运筹学习题集01

一．单纯性法1.用单纯形法求解下列线性规划问题（共 15 分）122121212max 25156224..5,0z x x x x x s t x x x x =+≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ 2.用单纯形法求解下列线性规划问题（共 15 分）12121212max 2322..2210,0z x x x x s t x x x x =+-≥-⎧⎪+≤⎨⎪≥⎩ 3.用单纯形法求解下列线性规划问题（共 15 分）1234123412341234max 24564282..2341,,,z x x x x x x x x s t x x x x x x x x =-+-+-+≤⎧⎪-+++≤⎨⎪≥⎩4.用单纯形法求解下列线性规划问题（共 15 分）123123123123123max 2360210..20,,0z x x x x x x x x x s t x x x x x x =-+++≤⎧⎪-+≤⎪⎨+-≤⎪⎪≥⎩ 5.用单纯形法求解下列线性规划问题（共 15 分）12312312123max 224..26,,0z x x x x x x s t x x x x x =-++++≤⎧⎪+≤⎨⎪≥⎩6.用单纯形法求解下列线性规划问题（共 15 分）121212max 105349..528z x x x x s t x x =++≤⎧⎪+≤⎨7.用单纯形法求解下列线性规划问题（共 16 分）12121212max 254212..3218,0z x x x x s t x x x x =+≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩二．对偶单纯性法1.灵活运用单纯形法和对偶单纯形法解下列问题（共 15 分） 12121212max 62..33,0z x x x x s t x x x x =++≥⎧⎪+≤⎨⎪≥⎩ 2.灵活利用单纯形法和对偶单纯形法求解下列线性规划问题（共 15 分）121212212max 3510501..4,0z x x x x x x s t x x x =++≤⎧⎪+≥⎪⎨≤⎪⎪≥⎩ 3.用对偶单纯形法求解下列线性规划问题（共 15 分）1212121212min 232330210..050z x x x x x x s t x x x x =++≤⎧⎪+≥⎪⎪-≥⎨⎪≥⎪⎪≥⎩4.灵活运用单纯形法和对偶单纯形法求解下列线性规划问题（共 15 分）124123412341234min 26..2335,,,0z x x x x x x x s t x x x x x x x x =+-+++≤⎧⎪-+-≥⎨⎪≥⎩5.运用对偶单纯形法解下列问题（共 16 分）12121212max 24..77,0z x x x x s t x x x x =++≥⎧⎪+≥⎨⎪≥⎩ 6.灵活运用单纯形法和对偶单纯形法解下列问题（共 15 分）12121212max 62..33,0z x x x x s t x x x x =++≥⎧⎪+≤⎨⎪≥⎩三．0-1整数规划1.用隐枚举法解下列0-1型整数规划问题（共 10 分）12345123451234512345123345max 567893223220..32,,,,,01z x x x x x x x x x x x x x x x s t x x x x x x x x x x x or =++++-++-≥⎧⎪+--+≥⎪⎨--+++≥⎪⎪=⎩2.用隐枚举法解下列0-1型整数规划问题（共 10 分）12312312323123min 4322534433..1,,01z x x x x x x x x x s t x x x x x or =++-+≤⎧⎪++≥⎪⎨+≥⎪⎪=⎩ 3.用隐枚举法解下列0-1型整数规划问题（共 10 分）1234512345123451234512345max 20402015305437825794625..81021025,,,,01z x x x x x x x x x x x x x x x s t x x x x x x x x x x =++++++++≤⎧⎪++++≤⎪⎨++++≤⎪⎪=⎩或4.用隐枚举法解下列0-1型整数规划问题（共 10 分）12345123451234512345max 2534327546..2420,,,,01z x x x x x x x x x x s t x x x x x x x x x x =-+-+-+-+≤⎧⎪-+-+≤⎨⎪=⎩或 5.用隐枚举法解下列0-1型整数规划问题（共 10 分）12341234123412341234min 25344024244..1,,,01z x x x x x x x x x x x x s t x x x x x x x x =+++-+++≥⎧⎪-+++≥⎪⎨+-+≥⎪⎪=⎩或6.7.用隐枚举法解下列0-1型整数规划问题（共 10 分）123451234513451245max 325232473438..116333z x x x x x x x x x x x x x x s t x x x x =+--+++++≤⎧⎪+-+≤⎪⎨-+-≥⎪⎪ 1231231231223max 3252244..346z x x x x x x x x x s t x x x x =-++-≤⎧⎪++≤⎪⎪+≤⎨⎪+≤⎪1.利用库恩-塔克（K -T ）条件求解以下问题（共 15 分）22121122121212max ()104446..418,0f X x x x x x x x x s t x x x x =+-+-+≤⎧⎪+≤⎨⎪≥⎩2.利用库恩-塔克（K -T ）条件求解以下非线性规划问题。

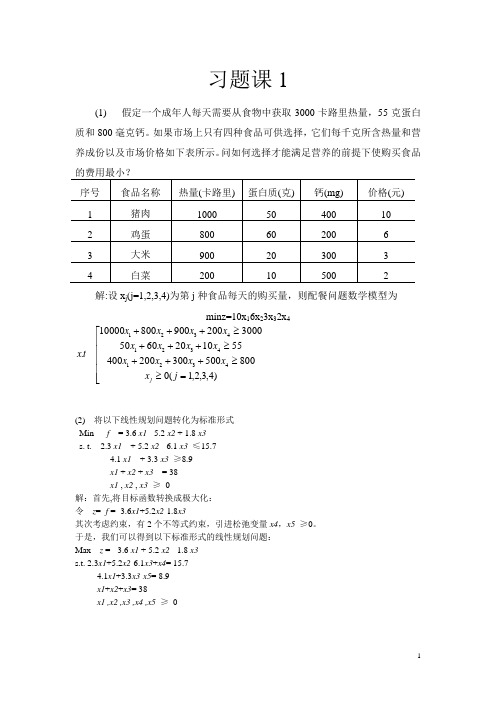
习题课1(1) 假定一个成年人每天需要从食物中获取3000卡路里热量，55克蛋白质和800毫克钙。

如果市场上只有四种食品可供选择，它们每千克所含热量和营养成份以及市场价格如下表所示。

问如何选择才能满足营养的前提下使购买食品解:设x j (j=1,2,3,4)为第j 种食品每天的购买量，则配餐问题数学模型为 minz=10x 16x 23x 32x 4⎢⎢⎢⎢⎢⎣⎡=≥≥+++≥+++≥+++)4,3,2,1(08005003002004005510206050300020090080010000.432143214321j x x x x x x x x x x x x x tx j(2) 将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x1 , x2 , x3 ≥ 0解：首先,将目标函数转换成极大化： 令 z = -f = -3.6x1+5.2x2-1.8x3其次考虑约束，有2个不等式约束，引进松弛变量x4，x5 ≥0。

于是，我们可以得到以下标准形式的线性规划问题： Max z = - 3.6 x1 + 5.2 x2 - 1.8 x3 s.t. 2.3x1+5.2x2-6.1x3+x4= 15.7 4.1x1+3.3x3-x5= 8.9 x1+x2+x3= 38x1 ,x2 ,x3 ,x4 ,x5 ≥ 0(3)用图解法求解下列线性规划问题本例中目标函数与凸多边形的切点是B (2,5)，则X *=(2,5)为最优解，m a x Z =20(4) 找出下列线性规划问题的全部基解，基可行解，并找出最优解基本解：X 1=(0,1,4,12,18)’ X 2=(4,0,0,12,6)’ X 3=(6,0,-2,12,0)’ X 4 =(4,3,0,6,0)’ X 5=(0,6,4,0,6)’ X 6=(2,6,2,0,0)’ X 7=((4,6,0,0,-6)’ X 8=(0,9,4,-6,0)’ 其中基本可行解为： X 1， X 2， X 4， X 5 ，X 6 最优解为X *＝X 6 =(2,6,2,0,0)’ Z *=36⎪⎪⎩⎪⎪⎨⎧≥≥≤≤+≤++=04155162325max 211212121x x x x x x x x x z ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤≤++=018236453max 21212121x x x x x x x x z习题课2(1) 用单纯形表求解LP问题Max z = 1500 x1 + 2500 x2s.t. 3 x1 + 2 x2 + x3 = 652 x1 + x2 + x4 = 403 x2 + x5 = 75x1 , x2 , x3 , x4 , x5 ≥0最优解x1 = 5 x2 = 25 x4 = 5（松弛标量，表示B设备有5个机时的剩余）最优值z* = 70000(2)用单纯形法解线性规划问题(唯一解)解：化为标准型列出单纯形表Z*=17/2, X*=(7/2,3/2, 15/2,0,0)’⎪⎪⎩⎪⎪⎨⎧≥=++=++=+++++=-0524261550002max 515214213254321x x x x x x x x x x x x x x z习题课3(1) 用单纯形法求解线性规划问题化成标准形式有加入人工变量则为列出单纯形表 ⎪⎪⎩⎪⎪⎨⎧≥≥≥=+≥-+-≤+++-=000931243max 3213232132131x x x x x x x x x x x x x z ⎪⎪⎩⎪⎪⎨⎧≥=+=--+-=++++++-=-093124003max 5132532143215431x x x x x x x x x x x x x x x z ⎪⎪⎩⎪⎪⎨⎧≥=++=+--+-=+++--+++-=-093124003max 71732653214321765431x x x x x x x x x x x x x Mx Mx x x x x z人工变量已不在基变量中，X*=(0,5/2,3/2,0,0,0,0)’ Z*=3/2注意：(1)在L P 问题的最优解中，人工变量都处在非基变量位置(即取0值)，则原问题有最优解，且去掉人工变量后的解为原问题的最优解。

第一章 线性规划及单纯形法一、写出下列线性规划的标准形式，用单纯形法求解，并指出其解属于哪种情况。

1、P55,1.3(a)21510m ax x x Z +=⎪⎩⎪⎨⎧≥≤+≤+0x ,x 8x 2x 59x 4x 3.t .s 212121 解：将模型化为标准型21510x x Z Max +=⎪⎩⎪⎨⎧≥=++=++0,,,825943..4321421321x x x x x x x x x x t s 单纯形表如下因所有检验数0j ≤σ，已达最优解，最优解是)2,1(*=X ，最优目标值为2。

由检验数的情况可知，该问题有唯一最优解。

2、 P55,1.3(b)21x x 2Z m ax +=s.t⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,524261552121212x x x x x x x解：将模型化为标准型21x x 2Z Max +=t s . ⎪⎪⎩⎪⎪⎨⎧≥=++=++=+0x ,...,x ,x ,5x x x ,24x x 2x 6,15x x 552152142132 单纯形表如下因所有检验数0j ≤σ，已达最优解，最优解是)0,0,2,2,2(X *=，最有目标值为217。

由检验数的情况可知，该问题有唯一最优解。

3、3212x x x Z Min -+=，t s . ⎪⎪⎩⎪⎪⎨⎧≥≤++≤+-≤-+0,,,5,822,422321321321321x x x x x x x x x x x x 解：将模型化为标准型：3212x x x Z Min -+=t s . ⎪⎪⎩⎪⎪⎨⎧≥=+++=++-=+-+0,,,5,822,422321632153214321x x x x x x x x x x x x x x x 用单纯形法迭代最优解为（0，0，4），最优值为-4。

4、43213x x x x Z Min +++=t s . ⎪⎪⎩⎪⎪⎨⎧≥=++=++-0,,,,,63,4224321421321x x x x x x x x x x 解：因为所有检验数均已非负，故已是最优解，最优解为（0，2，0，4），--10分最优目标值：6Z =*。

《运筹学》试题及参考答案一、填空题（每空2分，共10分）1、在线性规划问题中，称满足所有约束条件方程和非负限制的解为可行解。

2、在线性规划问题中，图解法适合用于处理变量为两个的线性规划问题。

3、求解不平衡的运输问题的基本思想是设立虚供地或虚需求点，化为供求平衡的标准形式。

4、在图论中，称无圈的连通图为树。

5、运输问题中求初始基本可行解的方法通常有最小费用法、西北角法两种方法。

二、（每小题5分，共10分）用图解法求解下列线性规划问题：1）max z =6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x ，解：此题在“《运筹学》复习参考资料.doc ”中已有，不再重复。

2）min z =－3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解：可行解域为abcda ，最优解为b 点。

⑴⑵⑶⑷⑸⑹、⑺由方程组⎩⎨⎧==+02242221x x x 解出x 1=11，x 2=0∴X *=⎪⎪⎭⎫⎝⎛21x x =（11，0）T∴min z =－3×11+2×0=－33三、（15分）某厂生产甲、乙两种产品，这两种产品均需要A 、B 、C 三种资源，每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示：AB C 甲94370乙46101203602003001）建立使得该厂能获得最大利润的生产计划的线性规划模型；（5分）2）用单纯形法求该问题的最优解。

（10分）解：1）建立线性规划数学模型：设甲、乙产品的生产数量应为x 1、x 2，则x 1、x 2≥0，设z 是产品售后的总利润，则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x ，2）用单纯形法求最优解：加入松弛变量x 3，x 4，x 5，得到等效的标准模型：max z =70x 1+120x 2+0x 3+0x 4+0x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下：四、（10分）用大M 法或对偶单纯形法求解如下线性规划模型：min z =5x 1＋2x 2＋4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x 解：用大M 法，先化为等效的标准模型：max z /=－5x 1－2x 2－4x 3s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7，得到：max z /=－5x 1－2x 2－4x 3－M x 6－M x 7s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下：五、（15分）给定下列运输问题：（表中数据为产地A i 到销地B j 的单位运费）B 1B 2B 3B 4s iA 1A 2A 312348765910119108015d j82212181）用最小费用法求初始运输方案，并写出相应的总运费；（5分）2）用1）得到的基本可行解，继续迭代求该问题的最优解。

运筹学题库第⼀章1 求解下述线性规划问题≥=-≥++-=0,1524..43min21212121x x x x x x t s x x z2 设某种动物每天⾄少需要700g 蛋⽩质、30g 矿物质、100mg 维⽣素，现有五种饲料可供选择，每种饲料每公⽄营养成分的含量及单价如表所⽰。

3某医院昼夜24h 各时段内需要的护⼠数量如下：2：00—6：00 10⼈，6：00—10：00 15⼈，10：00—14：00 25⼈，14：00—18：00 20⼈，18：00—22：00 18⼈，22：00—2：00 12⼈。

护⼠分别于2：00，6：00，10：00，14：00，18：00，22：00分6批上班，并连续⼯作8⼩时。

试建⽴模型，要求既满⾜值班需要，⼜使护⼠⼈数最少。

4 某⼈有⼀笔30万元的资⾦，在今后三年内有以下投资项⽬：（1）三年内的每年年初均可投资，每年获利为投资额的20%，其本利可以起⽤于下⼀年投资；（2）只允许第⼀年年初投⼊，第⼆年年末可收回，本利合计为投资额的150%，但此类投资限额不超过15万元；（3）于三年内第⼆年初允许投资，可于第三年末收回，本利合计为投资额的160%，这类投资限额20万元。

（4）于三年内的第三年初允许投资，⼀年回收，可获利40%，投资限额为10万元。

试为该⼈确定⼀个使第三年末本利和为最⼤的投资计划。

⽹上下载部分：某航空公司为满⾜客运量⽇益增长的需要，正考虑购置⼀批新的远程、中程、短程的喷⽓式客机。

每架远程的喷⽓式客机价格670万元，每架中程的喷⽓式客机价格500万元，每架短程的喷⽓式客机价格350万元。

该公司现有资⾦15000万元可以⽤于购买飞机。

根据估计年净利润每架远程客机42万元，每架中程客机30万元，每架短程客机23万元。

设该公司现有熟练驾驶员可⽤来配备30架新的飞机。

维修设备⾜以维修新增加40架短程的喷⽓式客机，每架中程客机的维修量相当于4/3架短程客机，每架远程客机的维修量相当于5/3架短程客机。

1. 判断下述论述的正误(在括号填入T 或F ) 或填空:(1) 凸集的顶点个数必为有限个.(1) 任何凸集均可找到一LP模型与之对应. ( )(2) LP模型的可行域的顶点必为有限个. ( )(3) LP模型的基本可行解必为有限个. ( )(4) 某LP模型有且仅有两个最优解. ( )(5) 某LP模型有且仅有有限个(大于等于2)最优解. ( )(6) 某LP模型有无穷多个最优解. ( )(7) 若LP模型存在可行解, 则必存在最优解( )(8) 若LP模型的可行域非空有界, 则其顶点中必存在最优解( )(9) 若LP模型的可行域非空, 则其顶点中必存在最优解( )(10) 若X是某LP模型的最优解, 则X必为该LP模型可行域的某一个顶点. ( )(11) 若X是某LP模型的基本解, 则X必为该LP模型可行域的某一个顶点.( )(12) 某LP的两个基本可行解中零分量的个数必相同. ( )(13) 在单纯形算法中, 采用最小比值原则确定换出变量是为了保持解的可行性. ( )(14) 对偶单纯形算法中, 采用最小比值原则确定换出变量是为了保持对偶解的可行性. ( )(15) 若增加极大化LP模型的约束方程个数, 则可能会使其最优值变大. ( )(16) 若增加极小化LP模型的约束方程个数, 则可能会使其最优值变小. ( )(15) 若减少极大化LP模型的约束方程个数, 则可能会使其最优值变大. ( )(16) 若减少极小化LP模型的约束方程个数, 则可能会使其最优值变小. ( )(17) 在运输问题中, 任一组M+N个变量必含有闭回路. ( )(18) 在运输问题中, 可任选一组M+N-1个变量作为基变量. ( )(19) 设μ是用FORT-FULKERSON方法求解网络最大流过程中所的得一条增广路，则μ+ 上必无零流弧. ( ) (20) 设μ为是用FORT-FULKERSON方法求解网络最大流过程中所的得一条增广路,则μ- 上必无饱和弧.( )(21) 用Dijkstra算法求网络的最短路时, 使用条件是该网络不含负回路. ( )(22) 由P个顶点, P-1条边组成的图G必为树. ( )(23) 某图G如下所示, 图a, b, c, d, e 中, ____________是G的真子图,____________是G的生成子图.(24) 某连通图G的各顶点的次分别为2, 3, 1, 2, 1, 2, 1, 2, 则G ________.A) 是树B) 不是树C) 不一定是树D) 条件不够, 无法判断.(24) 某图G的顶点数p 等于其边数q + 1, 则G ________.a 是树b 不是树c 条件不够, 无法判断.(24) 连通图G的可达阵M的元素m ij 必为1. ( )(24) 点v i 是图G的孤立点, 则图G的可达阵M的元素m ij 必为0. ( )(26) 用对偶法求解最大流-最小费用问题的过程中, 均可用Dijkstra算法求所绘的增广费用网络的最短路. ( ) (31) 建立动态规划模型的四个要素一个方程是指:__________________________________________________________________________________________________________________________________________________________________________. (33) 用表上作业法求解运输问题时, 常用的确定初始方案的两个方法是: _________________________和______________________, 常用的确定检验数的两个方法是:____________________和_________________________.(34) 已知X1 = (1, 2), X2 = (2, 3)是某LP的两个可行解, 则_____也是该LP的可行解.a. X = (3, 4)b. X = (1.5, 2.5)c. X = (1.2, 1.8)d. 条件不够, 无法判断.(34) 已知X1 = (1, 2), X2 = (2, 4)是某LP的两个基本可行解, 则_____必不是该LP的可行解.A) X = (3, 4) B) X = (1.5, 3) C) X = (2.5, 5) D) X = (5, 2)E) 条件不够, 无法判断.(35) 在单纯形的最优表上, 最优解不唯一, 则_____________a. 非基变量的检验数必有为零者b. 非基变量的检验数不必有为零者.(36) 已知原问题有可行解, 但无最优解. 则原问题的对偶问题__________.a. 无可行解b. 有可行解, 但无最优解c. 有可行解且有最优解(37) 已知某极大化LP问题及其对偶问题均有可行解, 而Y1 , Y2 为对偶问题的两个可行解,它们对应的目标函数值分别为4, 7. 则原问题的最优值Z满足__________.a. Z < 4b. 7 < Zc. 4 < Z < 7(38) 极小化(MinZ)LP问题可转化为目标函数取极大化即_______的问题求解. 而原问题的目标函数值等于__________.a. MaxZb. Max(-Z)c. -Max(-Z)d. -Max(39) 对产销不平衡的运输问题, 可通过___________________或_________________的方法, 将其转化产销平衡的运输问题求解.(40) 通常, 运输问题的变量个数为______, 其基由_______个变量组成.a. M + Nb. M * Nc. M + N - 1d. M + N + 1(41) 在网络分析中, 所求得的最大流_________唯一, 所求得的最短路_________唯一.a. 一定b. 一定不c. 不一定1. 求解LP的单纯形法中，先确定变量，后确定变量。

第一章习题解答1.1 用图解法求解下列线性规划问题。

并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。

+=32min 21x x Z +=23max 21x x Z ⎪⎩⎪⎨⎧≥≥+≥+0,422664.)1(212121x x x x x x st ⎪⎩⎪⎨⎧≥≥+≤+0,124322.)2(212121x x x x x x st ⎪⎩⎪⎨⎧≤≤≤≤≤++=85105120106.max )3(212121x x x x st x x Z ⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答无穷多最优解，,422664.32min )1(21212121⎪⎩⎪⎨⎧≥≥+≥++=x x x x x x st x x Z 是一个最优解3,31,121===Z x x 该问题无解⎪⎩⎪⎨⎧≥≥+≤++=0,124322.23max )2(21212121x x x x x x st x x Z 第一章习题解答85105120106.max )3(212121⎪⎩⎪⎨⎧≤≤≤≤≤++=x x x x st x x Z 唯最优解16,6,1021===Z x x 唯一最优解，该问题有无界解⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答1.2 将下述线性规划问题化成标准形式。

1422245243min )1(432143214321⎪⎪⎧≤+−+−=−+−+−+−=x x x x x x x x x x x x Z .,0,,23243214321⎪⎪⎩⎨≥≥−++−无约束x x x x x x x x st ⎪⎩⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min )2(x x x x x x x x x st x x x Z 第一章习题解答.2321422245243min )1(4321432143214321⎪⎪⎪⎨⎧≥−++−≤+−+−=−+−+−+−=x x x x x x x x x x x x st x x x x Z ,0,,4321⎪⎩≥无约束x x x x ⎪⎪⎩⎪⎪⎨⎧≥=−+−++−=+−+−+=−+−+−+−+−=0,,,,,232142222455243max 64241321642413215424132142413214241321x x x x x x x x x x x x x x x x x x x x x x x st x x x x x Z 第一章习题解答⎪⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min)2(x x x x x x x x x st x x x Z ⎩⎪⎩⎪⎨⎧≥=++−+=−++−+−+=0,,,,6243322max 43231214323121323121323121x x x x x x x x x x x x x x st x x x x Z第一章习题解答634334max )3(3212121⎪⎪⎧=−+=++=x x x x x st x x Z 517,0,1,59,524,,1,0424321421=====⎪⎪⎩⎨=≥=++Z x x x x j x x x x j 该题是唯一最优解：）（"第一章习题解答⎪⎧≤++−≤++++=151565935121510max 321321x x x x x x x x x Z 该题无可行解。