2017年中考数学精选压轴题(华东师大版)

1、已知，在平行四边形OABC 中，OA=5，AB=4，∠OCA=90°，动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动，同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动．设移动的时间为t 秒． （1）求直线AC 的解析式；（2）试求出当t 为何值时，△OAC 与△PAQ 相似；（3）若⊙P 的半径为58，⊙Q 的半径为23；当⊙P 与对角线AC 相切时，判断⊙Q 与直线AC 、BC 的位置关系，并求出Q 点坐标。

解：（1）42033y x =-+（2）①当0≤t ≤2.5时，P 在OA 上，若∠OAQ=90°时， 故此时△OAC 与△PAQ 不可能相似．当t>2.5时，①若∠APQ=90°，则△APQ ∽△OCA ，∵t>2.5，∴符合条件．②若∠AQP=90°，则△APQ ∽△∠OAC ，∵t>2.5，∴符合条件．综上可知，当时，△OAC 与△APQ 相似．（3）⊙Q 与直线AC 、BC 均相切，Q 点坐标为（109,531）。

2、如图，以矩形OABC 的顶点O 为原点，OA 所在的直线为x 轴，OC 所在的直线为y 轴，建立平面直角坐标系．已知OA ＝3，OC ＝2，点E 是AB 的中点，在OA 上取一点D ，将△BDA 沿BD 翻折，使点A 落在BC 边上的点F 处． （1）直接写出点E 、F 的坐标；（2）设顶点为F 的抛物线交y 轴正半轴．．．于点P ，且以点E 、F 、P 为顶点的三角形是等腰三角形，求该抛物线的解析式；（3）在x 轴、y 轴上是否分别存在点M 、N ，使得四边形MNFE 的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．解：（1）(31)E ，；(12)F ，．（2）在Rt EBF △中，90B ∠=，2222125EF EB BF ∴=+=+=．设点P 的坐标为(0)n ，，其中0n >，顶点(12)F ，， ∴设抛物线解析式为2(1)2(0)y a x a =-+≠．（第2题）①如图①，当EF PF =时，22EF PF =，221(2)5n ∴+-=．解得10n =（舍去）；24n =．(04)P ∴，．24(01)2a ∴=-+．解得2a =．∴抛物线的解析式为22(1)2y x =-+②如图②，当EP FP =时，22EP FP =，22(2)1(1)9n n ∴-+=-+．解得52n =-（舍去）．③当EF EP =时，53EP =<，这种情况不存在．综上所述，符合条件的抛物线解析式是22(1)2y x =-+． （3）存在点M N ，，使得四边形MNFE 的周长最小． 如图③，作点E 关于x 轴的对称点E '，作点F 关于y 轴的对称点F '，连接E F ''，分别与x 轴、y 轴交于 点M N ，，则点M N ，就是所求点．(31)E '∴-，，(12)F NF NF ME ME '''-==，，，．43BF BE ''∴==，．FN NM ME F N NM ME F E ''''∴++=++=22345=+=．又5EF =，∴55FN NM ME EF +++=+，此时四边形MNFE 的周长最小值是55+．3、如图，在边长为2的等边△ABC 中，AD ⊥BC,点P 为边AB 上一个动点，过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x .（1）①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;（2）记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值; （3）以P 、E 、F 为顶点的三角形与△EDG 是否可能相似？如果能相似，请求出BP 的长，如果不能，请说明理由。

2017年全国36省市中考数学填空压轴题汇编（含详解）1.（长沙市）如图，将正方形ABCD 折叠，使顶点A 与CD 边上的一点H 重合（H 不与端点D C ,重合），折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与边BC 交于点G ，设正方形ABCD 的周长为m ，CHG ∆的周长为n ，则mn 的值为（ ） A ．22 B ．21 C ．215- D ．随H 点位置的变化而变化2.（安徽省）如图，在矩形ABCD 中，5AB =，3AD =.动点P 满足13PAB ABCD S S ∆=矩形.则点P 到A ，B 两点距离之和PA PB +的最小值为（ ）A B C. D3.（北京市）下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断：当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620.其中合理的是（）A．①B．② C. ①②D．①③4.（福建省宁德市）如图，在△ABC中，AB=AC，点D，E分别在边BC 和AC 上，若AD=AE，则下列结论错误的是（）A．∠ADB=∠ACB+∠CAD B．∠ADE=∠AEDC ．∠CDE=∠BAD D ．∠AED=2∠ECD5.（福建省）如图，网格纸上正方形小格的边长为1．图中线段AB 和点P 绕着同一个点做相同的旋转，分别得到线段A B ''和点P '，则点P '所在的单位正方形区域是（ ）A ．1区B ．2区C ．3区D ．4区 6.（兰州市） 如图1，在矩形中，动点从出发，沿方向运动，当点到达点时停止运动，过点做，交于点，设点运动路程为，，如图2所表示的是与的函数关系的大致图象，当点在上运动时，的最大长度是，则矩形的面积是( )图1 图2 A. B.C.6D. 7.（广州市），函数与在同一直角坐标系中的大致图象可ABCD E A AB BC →E C E FE AE CD F E x FC y y x E BC FC 25ABCD 23552540a ≠a y x=2y ax a =-+能是（）8.（贵州省安顺市）二次函数y=ax2+bx+c（≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③4a+c＜2b；④m（am+b）+b＜a（m ≠1），其中结论正确的个数是（）A．1 B．2 C．3 D．49.（贵州省贵阳市）如图，四边形ABCDC，∠ABC+∠DCB=90°，且BC=2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3，若S1=3，S3=9，则S2的值为（）A．12 B．18 C．24 D．4810.（海南省）如图6，△ABC 的三个顶点分别为A （1，2），B （4，2），C （4，4）．若反比例函数k y x=在第一象限内的图象与△ABC 有交点，则k 的取值范围是（ ）21 9.A ．1≤k ≤4B ．2≤k ≤8C ．2≤k ≤16D ．8≤k ≤1611（河北省）A ．1.4B ．1.1C ．0.8D ．0.512.（河南省）如图，将半径为2，圆心角为的扇形绕点逆时针旋转，点，的对应点分别为，，连接，则图中阴影部分的面积是（ ）120︒OAB A 60︒O B 'O 'B 'BBA ．B ． C. D ．13.（黑龙江省大庆市）如图，，，点在轴上，与轴交于点，且，，则与轴交点的横坐标为（ ）A ．B ． C. D ．14.（哈尔滨市）周日，小涛从家沿着一条笔直的公路步行去报亭看报，看了一段时间后，他按原路返回家中，小涛离家的距离y （单位：m ）与他所用的时间t （单位：min ）之间的函数关系如图所示，下列说法中正确的是（ ）A ．小涛家离报亭的距离是900mB ．小涛从家去报亭的平均速度是60m/minC ．小涛从报亭返回家中的平均速度是80m/minD ．小涛在报亭看报用了15min23π3π23π23π15.（黑龙江省鹤岗市）观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…．则第2017个图形中有个三角形．16.（黑龙江省佳木斯市）如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（）①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG ：S△HBG=tan∠DAG ⑤线段DH的最小值是2﹣2．A．2 B．3 C．4 D．517.（湖北省鄂州市）如图四边形ABCD中，AD∥BC，∠BCD=90°，AB =BC+AD，∠DAC =45°，E 为CD 上一点，且∠BAE =45°，若CD =4，则△ABE 的面积为（ ） A.127 B.247 C.487 D.50718.（湖北省荆门市）已知：如图，在平面直角坐标系xoy 中，等边AOB ∆的边长为6，点C 在边OA 上，点D 在边AB 上，且3OC BD =.反比例函数()0k y k x=≠的图象恰好经过点C 和点D .则k 的值为 （ ）A B ． C. D 19.（武汉市）如图，在Rt △ABC 中，∠C ＝90°，以△ABC 的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多为（ ）A ．4B ．5C ．6D ．720.（湖北省宜昌市）某学校要种植一块面积为100m 2的长方形草坪，要求两边长均不小于5m ，则草坪的一边长为y （单位：m ）随另一边长x （单位：m ）的变化而变化的图象可能是（ ）21.（湖南省衡阳市）如图，已知点A 、B 分别在反比例函数1y x =（0x >），4y x=-（0x >）的图像上，且OA ⊥OB ，则OB OA的值为（ ） A B ．2 D ．422.（湖南省益阳市）如图，空心卷筒纸的高度为12cm ，外径（直径）为10cm ，内径为4cm ，在比例尺为1:4的三视图中，其主视图的面积是2·1·c ·n ·j ·yA ．214πcm 2B ．2116πcm 2C ．30cm 2D ．7.5cm 223.（吉林省长春市）如图，在平面直角坐标系中，平行四边形OABC 的顶点A 的坐标为（﹣4，0），顶点B 在第二象限，∠BAO=60°，BC 交y 轴于点D ，DB ：DC=3：1．若函数y=k x（k ＞0，x ＞0）的图象经过点C ，则k 的值为（ ）A ．3 B ．2 C ．3D 24.（江苏省南通市） 如图，矩形ABCD 中，10,5AB BC ==,点,,,EFGH 分别在矩形ABCD 各边上，且,AE CG BF DH ==，则四边形EFGH 周长的最小值为（ ）A ．B ．C ．D ．25.（江苏省常州市）如图，已知□ABCD的四个内角的平分线分别相交于点E、F、G、H，连接AC，若EF=2,FG=GC=5,则AC的长是( ).A．12 B．13 C．D．26.（江苏省淮安市）如图，在矩形纸片ABCD中点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC=∠ECA，则AC 的长是（）A．B．6 C．4 D．527.（江苏省连云港市）如图所示，一动点从半径为2的⊙O上的A0点出发，沿着射线A0O方向运动到⊙O上的点A1处，再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处；接着又从A2点出发，沿着射线A2O方向运动到⊙O上的点A3处，再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处；…按此规律运动到点A2017处，则点A2017与点A0间的距离是（）A ．4B ．2√3C ．2D ．028.（南京市）过三点（2，2），（6，2），（4，5）的圆的圆心坐标为（ ） A ．（4，） B ．（4，3） C.（5，） D ．（5，3） 29.（江苏省苏州市）如图，在菱形CD AB 中，60∠A =，D 8A =，F 是AB 的中点．过点F 作F D E ⊥A ，垂足为E ．将F ∆AE 沿点A 到点B 的方向平移，得到F '''∆A E ．设P 、'P 分别是F E 、F ''E 的中点，当点'A 与点B 重合时，四边形CD 'PP 的面积为A． B．C. D．8-30.（江苏省泰州市）如图，P 为反比例函数y=kx（k ＞0）在第一象限内图象上的一点，过点P 分别作x 轴，y 轴的垂线交一次函数y=﹣x ﹣4的图象于点A 、B ．若∠AOB=135°，则k 的值是（ ）A B C 176176A．2 B．4 C．6 D．831.（江苏省无锡市）如图，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE，则线段CE的长等于（）32.（江苏省徐州市）若函数y=x2﹣2x+b的图象与坐标轴有三个交点，则b的取值范围是（）A．b＜1且b≠0 B．b＞1 C．0＜b＜1 D．b＜133.（江苏省盐城市）如图，将函数y=（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）A．B．C．D．34.（江苏省扬州市）如图，已知△ABC的顶点坐标分别为A（0，2）、B（1，0）、C（2，1），若二次函数y=x2+bx+1的图象与阴影部分（含边界）一定有公共点，则实数b的取值范围是（）A．b≤﹣2 B．b＜﹣2 C．b≥﹣2 D．b＞﹣235.（辽宁省大连市）如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，点E是AB的中点，CD=DE=a，则AB的长为（）A．2a B．2 a C．3a D．36.（辽宁省葫芦岛市）如图，菱形ABCD的边长为2，∠A=60°，点P和点Q分别从点B和点C出发，沿射线BC向右运动，过点Q作QH⊥BD，垂足为H，连接PH，设点P运动的距离为x（0＜x≤2），△BPH的面积为s，则能反映s与x之间的函数关系的图象大致为（）37.（辽宁省营口市）如图，直线l的解析式为4=-+，它与x轴和y轴分别相y x交于,A B两点，平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于,C D两点，运动时间为t秒（04t≤≤），以CD为斜边作等腰直角三角形CDE（,E O两点分别在CD两侧），若CDE∆的重合部分的面积为S，则S与t之间的函数关系的图角大致∆和OAB是（）参考答案：1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.20.。

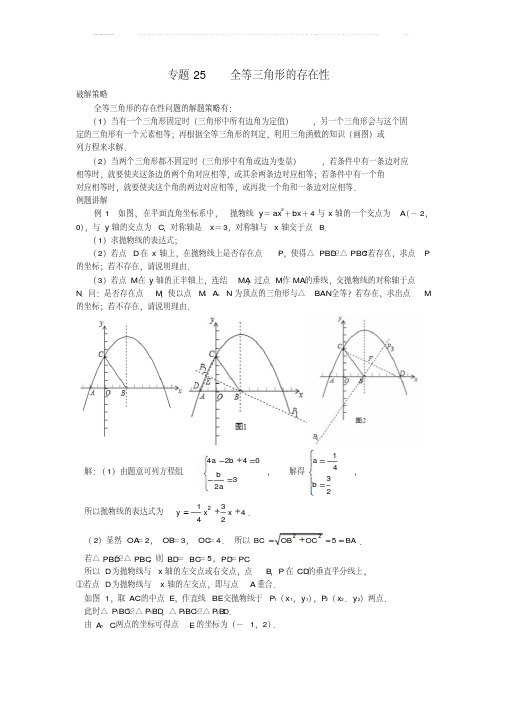
2017全国各地中考数学压轴题汇编之1D角三角形？若存在，请求出运动时间t ；若不存在，请说明理由；（4）如图②，点N 的坐标为（32 ，0），线段PQ 的中点为H ，连接NH ，当点Q 关于直线NH 的对称点Q ′恰好落在线段BC 上时，请直接写出点Q ′的坐标．CQ ABPO yx图① CQ HABNPO yx图②A【分析】（1）将A （－3，0）、B （4，0）代入y ＝213x bx c -++即可求解；（2）若△APQ 为直角三角形，则∠APQ ＝90°（∠PAQ 与∠PQA 不可能为直角）．连接QC ，则AQ 2－AP 2＝QC 2－PC 2＝PQ 2，据此列出关于t 的方程求解，若t 的值满足0≤t ≤4，则△APQ 可能是直角三角形，否则不可能；（3）①过点P 作DE ∥x 轴，分别过点M 、Q 作MD ⊥DE ，QE ⊥DE ，垂足分别为D 、E ，构成“一线三直角”全等模型，用含t 的式子表示点M 的坐标；②将点M 的坐标代入二次函数的表达式求解；（4）①分别求直线BC 、直线NQ ′的函数表达式；②解直线BC 、NQ ′的函数达式组成的方程组．【解析】（1）b ＝13，c ＝4． （2）在点P 、Q 运动过程中，△APQ 不可能是直角三角形．理由如下：若△APQ 是直角三角形，因为在点P 、Q 运动过程中，∠PAQ 、∠PQA 始终为锐角，所以∠APQ ＝90°．∴AQ 2－AP 2＝QC 2－PC 2＝PQ 2． 连接QC ．由（1）知抛物线的函数表达式为y ＝211433xx -++，当x＝0时，y ＝4．∴C （0，4）． ∴OC ＝4． ∵A （－3，0）， ∴OA ＝3．由题意，得AP ＝OQ ＝t ． ∴AQ ＝OA ＋OQ ＝3t +．在Rt △AOC 中，由勾股定理得AC5．∴PC ＝5t -．在Rt △OCQ 中，QC 2＝OQ 2＋OC 2＝224t +．∵∠APQ ＝90°，∴AQ 2－AP 2＝QC 2－PC 2＝PQ 2． ∴22(3)t t +-＝2224(5)tt +--．解得t ＝4.5． 由题意知0≤t ≤4．∴t ＝4.5不符合题意，舍去．∴在点P 、Q 运动过程中，△APQ 不可能是直角三角形．（3）如图，过点P 作DE ∥x 轴，分别过点M 、Q 作MD ⊥DE 、QE ⊥DE ，垂足分别为点D 、E ，MD 交x 轴于点F ，过点P 作PG ⊥x 轴，垂足为点G ，则PG ∥y 轴，∠D ＝∠E ＝90°． ∴△APG ∽△ACO ．∴PG OC ＝AG OA ＝AP AC ，即4PG ＝3AG ＝5t ． ∴PG ＝45t ，AG ＝35t ． CQ ABPO yx∴PE ＝GQ ＝GO ＋OQ ＝AO －AG ＋OQ ＝335t t -+＝235t +，DF ＝EQ ＝45t ．∵∠MPQ ＝90°，∠D ＝90°，∴∠DMP ＋∠DPM ＝∠EPQ ＋∠DPM ＝90°． ∴∠DMP ＝∠EPQ ． 又∵∠D ＝∠E ，PM ＝PQ ， ∴△MDP ≌△PEQ ．∴PD ＝EQ ＝45t ，MD ＝PE ＝235t +． ∴AM ＝MD －DF ＝24355t t +-＝235t -， OF ＝FG ＋GO ＝PD ＋OA －AG ＝43355t t +-＝135t +． ∴M （135t --，235t -+）． ∵点M 在x 轴下方的抛物线上，∴235t -+＝21111(3)(3)43535t t ---+--+．解得t．∵0≤t ≤4，∴t．（4）Q ′（67，227）．CQ A BPO yxMD EFG提示：连接OP，取OP中点R，连接RH、NR，延长NR交线段BC于点Q′．∵点H为PQ的中点，点R为OP的中点，∴RH＝12OQ＝12t，RH∥OQ．∵A（－3，0）、N（32-，0），∴点N为OA的中点．又∵点R为OP的中点，∴NR＝12AP＝12t，RN∥AC．∴RH＝NR．∴∠RNH＝∠RHN．∵RH∥OQ，∴∠RHN＝∠HNO．∴∠RNH＝∠HNO，即NH是∠QNQ′的平分线．设直线AC的函数表达式为y＝mx n+，把A（－3，0）、C （0，4）代入，得034m n n =-+⎧⎨=⎩，．解得m ＝43，n ＝4． ∴直线AC 的函数表达式为y ＝443x +． 同理可求，直线BC 的函数表达式为y ＝4x -+．设直线NR 的函数表达式为y ＝43x s +，把N （32-，0）代入，得0＝43()32s ⨯-+． 解得s ＝2．∴直线NR 的函数表达式为y ＝423x +． 解方程组4234y x y x ⎧=+⎪⎨⎪=-+⎩，得67227x y ⎧=⎪⎪⎨⎪=⎪⎩．，∴Q ′（67，227）．2．(2017江苏南京，27，11分)折纸的思考．【操作体验】用一张矩形纸片折等边三角形．第一步，对折矩形纸片ABCD （AB ＞BC ）（图①），使AB 与DC 重合，得到折痕EF ，把纸片展平（图②）．第二步，如图③，再一次折叠纸片，使点C 落在EF 上的P 处，并使折痕经过点B ，得到折痕BG ，CQ H A B NPO yxRQ折出PB，PC，得到△PB C．（1）说明△PBC是等边三角形．【数学思考】（2）如图④．小明画出了图③的矩形ABCD和等边三角形PB C．他发现，在矩形ABCD中把△PBC经过图形变化，可以得到图⑤中的更大的等边三角形．请描述图形变化的过程．（3）已知矩形一边长为3cm，另一边长为acm．对于每一个确定的a的值，在矩形中都能画出最大的等边三角形．请画出不同情形的示意图，并写出对应的a的取值范围．【问题解决】（4）用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片，所需正方形铁片的边长的最小值为cm．【分析】（1）由折叠的性质，线段垂直平分线的性质可判断；（2）根据旋转的性质和位似变换直接作图，写出过程即可；（3）根据图形，由勾股定理和等边三角形的性质求解；（4）由勾股定理和正方形的性质的性质直接求解．【解析】（1）由折叠，PB＝PC，EF是BC的垂直平分线，∴PB＝PC，∴PB＝PC＝BC，∴△PBC是等边三角形．（2）本题答案不惟一．例如，如图，以点B为中心，在矩形ABCD中把△PBC 逆时针方向旋转适当的角度，得到△P1B1C1；再以点B为位似中心，将△P1B1C1放大，使C1的对应点C2落在CD上，得到△P2BC2．（3）当等边三角形的边长为3cm，acm为高时，则a＝3√3，2当等边三角形的边长为a cm，3cm为高时，则a＝2√3，然后分0＜a ≤3√32，3√32＜a ＜2√3，a ≥2√3画出示意图．（4）165． 当以4cm 的直角边与正方形的边重合时，边长为4cm ，正方形的面积为16cm 2；当直角三角形的一个顶点与正方形的顶点重合，两外两个顶点在边上时，如图，∵四边形ABCD 是正方形，∴BC ＝CD ，∠C ＝∠D ＝90°．∵∠BFE ＝90°，∴∠BFC＋∠EFD＝90°，∠BFC＋∠CBF＝90°，∴∠EFD＝∠CBF，∴△BCF∽△FDE，∴BC∶DF＝BF∶EF．设BC＝a，由BF＝4，得CF＝√16−a2，则DF＝a－√16−a2，可知a∶( a－√16−a2)＝4∶1解得a＝16．5．正方形得面积为25625因为256＜16，25．所以a＝1653．（2017江苏连云港，27，14分）问题呈现：如图1，点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA 上，AE ＝DG ，求证：2S 四边形EFGH ＝S 矩形ABCD ．（S 表示面积）实验探究：某数学实验小组发现：若图1中AH ≠BF ，点G 在CD 上移动时，上述结论会发生变化，分别过点E 、G 作BC 边的平行线，再分别过点F 、H 作AB 边的平行线，四条平行线分别相交于点A 1、B 1、C 1、D 1，得到矩形A 1B 1C 1D 1． 如图2，当AH ＞BF 时，若将点G 向点C 靠近（DG ＞AE ），经过探索，发现：2S 四边形EFGH ＝S 矩形ABCD ＋1111A B C D S 矩形．如图3，当AH ＞BF 时，若将点G 向点D 靠近（DG ＜AE ），请探索S 四边形EFGH 、S 矩形ABCD 与1111A B C D S矩形之间的数量关系，并说明理由．迁移应用：请直接应用“实验探究”中发现的结论解答下列问题：（1）如图4，点E 、F 、G 、H 分别是面积为25的正方形ABCD 各边上的点，已知AH ＞BF ，AE＞DG，S＝11，HF EG的长．（2）如图5，在矩形ABCD中，AB＝3，AD＝5，点E、H分别在边AB、AD上，BE＝1，DH＝2，点F、G分别是边BC、CD上的动点，且FG连接EF、HG，请直接写出四边形EFGH面积的最大值．【分析】问题呈现：根据矩形的性质，通过割补法利用三角形的面积和矩形的面积可得到结论；实验探究：由题意得当将点G向点D靠近(DG AE)时，通过割补法利用三角形的面积和矩形的面积可得到结论；迁移应用：(1)由上面的结论，结合图形，通过割补法利用三角形的面积和矩形的面积可得到结论；（2）直接根据规律写出结果即可.【解析】问题呈现：证明：如图1中，∵四边形ABCD 是矩形， ∴AB ∥CD ，∠A ＝90°， ∵AE ＝DG ，∴四边形AEGD 是矩形， ∴S △HGE ＝12S 矩形AEGD ， 同理S △EGF ＝12S 矩形BEGC ， ∴S 四边形EFGH ＝S △HGE ＋S △EFG ＝12S 矩形BEGC ． 实验探究：结论：2S 四边形EFGH ＝S 矩形ABCD －1111A B C D S矩形．理由：∵1EHC S△＝121AEC HS 矩形，1HGD S△＝121HDGD S 矩形，1EFB S△＝121EBFB S 矩形，1FGA S △＝121CFA GS 矩形，∴S 四边形EFGH ＝1EHC S △＋1HGD S△＋1EFB S△＋1FGA S△－1111A B C D S矩形，∴2S 四边形EFGH ＝21EHCS △＋21HGD S△＋21EFB S△＋21FGA S△－21111A B C D S矩形，∴2S 四边形EFGH ＝S 矩形ABCD －1111A B C D S 矩形．迁移应用：解：（1）如图4中，∵2S 四边形EFGH ＝S 矩形ABCD －1111A B C D S 矩形．∴1111A B C D S矩形＝25－2×11＝3＝A 1B 1·A 1D 1，∵正方形的面积为25，∴边长为5， ∵A 1D 12＝HF 2－52＝29－25＝4， ∴A 1D 1＝2，A 1B 1＝32， ∴EG 2＝A 1B 12＋52＝1094， EG（2）∵2S 四边形EFGH ＝S 矩形ABCD ＋1111A B C D S 矩形．∴四边形A 1B 1C 1D 1面积最大时，矩形EFGH 的面积最大．①如图5－1中，当G与C重合时，四边形A1B1C1D1面积最大时，矩形EFGH的面积最大．B1C1D1面积＝1·2)＝此时矩形A②如图5－2中，当G与D重合时，四边形A1B1C1D1面积最大时，矩形EFGH的面积最大．此时矩形A1B1C1D1面积＝2·1＝2，∵22，∴矩形EFGH的面积最大值＝1724．（2017江苏南通，28，13分）已知直线y＝kx ＋b与抛物线y＝ax2（a＞0）相交于A、B两点（点A在点B的左侧），与y轴正半轴相交于点C，过点A作AD⊥x轴，垂足为D．（1）若∠AOB＝60°，AB∥x轴，AB＝2，求a 的值；（2）若∠AOB＝90°，点A的横坐标为－4，AC ＝4BC，求点B的坐标；（3）延长AD、BO相交于点E，求证：DE＝CO．【分析】（1）如图1，由条件可知△AOB为等边三角形，则可求得OA的长，在Rt△AOD中可求得AD和OD的长，可求得A点坐标，代入抛物线解析式可得a的值；（2）如图2，作辅助线，构建平行线和相似三角形，根据CF∥BG，由A的横坐标为－4，得B 的横坐标为1，所以A（－4，16a），B（1，a），证明△ADO∽△OEB，则AD OD＝，得a的值及BOE BE的坐标；（3）如图3，设AC＝nBC由（2）同理可知：A 的横坐标是B的横坐标的n倍，则设B（m，am2），则A（－mn，am2n2），分别根据两三角形相似计算DE和CO的长即可得出结论．【解析】解：（1）如图1，∵抛物线y＝ax2的对称轴是y轴，且AB∥x轴，∴A与B是对称点，O是抛物线的顶点，∴OA＝OB，∵∠AOB＝60°，∴△AOB是等边三角形，∵AB＝2，AB⊥OC，∴AC＝BC＝1，∠BOC＝30°，∴OC，∴A（－1把A（－1代入抛物线y＝ax2（a＞0）中得：a（2）如图2，过B作BE⊥x轴于E，过A作AG ⊥BE，交BE延长线于点G，交y轴于F，∵CF∥BG，∴AC AF＝，BC FG∵AC＝4BC，＝4，∴AFFG∴AF＝4FG，∵A的横坐标为－4，∴B的横坐标为1，∴A（－4，16a），B（1，a），∵∠AOB＝90°，∴∠AOD＋∠BOE＝90°，∵∠AOD ＋∠DAO ＝90°， ∴∠BOE ＝∠DAO ， ∵∠ADO ＝∠OEB ＝90°， ∴△ADO ∽△OEB ，∴AD OD OE BE＝， ∴1641a a＝， ∴16a 2＝4， a ＝±12， ∵a ＞0， ∴a ＝12； ∴B （1，12）； （3）如图3，设AC ＝nBC ，由（2）同理可知：A 的横坐标是B 的横坐标的n 倍，则设B （m ，am 2），则A （－mn ，am 2n 2）， ∴AD ＝am 2n 2， 过B 作BF ⊥x 轴于F ， ∴DE ∥BF ， ∴△BOF ∽△EOD ，∴OB OF BF OE OD DE＝＝， ∴2OB m am OE mn DE＝＝，∴1OB OE n＝，DE ＝am 2n ， ∴11OB BE n＝＋，∵OC ∥AE ， ∴△BCO ∽△BAE ，∴11CO OB AE BE n ＝＝＋， ∴22211CO am n am n n＝＋＋， ∴CO ＝()211am n n n＋＋＝am 2n ，∴DE ＝CO ．5．(2017江苏苏州，28，10分)如图，二次函数y ＝x 2＋bx ＋c 的图象与x 轴交于 A 、B 两点，与y 轴交于点C ，OB ＝OC ．点D 在函数图象上，CD ∥x 轴，且CD ＝2，直线l 是抛物线的对称轴，E 是抛物线的顶点． (1)求b 、c 的值；(2)如图①，连接BE ，线段OC 上的点F 关于直线l 的对称点F '恰好在线段BE 上，求点F 的坐标；(3)如图②，动点P 在线段OB 上，过点P 作x 轴的垂线分别与BC 交于点M ，与抛物线交于点N ．试问：抛物线上是否存在点Q ，使得△PQN与△APM的面积相等，且线段NQ的长度最小？如果存在，求出点Q的坐标；如果不存在，说明理由．【分析】(1)由条件可求得抛物线对称轴，则可求得b的值；由OB＝OC，可用c表示出B点坐标，代入抛物线解析式可求得c的值；(2)可设F(0，m)，则可表示出F′的坐标，由B、E的坐标可求得直线BE的解析式，把F′坐标代入直线BE解析式可得到关于m的方程，可求得F点的坐标；(3)设点P坐标为(n，0)，可表示出PA、PB、PN 的长，作QR⊥PN，垂足为R，则可求得QR的长，用n可表示出Q、R、N的坐标，在Rt△QRN 中，由勾股定理可得到关于n的二次函数，利用二次函数的性质可知其取得最小值时n的值，则可求得Q点的坐标，【解析】解：(1)∵CD∥x轴，CD＝2，∴抛物线对称轴为x＝1．∴-b＝2，b＝-2．2∵OB＝OC，C(0，c)，∴B点的坐标为(－c，0)，∴0＝c2＋2c＋c，解得c＝－3或c＝0(舍去)，∴c＝－3；(2)设点F的坐标为(0，m)．∵对称轴为直线x＝1，∴点F关于直线l的对称点F的坐标为(2，m)．由(1)可知抛物线解析式为y＝x2－2x－3＝(x－1)2－4，∴E(1，－4)，∵直线BE经过点B(3，0)，E(1，－4)，∴利用待定系数法可得直线BE的表达式为y＝2x－6．∵点F在BE上，∴m＝2×2－6＝－2，即点F的坐标为(0，－2)；(3)存在点Q满足题意．设点P坐标为(n，0)，则PA＝n＋1，PB＝PM＝3－n，PN＝－n2＋2n＋3．作QR⊥PN，垂足为R，∵S△PQN＝S△APM，∴12(n＋1)(3-n)＝12(-n2＋2n＋3)·QR，∴QR＝1．①点Q在直线PN的左侧时，Q点的坐标为(n－1，n2－4n)，R点的坐标为(n，n2－4n)，N点的坐标为(n，n2－2n－3)．∴在Rt△QRN中，NQ2＝1＋(2n－3)2，∴n＝32时，NQ取最小值1．此时Q点的坐标为(1 2，-154)；②点Q在直线PN的右侧时，Q点的坐标为(n＋11，n2－4)．同理，NQ2＝1＋(2n－1)2，∴n＝12时，NQ取最小值1．此时Q点的坐标为(3 2，-154)．综上可知存在满足题意的点Q，其坐标为(12，-154)或(32，-154)．6．（2017江苏泰州，26，14分）平面直角坐标系xOy中，点A、B的横坐标分别为a、a+2，二次函数y=－x2+（m－2）x+2m的图象经过点A、B，且a、m满足2a－m=d（d为常数）．（1）若一次函数y1=kx+b的图象经过A、B两点．①当a=1、d=－1时，求k的值；②若y1随x的增大而减小，求d的取值范围；（2）当d=－4且a≠－2、a≠－4时，判断直线AB与x轴的位置关系，并说明理由；（3）点A、B的位置随着a的变化而变化，设点A、B运动的路线与y轴分别相交于点C、D，线段CD的长度会发生变化吗？如果不变，求出CD 的长；如果变化，请说明理由．【分析】（1）①当a=1、d=－1时，m=2a－d=3，于是得到抛物线的解析式，然后求得点A和点B 的坐标，最后将点A和点B的坐标代入直线AB 的解析式求得k的值即可；②将x=a，x=a+2代入抛物线的解析式可求得点A 和点B的纵坐标，然后依据y1随着x的增大而减小，可得到－（a－m）（a+2）＞－（a+2－m）（a+4），结合已知条件2a－m=d，可求得d的取值范围；（2）由d=－4可得到m=2a+4，则抛物线的解析式为y=－x2+（2a+2）x+4a+8，然后将x=a、x=a+2代入抛物线的解析式可求得点A和点B的纵坐标，最后依据点A和点B的纵坐标可判断出AB 与x轴的位置关系；（3）先求得点A 和点B 的坐标，于是得到点A 和点B 运动的路线与字母a 的函数关系式，则点C （0，2m ），D （0，4m －8），于是可得到CD 与m 的关系式．【解析】解：（1）①当a =1、d =－1时，m =2a －d =3，所以二次函数的表达式是y =－x 2+x +6．∵a =1，∴点A 的横坐标为1，点B 的横坐标为3，把x =1代入抛物线的解析式得：y =6，把x =3代入抛物线的解析式得：y =0，∴A （1，6），B （3，0）．将点A 和点B 的坐标代入直线的解析式得：⎩⎨⎧=+=+036b k b k ，解得：⎩⎨⎧=-=93b k ， 所以k 的值为－3．②∵y =－x 2+（m －2）x +2m =－（x －m ）（x +2）， ∴当x =a 时，y =－（a －m ）（a +2）；当x =a +2时，y =－（a +2－4）（a +4），∵y1随着x的增大而减小，且a＜a+2，∴－（a－m）（a+2）＞－（a+2－m）（a+4），解得：2a－m＞－4，又∵2a－m=d，∴d的取值范围为d＞－4．（2）∵d=－4且a≠－2、a≠－4，2a－m=d，∴m=2a+4．∴二次函数的关系式为y=－x2+（2a+2）x+4a+8．把x=a代入抛物线的解析式得：y=a2+6a+8．把x=a+2代入抛物线的解析式得：y=a2+6a+8．∴A（a，a2+6a+8）、B（a+2，a2+6a+8）．∵点A、点B的纵坐标相同，∴AB∥x轴．（3）线段CD的长随m的值的变化而变化．∵y=－x2+（m－2）x+2m过点A、点B，∴当x=a时，y=－a2+（m－2）a+2m，当x=a+2时，y=－（a+2）2+（m－2）（a+2）+2m，∴A（a，－a2+（m－2）a+2m）、B（a+2，－（a+2）2+（m－2）（a+2）+2m）．∴点A运动的路线是的函数关系式为y1=－a2+（m－2）a+2m，点B运动的路线的函数关系式为y2=－（a+2）2+（m－2）（a+2）+2m．∴点C（0，2m），D（0，4m－8）．∴DC=|2m－（4m－8）|=|8－2m|．∴线段CD的长随m的值的变化而变化．当8－2m=0时，m=4时，CD=|8－2m|=0，即点C 与点D重合；当m＞4时，CD=2m－8；当m＜4时，CD=8－2m．7．（2017江苏无锡，28，8分）如图，已知矩形ABCD中，AB＝4，AD＝m，动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP，作点D关于直线PC的对称点E，设点P的运动时间为t（s）．（1）若m＝6，求当P，E，B三点在同一直线上时对应的t的值．（2）已知m满足：在动点P从点D到点A的整个运动过程中，有且只有一个时刻t，使点E到直线BC的距离等于3，求所有这样的m的取值范围．【分析】（1）如图1中，设PD＝x．则PA＝6－x．首先证明BP＝BC＝6，在Rt△ABP中利用勾股定理即可解决问题；（2）分两种情形求出AD的值即可解决问题：①如图2中，当点P与A重合时，点E在BC的下方，点E到BC的距离为3．②如图3中，当点P与A重合时，点E在BC的上方，点E到BC 的距离为3；【解析】解：（1）如图1中，设PD＝x．则PA ＝6－x．∵P、B、E共线，∴∠BPC＝∠DPC，∵AD∥BC，∴∠DPC＝∠PCB，∴∠BPC＝∠PCB，∴BP＝BC＝6，在Rt△ABP中，∵AB2＋AP2＝PB2，∴42＋（6－x）2＝62，6＋，∴x＝6－∴PD＝6－∴t＝（6－s时，B、E、P共线．（2）如图2中，当点P与A重合时，点E在BC的下方，点E到BC的距离为3．作EQ⊥BC于Q，EM⊥DC于M．则EQ＝3，CE＝DC＝4易证四边形EMCQ是矩形，∴CM＝EQ＝3，∠M＝90°，∴EM 227CM，∵∠DAC＝∠EDM，∠ADC＝∠M，∴△ADC∽△DME，，AD DCDM EM∴AD，77∴AD＝，如图3中，当点P与A重合时，点E在BC的上方，点E到BC的距离为3．作EQ⊥BC于Q，延长QE交AD于M．则EQ ＝3，CE＝DC＝4在Rt△ECQ中，QC＝DM＝7，由△DME∽△CDA，，∴DM EMCD AD，AD，∴AD综上所述，在动点P从点D到点A的整个运动过程中，有且只有一个时刻t，使点E到直线BC≤m＜．的距离等于3，这样的m的取值范围E在边片ABCD中，已知AB＝1，BCCD上移动，连接AE，将多边形ABCE沿直线AE翻折，得到多边形AB′C′E，点B、C的对应点分别为点B′、C′．(1)当B′C′恰好经过点D时(如图1)，求线段CE 的长；(2)若B′C′分别交边AD，CD于点F，G，且∠DAE ＝22.5°(如图2)，求△DFG的面积；(3)在点E从点C移动到点D的过程中，求点C′运动的路径长．【分析】(1)如图1中，设CE＝EC′＝x，则DE＝1－x，由△ADB′′∽△DEC，可得ADDE ＝DBEC，列出方程即可解决问题；(2)如图2中，首先证明△ADB′，△DFG都是等腰直角三角形，求出DF即可解决问题；(3)如图3中，点C的运动路径的长为CC的长，求出圆心角、半径即可解决问题．【解析】解：(1)如图1中，设CE＝EC′＝x，则DE＝1－x，∵∠ADB′＋∠EDC′＝90°，∠B′AD＋∠ADB′＝90°，∴∠B′AD＝∠EDC′，∵∠B′＝∠C′＝90°，AB′＝AB＝1，AD∴DB′∴△ADB′′∽△DEC，∴ADDE ＝DBEC，，∴x2．∴CE2．(2)如图2中，∵∠BAD ＝∠B ′＝∠D ＝90°，∠DAE ＝22.5°， ∴∠EAB ＝∠EAB ′＝67.5°， ∴∠B ′AF ＝∠B ′FA ＝45°，∴∠DFG ＝∠AFB ′＝∠DGF ＝45°， ∴DF ＝FG ，在Rt △AB ′F 中，AB ′＝FB ′＝1， ∴AF′， ∴DF ＝DG∴S△DFG ＝122＝52． (3)如图3中，点C 的运动路径的长为CC 的长，在Rt △ADC 中，∵tan ∠DAC ＝CD AD， ∴∠DAC ＝30°，AC ＝2CD ＝2， ∵∠C ′AD ＝∠DAC ＝30°， ∴∠CAC ′＝60°，∴CC 的长＝602180π＝23π．9．(2017江苏徐州，28，10分)如图，已知二次函数y ＝49x 2－4的图象与x 轴交于A ，B 两点，与y 轴交于点C ，⊙CP 为⊙C 上一动点．(1)点B ，C 的坐标分别为B ( )，C ( )； (2)是否存在点P ，使得△PBC 为直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由； (3)连接PB ，若E 为PB 的中点，连接OE ，则OE 的最大值＝ ．【分析】(1)在抛物线解析式中令y ＝0可求得B 点坐标，令x ＝0可求得C 点坐标；(2)①当PB 与⊙相切时，△PBC 为直角三角形，如图1，连接BC ，根据勾股定理得到BC ＝5，BP 2＝P 2作P 2E ⊥x 轴于E ，P 2F ⊥y 轴于F ，根据相似三角形的性质得到2222P F CP P E BP＝2，设OC ＝P 2E ＝2x ，CP 2＝OE ＝x ，得到BE ＝3－x ，CF＝2x －4，于是得到FP 2＝115，EP 2＝225，求得P 2(115，－225)，过P 1作P 1G ⊥x 轴于G ，P 1H ⊥y 轴于H ，同理求得P 1(－1，－2)，②当BC ⊥PC 时，△PBC 为直角三角形，根据相似三角形的判定和性质即可得到结论；(3)如图3中，连接AP ，∵OB ＝OA ，BE ＝EP，推出OE＝1AP，可知当AP最大时，OE的值最2大，x2－4中，令y＝0，则x 【解析】解：(1)在y＝49＝±3，令x＝0，则y＝－4，∴B(3，0)，C(0，－4)；故答案为：3，0；0，－4；(2)存在点P，使得△PBC为直角三角形，①当PB与⊙相切时，△PBC为直角三角形，如图(2)a，连接BC，∵OB＝3．OC＝4，∴BC＝5，∵CP⊥BP2，CP2∴BP 2＝过P 2作P 2E ⊥x 轴于E ，P 2F ⊥y 轴于F ， 则△CP 2F ∽△BP 2E ，四边形OCP 2B 是矩形，∴2222P F CP P E BP=＝2， 设OC ＝P 2E ＝2x ，CP 2＝OE ＝x ， ∴BE ＝3－x ，CF ＝2x －4，∴BE CF ＝324x x --＝2， ∴x ＝115，2x ＝225， ∴FP 2＝115，EP 2＝225， ∴P 2(115，－225)， 过P 1作P 1G ⊥x 轴于G ，P 1H ⊥y 轴于H ， 同理求得P 1(－1，－2)，②当BC ⊥PC 时，△PBC 为直角三角形，如图(2)b 过P 4作P 4H ⊥y 轴于H ，则△BOC∽△CHP4，∴4CH P HOB OC＝4P C BC＝，∴CH，P4H∴P4－4)；同理P3(－－4)；综上所述：点P的坐标为：(－1，－2)或(115，－225)或－4)或(－－4)；(3)如图(3)，连接AP，∵OB＝OA，BE＝EP，∴OE ＝12AP ， ∴当AP 最大时，OE 的值最大，∵当P 在AC 的延长线上时，AP 的值最大，最大值＝5∴OE的最大值为10．(2017江苏盐城，27，14分)如图，在平面直角坐标系中，直线y ＝12x ＋2与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝12x 2＋bx ＋c 经过A 、C 两点，与x 轴的另一交点为点B ． (1)求抛物线的函数表达式；(2)点D 为直线AC 上方抛物线上一动点； ①连接BC 、CD ，设直线BD 交线段AC 于点E ，△CDE 的面积为S 1，△BCE 的面积为S 2，求12S S 的最大值；②过点D 作DF ⊥AC ，垂足为点F ，连接CD ，是否存在点D ，使得△CDF 中的某个角恰好等于。

一、解答题1．在ABC中，AB AC=，D是边AC上一点，F是边AB上一点，连接BD、CF交于点E，连接AE，且．(1)如图1，若90∠=︒，，，求点B到AE的距离；BAC(2)如图2，若E为BD中点，连接FD，FD平分，G为CF上一点，且，求证：；(3)如图3，若，12△沿着AB翻折得，点H为的BC=，将ABD中点，连接HA、HC，当周长最小时，请直接写出的值．x－5与x轴、y轴分别交于B、C两点，点A为y轴正半轴上一2．如图1，直线y＝12S＝75．点，且ABC（1）请直接写出点B、C的坐标及直线AB的解析式：、、；（2）如图2，点P为线段OB上一点，若∠BCP＝45°，请写出点P的坐标：，并简要写出解答过程；（3）如图3，点D是AB的中点，M是OA上一点，连接DM，过点D作DN⊥DM交OB 于点N，连接BM，若∠OBM＝2∠ADM，请写出点M的坐标，并简要写出解答过程．3．已知有理数a，b，c在数轴上对应的点分别为A，B，C，其中b是最小的正整数，a，c满足()2++-=．a c250a______，b=______，c=______；（1）填空：=（2）点A，B，C分别以每秒4个单位长度，1个单位长度，1个单位长度的速度在数轴上同时向右运动，设运动时间为t 秒． ①当AC 长为6时，求t 的值；②当点A 在点C 左侧时（不考虑点A 与B ，C 重合的情况），是否存在一个常数m 使得2AC m AB +⋅的值在某段运动过程中不随t 的改变而改变？若存在，求出m 的值；若不存在，请说明理由．4．在平面直角坐标系中，直线24y x =-+与x 轴、y 轴分别相交于A 、B 两点，C 为AB 的中点，点D 在线段OB 上（BD OD <），连接CD ，将BCD △绕点C 逆时针旋转得到B CD ''△，旋转角为()0180αα︒<<︒，连接BB '，B D '．（1）求tan OBA ∠的值；（2）如图，当点D '恰好落在y 轴上时，B C '交y 轴于点E ，求证：BEB CED ''△△； （3）当点D 的坐标为(0,3)，且ODB OBA ∠'=∠时，求点B ′的坐标．5．已知如图，在ABCD 中，点E 是AD 边上一点，连接,,,BE CE BE CE BE CE =⊥，点F 是EC 上一动点，连接BF ．（1）如图1，当BF AB ⊥时，连接DF ，延长,BE CD 交于点K ，求证：FD DK =； （2）如图2，以BF 为直角边作等腰,90Rt FBG FBG ∠=︒△，连接GE ，若2,5DE CD ==，当点F 在运动过程中，求BEG 周长的最小值．6．如图，在直角梯形ABCD 中，AB ∥CD ，∠B ＝90°，AB ＝4，BC ＝8，CD ＝2m （m ＞2），P为CD中点，以P为圆心，CP为半径作半圆P，交线段AC于点E，交线段AD于点F．（1）当E为CA中点时，①求证：E是弧CF的中点．②求此时m的值．（2）连结PF，若PF平行△ABC的某一边时求出满足条件的m值．（3）连结PE，将PE绕着点E顺时针旋转90°得到EP'，连结AP'，当AP'⊥AC时，求此时CE的长．7．如图，抛物线y＝ax2+bx+6与x轴交于A（2，0），B（8，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P是抛物线上一动点，当∠PCB12=∠BCO时，求点P的横坐标．8．等腰直角三角形ABC中，90ACB∠=︒，AE为BAC∠的角平分线，交BC于点E，点D 为AB的中点，连结CD交AE于点G，过点C作CF AE⊥，垂足为点F，交AB于点H．（1）如图1，AG 与CH 的数量关系为__________；CFAG的值为__________； （2）如图2，以点C 为位似中心，将CAE 做位似变换，得到CA E ''△，使CA E ''△与CAE 的相似比为()01k k <<，A E ''与CD 、CH 的交点分别为G '，F '，隐去线段AE ，试求'''CF A G 的值； （3）如图3，将（2）中的等腰直角三角形改为等腰三角形，30B ∠=︒，且其他条件不变， ①CF A G '''的值为__________； ②若'3CF =，直接写出A G C ''△的面积．9．平面直角坐标系xOy 中，抛物线231y ax ax =-+与y 轴交于点A ． （1）求点A 的坐标及抛物线的对称轴；（2）当12x -≤≤时，y 的最大值为3，求a 的值；（3）已知点(0,2)P ，(1,1)Q a +．若线段PQ 与抛物线只有一个公共点，结合函数图象，求a 的取值范围．10．如图，菱形ABCD ，，点E 为平面内一点，连接AE ．(1)如图1，点E 在BC 的延长线上，将AE 绕点A 顺时针旋转60°得AF ，连接EF 交AB 延长线于点H ，若∠AEB ＝15°，，求AE 的长；(2)如图2，点E 在CA 的延长线上，将AE 绕点A 逆时针旋转60°得AF ，点M 为CE 的中点，连接BM ，证明：FM 3；(3)如图3，将AB 沿AS 翻折得AE （∠BAE ＜120°），连DE 交AS 于点S ，当DS 取得最大值时，连接TD ，若，AD =6，求TD ﹣TE 的最大值．11．如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，3OA OC ==，顶点为D ，对称轴交x 轴于点E ． （1）求抛物线的解析式、对称轴及顶点D 的坐标．（2）点P 在抛物线上，直线AP 与y 轴交于点F ，若AOF 与BOC 全等，求出点P 的坐标．（3）点P 在抛物线上，直线AP 与y 轴交于点T ，若tan 2:3PAB ∠=，求出点P 的坐标．（4）在线段AC上是否存在点M，使得AOM与ABC相似，若存在，求出点M的坐标；若不存在，请说明理由．PQ y轴，PO与AC相交于点Q，连（5）第三象限内的抛物线上有一动点P，过点P作//△与ABC相似，若存在，求出点P的坐接BC．请问抛物线上是否存在点P，使得PCQ标；若不存在，请说明理由．（6）x轴下方的抛物线上有一动点P，过点P作PF x轴于点F，PF与AC相交于点G．请问抛物线上是否存在点P，使得AFG与CPG△相似？若存在，求出点P的坐标；若不存在，请说明理由．⊥于点Q，连接BC和PC．请问抛物线上是（7）抛物线上有一动点P，过点P作PQ AC△与BOC相似？若存在，求出点P的坐标；若不存在，请说明理否存在点P，使得PCQ由．（8）在抛物线上是否存在点P，过点P作PH x⊥轴于点H，使得PAH与BOC相似，若存在，求出点P的坐标；若不存在，请说明理由．（9）抛物线的顶点为点D，连接AD，CD，在抛物线上有一动点M，过点M作MN x轴于点N．请问抛物线上是否存在点M，使得AMN与ACD△相似？若存在，求出点M的坐标；若不存在，请说明理由．12．（1）回归教材：北师大七年级下册P44，如图1所示，点P是直线m外一点，，点O是垂足，点A、B、C在直线m上，比较线段PO，PA，PB，PC的长短，你发现了什么？最短线段是______，于是，小明这样总结：直线外一点与直线上各点连接的所有线段中，______．（2）小试牛刀：如图2所示，Rt ABC △中，AB c =，，．则点P 为AB 边上一动点，则CP 的最小值为______．（3）尝试应用：如图3所示ABC 是边长为4的等边三角形，其中点P 为高AD 上的一个动点，连接BP ，将BP 绕点B 顺时针旋转60°得到BE ，连接PE 、DE 、CE ．①请直接写出DE 的最小值． ②在①的条件下求的面积．（4）拓展提高：如图4，顶点F 在矩形ABCD 的对角线AC 上运动，连接AE ．．3AB =，4BC =，请求出AE 的最小值．13．如图，已知抛物线23y ax bx =++（a 、b 为常数，且a ≠0）与x 轴交于点A （-1，0）和点B ，与y 轴交于点C ，其对称轴是直线x =1，顶点为P ，连接BP ，CP ．(1)求抛物线的表达式；(2)判断△BCP的形状，并说明理由；(3)该抛物线上是否存在点Q，使得∠QBC=∠ACO？若存在，请直接写出满足条件的所有点Q是坐标；若不存在，请说明理由．14．如图，在平面直角坐标系中抛物线y＝ax2＋bx＋c经过原点，且与直线y＝﹣kx＋6交于则A（6，3）、B（﹣4，8）两点．(1)求直线和抛物线的解析式；(2)点P在抛物线上，解决下列问题：①在直线AB下方的抛物线上求点P，使得△PAB的面积等于20；②连接OA，OB，OP，作PC⊥x轴于点C，若△POC和△ABO相似，请直接写出点P的坐标．15．如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋2与直线y＝x﹣2交于点A（m，0）和点B（﹣2，n），与y轴交于点C．(1)求抛物线的解析式及顶点D的坐标；(2)若向下平移抛物线，使顶点D落在x轴上，原来的抛物线上的点P平移后的对应点为P ，若，求点P的坐标；(3)在抛物线上是否存在点Q，使△QAB的面积是△ABC面积的一半？若存在，直接写出点Q的坐标；若不存在，请说明理由．16．我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，﹣3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．(1)求“蛋圆”抛物线部分的解析式及“蛋圆”的弦CD的长；(2)已知点E是“蛋圆”上的一点（不与点A，点B重合），点E关于x轴的对称点是点F，若点F也在“蛋圆”上，求点E坐标；(3)点P是“蛋圆”外一点，满足∠BPC＝60°，当BP最大时，直接写出点P的坐标．17．如图，在平面直角坐标系中，一抛物线的对称轴为直线x＝1，且该抛物线与y轴负半轴交于C点，与x轴交于A，B两点，其中B点的坐标为（3，0），且OB＝OC．(1)求此抛物线的函数表达式；(2)若平行于x轴的直线与该抛物线交于M、N两点（其中点M在点N的右侧），在x轴上是否存在点Q，使△MNQ是以MN为一直角边的等腰直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．18．已知二次函数经过点A（﹣3，0）、B（1，0）、C（0，3）．(1)求该抛物线解析式；(2)如图1，点M 为抛物线上第二象限内一动点，BM 交y 轴于点N ，当BM 将四边形ABCM 的面积分为1：2两部分时，求点M 的坐标；(3)如图2，点P 为对称轴上D 点下方一动点，点Q 为直线y ＝x 第一象限上的动点，且DP ＝2OQ ，求BP +2BQ 的最小值并求此时点P 的坐标．19．如图，在平面直角坐标系中，已知二次函数图像222(1)2y x a x a a =-+++的顶点为P ，点B 39(2,)16- 是一次函数5119216y x =+上一点．(1)当a ＝0时，求顶点P 坐标；(2)若a ＞0，且一次函数2y x b =-+的图象与此抛物线没有交点，请你写出一个符合条件的一次函数关系式（只需写一个，不必写出过程）； (3)作直线OC ：12y x =与一次函数5119216y x =+交于点C ．连结OB ，当抛物线与△OBC 的边有两个交点时，求a 的取值范围．20．在平面直角坐标系xOy 中，⊙O 的半径为1．对于线段AB ，给出如下定义：若线段AB 沿着某条直线l 对称可以得到⊙O 的弦A ′B ′，则称线段AB 是⊙O 的以直线l 为对称轴的“反射线段”，直线l 称为“反射轴”．（1）如图，线段CD ，EF ，GH 中是⊙O 的以直线l 为对称轴的“反射线段”有 ； （2）已知A 点坐标为（0，2），B 点坐标为（1，1），①若线段AB 是⊙O 的以直线l 为对称轴的“反射线段”，求反射轴l 与y 轴的交点M 的坐标．②若将“反射线段”AB 沿直线y ＝x 的方向向上平移一段距离S ，其反射轴l 与y 轴的交点的纵坐标yM 的取值范围为12≤yM 136≤，求S ． （3）已知点M ，N 是在以原点为圆心，半径为2的圆上的两个动点，且满足MN ＝1，若MN 是⊙O 的以直线l 为对称轴的“反射线段”，当M 点在圆上运动一周时，求反射轴l 未经过的区域的面积．（4）已知点M ，N 是在以（2，013MN 2=MN 是⊙O 的以直线l 为对称轴的“反射线段”，当M 点在圆上运动一周时，请直接写出反射轴l 与y 轴交点的纵坐标的取值范围．【参考答案】参考答案**科目模拟测试一、解答题31．(2)证明见解析(3)【解析】【分析】（1）如图所示，过点B作BG⊥AE交AE延长线于G，先证明∠ACF=∠GAB，即可证明△ABG≌△CAE得到BG=AE，由勾股定理得，再由，得到，则点B到AE的距离为（2）如图所示，延长AE到H使得，AE=HE，连接DH，CH，先证明△AEB≌△HED得到AB=HD=AC，∠ABE=∠HDE，则∠HCD=∠HDC，AB∥DH，从而推出∠BAC=∠HDC=∠HCD，再证明CE是AH的垂直平分线，得到AC=HC，则∠ACE=∠HCE，即∠HCA=2∠ACE，然后推出∠FGD=∠HCD=∠HDC=∠FAC=2∠GCD，GD=GC，即可证明△AFD≌△GFD（AAS），得到AF=GF，则CF=GF+CG=AF+DG；（3）如图所示，连接，延长交BC于F，作直线BE⊥BC，由翻折的性质可知，，，，然后证明，得到，则点D在线段BC的垂直平分线上，即AF⊥BC，求出，由H是的中点，得到直线A关于点H的对称点A'在直线BE上，则要使△AHC的周长最小，则要最小，即最小，即当A'、C、H、三点共线时有最小值，如图所示，连接交于，交AF于P，连接BP，先证明，得到，由平行线之间的间距相等，得到，然后求出，再证明，求出，由此求解即可．(1)解：如图所示，过点B作BG⊥AE交AE延长线于G，∵AE⊥CF，AG⊥BG，∴∠BAC=∠AGB=∠AEF=∠AEC=90°，∠AFC+∠ACF=90°，∴∠FAE+∠AFE=90°，∴∠ACF=∠GAB，又∵AB=CA，∴△ABG≌△CAE（AAS），∴BG=AE，在直角△AFC中，由勾股定理得，∵，∴，∴点B到AE的距离为32；(2)解：如图所示，延长AE到H使得，AE=HE，连接DH，CH，∵FD平分∠AFC，∴∠AFD=∠CFD，∵E是BD的中点，∴BE=DE，又∵AE=HE，∠AEB=∠HED，∴△AEB≌△HED（SAS），∴AB=HD=AC，∠ABE=∠HDE，∴∠HCD=∠HDC，∴∠BAC=∠HDC=∠HCD，∴∠ACE=∠HCE，即∠HCA=2∠ACE，∵∠GDC=∠GCD，∠FGD=∠GDC+∠GCD，∴∠FGD=∠HCD=∠HDC=∠FAC=2∠GCD，GD=GC，又∵FD=FD，∠AFD=∠GFD，∴△AFD≌△GFD（AAS），∴AF=GF，∴CF=GF+CG=AF+DG；(3)解：如图所示，连接，延长交BC于F，作直线BE⊥BC，由翻折的性质可知，，，，∴，又∵AB=AC，，∴，∴，∴点D在线段BC的垂直平分线上，即AF⊥BC，∴，∵H是的中点，∴直线A关于点H的对称点A'在直线BE上，∴，∴要使△AHC的周长最小，则要最小，即最小，∴当A'、C、H、三点共线时有最小值，如图所示，连接交于，交AF于P，连接BP，∵BE⊥BC，AF⊥BC，∴，∴，，又∵，∴，∴， ∵，BC ⊥BE ， ∴,∵平行线之间的间距相等，∴∵AB =AC ，∠BAC =120°， ∴∠ABC =∠ACB =30°， ∴AB =2AF ， ∴， ∴，∴，∵P 在线段BC 的垂直平分线上， ∴PB =PC ， ∴∠PBC =∠PCB ， ∵，∴，∴， ∴，∴，∴，∴，∴【点睛】本题主要考查了全等三角形的性质与判定，线段垂直平分线的性质，等腰三角形的性质与判定，含30度角的直角三角形的性质，勾股定理，平行线的性质与判定等等，熟练掌握相关知识是解题的关键．2．（1）()()10,0,0,5B C -，10y x =-+；（2）5(,0)3；（3）15(0,)2【解析】 【分析】（1）分别令,0x y =进而求得直线与坐标轴的交点，根据已知条件待定系数法求解析式即可；（2）过点B 作BQ CP ⊥于点Q ，过B 点作ED x ⊥轴，过,C Q 分别作,CD QE 平行于x 轴，交ED 于点,E D ，证明CBD ≌BQE △，可得,CD BE BD QE ==，根据图形与坐标的关系，即可求得(10,10),(5,10)E Q ，设直线CQ 的直线解析式为y mx n =+，待定系数法求解析式即可，令0y =，进而求得P 点的坐标；（3）连接OD ，证明DMN 是等腰直角三角形，设DO 交MN 于点E ,设ADM α∠=,则2MBO α∠=过点N 作SN x ⊥轴，作OBM ∠的角平分线BS 交NS 于点S ，过点S 作,ST SR分别垂直于,MO MB ，垂足分别为,T R ，连接MS ，证明SNB NOM △≌△，SRB △≌SNB △，进而证明Rt STM △≌Rt SRM △，设ON x =，则,10,,AM x BN x SN ON x ==-==在Rt MOB 中，222MB MO OB =+，勾股定理列出方程，求得AM ，进而求得MO ，从而求得M 的坐标． 【详解】 （1）直线y ＝12x －5与x 轴、y 轴分别交于B 、C 两点，令0x =，则5y =-，令0y =，则10x =，()()10,0,0,5B C ∴- 10,5OB OC ∴== 75ABC S =△1752AC OB ∴⋅⨯= 15AC ∴=点A 为y 轴正半轴上一点，AC AO CO =+10AO(0,10)A ∴设直线AB 的解析式为y kx b =+，将(0,10)A ，()10,0B 代入，得10100b k b =⎧⎨+=⎩解得110k b =-⎧⎨=⎩∴直线AB 的解析式为10y x =-+故答案为：()()10,0,0,5B C -，10y x =-+（2）如图，过点B 作BQ CP ⊥于点Q ，过B 点作ED x ⊥轴，过,C Q 分别作,CD QE 平行于x 轴，交ED 于点,E D ，45,BCP BQ BC ∠=︒⊥45BQC ∴∠=︒BCQ ∴△是等腰直角三角形 BC BQ ∴=，90CBD QBE ∴∠+∠=︒ED x ⊥轴，//CD x 轴，//QE x 轴，,CD ED QE DE ∴⊥⊥90CBD BCD ∴∠+∠=︒，90D E ∠=∠=︒BCD QBE ∴∠=∠在CBD 与BQE △中D E BCD QBE CB QB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴CBD ≌BQE △ ,CD BE BD QE ∴== (10,0),(0,5)B C - 10,5CD BD ∴==5QE BD ∴==，10BE CD == (10,10),(5,10)E Q ∴设直线CQ 的直线解析式为y mx n =+，将(0,5)C -,(5,10)Q 代入，则5510n m n =-⎧⎨+=⎩解得35m n =⎧⎨=-⎩直线CQ 的直线解析式为35y x =- 令0y =，则53x =即5 (,0) 3P故答案为：5 (,0) 3（3）如图，连接OD，(0,10)A，()10,0BOA OB∴=90AOB∠=︒AOB∴是等腰直角三角形DN DM⊥90MDN∴∠=︒D点是AB的中点，AD DB OD∴==，OD AD⊥45DON DAM∴∠=∠=︒ODN ODM ODM ADM∴∠+=∠+∠ODN ADM∴∠=∠DAM DON∴△≌△AM ON∴=，DM DN=,ODN ADM∠=∠DMN∴是等腰直角三角形，设DO 交MN 于点E ,设ADM α∠=,则2MBO α∠=45EOM ∠=︒，45DNM ∠=︒MOE MND ∴∠=∠MEO NED ∠=∠OMN ODN ADM α∴∠=∠=∠=过点N 作SN x ⊥轴，作OBM ∠的角平分线BS 交NS 于点S ，过点S 作,ST SR 分别垂直于,MO MB ，垂足分别为,T R ，连接MS ，如图，22OBM ADM α∠=∠=，BS 平分OBM ∠SBN SBR α∴∠==∠OA OB =,AM ON =OM NB ∴=又90,MON BNS OMN SBN α∠=∠=︒∠=∠=SNB NOM ∴△≌△ST SN ∴=∴四边形STON 是正方形在SRB △与SNB △中90SBN SBR SB SBSRB SNB α∠=∠=⎧⎪=⎨⎪∠=∠=︒⎩∴SRB △≌SNB △NB RB ∴=，SR SN =SR ST ∴=,ST OA SR MB ⊥⊥90STM SRM ∴∠=∠=︒在Rt STM △和Rt SRM △中MS MS ST SR =⎧⎨=⎩∴Rt STM △≌Rt SRM △MT MR ∴=设ON x =，则,10,,AM x BN x SN ON x ==-==102MT MO TO AO AM TO x MR =-=--=-=，10NB OB ON x BR =-=-=在Rt MOB 中，222MB MO OB =+即()222MR RB OB OM +=+()()22210210=1010x x x ∴-+-+- 整理得2225500x x -+=即()()25100x x --= 解得125,102x x ==（舍） 52AM ON ∴== 5151022MO ∴=-= 15(0,)2M ∴ 【点睛】本题考查了一次函数，坐标与图形，等腰三角形的性质，勾股定理，三角形全等的性质与判定，角平分线的定义，解一元二次方程，添加辅助线是解题的关键．3．（1）2,1,5-；（2）①13或133；②存在，m 的值为2-或2． 【解析】【分析】（1）根据正整数的定义、绝对值的非负性、偶次方的非负性分别可求出,,b a c 的值；（2）①先求出运动t 秒后，点,A C 所表示的数，再分点A 在点C 左侧和点A 在点C 右侧两种情况，然后根据数轴的定义建立方程，解方程即可得；②先求出运动t 秒后，点,,A B C 所表示的数，从而可得AC 的长，再分点A 在点B 左侧和点A 在点B 右侧两种情况，分别求出AB 的值，代入化简，然后根据整式的无关型问题求解即可得．【详解】解：（1）b 是最小的正整数，1b ∴=，()2250a c ++-=，20,50a c ∴+=-=， 解得2,5a c =-=，故答案为：2,1,5-；（2）①由题意，运动t 后，点A 所表示的数是42t -，点C 所表示的数是5t +， 当点A 在点C 左侧时，5(42)6AC t t =+--=，解得13t =， 当点A 在点C 右侧时，42(5)6AC t t =--+=，解得133t =， 综上，t 的值为13或133； ②由题意，运动t 后，点A 所表示的数是42t -，点B 所表示的数是1t +，点C 所表示的数是5t +， 当421t t -=+时，13t =， 当425t t -=+时，73t =， 因为点A 在点C 左侧，所以5(42)73AC t t t =+--=-，当点A 在点B 左侧，即01t <<时，1(42)33AB t t t =+--=-，则22(73)(33)314(36)AC m AB t m t m m t +⋅=-+-=+-+，由360m +=得：2m =-，即在01t <<运动时间内，当2m =-时，2AC m AB +⋅的值不随t 的改变而改变；当点A 在点B 右侧，即713t <<时，42(1)33AB t t t =--+=-， 则22(73)(33)143(36)AC m AB t m t m m t +⋅=-+-=-+-，由360m -=得：2m =， 即在713t <<运动时间内，当2m =时，2AC m AB +⋅的值不随t 的改变而改变； 综上，存在一个常数m 使得2AC m AB +⋅的值在某段运动过程中不随t 的改变而改变，m 的值为2-或2．【点睛】本题考查了数轴、一元一次方程的应用、绝对值和偶次方的非负性、整式等知识点，较难的是题（2）②，正确分两种情况讨论是解题关键．4．（1）12；（2）证明见解析；（3）B ′的坐标为(1,1)-或． 【解析】【分析】（1）利用一次函数的解析式先求解,A B 的坐标，再求解,OA OB 的长度，再利用正切的定义可得答案；（2）由旋转的性质可得CBD CB D ∠=∠''，证明BEC B ED ∽ ，可得BE B E EC ED ''=，结合BEB CED ，从而可得结论；（3）当B '在y 轴左边，过点B '作B M y '⊥轴于点M ，过点C 作CNB M ，交B M '的延长线于点N ，先利用等角正切相等可得：1.32ab 可得32,b a 再利用勾股定理可得222(1)(2)a b -+-=，再解方程组即可，当B '在y 轴右边时，同理可得B '点坐标．【详解】解：（1）直线24y x =-+与x 轴、y 轴分别相交于A 、B 两点，令0,x = 则4,y =令0,y = 则2,x =(2,0)A ∴，(0,4)B ，即2OA =，4OB =，AB ∴= 21tan .42OAOBA OB （2）由旋转的性质可得CBD CB D ∠=∠''，又BEC B ED ∠=∠''，BEC ∴∆∽△B ED ''，∴BE EC B E ED =''，∴BE B E EC ED ''=， 又BEB CED ∠=∠''，BEB CED ∆'∴∆'∽；（3）2,0,0,4,A B C 为AB 的中点，152BC B C AB ∴==='，(1,2)C ， 设(,)B a b '，①当B '在y 轴左侧时，如图，此时0a <，过点B '作B M y '⊥轴于点M ，过点C 作CN B M ，交B M '的延长线于点N ，ODB OBA ∠'=∠，tan tan ODB OBA ∴='∠∠， ∴12B M OA DM OB ='=， ∴132a b -=-， 32b a ∴=+，①1,2,C (,)B a b '，1B N a ∴'=-，2CN b =-，由勾股定理，得222B N CN B C '='+，即222(1)(2)(5)a b -+-=，②联立①②，解得11a b =-⎧⎨=⎩或35{215a b ==， 0a <，(1,1)B ∴-'；②当B '在y 轴右侧时，如图，此时0a >，过点B '作B M y '⊥轴于点M ，过点C 作CN B M 于点N ，同理可得：12B M OA DM OB ='=， ∴132a b =-， 32b a ∴=-，①(1,2)C ，(,)B a b '， 1B N a ∴'=-，2CN b =-，由勾股定理，得222B N CN B C '='+， 即222(1)(2)(5)a b -+-=，② 联立①②，解得326{946a b +=-326{946a b -+=，0a >， 326(B '+∴946-； 综上，B ′的坐标为(1,1)-或326(+946-． 【点睛】本题主要考查一次函数的性质，相似三角形的判定和性质，勾股定理，一元二次方程的解法，锐角三角函数的应用等知识，熟练掌握相似三角形的判定和性质以及勾股定理等知识是解题的关键．5．（1）证明见解析；（2）353【解析】【分析】（1）通过证明△CEK≌△BEF及△KED≌△FED即可证明FD DK=；（2）延长CE到点P，使EP＝CE，先证明点G在过点P且与CE垂直的直线PN上运动，再作点E关于点P的对称点Q，连接BQ交PN于点G，此时△BEG的周长最小，求出此时GE+GB+BE的值即可．【详解】证明：（1）∵四边形ABCD是平行四边形，∴AB CD∥，∴∠K＝∠ABE，∵BF⊥AB，,⊥BE CEBEF CEK∴∠ABF＝90°，90,∴∠ABE＝90°﹣∠EBF＝∠BFE，∴∠K＝∠BFE，∵BE＝CE，∴△CEK≌△BEF（AAS），∴CK＝BF，EK＝EF，∵AD BC∥，∴∠KED＝∠EBC，∠FED＝∠ECB，∵BE＝CE，∴∠EBC＝∠ECB，∴∠KED＝∠FED，∴ED＝ED，∴△KED≌△FED（SAS），∴DK＝DF，（2）如图，作BN⊥BE，GN⊥BN于点N，延长NG交射线CE于点P，则∠EBN＝∠FBG＝90°，∴∠NBG＝∠EBF＝90°﹣∠GBE，∵∠N＝∠BEF＝90°，BG＝BF，∴△BNG ≌△BEF （AAS ），∴BN ＝BE ；∵∠EBN ＝∠N ＝∠BEP ＝90°，∴四边形BEPN 是正方形，∴PE ＝BE ＝CE ，∴当点F 在CE 上运动时，点G 在PN 上运动；延长EP 到点Q ，使PQ ＝PE ，连接BQ 交PN 于点G ，∵PN 垂直平分EQ ，∴点Q 与点E 关于直线PN 对称，∵两点之间，线段最短，∴此时GE +GB ＝GQ +GB ＝BQ 最小，∵BE 为定值，∴此时GE +GB +BE 最小，即△BEG 的周长最小；作DH ⊥CE 于点H ，则∠DHE ＝∠DHC ＝90°，∵∠ECB ＝∠EBC ＝45°，∴∠HED ＝∠ECB ＝45°，∴∠HDE ＝45°＝∠HED ，∴DH ＝EH ，∴DH 2+EH 2＝2DH 2＝DE 2＝2， ∴DH ＝EH ＝1；∴CH 2222512DH ，∴BE ＝CE ＝EH +CH ＝1+2＝3，∴EQ ＝2PE ＝2BE ＝6，∵∠BEQ ＝90°，∴BQ =∴GE +GB +BE ＝3，∴△BEG 周长的最小值为3．【点睛】本题重点考查平行四边形的性质、正方形的判定与性质、等腰直角三角形的性质、全等三角形的判定与性质、勾股定理、以及运用轴对称的性质求线段和的最小值问题的求解等知识与方法，深入探究与挖掘题中的隐含条件并且正确地作出辅助线是解题的关键，此题综合性强，难度大，属于考试压轴题．6．（1）①见解析；②5m =；（2）m 的值为6；（3）CE =【解析】【分析】（1）①连接DE ，证明ADC ∆是等腰三角形，根据“三线合一”的性质可得ADE CDE ∠=∠，证得EC EF =，从而可得结论；②根据勾股定理得到AC 45=，由E 为AC 中点得EC 25=，再证明DEC CBA ，由相似三角形的性质列出比例式，求出m 的值即可；（2）分PF //AC 和PF //BC 两种情况求解即可； （3）设CE =x ，作PG ⊥AC ，则2x GE =，45AE x =- 证明PGE EAP '≅得AP GE '=，再证明AP EBAC '，列比例式求出x 的值即可．【详解】解：（1）如图，连接DE∵CD 是圆P 的直径，∴∠DEC =90°，即DE ⊥AC∵E 为CA 中点 ∴AE =CE∴AD =CD∴ADE CDE ∠=∠∴EC EF =∴E 是CF 的中点；②在Rt △ABC 中，∠B ＝90°，AB ＝4，BC ＝8， ∴22224845AC AB BC +=+∵E 是AC 的中点 ∴11452522EC AC ==⨯= ∵AB //CD ，90B ∠=︒∴90B DCB ∠+∠=︒∴90DCB ∠=︒，即90DCE BCA ∠+∠=︒∵90CDE DCE ∠+∠=︒∴CDE BCA ∠=∠又90B DEC ∠=∠=︒∴DEC CBA ∆∆∽∴CE DC AB AC =2545解得，5m =；（2）分两种情况：①当PF//AC时，如图，则有PDF CDA∆∆∴PF PDAC CD=，即245PF mm=∴25=PF∴25m=②当PF//BC时，如图，过点A作AH⊥DC，垂足为H，则四边形AHCB是矩形，∴AH//BC，HC=AB=4，AH=BC=8∴PF//AH∵90DCB∠=︒∴90FPD∠=︒∴45PDF PFD∠=∠=︒∴45HAD HDA∠=∠=︒∴DH=AH，即248m-=解得，6m=综上，m的值为256；（3）过点P作PG AC⊥于点G，如图，∵PE =PC∴1,2GE CE EPG CPG =∠=∠∵90PEP '∠=︒ ∴90P EA PEG '∠+∠=︒ 又90PEG GPE ∠+∠=︒ ∴P EA EPG '∠=∠又90P AE PGE '∠=∠=︒，PE P E '= ∴P AE EPG '∆≅∆ ∴AP GE '=设CE x =，则45,2x AE x GE AP '===∵90,90BCA DCA GPC PCH ∠+∠=︒∠+∠=︒ ∴GPC BCA ∠=∠ ∴EPG BCP ∠=∠ ∴P EA BCA '∠=∠ 又90P AE B '∠=∠=︒ ∴AP EBAC '∆∆∴AP ABAE BC'=42825x= ∴5x =25CE =【点睛】本题主要考查了全等三角形的判定与性质，圆的基本概念，相似三角形的判定与性质，正确作出辅助线以及进行分类讨论是解答本题的关键．7．（1）2315684y x x =-+；（2）143x =或34633x =【解析】 【分析】（1）由题意代入A （2，0），B （8，0）两点求出a 、b 的值，即可得出抛物线的解析式；（2）根据题意分点P 在BC 下方的抛物线上和点P 在BC 上方的抛物线上两种情况，结合全等三角形的判定与性质以及相似三角形的判定与性质进行分析即可得出答案. 【详解】解：（1）由题意代入A （2，0），B （8，0）两点，可得： 042606486a b a b =++⎧⎨=++⎩，解得：38154a b ⎧=⎪⎪⎨⎪=-⎪⎩， 所以抛物线的解析式为：2315684y x x =-+；（2）当点P 在BC 下方的抛物线上时，此时∠PCB 12=∠BCO 即CP 平分∠BCO ，如图，作CP 平分∠BCO ，交x 轴于点D ，过D 作DE BC ⊥垂足为E ， ∵CP 平分∠BCO ，DE BC ⊥， ∴OD DE =，DCO DCE ∠=∠，∵OD DE =，DCO DCE ∠=∠，90COD CED ︒∠=∠=, ∴,6,DOC DEC CO CE ≅==∴22226810,4BC CO BO BE BC CE ++=-=, 设OD DE m ==，8BD m =-,勾股定理可得：222DE B D E B +=,即2224(8)m m +=-, 解得：3m =,即3OD DE ==，D 的坐标为（3，0）， 设CD 的解析式为：(0)y kx b k =+≠，代入C 、D 可得：603b k b =⎧⎨=+⎩，解得：26k b =-⎧⎨=⎩，所以CD 的解析式为：26y x =-+， ∵P 为直线CD 与抛物线的交点，84解得：0x =（舍去）或143x =，即P 的横坐标为143x =， 当点P 在BC 上方的抛物线上时，此时∠PCB 12=∠BCO ，如图， 作∠PCB 12=∠BCO 交抛物线于点P ，延长DE 交CP 于点F ，过E 作EH ⊥x 轴交于点H ，∵∠PCB 12=∠BCO ，DCB DCO ∠=∠， ∴,PCB DCB ∠=∠∵,,PCB DCB CE CE DEC FEC ∠=∠=∠=∠, ∴,DEC FEC DE DF ≅=,∵,90CBO EBH COB EHB ︒∠=∠∠=∠=, ∴EHB COB ∽, ∴4,1068BE EH BH EH BHBC CO BO ====, 可得121624,,555EH BH OH BO BH ===-=, ∴2412(,)55E , 设F 为(,)m n ，由DE DF =可得324012,2525m n ++==，解得：3324,55m n ==， 即F 为3324(,)55， 设CF 的解析式为：(0)y kx b k =+≠，代入C 、F 可得：6243355b k b =⎧⎪⎨=+⎪⎩，解得：2116k b ⎧=-⎪⎨⎪=⎩，所以CD 的解析式为：2611y x =-+， ∵P 为直线CF 与抛物线的交点，1184解得：0x =（舍去）或34633x =，即P 的横坐标为34633x =， 综上所述P 的横坐标为143x =或34633x =.【点睛】本题考查二次函数的综合问题，熟练掌握待定系数法求二次函数解析式和全等三角形的判定与性质以及相似三角形的判定与性质和角平分线性质是解题的关键.8．（1）AG =CH ；12；（2）'''CF A G 的值为12；（3【解析】 【分析】（1）由已知条件ASA 推论出CDH ADG ≅△△，得出AG =CH ；再推论出ACF AHF ≅△△，得出CF HF =，因为12CF CH =，所以12CF AG =； （2）过点A '作//A B AB ''，同（1）理得：CH AG '='' 所以 12CF A G '=''； （3）①由已知条件推论出CD H A D G '''''△△，得出CH CD A G A D ''=''''，因为30B ∠=︒，推出CH A G '=''，由12CF CH '='可转化得，CF A G '=''；②由CF A G '=''，'CF 6AG ''=，由面积公式得到12A G C S A G CF ''='''=△ 【详解】解：（1）AC AB = 90ACB ∠=︒ 点D 为AB 的中点CD AB ∴⊥ AD DB CD == 90DCH CHD ∴∠+∠=︒ CF AE ⊥90GAD CHD ∴∠+∠=︒ DCH GAD ∴∠=∠在CDH △和ADG 中90DCH GADCD AD CDH ADG ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩CDH ADG ∴≅△△ CH AG ∴=AE ∵为BAC ∠的角平分线 CF AE ⊥CAF HAF CFA AFH ∴∠=∠∠=∠在ACF 和AHF △中 CAF HAF AF AFCFA AFH ∠=∠⎧⎪=⎨⎪∠=∠⎩ACF AHF ∴≅△△CF HF ∴=12CF CH ∴= 12CF AG ∴= （2）过点A '作//A B AB ''，交CD 于D '，CH 于H '，CB 于B ′在CA B ''△中A E '为CAB ∠''的角平分线 CF A E ⊥''同（1）理得：CH AG '='' 12CF A G '∴='' '''CF A G ∴的值为12； （3）过点A '作//A B AB ''，交CD 于D '，CH 于H '，CB 于B ′①AC AB = 30ABC ∠=︒ 点D 为AB 的中点CD AB ∴⊥ //A B AB ''CD A B ∴⊥'' 30A B C ABC ∠''=∠=︒ 30CA B CAB ∠''=∠=︒ 90D CH CH D ∴∠''+∠''=︒ 60AC D ∠'''=︒ CF A E '⊥''90G A D CH D ∴∠'''+∠''=︒ D CH G A D ∴∠''=∠''' 90CD H G D A ∠''=∠'''=︒ CD H A D G ∴'''''△△CH CD A G A D ''∴=''''tan 30CD A D '︒==''CH CD A G A D ''∴=='''CH A G ∴'='' 由题意知A E ''为B AC ∠''的角平分线 CF A E '⊥''CA F H A F CF A A F H ∴∠''=∠'''∠''=∠'''在A CF ''△和A H F '''△中 CA F H A F A F A F CF A A F H ∠''=∠'''⎧⎪''=''⎨⎪∠''=∠'''⎩ACF A H F ∴''≅'''△△ CF H F ∴'=''12CF CH '∴='12=CF A G '∴=''②CF A G '='''CF =6A G ∴''===11622A G C S A G CF ''∴='''=⨯=△【点睛】本题是相似形的综合题目，考察了等腰三角形、直角三角形以及全等三角形的判定和性质、和相似三角形判定和性质等知识；本题难度较大，综合性强．9．（1）(0,1)A ，32x =；（2）12a =或89a =-；（3）10a -<或2a ． 【解析】 【分析】（1）把0x =代入抛物线的解析式求解抛物线与y 轴的交点坐标即可，再利用抛物线的对称轴方程2bx a=-求解抛物线的对称轴即可； （2）分两种情况讨论，①当0a >时，抛物线的开口向上，12x -≤≤且()353112,2222--=>-= 此时1x =-，y 取最大值；②当0a <时，抛物线的开口向下，12x -≤≤且()353112,2222--=>-=此时32x =，y 取最大值，再分别列方程求解a 即可；（3）分两种情况分别画出符合题意的图形，①当0a >时，如图，当点Q 在点A 的左侧（包括点)A 或点Q 在点B 的右侧（包括点)B 时，线段PQ 与抛物线只有一个公共点；②当0a <时，如图，当Q 在点A 与点B 之间（包括点A ，不包括点)B 时，线段PQ 与抛物线只有一个公共点，再根据点的位置列不等式即可得到答案. 【详解】解：（1）令0x =，则1y =．(0,1)A ． 抛物线的对称轴为3322a x a -=-=． （2）2234931()24ay ax ax a x -=-+=-+， 抛物线的对称轴为32x =． ①当0a >时，抛物线的开口向上，12x -≤≤且()353112,2222--=>-= 此时1x =-，y 取最大值. ∴()213(1)13a a --⨯-+= ∴12a =. ②当0a <时，抛物线的开口向下，12x -≤≤且()353112,2222--=>-= ∴ 此时32x =，y取最大值. ∴233()31322a a -⨯+= ∴89a =-.综上所述，12a =或89a =-． （3）∵抛物线231y ax ax =-+的对称轴为32x =．设点A 关于对称轴的对称点为点B ，(3,1)B ∴.(1,1)Q a +， ∴点,,Q A B 都在直线1y =上．①当0a >时，如图，当点Q 在点A 的左侧（包括点)A 或点Q 在点B 的右侧（包括点)B 时，线段PQ 与抛物线只有一个公共点．10a ∴+或13a +．1a ∴-（不合题意，舍去）或2a∴ 2a .②当0a <时，如图，当Q 在点A 与点B 之间（包括点A ，不包括点)B 时，线段PQ 与抛物线只有一个公共点．013a ∴+<． 12a ∴-<．又0a <，10a ∴-<综上所述，a 的取值范围为10a -<或2a ． 【点睛】本题考查的是抛物线与坐标轴的交点问题，求解抛物线的对称轴方程，抛物线的最值问题，抛物线与线段的交点问题，掌握数形结合的方法，清晰的分类讨论是解题的关键.10．(1)43； (2)见解析 (3)−3√6+3√2【解析】 【分析】（1）过点H 作HL ⊥EF ，交AF 于L ，根据菱形ABCD ，，得出∠DAB =180°-，AD ∥BC ，可得∠DAE =∠AEB ，可求∠DAE =15°，先证△AEF 为等边三角形，得出∠F=60°，根据余角性质可求∠HLF=90°-∠F=30°，利用30°直角三角形性质可求LF=2HF=2×4=8，根据勾股定理，再证∠AHL=∠HAF，得出AL=LH=（2）过B作BL⊥AC于L，过F作FK⊥AE于K，设AE=m，AC=n，将AE绕点A逆时针旋转60°得AF，得出△AEF为等边三角形，可得AF=EF，可求∠AFK=∠EFK=30°，AK=EK=，根据勾股定理在Rt△AKF中，，根据菱形ABCD，可求AL=CL=,∠CBL=∠ABL=60°，进而可求∠LCB=90°-∠CBL=30°，利用30°直角三角形性质得出BC=2BL，在Rt△BCL中，根据勾股定理，得出，根据点M为CE中点，可得CM=EM=，得出MK=ME-KE=，M L=MC-CL=，再利用勾股定理股定理即可；（3）连结SB，过E作TL⊥DE，，过G作GI⊥AD于I，过T作TJ⊥AB于J，在TD上截取TE′=TE，根据将AB沿AS翻折得，∠BAS=∠EAS，AB=AE，可证△ABS≌△AES（SAS），可得∠ABS=∠AES，根据四边形ABCD为菱形，证明A、S、B、D 四点共圆，得出点S在△ABD的外接圆劣弧AB上运动，当AS⊥AB时，DS长最大，∠ADH=90°-∠DAH=30°，AH=3，DH=，点T在以点A为圆3为半径的圆上运动，当点A关于TJ直线的对称点在∠ADH的角平分线DT上时，的值最大，设点A的对称点为G， Rt△AIG中，根据勾股定理即，解得，在Rt△DGH中，根据勾股定理求得DG，可求DT，再证四边形JTLH为矩形，可得JH=TL=，在DL上截取DN=TN，可得∠NDT=∠NTD=15°，得出∠FNL=∠NDT+∠NTD=30°可求DN=TN=2TL，根据在Rt△TNL 中，根据勾股定理NL=，在Rt△AHE中，∠EAH=60°，根据DE=sin60°×AEDE LE=DE-DL=TL求出TE即可．(1)解：过点H作HL⊥EF，交AF于L，∵菱形ABCD，∴∠DAB=180°-，AD∥BC，∴∠DAE=∠AEB，∵，∴∠DAE=15°，∵AE绕点A顺时针旋转60°得AF，∴△AEF为等边三角形，∴∠F=60°，∵HL⊥EF，∴∠HLF=90°-∠F=30°，∴LF=2HF=2×4=8，根据勾股定理，∵∠DAE+∠EAH=∠EAH+∠HAF=60°∴∠DAE=∠HAF=15°，∵∠HLF为△AHL的外角，∴∠AHL=∠HLF-∠HAF=30°-15°=15°，∴∠AHL=∠HAF，∴AL=LH=43，∴AE=AF=AL+LF=43+8；(2)证明：过B作BL⊥AC于L，过F作FK⊥AE于K，设AE=m，AC=n，∵将AE绕点A逆时针旋转60°得AF，∴AE=AF=m，∠EAF=60°，∴△AEF为等边三角形，∴AF=EF，∵FK⊥AE，∴∠AFK=∠EFK=30°，AK=EK=，在Rt△AKF中，，∵菱形ABCD，，BL⊥AC，∴AL=CL=,∠CBL=∠ABL=60°，。

教育精品学习资源 教育精品学习资源 专题16 压轴题 一、选择题 1.（2017贵州遵义第12题）如图，△ABC中，E是BC中点，AD是∠BAC的平分线，EF∥AD交AC于F．若AB=11，AC=15，则FC的长为（ ）

A．11 B．12 C．13 D．14 【答案】C.

考点：平行线的性质；角平分线的性质． 2. （2017湖南株洲第10题）如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ） 教育精品学习资源 教育精品学习资源 A．5 B．4 C．3+2 D．2+2 【答案】D.

考点：旋转的性质；平行线的判定与性质；等腰直角三角形． 3. （2017湖北咸宁第8题）在平面直接坐标系xOy中，将一块含义45角的直角三角板如图放置，直角顶

点C的坐标为)0,1(，顶点A的坐标为)2,0(，顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此点C的对应点C的坐标为（）

A．)0,23( B．)0,2( C. )0,25( D．)0,3( 【答案】C. 教育精品学习资源 教育精品学习资源 将B（3，1）代入y=kx， ∴k=3， ∴y=3x， ∴把y=2代入y=3x， ∴x=32， 当顶点A恰好落在该双曲线上时， 此时点A移动了32个单位长度， ∴C也移动了32个单位长度， 此时点C的对应点C′的坐标为（52，0） 故选C. 教育精品学习资源

《中考压轴题全揭秘》第二辑原创模拟预测题专题36：动态几何之线面动形成的全等、相似三角形存在性问题数学因运动而充满活力，数学因变化而精彩纷呈．动态题是近年来中考的的一个热点问题，以运动的观点探究几何图形的变化规律问题，称之为动态几何问题，随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题，就其运动对象而言，有点动、线动、面动三大类，就其运动形式而言，有轴对称（翻折）、平移、旋转（中心对称、滚动）等，就问题类型而言，有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等．解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况．以动态几何问题为基架而精心设计的考题，可谓璀璨夺目、精彩四射．动态几何形成的存在性问题是动态几何中的基本类型，包括等腰（边）三角形存在问题；直角三角形存在问题；平行四边形存在问题；矩形、菱形、正方形存在问题；梯形存在问题；全等三角形存在问题；相似三角形存在问题；其它存在问题等．本专题原创编写动点形成的全等、相似三角形存在性问题模拟题．在中考压轴题中，线面动形成的全等、相似三角形存在性问题的重点和难点在于应用数形结合的思想准确地进行分类．原创模拟预测题1．已知，如图①，在▱ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM 停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ，MQ，MC，解答下列问题：（1）当t为何值时，PQ∥MN？（2）设△QMC的面积为y（cm2），求y与x之间的函数关系式；（3）是否存在某一时刻t，使S△QMC：S四边形ABQP=1：4？若存在，求出t的值；若不存在，请说明理由．（4）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．原创模拟预测题2．如图1，在△ABC中，∠C=90°，点D在AC上，且CD＞DA，DA=2，点P，Q同时从点D出发，以相同的速度分别沿射线DC、射线DA运动，过点Q作AC的垂线段QR，使QR=PQ，连接PR ，当点Q 到达点A 时，点P ，Q 同时停止运动．设PQ =x ，△PQR 与△ABC 重叠部分的面积为S ，S 关于x 的函数图象如图2所示（其中087x <≤，87x m <≤时，函数的解析式不同）． （1）填空：n 的值为 ；（2）求S 关于x 的函数关系式，并写出x 的取值范围．原创模拟预测题3．如图，在平面直角坐标系中，抛物线23y ax bx =++与x 轴交于A （﹣3，0），B （1，0）两点．与y 轴交于点C ，点D 与点C 关于抛物线的对称轴对称．（1）求抛物线的解析式，并直接写出点D 的坐标；（2）如图1，点P 从点A 出发，以每秒1个单位长度的速度沿A →B 匀速运动，到达点B 时停止运动．以AP 为边作等边△APQ （点Q 在x 轴上方），设点P 在运动过程中，△APQ 与四边形AOCD 重叠部分的面积为S ，点P 的运动时间为t 秒，求S 与t 之间的函数关系式；（3）如图2，连接AC ，在第二象限内存在点M ，使得以M 、O 、A 为顶点的三角形与△AOC 相似．请直接写出所有符合条件的点M 坐标．。