第二章轴对称与轴对称图形的重难点知识树

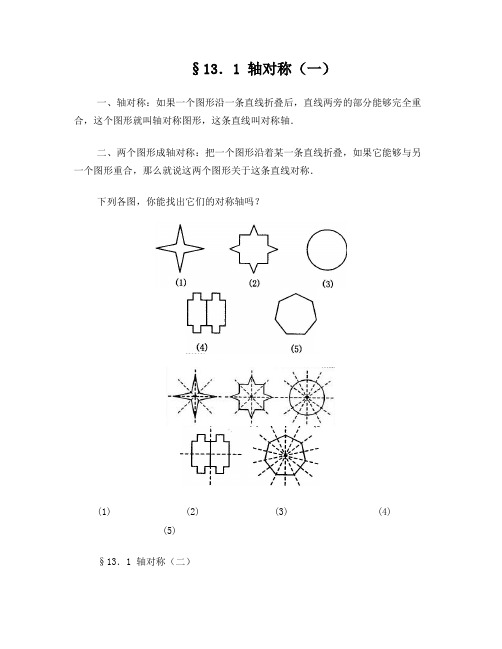
§13．1 轴对称（一）一、轴对称：如果一个图形沿一条直线折叠后，直线两旁的部分能够完全重合，这个图形就叫轴对称图形，这条直线叫对称轴．二、两个图形成轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称．下列各图，你能找出它们的对称轴吗？(1) (2) (3) (4)(5)§13．1 轴对称（二）一、线段垂直平分线的定义：经过线段中点并且垂直于这条线段的直线，叫做线段的垂直平分线．二、图形轴对称的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对称点所连线段的垂直平分线．类似地，轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线．三、线段垂直平分线的性质：线段垂直平分线的点到这条线段两个端点的距离相等；反过来，与这条线段两个端点距离相等的点都在它的垂直平分线上．[探究1]线段垂直平分线上的点与这条线段两个端点的距离相等．即AP1=BP1，AP2=BP2，…证明．证法一：利用判定两个三角形全等．如下图，在△APC和△BPC中，△APC≌△BPCPA=PB.证法二：利用轴对称性质．由于点C是线段AB的中点，将线段AB沿直线L对折，线段PA与PB是重合的，•因此它们也是相等的．[探究2]1.作线段AB，取其中点P，过P作L，在L上取点P1、P2，连结AP1、AP2、BP1、BP2．会有以下两种可能．2．讨论：要使L与AB垂直，AP1、AP2、BP1、BP2应满足什么条件？探究过程：1．如上图甲，若AP1≠BP1，那么沿L将图形折叠后，A与B不可能重合，也就是∠APP1≠∠BPP1，即L与AB不垂直．2．如上图乙，若AP1=BP1，那么沿L将图形折叠后，A与B恰好重合，就有∠APP1=∠BPP1，即L与AB重合．当AP2=BP2时，亦然．§12．2作轴对称图形一．如何由一个平面图形得到它的轴对称图形．【探究】四边形ABCD的四个顶点的坐标分别为A(－5,1)、B(－2,1)、C(－2,5)、D(－5,4)，分别作出与四边形ABCD关于x轴和y轴对称的图形．（归纳：与已知点关于y 轴或x轴对称的点的坐标的规律；）【引申】分别作出△PQR关于直线x=1(记为m)和直线y=－1(记为n)对称的图形，你能发现它们的对应点的坐标之间分别有什么关系吗？若△PQR中P(x,y)关于x=1(记为m)轴对称的点的坐标P(x,y) ，则，y= y．若△PQR中P(x,y)关于y=－1(记为n)轴对称的点的坐标P(x,y) ，则x= x，=n．13．3. 1等腰三角形等腰三角形的定义：有两条边相等的三角形叫做等腰三角形．相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角．同学们在自己作出的等腰三角形中，注明它的腰、底边、顶角和底角．思考：1．等腰三角形是轴对称图形吗？请找出它的对称轴．2．等腰三角形的两底角有什么关系？3．顶角的平分线所在的直线是等腰三角形的对称轴吗？4．底边上的中线所在的直线是等腰三角形的对称轴吗？底边上的高所在的直线呢？结论：等腰三角形是轴对称图形．它的对称轴是顶角的平分线所在的直线．因为等腰三角形的两腰相等，所以把这两条腰重合对折三角形便知：等腰三角形是轴对称图形，它的对称轴是顶角的平分线所在的直线．沿等腰三角形的顶角的平分线对折，发现它两旁的部分互相重合，由此可知这个等腰三角形的两个底角相等，而且还可以知道顶角的平分线既是底边上的中线，也是底边上的高．由此可以得到等腰三角形的性质：1．等腰三角形的两个底角相等（简写成“等边对等角”）．2．等腰三角形的顶角平分线，底边上的中线、•底边上的高互相重合（通常称作“三线合一”）．例题与练习1．如图2其中△ABC是等腰三角形的是 [ ]2．①如图3，已知△ABC中，AB=AC．∠A=36°，则∠C______(根据什么？)．②如图4，已知△ABC中，∠A=36°，∠C=72°，△ABC是______三角形(根据什么？)．③若已知∠A＝36°，∠C＝72°，BD平分∠ABC交AC于D，判断图5中等腰三角形有______．④若已知 AD＝4cm，则BC______cm．3．以问题形式引出推论l______．4．以问题形式引出推论2______．13．3.2等边三角形等边三角形定义：在等腰三角形中，有一种特殊的情况，就是底边与腰相等，这时，三角形三边都相等。

初二数学上册第二章知识点：轴对称初二数学上册第二章知识点：轴对称?一、定义1、如果一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

我们也说这个图形关于这条直线[成轴]对称。

2、把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称。

这条直线叫做对称轴，折叠后重合的点是对应点，叫做对应点。

3、经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

4、有两边相等的三角形叫做等腰三角形。

5、三条边都相等的三角形叫做等边三角形。

二、重点1、把成轴对称的两个图形看成一个整体，它就是一个轴对称图形。

2、把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条轴对称。

3、垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等。

4、垂直平分线的判定：与一条线段两个端点距离相等的点，等腰三角形顶角平分线，底边上的高，底边上的中线到两腰的距离相等。

]8、等腰三角形的判定方法：如果一个三角形有两个角相等，那么这两个角所对的边也相等[等角对等边]。

[如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形。

]9、等边三角形的性质：等边三角形的三个内角都相等，并且每一个角都等于60°。

10、等边三角形的判定：等边三角形的三个内角都相等，并且每一个角都等于60°。

三个角都相等的三角形是等边三角形。

有一个角是60°的等腰三角形是等边三角形。

11、直角三角形的性质之一：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

12、在一个三角形中，如果两条边不等，那么它们所对的角也不等，大边所对的角较大。

三、注意1、(x，y)关于原点对称(-x。

轴对称（一）一、目标认知学习目标：通过具体实例认识轴对称，探索它的基本性质，理解对应点所连的线段被对称轴垂直平分的性质；能按要求作出简单平面图形经过一次或两次轴对称后的图形；探索简单图形之间的轴对称关系，并能指出对称轴；欣赏生活中的轴对称图形，结合现实生活中的典型实例了解并欣赏物体的镜面对称。

重点：1.轴对称概念及有关性质；2.基本图形（如线段、角）的轴对称性3.画和轴对称有关的图形难点：轴对称的性质的探索和掌握。

二、知识要点梳理知识点一：轴对称图形及对称轴要点诠释：如果一个图形沿着一条直线对折，对折的两部分能够完全重合，这样的图形就是轴对称图形。

这条直线叫这个图形的对称轴.知识点二：轴对称及对称点要点诠释：把一个图形沿某条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.知识点三：线段的垂直平分线要点诠释：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

知识点四：轴对称的性质要点诠释：1.如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

2.轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

知识点五：线段垂直平分线的性质要点诠释：线段垂直平分线上的点与这条线段两个端点的距离相等。

知识点六：点在线段垂直平分线上的判定要点诠释：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

三、规律方法指导1．由一个平面图形得到它的轴对称图形叫做轴对称变换．•成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到．2．轴对称变换的性质：（1）经过轴对称变换得到的图形与原图形的形状、大小完全一样（2）经过轴对称变换得到的图形上的每一点都是原图形上的某一点关于对称轴的对称点．（3）连接任意一对对应点的线段被对称轴垂直平分．3．作一个图形关于某条直线的轴对称图形的步骤：（1）作出一些关键点或特殊点的对称点．（2）按原图形的连接方式连接所得到的对称点，即得到原图形的轴对称图形．4．点P（x，y）关于x轴对称的点的坐标是（x，-y）；点P（x，y）关于y轴对称的点的坐标是（-x，y）；点P（x，y）关于原点对称的点的坐标是（-x，-y）．5．点P（x，y）关于直线x=m对称的点的坐标是（2m-x，y）；点P（x，y）关于直线y=n对称的点的坐标是（x，2n-y）；轴对称经典例题透析类型一：最短路程问题1、在锐角∠AOB内有一定点P，试在OA、OB上确定两点C、D，使△PCD的周长最短．思路点拨:△PCD的周长等于PC+CD+PD，要使△PCD的周长最短，•根据两点之间线段最短，只需使得PC+CD+PD的大小等于某两点之间的距离，于是考虑作点P关于直线OA•和OB的对称点E、F，则△PCD的周长等于线段EF的长．举一反三：【变式1】草原上两个居民点A、B在河流a的同旁，一汽车从A出发到B，途中需要到河边加水。

轴对称知识点汇总轴对称知识在数学中是一个常考点，那么应该掌握的知识又有什么呢?下面轴对称知识点汇总是小编为大家带来的，希望对大家有所帮助。

轴对称知识点汇总一、轴对称与轴对称图形：1.轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，两个图形中的对应点叫做对称点，对应线段叫做对称线段。

2.轴对称图形：如果一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴。

注意：对称轴是直线而不是线段3.轴对称的性质：(1)关于某条直线对称的两个图形是全等形;(2)如果两个图形关于某条直线对称，那么对称轴是对应点连线的垂直平分线;(3)两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上;(4)如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

4.线段垂直平分线：(1)定义：垂直平分一条线段的直线是这条线的垂直平分线。

(2)性质：①线段垂直平分线上的点到这条线段两个端点的距离相等;②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

注意：根据线段垂直平分线的这一特性可以推出：三角形三边的垂直平分线交于一点，并且这一点到三个顶点的距离相等。

5.角的平分线：(1)定义：把一个角分成两个相等的角的射线叫做角的平分线.(2)性质：①在角的平分线上的点到这个角的两边的距离相等.②到一个角的两边距离相等的点，在这个角的平分线上.注意：根据角平分线的性质，三角形的三个内角的平分线交于一点，并且这一点到三条边的距离相等.6.等腰三角形的性质与判定：性质：(1)对称性：等腰三角形是轴对称图形，等腰三角形底边上的中线所在的直线是它的对称轴，或底边上的高所在的直线是它的对称轴，或顶角的平分线所在的直线是它的对称轴;(2)三线合一：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合;(3)等边对等角：等腰三角形的两个底角相等。

《轴对称》知识点总结及章节检测解析一、知识点总结：1.轴对称的定义：如果一个图形经过其中一条直线折叠后，能够与自身完全重合，则这条直线被称为这个图形的轴对称线，这个图形是轴对称的。

2.旋转对称：如果一个图形能够围绕其中一点旋转一定的角度后，能够与自身完全重合，则这个图形是旋转对称的。

3.轴对称图形的特点：轴对称图形的特点是，对称轴两侧的各点关于对称轴对应，即对称轴上的一点与对应点互为图形的对称点。

4.轴对称的判定方法：判断一个图形是否为轴对称图形，可以按照以下方式进行判定：(1)观察是否能找到一个或多个对称轴；(2)沿对称轴将图形折叠，看是否能够重合。

5.制作轴对称图形：制作一个轴对称图形可按照以下步骤进行：(1)在纸上画出一条轴对称线；(2)沿着对称线将图形的一边折叠；(3)检查折叠后的图形与未折叠的图形是否重合，如重合则完成。

二、章节检测解析：以小学三年级数学教材为例，进行《轴对称》的章节检测解析。

教材章节：第三章图形与设计1.知识点掌握情况：首先，学生需要了解轴对称的概念、特点和判定方法，并能够制作轴对称图形。

2.基础练习题：对于基础的练习题，要求学生绘制给定图形的对称线，并判断是否为轴对称图形。

3.综合应用题：在综合应用题中，要求学生设计自己的轴对称图形，并描述其特点。

4.拓展思考题：为了拓展学生的思维，可以提出一些拓展思考题，如“如何判断一个图形是否为旋转对称图形”、“如何找到一个图形的所有对称轴”等。

总结：通过针对《轴对称》这一章节的检测解析，学生可以对轴对称的知识点进行复习和巩固。

同时，综合应用题和拓展思考题能够提高学生的思维能力和创造力。

初二数学上册第二章知识总结：轴对称学习是一个边学新知识边巩固的过程，对学过的知识一定要多加练习，如此才能进步。

因此，精品编辑老师为大伙儿整理了初二数学上册第二章知识总结，供大伙儿参考。

一、定义1、假如一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，那个图形就叫做轴对称图形。

这条直线确实是它的对称轴。

我们也说那个图形关于这条直线[成轴]对称。

2、把一个图形沿着某一条直线折叠，假如它能够与另一个图形重合，那么就说这两个图形关于这条直线对称。

这条直线叫做对称轴，折叠后重合的点是对应点，叫做对应点。

3、通过线段中点同时垂直于这条线段的直线，叫做这条线段的垂直平分线。

假如两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

4、有两边相等的三角形叫做等腰三角形。

5、三条边都相等的三角形叫做等边三角形。

二、重点1、把成轴对称的两个图形看成一个整体，它确实是一个轴对称图形。

2、把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条轴对称。

3、垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等。

4、垂直平分线的判定：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

5、如何做对称轴：假如两个图形成轴对称，其对称轴确实是任何一对对应点所连线段的垂直平分线。

因此，我们只要找到一对再对应点，作出连接它们的线段的垂直平分线就能够得到那个图形的对称轴。

同样，关于轴对称图形，只要找到任意一组对应点所连线段的垂直平分线，就得到此图形的对称轴。

6、轴对称图形的性质：对称轴方向和位置发生变化时，得到的图形的方向和位置也会发生变化。

由个平面图形能够得到它关于一条直线成轴对称的图形，那个图形与原图形的形状，大小完全相等。

新图形上的每一点，差不多上原图形上的某一点关于直线的对称点。

连接任意一对对应点的线段被对称轴垂直平分。

7、等腰三角形的性质：等腰三角形的两个底角相等[等边对等角]等腰三角形的顶角平分线，底边上的中线，底边上的高相互重合[三线合一][等腰三角形是轴对称图形，底边上的中线(，底边上的高，顶角平分线)所在直线确实是它的对称轴。

知识归纳：轴对称和轴对称图形
轴对称
1、一个图形沿着某一条直线折叠，如果直线两侧的图形能够重合，就说这一个图形是轴对称图形。

这条直线叫做图形的对称轴。

2、轴对称图形一定有对称轴，而且至少有1条对称轴，常见的例如：等腰三角形、等腰梯形、线段、角；有两条对称轴的常见图形有长方形；有三条对称轴的常见图形有等边三角形；正方形有4条对称轴；五角星和正五边形有5条对称轴；圆有无数条对称轴。

轴对称图形的画法
1、轴对称图形的性质：
（1）对称轴两边的图形一定完全相同
（2）对应点也关于对称轴对称
（3）对应点的连线垂直于对称轴
（4）对应点到对称轴的距离相等
2、轴对称图形的画法：
（1）根据题意确定已知图形以及对称轴位置
（2）找出已知图形的关键点
（3）一次过每个点作垂直于对称轴的虚线
（4）在对称轴另一侧确定各对应点位置
（5）标明各点对应名称，顺次连接各对应点得到轴对称图形。

确定轴对称图形的对称轴
沿某条直线对折之后，两边的图形能够完全重叠，这条直线就是
图形的对称轴。

轴对称和成轴对称。

初二数学上册第二章知识总结：轴对称初二数学上册第二章知识总结：轴对称学习是一个边学新知识边巩固的过程，对学过的知识一定要多加练习，这样才能进步。

因此，精品编辑老师为大家整理了初二数学上册第二章知识总结，供大家参考。

一、定义1、如果一个图形沿着一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

我们也说这个图形关于这条直线[成轴]对称。

2、把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称。

这条直线叫做对称轴，折叠后重合的点是对应点，叫做对应点。

3、经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

4、有两边相等的三角形叫做等腰三角形。

5、三条边都相等的三角形叫做等边三角形。

二、重点1、把成轴对称的两个图形看成一个整体，它就是一个轴对称图形。

2、把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条轴对称。

等腰三角形两底角平分线相等。

等腰三角形底边上高的点到两腰的距离之和等于底角到一腰的距离。

等腰三角形顶角平分线，底边上的高，底边上的中线到两腰的距离相等。

]8、等腰三角形的判定方法：如果一个三角形有两个角相等，那么这两个角所对的边也相等[等角对等边]。

[如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形。

]9、等边三角形的性质：等边三角形的三个内角都相等，并且每一个角都等于60。

10、等边三角形的判定：等边三角形的三个内角都相等，并且每一个角都等于60。

三个角都相等的三角形是等边三角形。

有一个角是60的等腰三角形是等边三角形。

11、直角三角形的性质之一：在直角三角形中，如果一个锐角等于30，那么它所对的直角边等于斜边的一半。

12、在一个三角形中，如果两条边不等，那么它们所对的角也不等，大边所对的角较大。