吊车梁最大弯矩的计算器编程辅助计算_胡雅琪
- 格式:pdf
- 大小:474.17 KB
- 文档页数:2

移动荷载作用下主梁绝对最大弯矩的计算摘要:在设计起重机梁等承受移动荷载的结构时,利用内力包络图可以求的在横荷载和移动活荷载共同作用下各杆件、各截面可能出现的最大内力、最小内力。
其中弯矩包络图表示各截面的最大弯矩值,其中弯矩最大者称为绝对最大弯矩。
我们已经学习了简支梁绝对最大弯矩的求法,那么主梁在移动荷载作用下绝对最大弯矩的求法是怎样的呢?本文根据简支梁绝对最大弯矩的求法,给出了一组平行荷载直接沿着纵梁移动时,主梁承受结点荷载作用下绝对最大弯矩的计算方法。
关键词:结点荷载,绝对最大弯矩,主梁,影响线桥梁或房屋建筑中的某些主梁,是通过一些次梁(纵梁和横梁)将荷载传递到主梁上的。
主梁这些荷载的传递点称为主梁的结点。
从移动荷载来说,不论是荷载作用在次梁的哪些位置,其作用都是通过这些固定的结点传递到主梁上。
如下图所示:本文研究的主要问题是一组平行荷载直接沿着纵梁移动时怎样判断主梁绝对最大弯矩的发生的截面位置和计算主梁的绝对最大弯矩(假定相邻两横梁间的距离、节间距是相等的)。
1.主梁绝对最大弯矩的发生截面位置回想我们学过的简支梁,有两种计算方法。
一种是近似计算,划分30个以上等分截面,画出梁的弯矩包络图,采取电算的方法。
另一种是精确计算,也是最常用的方法。
它的求法是:由于荷载在任一位置时,梁的弯矩图顶点永远发生在集中荷载下。
因此可以断定,绝对最大弯矩必定发生在某一集中何在的作用点。
取一集中荷载Fpcr,它的弯矩为:FR为梁上实际荷载的合力,Mcr为FPcr 以左梁上实际荷载对FPcr作用点的力矩,a为FR 与FPcr 作用线之间的距离。
经分析可得,Fpcr作用点弯矩最大时,梁的中线正好平分Fpcr与FR之间的距离。
如下图所示:比较各个荷载作用点的最大弯矩,选择其中最大的一个,就是绝对最大弯矩。
与简支梁类似,当一组平行荷载直接沿着纵梁移动时,主梁在任意时刻的弯矩图总是呈折线图形,弯矩图的顶点永远位于集中荷载作用点,也就是各结点截面。
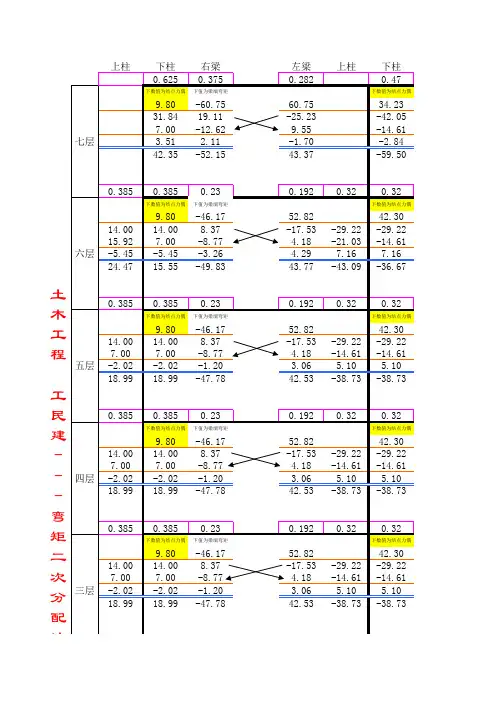
土木工程
工民建---弯矩二次分配法计
算
在计算竖向恒载和活载作用下框架结构弯矩时要多次使用弯矩二次分配法,此表为恒载作用输入每一层的各节点梁柱分配系数和各节点固端弯矩,即可自动计算生成所有其他数据,注据,否则公式被取消了就无法得出正确结果!!!!(计算的各节点最终弯矩代数和均为0,
图5-29 恒载作用下的
次分配法计算器
配法,此表为恒载作用下12轴线框架的计算过程,如果大家也是三跨的梁可以参用这个计算器,自动计算生成所有其他数据,注意千万不要改动了表上除各节点梁柱分配系数和各节点固端弯矩以外的数的各节点最终弯矩代数和均为0,有的为0.01的是因为四舍五入造成的)
作用下的框架弯矩内力二次分配图
-31.84 -11.39 -0.77
-22.77 -11.39 6.51
-22.77 -11.39 4.77
-22.77 -11.39 4.77
-22.77 -11.39 4.77
-22.77
-12.36
5.14
-19.58
0.08以参用这个计算器,点固端弯矩以外的数。
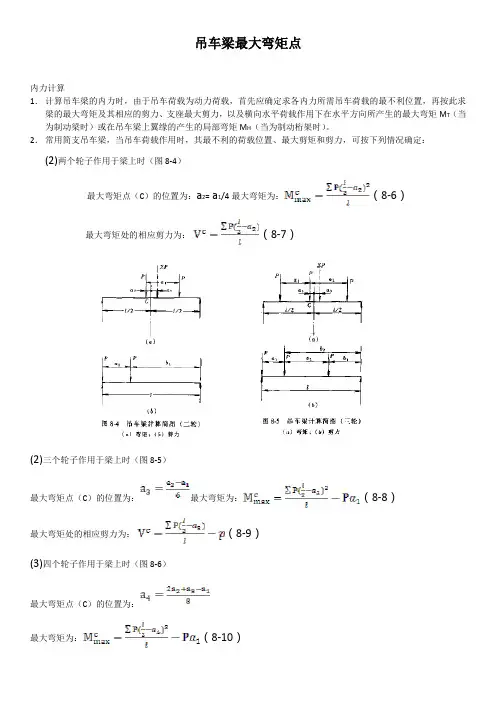
吊车梁最大弯矩点内力计算1.计算吊车梁的内力时,由于吊车荷载为动力荷载,首先应确定求各内力所需吊车荷载的最不利位置,再按此求梁的最大弯矩及其相应的剪力、支座最大剪力,以及横向水平荷载作用下在水平方向所产生的最大弯矩M T(当为制动梁时)或在吊车梁上翼缘的产生的局部弯矩M H(当为制动桁架时)。
2.常用简支吊车梁,当吊车荷载作用时,其最不利的荷载位置、最大剪矩和剪力,可按下列情况确定:(2)两个轮子作用于梁上时(图8-4)最大弯矩点(C)的位置为:a2= a1/4最大弯矩为:(8-6)最大弯矩处的相应剪力为:(8-7)(2)三个轮子作用于梁上时(图8-5)最大弯矩点(C)的位置为:最大弯矩为:(8-8)最大弯矩处的相应剪力为:(8-9)(3)四个轮子作用于梁上时(图8-6)最大弯矩点(C)的位置为:最大弯矩为:(8-10)最大弯矩处的相应剪力为:(8-11)当时最大弯矩及其相应剪力均与公式(8-10)及公式(8-11)相同,但公式中的应用代入(4)六个轮子作用于梁上时(图8-7):最大弯矩点(C)的位置为:最大弯矩为:(8-12)最大弯矩处的相应剪力为:(8-13)当及时,最大弯矩点(C点)的位置为:其最大弯矩及相应剪力均与公式(8-12)及公式(8-13)相同,但公式中的应用代入(5)最大剪力应在梁端支座处。
因此,吊车竖向荷载应尽可能靠近该支座布置(图8-4b)至图8-7b),并按下式计算支座最大剪力:(8-14)式中n—作用于梁上的吊车竖向荷载数。
选择吊车梁截面时所用的最大弯矩和支座最大剪力,可用吊车竖向荷载作用下所产生的最大弯矩和支座最大剪力乘以表8-2的(为考虑吊车梁等自重的影响系数)值,即(8-15)(8-16)3.吊车横向水平荷载作用下,在水平方向所产生的最大弯矩,可根据图8-4(a)至图8-7(a)所示荷载位置采用下列公式计算:当为轻、中工作制(A1-A5)吊车梁的制动梁时,(8-17)当为重级或特重级工作制(A6-A8)吊车梁的制动梁时,(8-18)(2)吊车横向水平荷载作用下制动桁架在吊车梁翼缘所产生的局部弯矩可近似地按下列公式计算(图8-8):当为起重量Q≥75t的轻、中级工作制吊车的制动桁架时(8-19)当为起重量Q≥75t的重级工作制(特重级不受起重量限制)吊车的制动桁架时(8-20)当为起重量Q≤50t的轻、中级工作制吊车的制动桁架时(8-21)当为起重量Q≤50t的重级工作制(特重级不受起重量限制)吊车的制动桁架时(8-22)。

移动荷载作用下主梁绝对最大弯矩的计算摘要:在设计起重机梁等承受移动荷载的结构时,利用内力包络图可以求的在横荷载和移动活荷载共同作用下各杆件、各截面可能出现的最大内力、最小内力。
其中弯矩包络图表示各截面的最大弯矩值,其中弯矩最大者称为绝对最大弯矩。
我们已经学习了简支梁绝对最大弯矩的求法,那么主梁在移动荷载作用下绝对最大弯矩的求法是怎样的呢?本文根据简支梁绝对最大弯矩的求法,给出了一组平行荷载直接沿着纵梁移动时,主梁承受结点荷载作用下绝对最大弯矩的计算方法。
关键词:结点荷载,绝对最大弯矩,主梁,影响线桥梁或房屋建筑中的某些主梁,是通过一些次梁(纵梁和横梁)将荷载传递到主梁上的。
主梁这些荷载的传递点称为主梁的结点。
从移动荷载来说,不论是荷载作用在次梁的哪些位置,其作用都是通过这些固定的结点传递到主梁上。
如下图所示:本文研究的主要问题是一组平行荷载直接沿着纵梁移动时怎样判断主梁绝对最大弯矩的发生的截面位置和计算主梁的绝对最大弯矩(假定相邻两横梁间的距离、节间距是相等的)。
1.主梁绝对最大弯矩的发生截面位置回想我们学过的简支梁,有两种计算方法。
一种是近似计算,划分30个以上等分截面,画出梁的弯矩包络图,采取电算的方法。
另一种是精确计算,也是最常用的方法。
它的求法是:由于荷载在任一位置时,梁的弯矩图顶点永远发生在集中荷载下。
因此可以断定,绝对最大弯矩必定发生在某一集中何在的作用点。
取一集中荷载F pcr ,它的弯矩为:F R 为梁上实际荷载的合力,M cr 为F Pcr 以左梁上实际荷载对F Pcr 作用点的力矩,a 为F R 与 F Pcr 作用线之间的距离。
经分析可得,F pcr 作用点弯矩最大时,梁的中线正好平分F pcr 与F R 之间的距离。
如下图所cr R cr yA M x La x L F M x F M ---=-=示:比较各个荷载作用点的最大弯矩,选择其中最大的一个,就是绝对最大弯矩。
与简支梁类似,当一组平行荷载直接沿着纵梁移动时,主梁在任意时刻的弯矩图总是呈折线图形,弯矩图的顶点永远位于集中荷载作用点,也就是各结点截面。

吊车梁最大弯矩引言吊车梁是用于起吊和搬运重物的工程机械设备,在工地和港口等场所被广泛使用。
在设计吊车梁时,需要考虑到各种力的作用,其中最大弯矩是一个重要的参数。
本文将介绍吊车梁最大弯矩的概念、计算方法和影响因素。
概念吊车梁最大弯矩是指吊车梁在使用过程中所能承受的最大弯曲力矩。
当吊车梁承受的力矩超过其所能承受的最大弯矩时,就会发生弯曲变形或破坏。
计算方法吊车梁最大弯矩的计算需要考虑各种加载情况,包括静态加载和动态加载。
以下是一些常见的计算方法:1.静态加载:当吊车梁处于静止状态时,可以使用静力学方法进行计算。
根据支持条件和施加载荷,可以通过应力和变形分析确定吊车梁的最大弯矩。
常用的方法包括叠加法、力矩法和三力共点法。
2.动态加载:当吊车梁处于运动状态时,需要考虑动力学效应。
除了考虑物体的重力外,还需要考虑各种运动和惯性力。
常见的方法包括动力学分析和有限元分析。
无论是静态加载还是动态加载,吊车梁的材料属性和几何形状都会对最大弯矩产生影响。
因此,在计算吊车梁最大弯矩时,需要准确地了解吊车梁的材料特性和结构参数。
影响因素吊车梁最大弯矩的大小受到许多因素的影响,包括但不限于以下几点:1.载荷重量:吊车梁所承受的物体重量是影响最大弯矩大小的关键因素。
当物体重量增加时,吊车梁所受弯矩也随之增加。
2.吊车梁的长度和截面形状:吊车梁的长度和截面形状会直接影响吊车梁的刚度和强度。
通常情况下,吊车梁越长,其最大弯矩也会越大。
而且,吊车梁的截面形状也会影响其抗弯能力,如梁的高度、宽度和厚度等。
3.材料特性:吊车梁所使用的材料的特性也会对最大弯矩产生影响。
材料的弹性模量、屈服强度和断裂韧性等都会影响吊车梁的强度和刚度。
4.支持条件:吊车梁的支持条件会对其最大弯矩和变形产生影响。
不同的支持方式,如简支、固定支承或悬臂支承等,会导致不同的弯矩分布和变形形态。
除了以上因素,环境条件如温度、湿度和风荷载等也会对吊车梁的最大弯矩产生一定影响。

2022年注册结构工程师《专业考试二级》上午真题2022年注册结构工程师《专业考试二级》上午真题单选题(共25题,共25分)1.某普通钢筋混凝土等截面连续梁,结构设计使用年限为50年,安全等级为二级,其计算简图和支座B左侧边缘(1—1)截面处的配筋示意如题~3图所示。
混凝土强度等级C35,钢筋HRB400,梁截面b×h =300mm×650mm。
假定,作用在梁上的永久均布荷载标准qGk=15kN/m(包括自重),AB段可变均布荷载标准值qLK1=18kN/m,可变集中荷载标准值Pk =200kN,BD段可变均布荷载标准值qLk2=25kN/m。
试问,支座B 处梁的最大弯矩设计值MB(kN·m),与下列何项数值最为接近?()提示:永久荷载与可变荷载的荷载分项系数分别取1.3、1.5。
A.360B.380C.400D.4202.某普通办公楼为钢筋混凝土框架结构,楼盖为梁板承重体系,其楼层平面及剖面如如图所示。
屋面为不上人屋面,隔墙均为固定隔墙,假定二次装修荷载作为永久荷载考虑。
试问,当设计柱KZ1时,考虑活荷载折减,在第三层柱顶1—1截面处,由楼面荷载产生的柱轴力标准值Nk的最小取值(kN),与下列何项数值最为接近?()如图提示:柱轴力仅按柱网尺寸对应的负荷面积计算。
A.140B.150C.180D.2103.某六层钢筋混凝土框架结构,抗震等级为三级,结构层高3.9m,所有框架梁顶均与楼板面平。
假定,其中某框架柱混凝土强度等级为C40,轴压0.7,箍筋的保护层厚度c=20mm,截面及配筋如如图所示,与柱顶相连的框架梁的截面高度为850mm,框架柱在地震组合下的反弯点在柱净高中部。
试问下列表述何项正确?()提示:按《混凝土结构设计规范》(GB 50010—2022)(2022年版)作答,体积配箍率计算时不考虑重叠部分箍筋。
A.该框架柱的体积配箍率为0.96%,箍筋配置满足《混凝土结构设计规范》(GB 50010—2022)(2022年版)的构造要求B.该框架柱的体积配箍率为1.11%,箍筋配置满足《混凝土结构设计规范》(GB 50010—2022)(2022年版)的构造要求C.该框架柱的体积配箍率为0.96%,箍筋配置不满足《混凝土结构设计规范》(GB 50010—2022)(2022年版)的构造要求D.该框架柱的体积配箍率为1.11%,箍筋配置不满足《混凝土结构设计规范》(GB 50010—2022)(2022年版)的构造要求4.某五层现浇钢筋混凝土框架结构,双向柱距均为8.1m,房屋总高度18.3m。

吊车梁最大弯矩引言吊车梁是一种常见的工业设备,用于吊装和搬运重物。
在使用吊车梁时,了解吊车梁的最大弯矩是非常重要的,它可以帮助我们评估吊车梁的承载能力和使用限制。
本文将介绍什么是吊车梁的最大弯矩,以及如何计算和应用这个参数。
什么是吊车梁最大弯矩吊车梁最大弯矩是指吊车梁在承受重物吊装过程中,材料受到曲线形变的最大程度。
在吊车梁的设计过程中,工程师需要考虑到最大弯矩,以确保吊车梁具备足够的强度和刚度来承受所需的载荷。
如何计算吊车梁的最大弯矩计算吊车梁的最大弯矩通常需要考虑以下几个因素:1. 负载吊车梁的最大弯矩与所搬运的负载有直接的关系。
负载的重量和形状将影响吊车梁的受力情况。
需要确定负载的重量、尺寸和形状,并考虑重心位置。
2. 吊杆长度和支撑方式吊车梁的长度和支撑方式也会影响最大弯矩的计算。
通常来说,吊车梁越长,承载能力越低。
吊车梁的支撑方式(如悬臂或固定支撑)也会对最大弯矩产生影响。
3. 材料的性能吊车梁所使用的材料也是计算最大弯矩的重要因素之一。
不同材料具有不同的力学性能,包括弹性模量、屈服强度和弯曲强度等。
材料的性能参数将用于计算吊车梁的最大弯矩。
4. 弯曲分布吊车梁在受到负载作用时,会发生弯曲。
弯曲分布是指吊车梁上不同位置的弯曲程度。
通常,最大弯矩发生在负载的重心位置。
在实际计算中,可以利用以下公式来计算吊车梁的最大弯矩:M = (W * L^2) / (8 * S)其中,M表示最大弯矩,W表示负载的重量,L表示吊杆的长度,S表示材料的抗弯承载力。
吊车梁最大弯矩的应用了解吊车梁的最大弯矩对于工程师和操作人员来说都是非常重要的。
它可以帮助我们评估吊车梁的承载能力,确定最大负载能力和操作限制。
如果超过了吊车梁的最大弯矩,可能会导致吊车梁的破坏或事故发生。
因此,在吊装作业中,必须根据吊车梁的最大弯矩选择适当的吊装设备和工艺。
此外,吊车梁的最大弯矩还可以用于吊装过程中的安全措施。
通过合理计算和设定最大弯矩的警戒线,在操作过程中及时监测和预警吊车梁的受力情况。

一台吊车(两个轮子)吊车梁计算1.输入吊车参数跨度(mm)轮压P(t)轮距(mm)车宽(mm)P设计值800016.550006330245.0798起重量Q小车重g水平荷载T2T弯矩Mt103 5.3562610.7125210126.682.输入截面参数上翼缘B1上翼缘t1下翼缘B2下翼缘t2腹板ho腹板tw螺孔位置ao 32012200124766903.强度验算Af1n Af2n Awn An3324240028568580中和轴yn Ixn Wxn1Wxn2Iyn1Wyn1fy正应力1 223.72313887848621737795140722928588400178677.5235323.3094.整体稳定验算Af1Af2Aw面积A3840240028569096中和轴y Ix Wx1Wx2Iy Wy iy211.372411857405194849514269494076800025480066.94752I1I2eitaB kesi beitaB lambdaY faiB faiB1 3276800080000000.4860280.60.838119.49660.9939590.7612395.挠度验算挠度 mm v/L24.9661320.43448两台吊车(三个轮子)吊车梁计算跨度L轮压P1轮压P2轮距a1轮距a2车宽B1车宽B2a1 6000 3.767.32500300030003500500起重量Q1起重量Q2小车重g1小车重g2水平刹车T1水平刹车T2弯矩Mt 5101 1.5 2.47212 4.7382310748.37上翼缘B1上翼缘t1下翼缘B2下翼缘t2腹板ho腹板tw螺孔位置ao 3001220012476890Af1n Af2n Awn An3072240038089280中和轴yn Ixn Wxn1Wxn2Iyn1Wyn1fy正应力1 232.3313947839641699230147489622723200151488235215.7027Af1Af2Aw A3600240038089808中和轴y Ix Wx1Wx2Iy Wy iy220.14684203751061909522150212735000000233333.359.73705I1I2eitaB kesi beitaB lambdaY faiB faib1 2700000080000000.4342860.480.8164100.4402 1.4136680.847275挠度v/L7.303707821.50068两台吊车(四个轮子)吊车梁计算跨度L轮压P1轮压P2轮距a1轮距a2车宽B1车宽B2a3 6000 3.767.32500300030003500500起重量Q1起重量Q2小车重g1小车重g2水平刹车T1水平刹车T22T1+2T2 5101 1.5 2.47212 4.7382314.4207上翼缘B1上翼缘t1下翼缘B2下翼缘t2腹板ho腹板tw螺孔位置ao 3001220012476890Af1n Af2n Awn An3072240038089280中和轴yn Ixn Wxn1Wxn2Iyn1Wyn1fy正应力1 232.3313947839641699230147489622723200151488235205.9632Af1Af2Aw面积A3600240038089808中和轴y Ix Wx1Wx2Iy Wy iy220.14684203751061909522150212735000000233333.359.73705I1I2eitaB kesi beitaB lambdaY faiB faib1 2700000080000000.4342860.480.8164100.4402 1.4136680.847275挠度v/L6.965991861.327592P ao弯矩(Nm)剪力(kN)490.15962500463354336.9847孔径do梁高h21.5500正应力2剪应力329.267176.9878正应力1352.1305P1设计值P2设计值P1+2P2a0弯矩M剪力V 55.84849108.4292272.7071090.414245964.9200.4208孔径do h22500正应力2剪应力166.767678.94727正应力1198.0927P1设计值P2设计值2P1+2P2ao弯矩M(Nm)剪力V(kN) 55.84849108.4292328.5555-395.118234591.7142.6414ao Mt-385.71410286.89孔径do梁高h22500正应力2剪应力159.056456.18752正应力1189.0853。

第7章辅助计算工具辅助计算工具灵活、方便、实用,专业性强,功能强大。
它的成功开发和推出,必将使用户的设计效率大为提高。
其主要功能如下:1、矩形截面配筋及裂缝计算2、圆形截面配筋及裂缝计算3、I型或T型截面配筋及裂缝计算4、单排桩墩顶位移计算5、简支结构布载计算6、群桩计算7、土中最大弯矩计算8、桩长计算9、螺旋箍筋长度计算10、浏览钢筋外径、内径、每米重数据表11、浏览钢筋长度折减表12、直+缓+圆+缓+直的线形附近计算点的大地坐标和高程计算13、桥下通航控制高程拉坡计算7.1矩形截面配筋及裂缝计算打开桥梁通主菜单的“辅助工具”下拉式菜单“截面配筋计算及验算”的“矩形截面配筋计算”,选择并弹出“矩形截面配筋计算”数据输入窗体,根据提示输入矩形截面配筋计算的基本数据,数据输入完毕点击“配筋计算”按钮,窗体右下方马上显示其计算结果。
受力方式:纯弯构件或压弯构件。
设计方式:单筋设计、双筋设计或上下钢筋面积不等。
设计或验算:计算钢筋面积或验算截面强度。
截面抗弯弯矩、截面抗弯轴压力:应计入荷载安全系数,计算钢筋面积使用。
截面抗裂弯矩、截面抗裂轴压力:不计荷载安全系数,计算裂缝值使用。
内力提高系数:取1。
裂缝系数C2:计算裂缝用的C2值。
数据组选择框:用户可以点击任意一组数据进行数据的输入或修改。
当快速双击任意一组数据,弹出对话框,选择其他一组数据可将其数据调入修改。
浏览计算结果:点击“浏览打印”按钮,即可浏览计算结果,再点击“打印按钮”,计算结果可通过打印机输出。
注意:系统提供了六数据组~十数据组的数据,分别对应【结构设计原理】第56页例3-1单筋设计、第62页例3-4B、第124页例7-1单筋设计、第125页例7-3A受压钢筋受力并计算受拉钢筋根数、第131页例7-6双筋设计等考题数据。
7.2圆形截面配筋及裂缝计算打开桥梁通主菜单的“辅助工具”下拉式菜单的“截面配筋计算及验算”,选择并弹出“圆形截面配筋计算”数据输入窗体,根据提示输入圆形截面配筋计算的基本数据,数据输入完毕点击“配筋计算”,窗体的右下方马上显示其计算结果。

吊车梁最大弯矩引言在建筑和工程行业中,吊车梁被广泛应用于货物的运输和搬运。
吊车梁在承载重物的过程中承受着巨大的力和压力。
了解吊车梁的最大弯矩是设计和使用吊车梁的关键因素之一。
本文将介绍吊车梁最大弯矩的概念、计算方法以及影响吊车梁最大弯矩的因素。
吊车梁最大弯矩的概念吊车梁最大弯矩是指吊车梁在受力作用下所承受的最大弯曲力矩。
弯矩是指物体在受力作用下发生弯曲时两个端点或受力点之间产生的力矩。
对于吊车梁来说,最大弯矩通常发生在吊梁两端点之间。
吊车梁最大弯矩的计算方法吊车梁最大弯矩的计算涉及到结构力学的知识。
一般来说,可以使用以下公式来计算吊车梁最大弯矩:M = W * L / 4其中,M是吊车梁的最大弯矩,W是吊车梁所承受的重力或外力的大小,L是吊车梁的长度。
这个公式适用于简单的悬挑梁和梁的均布载荷情况。
如果吊车梁存在复杂的载荷分布或结构形状,可以使用更复杂的计算方法来确定吊车梁的最大弯矩。
影响吊车梁最大弯矩的因素吊车梁的最大弯矩不仅与承受的载荷有关,还受到以下几个因素的影响:1. 材料强度吊车梁的材料强度是指其在受力作用下能够承受的最大力。
材料的强度越高,吊车梁的最大弯矩也就越大。
2. 吊车梁的截面形状吊车梁的截面形状对其最大弯矩有影响。
一般来说,截面形状越大,吊车梁的最大弯矩也就越大。
3. 吊车梁的长度吊车梁的长度越长,其最大弯矩也会相应增大。
4. 载荷分布吊车梁所承受的载荷分布也会对其最大弯矩产生影响。
如果载荷不均匀分布在吊车梁上,可能会导致某些部分承受更大的力,从而使最大弯矩增大。
结论吊车梁最大弯矩是设计和使用吊车梁时需要考虑的重要参数之一。
了解吊车梁最大弯矩的计算方法和影响因素有助于确保吊车梁的安全和稳定性。
应根据实际情况选择合适的材料和结构形状,并合理考虑载荷分布,以确保吊车梁能够承受所需的最大负载。

吊吊车车梁梁计计算算书书一. 设计资料吊车情况:1台吊车;编号:3 工作制:轻级, 吊钩形式: 硬钩;起重量:Q=20吨,小车重:g=1吨;最大轮压:P max =100千牛最小轮压:P min =20千牛吊车一侧的轮数:n=2个吊车轮子间间距:a 1=3m钢材类型:Q235B支座类型:平板式;吊车梁跨度:L=6m吊车梁计算长度:L y =6m轨道高度:0.14允许挠度比:1/600=0.001667二. 设计荷载和内力考虑轨道重量及吊车梁自重的增大系数:1.02动力系数:1.05;max 1P P Q γα=竖向荷载标准值:P=1.02×1.05×100=107.1千牛竖向荷载设计值:P=1.4×107.1=149.94千牛 10201⨯+=n Q Q T η 横向荷载标准值:T=0.1×(200+10)/2=10.5千牛横向荷载设计值:T=1.4×10.5=14.7千牛吊车梁的最大竖向设计弯矩: ()L a L P M 420-∑= M max =253.024千牛·米吊车梁的最大竖向设计弯矩处相应的设计剪力:V=112.455千牛 吊车梁端支座处的最大设计剪力: ⎪⎭⎫ ⎝⎛-+=L a P P V 1211 V max =224.91千牛吊车梁的最大水平设计弯矩:M t =24.806千牛·米三. 截面特性吊车梁高度h=56cm腹板厚度t=1.2cm上翼缘宽度b f =32cm上翼缘厚度t f =1.4cm下翼缘宽度b f1=32cm下翼缘厚度t f1=1.4cm吊车梁面积A=153.44cm 2;吊车梁X 轴惯性矩I x =81849.495cm 4;吊车梁Y 轴惯性矩I y =7653.527cm 4;吊车梁X 轴抵抗矩W x =2923.196cm 3;吊车梁Y 轴抵抗矩W y =478.345cm 3;吊车梁X 轴转动惯量r x =23.096cm;吊车梁Y 轴转动惯量r y =7.063cm;吊车梁最大面积矩S max =1647.576cm 3;四. 验算1 强度验算: f W M W M nyy nx x ≤+=max σ 上翼缘正应力σ=253.024×106/2923196.251+24.806×106/238933.329=190.378N/mm2≤215N/mm 2,合格。
弯矩标准最大值mk计算公式(一)弯矩标准最大值(mk)计算公式弯矩标准最大值(mk)是结构工程中用来评估材料或构件在受力下的弯曲能力的重要参数。
针对该计算公式,本文将列举相关计算公式,并举例解释说明,旨在帮助读者更好地理解和应用此公式。
弯矩标准最大值(mk)的定义弯矩标准最大值(mk)是指材料或构件在受力作用下所产生的最大弯矩值。
弯矩是在弯曲过程中产生的力矩,用于描述结构在弯曲时受力的情况。
弯矩标准最大值(mk)计算公式根据结构工程的相关理论和计算方法,根据不同的受力情况,计算弯矩标准最大值(mk)的公式也会有所不同。
下面将列举一些常用的计算公式及其应用场景。
弯矩标准最大值(mk)计算公式1:悬臂梁的弯矩对于悬臂梁的受力情况,其弯矩标准最大值(mk)可以通过以下公式计算:mk = (FL) / 4其中: mk:弯矩标准最大值() F:受力作用力(N) L:悬臂梁的长度(m)例如,假设悬臂梁的受力作用力为1000 N,悬臂梁的长度为 2 m,则根据上述公式计算得出弯矩标准最大值(mk)为500 。
弯矩标准最大值(mk)计算公式2:均布载荷的梁的弯矩对于均布载荷作用在梁上的情况,可以使用以下公式计算弯矩标准最大值(mk):mk = (wL^2) / 8其中: mk:弯矩标准最大值() w:均布载荷的大小(N/m) L:梁的长度(m)例如,假设梁的长度为4 m,均布载荷的大小为100 N/m,则根据上述公式计算得出弯矩标准最大值(mk)为200 。
弯矩标准最大值(mk)计算公式3:集中力作用的梁的弯矩对于集中力作用在梁上的情况,可以使用以下公式计算弯矩标准最大值(mk):mk = F * a其中: mk:弯矩标准最大值() F:集中力的大小(N) a:力的集中位置到梁的支点的距离(m)例如,假设集中力的大小为500 N,力的集中位置到梁的支点的距离为 m,则根据上述公式计算得出弯矩标准最大值(mk)为750 。
对《钢结构设计手册》吊车梁最大弯矩计算公式的商榷[摘要] 对吊车梁绝对最大弯矩的计算,通常采用手册给出的公式,直接计算得到。
然而,该公式仅在一定情况下是正确的。
通过结构力学影响线分析,指出其不足之处,而且给出了简便的改进计算方法。
[关键词] 吊车梁 最不利截面 绝对最大弯矩 影响线1问题的提出吊车梁设计时,必须首先计算出该梁在吊车荷载下的绝对最大弯矩。
由于吊车轮压为移动荷载,因此需要利用影响线方法求得。
其原理是,对钢梁上的i 截面,画出其弯矩影响线,则对应于不同荷载位置时i 截面的弯矩值可以方便得到。
吊车荷载从一端驶入,另一端驶出,该截面存在一个弯矩的最大值。
比较所有n 个这样的截面,就得到全梁的绝对最大弯矩值。
以上计算过程适合计算机实现。
一般手算方法则是先确定最不利截面位置,然后计算对应于此位置处的弯矩,这可以利用手册给出的公式直接得到。
A B 图1 吊车荷载布置图 《钢结构设计手册》[1][2]指出,6个轮子作用于梁上时(如图1所示),最大弯矩点(C 点)的位置为:1222321543a a a a a a −−++=(1) 对应于此点的最大弯矩值为)2()2(212c max a a P la l P M +−−=∑ (2) 并以此作为全梁的绝对最大弯矩。
然而,算例计算和公式推导表明,按上述方法得到的截面C 并不总是全梁的最不利截面,进而导致按此位置求得的弯矩值亦并非绝对最大弯矩。
2 绝对最大弯矩的确定对于一简支梁,承受间距不变的移动集中荷载,这时,绝对最大弯矩必然发生在某个集中荷载作用点处的截面上。
根据这一思路,求出各荷载作用点处截面的最大弯矩,再加以比较,即可确定绝对最大弯矩[3]。
为叙述方便,将图1中6个轮压从左至右依次称为、……。
考虑到简支梁的绝对最大弯矩总是发生在梁的中点附近,而且吊车荷载通常有=1P 2P 6P i P P (i =1,2, ……6)存在,所以,、和、作用于影响线顶点不会形成绝对最大弯矩,和则有可能。
梁内力图和最大内力值的自动计算工具袁晓光【期刊名称】《南通大学学报(自然科学版)》【年(卷),期】2018(017)004【摘要】材料力学中的内力图是确定杆件危险截面的重要依据, 利用Excel良好的交互性、丰富的内置函数、Vba强大的面向对象编程能力和对电子表格数据方便操作性, 研究并开发了自动化求解梁内力图和最大内力值的计算工具, 可以动态显示梁在集中力、分布力、集中弯矩和一般复杂载荷作用下的内力图, 该工作可为材料力学教学及与力学相关的工程应用提供一种新的思路和途径.%The risky beam section is determined by the internal force diagrams in material mechanics.A calculating tool is developed in the environment of Excel and Vba, which is capable of friendly interface, advanced programming, and data drawing. Thus, it can yield force diagram under the loading of concentrated force, distributed force, and force couple. It presents a new approach for the material mechanics teaching and engineering application.【总页数】5页(P90-94)【作者】袁晓光【作者单位】南通大学交通学院, 江苏南通 226019【正文语种】中文【中图分类】O341【相关文献】1.利用悬臂梁内力图规律绘制刚架的内力图 [J], 王淑琴2.口诀法绘制平面梁的内力图--平面梁的内力图教学的创新实践 [J], 徐文毅3.泵站厂房中吊车竖向荷载下吊车梁最大内力值及作用面的计算方法 [J], 戴康程;叶政权;葛恒军;陈锐;袁海霞4.热机专业阀门压力值自动计算程序的应用 [J], 米景平5.弯曲梁内力图计算模型及程序的实现——基于VB环境下静定梁内力图程序实现[J], 陈文平因版权原因,仅展示原文概要,查看原文内容请购买。
普通梁体最大弯矩绝对值的简化计算方法
徐秀维
【期刊名称】《科技资讯》
【年(卷),期】2008(000)018
【摘要】针对简支梁绝对最大弯矩的计算方法,教学实践中提倡一种划分截面近似算法,该法以影响线、计算机分别作为理论分析与计算工具,可同步解决恒载和移动活载作用下简支梁绝对最大弯矩的近似计算和弯矩包络图的绘制.
【总页数】2页(P65,67)
【作者】徐秀维
【作者单位】常州工程职业技术学院,江苏常州,213164
【正文语种】中文
【中图分类】TU3
【相关文献】
1.箱型梁极限弯矩简化计算方法 [J], 冯亮;董胜;王保森;甄春博
2.部分预应力砼梁在短期荷载下裂缝闭合弯矩的简化计算方法探讨 [J], 周善来
3.主梁绝对最大弯矩的计算方法与特性研究 [J], 王彦明;王威强
4.宽支座连续梁弯矩简化计算方法研究 [J], 高鹏;黄珊珊;欧阳峰;陈达
5.移动集中荷载作用下梁绝对最大弯矩的简便计算方法 [J], 栾凤艳
因版权原因,仅展示原文概要,查看原文内容请购买。