矿产资源储量计算表 平行断面法适用

矿山地质矿产储量计算手册第一节工业指标1.1储量计算工业指标一般包括：边界品位、最低工业品位、最小可采厚度、最低工业米百分值、夹石剔除厚度。

生产矿山原则上执行原开采设计时期由矿山主管部门确定的工业指标。

1.2矿山应根据矿床地质条件的变化，生产技术的发展，工艺流程的改进，经营管理水平的提高以及产品成本、市场价格、利润等情况，分析和研究工业指标是否适应生产发展的需要，提出合理的工业指标建议。

1.3矿山改变现行的工业指标，必须通过试算对比提出修改意见，并附有技术经济分析资料，报主管部门批准。

在未批复前不得改变原工业指标。

第二节储量分类和分级2.1根据国家当前技术经济条件，并考虑发展需要，将金属矿产储量分为两类：1、能利用（表内）储量：符合当前工业技术经济条件可以被工业开采利用的矿产储量；2、暂不能利用（表外）储量：由于有益组分或矿物含量低；矿体厚度薄；矿山开采技术条件或水文地质条件特别复杂；或对这种矿产加工技术方法尚未解决，不符合当前工业技术经济条件；或为其他条件所限制时暂时不能被开采利用而将来可能利用的矿产储量。

2.2根据对矿床的勘探程度，将矿成产储量划分为A、B、C、D四级。

其划分标准在新规范未下达前，原则上执行1977年国家地质总局下达的《金属矿产地质勘探规范总则》。

各矿山应根据矿产储量分类规范的原则和矿山生产的实际，制定具体的储量计算细则。

2.3根据不同工作程度，在计算主元素储量的同时，计算伴生有用组分的储量，其级别的划分按上述规范要求执行。

第三节矿体连接和矿块圈定3.1矿体圈定应在基本查清矿体赋存条件、变化规律、控矿规律的基础上，以储量计算工业指标为标准，按工程揭露的实际情况，用自然曲线连接。

3.2单项工程矿体的圈定应符合下列规定：1、按边界品位圈出矿体边界线。

2、矿体内低于边界品位、其厚度大于夹石剔除厚度的样品作夹石圈出。

当低于边界品位的样品，其厚度小于夹石剔除厚度时，应视为表内矿体，参与工程平均品位计算。

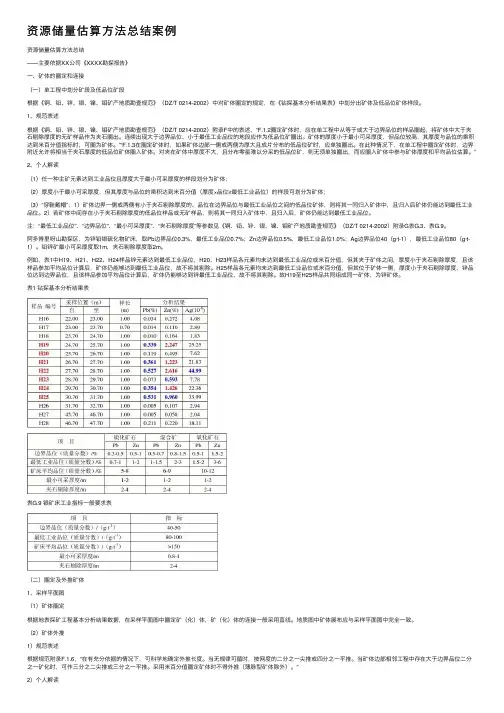
资源储量估算⽅法总结案例资源储量估算⽅法总结——主要依据XX公司《XXXX勘探报告》⼀、矿体的圈定和连接（⼀）单⼯程中划分矿段及低品位矿段根据《铜、铅、锌、银、镍、钼矿产地质勘查规范》（DZ/T 0214-2002）中对矿体圈定的规定，在《钻探基本分析结果表》中划分出矿体及低品位矿体样段。

1、规范表述根据《铜、铅、锌、银、镍、钼矿产地质勘查规范》（DZ/T 0214-2002）附录F中的表述，“F.1.2圈定矿体时，应在单⼯程中从等于或⼤于边界品位的样品圈起，将矿体中⼤于夹⽯剔除厚度的⽆矿样品作为夹⽯圈出。

连续出现⼤于边界品位、⼩于最低⼯业品位的地段应作为低品位矿圈出。

矿体的厚度⼩于最⼩可采厚度，但品位较⾼，其厚度与品位的乘积达到⽶百分值指标时，可圈为矿体。

”“F.1.3在圈定矿体时，如果矿体边部⼀侧或两侧为厚⼤且成⽚分布的低品位矿时，应单独圈出。

在此种情况下，在单⼯程中圈定矿体时，边界附近允许将相当于夹⽯厚度的低品位矿体圈⼊矿体。

对夹在矿体中厚度不⼤，且分布零星难以分采的低品位矿，则⽆须单独圈出，⽽应圈⼊矿体中参与矿体厚度和平均品位估算。

”2、个⼈解读（1）任⼀种主矿元素达到⼯业品位且厚度⼤于最⼩可采厚度的样段划分为矿体；（2）厚度⼩于最⼩可采厚度，但其厚度与品位的乘积达到⽶百分值（厚度×品位≥最低⼯业品位）的样段可划分为矿体；（3）“穿鞋戴帽”：1）矿体边界⼀侧或两侧有⼩于夹⽯剔除厚度的、品位在边界品位与最低⼯业品位之间的低品位矿体，则将其⼀同归⼊矿体中，且归⼊后矿体仍能达到最低⼯业品位。

2）若矿体中间存在⼩于夹⽯剔除厚度的低品位样品或⽆矿样品，则将其⼀同归⼊矿体中，且归⼊后，矿体仍能达到最低⼯业品位。

注：“最低⼯业品位”、“边界品位”、“最⼩可采厚度”、“夹⽯剔除厚度”等参数见《铜、铅、锌、银、镍、钼矿产地质勘查规范》（DZ/T 0214-2002）附录G表G.3、表G.9。

阿多得⾥呀⼭勘探区，为锌铅银硫化物矿床，取Pb边界品位0.3%，最低⼯业品位0.7%；Zn边界品位0.5%，最低⼯业品位1.0%；Ag边界品位40（g·t-1），最低⼯业品位80（g·t-1）。

常用储量计算方法及其应用条件[导读]将矿体用若干个剖面截成若干个块段，分别计算每个块段的储量，然后将各块段的储量和起来既得到矿体的储量。

这种用断面划分块段求储量的方法叫断面法。

如果是用一系列垂直剖面划分块段而计算储量者，叫做垂直断面法；用以犀利水平断面划分块段计算储量者，叫水平断面法。

在垂直断面法中，如果断面与断面之间平行，称为平行断面法；若不平行则为不平行断面法。

一、断面法将矿体用若干个剖面截成若干个块段，分别计算每个块段的储量，然后将各块段的储量和起来既得到矿体的储量。

这种用断面划分块段求储量的方法叫断面法。

如果是用一系列垂直剖面划分块段而计算储量者，叫做垂直断面法；用以犀利水平断面划分块段计算储量者，叫水平断面法。

在垂直断面法中，如果断面与断面之间平行，称为平行断面法；若不平行则为不平行断面法。

平行断面法的优点在于断面图保持了矿体断面的真实形状，直观的反映了地质构造特征；储量计算时，可根据出量级别、矿石类型、工业品级等的要求任意划分块段，具有相当的灵活性。

任意形状的矿床都可用断面法。

因其优点较多，称为目前最常用的储量计算方法。

二、算术平均法这种方法的基本特点是将整个矿体的各种参数都用简单算术平均法求得其平均值，从而计算矿体的储量。

他一般是利用水平投影图或垂直纵投影图来进行的，有时也在平行矿体倾斜面的投影图上进行。

算术平均法是所有储量计算方法中最简单的方法，也无须做复杂的图件。

因此，在矿点检查、矿区评价阶段常用这种方法计算。

当探矿工程数量较少，分布又不均匀，矿体各项指标值变化较大时，此法仅能得出粗略的计算结果。

此法没有按矿石类型、工业品级、储量级别等划分块段分别计算。

因此在勘探阶段很少用这种方法。

三、地质块断法在计算方法上，地质块断法和算术平均法基本一样，所不同者仅在于它不是将整个矿体一起计算，而是按需要将矿体划分成若干块断，每个块断都用算术平均法计算出块断的储量。

有时根据指标值的变化特点，也用加权平均法计算。

平行断面法与地质块段法地质学是一个广泛的领域，它涉及各种各样的技术和方法。

其中，平行断面法和地质块段法是两种被广泛应用的方法。

本文将讲解这两种方法的优点和应用情况。

一、平行断面法平行断面法是研究岩石和地质构造的一种方法。

它是通过将地质剖面在一定的间隔距离上作垂直切割，然后在连通的部位上绘制平行的线条，从而描绘出地质构造和岩石形成的情况。

平行断面法的主要优点在于可以显示岩石和地质构造在空间中的成型情况，使研究者可以更好地理解地球的构造、演化和地质历史。

在石油勘探和开发领域，平行断面法也被广泛应用。

它可以帮助研究者找到目标油气层，也可以提供有关岩石孔隙度、渗透率等重要参数的信息。

二、地质块段法地质块段法是一种在地质勘探、矿产勘探和土地利用规划中广泛应用的方法。

它是通过将区域内的地质面按照一定参数进行分割，然后在每一个地质块中进行详细的研究和分析，从而得到每一个地质块的地质特征和属性。

地质块段法的主要优点在于可以提高地质调查和矿产勘探的效率、可靠性和准确性。

它也是进行土地利用规划的一种有效的方法，可以帮助规划者更好地了解土地利用的可能性和风险。

三、应用情况平行断面法和地质块段法是地质学研究和勘探中常用的两种方法。

在石油勘探、矿物勘探、地震勘探等领域中被广泛应用。

两种方法的优点和适用情况不同，需要根据实际情况和研究目的进行选择和应用。

在石油勘探中，平行断面法可以帮助研究人员进行地质模拟和预测，预报油气储层的分布情况和产量。

地质块段法则可用于进行储油层及表面水矿化防治研究。

在矿物勘探中，平行断面法常用于矿床勘探、矿物矿化特征分析、矿物资源可持续性评价等方面。

地质块段法则常用于地质变形区水文地质背景研究、矿产资源预测和洞脉型矿体的富集规律研究。

在土地利用规划中，平行断面法可以用于地质遥感和数字地球建设中，帮助规划者更好地了解土地形成的背景和特征。

地质块段法则可用于近地面物质勘探、地下矿产资源分析等方面。

综上所述，平行断面法和地质块段法是两种常用的地质学研究方法。

断面法计算方法！断面法定义：矿体被一系列勘探断面分为若干个矿段或称块段，先计算各断面上矿体面积，再计算各个矿段的体积和储量，然后将各个块段储量相加即得矿体的总储量，这种储量计算方法称为断面法或剖面法。

根据断面间的空间位置关系分为水平断面法和垂直断面法，凡是用勘探（线）网法进行勘探的矿床，都可采用垂直断面法；对于按一定间距，以穿脉、沿脉坑道及坑内水平钻孔为主勘探的矿床，一般采用水平断面法计算矿床资源量和储量。

根据断面间的关系分为平行断面法和不平行断面法。

1平行断面法无论是垂直平行断面法还是水平平行断面法，均是把相邻两平行断面间的矿段，作为基本储量计算单元。

首先在两断面图上分别测定矿体面积，然后计算块段的体积和储量。

体积（V）的计算有下述几种情况：1）设两断面上矿体面积为S1、S2，两断面间距为L（图4-7-4）则：图4-7-4 平行断面间的矿段图4-7-5 断面间内插断面（Sm）的三种求法示意图2）矿体边缘矿块只有一个矿体断面控制那么根据矿体形态及尖灭特点，用下述体积（V）计算公式：图4-7-6 矿体端部块段形态（a）锥形体；（b）楔形体断面法，在平均品位计算时，若需使用加权平均法计算，则单工程内线平均品图4-7-7 不平行断面间矿块（a）锥形体；（b）楔形体其他参数和块段矿石储量与金属储量计算同于平行断面法。

适用条件：断面法在地质勘探和矿山地质工作中应用极为广泛。

它原则上适用于各种形状、产状的矿体。

优点是能保持矿体断面的真实形状和地质构造特点，反映矿体在三维地质空间沿走向及倾向的变化规律；能在断面上划分矿石工业品级、类型和储量类别块段；不需另作图件，计算过程也不算复杂；计算结果具有足够的准确性。

缺点是，当工程未形成一定的剖面系统时或矿体太薄、地质构造变化太复杂时，编制可靠的断面图较困难，品位的“外延”也会造成一定误差。

常用储量计算方法及其应用条件1、断面法：将矿体用若干个剖面截成若干个块段，分别计算每个块段的储量，然后将各块段的储量和起来既得到矿体的储量。

这种用断面划分块段求储量的方法叫断面法。

如果是用一系列垂直剖面划分块段而计算储量者，叫做垂直断面法；用以犀利水平断面划分块段计算储量者，叫水平断面法。

在垂直断面法中，如果断面与断面之间平行，称为平行断面法；若不平行则为不平行断面法。

平行断面法的优点在于断面图保持了矿体断面的真实形状，直观的反映了地质构造特征；储量计算时，可根据出量级别、矿石类型、工业品级等的要求任意划分块段，具有相当的灵活性。

任意形状的矿床都可用断面法。

因其优点较多，称为目前最常用的储量计算方法。

2、算术平均法：这种方法的基本特点是将整个矿体的各种参数都用简单算术平均法求得其平均值，从而计算矿体的储量。

他一般是利用水平投影图或垂直纵投影图来进行的，有时也在平行矿体倾斜面的投影图上进行。

算术平均法是所有储量计算方法中最简单的方法，也无须做复杂的图件。

因此，在矿点检查、矿区评价阶段常用这种方法计算。

当探矿工程数量较少，分布又不均匀，矿体各项指标值变化较大时，此法仅能得出粗略的计算结果。

此法没有按矿石类型、工业品级、储量级别等划分块段分别计算。

因此在勘探阶段很少用这种方法。

该法的实质是把形态不规则的矿体，改变为一个理想的具有同等厚度的板状体，其周边就是矿体的边界。

计算方法是先根据探矿工程平面图（或投影图）上圈出矿体边界，测定其面积（若为投影面积，需换算成真面积。

见后面块段法的面积换算）。

然后用算术平均法求出矿体的平均厚度、平均品位、平均体重。

最后按下面公式计算：矿体体积：V＝SxM式中：V一矿体体积（下同）；S一矿体面积；M一矿体平均厚度。

矿石储量: Q＝VxD式中：Q一矿石储量（下同；D一矿石平均体重。

矿体金属储量：P=QxC式中：P一金属储量: C一矿石平均品位。

3、地质块断法：在计算方法上，地质块断法和算术平均法基本一样，所不同者仅在于它不是将整个矿体一起计算，而是按需要将矿体划分成若干块断，每个块断都用算术平均法计算出块断的储量。

【技术方法】平行剖面法体积估算公式相对偏差研究——以浦中建筑石料矿资源储量估算为例祝有军(中国建筑材料工业地质勘查中心浙江总队，浙江 杭州　310022)【摘　要】地质勘查工作，平行断面法是固体矿产资源储量(体积)估算的基本方法之一。

本文通过理论推演和实例论证认为：平行断面法的体积计算公式，可以归纳为2个基本公式表达，即台(锥)体V =1/3(S 1+√S 1S 2+S 2)L 及楔形体V =1/2SL 。

矿块体积估算的偏差ε分析和推导结果显示：dε/dβ≤0，说明在S 1=βS 2(0≤β≤1)关系条件下，ε与β呈单调递减关系，β越小，采用梯形公式和台体公式计算结果之间的差别就越大。

矿区实例结果分析实际论证的结果与理论结果高度吻合。

本研究为在非金属矿区资源储量估算矿块体积公式合理的选择提供了理论基础，并可推广到实际应用中。

【关键词】资源储量估算方法；平行剖面法；台体；楔形体；公式；偏差【中图分类号】P624.7；TD872 【文献标识码】A 【文章编号】1007-9386(2023)03-0072-04Study on Volume Estimation Formula of Parallel Profile MethodZHU You-jun(Zhejiang Branch of China National Geological Exploration Center of Building Materials Industry, Hangzhou 310022, China)Abstract: In geological exploration, the parallel section method is one of the basic methods to estimate the reserves (volume) of solid mineral resources. Through theoretical deduction and practical demonstration, this paper argues that the formula for calculating the volume of the parallel section method can be summed up into two basic formulas, namely, pyramidal body V =1/3(S 1+ √S 1S 2+S 2)L and wedge body V =1/2SL . The deviationεanalysis and derivation results of ore block volume estimation show that: dε/dβ≤0, indicating that under the relation of S 1=βS 2(0 ≤ β ≤ 1), ε and β show monotonically decreasing relationship, the smaller the β, the greater the difference between the results calculated by the trapezoidal formula and the platform formula. The results of the practical demonstration and the theoretical results are highly consistent. This study provides a theoretical basis for the reasonable selection of mineral block volume formula in non-metallic mining area reserves estimation, and can be extended to practical applications.Key words: resource reserve estimation method; parallel section method; platform body; wedge body; formula; deviation地质勘查工作中，矿体资源储量估算常用方法有垂直剖面法和投影法。

根据场地内山体特征，本次采用钻孔岩土比例法进行计算，方量计算按以下步骤进行：
（一）首先在各个钻孔勘探剖面图上测定各类岩土所占总孔深比例；
（二）其次，由两个勘探剖面面积计算各类岩土的方量。

为此，必须根据相邻两剖面之面积S的大小来分别选择不同的公式进行计算。

当相邻两剖面上料场之相对面积差（S1-S2）/S1＜40%时，一般选用梯形体积公式，其公式为：
V=L×(S1+S2)/2 （公式一）当相邻两剖面上料场之相对面积差（S1-S2）/S1＞40%时，一般选用截锥体积公式，其公式为：
V=L×(S1+S2+√S1S2)/3 （公式二）当相邻两剖面上某一条剖面面积S2=0，且尖灭端呈楔形尖灭时，一般选用楔形尖灭体积公式，其公式为：
V=L×S1/2 （公式三）当相邻两剖面上某一条剖面面积S2=0，且尖灭端呈锥形尖灭时，一般选用锥形尖灭体积公式，其公式为：
V=L×S1/3 （公式三）式中：
V－计算对象的方量（立方米）；
L－两相邻剖面之间距（m）；
S1、S2－两相邻剖面上的料场面积（平方米）。

由于场地地形复杂，本次计算，上述四种公式均有采用。

矿山资源量与储量计算方法资源量与储量计算方法储量（包括资源量，下同）计算方法的种类很多，有几何法（包括算术平均法、地质块段法、开采块段法、断面法、等高线法、线储量法、三角形法、最近地区法/多角形法），统计分析法（包括距离加权法、克里格法），以及SD 法等等。

（一）地质块段法计算步骤：1.首先，在矿体投影图上，把矿体划分为需要计算储量的各种地质块段，如根据勘探控制程度划分的储量类别块段，根据地质特点和开采条件划分的矿石自然（工业）类型或工业品级块段或被构造线、河流、交通线等分割成的块段等；2.然后，主要用算术平均法求得各块段储量计算基本参数，进而计算各块段的体积和储量；3.所有的块段储量累加求和即整个矿体（或矿床）的总储量。

地质块段法储量计算参数表格式如表下所列。

表地质块段法储量计算表需要指出，块段面积是在投影图上测定。

一般来讲，当用块段矿体平均真厚度计算体积时，块段矿体的真实面积S需用其投影面积S′及矿体平均倾斜面与投影面间的夹角α进行校正。

在下述情况下，可采用投影面积参加块段矿体的体积计算：①急倾斜矿体，储量计算在矿体垂直纵投影图上进行，可用投影面积与块段矿体平均水平（假）厚度的乘积求得块段矿体体积。

图在矿体垂直投影图上划分开采块段(a)、(b)—垂直平面纵投影图； (c)、(d)—立体图1—矿体块段投影； 2—矿体断面及取样位置②水平或缓倾斜矿体，在水平投影图上测定块段矿体的投影面积后，可用其与块段矿体的平均铅垂（假）厚度的乘积求得块段矿体体积。

优点：适用性强。

地质块段法适用于任何产状、形态的矿体，它具有不需另作复杂图件、计算方法简单的优点，并能根据需要划分块段，所以广泛使用。

当勘探工程分布不规则，或用断面法不能正确反映剖面间矿体的体积变化时，或厚度、品位变化不大的层状或脉状矿体，一般均可用地质块段法计算资源量和储量。

缺点：误差较大。

当工程控制不足，数量少，即对矿体产状、形态、内部构造、矿石质量等控制严重不足时，其地质块段划分的根据较少，计算结果也类同其他方法误差较大。

垂直平行断面法局部结合垂直纵投影地质块段法在凡口铅锌矿进行资源储量估算的应用发布时间：2021-12-23T05:05:27.425Z 来源：《中国科技人才》2021年第27期作者：赵剑波[导读] 凡口铅锌矿资源丰富，储量大、品位高，是我国著名的大型地下开采矿山。

广东省有色地质勘查院 510080摘要：凡口铅锌矿是持续开采60年的大型地下开采矿山，在多中段多采场同时进行开采，本核实期共有400多个采场有采出矿量，少部分采空区边界线位于勘探线间。

本文主要介绍采用垂直平行断面法，局部结合垂直纵投影地质块段法做补充的方法进行资源量估算，方法合理，符合矿山生产实际，估算结果较为准确。

1.前言凡口铅锌矿资源丰富，储量大、品位高，是我国著名的大型地下开采矿山。

矿山于1968年投产，至今已持续开采60余年，2009年第三次技改扩产完成，形成日处理矿石5500吨、年采选矿石量168万吨、年产铅锌金属量18万吨的生产能力。

在前人提交的3份地质勘查报告基础上，矿山于2009年进行了资源储量核实，采用垂直平行断面法进行资源储量估算（与前人地勘报告一致）。

鉴于2010～2017年期间，矿山一直在进行正常生产开采和生产探矿，区内矿产资源储量发生较大变化，2018年采矿权人委托广东省有色地质勘查院进行铅锌矿资源储量核实工作，目的是查明矿山保有资源储量及分布情况。

2.矿山开采生产现状矿山分金星岭、狮岭、狮岭南三个开采区段。

上部中段高度为40m、深部中段为50m～55m。

到目前为止，矿山已开拓完成的中段有金星岭+50m～-320m共10个中段、狮岭0m～-650m共17个中段、狮岭南-120m～-500m共10个中段，其中采矿中段有金星岭-40m～-320m共8个中段、狮岭-40m～-455m和-550m～-650m共14个中段、狮岭南-120m～-500m共10个中段。

已结束的只有狮岭±0m中段，目前正在开拓的中段有狮岭-710m。

目前已有的储量计算方法很多，下面着重介绍找矿，评价阶段常用的算术平均法和地质块段法。

（一）算术平均法该法的实质是把形态不规则的矿体，改变为一个理想的具有同等厚度的板状体，其周边就是矿体的边界。

计算方法是先根据探矿工程平面图（或投影图）上圈出矿体边界，测定其面积（若为投影面积，需换算成真面积。

见后面块段法的面积换算）。

然后用算术平均法求出矿体的平均厚度、平均品位、平均体重。

最后按下面公式计算：矿体体积：V＝SxM式中：V一矿体体积（下同）；S一矿体面积；M一矿体平均厚度。

矿石储量: Q＝VxD式中：Q一矿石储量（下同；D一矿石平均体重。

矿体金属储量：P=QxC式中：P一金属储量: C一矿石平均品位。

（二）地质块段法地质块段法实际上是算术平均法的一种，其不同之处是将矿体按照不同的勘探程度、储量级别、矿床的开采顺序等划分成数个块段，然后按块段分别计算储量，整个矿体储量即是各块段储量之和。

具体计算方法是首先根据矿体产状，选用矿体水平投影图（缓倾斜矿体）或矿体垂直纵投影图，在图上圈出矿体可采边界线，按要求划分块段。

然后分别测定各块段面积S (系矿块投影面积），根据各探矿工程所获得的资料，用算术平均法计算每个块段的平均品位C，平均体重D和平均厚度M（为平均视厚度，即垂直或水平厚度）。

因为矿体的真面积与真厚度之乘积等于投影面积与投影面之法线厚度之积具体按下面步骤计算：1．块段体积：V＝S x M如果测定的面积为块段的垂直投影面积，则块段平均厚度M为块段的水平厚度；若测定的面积为块段的水平投影面积，则块段平均厚度为矿块的垂直厚度。

2．块段的矿石量：Q＝V XD3．块段的金属量：P＝QxC矿体的总储量即为各块段储量之和。

如果计算时采用的矿体平均厚度为真厚度，而面积是测定的投影面积，这时应把真厚度换算成视厚度（即水平或垂直厚度）。

或者将投形面积换算成矿体的真面积。

面积换算公式如下：S= Sˊ/sinβ式中：S一矿块真面积；Sˊ一矿块投影面积；β一矿体倾角。

我国固体矿产资源储量计算方法简介张福家白瑞和王师宇（辽宁省国土资源厅储量处辽宁沈阳1100？？）（中国建筑材料工业地质勘查中心辽宁总队，辽宁沈阳110004）摘要：本文简要介绍我国固体矿产资源储量计算方法和三维储量计算功能的矿业软件，详细介绍Micromine软件在固体矿产报告编写资源储量计算方法的应用。

关键词：断面法、地质块段法、地质统计学、SD法、建模方法（同步前进法和最短对角线法、切开缝合法）、克里格法、距离反比法、封闭多面体估算法固体矿产资源是指在地壳内或地表由地质作用形成的具有经济意义，根据产出形式、数量和质量，预期最终开采在技术上可行、经济上合理的固体自然富集物。

固体矿产资源的可利用储量以及矿化元素空间分布是矿山进行采选设计的基础，直接影响到矿山企业的宏观决策。

传统的储量计算方法是在简单几何图形的基础上近似地计算矿体体积，计算过程不直观、精度差。

随着信息技术的发展，以计算机为工具，以三维矿体模型为基础进行储量计算可有效地解决传统储量计算方法中存在的问题，显著提高储量计算的效率，能够大幅降低工作人员的计算量，降低此项工作的经营成本。

其与传统的储量计算方法相比，计算过程更为直观，结果更为精确，是储量计算的发展趋势。

一、我国固体矿产资源储量计算方法我国固体矿产资源储量计算方法大体分为三类：第一类是传统的简单几何图形储量计算方法；第二类是地质统计学的储量计算方法；第三类是SD储量计算方法。

第一类是传统的储量计算方法；常用的有断面法、算术平均法、地质块段法、多角形法、等值线法等。

在这些方法中至今最为常用的是断面法和地质块段法。

①断面法断面法（剖面法）是按一定间距，用若干勘探剖面将矿体截分为若干个块段（除矿体两端的边缘部分外，各块段均由两个剖面控制），通过对断面上矿体截面面积的测定，计算出断面之间的矿块体积和矿石储量。

根据断面的相互关系，可进一步将其划分为平行断面法和不平行断面法。

根据断面所处的空间状态，可进一步将其划分为垂直断面法和水平断面法。