线性代数第一章第二节
- 格式:ppt
- 大小:2.02 MB
- 文档页数:34
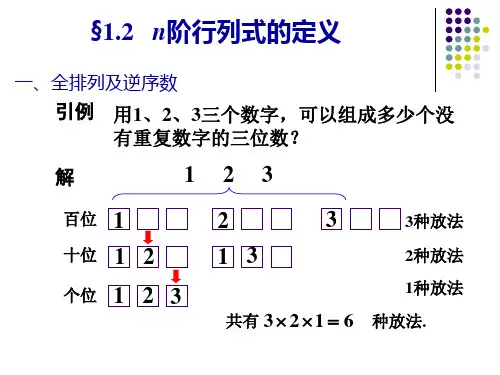



线性代数教案第(1)次课授课时间()1.教学内容: 二、三阶行列式的定义;全排列及其逆序数;阶行列式的定义2.时间安排: 2学时;3.教学方法: 讲授与讨论相结合;4.教学手段: 黑板讲解与多媒体演示.基本内容备注第一节 二、三阶行列式的定义一、二阶行列式的定义从二元方程组的解的公式,引出二阶行列式的概念。
设二元线性方程组 ⎩⎨⎧=+=+22222211212111b x a x a b x a x a用消元法,当021122211≠-a a a a 时,解得211222111212112211222112121221,a a a a b a b a x a a a a b a b a x --=--=令2112221122211211a a a a a a a a -=,称为二阶行列式 ,则如果将D 中第一列的元素11a ,21a 换成常数项1b ,2b ,则可得到另一个行列式,用字母1D 表示,于是有2221211a b a b D =按二阶行列式的定义,它等于两项的代数和: ,这就是公式(2)中 的表达式的分子。
同理将 中第二列的元素a 12,a 22 换成常数项b1,b2 ,可得到另一个行列式,用字母 表示,于是有2121112b a b a D =按二阶行列式的定义,它等于两项的代数和: ,这就是公式(2)中 的表达式的分子。
于是二元方程组的解的公式又可写为⎪⎪⎩⎪⎪⎨⎧==D D x D D x 2211 其中0≠D例1. 解线性方程组 .1212232121⎪⎩⎪⎨⎧=+=-x x x x 同样,在解三元一次方程组⎪⎩⎪⎨⎧=++=++=++333323213123232221211313212111bx a x a x a b x a x a x a b x a x a x a 时,要用到“三阶行列式”,这里可采用如下的定义.二、三阶行列式的定义设三元线性方程组⎪⎩⎪⎨⎧=++=++=++333323213123232221211313212111bx a x a x a b x a x a x a b x a x a x a用消元法解得定义 设有9个数排成3行3列的数表333231232221131211a a a a a a a a a 记 333231232221131211a a a a a a a a a D =322113312312332211a a a a a a a a a ++=332112322311312213a a a a a a a a a ---,称为三阶行列式,则三阶行列式所表示的6项的代数和,也用对角线法则来记忆: 从左上角到右下角三个元素相乘取正号,从右上角到左下角三个元素取负号,即例2.计算三阶行列式 .(-14) 例3.求解方程 ( ) 例4.解线性方程组 解 先计算系数行列式573411112--=D 069556371210≠-=----+-= 再计算 321,,D D D515754101121-=--=D ,315534011222=--=D ,55730112123=---=D得 23171==D D x ,69312-==D D y ,6953-==D D z第( 2 )次课授课时间()第( 3 )次课授课时间()1.教学内容: 行列式按行(列)展开;2.时间安排: 2学时;3.教学方法: 讲授与讨论相结合;教学手段: 黑板讲解与多媒体演示.基本内容备注第5节 行列式按行(列)展开定义 在 阶行列式中, 把元素 所处的第 行、第 列划去, 剩下的元素按原排列构成的 阶行列式, 称为 的余子式, 记为;而 称为 的代数余子式.引理 如果 阶行列式中的第 行除 外其余元素均为零, 即: .则: .证 先证简单情形:再证一般情形:定理 行列式等于它的任意一行(列)的各元素与对应的代数余子式乘积之和, 即按行: 按列: 证:(此定理称为行列式按行(列)展开定理)nnn n ini i n a a a a a a a a a D212111211000000+++++++++=nnn n in n nnn n i n nn n n i n a a a a a a a a a a a a a a a a a a a a a 21112112121121121111211000000+++=).,2,1(2211n i A a A a A a in in i i i i =+++=例1 : . 解:例2: 21122112----=n D解: 21122112----=n D 211221100121---=+++nr r)()()()()()21331122213311n n n n n n n x x x x x x x x x x x -----, 并提出因子 )()2321111--n n n x x x x x x()1-n 阶范德蒙行列式(1n x x -行列式一行(列)的各元素与另一行(列)对应各元素的代数余子式乘积之和为零第( 4 )次课授课时间()1.教学内容: 克拉默法则;2.时间安排: 2学时;教学方法: 讲授与讨论相结合;4.教学手段: 黑板讲解与多媒体演示.4.教学手段:黑板讲解与多媒体演示.基本内容备注第(5)次课授课时间()1.教学内容: 矩阵;矩阵的运算;2.时间安排: 2学时;3.教学方法: 讲授与讨论相结合;4.教学手段: 黑板讲解与多媒体演示。



线性代数⽬录第⼀章 线性⽅程组与矩阵 1第⼀节 矩阵的概念及运算 1 ⼀、矩阵的定义 1 ⼆、矩阵的线性运算 3 三、矩阵的乘法 4 四、矩阵的转置 6习题1-1 7第⼆节 分块矩阵 8 ⼀、分块矩阵的概念 8 ⼆、分块矩阵的运算 10习题1-2 13第三节 线性⽅程组与矩阵的初等变换 14 ⼀、矩阵的初等变换 14 ⼆、求解线性⽅程组 18习题1-3 22第四节 初等矩阵与矩阵的逆矩阵 23 ⼀、⽅阵的逆矩阵 24 ⼆、初等矩阵 25 三、初等矩阵与逆矩阵的应⽤ 26习题1-4 29本章⼩结 31拓展阅读 32测试题⼀ 33第⼆章 ⽅阵的⾏列式 35第⼀节 ⾏列式的定义 35 ⼀、排列 35 ⼆、n 阶⾏列式 37 三、⼏类特殊的n 阶⾏列式的值 39习题2-1 41第⼆节 ⾏列式的性质 41 ⼀、⾏列式的性质 41 ⼆、⾏列式的计算举例 45 三、⽅阵可逆的充要条件 48习题2-2 50第三节 ⾏列式按⾏(列)展开 51 ⼀、余⼦式与代数余⼦式 52 ⼆、⾏列式按⾏(列)展开 52习题2-3 57第四节 矩阵求逆公式与克莱默法则 58 ⼀、伴随矩阵与矩阵的求逆公式 58 ⼆、克莱默法则 59习题2-4 62本章⼩结 63拓展阅读 64测试题⼆ 65第三章 向量空间与线性⽅程组解的结构 67第⼀节 向量组及其线性组合 67 ⼀、向量的概念及运算 67 ⼆、向量组及其线性组合 69 三、向量组的等价 71习题3-1 74第⼆节 向量组的线性相关性 74⼀、向量组的线性相关与线性⽆关 75⼆、向量组线性相关性的⼀些重要结论 77习题3-2 80第三节 向量组的秩与矩阵的秩 81 ⼀、向量组秩的概念 81 ⼆、矩阵秩的概念 82 三、矩阵秩的求法 83 四、向量组的秩与矩阵的秩的关系 85习题3-3 87第四节 线性⽅程组解的结构 88 ⼀、线性⽅程组有解的判定定理 88 ⼆、齐次线性⽅程组解的结构 90 三、⾮齐次线性⽅程组解的结构 94习题3-4 96第五节 向量空间 97 ⼀、向量空间及其⼦空间 97 ⼆、向量空间的基、维数与坐标 99 三、基变换与坐标变换 101习题3-5 103本章⼩结 105拓展阅读 106测试题三 107第四章 相似矩阵及⼆次型 109第⼀节 向量的内积、长度及正交性 109 ⼀、向量的内积、长度 109 ⼆、正交向量组 110 三、施密特正交化过程 112 四、正交矩阵 113习题4-1 115第⼆节 ⽅阵的特征值与特征向量 115 ⼀、⽅阵的特征值与特征向量的概念及其求法 116 ⼆、⽅阵的特征值与特征向量的性质 119习题4-2 121第三节 相似矩阵 122 ⼀、⽅阵相似的定义和性质 122 ⼆、⽅阵的相似对⾓化 123习题4-3 124第四节 实对称矩阵的相似对⾓化 125 ⼀、实对称矩阵的特征值和特征向量的性质 125 ⼆、实对称矩阵的相似对⾓化 126习题4-4 129第五节 ⼆次型及其标准形 129 ⼀、⼆次型及其标准形的定义 130 ⼆、⽤正交变换化⼆次型为标准形 131 三、⽤配⽅法化⼆次型为标准形 134习题4-5 135第六节 正定⼆次型与正定矩阵 136 ⼀、惯性定理 136 ⼆、正定⼆次型与正定阵 137习题4-6 138本章⼩结 139拓展阅读 140测试题四 141第五章 线性空间与线性变换 143第⼀节 线性空间的定义与性质 143 ⼀、线性空间的定义 143 ⼆、线性空间的性质 145 三、线性空间的⼦空间 146习题5-1 147第⼆节 维数、基与坐标 147 ⼀、线性空间的基、维数与坐标 147 ⼆、基变换与坐标变换 149习题5-2 150第三节 线性变换 151 ⼀、线性变换的定义 151 ⼆、线性变换的性质 153 三、线性变换的矩阵表⽰式 154习题5-3 158本章⼩结 161拓展阅读 162测试题五 163部分习题答案 165。


线性代数知识点总结第一章 行列式第一节:二阶与三阶行列式把表达式11221221a a a a -称为11122122a a a a 所确定的二阶行列式,并记作11122112a a a a ,即1112112212212122.a a D a a a a a a ==-结果为一个数。
(课本P1) 同理,把表达式112233122331132132112332122133132231,a a a a a a a a a a a a a a a a a a ++---称为由数表111213212223313233a a a a a a a a a 所确定的三阶行列式,记作111213212223313233a a a a a a a a a 。
即111213212223313233a a a a a a a a a =112233122331132132112332122133132231,a a a a a a a a a a a a a a a a a a ++--- 二三阶行列式的计算:对角线法则(课本P2,P3) 注意:对角线法则只适用于二阶及三阶行列式的计算。
利用行列式计算二元方程组和三元方程组:对二元方程组11112212112222a x a xb a x a x b +=⎧⎨+=⎩设11122122a a D a a =≠1121222b a D b a =1112212.a b D a b =则1122221111122122b a b a Dx a a D a a ==,1112122211122122.a b a b Dx a a Da a ==(课本P2)对三元方程组111122133121122223323113223333a x a x a x b a x a x a x b a x a x a x b ++=⎧⎪++=⎨⎪++=⎩,设1112132122233132330a a a D a a a a a a =≠,1121312222333233b a a D b a a b a a =,1111322122331333a b a D a b a a b a =,1112132122231323a ab D a a b a a b =, 则11D x D =,22Dx D =,33D x D=。

