测量误差的分类以及解决方法
- 格式:doc
- 大小:603.50 KB
- 文档页数:11


GNSS测量中常见误差源及其校正方法导语:全球卫星导航系统(GNSS)已经成为现代测量和定位领域中不可或缺的技术工具。
然而,由于各种因素的干扰,GNSS测量结果可能会出现误差。
本文将讨论一些常见的GNSS测量误差源以及相应的校正方法。
一、信号传播误差在GNSS测量中,信号从卫星到接收机的传播过程中会受到大气层、多径效应等因素的影响,从而引入误差。
其中,大气层误差是最主要的误差源之一。
大气层中的水蒸气、电离层密度等因素会影响信号的传播速度和路径,进而引起测量结果的偏差。
校正大气层误差的方法包括双频差分测量和大气层模型计算。
二、钟差误差GNSS卫星上的原子钟是精确度非常高的,但是由于各种因素的影响,例如温度、空间辐射等,钟差误差仍然无法避免。
钟差误差会导致接收机收到的卫星信号的到达时间产生偏差,进而影响测量结果的准确性。
为了校正钟差误差,常见的方法是利用双频差分测量或者接收机内部的钟差模型进行补偿。
三、多路径误差多径效应是由于信号在传播过程中,同时经过直射路径和反射路径,造成接收机接收到多个信号,从而引起测量结果偏差的现象。
这种误差特别突出在城市环境或者山区等多反射面的地形中。
为了解决多路径误差,一种常见的方法是使用反射面特征分析技术,提高接收机的可靠度和抗干扰能力。
四、动态误差GNSS测量的准确性在很大程度上取决于接收机和测量对象的相对运动状态。
动态误差主要来自于运动的加速度、速度等变化过程中引起的信号多普勒效应、载波缺失等问题。
对于动态误差的校正,可以通过使用惯性测量单元(IMU)配合GNSS仪器进行联合定位,从而提高定位的精度和稳定性。
五、卫星几何误差卫星几何误差是由于卫星的位置分布、卫星与接收机的相对位置等因素引起的。
当卫星几何配置良好时,测量误差较小,但当卫星分布较差或者接收机与卫星的角度较小时,测量误差将增大。
为了解决卫星几何误差问题,可以通过使用多频多系统的GNSS接收机,提高系统的可靠性。
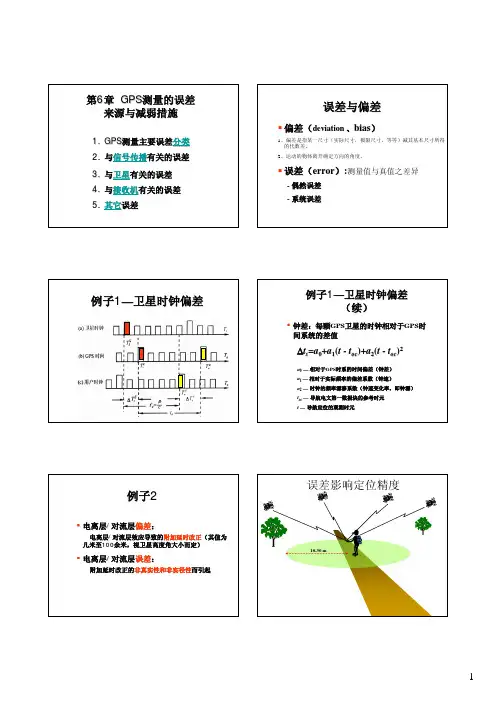
误差影响定位精度10-30 m接收机天线相位中心的偏移和变化消除或消弱各种误差影响的方法①•模型改正法–原理:利用模型计算出误差影响的大小,直接对观测值进行修正–适用情况:对误差的特性、机制及产生原因有较深刻了解,能建立理论或经验公式–所针对的误差源•相对论效应•电离层延迟•对流层延迟•卫星钟差–限制:有些误差难以模型化改正后的观测值=原始观测值+模型改正•求差法–原理:通过观测值间一定方式的相互求差,消去或消弱求差观测值中所包含的相同或相似的误差影响–适用情况:误差具有较强的空间、时间或其它类型的相关性。
–所针对的误差源•电离层延迟•对流层延迟•卫星轨道误差•…–限制:空间相关性将随着测站间距离的增加而减弱消除或消弱各种误差影响的方法②消除或消弱各种误差影响的方法③•参数法–原理:采用参数估计的方法,将系统性偏差求定出来–适用情况:几乎适用于任何的情况–限制:不能同时将所有影响均作为参数来估计消除或消弱各种误差影响的方法④•回避法–原理:选择合适的观测地点,避开易产生误差的环境;采用特殊的观测方法;采用特殊的硬件设备,消除或减弱误差的影响–适用情况:对误差产生的条件及原因有所了解;具有特殊的设备。
–所针对的误差源•电磁波干扰•多路径效应–限制:无法完全避免误差的影响,具有一定的盲目性6.1 GPS测量误差分类及对距离测量的影响与信号传播有关的误差与卫星有关的误差与接收机有关的误差其它误差•对流层折射•电离层折射•多路径效应•星历误差•卫星钟差•相对论效应•接收机钟差•位置误差•天线相位中心的偏差及变化•各通道间的信号延迟误差•地球潮汐1.5-15m1.5-15m1.5-5m1. m6.2 与信号传播有关的误差电离层折射对流层折射多路径误差电离层中的气体分子由于大气折射效应)利用电离层改正)(2cos P T t P-π∑3ϕαDC =5ns T P =14hαn 和βn :由导航tropion N δρδρλ++- 6.2.2对流层折射▪离地面高度40km 以下的大气层,是一种非电离大气层。

导致试验机测量结果产生误差的原因及解决方法试验机是一种关键的测试设备,用于测量材料、产品和构件的力学特性。
准确的试验机测量结果对于各种行业都至关重要,如汽车、航空、建筑等。
然而,试验机测量结果有时会出现误差。
本文将探讨导致试验机测量结果产生误差的原因以及解决方法。
原因试验机测量结果产生误差的原因有很多,以下是几种常见的原因:1. 试验机标定不准确试验机标定不准确是导致测量结果出现误差的主要原因之一。
试验机在出厂之前需要进行标定,并根据标准进行调整。
如果标定不准确,则测量结果也可能会出现误差。
为确保准确性,试验机需要定期进行标定。
2. 试验样品制备问题试验样品制备不当也会影响试验机测量结果的准确性。
如果样品的几何形状、尺寸或表面处理不正确,则试验机测量结果可能会出现误差。
为减少误差,制备试验样品时需要按照标准操作,并使用适当的设备和工具。
3. 环境条件的影响试验机测量结果还受环境因素的影响,如温度、湿度、气压等。
这些因素可能导致试验样品和试验机发生变形,进而影响测量结果的准确性。
因此,在进行试验前需要将试验机和试验样品放置在恒定的环境条件下,以减少环境因素对测量结果的影响。
4. 试验机操作错误试验机操作错误也可能导致测量结果产生误差。
如操作人员未正确设置试验参数,试验过程中未进行正确的数据记录和处理等。
因此,操作人员需要接受专业的培训,并按照正确的操作流程进行操作。
解决方法为了减少试验机测量结果中的误差,我们可以采取以下措施:1. 正确标定试验机为确保试验机的准确性,我们需要对试验机进行定期标定。
在标定时,需要注意设定标准和试验机参数等,并检查标定结果的准确性。
如果标定不正确,则需要进行相应的修正。
2. 合理制备试验样品试验样品的制备对试验机的测量结果非常关键。
为了减少误差,我们需要按照标准制备试验样品,包括几何形状、尺寸和表面处理等。
同时,需要使用适当的设备和工具进行试验样品的制备。
3. 控制环境条件环境条件对试验机测量结果非常敏感。


工程测量中三角高程测量的误差分析及解决方法戚忠中国水利水电第四工程局有限公司测绘中心,青海西宁,邮编810007一引言一直以来,为保证精度,高等级高程测量都采用几何水准的方法。
而在某些特定环境下,几何水准往往会耗费大量的人力、物力,且受地形等条件因素影响较大!鉴于几何水准在某些特定情形下无法进行的问题,探讨如何提高三角高程测量的精度,以保证其测量成果的可行性和可靠性,使得三角高程测量成果足以替代几何水准。
随着高精度全站仪的问世,结合合理的方式、方法,运用三角高程替代几何水准测量是切实可行的。
三角高程代替几何水准可以解决跨河水准及高边坡、危险地段无法进行精密几何水准测量的难题,保障危险地段测量人员和仪器设备的安全,提高了工作效率,降低了测量成本。
二三角高程测量误差分析常见的三角高程测量有单向观测法、中间法和对象观测法,对向观测法可以消除部分误差,故在三角高程测量中采用较为广泛。
对向观测法三角高程测量的高差公式为:(1)式中:D为两点问的距离;a为垂直角;为往返测大气垂直折光系数差;i为仪器高;v为目标高; R为地球曲率半径(6370 km);为垂线偏差非线性变化量;令。
对式(1)微分,则由误差传播定律可得高差中误差:(2) 由式(2)可知影响三角高程测量精度主要有:1.竖直角(或天顶距)、2.距离、3.仪器高、4.目标高、5.球气差。
第1、2项可以通过试验观测数据分析选择精度合适的仪器及其配套的反光棱镜、温度计、气压表等,我们选择的是徕卡TCA2003及其配套的单棱镜、国产机械通风干湿温度计、盒式气压计;第3、4项,一般要求建立稳定的观测墩和强制对中装置,采用游标卡尺在基座3个方向量取,使3个方向量取的校差小于0.2 mm,并在测前、测后进行2次量测;第5项球气差也就是大气折光差,也是本课题的研究重点。
三减弱大气折光差的方法和措施大气折光差:是电磁波经过大气层时,由于传播路径产生弯曲及传播速度发生变化而引起观测方向或距离的误差。

长度计量仪器测量过程中误差控制摘要:随着科技的飞速发展,长度测量仪器已经成为社会各行各业不可或缺的重要组成部分,它们能够准确地反映出物体的尺寸和形状。
然而,由于外界因素的影响,在检测过程中经常会出现误差,这会对测量结果造成不利影响。
在这篇文章中,我们将会详细介绍长度测量仪器,探讨导致测量结果偏差的原因,并给出一些有效的解决方案。
关键词:长度计量仪器;测量误差;控制措施引言随着时代的进步,长度测量仪器在各个行业都得到了广泛的应用,从工业到家庭,从农业到医疗,它们都在不断地推动着社会的进步和发展。
但是由于受到外界因素的影响,往往在测量结果上存在误差,为了进一步提高测量的精准程度,本文对长度计量仪器的误差控制进行详细的分析和探究。
一、长度计量仪器的概述通过长度计量,我们可以准确地比较被测量物体的实际尺寸,并且可以通过实验来检验其精确性。
通常来说,在进行长度测量时,被测物的表面是最重要的参考,由点和线组成。
因此,在进行测量之前,必须首先确定表面,只有确定了表面,才能进行下一步的测量。
在完成测量定位之后,为了确保物体能够被准确、可靠地测量,应采用最简单的方法,以确保测量结果的精确性。
随着实际情况的变化,基面的变化会对测量产生重大影响,从而使得测量结果出现较大的偏差。
为了确保长度测量的精确性,应当根据实际情况选择合适的标准器,以此来提升被测量物体的精度。
二、长度计量仪器测量误差分类2.1系统误差因为超出了预期的工作环境,以及不当的测量技术,导致了有序的精度波动。
由于已有的尺寸精度不够,导致了线纹尺的线距误差,这是一种严重的误差;测量结果具有原始错误。
由于气温改变引起错误。
由于安装方式的错误,可能会导致圆光栅的位置出现偏移或者其他问题。
通常来说,系统误差可以通过计算和测量得到,并且有可能被纠正。
使用正确度(correct-ness)来衡量它的重要性。
2.2随机误差又称偶然性错误。
当多次测量相同长度时,由于实际情况的复杂性,误差的绝对值和符号会发生不可预料的变化。

电力电子技术中的电流测量误差及解决方法在电力电子技术中,准确测量电流是非常重要的。
然而,在实际的电流测量中,总会存在一定的误差。
本文将探讨电力电子技术中的电流测量误差,并提出解决这些误差的方法。
一、电流测量误差的来源1.1 电阻的温度系数电流测量通常基于电阻原理,而电阻的电阻值在不同的温度下是会变化的。
因此,在温度变化的影响下,电流测量的精度可能会受到影响。
1.2 导线接触电阻导线在电流传输过程中会产生一定的接触电阻,这会导致测量电流时的误差。
接触电阻的大小和质量与导线的材料和接触面积有关。
1.3 测量装置本身的误差测量电流所使用的装置本身可能存在一定的误差。
这些误差可以来自于器件的精度、老化、磁场干扰等因素。
二、解决电流测量误差的方法2.1 温度补偿为了解决电阻的温度系数引起的误差,可以采用温度补偿的方法。
通过引入温度传感器,可以实时检测电阻的温度,并根据测量结果对电流进行相应的修正,从而提高测量的准确性。
2.2 导线优化为了减小导线接触电阻带来的误差,在实际的电流测量中,可以采用优质导线和合适的导线截面积。
此外,保持导线的接触面干净,确保良好的接触也是减小接触电阻的关键。
2.3 校准和修正针对测量装置本身的误差,可以通过校准和修正的方式来提高测量的精度。
定期对测量设备进行校准,修正其存在的误差,以确保测量结果的准确性。
2.4 磁场屏蔽由于电流测量中可能存在磁场干扰,可以采用合适的磁场屏蔽材料来减小这种干扰。
通过使用屏蔽罩或磁场隔离装置等手段,将磁场影响降至最低,提高测量的准确性。
2.5 精密测量装置的选择在实际应用中,选择精密测量装置也是减小电流测量误差的一种方法。
通过选用具有更高精度的测量设备,可以提高测量的准确性和可靠性。
三、总结在电力电子技术中,电流测量是非常重要的,但存在一定的误差是不可避免的。
本文讨论了电流测量误差的来源,并提出了相应的解决方法。
通过采用温度补偿、导线优化、校准和修正、磁场屏蔽和选择精密测量装置等措施,可以提高电流测量的准确性和可靠性,从而更好地应用于电力电子技术中。

卷尺使用中常见的误差和解决方法分析卷尺是我们日常生活中常见的测量工具,用于测量长度、宽度等物体的尺寸。
然而,在使用卷尺的过程中,我们常常会遇到一些误差,导致测量结果不准确。
本文将分析卷尺使用中常见的误差,并提供解决方法,以帮助读者更准确地使用卷尺。
首先,卷尺的刻度误差是最常见的问题之一。
由于制造工艺、使用年限等原因,卷尺上的刻度可能会出现偏差。
为了解决这个问题,我们可以使用标准卷尺进行校准。
校准方法很简单,只需要将标准卷尺与待校准的卷尺放在一起,对比两者的刻度,找出差异并进行调整。
其次,使用卷尺时的读数误差也是常见的问题。
由于视觉差异、读数不准确等原因,我们可能会读取到错误的数值。
为了减少读数误差,我们可以采取以下措施。
首先,要保持视线垂直于卷尺刻度,避免因视角问题造成的读数偏差。
其次,要仔细观察卷尺上的刻度,确保读数的准确性。
如果有必要,可以使用放大镜等工具来帮助读数。
最后,要进行多次测量,并取平均值作为最终结果,以降低个别读数误差的影响。
此外,卷尺的材质和使用环境也会对测量结果产生影响。
例如,卷尺的材质可能会受到温度、湿度等因素的影响而发生膨胀或收缩,导致测量结果不准确。
为了解决这个问题,我们可以在测量前将卷尺放置在稳定的环境中,等待其温度和湿度适应,再进行测量。
此外,还可以选择使用具有较低热胀冷缩系数的材质制造的卷尺,以减少温度变化对测量结果的影响。
最后,使用卷尺时的操作误差也是需要注意的问题。
例如,我们在测量时可能没有将卷尺完全贴合物体表面,导致测量结果偏大或偏小。
为了避免这个问题,我们应该尽量将卷尺贴合物体表面,并确保卷尺的刻度与物体的边缘对齐。
此外,我们还应该注意测量时的力度,避免用力过大或过小,以确保测量结果的准确性。
综上所述,卷尺使用中常见的误差包括刻度误差、读数误差、材质和环境误差以及操作误差。
为了解决这些问题,我们可以采取相应的措施,如使用标准卷尺进行校准、保持视线垂直、进行多次测量并取平均值、将卷尺放置在稳定环境中等。


工程测量观测误差的形成原因及解决方法摘要:通过对工程测量观测误差成因的分析,得出了造成观测误差的主要原因是仪器误差、观测误差和外部环境的影响。
文章结合有关资料,从仪器设备的日常维护、观察技能、观察人员与观察工作的态度等方面,归纳出了如何控制这些误差。
关键词:工程测量;观测误差;形成原因;仪器误差前言:随着我国社会的迅速发展,我国的工程建设工程越来越多,而工程测量是其中的一个重要方面,它直接关系到工程的质量和安全性[1]。
在施工中,由于工程的计量错误,将会对项目的整体质量产生直接的影响。
故对对工程测量中存在的误差来源和控制对策进行分析具有重要的重要的指导作用。
一、工程测量误差形成原因(一)仪器误差在实际应用中,观测员依靠测量仪器(图一)来获得观测资料,但由于各测量仪具有特定的精度和应用需求,因此也会对观测结果产生影响[2]。
按测试的技术需求,选用各种类型的仪表,而较低档的仪表难以胜任较高的测试工作。
如果使用6英寸精密的全站仪作控制线,其结果远没有6英寸精密仪表来得精确。
又比如,水平仪的基本要求是水平仪,即采用了水平线上的泡沫点的居中。
气泡是否处于中心,需要肉眼来观测,因为受生物力学的制约,无法准确分辨出气泡的中心。
水平管中流体与管道表面的摩擦和粘着,称为水平管的泡心偏差。
其尺寸与水平管内壁弯度相关。
对比两者,前者占主导地位。
另外,还要配备相应的测量仪。
比如,在测量时,由于水平尺的雕刻问题,都会对测量的结果造成一定的影响。
随着现代电子学的发展,各类高精度的测控设备层出不穷,经纬仪和电磁波测距已经逐步被数字水准仪和电子全站仪所代替。
但是,再先进的仪器也只是使它的精确性得到改善,而它自身的错误是无法避免的。
我们只有在实际操作中进行控制。
图一工程测量仪(二)自然条件的影响在观察时,由于地形、温度、湿度、风力、大气折射、交通条件等,这些都会对测量结果产生不同程度的影响[3]。
而且,由于各种因素的变动,会对观察的结果造成一定的影响,从而导致测量的结果出现偏差。
机械测量误差原因及处理方法在机械制造中,为了保证从零件加工、部件组装到机器的装配调试成功,实现其使用功能和正常运行,必须对零件的加工工艺过程进行控制,其中就要对零件进行测量,保证各零件的测量结果都在各要求的范围值内。
但是在测量的过程中,由于各种因素会造成少许的误差,这些因素必须去了解,并有效的解决,方可使整个测量过程中误差减至最少。
测量误差的来源测量误差产生的原因很多,但概括起来主要有以下三个方面:1、仪器的原因①仪器结构、制造方面,每一种仪器具有一定的精确度,因而使观测结果的精确度受到一定限制。
例如:•DJ6型光学经纬仪基本分划为1′,难以确保分以下估读值完全准确无误。
•使用只有厘米刻划的普通钢尺量距,难以保证厘米以下估读值的准确性。
②仪器构造本身也有一定误差。
例如:•水准仪的视准轴与水准轴不平行,则测量结果中含有i 角误差或交叉误差。
•水准尺的分划不均匀,必然产生水准尺的分划误差。
2、人的原因观测者感官鉴别能力有一定的局限性。
观测者的习惯因素、工作态度、技术熟练程度等也会给观测者成果带来不同程度的影响。
由于人为因素所造成的误差,包括误读、误算和视差等。
而误读常发生在游标尺、分厘卡等量具。
游标尺刻度易造成误读一个最小读数,如在10.00 mm处常误读成10.02 mm或9.98 mm。
分厘卡刻度易造成误读一个螺距的大小,如在10.20 mm常误读成10.70 mm或9.70 mm。
误算常在计算错误或输入错误数据时所发生。
视差常在读取测量值的方向不同或刻度面不在同一平面时所发生,两刻度面相差约在0.3~0.4 mm之间,若读取尺寸在非垂直于刻度面时,即会产生的误差量。
3、外界条件例如:外界环境如温度、湿度、风力、大气折光等因素的变化,均使观测结果产生误差。
测量误差的分类先作两个前提假设:•观测条件相同.•对某一量进行一系列的直接观测在此基础上分析出现的误差的数值、符号及变化规律。
先看两个实例:例1:用名义长度为30米而实际长度为30.04米的钢尺量距。
测量误差的分类(一)按误差表现的规律划分(1)系统误差对同—被测量进行多次重复测量时、化.这种误差称为系统误差。
各误差出走不变或者按照一定规雕变系统误茬主公足巾于测量系统本身不完备或者环境条件的变化造成的。
如所使用仪器仪表的误差、测量方法的不完善、各种环境因素的波动,以及测量者个体差异等原出。
系统误差反映泅Ij员值偏离真佰的程度,可川“厂确皮”词表让。
系统误差是村规律性的。
技其表现的特点。
钽电容可分为固定4;变的恒值系差川遵循·定规律变化的变仪系差。
系统误差一般可通过实验或分析的方法,企明义变化的视汗及,“生的原冈.因此它是可以预测的,也是可以消除的。
(2)随机误差对问一被测量进行多次重复测量叫.若误差的大小随机变化、不可预知,这种误差称为随机误差:随机误差足hfR多复杂因素凶微小生比引赵的.尽管这些不可控微小闽累中的一项对测量佰的影响签微,但这些因素的综合作用却造成了各次测量值的差异。
随机误差反映厂测量结果的‘相密度”,即各个训虽值之间祁11接近的程度。
对随机误差的义个单佰来说.是没匈规律、个uJ预料的.们从多次测量的总体上看,随机误差又服队——定的统计规律.大多数服从比态分布规律,闸此可以用概率论和数理统11的方法,从理沦J:估计其对测殴结果的影响。
(3)粗大误楚测虽结http://www.ebv.hk果明显地偏阂英文际值所对应的误差,称为粗大误差或疏忽误差,又叫过:尖误差。
(们缓变误差数汉阳列间而缓慢坐化的误差称为缓变误差。
缓变误差产生的原出十要是测量仪人零件的老化、夫效、坐形等原因造成的。
这种误差在短叫间内不易察觉。
们在较长的时间后台显露山来。
通常叫以采用定期校验的方法及时修正缓变误差。
(二)按被测星与时间关系划分(])静态误差被测丛稳定4;变时所广小的测量误点称为静态误差。
(2,动怂误差被测量随时间迅速变化时.系统的输小鱼在列间上邮跟小亡输入的变化,这时所,‘;生的误茸ATMEL代理商列;为动怂误差。
简述测量误差的概念和分类
测量误差是指实际测量值与真实值之间的差异。
由于各种原因,任何测量都无法完全准确地得到真实值,因此会存在测量误差。
测量误差可以分为系统误差和随机误差两类。
1. 系统误差:系统误差是指由于测量仪器的固有缺陷或操作者的偏差等原因导致的测量值与真实值之间的差异。
系统误差是一种有规律的误差,通常表现为测量值有一个固定的偏离真实值的趋势。
系统误差可以进一步分为常数误差和比例误差。
- 常数误差:常数误差是指测量值与真实值之间存在一个恒定
的偏差,无论测量值的大小如何,偏差都保持不变。
常数误差可以通过对测量结果进行适当的修正来减小。
- 比例误差:比例误差是指测量值与真实值之间存在一个比例
关系,测量值与真实值之间的差异随测量值的增大而增大或减小。
比例误差通常由于仪器的灵敏度不一致或者误差放大等原因造成。
2. 随机误差:随机误差是指由于各种不确定因素导致的测量值的随机变动。
随机误差是无规律的,通常表现为测量值的一系列波动,使得测量值呈现出一种分散的趋势。
随机误差可通过多次重复测量取平均值或应用统计方法来减小。
测量误差的存在是不可避免的,但可以通过使用合适的仪器和方法,以及进行适当的校正和修正来减小误差,从而增加测量结果的准确性和可靠性。
测量误差的分类以及解决方法1、系统误差能够保持恒定不变或按照一定规律变化的测量误差,称为系统误差。
系统误差主要是由于测量设备、测量方法的不完善和测量条件的不稳定而引起的。
由于系统误差表示了测量结果偏离其真实值的程度,即反映了测量结果的准确度,所以在误差理论中,经常用准确度来表示系统误差的大小。
系统误差越小,测量结果的准确度就越高。
2、偶然误差偶然误差又称随机误差,是一种大小和符号都不确定的误差,即在同一条件下对同一被测量重复测量时,各次测量结果服从某种统计分布;这种误差的处理依据概率统计方法。
产生偶然误差的原因很多,如温度、磁场、电源频率等的偶然变化等都可能引起这种误差;另一方面观测者本身感官分辨能力的限制,也是偶然误差的一个来源。
偶然误差反映了测量的精密度,偶然误差越小,精密度就越高,反之则精密度越低。
系统误差和偶然误差是两类性质完全不同的误差。
系统误差反映在一定条件下误差出现的必然性;而偶然则反映在一定条件下误差出现的可能性。
3、疏失误差疏失误差是测量过程中操作、读数、记录和计算等方面的错误所引起的误差。
显然,凡是含有疏失误差的测量结果都是应该摈弃的。
解决方法:仪表测量误差是不可能绝对消除的,但要尽可能减小误差对测量结果的影响,使其减小到允许的范围内。
消除测量误差,应根据误差的来源和性质,采取相应的措施和方法。
必须指出,一个测量结果中既存在系统误差,又存在偶然误差,要截然区分两者是不容易的。
所以应根据测量的要求和两者对测量结果的影响程度,选择消除方法。
一般情况下,在对精密度要求不高的工程测量中,主要考虑对系统误差的消除;而在科研、计量等对测量准确度和精密度要求较高的测量中,必须同时考虑消除上述两种误差。
1、系统误差的消除方法(1)对测量仪表进行校正在准确度要求较高的测量结果中,引入校正值进行修正。
(2)消除产生误差的根源即正确选择测量方法和测量仪器,尽量使测量仪表在规定的使用条件下工作,消除各种外界因素造成的影响。
采用特殊的测量方法如正负误差补偿法、替代法等。
例如,用电流表测量电流时,考虑到外磁场对读数的影响,可以把电流表转动180度,进行两次测量。
在两次测量中,必然出现一次读数偏大,而另一次读数偏小,取两次读数的平均值作为测量结果,其正负误差抵消,可以有效地消除外磁场对测量的影响。
2、偶然误差的消除方法消除偶然误差可采用在同一条件下,对被测量进行足够多次的重复测量,取其平均值作为测量结果的方法。
根据统计学原理可知,在足够多次的重复测量中,正误差和负误差出现的可能性几乎相同,因此偶然误差的平均值几乎为零。
所以,在测量仪器仪表选定以后,测量次数是保证测量精密度的前提。
.容:四、测量系统变差的类型1.测量过程变差2.测量过程变差分析3.测量过程FMEA MSA分析计划位置变差宽度变差测量系统变差对产品决策的影响产品特殊特性及顾客风险分析对过程决策的影响GRR对能力指数Cp的影响测量系统预测性和预防性维护五、计量型测量系统研究1.确定测量系统偏倚的2.确定测量系统稳定性3.确定测量系统线性4.确定重复性和再现性1.测量过程控制图2. 独立样本法3. 控制图样本法4. GRR分析5. Excel应用6. Minitab的应用六、计数型测量系统研究1.假设检验分析2.交叉表3. 量具性能曲线1.交叉表方法2.置信区间计算3.复杂测量系统实践测量分析系统在测试数据分析中的应用周群波[1]王舒[2](杭州鸿雁电器有限公司杭州310012)摘要通过对测量数据产生偏差的原因进行分析,有针对性地描述了测量分析系统(MSA)在测试数据分析中的具体应用情况,说明MSA的应用可以减少实验室在仪器设备、人员操作、环境、方法以及应样品的差异造成的测试结果的偏差,从而有效提高实验室的检测能力和检测精度。
关键词误差测量系统分析应用1 引言在一般实验室中,检测人员对得出的实验数据的处理通常是记录下来,然后跟标准中的要求进行比较得出一个合格与否的结论。
而所使用的设备和测量仪器的好坏仅依靠一年一次的校准、检定或者定期的期间核查来做为判定依据,这样就可能无法保证实验数据的可靠性,其所代表的产品批次的质量也不能得到完全的证实。
从而浪费了大量的实验数据极其所包含的大量信息。
而如果我们能应用测量系统分析(MSA),也就是通过使用一些合适的统计技术对这些数据进行分析,就可以减少因设备引起的误差,并得到测试中所隐含的信息,从而大大提高测试数据的可靠性。
2 测试数据偏差分析对测试过程而言,产生测试数据偏差的因素一般有三种:随机误差、系统误差和测试设备本身随时间而产生的偏倚。
随机误差指在对同一测量的多次测量中,受偶然因素影响而以不可预知的方式变化的误差,它由设备的精度决定。
系统误差指在对同一测量的多次测量中,它保持不变或按某种规律而变化的误差,是除测量仪器精度以外的其他测量系统的因素所造成的。
我们平时所说的产品质量特性的测试结果就是该产品由于受到随机误差和系统误差的综合影响而表现出质量的差异和波动。
偏倚是由测试设备产生的另一种误差,指设备本身产生变化而引起的测量值与真实值之间的不一致。
也就是说随时间变化设备的同一数据产生了漂移。
针对上述三种因素,我们可以应用不同的测量统计分析技术来消除混沌的和不合理的误差来源,现分述如下:2.1 随机误差随机误差通常用重复性变差(EV)表示,即由一个评价人使用相同的测量仪器对同一个样品上同一特征进行多次测试所得到的测量变差;它是设备本身所固有的,也叫设备变差。
重复性产生的变差是随机的,因此所测得数据是服从正态分布的,可以用EXCEL中提供的统计函数AVERAGE计算数据组的均值,用函数STDEV计算数据组的偏差,根据均值和偏差得出测量值的上下限值。
将新测得的数值加入到以往的数据组中进行计算。
看测得的数值是否在上下限即统计容许区间内就可判断数据的正确性及可靠性即设备精度是否可靠。
实验室中对设备的期间核查就可应用这种方法来进行判断。
例如由同一个检测人员定期用同一把数显卡尺对一个基准件测量其尺寸,测得一组n=12个数据:5.99、5.98、5.98、5.99、6.00、6.01、6.00、6.01、6.02、6.00、5.99、6.01,用AVERAGE计算数据组的均值为 5.9983,STDEV 计算数据组的偏差为0.0127,取1-a=0.95的容许区间即k(12,0.95,0.95)=2.12,可计算出上下区间Li=6.0008-2.12×0.0116=5.9714、Ls=6.0008+2.12×0.0116=6.0252,由此可见这组数据均是落在区间内的,测得的数据是可信任的。
2.2 系统误差系统误差用再现性变差(AV)表示,指不同的评价人使用相同的测量仪器对同一个样品上同一特征,进行测量所得的平均值的变差;也叫评价人变差。
在再现性的计算中包括了重复性。
从更广的定义上,再现性不仅可以用来判断因评价人的不同而导致结果的不同程度,同时还可以判断因:仪器设备、试验方法、试验室及环境(温度、湿度)的不同,即实验室与实验室的差别,而导致结果的不同程度。
可用于外部和内部的比对试验以及作为试验方法、环境等改进的依据。
我们在进行产品质量分析,根据测试结果所得到的数据,在分析哪个或哪几个因素对质量特性的差异影响显著时,需要用方差分析的方法将两种误差分离后再进行比较。
为减少计算量,一般利用EXCEL 中工具栏提供的数据分析项就可直接得出结果。
以下是单因素方差分析的具体计算方法:令:R=全部数据的平方和;Q=各组数据之和的平方除于本组数据个数n后再相加;P=全部数据之和的平方除于总的数据个数N。
于是:总方差S总=R-P随机误差S e=R-Q;系统误差S A=S总-S e= Q-P;统计量:MS A=S A/(组数-1)= Q-P/(组数-1);M S e=S e/(总的数据个数-组数)= R-Q/(总的数据个数-组数);F= MS A/ M S e=[ Q-P/(组数-1)]/ [R-Q/(总的数据个数-组数)]统计量F服从自由度为[(组数-1),(总的数据个数-组数)]的F分布,若计算的F值大于某一临界值F a可认为系统误差的影响是显著的。
一般以a=0.05做为显著性判断的临界值,a=0.01为特别显著。
一般用GRR来表示量具的重复性和再现性。
也就是说,GRR值等于系统内部变差和系统之间变差的和即GRR=[(AV)2+(EV)2]0.5.通常用%GRR来判断测量系统整体的可接受程度,%GRR <10%表示测量系统可接受, %GRR>30%表示测量系统不可接受。
%GRR=100[GRR/TV]=100 GRR/ [(GRR)2+(PV)2]0.5,其中TV为总变差,PV为样品特征值的变差由样品特征值平均值的极差(RP)乘以一个常数所决定。
2.3 偏倚偏倚(通常被称为“准确度”)指对相同样品上同一特征值与真值(参考值)的差异。
偏倚等于测量的平均值减去参考值。
造成过大的偏倚的可能原因有:仪器需要校准;仪器、设备或夹具磨损;基准的磨损或损坏,基准偏差;不适当的校准或使用基准设定;仪器质量不良;线性误差;使用错误量具;不同的测量方法;测量的特性不对;环境(温度、湿度等);变形(量具或试样)等。
得出一组偏倚值,可以按区间的计算方法算出偏倚值附近的1-a置信区间,若0落在置信区间内,则偏倚在这a水准上是可接受的(一般采用95%的置信度)。
偏倚不可接受时,应对测量系统进行仔细检查,找出原因加以解决。
如果测量系统的偏倚不等于零。
若有可能,应该采用硬件修正法、软件修正法或同时使用两种方法对量具进行重新校准以达到零偏倚。
如调整仪器零位和/或给设备添加修正值表对测量值进行修正。
3 结束语针对产生误差的不同原因,用不同的方法对测量数据进行整合统计分析,就可根据分析结论,从人、机、料、法、环各个环节对测量系统进行控制加以改进。
对复杂的或不可重复的测量系统,还可以进一步用稳定性研究和变差研究来进行分析,例如发动机或变速箱动力计试验等。
当然,在应用测量分析系统前首先要知道使用什么样的数据是重要的,要确定该系统要具备哪些可被接受的统计特征,否则就不能确定适当的统计特性,不能正确使用测量系统分析。
把测量系统分析(MSA)应用到实验室测试数据分析过程中,减少实验室在仪器设备、人员操作、环境、方法以及应样品的差异造成的测试结果的偏差,提高实验室的检测能力和检测精度,可以将产品的质量控制由事后检验提高到进行事先预防的过程控制,对推进质量管理,具有非常重要的意义。