运筹学上机试题1-运输问题

实验报告2：P153习题1某公司在三个地方有三个分厂，生产同一种产品，其产量分别为300箱、600箱、500箱。

需要供应四个地方的销售，这四地的产品需求分别为400箱、250箱、350箱、200箱。

三个分厂到四个产地的单位运价如表所示。

应如何安排运输方案，使得总运费为最小。

在此问题中，三个分厂的总产量为1400单位，而总需求量为1200单位。

因此此问题为供求不相等的运输问题，且供大于求。

为此，除已有的四个销地外，可假设一销地，且三个分厂运往此销地的单位运费均为0。

即将假设的销地看为存储的仓库。

求解过程最优解如下********************************************起至销点发点 1 2 3 4-------- ---- ----- ----- -----1 0 250 0 502 400 0 0 03 0 0 350 150此运输问题的成本或收益为: 19800此问题的另外的解如下：起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 0 250 50 02 400 0 0 03 0 0 300 200此运输问题的成本或收益为: 19800（2）如果2 分厂产量提高到600，则为产销不平衡问题最优解如下******************************************** 起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 0 250 0 02 400 0 0 2003 0 0 350 0此运输问题的成本或收益为: 19050注释：总供应量多出总需求量200第1 个产地剩余50第3 个产地剩余150（3）销地甲的需求提高后，也变为产销不平衡问题最优解如下******************************************** 起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 50 250 0 02 400 0 0 03 0 0 350 150此运输问题的成本或收益为: 19600总需求量多出总供应量150第1 个销地未被满足，缺少100第4 个销地未被满足，缺少50P255 习题1这是一个最短路问题，要求我们求出从v1 到v7 配送的最短距离。

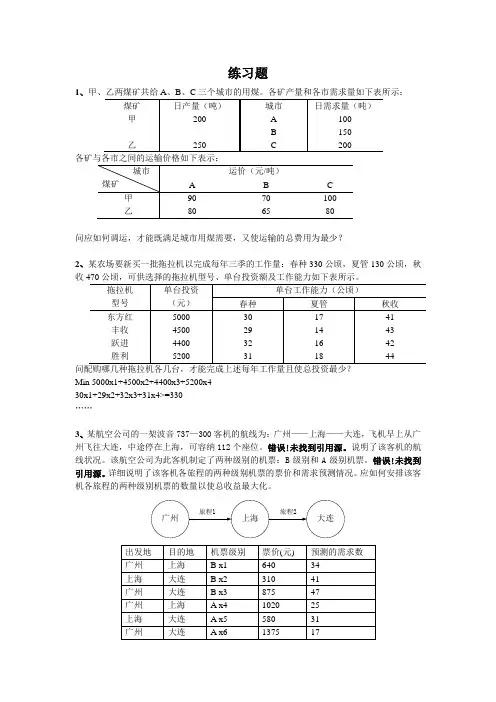
练习题1、各矿与各市之间的运输价格如下表示：问应如何调运，才能既满足城市用煤需要，又使运输的总费用为最少？2、某农场要新买一批拖拉机以完成每年三季的工作量：春种330公顷，夏管130公顷，秋收470公顷，可供选择的拖拉机型号、单台投资额及工作能力如下表所示。

Min 5000x1+4500x2+4400x3+5200x430x1+29x2+32x3+31x4>=330……3、某航空公司的一架波音737—300客机的航线为：广州——上海——大连，飞机早上从广州飞往大连，中途停在上海，可容纳112个座位。

错误！未找到引用源。

说明了该客机的航线状况。

该航空公司为此客机制定了两种级别的机票：B级别和A级别机票。

错误！未找到引用源。

详细说明了该客机各旅程的两种级别机票的票价和需求预测情况。

应如何安排该客机各旅程的两种级别机票的数量以使总收益最大化。

MaxX1+X3+X4+X6<=122;4、有A1，A2，A3三个水泥厂，每天要把生产的水泥运往B1，B2两地。

各厂的产量、各地的需求量（销量）以及各厂地间的运价见下表。

问如何设计调运方案才能使总运费最少？56、设有三个化肥厂（A、B、C）供应四个地区（Ⅰ、Ⅱ、Ⅲ、Ⅳ）的农用化肥。

假定等量的花费在这些地区的使用效果相同。

各化肥厂年产量，各地区需要量及从各化肥厂到各地区运送单位化肥的运价表如下表所示。

试求出总的运费最节省的化肥调拨方案。

若规定每人专门负责一个语种的翻译工作，那么，试回答下列问题：（1）应如何指派，使总的翻译效率最高？（2）若甲不懂德文，乙不懂日文，其他数字不变，则应如何指派？8、某市六个新建单位之间的交通线路的长度（公里）如下表所示。

其中单位A距市煤气供应网最近，为1.5公里。

应如何铺设煤气管道使其总长最短。

9、在下面的网络中，试求：①各点到点t的最短路；②点s到各点的最短路。

-2410、求出下图所示的网络的最大流。

11、试确定关键路径和总工期。

4 运输问题1、运输问题表上作业法的基本步骤。

答：表上作业法的基本步骤可参照单纯形法归纳如下：（1）找出初始基可行解：即要在阶产销平衡表上给出“”个数字格（基变量）；（2）求各非基变量（空格）的检验数，判断当前的基可行解是否是最优解，如已得到最优解，则停止计算，否则转到下一步；(3确定入基变量，若，那么选取为入基变量；(4确定出基变量，找出入基变量的闭合回路，在闭合回路上最大限度地增加入基变量的值，那么闭合回路上首先减少为“0”的基变量即为出基变量；（5）在表上用闭合回路法调整运输方案；（6）重复2、3、4、5步骤，直到得到最优解。

2、“最小元素法”和“伏格尔”法的基本思想及基本操作。

答：最小元素法的基本思想是就近供应，即从单位运价表中最小的运价开始确定产销关系，依此类推，一直到给出基本方案为止。

伏格尔法把费用增量定义为给定行或列次小元素与最小元素的差（如果存在两个或两个以上的最小元素费用增量定义为零）。

最大差对应的行或列中的最小元素确定了产品的供应关系，即优先避免最大的费用增量发生。

当产地或销地中的一方在数量上供应完毕或得到满足时，划去运价表中对应的行或列，再重复上述步骤，即可得到一个初始的基可行解。

3、闭合回路的构成以及利用闭合回路法求检验数的基本操作。

答：判断基可行解的最优性，需计算空格（非基变量）的检验数。

闭合回路法即通过闭合回路求空格检验数的方法。

从给定的初始方案的任一空格出发寻找闭合回路，闭合回路顶点所在格括号内的数字是相应的单位运价，单位运价前的“+”、“-”号表示运量的调整方向。

空格处单位运量调整所引起的运费增量就是空格的检验数。

仿照此步骤可以计算初始方案中所有空格的检验数。

4、利用位势法求检验数以及利用闭合回路进行方案调整的基本操作。

答：位势法求解非基变量检验数的基本步骤：第一步：把方案表中基变量格填入其相应的运价并令；让每一个基变量都有，可求得所有的位势；第二步：利用计算各非基变量的检验数方案的优化基本步骤：在负检验数中找出最小的检验数，该检验数所对应的变量即为入基变量。

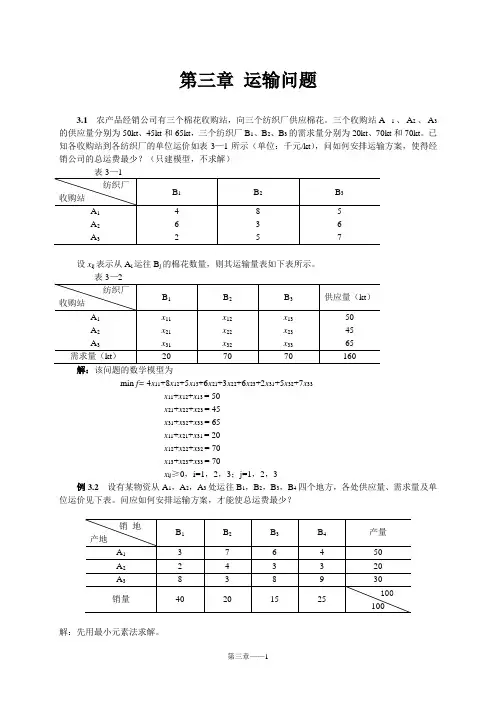
第三章运输问题3.1农产品经销公司有三个棉花收购站，向三个纺织厂供应棉花。

三个收购站A1、A2、A3的供应量分别为50kt、45kt和65kt，三个纺织厂B1、B2、B3的需求量分别为20kt、70kt和70kt。

已知各收购站到各纺织厂的单位运价如表3—1所示（单位：千元/kt），问如何安排运输方案，使得经销公司的总运费最少？（只建模型，不求解）设x ij表示从A i运往B j的棉花数量，则其运输量表如下表所示。

表3—2min f= 4x11+8x12+5x13+6x21+3x22+6x23+2x31+5x32+7x33x11+x12+x13 = 50x21+x22+x23 = 45x31+x32+x33 = 65x11+x21+x31 = 20x12+x22+x32 = 70x13+x23+x33 = 70x ij≥0，i=1，2，3；j=1，2，3例3.2设有某物资从A1，A2，A3处运往B1，B2，B3，B4四个地方，各处供应量、需求量及单位运价见下表。

问应如何安排运输方案，才能使总运费最少？解：先用最小元素法求解。

用位势法对基可行解进行最优性检验。

位势方程组为u1+v1=3 u1+v3=6 u1+v4=4u2+v1=2u3+v2=3u3+v3=8取u1=0，解上述方程组得u1=0u2=－1u3=2v1=3v2=1v3=6v4=4各非基变量的检验数为σ12 =c12－（u1+v2）=7－（0+1）= 4>0σ22 =c22－（u2+v2）=4－（－1+1）= 2>0σ23 =c23－（u2+v3）=3－（－1+6）= －2<0σ24 =c24－（u2+v4）=3－（－1+4）= 0σ31 =c31－（u3+v1）=8－（2+3）= 3>0σ34 =c34－（u3+v4）=9－（2+4）= 3>0由于σ23 =－2<0，故表中基可行解不是最优解。

由于σ该闭回路上，偶数顶点上的基变量最小值为5，以该调整量进行调整得到如表3—11的新的基可行解。

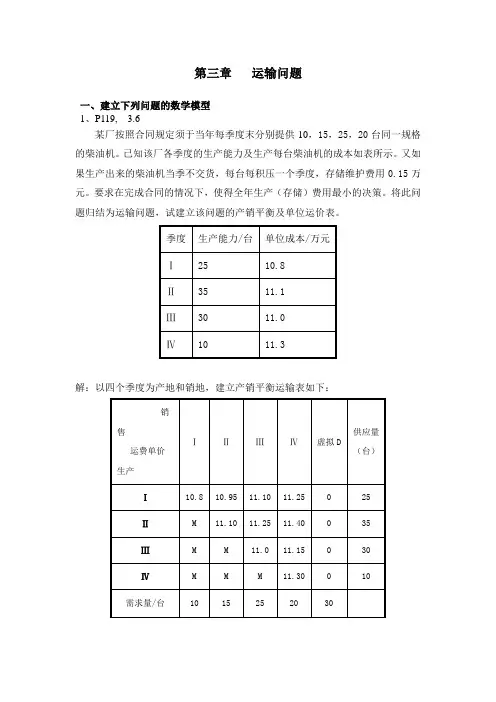
第三章运输问题一、建立下列问题的数学模型1、P119, 3.6某厂按照合同规定须于当年每季度末分别提供10，15，25，20台同一规格的柴油机。

已知该厂各季度的生产能力及生产每台柴油机的成本如表所示。

又如果生产出来的柴油机当季不交货，每台每积压一个季度，存储维护费用0.15万元。

要求在完成合同的情况下，使得全年生产（存储）费用最小的决策。

将此问题归结为运输问题，试建立该问题的产销平衡及单位运价表。

解：以四个季度为产地和销地，建立产销平衡运输表如下：2、P119, 3.7上题中若允许某些季度末交货时发生短缺，但全部合同必须于Ⅳ季度末完成。

又缺货时，每台每晚交一个季度，罚款0.1万元。

为使总的生产、存储和缺货罚款损失费用最小，重新列出用运输问题求解时的产销平衡和单位运价表。

解：以四个季度为产地和销地，建立产销平衡运输表如下：3、P119, 3.8某造船厂在某年算起的连续三年的年末各提供三条规格相同的货轮，已知该厂今后三年的的生产能力及生产成本如下表所示。

已知加班生产时每条货轮成本比正常生产时高70万元，又知造出的货轮如当年不交货，每条每积压一年增加维护费用40万元。

在签订合同时，已有以前积压的两条，该厂希望在第三年末交货后多留一条备用。

问该厂应如何安排生产计划，满足上述要求，并使得总费用最小。

请列出产销平衡表和单位运价表。

解4、P120, 3.9为确保飞行的安全，飞机上的发动机每半年必须强迫更换进行大修。

某维修厂估计某种型号的战斗机从下一个半年起的今后三年内每半年需更换的发动机数量分别为：100,70,80,120,150,140（台）。

更换发动机时，可以换上新的，也可以用经过大修的旧的发动机。

已知每台新发动机的购置费是10万元，而旧发动机的维修方式有两种：快修，每台2万元，半年交货（本期拆下，下期即可用上，半年为一期）；慢修，每台1万元，一年才能交货（本期拆下，下下期可用上）。

该厂新接手该项发动机的更换维修任务，又知三年后这种战斗机将退役，退役后这种发动机将报废。

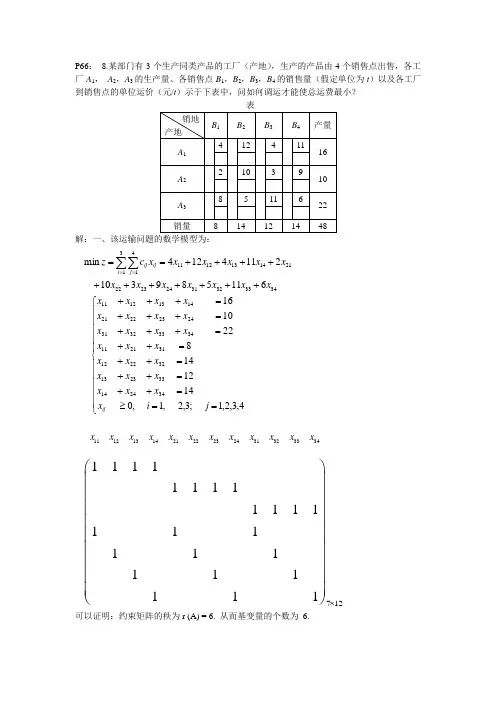
P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。

其余（非基）变量全等于零。

此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。