贵州省贵阳清镇市普通中学毕业生和专任教师数量综合情况3年数据研究报告2020版

（2023年）贵州省贵阳市公务员省考行政职业能力测验真题(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、1.常识判断(10题)1. 缺乏维生素A会得什么病?( )A.牙龈出血B.脚气C.皮肤病D.手脚肿胀2. 在国家垄断资本主义条件下，国家对经济生活进行干预和调节，其实质是( )+A.提高就业率，促使资本主义经济稳定增长B.保持经济总量平衡，抑制通货膨胀C.加强垄断资本对广大劳动人民的剥削D.维护垄断资产阶级的整体利益和长远利益3. 《 消费者权益保护法》规定，消费者享有知悉其购买、使用的商品或接受的服务的真实情况的权利，这里的“知情权”应不包括( )。

A.商品的价格B.商品的进货渠道C.商品的检验合格证明D.商品的生产日期4. 2009年12月4日，我国首款拥有自主知识产权的( )在上海诞生，国内众多消费电子厂商一直以来百分百依赖进口的局面被打破。

A.中国芯B.基因芯片C.商用微机电芯片陀螺仪D.蛋白质芯片5. 西方侵略者洗掠并烧毁了被誉为“万园之园”的圆明园是在( )。

A.第一次鸦片战争B.第二次鸦片战争C.甲午战争D.中法战争6. 我国《 合同法》中经常出现“当事人另有约定的，按照其约定”这一表述，它体现了民法基本原则中的( )。

A.平等原则B.意思自治原则C.诚实信用原则D.禁止权利滥用原则7. 关于公司名称、章程、住所、经营范围等的陈述，以下说法正确的是( )。

A.有限责任公司必须在公司名称中标明“有限责任公司”的字样，但股份有限公司就不必在公司名称中标明“股份有限公司”的字样了B.公司章程对公司所有员工都具有约束力C.甲公司在A市工商局登记设立，但其主要办事机构所在地是B市，则甲公司的住所地在B市D.某公司章程规定该公司只能生产塑胶产品，但该公司多次向胜利网络公司销售电脑配件，则该公司与胜利网络公司的销售合同无效8. 下列属于法人的是( )。

贵州省贵阳市（新版）2024高考数学统编版模拟(提分卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题神舟十五号飞行任务是中国载人航天工程2022年的第六次飞行任务，也是中国空间站建造阶段最后一次飞行任务，航天员乘组将在轨工作生活6个月.某校为了培养学生们的航天精神，特意举办了关于航天知识的知识竞赛，竞赛一共包含两轮.高三（9）班派出了和两位同学代表班级参加比赛，每轮竞赛和两位同学各答1题.已知同学每轮答对的概率是，同学每轮答对的概率是，每轮竞赛中和两位同学答对与否互不影响，每轮结果亦互不影响，则和两位同学至少答对3道题的概率为（ ）.A．B．C．D．第(2)题甲袋中有3个红球，3个白球和2个黑球；乙袋中有2个红球，2个白球和4个黑球.先从甲袋中随机取出一球放入乙袋，分别以，，表示事件“取出的是红球”、“取出的是白球”、“取出的是黑球”；再从乙袋中随机取出一球，以表示事件“取出的是白球”，则下列结论中不正确的是（ ）A ．事件，，是两两互斥的事件B．事件与事件为相互独立事件C．D．第(3)题已知直线不过坐标原点，且与椭圆相交于不同的两点的面积为，则的值是（ ）A．B．C．D ．不能确定第(4)题某幼儿园组织“宝贝计画”兴趣小组.“变变变”是“宝贝计画哲学”，源自《周易》“穷则变，变则通，通则久”，宝贝计画的终极理想是通过画画，让孩子还原想象､树立自信､感悟智慧､温存内心.某天中班有四个小朋友参加此项活动，每个人画了一幅《小猪佩奇》的画，他们先把作品放到一起再反扣在桌子上，每人从中随机的拿出一幅画，则四个小朋友拿到的都不是自己的作品的概率为（ ）A．B．C．D．第(5)题已知三棱柱ABC-A 1B 1C 1的侧面积为6+4，AA 1⊥平面ABC ，BC=，∠BAC=120°，则该三棱柱外接球表面积的最小值为（ ）A．B．C．D．第(6)题已知抛物线：的焦点为，点，直线与抛物线交于点（在第一象限内)，与其准线交于点，若，则点到轴距离为A．B．C．D．第(7)题庑殿顶是中国古代传统建筑中的一种屋顶形式，宋代称为“五脊殿”、“吴殿”，清代称为“四阿殿”，如图（1）所示.现有如图（2）所示的庑殿顶式几何体，其中正方形边长为3，，且到平面的距离为2，则几何体的体积为（）A．B．C．D．第(8)题已知平面区域中的点满足，若在圆面中任取一点，则该点取自区域的概率为（ ）A．B ．C ．D ．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题如图是电灯挂在圆形桌面正中央上方的示意图，电灯在点O 处，桌面直径为2m ，点M 是桌面边缘上一点，电灯与M 之间的光线与桌面所成角为，电灯与M 之间的距离为l ．根据光学原理，M 点处的照度I 满足关系式：（为常数，）．则下列说法正确的是（ ）A．记时的照度为，时的照度为，则B ．I 随l 的增大而减小C ．I 先随的增大而增大，后随的增大而减小D ．当时，I 取得最大值第(2)题若，则下列说法正确的是（ ）A ．的最小正周期是B．的对称轴方程为，C ．存在实数，使得对任意的，都存在且，满足，D ．若函数，，（是实常数），有奇数个零点，则第(3)题如图，在棱长为1的正方体中，点M 为线段上的动点（含端点），则（ ）A ．存在点M ，使得平面B ．存在点M ，使得∥平面C ．不存在点M ，使得直线与平面所成的角为D ．存在点M ，使得平面与平面所成的锐角为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知定义在上的函数满足，当时，.若在区间内，函数有三个不同零点，则实数的取值范围为__________.第(2)题某产品的广告费投入与销售额的统计数据如下表所示:广告费万元万元4235销售额万元万元49263954根据上表建立线性回归方程，预测当广告费投入6万元时，销售额约为_______万元.第(3)题已知数列满足是的等差中项，若，则实数的取值范围为__________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知椭圆与椭圆的左焦点均为F，且椭圆C的离心率与椭圆D的离心率的比值为．(1)求椭圆C的标准方程；(2)已知过点F的圆E与y轴交于点，与椭圆C在第一象限内的公共点为为M．点P在y轴正半轴上，且线段PQ为圆E的直径，线段MQ与x轴交于点N，求的值．第(2)题如图，在多面体中，为正三角形，平面，，，为的中点，为线段上的动点.(1)若，求点到平面的距离；(2)若平面，求平面与平面所成锐二面角的余弦值.第(3)题已知在数列中，，，其中，且，实数.(1)当时，求数列的通项公式；(2)是否存在常数，使得数列为等比数列？若存在，求出的值；若不存在，请说明理由.第(4)题为促进全面阅读，建设书香校园，鼓励学生参加阅读活动，某校随机抽查了男、女生各200名，统计他们在暑假期间每天阅读时长，并把每天阅读时长超过1小时的记为“阅读达标”，时长不超过1小时的记为“阅读不达标”，阅读达标与阅读不达标的人数比为，阅读达标的女生与男生的人数比为．(1)完成下面的列联表：性别阅读达标情况合计阅读达标阅读不达标男生女生合计(2)根据上述数据，依据小概率值的独立性检验，能否认为“阅读达标情况”与“性别”有关联？(3)从阅读达标的学生中按男、女生人数比例用分层随机抽样的方法抽取5人进行座谈，再从这5人中任选2人，记这2人中男生人数为X，求X的分布列和数学期望．参考公式：，．0.100.050.010.0012.7063.841 6.63510.828第(5)题已知为等差数列的前n项和，满足，___________.给出三个条件：①，②，③.试从上面三个条件中选择一个，补充在上面横线中，并给出下面两问的解答.(1)求的通项公式；(2)设，数列的前n项和为，若，求正整数n的值.注：如果选择多个条件分别解答，按第一个解答计分.。

2020年5月事业单位联考A类试卷和真题贵州1、47.小明上学要经过一段下坡路、一段上坡路和一段平路，共5.7千米。

下坡时的速度比平路快一半，上坡时的速度比平路慢1/3。

已知上坡、下坡和平路每段用时刚好相等，则下坡路多长?（）[单选题] *A. 2100米B. 2700米(正确答案)C. 3000米D. 3200米2、5.新年前夕，国家主席习近平通过中央广播电视总台和互联网，发表了二〇二一年新年贺词。

贺词指出，过去一年，“天问一号”、“嫦娥五号”、“奋斗者”号等科学探测实现重大突破。

关于我国科技成就，下列说法错误的是（）[单选题] *A. 2020年11月10日8时12分，奋斗者号在马里亚纳海沟成功坐底，坐底深度10909米，刷新中国载人深潜的新纪录B. 天问一号是执行中国第一次自主火星探测任务的探测器C. 嫦娥五号是中国探月工程五期发射的月球探测器，也是中国首个实施无人月面取样返回的月球探测器(正确答案)D. 长征五号B运载火箭是中国近地轨道运载能力最大的新一代运载火箭3、16.通用公文是党政机关、社会团体和企事业单位及其他社会组织在公务活动中普遍形成和使用的公文。

下列不属于通用公文的是（）[单选题] *A. 商洽函B. 工作报告C. 国书(正确答案)D. 知照性通知4、39.我国法定的法律解释体制，从总体上看是以全国人大常委会为主体的（）体制。

[单选题] *A垂直管理B集体领导C职能决策D分工配合(正确答案)5、51.某小区鼓励居民节约用水，对自来水用户按分段计费方式收取水费;在标准用水量以内，每吨的水费为1.2元，超过标准用水量的部分为每吨多交0.3元。

如果李家用水3吨，张家用水7吨，且张家比李家多交水费5.4元，则标准用水量为（）吨。

[单选题] *A. 3B. 4C. 5(正确答案)D. 66、35.疫情期间，吴某因出现发热、咳嗽等症状，被某市列为新冠肺炎疑似病人，并要求其在规定地点予以隔离治疗。

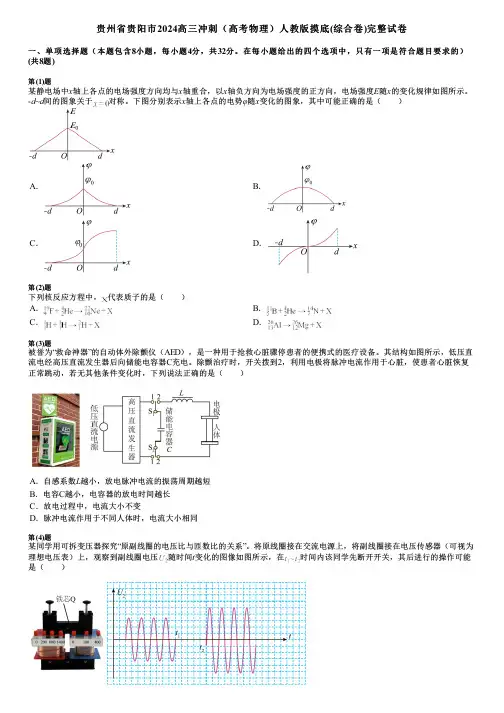
贵州省贵阳市2024高三冲刺（高考物理）人教版摸底(综合卷)完整试卷一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题某静电场中x轴上各点的电场强度方向均与x轴重合，以x轴负方向为电场强度的正方向，电场强度E随x的变化规律如图所示。

-d~d间的图象关于对称。

下图分别表示x轴上各点的电势φ随x变化的图象，其中可能正确的是（ ）A．B．C．D．第(2)题下列核反应方程中，代表质子的是（ ）A．B．C．D．第(3)题被誉为“救命神器”的自动体外除颤仪（AED），是一种用于抢救心脏骤停患者的便携式的医疗设备。

其结构如图所示，低压直流电经高压直流发生器后向储能电容器C充电。

除颤治疗时，开关拨到2，利用电极将脉冲电流作用于心脏，使患者心脏恢复正常跳动，若无其他条件变化时，下列说法正确的是（ ）A．自感系数L越小，放电脉冲电流的振荡周期越短B．电容C越小，电容器的放电时间越长C．放电过程中，电流大小不变D．脉冲电流作用于不同人体时，电流大小相同第(4)题某同学用可拆变压器探究“原副线圈的电压比与匝数比的关系”。

将原线圈接在交流电源上，将副线圈接在电压传感器（可视为理想电压表）上，观察到副线圈电压随时间t变化的图像如图所示，在时间内该同学先断开开关，其后进行的操作可能是（ ）A．增加了交流电源的频率B．拧紧了松动的铁芯QC．减少了副线圈的匝数D．增加了原线圈的匝数第(5)题下列有关四幅图像的说法正确的是（ ）A．图甲中振荡电路正在放电B．图乙中的发电机是旋转磁极式发电机C．图丙中的双线绕法可减小绕线的漏磁现象，从而减小磁场能的损失D．图丁中变化的磁场产生电场是一个普遍规律，与闭合电路是否存在无关第(6)题下列物理学历史的事件与观点符合事实的是（ ）A．伽利略在第谷的观察数据的基础上总结了行星运动定律B．居里夫人发现了天然放射性现象，打开了原子核的大门C．法拉第引入“电场线”“磁感线”等形象的方法来描述场D．爱因斯坦首先提出能量量子化的观点，成功解释了光电效应现象第(7)题下列实验能说明光具有波动性的是（ ）A．阴极射线实验B．α粒子轰击氮核实验C．光电效应实验D．杨氏双缝干涉实验第(8)题五一假期济宁太白湖公园的湖水里安装了一批圆形线状光源，将该光源水平放置于湖水下方处，该光源发出红光时，可在水面上观察到红色亮环，如图所示。

贵州省贵阳市2020年数学中考基础冲刺训练（二）一．选择题（每题3分，满分30分）1．已知x﹣2y＝﹣2，则3+2x﹣4y的值是（）A．0 B．﹣1 C．3 D．52．如图，在△ABC中有四条线段DE，BE，EF，FG，其中有一条线段是△ABC的中线，则该线段是（）A．线段DE B．线段BE C．线段EF D．线段FG3．下面是几个一样的小正方体摆出的立体图形的三视图，由三视图可知小正方体的个数为（）A．6个B．5个C．4个D．3个4．以下问题，适合用普查的是（）A．调查某种灯泡的使用寿命B．调查中央电视台春节联欢会的收视率C．调查我国八年级学生的视力情况D．调查你们班学生早餐是否有喝牛奶的习惯5．如图，在菱形ABCD中，AB＝2，∠B＝60°，E、F分别是边BC、CD中点，则△AEF 周长等于（）A．B．C．D．36．数轴上的点A表示的数是a，当点A在数轴上向右平移了6个单位长度后得到点B，若点A和点B表示的数恰好互为相反数，则数a是（）A．6 B．﹣6 C．3 D．﹣37．如果方程x2﹣8x+15＝0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，那么tan A的值为（）A．B．C．D．或8．用蓝色和红色可以混合在一起调配出紫色，小明制作了如图所示的两个转盘，其中一个转盘两部分的圆心角分别是120°和240°，另一个转盘两部分被平分成两等份，分别转动两个转盘，转盘停止后，指针指向的两个区域颜色恰能配成紫色的概率是（）A．B．C．D．9．在平面直角坐标系xOy中，若一次函数y＝kx﹣1（k≠0）的图象经过点P，且y的值随x 值的增大而减少，则点P的坐标可以为（）A．（2，1）B．（﹣2，1）C．（﹣2，﹣1）D．（2，﹣1）10．如图，抛物线y＝x2﹣7x+与x轴交于点A、B，把抛物线在x轴及其下方的部分记作C1，将C1向左平移得到C2，C2与x轴交于点B、D，若直线y＝x+m与C1、C2共有3个不同的交点，则m的取值范围是（）A．﹣＜m＜﹣B．﹣＜m＜﹣C．﹣＜m＜﹣D．﹣＜m＜﹣二．填空题（每题4分，满分20分）11．一次数学测试后，某班40名学生的成绩被分为5组，第1﹣4组的频数分别为12、10、6、8，则第5组的频率是．12．如图，点P是反比例函数y＝（k≠0）的图象上任意一点，过点P作PM⊥x轴，垂足为M．若△POM的面积等于2，则k的值等于．13．如图，正六边形ABCDEF的顶点B、C分别在正方形AGHI的边AG、GH上，如果AB＝4，那么CH的长为．14．若不等式组的解集是﹣1＜x≤1，则a＝，b＝．15．如图，在矩形ABCD中，AB＜BC，点E为CD边的中点，连接AE并延长与BC的延长线交于点F，过点E作EM⊥AF交BC于点M，连接AM与BD交于点N，现有下列结论：①AM＝MF；②ME2＝MC•AM；③＝（sin∠DAE）2；④点N是四边形ABME 的外接圆的圆心，其中正确结论的序号是．三．解答题16．（10分）体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况，从该校九年级136名女生中，随机抽取了20名女生，进行了1分钟仰卧起坐测试，获得数据如下：收集数据：抽取20名女生的1分钟仰卧起坐测试成绩（个）如下：38 46 42 52 55 43 59 46 253835 45 51 48 57 49 47 53 5849（1）整理、描述数据：请你按如下分组整理、描述样本数据，把下列表格补充完整：范围25≤x≤2930≤x≤3435≤x≤3940≤x≤4445≤x≤4950≤x≤5455≤x≤59人数（说明：每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分）（2）分析数据：样本数据的平均数、中位数、满分率如下表所示：平均数中位数满分率46.8 47.5 45%得出结论：①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为；②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下：平均数中位数满分率45.3 49 51.2%请你结合该校样本测试成绩和该区县总体测试成绩，为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估，并提出相应建议．17．（8分）某商场销售进价为每件x元的上衣，先按进价的2倍作为定价，而实际销售时按定价打八折出售．（1）试用代数式表示：①每件上衣最初的定价为元；②每件上衣打八折后的销售价为元；③n件上衣打八折后的利润为元；（2）若该商场这次共购进每件120元的上衣100件，按以上办法售出80件后，其余按定价的六折销售全部卖完，问该商场在这批上衣买卖中，除支付销售费用1000元外，盈亏情况如何？18．如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点D是边AC的中点，CF⊥BD，垂足为点F，延长CF与边AB交于点E．求：（1）∠ACE的正切值；（2）线段AE的长．19．（10分）某水果店2400元购进一批葡萄，很快售完；又用5000元购进第二批葡萄，所购件数是第一批的2倍，但进价比第一批每件多了5元．（1）求第一批葡萄每件进价多少元？（2）若以每件150元的价格销售第二批葡萄，售出80%后，为了尽快售完，决定打折促销，要使第二批葡萄的销售利润不少于640元，剩余的葡萄每件售价至少打几折（利润＝售价﹣进价）？20．（10分）如图，在等腰Rt△ABC中，∠BAC＝90°，延长BA至点D，连结DC，过点B 作BE⊥DC于点E，F为BC上一点，FC＝FE．连结AF，AE．（1）求证：FA＝FE．（2）若∠D＝60°，BC＝10，求△AEF的周长．21．（10分）某种机器使用若干年后即被淘汰，该机器有一易损零件，为调查该易损零件的使用情况，随机抽取了100台已被淘汰的这种机器，经统计：每台机器在使用期内更换的该易损零件数均只有8，9，10，11这四种情况，并整理了这100台机器在使用期内更换的该易损零件数，绘制成如图所示不完整的条形统计图．（1）请补全该条形统计图；（2）某公司计划购买一台这种机器以及若干个该易损零件，用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率．①求这台机器在使用期内共更换了9个该易损零件的概率；②若在购买机器的同时购买该易损零件，则每个200元；若在使用过程中，因备用该易损零件不足，再购买，则每个500元．请你帮该公司用花在该易损零件上的费用的加权平均数进行决策：购买机器的同时应购买几个该易损零件，可使公司的花费最少？22．（10分）为满足市场需求，某超市在新年来临前夕，购进一款商品，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，如果每盒售价每提高1元，则每天要少卖出20盒．（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？23．如图，AB为⊙O的直径，且AB＝4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点（不与点C重合），过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM．（1）求∠OMP的度数；（2）当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．24．我们知道：在小学已经学过“正方形的四条边都相等，正方形的四个内角都是直角”，试利用上述知识，并结合已学过的知识解答下列问题：如图1，在正方形ABCD中，G是射线DB上的一个动点（点G不与点D重合），以CG 为边向下作正方形CGEF．（1）当点G在线段BD上时，求证：∠DCG＝∠BCF；（2）连接BF，试探索：BF，BG与AB的数量关系，并说明理由；（3）若AB＝a（a是常数），如图2，过点F作FT∥BC，交射线DB于点T，问在点G 的运动过程中，GT的长度是否会随着G点的移动而变化？若不变，请求出GT的长度；若变化，请说明理由．25．如图，直线y＝x+2与x轴交于点B，与双曲线C1：（x＞0）交于点A，且A点的横坐标为2．（1）求双曲线C1的函数解析式；（2）若P为C1上的一动点，连接PO．①将PO绕O点顺时针旋转90°，得到点P′，问P′是否在某定曲线C1上运动，若是，试求C1的解析式，若不是，说明理由；②若△AOP的面积为，直接写出P点坐标为．参考答案一．选择题1．解：由x﹣2y＝﹣2，得到原式＝3+2（x﹣2y）＝3﹣4＝﹣1．故选：B．2．解：根据三角形中线的定义知线段BE是△ABC的中线，故选：B．3．解：综合三视图，这个立体图形的底层应该有3个，第二层应该有1个小正方体，因此构成这个立体图形的小正方体的个数是3+1＝4个．故选：C．4．解：A、调查某种灯泡的使用寿命，不能使用普查，错误；B、调查中央电视台春节联欢会的收视率被调查的对象都较大，不能使用普查，错误；C、调查我国八年级学生的视力情况被调查的对象都较大，不能使用普查，错误；D、调查你们班学生早餐是否有喝牛奶的习惯被调查的对象较小，故D宜使用普查；故选：D．5．解：如图，连接AC，∵菱形ABCD，∠B＝60°，∴△ABC是等边三角形，∵点E是BC的中点，∴AE＝，∠EAC＝30°，同理可得：AF＝，∠FAC＝30°，∴AE＝AF，∠EAC＝∠FAC，∴△AEF是等边三角形，∴△AEF的周长＝3×＝3．故选：B．6．解：由题意可得：B点对应的数是：a+6，∵点A和点B表示的数恰好互为相反数，∴a+a+6＝0，解得：a＝﹣3．故选：D．7．解：x2﹣8x+15＝0，（x﹣3）（x﹣5）＝0，则x﹣3＝0，x﹣5＝0，解得x＝3或5，①当3和5为直角边时：tan A＝．②当5为斜边时，另一直角边为4，tan A＝．故选：D．8．解：列表如下：红红蓝红紫蓝紫紫共有6种情况，其中配成紫色的有3种，所以恰能配成紫色的概率＝＝，故选：A．9．解：把（2，1）代入一次函数y＝kx﹣1得：2k﹣1＝1，k＝1，因此不可以；把（﹣2，1）代入一次函数y＝kx﹣1得：﹣2k﹣1＝1，k＝﹣1，因此可以；故选：B．10．解：∵抛物线y＝x2﹣7x+与x轴交于点A、B∴B（5，0），A（9，0）∴抛物线向左平移4个单位长度∴平移后解析式y＝（x﹣3）2﹣2当直线y＝x+m过B点，有2个交点∴0＝+mm＝﹣当直线y＝x+m与抛物线C2相切时，有2个交点∴x+m＝（x﹣3）2﹣2x2﹣7x+5﹣2m＝0∵相切∴△＝49﹣20+8m＝0∴m＝﹣如图∵若直线y＝x+m与C1、C2共有3个不同的交点，∴﹣＜m＜﹣故选：C．二．填空题11．解：根据题意得：40﹣（12+10+6+8）＝40﹣36＝4，则第5组的频率为4÷40＝0.1，故答案为：0.1．12．解：∵△POM的面积等于2，∴|k|＝2，而k＜0，∴k＝﹣4，故答案为：﹣4．13．解：正六边形的内角的度数＝＝120°，则∠CBG＝180°﹣120°＝60°，∴∠BCG＝30°，∴BG＝BC＝2，CG＝BC＝2，∴AG＝AB+BG＝6，∵四边形AGHI是正方形，∴GH＝AG＝6，∴CH＝HG﹣CG＝6﹣2，故答案为：6﹣2．14．解：∵解不等式①得：x＞1+a，解不等式②得：x≤﹣∴不等式组的解集为：1+a＜x≤﹣∵不等式组的解集是﹣1＜x≤1，∴1+a＝﹣1，﹣＝1，解得：a＝﹣2，b＝﹣3故答案为：﹣2，﹣3．15．解：∵四边形ABC都是正方形，∴AD∥BF，∴∠DAE＝∠F，∵∠AED＝∠FEC，DE＝EC，∴△ADE≌△FCE（AAS），∴AE＝EF，∵ME⊥AF，∴MA＝NF，故①正确，∵∠EMC＝∠EMF，∠ECM＝∠MEF，∴△MEC∽△MFE，∴ME：MF＝MC：ME，∴ME2＝MC•MF＝MC•AM，故②正确，∵∠AEM＝90°，∠ADE＝∠ECM＝90°，∴∠AED+∠MEC＝90°，∠MEC+∠EMC＝90°，∴∠AED＝∠EMC，∴△ADE∽△ECM，∴＝（）2＝（）2＝（tan∠DAE）2，故③错误，∵∠ABM＝∠AEM＝90°，∴A，B，M，E四点共圆，∴四边形的外接圆的圆心是线段AM的中点，显然点N不是AM的中点，故④错误．故答案为①②．三．解答题16．解：（1）补充表格如下：范围25≤x≤2930≤x≤3435≤x≤3940≤x≤4445≤x≤4950≤x≤5455≤x≤59人数 1 0 3 2 7 3 4 （2）①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为136×≈61，故答案为：61；②从平均数角度看，该校女生1分钟仰卧起坐的平均成绩高于区县水平，整体水平较好；从中位数角度看，该校成绩中等水平偏上的学生比例低于区县水平，该校测试成绩的满分率低于区县水平；建议：该校在保持学校整体水平的同时，多关注接近满分的学生，提高满分成绩的人数．17．解：（1）①每件上衣最初的定价为2x（元）；②每件上衣打八折后的销售价为2x•0.8＝1.6x（元）；③n件上衣打八折后的利润为n•（1.6x﹣x）＝0.6xn（元）；（2）0.6×120×80+2×120×0.6×20﹣120×20﹣1000＝5240（元），所以该商场在这批上衣买卖中盈利5240元．故答案为2x，1.6x，06xn．18．解：（1）∵∠ACB＝90°，∴∠ACE+∠BCE＝90°，又∵CF⊥BD，∴∠CFB＝90°，∴∠BCE+∠CBD＝90°，∴∠ACE＝∠CBD，∵AC＝4且D是AC的中点，∴CD＝2，又∵BC＝3，在Rt△BCD中，∠BCD＝90°．∴tan∠BCD＝＝，∴tan∠ACE＝tan∠CBD＝；（2）过点E作EH⊥AC，垂足为点H，在Rt△EHA中，∠EHA＝90°，∴tan A＝，∵BC＝3，AC＝4，在Rt△ABC中，∠ACB＝90°，∴tan A＝＝，∴＝，设EH＝3k，AH＝4k，∵AE2＝EH2+AH2，∴AE＝5k，在Rt△CEH中，∠CHE＝90°，∴tan∠ECA＝＝，∴CH＝k，∴AC＝AH+CH＝k＝4，解得：k＝，∴AE＝．19．解：（1）设第一批葡萄每件进价x元，根据题意，得：×2＝，解得x＝120．经检验，x＝120是原方程的解且符合题意．答：第一批葡萄每件进价为120元．（2）设剩余的葡萄每件售价打y折．根据题意，得：×150×80%+×150×（1﹣80%）×0.1y﹣5000≥640，解得：y≥7．答：剩余的葡萄每件售价最少打7折．20．（1）证明：∵BE⊥DC，∴∠EBC+∠ECB＝∠CEF+∠BEF＝90°，∵FC＝FE，∴∠ECB＝∠CEF，∴∠EBC＝∠BEF，∴BF＝FE＝FC，在Rt△BAC中，AF是斜边BC上的中线，∴FA＝FC，∴FA＝FE；（2）解：∵∠D＝60°，∠BAC＝90°，∴∠ACD＝30°，∵△ABC为等腰直角三角形，∴∠ABC＝∠ACB＝45°，∴∠ECF＝∠ACD+∠ACB＝30°+45°＝75°，由（1）得：FA＝FE，AF是斜边BC上的中线，∴AF⊥BC，AF＝BC＝5，∵FC＝FE，∴∠EFC＝180°﹣2∠ECF＝180°﹣2×75°＝30°，∴∠AFE＝90°﹣30°＝60°，∴△AEF是等边三角形，∴△AEF的周长＝3AF＝3×5＝15．21．解：（1）100﹣20﹣50﹣20＝10，补全的条形统计图如图所示：（2）①这台机器在使用期内共更换了9个该易损零件的概率为：P＝＝；②购买机器的同时购买8个该易损零件200×0.2+500×0.8＝440元，购买机器的同时购买9个该易损零件200×0.5+500×0.5＝350元，购买机器的同时购买10个该易损零件200×0.1+500×0.9＝470元，购买机器的同时购买11个该易损零件200×0.2+500×0.8＝440元，因此，购买机器的同时应购买9个该易损零件，可使公司的花费最少．22．解：（1）由题意得销售量y＝700﹣20（x﹣45）＝﹣20x+1600（x≥45）；（2）P＝（x﹣40）（﹣20x+1600）＝﹣20x2+2400x﹣64000＝﹣20（x﹣60）2+8000，∵x≥45，a＝﹣20＜0，＝8000元∴当x＝60时，P最大值即当每盒售价定为60元时，每天销售的利润P（元）最大，最大利润是8000元．23．解：（1）∵△OPE的内心为M，∴∠MOP＝∠MOC，∠MPO＝∠MPE，∴∠PMO＝180°﹣∠MPO﹣∠MOP＝180°﹣（∠EOP+∠OPE），∵PE⊥OC，即∠PEO＝90°，∴∠PMO＝180°﹣（∠EOP+∠OPE）＝180°﹣（180°﹣90°）＝135°，（2）如图，∵OP＝OC，OM＝OM，而∠MOP＝∠MOC，∴△OPM≌△OCM，∴∠CMO＝∠PMO＝135°，所以点M在以OC为弦，并且所对的圆周角为135°的两段劣弧上（和）；点M在扇形BOC内时，过C、M、O三点作⊙O′，连O′C，O′O，在优弧CO取点D，连DC，DO，∵∠CMO＝135°，∴∠CDO＝180°﹣135°＝45°，∴∠CO′O＝90°，而OA＝2cm，∴O′O＝OC＝×2＝，∴弧OMC的长＝＝π（cm），同理：点M在扇形AOC内时，同①的方法得，弧ONC的长为πcm，所以内心M所经过的路径长为2×π＝πcm．24．解：（1）∵四边形ABCD和四边形EFCG是正方形，∴CD＝CB，CG＝CF，∠BCD＝∠FCG＝90°，∵∠DCG＝90°﹣∠BCG，∠BCF＝90°﹣∠BCG，∴∠DCG＝∠BCF；（2）BF+BG＝AB，理由：在Rt△CDG和△CBF中，，∴△CDG≌CBF（SAS），∴DG＝BF，在Rt△ABD中，AD＝AB，∴BD＝AB，∵BD＝DG+BG＝BF+BG，∴BF+BG＝AB；（3）∵BD是正方形ABCD的对角线，∴∠CBD＝∠CDB＝45°，由（2）知，△CDG≌CBF（SAS），∴DG＝BF，∠CDG＝∠CBF＝45°，∴∠DBF＝∠CBD+∠CBF＝90°，∴∠FBT＝90°，∵FT∥CB，∴∠BTF＝∠CBD＝45°，∴∠BFT＝45°＝∠BTF，∴BF＝BT，∴DG＝BT，∴GT＝BG+BT＝BG+DG＝BD＝AB＝a．25．解：（1）当x＝2时，y＝x+2＝2+2＝4，∴点A坐标为（2，4），则k＝2×4＝8，∴双曲线C1的函数解析式为y＝；（2）①点P′在双曲线C2：y＝﹣上运动，设P （m ，） （m ＞0），如图，过点P 作PC ⊥x 轴于点C ，过点P ′作P ′D ⊥y 轴于点D ，则∠PCO ＝∠P ′DO ＝∠POP ′＝90°，∴∠POC ＝∠P ′OD ，又∵OP ＝OP ′，∴△OPC ≌△OP ′D （AAS ），∴OD ＝OC ＝m ，P ′D ＝PC ＝，∴P ′（m ，﹣），则点P ′在双曲线C 2：y ＝﹣上运动．②设P （n ，），如图2，过点A 作AE ⊥y 轴于点E ，作PF ⊥x 轴于点F ，延长EA 、FP 交于点M ，则四边形OEMF 是矩形，M （n ，4），∵A （2，4），∴AM ＝n ﹣2，PM ＝4﹣，∵S △AOP ＝S 矩形OEMP ﹣S △AOE ﹣S △POF ﹣S △AMP ， ∴＝4n ﹣4﹣4﹣（n ﹣2）（4﹣），整理，得：3n2﹣16n﹣12＝0，解得n＝6或n＝﹣（舍），当n＝6时，＝，∴点P（6，）．故答案为：（6，）．。

2023届贵州省贵阳市第一中学高考12月备考模拟性联考文科数学一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合，则表示的集合为（）{}{}1,0,1,2,2xA B y y =-==A B ⋂A. B. C. D. {}1-{1,0}-{1,2}{0,1,2}2. 复数，则（ ）3i11i z -=-+||z =C. 2D. 53. 某医疗公司引进新技术设备后，销售收入（包含医疗产品收人和其他收入）逐年翻一番，据统计该公司销售收入情况如图所示，则下列说法错误的是（）A. 该地区2021年的销售收入是2019年的4倍B. 该地区2021年的医疗产品收入比2019年和2020年的医疗产品收入总和还要多C. 该地区2021年其他收人是2020年的其他收入的3倍D. 该地区2021年的其他收入是2019年的其他收人的6倍4. 我国古代数学名著《九章算术》对立体几何有深入的研究，从其中一些数学用语可见，譬如“阳马”意指底面为矩形，一侧棱垂直于底面的四棱锥．某“阳马”的三视图如图所示，则它的最长侧棱与底面所成角的正切值为（）A. B. 1125. 已知焦点在坐标轴上且中心在原点的双曲线的一条渐近线方程为，若该双曲线2y x =过点，则它的方程为（）(1,1)A.B.C.D.2243y x -=2243x y -=2221y x -=2221x y -=6. 若不等式组所表示的平面区域被直线分成面积相等的两部分，0,2,35,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩(2)x m y =-则实数m 的值为（）A. 1B. C. D. 1213147. 已知直线与圆，则下列(2)(1)210()m x m y m m ++---=∈R 22:40C x x y -+=说法错误的是（ ）A. 对，直线恒过一定点m ∀∈RB. ，使直线与圆相切m ∃∈R C. 对，直线与圆一定相交m ∀∈R D. 直线与圆相交且直线被圆所截得的最短弦长为8. 以下关于的命题，正确的是（ ）21()sin cos cos 2f x x x x =-+A. 函数在区间上单调递增()f x 2π0,3⎛⎫ ⎪⎝⎭B. 直线是函数图象的一条对称轴π8x =()y f x =C. 点是函数图象的一个对称中心π,04⎛⎫ ⎪⎝⎭()y f x =D. 将函数图象向左平移个单位，可得到的图象()y f x =π82y x=9. 在中，分别为角的对边，且满足，则的ABC ,,a b c ,,A B C 22sin 2Cb a b -=ABC 形状为（）A. 直角三角形B. 等边三角形C 直角三角形或等腰三角形D. 等腰直角三角形10. 小明家订了一份牛奶，送奶人可能在早上6：30~7：00之间把牛奶送到小明家，小明出门去上学的时间在早上6：50~7：10之间，则小明在离开家之前能得到牛奶的概率是（ ）A. B. C. D. 1122378111211. 已知符号函数，函数满足1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩()f x ，当时，，则（ ）(1)(1),(2)()f x f x f x f x -=++=[0,1]x ∈π()sin 2f x x ⎛⎫= ⎪⎝⎭A. B. sgn(())0f x >404112f ⎛⎫= ⎪⎝⎭C. D. sgn((2))0(Z)f k k =∈sgn((2))|sgn |(Z)f k k k =∈12. 已知直线l 与曲线相切，切点为P ，直线l 与x 轴、y 轴分别交于点A ，B ，O 为e xy =坐标原点．若的面积为，则点P 的个数是（ ）OAB 1e A. 1B. 2C. 3D. 4二、填空题（本大题共4小题，每小题5分，共20分）13. 已知向量，若，则___________．(1,3),(3,4)a b == ()//()ma b a b -+ m =14. 153与119的最大公约数为__________．15. 若，则a 的值为___________．a =16. 如图，已知正方体的棱长为2，M ，N ，P 分别为棱1111ABCD A B C D -的中点，Q 为该正方体表面上的点，若M ，N ，P ，Q 四点共面，则点Q 的11,,AA CC AD 轨迹围成图形的面积为___________．三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤）17. 随着人民生活水平的不断提高，“衣食住行”愈发被人们所重视，其中对饮食的要求也愈来愈高．某地区为了解当地餐饮情况，随机抽取了100人对该地区的餐饮情况进行了问卷调查．请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图），解决下列问题．组别分组频数频率第1组[)50,60140.14第2组[)60,70m第3组[)70,80360.36第4组[)80,900.16第5组[)90,1004n合计（1）求m ，n ，x ，y 的值；（2）求中位数；（3）用分层抽样的方式从第四、第五组抽取5人，再从这5人中随机抽取2人参加某项美食体验活动，求抽到的2人均来自第四组的概率．18. 已知数列是递增的等比数列．设其公比为，前项和为，并且满足{}n a q n n S ，是与的等比中项．1534a a +=82a 4a （1）求数列的通项公式；{}n a （2）若，是的前项和，求使成立的最大正整数的n n b n a =⋅n T n b n 12100n n T n +-⋅>-n 值．19. 如图，在四棱锥中，底面是平行四边形，平面P ABCD -ABCD PD ⊥．,1,ABCD AD BD AB ===（1）求证：平面平面；PBD ⊥PBC （2）若二面角的大小为，求点D 到的距离．P BC D --60︒PBC 20. 已知椭圆过点．2222:1(0,0)x y C a b a b +=>>⎛ ⎝（1）求椭圆C 的方程；（2）已知直线与椭圆交于不同的两点P ，Q ，那么在x 轴上是否存在点M ，:2l y mx =+使且，若存在，求出该直线的方程；若不存在，请说明理由．MP MQ =MP MQ ⊥21. 已经函数．22e ()ln 2,()2()xf x a x xg x x ax a x =+=--∈R （1）求函数的单调性；()f x （2）若，求当时，a 的取值范围．()()()F x f x g x =+()0F x ≥请考生在第22、23两题中任选一题作答，并用2B 铅笔在答题卡上把所选题目的题号涂黑．注意所做题目的题号必须与所涂題题目的题号一致，在答题卡选答区城指定位置答题．如果多做，则按所做的第一题计分．22. 在平面直角坐标系中，曲线C 的参数方程为（为参数），xOy cos )cos )x y θθθθ⎧=-⎪⎨=+⎪⎩θ以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为O x l．πcos 4ρθ⎛⎫+=⎪⎝⎭（1）求直线和曲线的直角坐标方程；l C （2）从原点引一条射线分别交曲线和直线于两点，求的最O C l ,M N 22121||||OM ON +大值．23. 已知函数．()||2af x x a x =++-（1）当时，求不等式的解集；2a =()5f x ≤（2）设且的最小值为m ，若，求的最小值．0,0a b >>()f x 332m b +=32a b +2023届贵州省贵阳市第一中学高考12月备考模拟性联考文科数学一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合，则表示的集合为（）{}{}1,0,1,2,2xA B y y =-==A B ⋂A. B. C. D. {}1-{1,0}-{1,2}{0,1,2}【答案】C 【解析】【分析】由指数函数值域得，再根据交集的含义即可得到答案.{0}B yy =>∣【详解】根据指数函数值域可知，{0}B y y =>∣表示的集合为，A B ∴ {}1,2故选：C.2. 复数，则（ ）3i11i z -=-+||z =C. 2D. 5【答案】C 【解析】【分析】根据复数运算规则计算即可.【详解】 ，()221i 3i 3i 1i 22i 12i 1i 1i 1i 2z ------=-====-+++ ；2z ∴=故选：C.3. 某医疗公司引进新技术设备后，销售收入（包含医疗产品收人和其他收入）逐年翻一番，据统计该公司销售收入情况如图所示，则下列说法错误的是（）A. 该地区2021年的销售收入是2019年的4倍B. 该地区2021年的医疗产品收入比2019年和2020年的医疗产品收入总和还要多C. 该地区2021年其他收人是2020年的其他收入的3倍D. 该地区2021年的其他收入是2019年的其他收人的6倍【答案】D 【解析】【分析】设该地区2019年销售收入为，a 则由销售收入（包含医疗产品收人和其他收入）逐年翻一番，所以该地区2020年销售收入为，2a 该地区2021年销售收入为，4a 然后逐项分析即可.【详解】设该地区2019年销售收入为，a 则由销售收入（包含医疗产品收人和其他收入）逐年翻一番，所以该地区2020年销售收入为，2a 该地区2021年销售收入为，4a 选项A ：该地区2021年的销售收入是2019年的4倍，故选项A 正确；选项B ：由图可得该地区2021年的医疗产品收入为，40.7 2.8a a ⨯=该地区2019年的医疗产品收入为，0.90.9a a ⨯=该地区2020年的医疗产品收入为，20.8 1.6a a ⨯=由，0.9 1.6 2.5 2.8a a a a +=<故选项B 正确；选项C ：该地区2021年的其他收入为，40.3 1.2a a ⨯=2020年的其他收入为，20.20.4a a ⨯=所以该地区2021年其他收人是2020年的其他收入的3倍，故选项C 正确；选项D ：该地区2021年的其他收入为，40.3 1.2a a ⨯=2019年的其他收入为，0.10.1a a ⨯=所以该地区2021年的其他收入是2019年的其他收人的12倍，故选项D 不正确.故选：D.4. 我国古代数学名著《九章算术》对立体几何有深入的研究，从其中一些数学用语可见，譬如“阳马”意指底面为矩形，一侧棱垂直于底面的四棱锥．某“阳马”的三视图如图所示，则它的最长侧棱与底面所成角的正切值为（）A. B. 112【答案】C 【解析】【分析】首先还原几何体，并得到最长侧棱，根据线面角的定义，求线面角的正切值.【详解】如下图，还原几何体，其中平面，底面为矩形，SA ⊥ABCD，，，，1AB =2BC =AC =1SA =SB ==, SD==SC===SC 与底面所成的角是，SC SCA∠tanSASCAAC∠===故选：C5. 已知焦点在坐标轴上且中心在原点的双曲线的一条渐近线方程为，若该双曲线2y x=过点，则它的方程为（）(1,1)A. B. C. D.2243y x-=2243x y-=2221y x-=2221x y-=【答案】A【解析】【分析】根据渐近线设双曲线方程为，代入点坐标，计算得到答案.224y xλ-=【详解】双曲线的一条渐近线方程为，设双曲线方程为，2y x=224y xλ-=该双曲线过点，则，故双曲线方程为，(1,1)413λ-==2243y x-=故选：A6. 若不等式组所表示的平面区域被直线分成面积相等的两部分，0,2,35,xx yx y≥⎧⎪+≥⎨⎪+≤⎩(2)x m y=-则实数m的值为（）A 1 B. C. D.121314【答案】A【解析】【分析】画出不等式组所表示的平面区域,利用三角形面积公式，选择同一条边为底，高为一半即可.【详解】如图所示，不等式组所表示的平面区域为，0,2,35,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩ABC 为的中点，M BC 解得：、、、()0,2A 31,22B ⎛⎫ ⎪⎝⎭()0,5C 311,44M ⎛⎫ ⎪⎝⎭，此直线过定点.(2)x m y =-∴A 只要直线过点，(2)x m y =-M 就可以将分成面积相等的两部分.ABC 设直线的斜率为，k 则，即，解得.1124134k -==11m =1m =故选：A.7. 已知直线与圆，则下列(2)(1)210()m x m y m m ++---=∈R 22:40C x x y -+=说法错误的是（ ）A. 对，直线恒过一定点m ∀∈RB. ，使直线与圆相切m ∃∈RC. 对，直线与圆一定相交m ∀∈R D.直线与圆相交且直线被圆所截得的最短弦长为【答案】B 【解析】【分析】首先求出直线过定点，则可判断A ，求出圆心，，则()1,1P ()2,0C 2r =，根据点在圆内，则直线与圆一定相交，故可判断B,C ，对D选项，||2PC =<()1,1P 分析出时弦长最短，则.PC l ⊥l =【详解】直线，即，(2)(1)210m x m y m ++---=(2)210m x y x y +-+--=令，解得，即直线恒过定点，故A 正确；20210x y x y +-=⎧⎨--=⎩11x y =⎧⎨=⎩()1,1P 圆，即圆，圆心，半径，22:40C x x y -+=22:(2)4C x y -+=()2,0C 2r =则，即点在圆内，所以直线与圆一定相交，故B错||2PC ==<()1,1P 误，故C 正确，当时直线与圆相交且直线被圆所截得的弦长最短，最短弦长PCl ⊥，故D正确，l ==故选：B.8. 以下关于的命题，正确的是（ ）21()sin cos cos 2f x x x x =-+A. 函数在区间上单调递增()f x 2π0,3⎛⎫ ⎪⎝⎭B. 直线是函数图象的一条对称轴π8x =()y f x =C. 点是函数图象的一个对称中心π,04⎛⎫ ⎪⎝⎭()y f x =D. 将函数图象向左平移个单位，可得到的图象()y f x=π82y x=【答案】D【分析】根据三角函数恒等变换化简为21()sin cos cos 2f x x x x =-+，计算出，根据正弦函数的单调性，可判断π())4f x x =-ππ13π2(,4412x -∈-A;采用代入验证的方法可判断;根据三角函数的平移变换可得平移后的函数解析式，判B,C 断D.【详解】由题意得，2111π()sin cos cos sin 2cos 2)2224f x x x x x x x =-+=-=-当时，，由于函数在不单调，2π0,3x ⎛⎫∈ ⎪⎝⎭ππ13π2(,4412x -∈-sin y x =π13π(,)412-故函数在区间上不是单调递增函数，A 错误；()f x 2π0,3⎛⎫⎪⎝⎭当时，，故直线不是函数图象的对称轴，π8x =ππ8(4)f x⨯-==π8x =()y f x =B 错误；当时，，故点不是函数图象的对称中心，π4x =ππ1)42()4f x ⨯-==π,04⎛⎫ ⎪⎝⎭()y f x =C 错误；将函数图象向左平移个单位，可得到的()y f x =π8ππ)284y x x=+-=图象，D 正确，故选：D9. 在中，分别为角的对边，且满足，则的ABC ,,a b c ,,A B C 22sin 2Cb a b -=ABC 形状为（）A. 直角三角形B. 等边三角形C. 直角三角形或等腰三角形D. 等腰直角三角形【解析】【分析】根据三角恒等变换得，再由余弦定理解决即可.cos a b C =【详解】由题知，，22sin 2C b a b -=所以，21cos sin 222b a C Cb --==所以，得，cos b a b b C -=-cos a b C =所以，得，2222a b c a b ab +-=⋅222a cb +=所以的形状为直角三角形，ABC 故选：A10. 小明家订了一份牛奶，送奶人可能在早上6：30~7：00之间把牛奶送到小明家，小明出门去上学的时间在早上6：50~7：10之间，则小明在离开家之前能得到牛奶的概率是（ ）A. B. C. D. 11223781112【答案】D 【解析】【分析】根据题意，设送奶人到达时间为，小明出门去上学的时间为，则可以看x y (,)x y 成平面中的点，分析可得由试验的全部结果所构成的区域并求出其面积，同理可得事件所构成的区域及其面积，由几何概型公式，计算可得结果.A 【详解】设送奶人到达时间为，小明出门去上学的时间为，x y 记小明在离开家之前能得到牛奶为事件，A 以横坐标表示送奶人到达时间，以纵坐标表示小明出门去上学的时间，建立平面直角坐标系，小明在离开家之前能得到牛奶的事件构成的区域如图所示：由于随机试验落在长方形区域内任何一点是等可能的，所以符合几何概型的条件.根据题意，只要点落到阴影 部分，就表示小明在离开家之前能得到牛奶，即事件发生，A所以，120301010112()203012P A ⨯-⨯⨯==⨯故选：.D 11. 已知符号函数，函数满足1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩()f x ，当时，，则（ ）(1)(1),(2)()f x f x f x f x -=++=[0,1]x ∈π()sin 2f x x ⎛⎫= ⎪⎝⎭A. B. sgn(())0f x >404112f ⎛⎫= ⎪⎝⎭C. D. sgn((2))0(Z)f k k =∈sgn((2))|sgn |(Z)f k k k =∈【答案】C 【解析】【分析】计算得到A 错误，根据周期计算B 错误，根sgn((0))0f =40412f ⎛⎫= ⎪⎝⎭据定义计算C 正确，取，得到D 不正确，得到答案.1k =【详解】对选项A ：，错误；()sgn((0))sgn 00f ==对选项B ：，函数周期为，，错误；(2)()f x f x +=240411πsin 224f f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭对选项C ：，正确；()()sgn((2))sgn sin πsgn 00(Z)f k k k ===∈对选项D ：取，，，不正确.1k =()sgn((2))sgn((0))sgn 00f f ===|sgn1|1=故选：C12. 已知直线l 与曲线相切，切点为P ，直线l 与x 轴、y 轴分别交于点A ，B ，O 为e xy =坐标原点．若的面积为，则点P 的个数是（ ）OAB 1e A. 1 B. 2C. 3D. 4【答案】C 【解析】【分析】设出切点坐标，利用导数求切线斜率，写出切线方程，求出点A ，B 的坐标，表示的面积函数，求面积函数与直线有几个交点.OAB 1e y =【详解】设直线l 与曲线相切于，又，e xy =00(,)P x y e xy '=所以直线l 的斜率为，方程为，0e x k =000e e ()x x y x x -=-令，；令，,即，.0x =00(1)e xy x =-0y =01x x =-0(1,0)A x -00(0,(1)e )x B x -所以.0020001111(1)e (1)e 222x x OAB S OA OB x x x =⨯⨯=⨯-⨯-=-△设，则.21()(1)e 2x f x x =-[]211()2(1)(1)e (1)(1)e 22x xf x x x x x '⎡⎤=--+-=+-⎣⎦由，解得或；由，解得.()0f x '>1x <-1x >()0f x '<11x -<<所以在，上单调递增，在上单调递减.()f x ()1-∞-，()1+∞，()11-，，，，，且恒有21(1)e e f -=>43252511(4)2e 2e e e f -==⨯<(1)0f =2e 1(2)2e f =>成立，()0f x ≥如图，函数与直线有3个交点.()f x 1e y =所以点P 的个数为3.故选：C .二、填空题（本大题共4小题，每小题5分，共20分）13. 已知向量，若，则___________．(1,3),(3,4)a b == ()//()ma b a b -+m =【答案】1-【解析】【分析】根据平面向量的坐标运算以及向量平行的坐标表示可求出结果.【详解】因为，(1,3),(3,4)a b ==所以，，(3,34)ma b m m -=-- (4,7)a b +=因为，所以，解得.()//()ma b a b -+7(3)4(34)0m m ---=1m =-故答案为：.1-14. 153与119的最大公约数为__________．【答案】17【解析】【详解】因为，153119134,11934317,34172=⨯+=⨯+=⨯所以153与119的最大公约数为17.答案：1715. 若，则a 的值为___________．a =【答案】1【解析】【分析】利用对数的运算性质分别对分子分母化简即可得到结果.【详解】原式()()266666612log 3log 3log log 6332log 2-++⋅⨯=()()22666612log 3log 31log 32log 2-++-=.()666666621log 3log 6log 3log 212log 2log 2log 2--====故答案为：116. 如图，已知正方体的棱长为2，M ，N ，P 分别为棱1111ABCD A B C D -的中点，Q 为该正方体表面上的点，若M ，N ，P ，Q 四点共面，则点Q 的11,,AA CC AD轨迹围成图形的面积为___________．【答案】【解析】【分析】根据题意找出点Q 的轨迹围成图形为正六边形即可求解.PENFGM 【详解】如图，取的中点分别为，1111,,CD B C A B EFG 则点Q 的轨迹围成图形为正六边形，PENFGM，所以点Q的轨迹围成图形的面积为，6=故答案为:三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤）17. 随着人民生活水平的不断提高，“衣食住行”愈发被人们所重视，其中对饮食的要求也愈来愈高．某地区为了解当地餐饮情况，随机抽取了100人对该地区的餐饮情况进行了问卷调查．请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图），解决下列问题．组别分组频数频率第1组[)50,60140.14第2组[) 60,70m第3组[)70,80360.36第4组[)80,900.16第5组[)90,1004n 合计（1）求m，n，x，y的值；（2）求中位数；（3）用分层抽样的方式从第四、第五组抽取5人，再从这5人中随机抽取2人参加某项美食体验活动，求抽到的2人均来自第四组的概率．【答案】（1）30;0.04;0.030;0.004（2）71.67（3）35【解析】【分析】（1）根据频率分布表可求得，根据频率分布直方图中的含义即可求得其,m n ,x y 值；（2）根据频率分布直方图，利用中位数的估计方法，可计算得答案；（3）用分层抽样的方式从第四、第五组抽取5人，确定每组中的人数，列举从这5人中随机抽取2人参加某项美食体验活动的所有基本事件，列举出抽到的2人均来自第四组的基本事件，根据古典概型的概率公式，即可求得答案.【小问1详解】由题意可知,第四组的人数为，1000.1616⨯=故，；100143616430m =----=40.04100n ==又内的频率为 ，∴；[)60,70300.30100=0.300.03010x ==∵内的频率为 ，∴.[)90,1000.040.040.00410y ==【小问2详解】由频率分布直方图可知第一、二组频率之和为，0.140.300.44+=前三组频率之和为，0.140.300.360.80++=故中位数为：.0.500.447071.670.036-+≈【小问3详解】由题意可知，第4组共有16人，第5组共有4人，用分层抽样的方式从第四、第五组抽取5人,则第四、第五组抽取人数为4人和1人，设第4组的4人分别为 ，第5组的1人分别为A,a b c d ,,,则从中任取2人，所有基本事件为：共10个，(,),(,),(,),(,),(,),(,),(,),(,),(,),(,)a b a c a d a A b c b d b A c d c A d A又抽到的2人均来自第四组的基本事件有∶共6个，(,),(,),(,),(,),(,),(,)a b a c a d b c b d c d 故抽到的2人均来自第四组的的概率为.63105=18. 已知数列是递增的等比数列．设其公比为，前项和为，并且满足{}n a q n n S ，是与的等比中项．1534a a +=82a 4a （1）求数列的通项公式；{}n a （2）若，是的前项和，求使成立的最大正整数的n n b n a =⋅n T n b n 12100n n T n +-⋅>-n 值．【答案】（1）（）2n n a =*n ∈N （2）5【解析】【分析】（1）根据等比数列的性质结合条件是与的等比中项得到，联立82a 4a 1564a a =条件得到和，根据题目条件和等比数列的通项公式即可求解.1532a a +=1a 5a （2）根据（1）求得，利用错位相减求和得到，从而得到，通过2nn b n =⋅n T 12n n T n +-⋅函数法判断出是单调递减数列，即可求解.12n n T n +-⋅【小问1详解】因为是与的等比中项，所以，82a 4a 224864a a ==则由题意得：，即，解得：或，15243464a a a a +=⎧⎨=⎩15153464a a a a +=⎧⎨=⎩15232a a =⎧⎨=⎩15322a a =⎧⎨=⎩因为数列是递增的等比数列，所以，即，，{}n a 1451232a a a q =⎧⎨==⎩12a =2q =所以，111222n n nn a a q --==⨯=故数列的通项公式为（）.{}n a 2n na=*n ∈N 【小问2详解】由（1）得：（），2n n n b n a n =⋅=⨯*n ∈N则123n nT b b b b =++++ ，①1231222322n n =⨯+⨯+⨯++⨯ 即，②234121222322n n T n +=⨯+⨯+⨯++⨯ 则得：-①②123122222n n nT n +-=++++-⨯ 即（），()11122212212n n n n T n n +++-=⨯-=-+-*n ∈N 所以（），()11112122222n n n n n T n n n ++++-⋅=-+-⋅=-*n ∈N 设，则（），12n n n C T n +=-⋅122n n C +=-*n ∈N 因为在上单调递减，122x y +=-()0,∞+所以是单调递减数列，122n n C +=-又有，，652262100C =-=->-7622126100C =-=-<-所以当且时，成立，5n ≤*n ∈N 12100n nT n +-⋅>-故使成立的最大正整数的值为.12100n n T n +-⋅>-n 519. 如图，在四棱锥中，底面是平行四边形，平面P ABCD -ABCD PD ⊥．,1,ABCD AD BD AB ===（1）求证：平面平面；PBD ⊥PBC （2）若二面角的大小为，求点D 到的距离．P BC D --60︒PBC 【答案】（1）证明见解析；（2【解析】【分析】（1）利用线面垂直及面面垂直的判定定理可得结果；（2）根据等体积法即可求得点到平面的距离.C PBD 【小问1详解】在中, ，ADB1,===AD BD AB ，∴，222AD BD AB ∴+=AD BD ⊥∵平面,平面，∴.PD ⊥ABCD AD ⊂ABCD PD AD ⊥又∵,平面，∴平面，PD BD D ⋂=,PD DB ⊂PBD AD ⊥PBD 又，∴平面，//AD BC BC⊥PBD 又平面，所以平面平面BC ⊂PBC PBD ⊥PBC 【小问2详解】由（1）知平面，，，BC⊥PBD PB BC ∴⊥DB BC ⊥∴为二面角的平面角，∴.PBD ∠P BC D --60PBD ∠=在中, ，Rt PDB1,2===PD BD PB 所以，，111122=⨯⨯= BDC S 11212=⨯⨯= PBC S 设点D 到的距离,PBC d 由，有，P BCDD PBC V V --=1133△△⋅⋅=⋅⋅BDC PBCSPD S d即，解得1111323⨯=⨯⨯d d =即点D 到PBC20. 已知椭圆过点．2222:1(0,0)x y C a b a b +=>>⎛ ⎝（1）求椭圆C 的方程；（2）已知直线与椭圆交于不同的两点P ，Q ，那么在x 轴上是否存在点M ，:2l y mx =+使且，若存在，求出该直线的方程；若不存在，请说明理由．MP MQ =MP MQ ⊥【答案】（1）22142x y +=（2）详见解析【解析】【分析】（1）根据条件得到关于的方程组，即可求得椭圆方程；,,a b c （2）首先直线与椭圆方程联立，利用韦达定理表示线段中点坐标PQ ，再根据,以及，转化为坐标表示，代入韦2242,1212mN m m -⎛⎫ ⎪++⎝⎭MN PQ ⊥MP MQ ⊥达定理后，即可求,m n 【小问1详解】由条件可知，，解得：，，222221312a b c a a b c ⎧+=⎪⎪⎪=⎨⎪=+⎪⎪⎩24a =222b c ==所以椭圆C 的方程是；22142x y +=【小问2详解】假设在轴上存在点，使且，x (),0M n MP MQ =MP MQ ⊥联立，设，，222142y mx x y =+⎧⎪⎨+=⎪⎩()11P x y ()22,Q x y 方程整理为，()2212840m xmx +++=，解得：或，()226416120m m∆=-+>m>m <，，122812m x x m -+=+122412x x m =+1224212x x mm +-=+则线段的中点的横坐标是，中点纵坐标，PQ 2412mx m -=+2224221212m y m m -=+=++即中点坐标，，2242,1212mN m m -⎛⎫ ⎪++⎝⎭(),0M n 则，即，化简为，①MN PQ ⊥222112412m m m n m +=---+2220m n m n ++=又,0MP MQ ⋅= 则，，()()12120x n x n y y --+=()()()()1212220x n x n mx mx --+++=整理为，()()()2212121240m x x m n x x n ++-+++=，()()22224812401212m mm n n m m -+⨯+-⨯++=++化简为②()222124880n m m mn +-++=由①得，即，代入②得()2212mn m+=-()22212m n mn+=-，整理得③，又由①得，代224880mn m mn --++=22340m mn -++=2221mn m -=+入③得，即，222234021mm m m --+⋅+=+()()()222221324210m m m m m -++⋅-++=整理得，即.41m =1m =±当时，，当时，，满足，1m =23n =-1m =-23n =0∆>所以存在定点,此时直线方程是，当定点,此时直线方程是2,03M ⎛⎫- ⎪⎝⎭l 2y x =+2,03M ⎛⎫⎪⎝⎭l .2y x =-+21. 已经函数．22e ()ln 2,()2()xf x a x xg x x ax a x =+=--∈R （1）求函数的单调性；()f x （2）若，求当时，a 的取值范围．()()()F x f xg x =+()0F x ≥【答案】（1）见解析 （2）ea ≤【解析】【分析】（1）根据两种情况讨论.()24x af x x +'=0,0a a ≤>(2)求出，首先证明()ln e ()ln ln e xx xF x a x ax a x x x -=+-=-+()ln e e ln x x x x -≥-只需要求即可.()()ln e ln 0a x x x x -+-≥【小问1详解】()()2440a x af x x x x x+'=+=> (1)时，，所以在单调递增.0a ≥()240x a f x x +'=>()f x ()0,∞+(2)时，a<0()0,f x x '===时，时x ⎛∈ ⎝()0f x '<x ∞⎫∈+⎪⎪⎭()0f x ¢>所以在单调递减，在单调递增.()f x ⎛⎝∞⎫+⎪⎪⎭综上：时在单调递增0a ≥()f x ()0,∞+时在单调递减，在单调递增a<0()f x ⎛⎝∞⎫+⎪⎪⎭【小问2详解】()()()22e e ln 22ln x x F xf xg x a x x x ax a x axx x=+=++--=+-，要求，即求()()ln ln e ln ln e e xx xx a x x a x x -=-+=-+()0F x ≥()ln ln e 0x x a x x --+≥设，则，当，ln 1t x x =-+1110,1xt x x x -'=-===()()0,10,1,0x t x t ∞'∈∈+'><，所以在上单调递增，在单调递减，所以即t ()0,1()1,+∞ln1110t ≤-+=ln 1x x -≥设，，()()()e e 1,e e 0x x h x x x h x '=-≤-=-=()10x h x x '∴=<∈(],1-∞，所以在单调递减，在单调递增()[)01,h x x ∞∈'>+()h x (],1-∞[)1,+∞，故当且仅当时成立.所以当且()()1e e 0h x h ∴≥=-=e e xx ≥1x =()ln e e ln x x x x -≥-仅当即当且仅当时等号成立，ln 1x x -=1x =，又因为()()()ln ln e ln e ln 0x x a x x a x x x x --+≥-+-≥ln 1x x -≤-所以，所以.e 0a -≤e a ≤请考生在第22、23两题中任选一题作答，并用2B 铅笔在答题卡上把所选题目的题号涂黑．注意所做题目的题号必须与所涂題题目的题号一致，在答题卡选答区城指定位置答题．如果多做，则按所做的第一题计分．22. 在平面直角坐标系中，曲线C 的参数方程为（为参数），xOy cos )cos )x y θθθθ⎧=-⎪⎨=+⎪⎩θ以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为O x l．πcos 4ρθ⎛⎫+=⎪⎝⎭（1）求直线和曲线的直角坐标方程；l C （2）从原点引一条射线分别交曲线和直线于两点，求的最O C l ,M N 22121||||OM ON +大值．【答案】（1）直线的直角坐标方程为：，曲线的直角坐标方程为：l 10x y --=C.22164x y +=（2【解析】【分析】（1）消去参数可得曲线的直角坐标方程；利用两角和的余弦公式和θC ，可得直线的直角坐标方程；cos x ρθ=sin y ρθ=l （2）设射线方程为（），将曲线的直角坐标方程化为极坐标方程，θα=0,0πρθ≥≤<C 并将代入可得，将代入可得，再利用辅助角θα=||OM θα=cos sin 10ρθρθ--=||ON 公式可求出的最大值.22121||||OM ON +【小问1详解】由，得，cos )cos )x y θθθθ⎧=-⎪⎨=+⎪⎩2222(sin cos )(sin cos )32x y θθθθ+=-++2=即,22164x y +=所以曲线的直角坐标方程为：.C 22164x y +=由，πcos 4ρθ⎛⎫+= ⎪⎝⎭ππcos cos sin sin 44ρθρθ-=，cos sin θθ=cos sin 10ρθρθ--=将，代入得，cos x ρθ=sin y ρθ=10x y --=所以直线的直角坐标方程为：.l 10x y --=综上所述：直线的直角坐标方程为：，曲线的直角坐标方程为：l 10x y --=C .22164x y +=【小问2详解】设射线方程为（），θα=0,0πρθ≥≤<将，代入，得，cos x ρθ=sin y ρθ=22164x y +=2222cos sin 164ρθρθ+=得，2221cos sin 64θθρ=+将代入，得，得θα=2221cos sin 64θθρ=+2221cos sin 64ααρ=+21||OM ，22cos sin64αα=+由，πcos 4ρθ⎛⎫+=⎪⎝⎭1π4θρ=+将代入，得()，，得θα=1π)4θρ=+1π4αρ=+π5π[0,)(,2π)44α∈ ，221π2cos (||4ON α=+所以22121||||OM ON +222π2cos 3sin 2cos ()4ααα=+++2222cos 3sin 2(cos sin αααα=++-2222cos 3sin (cos sin )αααα=++-22222cos 3sin cos 2sin cos sin αααααα=++-+23sin sin 2αα=+-1cos 23sin 22αα-=+-17cos 2sin 222αα=--+72sin 22αα=++（其中，），7)2αϕ=-+sin ϕ=cos ϕ=tan 2ϕ=因为，所以，π5π[0,)(,2π)44α∈ π5π2[0,)(,4π)22α∈ 又，所以，ϕπ(0,)2∈ππ2(,)(2π,4π)22αϕ-∈- 所以当时，即，即（其中cos(2)1αϕ-=-2αϕ-=3π3π22ϕα=+sin ϕ=，）时，.cos ϕ=tan 2ϕ=22121||||OM ON +23. 已知函数．()||2a f x x a x =++-（1）当时，求不等式的解集；2a =()5f x ≤（2）设且的最小值为m ，若，求的最小值．0,0a b >>()f x 332m b +=32a b +【答案】（1）[3,2]-（2【解析】【分析】（1）分段讨论求解，（2）由绝对值三角不等式求最小值，再由基本不等式求解，m 【小问1详解】当时，，2a =21,2()213,2121,1x x f x x x x x x --<-⎧⎪=++-=-≤≤⎨⎪+>⎩故即或或，()5f x ≤2215x x <-⎧⎨--≤⎩2135x -≤≤⎧⎨≤⎩1215x x >⎧⎨+≤⎩解得，即原不等式的解集为32x -≤≤[3,2]-【小问2详解】由题意得，3()||||222a a f x x a x a a =++-≥+=即，，即，32m a =3333222m b a b +=+=2a b +=而即3232()()55b a a b a b a b ++=++≥+32b ab a =时等号成立，64a b =-=故32a b +。

贵州省选调考试试卷及答案（满分100分时间120分钟）第一部分常识判断1.2024年清明节假期，共518.9万人次中外人员出入境，较去年同期（）。

A.增长62.6%B.增长66.5%C.增长69.6%D.增长60.6%【答案】：C2.2024年5月3日，搭载（）探测器的长征五号遥八运载火箭，在中国文昌航天发射场发射升空。

A.嫦娥六号B.嫦娥八号C.玉兔六号D.玉兔八号【答案】：A3.2024年3月19日，香港特别行政区立法会审议通过了（）。

这是香港特别行政区落实维护国家安全宪制责任的重大举措，是全面履行维护国家安全法定义务的切实成果。

A.《维护国家安全条例》B.《港区国安法》C.《香港治安法》D.《维护香港治安法》【答案】：A4.2024年1月15日，工信部发布最新数据显示，中国造船业三大指标连续（）位居世界第一。

中国成为全球唯一一个三大指标实现全面增长的国家。

A.12年B.13年C.14年1/ 14D.11年【答案】：C5.我国科学家自主研发的"（）"，填补了国内高性能侵入式脑机接口技术的空白，并在国际上首次实现猕猴对二维运动光标的灵巧脑控。

A.北脑二号B.夸父三号C.萤火二号D.天目一号【答案】：A6.(单选题)下列植物中被称为“活化石”的是（）。

A.梧桐B.松柏C.银杉D.苏铁【答案】：C7.下列有关报告的描述不正确的是（）。

A.相关上级单位必须回复B.上行文C.陈述性语言为主D.事后行文【答案】：A8.当出租车租金上涨后，对公共汽车服务的（）。

A.需求量减少B.需求增加C.需求量增加D.需求减少【答案】：B9.下列因素变化不会引起需求曲线移动的是（）。

A.消费者的收入B.相关商品的价格2/ 14C.消费者的偏好D.商品本身的价格【答案】：D10.坐地日行八万里，巡天遥看一千河的诗句蕴含的哲学原理是A.物质运动的绝对与静止的相对性的统一。

B.物质运动的多样性和静止的单一性的统一。

2024年贵州专业技术继续教育公需科目考试试题及答案单选题01、种业种植的收益远高于农产品生产，但其中的难点不包括（C）。

A、研究周期长B、跨学科领域C、人员匮乏D、投资额巨大02、下列选项中，关于党的二十大报告中提出的构建新发展格局的理解，表述不正确的是（B）。

A、是适应我国发展新阶段要求、贯彻新发展理念塑造国际合作和竞争新优势的必然选择B、是被迫之举和权宜之计C、是以全国统一大市场基础上的国内大循环为主体，不是各地都搞自我小循环D、是具有显著制度优势和坚实改革基础的03、党的二十大报告中明确提出，在人才建设方面的基本要求是 （A）。

A、聚天下英才而用之B、深化人才发展体制机制改C、营造环境04、元宇宙的英文是Metaverse，这个词最早起源尼尔·斯蒂芬森的小说（C)。

A、《佐迪亚克》B、《神经漫游者》C、《雪崩》05、1930年冬，中央交通局开通上海至中央苏区的第一条地下交通路线，设有（D）和闽西两个交通大站、三个交通中站和多个交通小站。

A、汕头B、长汀C、武汉D、香港06、下面对人工智能是通用目的战略技术（Generalpurposetechnologies）描述不正确的是（D）。

A、通用目的技术是使能技术(enablingtechnology)，但不是完整的最终解决方案B、人工智能犹如历史上蒸气机、电力、计算机和互联网等发明创造，是一种通用使能技术，正深刻地以史无前例速度改变人类社会和经济发展C、人工智能天然具备推动学科交叉的潜力，其与不同学科专业知识结合，形成AlI+X的新研究格局D、人工智能是通用目的技术，因此就是解决方案的全部，与其他技术没有任何联系07、红色交通线，是指中国共产党在领导革命斗争中，根据需要开辟和建立的人、财、物转运输送和（A）的秘密交通路线。

A、通信联络B、情报传送C、武器装备D、信息资料08、以纯休闲为核心的农业受到很大冲击，核心原因在于其无法满足农业的（D）。

2020年贵州省考B卷公文写作假如你随C市商务局考察团到H市调研“夜间经济”发展情况，请结合“给定资料2”,写一份调研报告提纲。

(40分)要求:(1)紧扣资料,内容全面;(2)层次分明，有逻辑性;(3）不超过400字。

2.八月的H市,已进入高温炙灼模式。

夜,却未因此而平静。

晚上十点,市区最大商场的主体部分已经打烂,人们陆续从商场大门走出。

与此同时,另一批“意犹未尽”的顾客走进地下一层和地下二层东侧的“21街区”。

这片主营餐饮的区域,营业时间一直会延长到凌两点,是名副其实的“深夜食堂”。

人们在炸糕店前排队买着炸糕、在奶茶店外挑选着饮料、手捧着冰淇淋和炸鸡….….街区内无论面条米饭、饺子煎包,各式中餐西餐种类都很丰富。

H市商务局的陈科长介绍说,所谓“夜间经济”,是指从当日下午6点到次日早上6点发生的经济文化活动。

在不少人看来,夜间经济无非就是“啤酒烤串加唱歌”。

事实上,夜间经济的内涵远比“吃吃喝喝”丰富得多。

它已经由早期的灯光夜市转变为括“食、游、购、娱、体、展、演”等在内的多元夜间消费市场。

H市一家著名的24小时书店,就给人们的夜生活增加了一种新的方式。

位于临窗位置的阅读区,摆放着一张长桌和七把圆形座椅,其中六把已被读者占用。

年轻姑娘小赵戴着耳机,全神贯注地看着手机播放的“中国会计网校”课程。

休息间隙,小赵告诉记者,自己参加工作不到一年,打算自学考“注会”。

合租环境比吵闹,下班后就来书店学到10点多再回去。

“这里环境好,手机用来听课,也没有电脑玩儿,效率还是很高的。

”“再来,加把劲儿!”听着一旁教练的口令,扎着马尾辫的女孩咬了下嘴唇,抹下额头的汗珠,继续奋力向前推着沉重的哑铃。

已是夜里九点半,位于H市南二附近的一家健身工作室灯火通明。

“每天人最多的时候是八点左右,现在好多人经练完走了。

”健身教练表示，“我们工作室成立近三年,明显感觉到健身的人增多。

来这里的大部分是附近的住户,下班之后过来健身。

正常,我们是晚上十关门,但有的人下班晚,跟教练约了,过来练到十一点、十二点也没问题,我们都等。

贵州省考2024行测真题及答案（满分100分时间120分钟）第一部分常识判断1.日前从商务部召开的中非经贸深度合作先行区专题新闻发布会上了解到，中国已连续（）保持非洲第一大贸易伙伴地位。

A.15年B.10年C.12年D.20年【答案】：A2.2024年3月份，中国制造业采购经理指数为（），经济回升向好势头进一步增强。

A.52.8%B.48.8%C.50.8%D.48%【答案】：C3.2024年3月6日，4000吨级全球最大轮式起重机在（）交付，能有效解决超高大功率风机安装难题。

A.江苏南通B.江苏徐州C.山东青岛D.辽宁大连【答案】：B4.财政部公布，2023年，国有企业营业总收入857306.1亿元，同比（）。

A.增长3.6%B.增长3.08%C.增长3.25%D.增长2.6%1/ 14【答案】：A5.2024年中央一号文件中关于“确保不发生规模性返贫”的举措包括（)。

①加大对重点地区帮扶支持力度②促进农村一二三产业融合发展③落实防止返贫监测帮扶机制④持续深化食物节约各项行动⑤持续加强产业和就业帮扶A.①②④B.①③⑤C.②③④⑤D.①②③⑤【答案】：B6.地球是一个赤道两极部分比凸出的扁球体，而不是几何学中所说的正球体，造成这种现象的主要原因是（）。

A.地球自身形成过程中造成的B.太阳与其他行星引力的结果C.地球自身引力的结果D.地球自转造成的【答案】：D7.公文处理应当坚持（）的原则，做到及时、准确、安全。

A.准确、精简、高效B.实事求是、严谨、高效C.实事求是、精简、庄重D.实事求是、精简、高效【答案】：D8.田园诗是中国古代歌咏田园生活的诗，其特色在于描写农村的朴实生活和田园的风光。

中国田园诗派的开创者是（）。

A.孟浩然B.陶渊明C.谢灵运D.王维【答案】：B9.根据我国《劳动合同法》有关规定，下列哪一项说法是正确的？（）。

2/ 14A.已建立劳动关系，未同时订立书面劳动合同的，应当自用工之日起十五日内订立书面劳动合同B.劳动合同部分无效，即使不影响其他部分效力的，其他部分也仍然无效C.用人单位与劳动者协商一致，可以变更劳动合同约定的内容。

中考通关——《艰辛探索与建设成就》【内容标准（2011版）】（4）知道“大跃进”和人民公社化运动的失误。

一、选择题1．（2020·贵州黔东南州·8）2020年“新冠肺炎、宅在家、戴口罩”成了最热门词汇，1958年可能出现的热门词汇是（）A．真理标准、拨乱反正、经济建设 B．改革开放、四个全面、公私合营C．鼓足干劲、力争上游、多快好省 D．阶级斗争、深圳特区、和平发展2．（2020·湖北孝感·14）学习历史需要区分历史事实与历史结论。

历史事实是指客观存在的历史人物或事件，历史结论是关于史实的基本判断和基本观点。

下列表述属于历史结论的是（）A．1949年10月1日，中华人民共和国成立B．到1952年底，约3亿无地少地的农民，分到了约7亿亩土地C．1956年，中国共产党在北京召开第八次全国代表大会D．1958年开始的“大跃进”运动急于求成，忽视了客观的经济规律3．（2020·河南·9）在全面建设社会主义的过程中，河南林县人民经过几年苦战，开凿太行山，引漳河水入境，修建了“人造天河”红旗渠，彻底告别“水缺贵如油”的历史，创造了人间奇迹。

这体现了林县人民（）A．防风治沙的决心 B．助人为乐的品格C．国际主义的视野 D．艰苦奋斗的精神4．（2020·陕西·6）下列四幅图片反映了新中国成立后农业生产关系的四次调整。

按调整先后顺序排列正确的是（）A．①②③④ B．②①④③C．②①③④ D．④③①②二、非选择题5．（2020·江苏淮安·27）（9分）新中国成立以来，中国共产党带领全国人民取得了辉煌成就。

阅读下列材料，回答问题。

材料一没有适当形式的政权机关，就不能代表国家。

中国现在可以采取全国人民代表大会、省人民代表大会、县人民代表大会、区人民代表大会直到乡人民代表大会的系统，并由各级人民代表大会选举政府。

——毛泽东《新民主主义论》材料二如果六十年代以来中国没有原子弹、氢弹，没有发射卫星，中国就不能叫有重要影响的大国，就没有现在这样的国际地位。

1 / 25贵州省2023年初中学业水平考试（中考）语文真题试卷姓名：__________ 班级：__________考号：__________1． 2023年5月26日，以“数实相融 算启未来”为主题的中国国际大数据产业博览会在贵州贵阳拉开xù mù ，吸引了国内外大数据领域的众多企业参会参展。

不期而．．．至．的数博会以“数”为媒，乘“云”而上！ 近年来，大数据已经渗透到经jì 发展和社会生活的方方面面。

降低成本的智能化矿山建设、与洪水赛跑的“东方祥云”预报系统、《熊出没•伴我“雄芯”》电影的后期渲．染．等，都有大数据的功劳。

除此之外，大数据还赋予了传统文化更有意思的演绎．．形式，助力文化跨界传播……总之，贵州持续推动大数据赋能各行各业转型升级，shuò 果累累。

如今，贵州大数据这棵“智慧树”正生机勃发，日益茁壮。

大数据正以锐不可当．．．．之势引领贵州阔步前进！（1）请根据上面文段的语境和拼音，用楷体字写出横线处的汉字。

（2）上面文段中加点词语使用不恰当的一项是（ ） A ．不期而至B ．渲染C ．演绎D ．锐不可当2．根据所给信息默写相应内容。

①青青子衿， 。

《诗经•郑风》②大道之行也， 。

《礼记•大道之行也》③ ，暂凭杯酒长精神。

刘禹锡《酬乐天扬州初逢席上见赠》 ④零落成泥碾作尘， 。

陆游《卜算子•咏梅》 ⑤ ，断肠人在天涯。

马致远《天净沙•秋思》 ⑥山 起来了，水涨起来了……朱自清《春》⑦《白雪歌送武判官归京》中，以春景写冬景，表现边塞奇异风光的句子是： ， 。

⑧《登飞来峰》中，蕴含着认识达到一定高度，就不会被事物的假象所迷惑这一道理的句子是： ， 。

2 / 25…○…………装…………○…………装………※※请※※不※※要※※3．下列文学、文化常识表述有误的一项是（ ）A ．《湖心亭看雪》是明末清初文学家张岱的作品，选自《陶庵梦忆》。

B ．加冠，古时男子二十岁举行加冠（束发戴帽）仪式，表示已成人。

绝密★启用前备战2021年中考数学【名校地市好题必刷】全真模拟卷（贵州省贵阳市专用）第六模拟同学你好！答题前请认真阅读以下内容：1.全卷共8页，共25道小题，满分150分，答题时间120分钟，考试形式为闭卷.2.一律在答题卡相应位置作答，在试题卷上答题视为无效.一、选择题（本题共10小题，每小题3分，共30分）1.﹣（﹣3）4等于（）A.﹣12B.12C.﹣81D.81【解答】解：﹣（﹣3）4＝﹣81，故选：C.2.如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图正确的是（）A.主视图、左视图和俯视图都相同B.仅俯视图不同C.仅左视图不同D.仅主视图不同【解答】解：解法一：从正面看，两个几何体均为第一层和第二层都是两个小正方形，故主视图相同；从左面看，两个几何体均为第一层和第二层都是两个小正方形，故左视图相同；从上面看，两个几何体均为第一层和第二层都是两个小正方形，故俯视图相同.解法二：第一个几何体的三视图如图所示第二个几何体的三视图如图所示：观察可知这两个几何体的主视图、左视图和俯视图都相同，故选：A.3.已知a2+a﹣4＝0，那么代数式：a2（a+5）的值是（）A.4B.8C.12D.16 【解答】解：∵a2+a﹣4＝0，∴a2＝﹣a+4，a2+a＝4，∴a2（a+5）＝（﹣a+4）（a+5）＝﹣a2﹣a+20＝﹣（a2+a）+20＝﹣4+20＝16.故选：D.4.如图所示，长方形纸片ABCD中，点E是AB的中点，且AE＝1，DE的垂直平分线MN恰好经过点C，则BC边的长度为（）A.2B.C.D.1【解答】解：如图，连接EC.∵点E是AB的中点，且AE＝1，∴BE＝AE＝1，AB＝2AE＝2，∵四边形ABCD是矩形，∴CD＝AB＝2，∠B＝90°，∵MN垂直平分DE，∴CE＝CD＝2，∴BC＝＝＝；故选：B.5.某市今年中考体育测试，其中男生测试项目有200米跑、1000米跑、立定跳远、投掷实心球、一分钟跳绳、引体向上、篮球半场来回运球上篮七个项目.考生须从这七个项目中选取两个项目，其中200米跑必选，剩下六个项目选一个，则两名男生在体育测试中所选项目完全相同的概率为（）A. B. C. D.【解答】解：1000米跑、立定跳远、投掷实心球、一分钟跳绳、引体向上、篮球半场来回运球上篮分别用A，B，C，D，E，F表示，画图如下：共有36种等情况数，其中两名男生在体育测试中所选项目完全相同的有6种，则两名男生在体育测试中所选项目完全相同的概率为＝；故选：B.6.如图，四边形ABCD内接于⊙O，已知∠A＝80°，则∠C的度数是（）A.40°B.80°C.100°D.120°【解答】解：∵四边形ABCD内接于⊙O，∴∠C＝180°﹣∠A＝100°，故选：C.7.党的十九大为新时代农业农村改革发展明确了重点、指明了方向.报告中提出了“实施乡村振兴战略”.某地区经过三年的乡村振兴建设，农村的经济收入是振兴前的2倍.为更好地了解该地区农村的经济收入变化情况，统计了该地区乡村振兴建设前后农村的经济收入构成比例，绘制了如图的扇形统计图：则下列说法错误的是（）A.乡村振兴建设后，养殖收入是振兴前的2倍B.乡村振兴建设后，种植收入减少C.乡村振兴建设后，其他收入是振兴前的2倍以上D.乡村振兴建设后，养殖收入与第三产业收入的总和超过了经济收入的一半【解答】解：由题意可得，乡村振兴建设后，养殖收入是振兴前的2倍，故选项A正确；乡村振兴建设后，种植收入相当于振兴前的37%×2＝74%，相对于振兴前收入增加了，故选项B错误；乡村振兴建设后，其他收入是振兴前的2倍以上，故选项C正确；乡村振兴建设后，养殖收入与第三产业收入的总和占总收入的30%+28%＝58%，故选项D正确；故选：B.8.如图，数轴上A、B、C三点所表示的数分别为a、b、c，满足a+b﹣c＝0且AB＝BC.那么下列各式正确的是（）A.a+c＜0B.ac＞0C.bc＜0D.ab＜0【解答】解：∵AB＝BC，∴b﹣a＝c﹣b，∴a+c＝2b，∵a+b﹣c＝0，即c＝a+b，∴a+（a+b）＝2b，∴b＝2a，∴c＝a+b＝3a，∵a＜b＜c，∴a＞0，b＞0，c＞0，∴a+c＞0，则A选项错误；ac＞0，则B选项正确；bc＞0，则C错误；ab＞0，则D错误.故选：B.9.如图，等边三角形ABC的边长为8，点O是△ABC的内心，∠FOG＝120°，绕点O旋转∠FOG，分别交线段AB、BC于D、E两点，连接DE，给出下列四个结论：①点O也一定是△ABC的外心；②OD＝OE；③四边形ODBE的面积始终等于；④△BDE周长的最小值为6.上述结论中正确的个数是（）A.1B.2C.3D.4【解答】解：∵点O是等边△ABC的内心，∴点O是△ABC的外心，所以①正确；连接OB、OC，如图，∵点O是等边△ABC的内心和外心，∴OB平分∠ABC，OC平分∠ACB，OB＝OC，∴∠ABO＝∠OBC＝∠OCB＝30°，∴∠BOC＝120°，∵∠DOE＝120°，∴∠DOB＝∠EOC，在△BOD和△COE中，，∴△BOD≌△COE（ASA），∴OD＝OE，所以②正确；S△OBD＝S△OCE，＝S△OBC＝S△ABC＝××82＝，所以③错误；∴S四边形BDOE∵△BOD≌△COE，∴BD＝CE，∴△BDE的周长＝BD+BE+DE＝CE+BE+DE＝BC+DE＝8+DE，过O点作OH⊥DE于H，如图，∵OD＝OE，∠DOE＝120°，∴∠ODE＝∠OED＝30°，DH＝EH，∵OH＝OE，∴HE＝OH＝OE，∴DE＝OE，∴△BDE的周长＝8+OE，当OE⊥BC时，OE的值最小，△BDE的周长最小，此时OE＝，∴△BDE的周长的最小值为8+4＝12，所以④错误.故选：B.10.已知二次函数y＝kx2﹣6x﹣9的图象与x轴有两个不同的交点，则k的取值范围为（）A.k＞﹣1B.k＞﹣1且k≠0C.k≥﹣1D.k≥﹣1且k≠0【解答】解：令y＝0，则kx2﹣6x﹣9＝0.∵二次函数y＝kx2﹣6x﹣9的图象与x轴有两个不同的交点，∴一元二次方程kx2﹣6x﹣9＝0有两个不相等的解，∴，解得：k＞﹣1且k≠0.故选：B.二、填空题（本题共5小题，每小题4分，共20分）11.计算＝.【解答】解：原式﹣＝＝＝＝，故答案为：.12.如图，直线y＝﹣x+8与x轴、y轴分别交于点A、B，∠BAO的角平分线与y轴交于点M，则OM的长为3.【解答】解：过M点作MN⊥AB于N，如图，当y＝0时，﹣x+8＝0，解得x＝6，则A（6，0）；当x＝0时，y＝﹣x+8＝8，则B（0，8），∴AB＝＝10，∵AM平分∠OAB，∴MO＝MN，∵S△OMA+S△BMA＝S△OAB，∴×6•OM+×10•MN＝×6×8，即3OM+5MN＝24，∴8OM＝24，∴OM＝3.故答案为3.13.为积极响应“无偿献血，传递温暖”的号召，某高校一寝室的4个同学也用实际行动参与到爱心献血的活动中，他们其中有2个A型血，1个B型血，还有1个O型血，现从该寝室随机抽取两个同学参与第一批次献血，则两个同学都是A型血的概率为.【解答】解：用列表法列举出所有可能出现的结果如下：共有12种可能出现的结果，其中“两人都是A型血”的有2种，＝＝，∴P（两人都是A型血）故答案为：.14.以O为中心点的量角器与直角三角板ABC如图所示摆放，直角顶点B在零刻度线所在直线DE上，且量角器与三角板只有一个公共点P.若点P的读数为135°，则∠CBD的度数是45°.【解答】解：如图，∵点P的读数为135°，∴∠POB＝180°﹣135°＝45°.∵AB是⊙O的切线，∴∠OPB＝90°，∵∠ABC＝90°，∴OP∥BC，∴∠CBD＝∠POB＝45°，故答案是：45°.15.正方形ABCD中，AB＝4，点E、F分别在BC、CD上，且BE＝CF，线段BF、AE相交于点O，若图中阴影部分的面积为14，则△ABO的周长为2+4.【解答】解：∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠BCD＝90°，又∵BE＝CF，∴△ABE≌△BCF（SAS），∴S△ABE＝S△BCF，∠BAE＝∠CBF，，∠BAE+∠AEB＝90°＝∠CBF+∠AEB＝∠AOB，∴S△ABO＝S四边形ECFO∵图中阴影部分的面积为14，∴S△ABO＝×（4×4﹣14）＝1，∴×AO×BO＝1，∴2AO•BO＝4，∵AB2＝AO2+BO2＝16，∴（AO+BO）2＝20，∴AO+BO＝2，∴△ABO的周长＝AB+AO+BO＝2+4，故答案为：2+4.三、解答题（本题共10小题，共100分）16.阅读佳佳与明明的对话，解决下列问题：（1）“多边形内角和为2020°”，为什么不可能？（2）明明求的是几边形的内角和？（3）错当成内角的那个外角为多少度？【解答】解：（1）设多边形的边数为n，180°（n﹣2）＝2020°，解得，∵n为正整数，∴“多边形的内角和为2020°”不可能.（2）设应加的内角为x，多加的外角为y，依题意可列方程：（n﹣2）180°＝2020°﹣y+x，∵﹣180°＜x﹣y＜180，∴2020°﹣180°＜180°（n﹣2）＜2020°+180°，解得，又∵n为正整数，∴n＝13，n＝14.故明明求的是十三边形或十四边形的内角和.（3）十三边形的内角和＝180°×（13﹣2）＝1980°，∴y﹣x＝2020°﹣1980°＝40°，又x+y＝180°，解得：x＝70°，y＝110°；十四边形的内角和＝180°×（14﹣2）＝2160°，∴y﹣x＝2020°﹣2160°＝﹣140°，又x+y＝180°，解得：x＝160°，y＝20°；所以那个外角为110°或20°.17.某校七年级学生进行期末体育达标测试，每名学生需考3个项目（包括2个必考项目与1个选考项目），每个项目20分，总分60分.其中必考项目为：跳绳和实心球；选考项目为：A、篮球，B、足球，C、排球，D、立定跳远，E、50米跑，F、女生800米跑或男生1000米跑.某兴趣小组随机对同学们的选考项目做了调查，根据调查结果绘制了两幅不完整的条形统计图与扇形统计图.结合图中信息，回答下列问题：（1）在这次调查中，一共调查了50名学生，补全条形统计图和扇形统计图；（2）本次调查的选考项目的众数是C；（填A，B，C，D，E，F选项）（3）选考项目包括球类与非球类，请用树状图或列表法求甲、乙两名同学都选球类的概率.【解答】解：（1）5÷10%＝50（名），即在这次调查中，一共调查了50名学生，故答案为：50；D的人数为：50×20%＝10（名），C所占的百分比为×100%＝30%，补全条形统计图和扇形统计图：（2）在本次调查的选考项目的众数是C，故答案为：C；（3）画树状图如图所示，共有36种等可能的结果，甲、乙两名同学都选球类的有9种情况，∴P（甲、乙两名同学都选球类）＝＝.18.如图，平行四边形ABCD中，分别过A，C两点作AE⊥BD，CF⊥BD，垂足分别为E，F，连接CE、AF.（1）若AB＝4，EF＝，∠ABD＝30°，求△ABD的面积；（2）求证：AF＝CE.出结论.【解答】（1）解：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠ABE＝∠CDF，又∵AE⊥BD，CF⊥BD，∴∠AEB＝∠CFD＝90°，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS），∴BE＝DF，∵在Rt△ABE中，∠ABD＝30°，∴AE＝AB＝2，由勾股定理得：BE＝＝＝2，∴BD＝2BE+EF＝2×2+＝5，∴S△ABD＝AE•BD＝×2×5＝5；（2）证明：由（1）得：△ABE≌△CDF，∴AE＝CF，∵AE⊥BD，CF⊥BD，∴AE∥CF，∴四边形AECF是平行四边形，∴AF＝CE.19.被誉为“神秘的东方女儿国”“人类母系氏族领地的活化石”的国家级风景名胜区泸沽湖，其湖光山色如诗如画、如梦如幻、旖旎静谧.实验中学组织八年级部分学生乘车参观，若用1辆小客车和2辆大客车，则每次可运送学生115人；若用3辆小客车和1辆大客车，则每次可运送学生120人（注意：每辆小客车和大客车都坐满）.问每辆小客车和大客车各能运送学生多少人？【解答】解：设每辆小客车能运送学生x人，每辆大客车能运送学生y人，依题意，得：，解得：.答：每辆小客车能运送学生25人，每辆大客车能运送学生45人.20.一个不透明的口袋里装有除表面上分别标有1，2，3，4数字外，其余完全相同的四个小球，现从中摸球，每次摸球前先搅拌均匀.（1）从中不放回地任取两个球，求取得两球的数字和为4的概率；（2）从中任取一个球，记下数字后放回袋中，搅拌均匀后再从中任取一球，求取得的两球数字和为4的概率.【解答】解：（1）画树状图如下：共有12个等可能的结果，取得两球的数字和为4的有2个，∴取得两球的数字和为4的概率为＝；（2）画树状图如下：共有16个等可能的结果，取得两球的数字和为4的有3个，∴取得两球的数字和为4的概率为.21.如图，在某次军事演习时，中国空警机A在北偏东22°方向上发现有不明敌机在钓鱼岛P附近徘徊，并快速报告给东海司令部.此时正在空警机A的正西方向200km处巡逻的中国歼击机B接到任务，迅速赶往北偏东60°方向上的钓鱼岛P处，已知歼击机B的速度是2.2马赫（1马赫大约等于1200km/h）.请根据以上信息，求出歼击机B到达钓鱼岛P所需的时间.（结果精确到1s.参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，≈1.73）【解答】解：过点P作PC⊥BA交BA的延长线于C，设AC＝xkm，则BC＝（200+x）km，在Rt△PAC中，tan∠APC＝，∴PC＝≈＝2.5x，在Rt△BCP中，tan∠PBC＝，∴≈，解得，x≈60，则PC＝2.5x＝150，在Rt△PBC中，∠PBC＝30°，∴BP＝2PC＝300，∴歼击机B到达钓鱼岛P所需的时间为：×3600≈410（s），答：歼击机B到达钓鱼岛P所需的时间约为410s.22.为了优化环境，将对某一小区环境进行绿化，现有甲、乙两家绿化公司进行了投标，各自推出了绿化收费方案如下：甲公司绿化费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示.乙公司：绿化面积不超过1000平方米时，统一收取费用5000元；绿化面积超过1000平方米时，超过部分每平方米收取3元.（1）求甲、乙公司绿化费用y（元）与绿化面积x（平方米）的函数表达式；（2）如果该小区目前的绿化面积是1500平方米，试通过计算说明：选择哪家公司的绿化费用较少？【解答】解：（1）设甲公司y关于x的函数表达式为y＝kx+b（k≠0），∵函数图象经过（0，500），（100，1000），∴，解得，＝5x+500；即甲公司y关于x的函数表达式为y甲由题意可得，当0＜x≤1000时，y＝5000，乙＝3（x﹣1000）+5000＝3x+2000，当x＞1000时，y乙＝；由上可得，y乙＝5x+500＝8000，（2）当x＝1500时，y甲＝3x+2000＝6500，当x＝1500时，y乙∵8000＞6500，∴选择乙公司绿化费用较少.23.如图，点A、B在⊙O上，OC⊥AB于点D，交⊙O于点E，BC切⊙O于点B.（1）若AB＝8，DE＝2，求BC；（2）过点D的直线MN交⊙O于点M、N（均不与点E重合），试猜想：∠MCO与∠NCO的数量关系，并说明理由.【解答】解：（1）∵OC⊥AB于点D，AB＝8，∴BD＝，在Rt△BDO中，由勾股定理得，OD2+BD2＝OB2，即（r﹣2）2+4＝r2，解得r＝5，∴OD＝3，∵BC切⊙O于点B，∴∠OBC＝90°，∵∠COB＝∠BOD，∴tan∠COB＝tan∠BOD，∴，即，∴BC＝；（2）∠MCO＝∠NCO.理由如下：连接OM，ON，∵CB切⊙O于点B，∴OB⊥CB，∴∠DBC+∠OBD＝90°，∵∠DBC+∠BCO＝90°，∴∠BCO＝∠OBD，∴sin∠BCO＝sin∠OBD，∴，∴OB2＝OC•OD，∵ON＝OB，∴ON2＝OC•OD，∴，又∵∠NOD＝∠CON，∴△NOD∽△CON，∴∠DNO＝∠NCO，同理可得∠DMO＝∠MCO，∵OM＝ON，∴∠DMO＝∠DNO，∴∠MCO＝∠NCO.24.如图，在平面直角坐标系中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3），B（3，0）两点，该抛物线的顶点为C.（1）求此抛物线和直线AB的解析式；（2）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，试求出点P的坐标，并求出△PAB面积的最大值；（3）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过点M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，试求出点M的坐标；若不存在，请说明理由.【解答】解：（1）∵抛物线y＝ax2﹣2x+c经过A（0，﹣3），B（3，0）两点，∴，解得，∴抛物线的解析式为y＝x2﹣2x﹣3，∵直线y＝kx+b经过A（0，﹣3），B（3，0）两点，∴，解得，∴直线AB的解析式为y＝x﹣3；（2）如图1，作PQ∥y轴交直线AB于点Q，设P（m，m2﹣2m﹣3），则Qm，m﹣3），∴PQ＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，∴S△PAB＝×3×（﹣m2+3m）＝﹣m2+m＝﹣（m﹣）2+，∴当m＝时，△PAB面积有最大值，最大值是，此时P点坐标为（，﹣）.（3）存在，理由如下：∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点C的坐标为（1，﹣4），∵CE∥y轴，∴E（1，﹣2），∴CE＝2，①如图2，若点M在x轴下方，四边形CEMN为平行四边形，则CE＝MN，设M（a，a﹣3），则N（a，a2﹣2a﹣3），∴MN＝a﹣3﹣（a2﹣2a﹣3）＝﹣a2+3a，∴﹣a2+3a＝2，解得：a＝2，a＝1（舍去），∴M（2，﹣1），②如图3，若点M在x轴上方，四边形CENM为平行四边形，则CE＝MN，设M（a，a﹣3），则N（a，a2﹣2a﹣3），∴MN＝a2﹣2a﹣3﹣（a﹣3）＝a2﹣3a，∴a2﹣3a＝2，解得：a＝，a＝（舍去），∴M（，），综合可得M点的坐标为（2，﹣1）或（，），25.阅读下面内容，并解答问题.在学习了平行线的性质后，老师请学们证明命题：两条平行线被第三条直线所截，一组同旁内角的平分线互相垂直.小颖根据命题画出图形并写出如下的已知条件.已知：如图1，AB∥CD，直线EF分别交AB，CD于点E，F.∠BEF的平分线与∠DFE的平分线交于点G.求证：EG⊥FG.（1）请补充要求证的结论，并写出证明过程；（2）请从下列A、B两题中任选一题作答，我选择A或B题.A.在图1的基础上，分别作∠BEG的平分线与∠DFG的平分线交于点M，得到图2，则∠EMF的度数为45°.B.如图3，AB∥CD，直线EF分别交AB，CD于点E，F.点O在直线AB，CD之间，且在直线EF右侧，∠BEO的平分线与∠DFO的平分线交于点P，则∠EOF与∠EPF满足的数量关系为∠EOF＝2∠EPF.【解答】解：（1）结论：EG⊥FG；理由：如图1中，∵AB∥CD，∴∠BEF+∠DFE＝180°，∵EG平分∠BEF，FG平分∠DFE，∴，，∴. 在△EFG中，∠GEF+∠GFE+∠G＝180°，∴∠G＝180°﹣（∠GEF+∠GFE）＝180°﹣90°＝90°，∴EG⊥FG.故答案为EG⊥GF.（2）A.如图2中，由题意，∠BEG+∠DFG＝90°，∵EM平分∠BEG，MF平分∠DFG，∴∠BEM+∠MFD＝（∠BEG+∠DFG）＝45°，∴∠M＝∠BEM+∠MFD＝45°，B.如图3中，由题意，∠EOF＝∠BEO+∠DFO，∠EPF＝∠BEP+∠DFP，∵PE平分∠BEO，PF平分∠DFO，∴∠BEO＝2∠BEP，∠DFO＝2∠DFP，∴∠EOF＝2∠EPF，故答案为A或B，45°，∠EOF＝2∠EPF.。