晶体生长第七章 晶体生长动力学

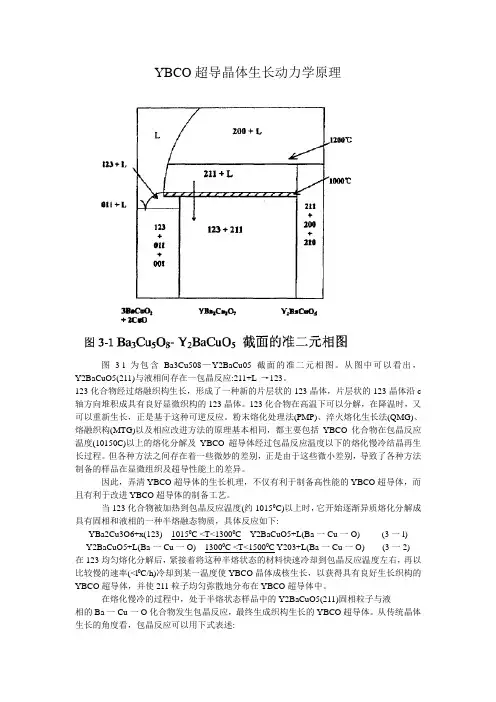
YBCO超导晶体生长动力学原理图3-l为包含Ba3Cu508—Y2BaCu05截面的准二元相图。

从图中可以看出，Y2BaCuO5(211)与液相间存在一包晶反应:211+L →123。

123化合物经过熔融织构生长，形成了一种新的片层状的123晶体，片层状的123晶体沿c 轴方向堆积成具有良好显微织构的123晶体。

123化合物在高温下可以分解，在降温时，又可以重新生长，正是基于这种可逆反应。

粉末熔化处理法(PMP)、淬火熔化生长法(QMG)、熔融织构(MTG)以及相应改进方法的原理基本相同，都主要包括YBCO化合物在包晶反应温度(10150C)以上的熔化分解及YBCO超导体经过包晶反应温度以下的熔化慢冷结晶再生长过程。

但各种方法之间存在着一些微妙的差别，正是由于这些微小差别，导致了各种方法制备的样品在显微组织及超导性能上的差异。

因此，弄清YBCO超导体的生长机理，不仅有利于制备高性能的YBCO超导体，而且有利于改进YBCO超导体的制备工艺。

当123化合物被加热到包晶反应温度(约10150C)以上时，它开始逐渐异质熔化分解成具有固相和液相的一种半熔融态物质，具体反应如下:YBa2Cu3O6+x(123) 10150C <T<13000C Y2BaCuO5+L(Ba一Cu一O) (3一l) Y2BaCuO5+L(Ba一Cu一O) 13000C <T<15000C Y203+L(Ba一Cu一O) (3一2)在123均匀熔化分解后，紧接着将这种半熔状态的材料快速冷却到包晶反应温度左右，再以比较慢的速率(<l0C/h)冷却到某一温度使YBCO晶体成核生长，以获得具有良好生长织构的YBCO超导体，并使211粒子均匀弥散地分布在YBCO超导体中。

在熔化慢冷的过程中，处于半熔状态样品中的Y2BaCuO5(211)固相粒子与液相的Ba一Cu一O化合物发生包晶反应，最终生成织构生长的YBCO超导体。

晶体生长原理晶体生长是指晶体在适当条件下从溶液或气相中吸收物质并逐渐增大的过程。

晶体生长是固体物理学和化学中的一个重要研究领域，对于材料科学、地质学、生物学等领域都具有重要意义。

晶体生长的原理涉及到热力学、动力学、表面化学等多个方面的知识，在实际应用中也有着广泛的应用价值。

晶体生长的原理可以归纳为以下几个方面：1. 原子或分子的扩散。

晶体生长的第一步是溶液或气相中的原子或分子通过扩散运动到达晶体表面。

这一过程受到温度、浓度梯度、表面形貌等多种因素的影响。

原子或分子在溶液或气相中的扩散速率决定了晶体生长的速度和形貌。

2. 晶体表面的吸附和解吸。

当原子或分子到达晶体表面时，它们会发生吸附和解吸的过程。

吸附是指原子或分子附着在晶体表面，解吸则是指原子或分子从晶体表面脱离。

吸附和解吸的平衡状态决定了晶体表面的活性，进而影响晶体生长的速率和形貌。

3. 晶体生长的动力学过程。

晶体生长的动力学过程包括原子或分子在晶体表面的扩散、吸附、解吸等过程，以及晶体内部的结构调整和排列。

这一过程受到温度、浓度、界面能等因素的影响，对晶体生长的速率和形貌起着决定性作用。

4. 晶体生长的形貌控制。

晶体生长的形貌受到晶体生长条件和晶体本身特性的影响。

在实际应用中，通过调控溶液或气相中的成分、温度、pH值等条件，可以实现对晶体生长形貌的控制，获得特定形状和尺寸的晶体。

总的来说，晶体生长是一个复杂的过程，受到多种因素的影响。

在实际应用中，通过深入研究晶体生长的原理，可以实现对晶体生长过程的控制，获得具有特定形貌和性能的晶体材料，为材料科学和其他领域的发展提供重要支持。

同时，对晶体生长原理的深入理解也有助于揭示自然界中晶体的形成和演化规律，对地质学、生物学等领域的研究具有重要意义。

1.如何知道晶体沿哪个晶面生长?一个晶体有多个晶面，怎么知道它沿哪个晶面生长？是不是沿XRD测出来的峰最强的那个晶面生长？扫描电镜可以观察晶体有多个面，如何知道每个面所对应的晶面？
答：一般是晶体的密排面，因为此晶面的自由能最低。

这个和温度有关，温度高就是热力学生长，能克服较大势垒，一般沿111面长成球或者四方。

温度低的话，就是动力学生长，沿着100面，成为柱状了。

对于完美无缺陷的晶体来说，原子间距最小的面最容易生长，如111面，长成球或者四方。

改变外界条件，如温度、PH值、表面活性剂等，都会影响晶体的生长。

对于缺陷晶体来说，除以上因素外，杂质缺陷、螺旋位错等也会影响晶体的生长。

如果按照正常生长的话，都是密排面生长，但是熔体的条件改变后生长方式发生改变，例如铝硅合金的变质，加入变质剂后就不是密排面生长，而是频繁的分枝，各个面可能都有。

完美条件下是沿吴立夫面生长，但总会有外界条件影响晶面的表面能，导致吴立夫面不是表面能最低的面，所以晶体露在外边的面就不一定是吴立夫面了，但应该是该生长条件下表面能最低的面。

HRTEM 和SAED可以表征生长方向~晶面能量越高，原子堆积速度越快，垂直该晶面方向的生长速度就快。

而这样的后果有两个：
1.晶体沿垂直该晶面的方向快速生长；
2.该晶面在生长过程中消失。

引晶是拉晶里面的一个步骤，一般拉晶是指单晶生长的整个过程，
其中包括清炉、装料、抽空、化料、引晶、放肩、转肩、等径、收尾、停炉。

拉晶有些人是叫长晶，引晶一般是指将籽晶（又称晶种）放入溶液硅中，然后沿着籽晶引出一段细晶，这过程主要是为了排除位错和缺陷，使后面的晶体能够较好的生长。

晶体生长的真实过程与理论模拟晶体是一种有序结构的凝聚态物质，在科学技术和工业生产中有着广泛的应用。

晶体生长是晶体学的重要分支，其研究对象是如何控制、促进晶体的形成和生长。

然而，晶体生长的真实过程十分复杂，需要运用不同的理论和模拟方法予以探究。

一、晶体生长的真实过程晶体生长的过程一般包括溶液的饱和和过饱和状态、分子在晶体表面的吸附和扩散、晶体表面的缺陷形成和扩张、晶体的生长等多个阶段。

其中，晶体表面的行为对于晶体形态的形成和晶体质量的提高具有重要意义。

1. 溶液的饱和和过饱和状态溶液的饱和度决定了晶体生长的起始条件。

在晶体生长前期，若溶液中的物质浓度低于饱和浓度，则晶体无法形成。

而当溶液中的物质浓度高于饱和浓度，就会形成过饱和状态，这时分子在晶体表面上的吸附和扩散过程增强，晶体生长速率加快。

2. 分子在晶体表面的吸附和扩散在晶体生长初期，一般先形成一个小的“种子晶体”，然后再在其周围不断加长。

分子在晶体表面的吸附和扩散对于晶体的初期生长具有决定性的作用。

当分子在晶体表面上吸附后，会发生扩散现象，即离开吸附位置，向周围运动。

3. 晶体表面的缺陷形成和扩张晶体表面的缺陷是晶体生长过程中不可避免的现象。

晶体表面的缺陷形成主要有以下几种：（1）附加缺陷：晶体表面受到外界扰动，例如震动、光照等，会产生附加缺陷。

（2）基础缺陷：晶体表面固有的未完整的原子排列也会形成缺陷。

这些缺陷会深入吸附分子和周围原子，并促进晶体的生长。

（3）生长缺陷：晶体生长过程中，表面上可能出现某些地方缺陷不断扩张，产生形态不规则的晶体。

4. 晶体的生长晶体的生长是指晶体形态的改变和晶格的不断扩大。

在晶体的生长过程中，分子会在晶体表面寻找最适合自己的位置，当其能量下降时，晶体就会加长。

通过调节溶液的饱和度、温度、压力等因素，可以控制晶体生长的速度和方向，从而得到有特定形态和尺寸的晶体。

二、理论模拟方法晶体生长的真实过程受到多种难以控制的因素的影响，这使得实验方法往往无法完全揭示晶体生长的机制和规律。

晶体生长原理与技术晶体生长是指无定形物质逐渐形成有序排列的晶体结构的过程。

晶体生长的原理和技术在材料科学、化学工程、地质学等领域都有着重要的应用。

本文将介绍晶体生长的基本原理和常见的生长技术，希望能够为相关领域的研究者和工程师提供一些参考。

晶体生长的原理主要包括热力学和动力学两个方面。

热力学上，晶体生长是在适当的温度、压力和化学势条件下，通过原子、分子或离子的有序排列形成晶体结构。

动力学上，晶体生长受到核形成、生长和形貌稳定性等多个因素的影响。

在实际应用中，热力学和动力学的相互作用决定了晶体生长的过程和结果。

晶体生长的技术包括自发晶体生长和人工晶体生长两种类型。

自发晶体生长是指在自然条件下晶体从溶液、气相或熔体中沉积生长的过程。

常见的自发晶体生长技术包括溶液结晶、气相沉积和熔融结晶等。

人工晶体生长是指通过人为控制条件来促进晶体生长的过程。

常见的人工晶体生长技术包括气相输运法、熔融法、溶液法和固相法等。

在晶体生长技术中，溶液法是应用最为广泛的一种技术。

溶液法是指将溶剂中的溶质逐渐沉积形成晶体的过程。

在溶液法中，溶剂的选择、溶质的浓度、溶液的温度和搅拌速度等因素都会对晶体生长的过程产生影响。

另外，溶液法还包括了一些特殊的技术，如悬浮溶液法、凝胶溶液法和水热法等，这些技术在不同领域都有着重要的应用。

除了溶液法，气相沉积也是一种常见的晶体生长技术。

气相沉积是指通过气相中的原子或分子沉积在基底表面上形成晶体的过程。

在气相沉积技术中，通常会选择适当的气相载体和反应条件来控制晶体的生长方向和形貌。

气相沉积技术在半导体材料、功能薄膜和纳米材料等领域有着广泛的应用。

总的来说，晶体生长是一个复杂的过程，涉及到热力学、动力学和多种技术的相互作用。

通过深入理解晶体生长的原理和技术，可以更好地控制和应用晶体材料，为材料科学和工程技术的发展提供新的思路和方法。

希望本文能够对相关领域的研究和实践有所帮助。

钼精矿的矿石结晶与晶体生长动力学钼是一种广泛用于工业和冶金的重要金属。

它的精矿中含有一定量的钼，通常通过矿石结晶和晶体生长来提取。

本文将探讨钼精矿的矿石结晶和晶体生长动力学的基本过程和影响因素。

矿石结晶是钼精矿中钼酸钠或其他化合物的结晶过程。

在这个过程中，溶液中的离子结合在一起形成晶体。

矿石结晶的动力学过程主要受到以下因素的影响：温度、浓度、溶液的流动性和晶体核心数量。

首先，温度对矿石结晶的影响很大。

随着温度的升高，溶液中的溶解度降低，使得晶体开始从溶液中析出。

较低的温度可以促进钼精矿晶体的生长，而过高的温度则可能导致晶体的溶解。

其次，溶液中的钼浓度也对矿石结晶起着重要作用。

当钼溶液的浓度超过饱和度时，晶体开始形成。

较高的钼浓度可以加速晶体的生长，但过高的浓度可能导致晶体形成的速度过快，导致晶体质量下降。

此外，溶液的流动性对矿石结晶起着影响。

较好的流动性有利于溶液中的离子迅速扩散并结合成晶体，从而促进了结晶过程。

溶液中的搅拌和涡流可以提高晶体的生长速度和质量。

最后，晶体核心数量是钼精矿矿石结晶的关键因素之一。

当溶液中存在足够多的晶核时，结晶过程可以迅速进行。

晶体核心的形成可以通过添加催化剂或种子结晶剂来促进。

晶体生长是矿石结晶后的重要过程。

晶体生长是指晶体从核心开始不断增加大小和改变形状的过程。

晶体生长的动力学过程受到以下因素的影响：溶液浓度、温度、溶液流动性和晶体表面形态。

首先，溶液浓度对晶体生长起着关键作用。

较高的溶液浓度有利于晶体的生长，但过高的浓度可能导致结晶速度过快，从而影响晶体的质量和形状。

其次，温度对晶体生长也有显著影响。

适当的温度可以促进晶体的生长，但过高或过低的温度都会干扰晶体的生长过程。

此外，溶液的流动性对晶体生长起着重要作用。

较好的流动性可以促进溶液中的离子扩散和结晶过程，从而促进晶体的生长。

最后，晶体表面的形态对晶体生长也有影响。

晶体表面的形态决定了晶体生长的速率和方向。

分子动力学模拟晶体生长分子动力学模拟是数值计算方法之一，它可以模拟分子在宏观尺度下的运动，被广泛应用于材料科学、化学、生物物理学等领域。

其中特别值得关注的一种应用就是晶体生长的模拟。

下面将分步骤详细阐述晶体生长的分子动力学模拟过程。

第一步：构建晶体模型在开始模拟之前，需要首先构建一个具有晶格结构的模型。

在晶体生长中，通常使用的方法是在一个盒子内放入所需的原子或分子，并以一定的方式排列得到最初的结构。

比如，对于一种简单的晶体，如NaCl，可以将Na和Cl离子放置在不同的网格点上，以此构建初始模型。

第二步：确定势能函数分子间作用力是晶体生长中的重要因素。

它们可以用势能函数来描述，在分子动力学模拟中，通常选取Lennard-Jones势函数和Coulomb势函数作为分子的相互作用势能。

在Lennard-Jones势能函数中，原子或分子之间的相互作用由短程范德华力（发生在原子或分子之间距离较近的位置）和长程库仑相互作用（发生在原子或分子之间距离较远的位置）构成。

第三步：选择积分方法在分子动力学模拟中，通常使用Verlet算法进行积分。

这个算法可以通过分子的位置和速度来计算分子的运动状态，基本思想是通过离散化时间来近似求解分子的运动方程。

在模拟过程中，可以通过调整时间步长和模拟时间来达到不同的精度。

第四步：设定模拟参数在设定模拟参数的过程中，需要考虑初始状态、温度、压力等因素。

初始状态可以通过仿真算法来生成，温度和压力则需要通过调整模拟过程中分子的速度和位置来进行控制。

具体来说，可以通过在模拟过程中增加或减小温度和压力，来模拟不同条件下的晶体生长。

第五步：模拟晶体生长在设置好以上参数后，就可以开始模拟晶体生长的过程了。

在模拟过程中，每个分子会与其它分子相互作用，这些作用力会导致分子不断移动和变形，直至最终达到稳定的晶体结构。

在晶体形成的过程中，可以通过观察晶体的生长速度、形态等指标，来评估模拟过程的结果。

结晶动力学Avrami方程1. 简介结晶动力学是研究物质从亚稳态向稳态转变的过程。

在材料科学、地球科学、化学工程等领域，结晶动力学的研究对于理解和控制材料的性能具有重要意义。

Avrami 方程是描述结晶过程中晶体生长速率与时间关系的数学模型，由Sergei Avrami于1939年提出。

2. Avrami方程的推导假设在结晶过程中，物质从初始状态开始，经过一段时间后形成了晶体。

Avrami 方程描述了这个过程中晶体形成的速率与时间的关系。

考虑一个简化模型，假设结晶是在均匀各向同性条件下进行的，并且每个结晶核都具有相同的生长速率。

此外，假设结晶是以立方体为单位进行生长，并且生长速率与已经形成的晶体数量成正比。

根据以上假设，可以得到Avrami方程：V=1−e−kt nV0其中，V表示已经形成的晶体数量，V0表示总共需要形成的晶体数量，k为结晶速率常数，t为时间，n为Avrami指数。

3. Avrami方程的物理意义Avrami方程的形式说明了晶体生长速率随时间的增加而减小。

方程中的指数n决定了晶体生长过程的性质。

当n=1时，Avrami方程变为：V=1−e−ktV0此时，Avrami方程描述了一维线性生长过程。

在这种情况下，晶体生长速率与时间成正比。

当n=2时，Avrami方程变为：V=1−e−kt2V0此时，Avrami方程描述了二维面状生长过程。

在这种情况下，晶体生长速率随时间的平方增加。

当n=3时，Avrami方程变为：V=1−e−kt3V0此时，Avrami方程描述了三维体积生长过程。

在这种情况下，晶体生长速率随时间的立方增加。

通过改变Avrami指数n的值，可以控制晶体生长过程的形态和速率。

4. Avrami方程在实际应用中的意义Avrami方程在材料科学和化学工程中具有广泛的应用。

通过实验测量晶体生长过程中已经形成的晶体数量和时间，可以拟合Avrami方程，从而确定结晶速率常数k和Avrami指数n。

晶体的生长方式和速度晶体的生长方式，是指液相中原子向某个晶粒表面的堆砌方式。

根据界面结构的不同，晶体可采取连续生长，侧向生长和从缺陷生长等方式;这三种生长方式相互联系又各具特征。

2012-4-2811）连续生长――粗糙界面的生长粗糙界面--原子只占50%左右的位置，存在50%左右的空位，可作为液相中原子向上堆砌的台阶。

这种台阶不限于一层原子，甚至存在于几个原子层内。

沉积到界面上的原子受到前方和侧面固态原子的作用，结合牢固且不易反弹或脱落，如图。

晶体在生长过程中界面上的台阶始终存在（保持粗糙界面）因此，液体中的原子可以在整个界面上连续沉积，促使界面便连续、均匀地垂直生长。

这种生长被称为连续生长、垂直生长或正常生长。

2012-4-282图2-6 粗糙界面上原子的堆砌过程2012-4-283•由于一个原子到达界面后不因弹性碰撞而被弹回几率A→1，故生长中几乎不存在热力学能障。

F•由于界面的多层结构和过渡性质，其动力学能障也比较小。

因此生长过程易为较小的动力学过冷所驱动，并能得到较高的生长速度。

•绝大多数金属关系？•定量：连续生长速度R与ΔTK2012-4-284如图7,当固/液界面温度低于平衡熔点温度Tm 时，原子从液相跳向固相界面所需活化能为ΔGb，则原子越过势垒ΔGb 从液态变为固态的频率υLS为：υ0—原子的振动频率。

) exp(KTGbLS∆−=νν图2-7 固/液界面的自由能2012-4-2852012-4-286如果原子从固相界面反弹回液相液相中所要克服的势垒是ΔG b ＋ΔG m 。

原子反弹回液相的频率υSL 示为：只有当原子由液态变为固态的频率大于由固态变为液态的频率时，晶体才能长大。

因此，原子沉积与反弹频率之差，即净频率为])(exp[0KT G G m b SL ∆+∆−=νν)]exp(1[KT G m Ls sL Ls net ∆−−=−=νννν2012-4-287由于式中ΔT K 为动力学过冷度。