人教版高中数学必修三 第二章 统计用样本估计总体练习题及答案

分层训练·进阶冲关A 组 基础练(建议用时20分钟)1.已知甲,乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为 ( A )A.32B.33C.34D.352.设样本数据1,2,…,10的均值和方差分别为1和4,若y i =i +a(a 为非零常数,i=1,2,…,10),则y 1,y 2,…,y 10的均值和方差分别为 ( A )A.1+a,4B.1+a,4+aC.1,4D.1,4+a3.如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( D )A.中位数为14B.众数为13C.平均数为15D.方差为194.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则 ( C )A.甲的成绩的平均数小于乙的成绩的平均数B.甲的成绩的中位数等于乙的成绩的中位数C.甲的成绩的方差小于乙的成绩的方差D.甲的成绩的极差小于乙的成绩的极差5.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据环保部门某日早6点至晚9点在A县,B县两个地区附近的PM2.5监测点统计的数据(单位;毫克/立方米)列出的茎叶图,A县、B县两个地区浓度的方差较小的是( A )A.A县B.B县C.A县,B县两个地区相等D.无法确定6.某项测试成绩满分为10分,现随机抽取30名学生参加测试,得分如图所示,假设得分值的中位数为me ,平均值为,众数为m,则( D )A.me =m= B.me=m<C.me <m< D.m<me<7.一组样本数据的频率分布直方图如图所示,试估计此样本数据的中位数为.8.某商场对一个月内每天的顾客人数进行统计,得到如图所示的茎叶图,则该样本的众数是45.9.已知一组数据;87,,90,89,93的平均数为90,则该组数据的方差为4.10.如图是甲,乙两位同学在5次数学测试中得分的茎叶图,则成绩较稳定(方差较小)的那一位同学的方差为2.11.某教师为了了解高三一模所教两个班级的数学成绩情况,将两个班的数学成绩(单位;分)绘制成如图所示的茎叶图.(1)分别求出甲,乙两个班级数学成绩的中位数、众数.(2)若规定成绩大于等于115分为优秀,分别求出两个班级数学成绩的优秀率.【解析】(1)由所给的茎叶图知,甲班50名同学的成绩由小到大排序,排在第25,26位的是108,109,出现次数最多的是103,故甲班数学成绩的中位数是108.5,众数是103;乙班48名同学的成绩由小到大排序,排在第24,25位的是106,107,数量最多的是92和101,故乙班数学成绩的中位数是106.5,众数为92和101.(2)由茎叶图中的数据可知,甲班中数学成绩为优秀的人数为20,优秀率为=;乙班中数学成绩为优秀的人数为18,优秀率为=.12.为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生的各项平均成绩(满分100分),按照以下区间分为7组;[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到频率分布直方图(如图).已知测试平均成绩在区间[30,60)内的有20人.(1)求m的值及中位数n.(2)若该校学生测试平均成绩小于n,则学校应适当增加体育活动时间.根据以上抽样调查数据,该校是否需要增加体育活动时间?【解析】(1)由频率分布直方图知第1组、第2组和第3组的频率分别是0.02,0.02和0.06,则m×(0.02+0.02+0.06)=20,解得m=200.由图知,中位数n位于[70,80)内,则0.02+0.02+0.06+0.22+0.04(n-70)=0.5,解得n=74.5.(2)设第i(i=1,2,3,4,5,6,7)组的频率和频数分别为p i 和i ,由图知,p 1=0.02,p 2=0.02,p 3=0.06,p 4=0.22,p 5=0.40,p 6=0.18,p 7=0.10,则由i =200×p i ,可得1=4,2=4,3=12,4=44,5=80,6=36,7=20,故该校学生测试平均成绩是==74<74.5,所以该校应该适当增加体育活动时间.B 组 提升练(建议用时20分钟) 13.如图所示的茎叶图是甲、乙两位同学在期末考试中的六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则,y 的值分别为 ( D )A.2,4B.4,4C.5,6D.6,414.一个样本a,3,5,7的平均数是b,且a,b 是方程2-5+4=0的两根,则这个样本的方差是( C ) A.3 B.4 C.5 D.615.某校女子篮球队7名运动员身高(单位;厘米)分布的茎叶图如图,已知记录的平均身高为175 cm,但有一名运动员的身高记录不清楚,其末位数记为,那么的值为 2 .16.在一个容量为5的样本中,数据均为整数,已测出其平均数为10,但墨水污损了两个数据,其中一个数据的十位数字1未被污损,其余三个数据为9,10,11,那么这组数据的方差s2可能的最大值是32.8.17.一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动.在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制) 的茎叶图如图所示.(1)根据这10名同学的测试成绩,估计该班男、女生国学素养测试的平均成绩.(2)比较这10名同学中男生和女生的国学素养测试成绩的方差的大小.(只需直接写出结果)【解析】(1)设这10名同学中男、女生的平均成绩分别为,.则==73.75(分),==76(分).(2)女生国学素养测试成绩的方差大于男生国学素养测试成绩的方差.18.某同学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该盒饭,以(单位;盒,100≤≤200)表示这个开学季内的市场需求量,y(单位;元)表示这个开学季内经销该产品的利润.(1)根据频率分布直方图估计开学季内市场需求量的平均数和众数.(2)将y表示为的函数.(3)根据频率分布直方图估计利润y不少于1 350元的概率(将频率视为概率). 【解析】(1)由频率分布直方图得,开学季内市场需求量的众数的估计值是150盒.需求量为[100,120)的频率为0.005×20=0.1,需求量为[120,140)的频率为0.01×20=0.2,需求量为[140,160)的频率为0.015×20=0.3,需求量为[160,180)的频率为0.012 5×20=0.25,需求量为[180,200]的频率为0.007 5×20=0.15,110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153,故平均数的估计值为153盒.(2)因为每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元,所以当100≤≤150时,y=10-5(150-)=15-750,当150<≤200时,y=10×150=1 500,所以y=(∈N).(3)因为利润不少于1 350元,所以由15-750≥1 350,得≥140.所以由(1)知利润不少于1 350元的概率P=1-0.1-0.2=0.7.C组培优练(建议用时15分钟)19.如图是民航部门统计的2017年春运期间几个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是( D )A.深圳的变化幅度最小,北京的平均价格最高B.深圳和厦门的春运期间往返机票价格同去年相比有所下降C.平均价格从高到低居于前三位的城市为北京、深圳、广州D.平均价格的涨幅从高到低居于前三位的城市为天津、西安、厦门20.随着移动互联网的发展,与餐饮美食相关的手机应用软件层出不穷.现从使用A和B两款订餐软件的商家中分别随机抽取50个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下;(1)试估计使用A款订餐软件的50个商家的“平均送达时间”的众数及平均数.(2)根据以上抽样调查数据,将频率视为概率,回答下列问题;①能否认为使用B款订餐软件“平均送达时间”不超过40分钟的商家达到75%?②如果你要从A和B两款订餐软件中选择一款订餐,你会选择哪款?说明理由. 【解析】(1)由已知,使用A款订餐软件的50个商家的“平均送达时间”的众数为55.使用A款订餐软件的50个商家的“平均送达时间”的平均数为15×0.06+25×0.34+35×0.12+45×0.04+55×0.4+65×0.04=40.(2)①使用B款订餐软件“平均送达时间”不超过40分钟的商家的比例估计值为0.04+0.20+0.56=0.80=80%>75%.故可以认为使用B款订餐软件“平均送达时间”不超过40分钟的商家达到75%.②使用B款订餐软件的50个商家的“平均送达时间”的平均数为15×0.04+25×0.2+35×0.56+45×0.14+55×0.04+65×0.02=35<40,所以选B款订餐软件.。

,/ .2．2.1用样本的频率分布估计总体分布(一)学习目标 1.体会分布的意义和作用；2.学会用频率分布表，画频率分布直方图表示样本数据；3.能通过频率分布表或频率分布直方图对数据做出总体统计．思考还记得我们抽样的初衷吗？梳理(1)用样本的__________估计总体的分布．(2)用样本的__________估计总体的数字特征．知识点二数据分析的基本方法思考通过抽样获得的原始数据有什么缺点？梳理(1)借助于图形分析数据的一种基本方法是用图将它们画出来，此方法可以达到两个目的，一是从数据中________信息，二是利用图形________信息．(2)借助于表格分析数据的另一种方法是用紧凑的________改变数据的排列方式，此方法是通过改变数据的____________，为我们提供解释数据的新方式．知识点三频率分布表与频率分布直方图思考1要做频率分布表，需要对原始数据做哪些工作？思考2如何决定组数与组距？思考3同样一组数据，如果组距不同，得到的频率分布直方图也会不同吗？梳理一般地，频数指某组中包含的个体数，各组频数和＝样本容量；频率＝频数样本容量，各组频率和＝1.在频率分布直方图中，纵轴表示________，数据落在各小组内的频率用________________来表示，各小长方形的面积的总和等于____．类型一频率分布直方图命题角度1有关概念的理解例1关于频率分布直方图，下列说法正确的是()A．直方图中小长方形的高表示取某数的频率B．直方图中小长方形的高表示该组上的个体在样本中出现的频率C．直方图中小长方形的高表示该组上的个体在样本中出现的频数与组距的比值D．直方图中小长方形的高表示该组上的个体在样本中出现的频率与组距的比值反思与感悟由频率的定义不难得出，各组数据的频率之和为1，因为各组数据的个数之和为样本容量．在列频率分布表时，可以利用这种方法检查是否有数据的丢失．跟踪训练1一个容量为20的样本数据，将其分组如下表：A．0.5 B．0.25 C．0.6 D．0.7命题角度2绘制频率分布直方图例2某中学从高一年级随机抽取50名学生进行智力测验，其得分如下(单位：分)：4864528671486441867971688284686462688157905274735678476655645688694073976856675970527944556962583258根据上面的数据，回答下列问题：(1) 这次测验成绩的最高分和最低分分别是多少？(2)将区间[30,100]平均分成7个小区间，试列出这50名学生智力测验成绩的频率分布表，进而画出频率分布直方图；(3)分析频率分布直方图，你能得出什么结论？反思与感悟组距和组数的确定没有固定的标准，将数据分组时，组数应力求合适，以使数据的分布规律能较清楚地呈现出来．组数太多或太少，都会影响我们了解数据的分布情况．数据分组的组数与样本容量有关，一般样本容量越大，所分组数越多．当样本容量不超过100时，按照数据的多少，常分成5至12组．跟踪训练2一个农技站为了考察某种大麦穗生长的分布情况，在一块试验田里抽取了100株麦穗，量得长度如下(单位：cm)：6．5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.65．8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.86．2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.56．8 6.0 6.3 5.5 5.0 6.3 5.2 6.07.0 6.46．4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.77.46．0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.65．3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.05．6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.75．8 5.37.0 6.0 6.0 5.9 5.4 6.0 5.2 6.06．3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3根据上面的数据列出频率分布表、绘制出频率分布直方图，并估计在这块试验田里长度在5.75～6.35 cm之间的麦穗所占的百分比．例3如表所示给出了在某校500名12岁男孩中，用随机抽样得出的120人的身高(单位：cm).(1)列出样本频率分布表；(2)画出频率分布直方图；(3)估计身高小于134 cm的人数占总人数的百分比．反思与感悟频率分布表和频率分布直方图之间的密切关系是显然的，它们只不过是相同的数据的两种不同的表达方式，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚地看到整个样本数据的频率分布情况，并由此估计总体的分布情况．跟踪训练3从某校高三学生中抽取50名参加数学竞赛，成绩分组(单位：分)及各组的频数如下：[40,50)，2；[50,60)，3；[60,70)，10；[70,80)，15；[80,90)，12；[90,100]，8.(1)列出样本的频率分布表(含累积频率)；(2)画出频率分布直方图；(3)估计成绩在[60,90)分的学生比例．例4从某校随机抽取100名学生，获得了他们一周课外阅读时间(单位：小时)的数据，整理得到数据分组及频数分布表和频率分布直方图：(1)从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；(2)求频率分布直方图中的a，b的值；(3)假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)．反思与感悟在频率分布直方图中，各小长方形的面积等于相应各组的频率，小长方形的高与频数成正比，各组频数之和等于样本容量，频率之和等于1.跟踪训练4某学校组织学生参加数学测试，某班学生的成绩频率分布直方图如图，数据的分组依次为[20,40)，[40,60)，[60,80)，[80,100]，若低于60分的人数是15，则该班的学生总人数是()A．45 B．50 C．55 D．601．如图所示是一容量为100的样本的频率分布直方图，则由图中的数据可知，样本落在[15,20]内的频数为()A．20 B．30C．40 D．502．已知样本数据：10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,11.那么频率为0.2的是() A．[5.5,7.5) B．[7.5,9.5)C．[9.5,11.5) D．[11.5,13.5]3．如图是将高三某班60名学生参加某次数学模拟考试所得的成绩(成绩均为整数)整理后画出的频率分布直方图，则此班的优秀(120分及以上为优秀)率为________．4．根据国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阈值与检验》(GB19522～2004)中规定车辆驾驶人员血液酒精含量：“饮酒驾车”的临界值为20 mg/100mL ；“醉酒驾车”的临界值为80 mg/100 mL.某地区交通执法部门统计了5月份的执法记录数据(每个分组包括最小值不包括最大值)：根据上述表格，可估计该地区全年“饮酒驾车”发生的频率等于________．5．暑假期间某班为了增强学生的社会实践能力，把该班学生分成四个小组到一果园帮果农测量果树的产量，某小组来到一片种植苹果的山地，他们随机选取20株作为样本测量每一株的果实产量(单位：kg)，获得的数据按照区间[40,45)，[45,50)，[50,55)，[55,60]进行分组，得到如下频率分布表：已知样本中产量在区间[45,50)内的株数是产量在区间[50,60]内的株数的43倍．(1)分别求出a ，b ，c 的值； (2)作出频率分布直方图．1．频率分布是指一个样本数据在各个小范围内所占比例的大小，总体分布是指总体取值的频率分布规律，我们通常用样本的频率分布表或频率分布直方图去估计总体的分布． 2．频率分布表和频率分布直方图，是对相同数据的两种不同表达方式，用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况．通过作图既可以从数据中提取信息，又可以利用图形传递信息．3．样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚地看到整个样本数据的频率分布情况，并由此估计总体的分布情况．答案精析问题导学 知识点一思考 用样本去估计总体，为决策提供依据． 梳理(1)频率分布 (2)数字特征 知识点二思考 因为通过抽样获得的原始数据多而且杂乱，无法直接从中理解它们的含义，并提取信息，也不便于我们用它来传递信息． 梳理(1)提取 传递 (2)表格 构成形式 知识点三思考1 分组，频数累计，计算频数和频率． 思考2 若极差组距为整数，则极差组距＝组数．若极差组距不为整数，则⎣⎢⎡⎦⎥⎤极差组距＋1＝组数．注意：[x ]表示不大于x 的最大整数．思考3 不同．对于同一组数据分析时，要选好组距和组数，不同的组距与组数对结果有一定的影响． 梳理频率/组距 小长方形的面积 1 题型探究例1 D [注意频率分布直方图和条形图的区别，在直方图中，纵轴(小长方形的高)表示频率与组距的比值，其相应组距上的频率等于该组距上的小长方形的面积．] 跟踪训练1 D [样本在区间(－∞，50)上的频率为2＋3＋4＋520＝1420＝0.7.] 例2 解 (1)这次测验成绩的最低分是32分，最高分是97分． (2)根据题意，列出样本的频率分布表如下：(3)从频率分布直方图可以看出，这50名学生的智力测验成绩大体上呈两头小、中间大，左右基本对称，说明这50名学生中智力特别好或特别差的占极少数，而智力一般的占多数，这是一种最常见的分布．跟踪训练2 解 (1)计算极差：7.4－4.0＝3.4； (2)决定组距与组数：若取组距为0.3，因为3.40.3≈11.3，需分为12组，组数合适，所以取组距为0.3，组数为12；(3)决定分点：使分点比数据多一位小数，并且把第1小组的起点稍微减小一点，那么所分的12个小组可以是3.95～4.25,4.25～4.55,4.55～4.85，…，7.25～7.55； (4)列频率分布表：(5)从表中看到，样本数据落在5.75～6.35之间的频率是0.28＋0.13＝0.41，于是可以估计，在这块试验田里长度在5.75～6.35 cm之间的麦穗约占41%.例3解(1)样本频率分布表如下：(2)(3)由样本频率分布表可知，身高小于134 cm的男孩出现的频率为0.04＋0.07＋0.08＝0.19，所以我们估计身高小于134 cm的人数占总人数的19%.跟踪训练3解(1)频率分布表如下：(2)(3)成绩在[60,90)分的学生比例，即学生成绩在[60,90)分的频率0.2＋0.3＋0.24＝0.74＝74%.所以估计成绩在[60,90)分的学生比例为74%.例4 解 (1)根据频数分布表知，100名学生中一周课外阅读时间不少于12小时的学生共有6＋2＋2＝10(名)，所以样本中的学生一周课外阅读时间少于12小时的频率是1－10100＝0.9.故从该校随机选取一名学生，估计其该周课外阅读时间少于12小时的概率为0.9.(2)课外阅读时间落在组[4,6)内的有17人，频率为0.17，所以a ＝频率组距＝0.172＝0.085.课外阅读时间落在组[8,10)内的有25人，频率为0.25，所以b ＝频率组距＝0.252＝0.125.(3)样本中的100名学生该周课外阅读时间的平均数在第4组．跟踪训练4 B [结合频率分布直方图，得分低于60分的人数占总人数的频率为20×(0.005＋0.01)＝0.30，所以总人数为150.30＝50，故选B.] 当堂训练1．B [样本数据落在[15,20]内的频数为100×[1－5×(0.04＋0.1)]＝30.] 2．D [列出频率分布表，依次对照就可以找到答案，频率分布表如下：从表中可以看出频率为3．30%解析 优秀率为10×(0.022 5＋0.005＋0.002 5)＝0.3＝30%. 4．0.09解析 5月份“饮酒驾车”发生的频率等于11＋5＋2200＝0.09.可估计全年“饮酒驾车”发生的频率为0.09. 5．解 (1)易得c ＝1.0.由题意得⎩⎪⎨⎪⎧a ＝43(0.1＋b )，0.3＋a ＋0.1＋b ＝1.0，∴a ＝0.4，b ＝0.2.(2)根据频率分布表画出频率分布直方图，如图所示．。

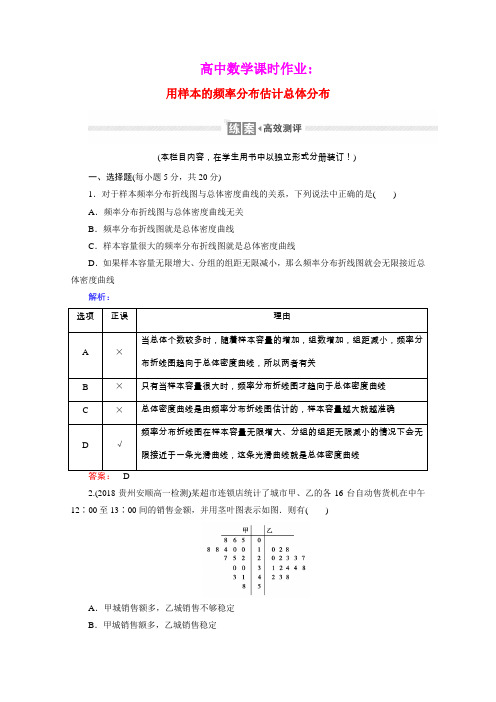
高中数学课时作业:用样本的频率分布估计总体分布(本栏目内容，在学生用书中以独立形式分册装订！)一、选择题(每小题5分，共20分)1．对于样本频率分布折线图与总体密度曲线的关系，下列说法中正确的是()A．频率分布折线图与总体密度曲线无关B．频率分布折线图就是总体密度曲线C．样本容量很大的频率分布折线图就是总体密度曲线D．如果样本容量无限增大、分组的组距无限减小，那么频率分布折线图就会无限接近总体密度曲线解析：选项正误理由当总体个数较多时，随着样本容量的增加，组数增加，组距减小，频率分A ×布折线图趋向于总体密度曲线，所以两者有关B ×只有当样本容量很大时，频率分布折线图才趋向于总体密度曲线C ×总体密度曲线是由频率分布折线图估计的，样本容量越大就越准确频率分布折线图在样本容量无限增大、分组的组距无限减小的情况下会无D √限接近于一条光滑曲线，这条光滑曲线就是总体密度曲线2.(2018·贵州安顺高一检测)某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12∶00至13∶00间的销售金额，并用茎叶图表示如图．则有()A．甲城销售额多，乙城销售不够稳定B．甲城销售额多，乙城销售稳定C．乙城销售额多，甲城销售稳定D．乙城销售额多，甲城销售不够稳定解析：十位数字是2,3,4时乙明显多于甲，估计乙销售额多，甲的数字过于分散，不够稳定，故选D.答案： D3.如图是某公司10个销售店某月销售某产品数量(单位：台)的茎叶图，则数据落在区间[22,30)内的频率为()A．0.2 B．0.4C．0.5 D．0.6解析：利用频率及茎叶图的知识直接运算求解．由题意知，这10个数据落在区间[22,30)内的有22、22、27、29，共4个，所以其频率为410＝0.4，故选B.答案： B4．观察新生婴儿的体重，其频率分布直方图如图所示，则新生婴儿体重在[2 700,3 000)内的频率为()A．0.001 B．0.1C．0.2 D．0.3解析：由频率分布直方图的意义可知，各小长方形的面积＝组距×频率组距＝频率，即各小长方形的面积等于相应各组的频率．在区间[2 700,3 000)内频率的取值为(3 000－2 700)×0.001＝0.3.故选D.答案： D二、填空题(每小题5分，共15分)5．一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如图)．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在[2 500，3 000)(元)月收入段应抽出________人．解析：由题意得在[2500,3000)(元)月收入段应抽出的人数为0.0005×500×100＝25.答案：256．某省选拔运动员参加运动会，测得7名选手的身高(单位：cm)分布茎叶图如图所示，记录的平均身高为177 cm，其中有一名候选人的身高记录不清，其末位数为x，那么x的值为________．解析：依题意得180×2＋1＋170×5＋3＋x＋8＋9＝177×7，x＝8.答案：87．下面是某中学期末考试各分数段的考生人数分布表：分数频数频率[300,400) 5[400,500)900.075[500,600)499[600,700)0.425[700,800)？[800,900]8则分数在[700,800)解析：由于在分数段[400,500)内的频数是90，频率是0.075，则该中学共有考生90 0.075＝1 200，则在分数段[600,700)内的频数是1 200×0.425＝510，则分数在[700,800)内的频数，即人数为1 200－(5＋90＋499＋510＋8)＝88.答案：88三、解答题(每小题10分，共20分)8．为了调查甲、乙两个交通站的车流量，随机选取了14天，统计每天上午8：00～12：00间各自的车流量(单位：百辆)，得如图所示的统计图，试求：(1)甲、乙两个交通站的车流量的极差分别是多少？(2)甲交通站的车流量在[10,40]间的频率是多少？(3)甲、乙两个交通站哪个站更繁忙？并说明理由．解析：(1)甲交通站的车流量的极差为73－8＝65(百辆)，乙交通站的车流量的极差为71－5＝66(百辆)．(2)甲交通站的车流量在[10,40]间的频率为414＝2 7.(3)甲交通站的车流量集中在茎叶图的下方，而乙交通站的车流量集中在茎叶图的上方，从数据的分布情况来看，甲交通站更繁忙．9．下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高(单位：cm)．区间界限[122,126)[126,130)[130,134)[134,138)[138,142) 人数58102233区间界限[142,146)[146,150)[150,154)[154,158]人数20116 5(2)画出频率分布直方图；(3)估计身高小于134 cm的人数占总人数的百分比．解析：(1)样本频率分布表如下：分组频数频率[122,126)50.04[126,130)80.07[130,134)100.08[134,138)220.18[138,142)330.28[142,146)200.17[146,150)110.09[150,154)60.05[154,158]50.04合计120 1(2)其频率分布直方图如下：(3)由样本频率分布表可知身高小于134 cm的男孩出现的频率为0.04＋0.07＋0.08＝0.19，所以我们估计身高小于134 cm的人数占总人数的19%.。

人教新课标A版高中数学必修3 第二章统计 2.2样本估计总体 2.2.1用样本的频率分布估计总体同步测试（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题；共30分)1. （2分）(2017·鞍山模拟) 某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，若这200名学生中每周的自习时间不超过m小时的人数为164，则m的值约为（）A . 26.25B . 26.5C . 26.75D . 272. （2分）某路段检查站监控录像显示，在某时段内，有1000辆汽车通过该站，现在随机抽取其中的200辆汽车进行车速分析，分析的结果表示为如右图的频率分布直方图，则估计在这一时段内通过该站的汽车中速度不小于90km/h的约有A . 100辆B . 200辆C . 300辆D . 400辆3. （2分）为了解一片速生林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出了样本的频率分布直方图，那么在这100株树木中，底部周长小于110cm的株数是A . 30B . 60C . 70D . 804. （2分）某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒;…… 第六组，成绩大于等于18秒且小于等于19秒. 右图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y，则从频率分布直方图中可分析出x和y分别为（）A . 0.9，35B . 0.9，45C . 0.1，35D . 0.1，455. （2分）为了了解某校高三学生的视力情况，随机地抽查了该校100名高三学生，得到学生视力频率分布直方图，如右图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频率成等差数列．设最大频率为a；视力在4．6到5．0之间的学生人数为b，则a、b的值分别为A . 0.27，78B . 0.27，83C . 2.7，78D . 2.7，836. （2分）已知样本：10861013810121178911912910111211那么频率为0.2的范围是（）A . 5.5～7.5B . 7.5～9.5C . 9.5～11.5D . 11.5～13.57. （2分）一个容量为100的样本分成若干组，已知某组的频率为0.3，则该组的频数是（）A . 3B . 30C . 10D . 3008. （2分）某校高二（1）班一次阶段考试数学成绩的茎叶图和频率分布直方图可见部分如图，根据图中的信息，可确定被抽测的人数及分数在[90，100]内的人数分别为（）A . 20，2B . 24，4C . 25，2D . 25，49. （2分） (2017高二下·乾安期末) 某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图.根据该折线图，下列结论正确的是（）A . 月接待游客逐月增加B . 年接待游客量逐年减少C . 各年的月接待游客量高峰期大致在6、7月D . 各年1月至6月的月接待游客量相对于7月至12月，波动性较小，变化比较稳定10. （2分）某大学对名学生的自主招生水平测试成绩进行统计，得到样本频率分布直方图(如图)，则这名学生在该次自主招生水平测试中成绩不低于分的学生数是（）A .B .C .D .11. （2分）某商场在国庆黄金周的促销活动中，对10月2日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时到12时的销售额为（）A . 6万元B . 8万元C . 10万元D . 12万元12. （2分） (2016高二下·银川期中) 对某班学生一次英语测验的成绩分析，各分数段的分布如图（分数取整数），由此，估计这次测验的优秀率（不小于80分）为（）A . 92%B . 24%C . 56%D . 5.6%13. （2分）某地一种植物一年生长的高度如下表：则该植物一年生长在[30，40）内的频率是（）B . 0.65C . 0.40D . 0.2514. （2分）为了解某大学的学生是否爱好体育锻炼，用简单随机抽样方法在校园内调查了120位学生，得到如下2×2列联表：男女总计爱好a b73不爱好c25总计74则a﹣b﹣c等于（）A . 6B . 7C . 8D . 915. （2分） 5000辆汽车经过某一雷达测速区，其速度频率分布直方图如图所示，则时速超过70km/h的汽车数量为（）A . 50C . 1000D . 4500二、填空题 (共5题；共5分)16. （1分）一个高中研究性学习小组对本地区2002年至2004年快餐公司发展情况进行了调查，根据图中的信息可以得出这三年中该地区每年平均销售盒饭________ 万盒．17. （1分）某中学举行了一次田径运动会，其中有50名学生参加了一次百米比赛，他们的成绩和频率如图所示．若将成绩小于15秒作为奖励的条件，则在这次百米比赛中获奖的人数共有________ 人．18. （1分） (2017高一下·珠海期末) 下面是被严重破坏的频率分布表和频率分布直方图，根据残表和残图，则 p=________，q=________．分数段频数[60，70）p[70，80）90[80，90）60[90，100]20q19. （1分） (2017高一下·桃江期末) 如图是某班50名学生身高的频率分布直方图，那么身高在区间[150，170）内的学生约有________人．20. （1分）对某文科班50名同学的一次数学成绩进行了统计，全年级文科数学平均分是100分，这个班数学成绩的频率分布直方图如图：（总分150分）从这个班中任取1人，其数学成绩达到或超过年级文科平均分的概率是________．三、解答题 (共5题；共25分)21. （5分） (2017高一下·衡水期末) 2015年下学期某市教育局对某校高三文科数学进行教学调研，从该校文科生中随机抽取40名学生的数学成绩进行统计，将他们的成绩分成六段[80，90），[90，100），[100，110），[110，120），[120，130），[130，140）后得到如图所示的频率分布直方图．（1）求这40名学生中数学成绩不低于120分的学生人数；（2）若从数学成绩[80，100）内的学生中任意抽取2人，求成绩在[80，90）中至少有一人的概率．22. （5分）为了研究某种农作物在特定温度下（要求最高温度t满足：27℃≤t≤30℃）的生长状况，某农学家需要在十月份去某地进行为期十天的连续观察试验．现有关于该地区10月份历年10月份日平均最高温度和日平均最低温度（单位：℃）的记录如下：（Ⅰ）根据本次试验目的和试验周期，写出农学家观察试验的起始日期．（Ⅱ）设该地区今年10月上旬（10月1日至10月10日）的最高温度的方差和最低温度的方差分别为D1 ， D2 ，估计D1 ， D2的大小？（直接写出结论即可）．（Ⅲ）从10月份31天中随机选择连续三天，求所选3天每天日平均最高温度值都在[27，30]之间的概率．23. （5分）某初级中学共有学生2000名，各年级男、女生人数如下表：初一年级初二年级初三年级已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19．（1）求x的值；（2）现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？24. （5分）一个地区共有5个乡镇，共30万人，其人口比例为3∶2∶5∶2∶3，从这30万人中抽取一个300人的样本，分析某种疾病的发病率.已知这种疾病与不同的地理位置及水土有关，则应采取什么样的抽样方法?并写出具体过程.25. （5分） (2018高二上·宾阳月考) 某产品的三个质量指标分别为x，y，z，用综合指标S＝x＋y＋z评价该产品的等级．若S≤4,则该产品为一等品．先从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：（1）利用上表提供的样本数据估计该批产品的一等品率；（2）在该样本的一等品中，随机抽取2件产品，(ⅰ) 用产品编号列出所有可能的结果；(ⅱ) 设事件B为“在取出的2件产品中，每件产品的综合指标S都等于4”，求事件B发生的概率．参考答案一、单选题 (共15题；共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题；共5分) 16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题；共25分) 21-1、21-2、22-1、23-1、24-1、25-1、25-2、。

2.2.1 用样本的频率分布估计总体分布A级基础巩固一、选择题1．没有信息的损失，所有的原始数据都可以从图中得到的统计图是( )A．总体密度曲线B．茎叶图C．频率分布折线图D．频率分布直方图答案：B2．下图是某公司10个销售店某月销售某产品数量(单位：台)的茎叶图，则数据落在区间[22，30)内的频率为( )B．C．D．解析：数据总个数n＝10，又落在区间[22，30)内的数据个数为4，故所求的频率为410＝0.4.答案：B3．某雷达测速区规定：凡车速大于或等于70 km/h的汽车视为“超速”，并将受到处罚．下图是某路段的一个检测点对300辆汽车的车速进行检测所得结果的频率分布直方图，则从图中可得出将被处罚的汽车数为( )A．30辆B．40辆C．60辆D．80辆解析：车速大于或等于70 km/h的汽车数为×10×300＝60(辆)．答案：C4．一个社会调查机构就某地区居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如图)，为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在[2 500，3 000)(单位：元)月收入段应抽出的人数为( )A．5 B．25 C．50 D．2 500解析：组距＝500，在[2 500，3 000)的频率＝0.000 5×500＝，样本数为100，则在[2 500，3 000)内应抽100×＝25(人)．答案：B5．为了了解某校高三学生的视力情况，随机抽查了该校100名高三学生的视力情况，得到频率分布直方图如图所示，由于不慎将部分数据丢失，仅知道后5组的频数和为62.设视力在到之间的学生数为a，最大频率为，则a的值为( )A．27 B．48 C．54 D．64解析：由已知，视力在到之间的学生数为100×＝32，又视力在到之间的频率为1－＋0.5)×－62100＝，所以视力在到之间的学生数为100×＝22，所以视力在到之间的学生数a ＝32＋22＝54.答案：C二、填空题6．某市共有5 000名高三学生参加联考，为了了解这些学生对数学知识的掌握情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：分组/分频数频率[80，90)①②[90，100)[100，110)[110，120)36[120，130)[130，140)12③[140，150]合计④根据上面的频率分布表，可以①处的数值为________，②处的数值为________． 解析：由位于[110，120)的频数为36，频率＝36n＝，得样本容量n ＝120，所以[130，140)的频率＝12120＝，②处的数值＝1－－－－－－＝； ①处的数值为×120＝3. 答案：37．从某小学随机抽取100名同学，将他们的身高(单位：cm)数据绘制成频率分布直方图(如图)．由图中数据可知a ＝________．若要从身高在[120，130)，[130，140)，[140，150]三组内的学生中，用分层抽样的方法抽取18人参加一项活动，则从身高在[140，150]内的学生中抽取的人数应为________．解析：所有小矩形的面积和等于10×＋＋0.020＋a ＋0.035)＝1，解得a ＝；100名同学中，身高在[120，130)内的学生数是10××100＝30，身高在[130，140)内的学生数是10××100＝20，身高在[140，150]内的学生数是10××100＝10，则三组内的总学生数是30＋20＋10＝60，抽样比是1860＝310，所以身高在[140，150]内的学生中选取的人数应为10×310＝3.答案： 38．为了解某校教师使用多媒体进行教学的情况，采用简单随机抽样的方法，从该校200名授课教师中抽取20名教师，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如下：据此可估计该校上学期200名教师中，使用多媒体进行教学次数在[15，25)内的人数为________．答案：60三、解答题9．为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00－10：00间各自的点击量，得到如图所示的茎叶图．(1)甲网站点击量在[10，40]间的频率是多少？ (2)甲、乙两个网站哪个更受欢迎？请说明理由．解：(1)甲网站点击量在[10，40]内的有17，20，38，32，共有4天，则频率为414＝27. (2)甲网站的点击量集中在茎叶图的下方，而乙网站的点击量集中在茎叶图的上方，从数据的分布情况来看，甲网站更受欢迎．10．为了了解高一学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3，第二小组频数为12.(1)第二小组的频率是多少？样本容量是多少？(2)若次数在110以上(含110次)为达标，试估计该学校全体高一学生的达标率是多少？ 解：(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小，因此第二小组的频率为：42＋4＋17＋15＋9＋3＝0.08.又因为第二小组的频率＝第二小组的频数样本容量，所以样本容量＝第二小组的频数第二小组的频率＝120.08＝150.(2)由题意估计该学校高一学生的达标率约为17＋15＋9＋32＋4＋17＋15＋9＋3×100%＝88%.B 级 能力提升1．为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据(单位：kPa)的分组区间为[12，13)，[13，14)，[14，15)，[15，16)，[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组，如图所示是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为( )A ．6B ．8C ．12D ．18解析：志愿者的总人数为20（＋）×1＝50，所以第三组的人数为50×＝18，有疗效的人数为18－6＝12.答案：C2．在一次马拉松比赛中，35名运动员的成绩(单位：分钟)的茎叶图如图所示．若将运动员按成绩由好到差编为1～35号，再用系统抽样方法从中抽取7人，则其中成绩在区间[139，151]上的运动员人数是________．解析：由题意可知，这35名运动员的分组情况为，第一组(130，130，133，134，135)，第二组(136，136，138，138，138)，第三组(139，141，141，141，142)，第四组(142，142，143，143，144)，第五组(144，145，145，145，146)，第六组(146，147，148，150，151)，第七组(152，152，153，153，153)，故成绩在区间[139，151]上的运动员恰有4组，则运动员人数为4.答案：43．从高一学生中抽取50名参加调研考试，成绩的分组及各组的频数如下(单位：分): [40，50)，2；[50，60)，3；[60，70)，10；[70，80)，15；[80，90)，12；[90，100]，8.(1)列出样本的频率分布表；(2)画出频率分布直方图；(3)估计成绩在[70，80)分的学生所占总体的百分比．解：(1)频率分布表如下：成绩分组频数频率[40，50)2[50，60)3[60，70)10[70，80)15[80，90)12[90，100]8合计50(2)由题意知组距为10，取小矩形的高根据表格画出如下的频率分布直方图：(3)由频率分布直方图，可估计成绩在[70，80)分的学生所占总体的百分比是×10＝＝30%.。

人教新课标A版高中数学必修3 第二章统计 2.2用样本估计总体 2.2.2用样本的数字特征估计总体同步测试A卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题；共30分)1. （2分）某班级有50名学生，其中有30名男生和20名女生，随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86，94，88，92，90，五名女生的成绩分别为88，93，93，88，93。

下列说法一定正确的是（）A . 这种抽样方法是一种分层抽样。

B . 这种抽样方法是一种系统抽样。

C . 这五名男生成绩的方差大于这五名女生成绩的方差。

D . 该班级男生成绩的平均数小于该班女生成绩的平均数。

3. （2分）某设计运动员在一次测试中射击10次，其测试成绩如表：则该运动员测试成绩的中位数为（）A . 2B . 8C . 8.5D . 94. （2分） (2018高二上·哈尔滨月考) 一组数据中的每一个数据都乘以2，再减去80，得到一组新数据，若求得新数据的平均数是1.2，方差是4.4，则原来数据的平均数和方差分别是（）A . 40.6，1.1B . 48.8，4.4C . 81.2，44.4D . 78.8，75.65. （2分） (2018高一下·枣庄期末) 已知数据，，，…，是枣强县普通职工（，）个人的年收入，设个数据的中位数为，平均数为，方差为，如果再加上世界首富的年收入，则这个数据中，下列说法正确的是（）A . 年收入平均数大大增加，中位数一定变大，方差可能不变B . 年收入平均数大大增加，中位数可能不变，方差变大C . 年收入平均数大大增加，中位数可能不变，方差也不变D . 年收入平均数可能不变，中位数可能不变，方差可能不变6. （2分）(2020·鹤壁模拟) 中国铁路总公司相关负责人表示，到2018年底，全国铁路营业里程达到13.1万公里，其中高铁营业里程2.9万公里，超过世界高铁总里程的三分之二，下图是2014年到2018年铁路和高铁运营里程（单位：万公里）的折线图，以下结论不正确的是（）A . 每相邻两年相比较，2014年到2015年铁路运营里程增加最显著B . 从2014年到2018年这5年，高铁运营里程与年价正相关C . 2018年高铁运营里程比2014年高铁运营里程增长80%以上D . 从2014年到2018年这5年，高铁运营里程数依次成等差数列7. （2分） (2016高一下·永年期末) 甲、乙两名选手参加歌手大赛时，5名评委打的分数，用茎叶图表示（如图）s1 ， s2分别表示甲、乙选手分数的标准差，则s1与s2的关系是（填“＞”、“＜”或“=”）（）A . s1＞s2B . s1=s2C . s1＜s2D . 不确定8. （2分）某高校进行自主招生，先从报名者筛选出400人参加考试，再按笔试成绩择优选出100人参加面试．现随机抽取24名笔试者的成绩，如下表所示：分数段[60，65）[65，70）[70，75）[75，80）[80，85）[85，90）人数234591据此估计参加面试的分数线大约是（）A . 75B . 80C . 85D . 909. （2分）小波一星期的总开支分布图如图1所示，一星期的食品开支如图2所示，则小波一星期的鸡蛋开支占总开支的百分比为（）A . 30%B . 10%C . 3%D . 不能确定11. （2分）由正整数组成的一组数据x1 ， x2 ， x3 ， x4 ，其平均数和中位数都是2，且标准差等于1，则这组数据的立方和为（）A . 70B . 60C . 50D . 5612. （2分） (2019高三上·上海月考) 演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是（）A . 中位数B . 平均数C . 方差D . 极差13. （2分） (2016高二上·昌吉期中) 甲、乙两名运动员的5次测试成绩如下图所示：甲茎乙5 716 88 8 22 3 6 7设s1 ， s2分别表示甲、乙两名运动员测试成绩的标准差，分别表示甲、乙两名运动员测试成绩的平均数，则有（）A . ，s1＜s2B . ，s1＞s2C . ，s1＞s2D . ，s1=s215. （2分）(2017·浦东模拟) 若样本平均数为，总体平均数为μ，则（）A . =μB . ≈μC . μ是的估计值D . 是μ的估计值二、填空题 (共5题；共6分)17. （1分） (2018高一下·河南月考) 已知一组样本数据按从小到大的顺序排列为-1，0，4. ，这组数据的平均数与中位数均为5，则其方差为________．20. （2分）若样本数据x1 ， x2 ，…，x10的平均数为8，则数据2x1﹣1，2x2﹣1，…，2x10﹣1的平均数为________三、解答题 (共5题；共25分)21. （5分）要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽取10名学生，分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表)：编号12345678910x63674588817152995876y65785285928973985675（1）画出散点图；（2）判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系；（3）如果x与y具有线性相关关系，求出回归直线方程；23. （5分） (2018高一下·商丘期末) 有关部门要了解甲型H1N1流感预防知识在学校的普及情况，命制了一份有10道题的问卷到各个学校做问卷调查。

人教新课标A版高中数学必修3 第二章统计 2.2样本估计总体 2.2.1用样本的频率分布估计总体同步测试D卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题；共30分)1. （2分）某公司从代理的A，B，C，D四种产品中，按分层抽样的方法抽取容量为110的样本，已知A，B，C，D四种产品的数量比是2：3：2，：4，则该样本中D类产品的数量为（）A . 22B . 33C . 44D . 552. （2分） (2019高二下·新城期末) 现行普通高中学生在高一升高二时面临着选文理科的问题，学校抽取了部分男、女学生意愿的一份样本，制作出如下两个等高堆积条形图：根据这两幅图中的信息，下列统计结论是不正确的是（）A . 样本中的女生数量多于男生数量B . 样本中有理科意愿的学生数量多于有文科意愿的学生数量C . 样本中的男生偏爱理科D . 样本中的女生偏爱文科3. （2分） (2018高二下·陆川月考) 容量为100的样本，其数据分布在，将样本数据分为4组：，，，，得到频率分布直方图如图所示.则下列说法不正确的是（）A . 样本数据分布在的频率为B . 样本数据分布在的频数为40C . 样本数据分布在的频数为40D . 估计总体数据大约有分布在4. （2分）某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[20,45)岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是（）A . 31.6岁B . 32.6岁C . 33.6岁D . 36.6岁5. （2分）一批产品抽50件测试，其净重介于13克与19克之间，将测试结果按如下方式分成六组：第一组，净重大于等于13克且小于14克；第二组，净重大于等于14克且小于15克； ... 第六组，净重大于等于18克且小于19克．如图是按上述分组方法得到的频率分布直方图．设净重小于17克的产品数占抽取数的百分比为x，净重大于等于15克且小于17克的产品数为y，则从频率分布直方图中可分析出x和y分别为（）A . 0.1,45B . 0.9,45C . 0.1,35D . 0.9,356. （2分）对“小康县”的经济评价标准：①年人均收入不小于7000元；②年人均食品支出不大于收入的35%．某县有40万人，调查数据如下：年人均收入/元0200040006000800010 00012 00016 000人数/万人63556753则该县（）A . 是小康县B . 达到标准①，未达到标准②，不是小康县C . 达到标准②，未达到标准①，不是小康县D . 两个标准都未达到，不是小康县7. （2分）有一个容量为50的样本，其分组以及各组的频数如下：[12.5,15.5],3；[15.5,18.5],8；[18.5,21.5],9；[21.5,24.5],11;[24.5,27.5],10;[27.5,30.5],5;[30.5,33.5],4，根据累计频率分布，估计小于30的数据大约占样本总数A . 5%B . 10%C . 30%D . 93%8. （2分） (2017高二上·长春期末) 某班名学生在一次考试中数学成绩的频率分布直方图如图，若在这名学生中，数学成绩不低于100分的人数为33，则等于（）A . 45B . 48D . 559. （2分） (2020高二上·黄陵期末) 如图是某超市一年中各月份的收入与支出单位：万元情况的条形统计图已知利润为收入与支出的差，即利润收入一支出，则下列说法正确的是A . 利润最高的月份是2月份，且2月份的利润为40万元B . 利润最低的月份是5月份，且5月份的利润为10万元C . 收入最少的月份的利润也最少D . 收入最少的月份的支出也最少10. （2分）为了了解某地参加计算机水平测试的5000名学生的成绩，从中抽取了200名学生的成绩进行统计分析．在这个问题中，5000名学生成绩的全体是（）A . 总体B . 个体C . 从总体中抽取的一个样本D . 样本的容量11. （2分）某地一种植物一年生长的高度如下表：则该植物一年生长在[30，40）内的频率是（）B . 0.65C . 0.40D . 0.2512. （2分）如图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图，若80分以上为优秀，根据图形信息可知：这次考试的优秀率为（）A . 25%B . 30%C . 35%D . 40%13. （2分）某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，已知抽到的司机年龄都在[20，45）岁之间，根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是（）A . 31.6岁B . 32.6岁D . 36.6岁14. （2分）容量为20的样本，数据的分组及各组的频数如下：（10，20]，2；（20，30]，3；（30，40]，4；（40，50]，5；（50，60]，4；（60，70]，2．则样本在区间（10，50]上的频率为（）A . 0.5B . 0.7C . 0.25D . 0.0515. （2分）已知样本7，10，14，8，7，12，11，10，8，10，13，10，8，11，8，9，12，9，13，20，那么这组数据落在8.5～11.5的频率为（）A . 0.5B . 0.4C . 0.3D . 0.2二、填空题 (共5题；共5分)16. （1分）某网络公司为了调查一住宅区连接互联网情况，从该住宅区28000住户中随机抽取了210户进行调查，调查数据如右图，则估计该住宅区已接入互联网的住户数是________ ．17. （1分）一个高中研究性学习小组对本地区2002年至2004年快餐公司发展情况进行了调查，根据图中的信息可以得出这三年中该地区每年平均销售盒饭________ 万盒．18. （1分） (2015高三上·连云期末) 交通部门对某路段公路上行驶的汽车速度实施监控，从速度在50﹣90km/h的汽车中抽取150辆进行分析，得到数据的频率分布直方图如图所示，则速度在70km/h以下的汽车有________辆．19. （1分） (2016高一下·中山期中) 超速行驶已成为马路上最大杀手之一，已知某中段属于限速路段，规定通过该路段的汽车时速不超过80km/h，否则视为违规．某天，有1000辆汽车经过了该路段，经过雷达测速得到这些汽车运行时速的频率分布直方图如图所示，则违规的汽车大约为________辆．20. （1分）对某校400名学生的体重（单位：kg）进行统计，得到如图所示的频率分布直方图，则学生体重在60kg以上的人数为________三、解答题 (共5题；共25分)21. （5分） (2018高二上·汕头期末) 某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：上年度出险次数01234保费a 1.25a 1.5a 1.75a2a 随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：出险次数01234频数605030302010（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求的估计值；（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160％”.求的估计值；（Ⅲ）求续保人本年度的平均保费估计值.22. （5分）为了研究某种农作物在特定温度下（要求最高温度t满足：27℃≤t≤30℃）的生长状况，某农学家需要在十月份去某地进行为期十天的连续观察试验．现有关于该地区10月份历年10月份日平均最高温度和日平均最低温度（单位：℃）的记录如下：（Ⅰ）根据本次试验目的和试验周期，写出农学家观察试验的起始日期．（Ⅱ）设该地区今年10月上旬（10月1日至10月10日）的最高温度的方差和最低温度的方差分别为D1 ， D2 ，估计D1 ， D2的大小？（直接写出结论即可）．（Ⅲ）从10月份31天中随机选择连续三天，求所选3天每天日平均最高温度值都在[27，30]之间的概率．23. （5分）某校有教职员工150人，为了丰富教工的课余生活，每天下午4：00～5：00同时开放健身房和娱乐室，要求所有教工每天必须参加一个活动．据调查统计，每次去健身房的人有10%下次去娱乐室，而在娱乐室的人有20%下次去健身房．请问，随着时间的推移，去健身房的人数能否趋于稳定？24. （5分） (2017高二下·太原期中) 某大学餐饮中心为了了解新生的饮食习惯，利用简单随机抽样的方法在全校一年级学生中进行了抽样调查，调查结果如表所示：喜欢甜品不喜欢甜品合计南方学生602080北方学生101020合计7030100（1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；（2）根据（1）的结论，你能否提出更好的调查方法来了解该校大学新生的饮食习惯，说明理由．25. （5分）(2017·新课标Ⅲ卷文) 某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：以最高气温位于各区间的频率估计最高气温位于该区间的概率．（12分）（1）求六月份这种酸奶一天的需求量不超过300瓶的概率；（2）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量为450瓶时，写出Y的所有可能值，并估计Y大于零的概率．参考答案一、单选题 (共15题；共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题；共5分)16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题；共25分)21-1、22-1、23-1、24-1、24-2、25-1、25-2、。

分层训练·进阶冲关A 组 基础练(建议用时20分钟)1.已知甲,乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为 ( A )A.32B.33C.34D.352.设样本数据1,2,…,10的均值和方差分别为1和4,若y i =i +a(a 为非零常数,i=1,2,…,10),则y 1,y 2,…,y 10的均值和方差分别为( A )A.1+a,4B.1+a,4+aC.1,4D.1,4+a3.如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( D )A.中位数为14B.众数为13C.平均数为15D.方差为194.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则 ( C )A.甲的成绩的平均数小于乙的成绩的平均数B.甲的成绩的中位数等于乙的成绩的中位数C.甲的成绩的方差小于乙的成绩的方差D.甲的成绩的极差小于乙的成绩的极差5.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据环保部门某日早6点至晚9点在A 县,B 县两个地区附近的PM2.5监测点统计的数据(单位;毫克/立方米)列出的茎叶图,A 县、B 县两个地区浓度的方差较小的是 ( A )A.A 县B.B 县C.A 县,B 县两个地区相等D.无法确定6.某项测试成绩满分为10分,现随机抽取30名学生参加测试,得分如图所示,假设得分值的中位数为m e ,平均值为,众数为m 0,则 ( D )A.m e =m 0=B.m e =m 0<C.m e <m 0<D.m 0<m e <7.一组样本数据的频率分布直方图如图所示,试估计此样本数据的中位数为.8.某商场对一个月内每天的顾客人数进行统计,得到如图所示的茎叶图,则该样本的众数是45.9.已知一组数据;87,,90,89,93的平均数为90,则该组数据的方差为4.10.如图是甲,乙两位同学在5次数学测试中得分的茎叶图,则成绩较稳定(方差较小)的那一位同学的方差为2.11.某教师为了了解高三一模所教两个班级的数学成绩情况,将两个班的数学成绩(单位;分)绘制成如图所示的茎叶图.(1)分别求出甲,乙两个班级数学成绩的中位数、众数.(2)若规定成绩大于等于115分为优秀,分别求出两个班级数学成绩的优秀率.【解析】(1)由所给的茎叶图知,甲班50名同学的成绩由小到大排序,排在第25,26位的是108,109,出现次数最多的是103,故甲班数学成绩的中位数是108.5,众数是103;乙班48名同学的成绩由小到大排序,排在第24,25位的是106,107,数量最多的是92和101,故乙班数学成绩的中位数是106.5,众数为92和101. (2)由茎叶图中的数据可知,甲班中数学成绩为优秀的人数为20,优秀率为=;乙班中数学成绩为优秀的人数为18,优秀率为=.12.为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生的各项平均成绩(满分100分),按照以下区间分为7组;[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],并得到频率分布直方图(如图).已知测试平均成绩在区间[30,60)内的有20人.(1)求m的值及中位数n.(2)若该校学生测试平均成绩小于n,则学校应适当增加体育活动时间.根据以上抽样调查数据,该校是否需要增加体育活动时间?【解析】(1)由频率分布直方图知第1组、第2组和第3组的频率分别是0.02,0.02和0.06,则m×(0.02+0.02+0.06)=20,解得m=200.由图知,中位数n 位于[70,80)内,则0.02+0.02+0.06+0.22+0.04(n-70)=0.5,解得n=74.5.(2)设第i(i=1,2,3,4,5,6,7)组的频率和频数分别为p i 和i ,由图知,p 1=0.02,p 2=0.02,p 3=0.06,p 4=0.22,p 5=0.40,p 6=0.18,p 7=0.10,则由i =200×p i ,可得1=4,2=4,3=12,4=44,5=80,6=36,7=20,故该校学生测试平均成绩是==74<74.5,所以该校应该适当增加体育活动时间.B 组 提升练(建议用时20分钟) 13.如图所示的茎叶图是甲、乙两位同学在期末考试中的六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则,y 的值分别为 ( D )A.2,4B.4,4C.5,6D.6,414.一个样本a,3,5,7的平均数是b,且a,b 是方程2-5+4=0的两根,则这个样本的方差是 ( C )A.3B.4C.5D.615.某校女子篮球队7名运动员身高(单位;厘米)分布的茎叶图如图,已知记录的平均身高为175 cm,但有一名运动员的身高记录不清楚,其末位数记为,那么的值为2.16.在一个容量为5的样本中,数据均为整数,已测出其平均数为10,但墨水污损了两个数据,其中一个数据的十位数字1未被污损,其余三个数据为9,10,11,那么这组数据的方差s2可能的最大值是32.8.17.一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动.在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制) 的茎叶图如图所示.(1)根据这10名同学的测试成绩,估计该班男、女生国学素养测试的平均成绩.(2)比较这10名同学中男生和女生的国学素养测试成绩的方差的大小.(只需直接写出结果)【解析】(1)设这10名同学中男、女生的平均成绩分别为,.则==73.75(分),==76(分).(2)女生国学素养测试成绩的方差大于男生国学素养测试成绩的方差. 18.某同学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该盒饭,以(单位;盒,100≤≤200)表示这个开学季内的市场需求量,y(单位;元)表示这个开学季内经销该产品的利润.(1)根据频率分布直方图估计开学季内市场需求量的平均数和众数.(2)将y表示为的函数.(3)根据频率分布直方图估计利润y不少于1 350元的概率(将频率视为概率).【解析】(1)由频率分布直方图得,开学季内市场需求量的众数的估计值是150盒.需求量为[100,120)的频率为0.005×20=0.1,需求量为[120,140)的频率为0.01×20=0.2,需求量为[140,160)的频率为0.015×20=0.3,需求量为[160,180)的频率为0.012 5×20=0.25,需求量为[180,200]的频率为0.007 5×20=0.15,110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153,故平均数的估计值为153盒.(2)因为每售出1盒该盒饭获利润10元,未售出的盒饭,每盒亏损5元,所以当100≤≤150时,y=10-5(150-)=15-750,当150<≤200时,y=10×150=1 500,所以y=(∈N).(3)因为利润不少于1 350元,所以由15-750≥1 350,得≥140.所以由(1)知利润不少于1 350元的概率P=1-0.1-0.2=0.7.C组培优练(建议用时15分钟)19.如图是民航部门统计的2017年春运期间几个城市售出的往返机票的平均价格以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述不正确的是( D )A.深圳的变化幅度最小,北京的平均价格最高B.深圳和厦门的春运期间往返机票价格同去年相比有所下降C.平均价格从高到低居于前三位的城市为北京、深圳、广州D.平均价格的涨幅从高到低居于前三位的城市为天津、西安、厦门20.随着移动互联网的发展,与餐饮美食相关的手机应用软件层出不穷.现从使用A和B两款订餐软件的商家中分别随机抽取50个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下;(1)试估计使用A款订餐软件的50个商家的“平均送达时间”的众数及平均数.(2)根据以上抽样调查数据,将频率视为概率,回答下列问题;①能否认为使用B款订餐软件“平均送达时间”不超过40分钟的商家达到75%?②如果你要从A和B两款订餐软件中选择一款订餐,你会选择哪款?说明理由.【解析】(1)由已知,使用A款订餐软件的50个商家的“平均送达时间”的众数为55.使用A款订餐软件的50个商家的“平均送达时间”的平均数为15×0.06+25×0.34+35×0.12+45×0.04+55×0.4+65×0.04=40.(2)①使用B款订餐软件“平均送达时间”不超过40分钟的商家的比例估计值为0.04+0.20+0.56=0.80=80%>75%.故可以认为使用B款订餐软件“平均送达时间”不超过40分钟的商家达到75%.②使用B款订餐软件的50个商家的“平均送达时间”的平均数为15×0.04+25×0.2+35×0.56+45×0.14+55×0.04+65×0.02=35<40,所以选B款订餐软件.。

2．2.2 用样本的数字特征估计总体的数字特征第2课时方差、标准差课时目标1.理解方差、标准差的意义，会计算一组数据的方差和标准差，掌握用样本方差或标准差去估计总体方差或总体标准差的方法．2．会用平均数和方差对数据进行处理与比较．识记强化标准差及方差考察样本数据的分散程度的大小，最常用的统计量是标准差．标准差是样本数据到平均数的一种平均距离，一般用s表示．标准差的平方s2叫做方差，也为测量样本数据分散程度的工具．若样本数据是x1，x2，…，x n，x表示这组数据的平均数，则s＝1n[x1－x2＋x2－x2＋…＋x n－x2]；s2＝1n[(x1－x)2＋(x2－x)2＋…＋(x n－x)2]．课时作业一、选择题1．下列说法正确的是( )A．在两组数据中，平均值较大的一组方差较大C ．2x －＋3和s 2D ．2x －＋3和4s 2＋12s ＋9 答案：B解析：由平均数、方差的求法可得．6．甲、乙两位同学都参加了由学校举办的篮球比赛，他们都参加了全部的7场比赛，平均得分均为16分，标准差分别为5.09和3.72，则甲、乙两同学在这次篮球比赛活动中，发挥得更稳定的是( )A ．甲B ．乙C ．甲、乙相同D ．不能确定 答案：B解析：方差或标准差越小，数据的离散程度越小，表明发挥得越稳定．∵5.09>3.72，故选B.二、填空题7．已知样本9、10、11、x 、y 的平均数是10，方差是2，则xy ＝________. 答案：96解析：由平均数得9＋10＋11＋x ＋y ＝50，∴x ＋y ＝20，又由(9－10)2＋(10－10)2＋(11－10)2＋(x －10)2＋(y －10)2＝(2)2×5＝10，得x 2＋y 2－20(x ＋y )＝－192，(x ＋y )2－2xy －20(x ＋y )＝－192，xy ＝96.8．如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为________.答案：6.8解析：x ＝15(8＋9＋10＋13＋15)＝11，s 2＝15[(8－11)2＋(9－11)2＋(10－11)2＋(13－11)2＋(15－11)2]＝6.8.9．若k 1，k 2，…，k 8的方差为3，则2(k 1－3)，2(k 2－3)，…，2(k 8－3)的方差为________． 答案：12解析：设k 1，k 2，…，k 8的平均数为k ，则18[(k 1－k )2＋(k 2－k )2＋…＋(k 8－k )2]＝3，而2(k 1－3)，2(k 2－3)，…，2(k 8－3)的平均数为2(k －3)，解析：x 9＝x 8＋19(x 9－x 8)＝5＋19×(4－5)＝449，s 29＝89[s 28＋19(x 9－x 8)2]＝89[22＋19(4－5)2]＝29681. 13．下图为我国10座名山的“身高”统计图，请根据图中信息回答下列问题。

高中数学学习材料马鸣风萧萧*整理制作2.2 用样本估计总体 同步练测建议用时 实际用时满分 实际得分45分钟100分一、选择题（每小题6分，共30分）1．为了了解某地区10000名高三男生的身体发育情况，抽查了该地区100名年龄为17～18岁的高三男生体重(kg)，得到频率分布直方图如图．根据图示，请你估计该地区高三男生中体重在[56.5,64.5]的学生人数是( )第1题图A ．40B ．400C ．4 000D ．4 4002．甲、乙两名选手参加歌手大赛时，5名评委打的分数用茎叶图表示如图，s 1，s 2分别表示甲、乙选手分数的标准差，则s 1与s 2的关系是( )第2题图A ．s 1＞s 2B ．s 1＝s 2C ．s 1＜s 2D ．不确定3．某校甲、乙两个班级各有编号为1,2,3,4,5的五名学生进行投篮练习，每人投10次，投中的次数如下表： 学生 1号 2号 3号 4号 5号 甲班 6 7 7 8 7 乙班 67679则以上两组数据的方差中较小的一个为s 2，则s 2＝( )A. 25 B. 425C. 35D ．44.为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分(十分制)如图所示，假设得分值的中位数为m e，众数为m0，平均值为x，则()A．m e＝m0＝x B．m e＝m0＜xC．m e＜m0＜x D．m0＜m e＜x5．从甲、乙两种树苗中各抽测了10株树苗的高度，其茎叶图如图．第5题图A．甲种树苗的平均高度大于乙种树苗的平均高度，且甲种树苗比乙种树苗长得整齐B．甲种树苗的平均高度大于乙种树苗的平均高度，但乙种树苗比甲种树苗长得整齐C．乙种树苗的平均高度大于甲种树苗的平均高度，且乙种树苗比甲种树苗长得整齐D．乙种树苗的平均高度大于甲种树苗的平均高度，但甲种树苗比乙种树苗长得整齐二、填空题（每小题7分，共14分）6．甲、乙两名同学学业水平考试的9科成绩如茎叶图所示，请你根据茎叶图判断谁的平均分高________．(填“甲”或“乙”)第6题图7．某中学为了解学生数学课程的学习情况，在3 000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图(如图)．根据频率分布直方图推测，这 3 000名学生在该次数学考试中成绩小于60分的学生数是________．第7题图三、解答题（共56分）8．（16分）随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图(中间的数字表示身高的百位、十位数，旁边的数字分别表示身高的个位数)如图所示．第8题图(1)根据茎叶图判断哪个班的平均身高较高；(2)计算甲班的样本方差．9．（20分）从某学校高三年级800名学生中随机抽取50名测量身高，被抽取的学生的身高全部介于155 cm和195 cm之间，将测量结果按如下方式分成八组：第一组[155,160)；第二组[160,165)；…第八组[190,195]，如图是按上述分组方法得到的频率分布直方图．第9题图(1)根据已知条件填写下面表格： 组别 1 2 3 4 5 6 7 8 样本数(2)估计这所学校高三年级800名学生中身高在180 cm 以上(含180 cm)的人数．10．（20分）某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)，…，[140,150)后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：（1）求分数在[120,130)内的频率；(2)若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为100＋1102＝105.)作为这组数据的平均分，据此，估计本次考试的平均分；(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率．2.2 用样本估计总体答题纸得分：一、选择题题号 1 2 3 4 5答案二、填空题6． 7．三、解答题8.9.10.2.2 用样本估计总体 答案一、选择题1．C 解析：依题意得，该地区高三男生中体重在[56.5,64.5]的学生人数是10 000×(0.03＋2×0.05＋0.07)×2＝4 000.2．C 解析：由茎叶图可得x 甲＝78＋81＋84＋85＋925＝84，x 乙＝76＋77＋80＋94＋935＝84，所以s 21＝ (78－84)2＋(81－84)2＋(84－84)2＋(85－84)2＋(92－84)25＝22，s 22＝(76－84)2＋(77－84)2＋(80－84)2＋(94－84)2＋(93－84)25＝62，显然有s 1＜s 2. 3.A解析：甲班的平均数为x甲＝6＋7＋7＋8＋75＝7，甲班的方差为s2甲＝(6－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(7－7)25＝25；乙班的平均数为x 乙＝6＋7＋6＋7＋95＝7，乙班的方差为s 2乙＝(6－7)2＋(7－7)2＋(6－7)2＋(7－7)2＋(9－7)25＝65；∵65＞25，∴s 2＝25.4.D 解析：由图可知，30名学生的得分情况依次为：2个人得3分，3个人得4分，10个人得5分，6个人得6分，3个人得7分，2个人得8分，2个人得9分，2个人得10分．中位数为第15,16个数(分别为5,6)的平均数，即m e ＝5.5,5出现次数最多，故m 0＝5，x ＝2×3＋3×4＋10×5＋6×6＋3×7＋2×8＋2×9＋2×1030≈5.97.于是得m 0＜m e ＜ x .5．D 解析：根据茎叶图计算得甲种树苗的平均高度为27，而乙种树苗的平均高度为30，但乙种树苗的高度分布不如甲种树苗的高度分布集中．二、填空题6．乙 解析：由茎叶图可以看出，x 甲＝19(92＋81＋89×2＋72＋73＋78×2＋68)＝80，x 乙＝19(91＋83＋86＋88＋89＋72＋75＋78＋69)≈81.2, x 乙＞x 甲，故乙的平均数大于甲的平均数．7．600 解析：由题意知，在该次数学考试中成绩小于60分的频率为(0.002＋0.006＋0.012)×10＝0.2，故这3 000名学生在该次数学考试中成绩小于60分的学生数是3 000×0.2＝600.三、解答题8．解：(1)由茎叶图可知乙班身高比较集中在170～181之间，所以乙班的平均身高较高． (2)甲班的方差为：110[(182－170)2＋(179－170)2＋(178－170)2＋(171－170)2＋(170－170)2＋(168－170)2＋(168－170)2＋(164－170)2＋(162－170)2＋(158－170)2]＝54.2.9．解：(1)由频率分布直方图得第七组的频率为：1－(0.008×2＋0.016×2＋0.04×2＋0.06)×5＝0.06，∴第七组的人数为0.06×50＝3.同理可得各组人数如下：组别12345678样本数2410101543 2(2)由频率分布直方图得后三组的频率为0.016×5＋0.06＋0.008×5＝0.18.估计这所学校高三年级身高在180 cm以上(含180 cm)的人数为800×0.18＝144.10．解：(1)分数在[120,130)内的频率为1－(0.1＋0.15＋0.15＋0.25＋0.05)＝1－0.7＝0.3.(2)估计平均分为x＝95×0.1＋105×0.15＋115×0.15＋125×0.3＋135×0.25＋145×0.05＝121.(3)由题意，[110,120)分数段的人数为60×0.15＝9(人)．[120,130)分数段的人数为60×0.3＝18(人)．∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，∴需在[110,120)分数段内抽取2人，并分别记为m，n；在[120,130)分数段内抽取4人，并分别记为a，b，c，d；设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A，则基本事件共有(m，n)，(m，a)，…，(m，d)，(n，a)，…，(n，d)，(a，b)，…，(c，d)共15种．则事件A包含的基本事件有(m，n)，(m，a)，(m，b)，(m，c)，(m，d)，(n，a)，(n，b)，(n，c)，(n，d)共9种．∴P(A)＝915＝35.。