沪科版数学讲义_第20章__四边形

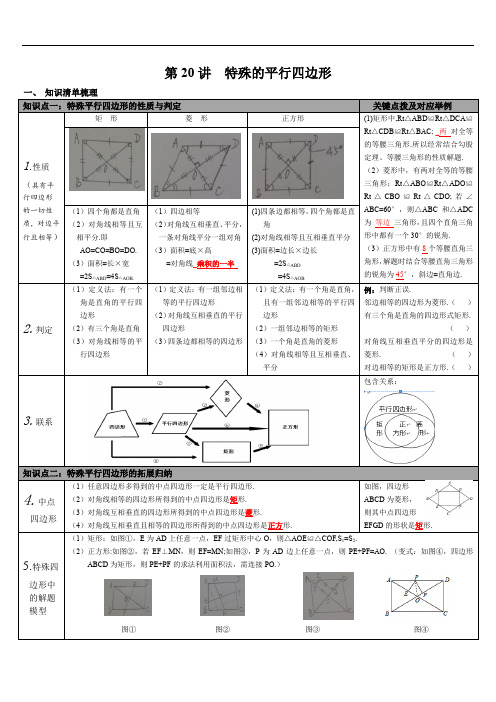
第20讲特殊的平行四边形一、知识清单梳理知识点一：特殊平行四边形的性质与判定关键点拨及对应举例1.性质（具有平行四边形的一切性质，对边平行且相等）矩形菱形正方形(1)矩形中,Rt△ABD≌Rt△DCA≌Rt△CDB≌Rt△BAC; _两对全等的等腰三角形.所以经常结合勾股定理、等腰三角形的性质解题.（2）菱形中，有两对全等的等腰三角形；Rt△ABO≌Rt△ADO≌Rt△CBO≌Rt△CDO;若∠ABC=60°，则△ABC和△ADC为等边三角形，且四个直角三角形中都有一个30°的锐角.（3）正方形中有8个等腰直角三角形，解题时结合等腰直角三角形的锐角为45°，斜边=直角边. （1）四个角都是直角（2）对角线相等且互相平分.即AO=CO=BO=DO.（3）面积=长×宽=2S△ABD=4S△AOB.（1）四边相等（2）对角线互相垂直、平分，一条对角线平分一组对角（3）面积=底×高=对角线_乘积的一半(1)四条边都相等，四个角都是直角(2)对角线相等且互相垂直平分(3)面积=边长×边长=2S△ABD=4S△AOB2.判定（1）定义法：有一个角是直角的平行四边形（2）有三个角是直角（3）对角线相等的平行四边形（1）定义法：有一组邻边相等的平行四边形（2）对角线互相垂直的平行四边形（3）四条边都相等的四边形（1）定义法：有一个角是直角，且有一组邻边相等的平行四边形（2）一组邻边相等的矩形（3）一个角是直角的菱形（4）对角线相等且互相垂直、平分例：判断正误.邻边相等的四边形为菱形.（）有三个角是直角的四边形式矩形.（）对角线互相垂直平分的四边形是菱形. （）对边相等的矩形是正方形.（）3.联系包含关系：知识点二：特殊平行四边形的拓展归纳4.中点四边形（1）任意四边形多得到的中点四边形一定是平行四边形.（2）对角线相等的四边形所得到的中点四边形是矩形.（3）对角线互相垂直的四边形所得到的中点四边形是菱形.（4）对角线互相垂直且相等的四边形所得到的中点四边形是正方形.如图，四边形ABCD为菱形，则其中点四边形EFGD的形状是矩形.5.特殊四边形中的解题模型（1）矩形：如图①，E为AD上任意一点，EF过矩形中心O，则△AOE≌△COF,S1=S2.（2）正方形:如图②，若EF⊥MN，则EF=MN;如图③，P为AD边上任意一点，则PE+PF=AO. （变式：如图④，四边形ABCD为矩形，则PE+PF的求法利用面积法，需连接PO.）图①图②图③图④。

第4讲四边形【学习目标】1. 掌握多边形内角和与外角和公式，灵活运用多边形内角和与外角和公式解决有关问题；通过观察和实地操作知道三角形具有稳定性，知道四边形没有稳定性，了解它们这些性质在生产、生活中的广泛应用．2. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系. 掌握它们的性质和判别方法, 并能运用这些知识进行证明和计算.3. 掌握三角形中位线定理，并能灵活应用.4. 理解用多边形进行镶嵌的应用，能灵活运用公式解决有关问题.体验并掌握探索、归纳图形性质的推理方法，进一步培养说理和进行简单推理的能力.【基础知识】一、多边形及有关概念1. 多边形的定义：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形.要点诠释：多边形通常还以边数命名，多边形有n条边就叫做n边形．三角形、四边形都属于多边形，其中三角形是边数最少的多边形.2. 正多边形：各个角都相等、各个边都相等的多边形叫做正多边形.如正三角形、正方形、正五边形等．要点诠释：各角相等、各边也相等是正多边形的必备条件，二者缺一不可. 如四条边都相等的四边形不一定是正方形，四个角都相等的四边形也不一定是正方形，只有满足四边都相等且四个角也都相等的四边形才是正方形.3.多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.要点诠释：(1)从n边形一个顶点可以引(n－3)条对角线，将多边形分成(n－2)个三角形；(2)n边形共有条对角线．二、多边形的内角和及外角和公式1.内角和公式：n边形的内角和为(n－2)·180°(n≥3，n是正整数) ．要点诠释：（1）一般把多边形问题转化为三角形问题来解决；(2)内角和定理的应用：①已知多边形的边数，求其内角和；②已知多边形内角和，求其边数.2.多边形外角和：n边形的外角和恒等于360°，它与边数的多少无关.要点诠释：(1)外角和公式的应用：①已知外角度数，求正多边形边数；②已知正多边形边数，求外角度数.(2)多边形的边数与内角和、外角和的关系：①n边形的内角和等于(n－2)·180°(n≥3，n是正整数)，可见多边形内角和与边数n有关，每增加1条边，内角和增加180°.三、平行四边形1.定义：两组对边分别平行的四边形叫做平行四边形.2.性质与判定性质：（1）．边的性质：平行四边形两组对边平行且相等；（2）．角的性质：平行四边形邻角互补，对角相等；（3）．对角线性质：平行四边形的对角线互相平分；（4）．平行四边形是中心对称图形，对角线的交点为对称中心.判定：（1）.两组对边分别平行的四边形是平行四边形；（2）.两组对边分别相等的四边形是平行四边形；（3）.一组对边平行且相等的四边形是平行四边形；（4）.两组对角分别相等的四边形是平行四边形；（5）.对角线互相平分的四边形是平行四边形.3.平行线的性质（1）平行线间的距离都相等（2）等底等高的平行四边形面积相等四、特殊的平行四边形1.矩形、菱形、正方形的定义有一个角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.有一组邻边相等并且有一个内角是直角的平行四边形叫做正方形.2.矩形的性质与判定性质：1.矩形具有平行四边形的所有性质；2.矩形的对角线相等；3.矩形的四个角都是直角；4.矩形是轴对称图形，它有两条对称轴.判定：1. 有三个角是直角的四边形是矩形.2. 对角线相等的平行四边形是矩形.3. 定义：有一个角是直角的平行四边形叫做矩形.3.菱形的性质与判定性质：1.菱形的四条边都相等；2.菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；3.菱形是轴对称图形，它有两条对称轴.判定：1. 四条边相等的四边形是菱形.2.对角线互相垂直的平行四边形是菱形.3. 定义：有一组邻边相等的平行四边形是菱形.4正方形的性质与判定性质：1.正方形四个角都是直角，四条边都相等.2.正方形的两条对角线相等并且互相垂直平分，每条对角线平分一组对角.3.正方形是轴对称图形，有4条对称轴；又是中心对称图形，两条对角线的交点是对称中心. 判定：1.有一组邻边相等的矩形是正方形.2.有一个内角是直角的菱形是正方形.5.三角形中位线定义：连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半.五、镶嵌的概念和特征用一些不重叠摆放的多边形把平面的一部分完全覆盖，通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)．这里的多边形可以形状相同，也可以形状不相同.要点诠释：（1）拼接在同一点的各个角的和恰好等于360°；相邻的多边形有公共边.(2)用正多边形实现镶嵌的条件：边长相等；顶点公用；在一个顶点处各正多边形的内角之和为360°.(3)只用一种正多边形镶嵌地面，当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角360°时，就能铺成一个平面图形.事实上，只有正三角形、正方形、正六边形的地砖可以用.【考点剖析】考点一：多边形内角和的问题例1．1．下列多边形中，内角和为360°的图形是（）A．B．C．D．【答案】B【分析】若多边形的边数是n，则其内角和计算公式为（n﹣2）•180°，据此进行解答即可.【详解】解：由多边形内角和公式可得，（n﹣2）•180°=360°，解得n=4，是四边形，故选择B.考点二：平行四边形例2．2．下列关于判定平行四边形的说法错误的是（）A．一组对角相等且一组对边平行的四边形B．一组对边相等且另一组对边平行的四边形C．两组对角分别相等的四边形D．四条边相等的四边形【答案】B【分析】根据平行四边形的判定定理即可得到结论．【详解】A. 一组对角相等且一组对边平行的四边形是平行四边形，故本选项不符合题意；B. 一组对边相等且另一组对边平行的四边形不一定是平行四边形，故本选项符合题意；C. 两组对角分别相等的四边形是平行四边形，故本选项不符合题意；D. 四条边相等的四边形是平行四边形，故本选项不符合题意；故选：B考点三：矩形性质理解例3．3．菱形具有而矩形不一定具有的性质是（）A．邻边相等B．对角线互相平分C．对角线相等D．邻角互补【分析】根据菱形的性质及矩形的性质，结合各选项进行判断即可得出答案．【详解】解：A、邻边相等，菱形具有而矩形不具有，故本选项正确；B、对角线互相平分，菱形具有而矩形也具有，故本选项错误；C、对角线相等，菱形不具有矩形具有，故本选项错误；D、邻角互补，菱形具有而矩形也具有，故本选项错误；故选：A．考点四：多边形的镶嵌例4．4．用一批完全相同的正多边形能镶嵌成一个平面图案的是（）A．正五边形B．正六边形C．正七边形D．正八边形【答案】B【分析】根据镶嵌的性质即可判断.【详解】A. 正五边形内角为108°,不能被360°整除,不符合题意;B. 正六边形内角为120°,可以被360°整除,符合题意;C. 正七边形内角为128.571°,不能被360°整除,不符合题意;D. 正八边形内角为135°,不能被360°整除,不符合题意;故选B.【真题演练】1．用形状、大小完全相同的图形不能镶嵌成平面图案的是( )A．正三角形B．正方形C．正五边形D．正六边形【答案】C【分析】本题考查了平面镶嵌的条件分别求出各个正多边形的每个内角的度数，结合镶嵌的条件即可作出判断．A 、正三角形的每个内角是60°，能整除360°，6个能镶嵌；B 、正方形的每个内角是90°，能整除360°，4个能镶嵌；C 、正五边形每个内角是1803605108︒︒︒-÷=，不能整除360°，不能镶嵌；D 、正六边形每个内角为120度，能整除360度，3个能镶嵌．故选C ．2．用一批完全相同的多边形地砖铺地面，不能进行镶嵌的是( )A ．正三角形B ．正方形C ．正八边形D ．正六边形 【答案】C【解析】【详解】A 、正三角形的每个内角是60°，能整除360°，能密铺；B 、正方形的每个内角是90°，4个能密铺；C 、正八边形的每个内角为：180°-360°÷8=135°，不能整除360°，不能密铺；D 、正六边形的每个内角是120°，能整除360°，能密铺．故选C ．3．边长相等的下列两种正多边形的组合，不能作平面镶嵌的是（ ）A ．正方形与正三角形B ．正五边形与正三角形C ．正六边形与正三角形D ．正八边形与正方形 【答案】B【分析】分别求出各个正多边形每个内角的度数，再结合镶嵌的条件即可作出判断．【详解】解：A.正三角形的每个内角是60°，正方形的每个内角是90°，∵3×60°+2×90°=360°，能作平面镶嵌．B.正三角形的每个内角是60°，正五边形每个内角是180°-360°÷5=108°，60m+108n=360°，m=6-95n ，显然n 取任何正整数时，m 不能得正整数，故不能作平面镶嵌．C.正三角形的每个内角是60°，正六边形的每个内角是120°，∵2×60°+2×120°=360°，能作平面镶嵌．D.正八边形的每个内角是135°，正方形的每个内角是90°，∵2×135°+90°=360°，能作平面镶嵌． 故选：B ．4．下列说法错误的是（）A．平行四边形的对角线互相平分B．矩形的对角线相等C．直角三角形斜边上的中线等于斜边的一半D．对角线互相垂直的四边形是菱形【答案】D【分析】根据菱形的判定、矩形和平行四边形和直角三角形斜边上的中线性质进行判定即可．【详解】A、平行四边形的对角线互相平分，说法正确，不符合题意；B、矩形的对角线相等，说法正确，不符合题意；C、直角三角形斜边上的中线等于斜边的一半，说法正确，不符合题意；D、对角线互相垂直且平分的四边形是菱形，故错误，故选：D．5．菱形具有而平行四边形不一定具有的性质是（）A．对角相等B．对角线相等C．对角线互相平分D．对角线互相垂直【答案】D【分析】利用菱形的性质和平行四边形的性质进行判断可求解．【详解】解：∵菱形具有的性质有：四边相等，两组对边平行且相等，两组对角分别相等，对角线互相平分，对角线互相垂直；平行四边形的性质有：两组对边分别平行且相等，两组对角分别相等，对角线互相平分，∵菱形具有而平行四边形不一定具有的性质是四边相等，对角线互相垂直，故选：D．6．下面说法正确的有（）∵等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高；∵如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形；∵等腰三角形的两个内角相等；∵到三角形三边距离相等的点是三边垂直平分线的交点；∵等腰三角形一腰上的高与底边的夹角是顶角的一半．A．2个B．3个C．4个D．5个【答案】C【分析】根据等腰三角形的性质、三角形的内心和外心、直角三角形斜边中线的性质一一判断即可．【详解】解：∵等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高，正确；∵如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形，正确；∵等腰三角形的两个内角相等，正确；∵在三角形中，到三角形三边距离相等的点是三条角平分线的交点，故此选项不正确；∵等腰三角形一腰上的高与底边的夹角是顶角的一半，正确；故选：C ．7．矩形具有，而菱形不一定具有的性质是（ ）A ．对角线互相平分B ．对角线相等C ．对边平行且相等D ．内角和为360° 【答案】B【分析】列举出矩形和菱形的所有性质，找出矩形具有而菱形不具有的性质即可．【详解】解：矩形的性质有：∵矩形的对边相等且平行，∵矩形的对角相等，且都是直角，∵矩形的对角线互相平分、相等；菱形的性质有：∵菱形的四条边都相等，且对边平行，∵菱形的对角相等，∵菱形的对角线互相平分、垂直，且每一条对角线平分一组对角；矩形和菱形都属于四边形，其内角和均为360°∵矩形具有而菱形不一定具有的性质是对角线相等，故选：B ．8．在菱形ABCD 中，对角线 2AC =，BD =S 菱形ABCD ＝（ ）A ．B ．C ．3D 【答案】B【分析】根据菱形的面积等于其对角线积的一半，进而求解．【详解】由题意知，菱形ABCD 的面积122=⨯⨯= 故选B ．【过关检测】1．下列性质中，平行四边形不一定具备的是（）A．对角互补B．邻角互补C．对角相等D．内角和是360°【答案】A【分析】利用平行四边形的性质逐个判断，即可得出结论．【详解】解：四边形ABCD是平行四边形，∵对角相等，不一定互补，故A符合题意，C不符合题意．AB∵CD，AD∵BC，∵邻角互补，故B不符合题意．任意四边形的内角和为360°，故D不符合题意．故选：A．2．下列关于平行四边形的特征的描述中，正确的个数有（）（1）对边相等；（2）对角相等；（3）对角线相等；（4）邻边相等；（5）邻角互补．A．2个B．5个C．3个D．4个【答案】C【分析】根据平行四边形的性质：平行四边形的对角相等，对角线互相平分，对边平行，即可判断各选项的正误．【详解】解：∵平行四边形的对角相等，对角线互相平分，对边平行，对边相等，邻角互补可知（1）（2）（5）正确，故选：C．3．能判定四边形ABCD为平行四边形的题设是( )A．AB∵CD，AD=BC B．AB=CD，AD=BC C．∵A=∵B，∵C=∵D D．AB=AD，CB=CD【答案】B【分析】根据两组对边分别平行的四边形是平行四边形，两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形可得答案．【详解】解：A、AB∵CD，AD=BC不能判定四边形ABCD为平行四边形，故此选项错误；B、AB=CD，AD=BC判定四边形ABCD为平行四边形，故此选项正确；C、∵A=∵B，∵C=∵D不能判定四边形ABCD为平行四边形，故此选项错误；D、AB=AD，CB=CD不能判定四边形ABCD为平行四边形，故此选项错误；故选：B．4．平行四边形的一个内角为40︒，与它相邻的另一个内角等于（）A．40︒B．50︒C．90︒D．140︒【答案】D【分析】利用平行四边形的邻角互补进而得出答案．【详解】解：∵平行四边形的一个内角为40°，∵与它相邻的另一个内角为：140°．故选：D．5．六边形的内角和为（）A．360°B．540°C．720°D．180°【答案】C【分析】根据多边形内角和=(n-2) ×180 °计算即可．【详解】解：根据多边形的内角和可得：六边形的内角和为（6﹣2）×180°=720°．故选C．6．若一个正多边形的一个内角是144°，则它的边数是（）A．6B．10C．12D．13【答案】B【分析】设这个正多边形的边数为n ，根据n 边形的内角和为(2)180n -⨯得(2)180144n n -⨯=⨯，然后解方程即可．【详解】解：设这个正多边形的边数为n ，则(2)180144n n -⨯=⨯，解得10n =．故选：B ．7．四边形的内角和等于（ ）A ．180°B ．270°C ．360°D ．150° 【答案】C【分析】n 边形的内角和是（n -2）•180°，代入公式就可以求出内角和．【详解】解：（4-2）•180°=360°．故选：C ．8．正五边形的每一个内角是（ ）A ．30B ．72︒C ．108︒D ．120︒【答案】C【分析】求出正五边形的每个外角即可解决问题．【详解】 解：正五边形的每个外角360725︒==︒，正五边形的每个内角，故选：C ．9．十二边形的内角和为（ ）A ．1620°B ．1800°C ．1980°D ．2160°【答案】B【分析】根据多边形内角和公式解答即可;【详解】解：十二边形的内角和为：（12﹣2）•180°＝1800°．故选B．10．从五边形的一个顶点出发，最多可以引出该五边形的对角线的条数是（）A．2B．3C．4D．5【答案】A【分析】n n>边形从一个顶点出发可引出条对角线即可得．根据(3)【详解】-=（条），从五边形的一个顶点出发，最多可以引出的对角线的条数为532故选：A．。

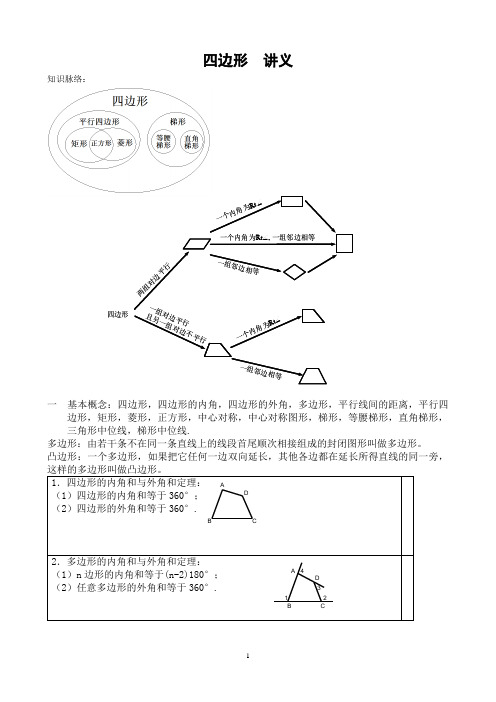
对行为一一为一四边形两组边平一个内角R t ∠一个内角为Rt ∠, 一组邻边相等组邻边相等组对边平行且另一组对边不平行一个内角R t ∠组邻边相等四边形 讲义知识脉络：一 基本概念：四边形，四边形的内角，四边形的外角，多边形，平行线间的距离，平行四边形，矩形，菱形，正方形，中心对称，中心对称图形，梯形，等腰梯形，直角梯形，三角形中位线，梯形中位线.多边形：由若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形。

凸边形：一个多边形，如果把它任何一边双向延长，其他各边都在延长所得直线的同一旁，1．四边形的内角和与外角和定理： （1）四边形的内角和等于360°； （2）四边形的外角和等于360°.2．多边形的内角和与外角和定理： （1）n 边形的内角和等于(n-2)180°； （2）任意多边形的外角和等于360°.A B C D1234A B C DABCD=BC 同底(等底ABCD =BCFE S(5)中心对称图形，对称中心是对角线的交点。

(6)若一直线过平行四边形两对角线的交点，则这直线被一组对边截下的线段以(7)正方形的面积：若正方形的边长为a ，对角线长为b ，则222b a S ==10．正方形的判定：⎪⎭⎪⎬⎫++++一组邻边等矩形）（一个直角）菱形（一个直角一组邻边等）平行四边形（321⇒四边形ABCD 是正方形.(3)∵ABCD 是矩形 又∵AD=AB∴四边形ABCD 是正方形(2)判定正方形的一般顺序： ①先证明它是平行四边形； ②再证明它是菱形(或矩形)；③最后证明它是矩形(或菱形)．11.梯形：只有一组对边平行，而另一组对边不平行的四边形叫做梯形。

等腰梯形的性质：因为ABCD 是等腰梯形⇒⎪⎩⎪⎨⎧.321）对角线相等（；）同一底上的底角相等（两底平行，两腰相等；）（12.等腰梯形的判定：⎪⎭⎪⎬⎫+++对角线相等）梯形（底角相等）梯形（两腰相等）梯形（321⇒四边形ABCD 是等腰梯形 (3)∵ABCD 是梯形且AD ∥BC ∵AC=BD ∴ABCD 四边形是等腰梯形(4)等腰梯形是轴对称图形，它只有一条对称轴，一底的垂直平分线是它的对称轴． （5）．梯形的面积(1) DE AB CD S ABCD ⋅+=)(21梯形． A BC D OABC DOCD A B二．中心对称图形：（1）定义：在平面内，一个图形绕某个点旋转180O，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心.做轴对称图形这条直线叫做对称轴这时,我们也说这个图形关于这条直线对称 （3）中心对称的有关定理※1．关于中心对称的两个图形是全等形.※2．关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分. ※3．如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称. 三． 常识：※1．若n 是多边形的边数，则对角线条数公式是：2)3n (n -. 2．规则图形折叠一般“出一对全等，一对相似”.3．如图：平行四边形、矩形、菱形、正方形的从属关系.4．常见图形中，仅是轴对称图形的有：角、等腰三角形、等边三角形、正奇边形、等腰梯形 …… ；仅是中心对称图形的有：平行四边形 …… ；是双对称图形的有：线段、矩形、菱形、正方形、正偶边形、圆 …… .注意：线段有两条对称轴. n 边形的的性质：（1）n 边形的内角和等于 180)2(⋅-n ． （2）任意多边形的外角和等于 360 （3）n 边形共有2)3(-n n 条对角线 （4）在平面内，内角都相等且边都相等的多边形叫做正多边形。

八年级数学下册第20章四边形复习导学案沪科版：（1）复习多边形的概念和内角和定理；iu（2）理解平行四边形及矩形、菱形、正方形的定义、性质定理和判定定理的内容；（3）会运用上述内容进行简单的计算或证明、学习重难点：重点是特殊平行四边形的性质和判定及其定理的内容，难点是定理的运用、学法指导：复习课本第20章重点内容，按导学案内容填空，在小组内讨论知识点的运用、课堂合作,复习知识点学生交流展示：1、多边形的概念（1）n边形的内角和是，正n边形的每个内角的度数可表示为；（2）n边形的外角和是，正n边形的每个外角的度数可表示为；（3）多边形的对角线：从n边形的一个顶点可以引条对角线、n边形的n个顶点处共有条对角线，由于每条对角线都计算了两次，所以 n边形应该有条对角线。

例、一个凸多边形的内角和是540,那么这个多边形的对角线有条。

2、四边形之间的关系 (填空)3、平行四边形(1)平行四边形的性质边 : 平行四边形的两组对边分别 , 两组对边分别 ;角 : 平行四边形的两组对角 ,四对邻角 ;对角线 :平行四边形的对角线；对称性：平行四边形是图形。

（2）平行四边形的判定边：两组对边的四边形是平行四边形；两组对边的四边形是平行四边形；一组对边的四边形是平行四边形；角：两组对角的四边形是平行四边形；对角线：对角线的四边形是平行四边形；（3）平行四边形的面积S 平行四边形 = （用a表示平行四边形的一边，h表示这条边上的高）。

例：如图，在平行四边形ABCD中，点E、F在对角线AC 上，且AE = CF，连DE、DF、BE、BF，试判断四边形DEBF的形状，并证明你的结论。

（请考虑用多种方法）4、矩形（长方形）（1）矩形的性质边 : 矩形的两组对边分别且 ;角 : 矩形的四个角 ;（既相等又互补）对角线 : 矩形的对角线且；对称性：矩形既是图形又是图形。

（2）矩形的判定①有三个角是的四边形是矩形；②有一个角是的四边形是矩形；③对角线的平行四边形是矩形；（3）矩形的周长和面积C矩形 = ， S矩形 = （用a、b分别表示矩形的两边）。