高三理科数学综合训练(4)

注：尊敬的各位读者，本文是笔者教育资料系列文章的一篇，由于时间关系，如有相关问题，望各位雅正。

希望本文能对有需要的朋友有所帮助。

如果您需要其它类型的教育资料，可以关注笔者知识店铺。

由于部分内容来源网络，如有部分内容侵权请联系笔者。

专题三：高考数学不等式问题的题型与方法（理科）一、考点回顾1．高考中对不等式的要求是：理解不等式的性质及其证明；掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用；掌握分析法、综合法、比较法证明简单的不等式；掌握简单不等式的解法；理解不等式│a│-│b│≤│a+b│≤│a│+│b│。

2．不等式这部分内容在高考中通过两面考查，一是单方面考查不等式的性质，解法及证明；二是将不等式知识与集合、逻辑、函数、三角函数、数列、解析几何、立体几何、平面向量、导数等知识交汇起来进行考查，深化数学知识间的融汇贯通，从而提高学生数学素质及创新意识．3．在不等式的求解中，换元法和图解法是常用的技巧之一，通过换元，可将较复杂的不等式化归为较简单的或基本不等式，通过构造函数，将不等式的解化归为直观、形象的图象关系，对含有参数的不等式，运用图解法，可以使分类标准更加明晰．4．证明不等式的方法灵活多样，但比较法、综合法、分析法仍是证明不等式的最基本方法．要依据题设、题断的结构特点、内在联系，选择适当的证明方法，要熟悉各种证法中的推理思维，并掌握相应的步骤，技巧和语言特点．比较法的一般步骤是：作差(商)→变形→判断符号(值)．5．在近几年全国各省市的高考试卷中，不等式在各种题型中都有出现。

在解答题中，不等式与函数、数列与导数相结合，难度比较大，使用导数解决逐渐成为一般方法6．知识网络其中：指数不等式、对数不等式、无理不等式只要求了解基本形式，不做过高要求.二、 经典例题剖析 1．有关不等式的性质此类题经常出现在选择题中，一般与函数的值域，最值与比较大小等常结合在一起例1．（2006年江西卷）若a >0，b >0，则不等式－b <1x<a 等价于（ ） A ．1b －<x <0或0<x <1a B.－1a <x <1b C.x <-1a 或x >1b D.x <1b －或x >1a解析：－b <1x <a 等价于－b <1x <0或0<1x <a 等价于x <1b －或x >1a答案：D点评：注意不等式ba b a 11>⇔<和适用条件是0>ab 例2.（2007年北京卷）如果正数a b c d ，，，满足4a b cd +==，那么（ ）Ａ．ab c d +≤，且等号成立时a b c d ，，，的取值唯一 Ｂ．ab c d +≥，且等号成立时a b c d ，，，的取值唯一 Ｃ．ab c d +≤，且等号成立时a b c d ，，，的取值不唯一 Ｄ．ab c d +≥，且等号成立时a b c d ，，，的取值不唯一解析：正数a b c d ，，，满足4a b cd +==，∴ 4=a b +≥，即4ab ≤，当且仅当a =b =2时，“=”成立；又4=2()2c d cd +≤，∴ c+d ≥4，当且仅当c =d =2时，“=”成立；综上得ab c d +≤，且等号成立时a b c d ，，，的取值都为2 答案：A点评：本题主要考查基本不等式，命题人从定值这一信息给考生提供了思维，重要不等式可以完成和与积的转化，使得基本不等式运用成为现实。

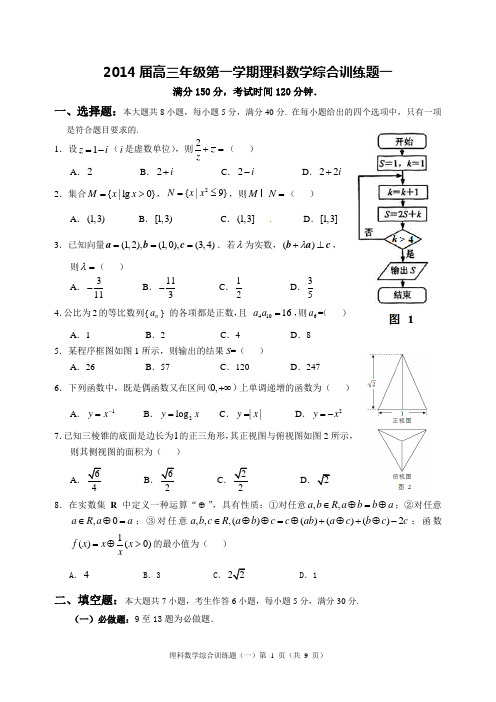
2014届高三年级第一学期理科数学综合训练题一满分150分，考试时间120分钟．一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1．设1z i =-（i 是虚数单位），则2z z+=（ ）A ．2 B ．2i + C ．2i - D ．22i +2．集合{|lg 0}M x x =>，2{|9}N x x =≤，则M N = （ ）A ．(1,3)B ．[1,3)C ．(1,3]D ．[1,3] 3．已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+⊥b a c ，则λ=（ ） A ．311-B ．113- C ．12 D ．354．公比为2的等比数列{n a } 的各项都是正数，且 41016a a =，则6a =（ ）A ．1B ．2C ．4D ．8 5．某程序框图如图1所示，则输出的结果S =（ ）A ．26B ．57C ．120D ．2476．下列函数中，既是偶函数又在区间0,+∞（）上单调递增的函数为（ ）A ．1y x -=B ．2log y x =C ．||y x =D ．2y x =- 7．已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图2所示，则其侧视图的面积为（ ）A B C ．2D 8．在实数集R 中定义一种运算“⊕”，具有性质：①对任意,,a b R a b b a ∈⊕=⊕；②对任意,0a R a a ∈⊕=；③对任意,,,()()()()2a b c R a b c c ab a c b c c ∈⊕⊕=⊕+⊕+⊕-；函数1()(0)f x x x x=⊕>的最小值为（ ）A ．4B ．3C ．．1二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分.（一）必做题：9至13题为必做题．9．不等式4|||2|≥++x x 的解集是_ __.10. 2个好朋友一起去一家公司应聘，公司人事主管通知他们面试时间时说：“我们公司要从面试的人中招3个人，你们都被招聘进来的概率是701” .根据他的话可推断去面试的人有_ __个（用数字作答）. 11．若圆22104x y mx ++-=与直线1y =-相切，其圆心在y 轴的左侧，则m =_ _. 12．在ABC ∆中，AC = ，BC =2，︒=∠60B ，则ABC ∆的面积等于 _.13．已知不等式组⎪⎪⎩⎪⎪⎨⎧≥-≤+≥≥ay x y x y x ,2,0,0表示一个三角形区域（包括三角形的内部及边界），则实数a 的取值范围为 __.（二）选做题：以下两题任选一道作答，两题都答的按第14题正误给分． 14．（坐标系与参数方程选做题） 已知直线113:(24x tl t y t=+⎧⎨=-⎩为参数）与直线2:245l x y -=相交于点B ，又点(1,2)A ，则AB = __.15．（几何证明选讲选做题）如图4，已知圆O 的半径为2，从圆O 外一点A 引切线AB 和割线AD ，C 为AD 与圆O 的交点，圆心O 到ADAB =AC 的长为__ __.三、解答题：本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤.16．（本小题满分12分）已知函数)0,0)(4sin()(πϕϕ<<>+=A x A x f 在16x π=时取得最大值2.（1）求()f x 的最小正周期； （2）求()f x 的解析式； （3）若,02πα⎡⎤∈-⎢⎥⎣⎦，164165f πα⎛⎫+= ⎪⎝⎭，求sin 24πα⎛⎫- ⎪⎝⎭的值.因台风灾害，我省某水果基地龙眼树严重受损，为此有关专家提出两种拯救龙眼树的方案，每种方案都需分四年实施．若实施方案1，预计第三年可以使龙眼产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第四年可以使龙眼产量为第三年产量的1.25倍、1.0倍的概率分别是0.5、0.5．若实施方案2，预计第三年可以使龙眼产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第四年可以使龙眼产量为第三年产量的1.2倍、1.0倍的概率分别是0.4、0.6．实施每种方案第三年与第四年相互独立，令()1,2i i ξ=表示方案i 实施后第四年龙眼产量达到灾前产量的倍数．（1）写出ξ1、ξ2的分布列；（2）实施哪种方案，第四年龙眼产量超过灾前产量的概率更大?（3）不管哪种方案，如果实施后第四年龙眼产量达不到、恰好达到、超过灾前产量，预计利润分别为10万元、15万元、20万元．问实施哪种方案的平均利润更大?18．（本小题满分13分）如图5，P A 垂直⊙O 所在平面ABC ，AB 为⊙O 的直径，P A =AB ，14BF BP =，C 是弧AB 的中点. （1）证明：BC ⊥平面P AC ； （2）证明：CF ⊥BP ；（3）求二面角F —OC —B 的平面角的正弦值. 19．（本小题满分14分）已知椭圆22122:1(0)x y C a b a b +=>>的离心率为e =:2l y x =+与以原点为圆心、以椭圆1C 的短半轴长为半径的圆O 相切.（1）求椭圆C 1的方程；（2）设椭圆1C 的左焦点为1F ，右焦点为2F ，直线1l 过点1F ，且垂直于椭圆的长轴，动直线2l 垂直于1l ，垂足为点P ，线段2PF 的中垂线交2l 于点M ，求点M 的轨迹2C 的方程；（3）设2C 与x 轴交于点Q ，不同的两点R 、S 在2C 上，且满足0=⋅RS QR ，求||QS的取值范围.已知S n 是数列{}n a 的前n 项和，且11=a ，)(2*1N n S na n n ∈=+. （1）求234,,a a a 的值； （2）求数列{}n a 的通项n a ； （3）设数列{}n b 满足21111,2n n n kb b b b a +==+，求证：当n k ≤时有1n b <.【参考答案与评分建议部分】一、选择题：本大题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案DCABBCAB二、填空题：本大题共6小题，每小题5分，共30分．9．(][)+∞-∞-,13, ；10．21；111213．(,2][0,2)-∞- ；14．52；15．3．三、解答题：本大题共6小题，共80分．16．（本小题满分12分） （1）()f x 的最小正周期为242T ππ==，…………………………………………………………2分 （2）由()f x 的最大值是2知，2A =，……………………………………………………………3分又()2sin 421616max f x f ππϕ⎛⎫⎛⎫==⨯+=⎪ ⎪⎝⎭⎝⎭，即sin 14πϕ⎛⎫+= ⎪⎝⎭， ………………………4分∵0ϕπ<<，∴5444πππϕ<+<，∴42ππϕ+=，∴4πϕ=， …………………………5分 ∴()2sin(4)4f x x π=+．………………………………………………………………………6分（3）由（2）得1162sin 441641645f πππαα⎡⎤⎛⎫⎛⎫+=++= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 即3sin()25πα+=，∴3cos 5α=，……………………………………………………………7分∵,02πα⎡⎤∈-⎢⎥⎣⎦，∴4sin 5α===-， …………………………8分∴4324sin 22sin cos 25525ααα⎛⎫==⨯-⨯=- ⎪⎝⎭，……………………………………………9分2237cos 22cos 121525αα⎛⎫=-=⨯-=- ⎪⎝⎭， ………………………………………………10分∴sin 2sin 2cos cos2sin 444πππααα⎛⎫-=- ⎪⎝⎭24725225250=-+=- ………………12分 17．（本小题满分13分） （1）ξ1的分布列为ξ1 0.8 0.9 1.0 1.125 1.25 P 10.20.150.350.150.15…………………………………………………3分ξ2的分布列为ξ2 0.8 0.96 1.0 1.2 1.44 P 20.30.20.180.240.08…………………………………………………6分 （2）由（1）可得ξ1＞1的概率P （ξ1＞1）= 0.15 + 0.15 = 0.3，…………………………………7分ξ2＞1的概率P （ξ2＞1）= 0.24 + 0.08 = 0.32， ………………………………………………8分 ∵P （ξ2＞1）＞P （ξ1＞1），∴实施方案2，第四年产量超过灾前概率更大．…………… 9分 （3）设实施方案1、2的平均利润分别为利润A 、利润B ，根据题意，利润A =（0.2 +0.15）×10 + 0.35×15 +（0.15 + 0.15）×20 = 14.75（万元）， ……………10分 利润B =（0.3 + 0.2）×10 + 0.18×15 + （0.24 + 0.08）×20 = 14.1（万元）， ……………11分 ∵利润A ＞利润B ，∴实施方案1平均利润更大． ………………………………………13分18．（本小题满分13分）（1）∵P A ⊥平面ABC ，BC ⊂平面ABC ，∴BC ⊥P A ．………………………………………………1分∵∠ACB 是直径所对的圆周角，∴90o ACB ∠=，即BC ⊥AC ．………………………………2分 又∵PA AC A = ，∴BC ⊥平面PAC ． ………………………………………………………3分 （2）∵P A ⊥平面ABC ，OC ⊂平面ABC ，∴OC ⊥P A ．………………………………………………4分∵C 是弧AB 的中点， ∴∆ABC 是等腰三角形，AC =BC ，又O 是AB 的中点，∴OC ⊥AB ．………………………………………………………………5分 又∵PA AB A = ，∴OC ⊥平面PAB ，又PB ⊂平面PAB ，∴BP OC ⊥．…………………6分 设BP 的中点为E ，连结AE ，则//OF AE ，AE BP ⊥，∴BP OF ⊥．………………………7分 ∵OC OF O = ，∴BP ⊥平面CFO . 又CF ⊂平面CFO ，∴C F B P ⊥．……………………8分 （3）由（2）知OC ⊥平面PAB ，∴OF OC ⊥，OC OB ⊥，………………………………………9分∴BOF ∠是二面角F OC B --的平面角．……………………………………………………10分 又∵BP OF ⊥，045FBO ∠=，∴045FOB ∠=，………………………………………………12分∴sin FOB ∠，即二面角F OC B --13分 19．（本小题满分14分）（1）由直线:2l y x =+与圆222x y b +=b =，即b =2分由e =222213b e a =-=，所以a =3分所以椭圆的方程是221:132x y C +=．…………………………………………………………4分 （2）由条件，知2||||MF MP =，即动点M 到定点2F 的距离等于它到直线1:1l x =-的距离，由抛物线的定义得点M 的轨迹2C 的方程是x y 42=． …………………………………………7分（3）由（2），知(0,0)Q ，设221212,,,44y y R y S y ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭，∴222121121,,,44y y y QR y RS y y ⎛⎫⎛⎫-==- ⎪ ⎪⎝⎭⎝⎭，…………………………………………………8分 由0=⋅，得()()222121121016y y y y y y -+-=， ………………………………………9分∵12y y ≠，∴21116y y y ⎛⎫=-+⎪⎝⎭，∴222121256323264y y y =++≥=， 当且仅当2121256y y =，即14y =±时等号成立． ………………………………………………11分又||QS ==………………………………………………12分∵2264y ≥，∴当2264y =，即28y =±时，min ||QS =13分故||QS的取值范围是)⎡+∞⎣．……………………………………………………………14分20．（本小题满分14分）（1）由111,2()n n a na S n N *+==∈得 2122a a ==， ……………………………………………1分32123a S a a ==+=，…………………………………………………………………………2分由43123322()a S a a a ==++得44a =． ……………………………………………………3分 （2）当1>n 时，由12n n na S += ① ，得1(1)2n n n a S --= ② ………………………………4分①－②得11(1)2()n n n n na n a S S +---=-，化简得1(1)n n na n a +=+，∴11n n a n a n++=（1>n ）．………………………………………………………………………5分 ∴22=a ，3232a a =，……，11n n a na n -=-， …………………………………………………6分 以上（1n -）个式子相乘得n n na n =-⨯⨯⨯=1232 （1>n ）， ………………………7分 又11=a ，∴()n a n n N *=∈ ．………………………………………………………………8分 （3）∵0>=n a n ，0211>=b ，n n kn b b a b +=+211， ∴{}n b 是单调递增数列，故要证：当n k ≤时，1n b <，只需证1k b <． …………………9分 ①当1k =时 ，1112b =<，显然成立． ……………………………………………………10分 ②当2k ≥时，∵01>>+n n b b ，n n kn b b a b +=+211， ∴n n n n b b b k b +<++111，∴1111n n b b k+->-， ………………………………………………11分 ∴112232111111111111kk k k k k k b b b b b b b b b b -----⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭112k k k k -+>-+=， ……………12分 ∴11k kb k <<+．………………………………………………………………………………13分 综上，当n k ≤时有1n b <． …………………………………………………………………14分故所求a的取值范围是(]2,0．………………………………………………………………14分。

专题1.33 《有理数》计算题综合训练（培优篇）（专项练习）一、解答题1．（1）计算：3100221-5--1-12-21-1-32（）（）÷+⨯ （2）解方程：1111333302222x ⎧⎫⎡⎤⎛⎫----=⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭2．有一列按一定顺序和规律排列的数： 第一个数是； 第二个数是； 第三个数是；…对任何正整数n ，第n 个数与第（n+1）个数的和等于．（1）经过探究，我们发现：设这列数的第5个数为a ，那么，，，哪个正确？请你直接写出正确的结论；（2）请你观察第1个数、第2个数、第3个数，猜想这列数的第n 个数（即用正整数n 表示第n 数），并且证明你的猜想满足“第n 个数与第（n+1）个数的和等于”；（3）设M 表示，，，…，，这2016个数的和，即，求证：．3．计算：(1)412411-÷； (2)3(72)95-÷； (3)1339(2)()1648-÷⨯； (4)1853()()334÷-÷-；(5) 14(81)2()(8)49-÷⨯-÷-； (6)1331(0.25)(1)244-÷÷-⨯-．4．计算：(1)3521(2)(1)13[()]2-⨯--+-； (2)[(－3)3－(－5)3]÷[(－3)－(－5)]；(3) 221143(2)(1)(1)33--⨯-⨯-÷-； (4)2016221(1)(0.5)[2(3)]36---÷⨯---．5．计算：(1) 0.125×(-7)×8； (2) -32-(-8)×(-1)5÷(-1)4； (4) [212-(79-1112+16)×36]÷5； (4) (-370)×(-14)+0.25×24.5+(-512)×(-25%).6．计算 （1）414)21(32)65(41-+-+-+-； （2）2111()()3642-+----；（3）74324.773276.3----； （4）.25.032581413125.0-+-+ 7．计算（1）331624⨯÷+； （2）)532(0)21(312-÷⨯--；（3）)157125(24)3153(15-⨯-+-⨯； （4）)8(161571)36()1855(-⨯+-⨯-；（4）)]3()6.0321(4[2-÷⨯-+---； （6）4211(10.5)[2(3)]3---⨯⨯--．8．阅读下面文字： 对于（﹣556）+（﹣923）+1734+（﹣312）可以如下计算：原式=[（﹣5）+（﹣56）]+[（﹣9）+（﹣23）]+（17+34）+[（﹣3）+（﹣12）]=[（一5）+（﹣9）+17+（一3）]+[（﹣56）+（﹣23）+34+（﹣12）]=0+（﹣114）=﹣114上面这种方法叫拆项法，你看懂了吗？ 仿照上面的方法，请你计算：（﹣112）+（﹣200056）+400034+（﹣199923）9．计算：（1）-2-（+10）； （2）0-（-3.6）；（3）（-30）-（-6）-（+6）-（-15）； （4）232(3)(2)(1)( 1.75)343-----+．10．计算下列各题：（1）3.587-（-5）+（-512）+（+7）-（+314）-（+1.587）；（2）（－1）5×{[－423÷（－2）2+（－1.25）×（－0.4）]÷（－19）－32}.10．（1）3131.75613848⎛⎫⎛⎫+----- ⎪ ⎪⎝⎭⎝⎭．（3）()31122.525 2.5485⎛⎫⨯--⨯+⨯- ⎪⎝⎭．（3）()()222017213313⎛⎫-⨯-+-÷- ⎪⎝⎭．11．已知282(41)3830x y y z x -+-+-=，求x ＋y ＋z 的值．12． 计算：112⎛⎫- ⎪⎝⎭ ×113⎛⎫- ⎪⎝⎭ ×114⎛⎫- ⎪⎝⎭ ×…×(1－149)×(1－150)．14．在数学活动中，小明为了求2341111122222n ++++⋅⋅⋅+的值(结果用n 表示)，设计如图所示的几何图形．请你利用这个几何图形求2341111122222n ++++⋅⋅⋅+的值．15．计算：1+111121231232000++⋅⋅⋅+++++++⋅⋅⋅+．16．阅读下面文字：对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 可以如下计算：原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦ ()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦1014⎛⎫=+- ⎪⎝⎭114=-上面这种方法叫拆项法，你看懂了吗？ 仿照上面的方法，计算： （1）115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭（2）235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭17．探索研究：（1）比较下列各式的大小（用“<”“>”或“=”连接） ①|3||2|+-_________|32|-；①1123+_______1123+； ①|6||3|+-________|63|-．（2）通过以上比较，请你归纳出当a ，b 为有理数时||||a b +与||a b +的大小关系．（直接写出结果）（3）根据（2）中得出的结论，当||20152015x x +=-时，x 的取值范围是________．若123415a a a a +++=，12345a a a a +++=，则12a a +=________．18．阅读材料：求l+2+22+32+42+…+22013的值．解：设S= l+2+22+32+42+…+20122+22013，将等式两边同时乘2， 得2S=2+22+32+42+52+…+22013+22014． 将下式减去上式，得2S -S=22014-l 即S=22014-l ， 即1+2+22+32+42+…+22013= 22014-l 仿照此法计算：(1)1+3+2333++…+100319．2014年“十一”黄金周期间，罗浮山风景区在7天假期中每天旅游的人数变化如下表（正 数表示比前一天多的人数，负数表示比前一天少的人数）：（1）请判断7天中游客人数最多的是哪天？最少的是哪天？它们相差多少万人？ （2）若9月30日的游客人数为0.3万人，则这7天的游客总人数是多少万人？20．观察下列各式：3211=，332123+=，33321236++=，33332123410+++=…()1请叙述等式左边各个幂的底数与右边幂的底数之间有什么关系？ ()2利用上述规律，计算：333331234...100+++++．21．下面是按一定规律排列的一列数： 第1个数：1－（1+12-）； 第2个数：2－（1+12-）[1+2(1)3-][1+3(1)4-]； 第3个数：3－（1+12-）[1+2(1)3-][1+3(1)4-][1+4(1)5-][1+5(1)6-]. …(1)分别计算这三个数的结果(直接写答案)；(2)写出第2 017个数的形式(中间部分用省略号，两端部分必须写详细)，然后推测出结果．22．数学老师布置了一道思考题：“计算121123031065⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭”，小红和小明两位同学经过仔细思考，用不同的方法解答了这个问题． 小红的解法：原式的倒数为()2112121123020351210310653031065⎛⎫⎛⎫⎛⎫-+-÷-=-+-⨯-=-+-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．所以121121303106510⎛⎫⎛⎫-÷-+-=- ⎪ ⎪⎝⎭⎝⎭． 小明的解法：原式12112151113303610530623010⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-÷+-+=-÷-=-⨯=- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦． 请你分别用小红和小明的方法计算：113224261437⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭．23．观察下列各等式，并回答问题：112⨯=1﹣12；123⨯=12﹣13；134⨯=13﹣14；145⨯=14﹣15；… （1）填空：1n(n 1)+=______（n 是正整数）（2）计算：112⨯ +123⨯+134⨯+145⨯+…+120042005⨯=______．（3）计算：112⨯ +123⨯+134⨯+145⨯+…+1n(n 1)+=______． （4）求113⨯+135⨯+157⨯+179⨯+…+120132015⨯的值．24．计算：196.9130.31310073317 1889.42377.124 111001150÷+⨯-÷+--+参考答案1．（1）3910-（2）90x=【解析】试题分析：（1）先去括号和绝对值符号后，再计算即可；（2）按等式性质称项、两边同时乘2，直至系数为1即可；试题解析：（1）原式＝() 125112478391192020 ---⨯--==-+;（2）12{12[12(12x-3)-3]-3}-3=01 2{12[12(12x-3)-3]-3}=31 2[12(12x-3)-3]-3=61 2[12(12x-3)-3]=91 2(12x-3)-3=181 2(12x-3)=2112x-3=4212x=45x=902．（1）第5个；（2）；证明过程见解析；（3）证明过程见解析.【解析】试题分析：（1）由已知规律可得；（2）先根据已知规律写出第n、n+1个数，再根据分式的运算化简可得；（3）将每个分式根据﹣=＜＜=﹣，展开后再全部相加可得结论．试题解析：（1）由题意知第5个数a==；（2）①第n个数为，第（n+1）个数为，①+=（+）=×=×=，即第n个数与第（n+1）个数的和等于；（3）①1﹣=＜=1，=＜＜=1﹣，﹣=＜＜=﹣，…﹣=＜＜=﹣，﹣=＜＜=﹣，①1﹣＜+++…++＜2﹣，即＜+++…++＜，①．考点：（1）分式的混合运算；（2）规律型；（3）数字的变化类3．(1)1311-;(2)1815-;(3)103-;(4)1;(5)－2;(6)－14【解析】试题分析：（1）（2）（3）利用带分数的性质，把复杂的数写成两个数的和，再用乘法分配律计算；（4）（5）（6）把乘数运算，带分数，统一成假分数的乘积形式，约分求解.试题解析：(1)4411411 12412123 11114411411⎛⎫⎛⎫-÷=-+⨯-⨯+⨯=-⎪ ⎪⎝⎭⎝⎭.(2)3311311 72972728 55995915⎛⎫⎛⎫⎛⎫-÷=-+⨯=-⨯+⨯=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(3)1339454810 2164816393⎛⎫⎛⎫⎛⎫-÷⨯=-⨯⨯=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(4)185103431 334385⎛⎫⎛⎫⎛⎫⎛⎫÷-÷-=⨯-⨯-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.(5)()()()()()1444812881816824999⎛⎫⎛⎫-÷⨯-÷-=-⨯⨯-÷-=÷-=- ⎪⎪⎝⎭⎝⎭. (6)()()13334710.251414244234⎛⎫⎛⎫-÷÷-⨯-=-⨯⨯-⨯-=- ⎪ ⎪⎝⎭⎝⎭. 4．(1) 154-；(2)49；(3)－22；(4)－10 【解析】（1）原式=18(1)134-⨯---， =18134--， =154-. （2）原式=[27(125)](35)---÷-+， =(27125)2-+÷， =982÷， =49.（3）原式=231634()()34--⨯⨯-⨯- =166--， =22-.（4）原式=341()6(29)66--⨯⨯--， =11()6(11)6--⨯⨯-， =111-， =10-. 考点：有理数的混合运算. 5．（1）-7；（2）-17；（3）310；(4)100. 【解析】 试题分析：这是一组有理数的混合运算题，在计算时，首先确定好正确的运算顺序，其次注意“符号”问题；具体解题过程中，（1）小题要注意乘法交换律和结合律的使用；（2）小题要特别注意“符号”方面的问题；（3）小题注意乘法分配律的使用；（4）小题注意乘法分配律的逆用. 试题解析：（1）原式=()0.12587⨯⨯- =()17⨯- =7-.（2）原式=()()9811---⨯-÷ =98-- =17-. （3）原式=()1122833625⎡⎤--+⨯⎢⎥⎣⎦ =51125⎛⎫-⨯ ⎪⎝⎭ =310. （4）原式=11137024.5 5.5444⨯+⨯+⨯ =()137024.5 5.54++ =100. 6．（1）615-; （2）1312- ; （3）－17 ; （4）283【解析】试题分析：进行有理数的加减混合运算时，可先统一成加法，再运用加法交换律，结合律进行运算．试题解析：解：（1）152********⎛⎫⎛⎫-+-+-+- ⎪ ⎪⎝⎭⎝⎭ =][11152444263⎡⎤⎛⎫⎛⎫⎛⎫-+-+-+-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ =-5+(-16) =156-（2）21113642⎛⎫⎛⎫-+---- ⎪ ⎪⎝⎭⎝⎭=21113642⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭=21113264⎛⎫⎛⎫-+-+-+ ⎪ ⎪⎝⎭⎝⎭=-43+14 = 1312-（3）343.7627.24377---- =()343.767.242377⎛⎫⎛⎫-+-+-+- ⎪ ⎪⎝⎭⎝⎭=-11+(-6) =-17（4）1120.125350.25483+-+- =()1112350.258483⎛⎫++-++- ⎪⎝⎭ =()111230.2558843⎛⎫+-++-+ ⎪⎝⎭ =0+3+253=2837．（1）70；（2）123；（3）542-；（4）－385.5；（5）2.2；（6）16.【解析】试题分析：（1）利用有理数的乘方和有理数乘除法法则计算即可；（2）按先乘除，后加减的顺序计算，注意有因数为0； （3）利用乘法分配率进行简算； （4）利用乘法分配率进行简算；（5）按先乘除，后加减，有括号先算括号内的；（6）按照有理数四则混合运算顺序进行计算即可．试题解析：（1）原式=16+18×3=16+54=70；（2）原式=1203-=123；（3）原式=315715()152424531215⨯-+⨯-⨯+⨯=5695105-+-+=1441255-+=-；（4）原式=515536367188180105687.5385.5 1816⨯+⨯-⨯-⨯=+--=-；（5）原式=2[4(10.4)(3)]2[40.6(3)]2[4(0.2)] ---+-÷-=---+÷-=---+-2.2=（6）原式=111711[29]1(7)123666 --⨯⨯-=--⨯-=-+=．8．5 4 -.【解析】试题分析：首先分析（-556）+（-923）+1734+（-312）的运算方法：将带分数分解为一个整数和一个分数；然后重新组合分组：整数一组，分数一组；再分别计算求值．试题解析：（﹣112）+（﹣200056）+400034+（﹣199923）=﹣1+（﹣12）+（﹣2000）+（﹣56）+4000+34+（﹣1999）+（﹣23），=﹣1+（﹣2000）+4000+（﹣1999）+（﹣12）+（﹣56）+34+（﹣23），=（﹣2）+34，=﹣54．点拨：首先阅读材料，结合有理数运算的法则，理解拆项法的原理及应用，然后仿照材料的方法，进行计算．9．（1）-12；（2）3.6（3）-15；（4）-1．【解析】试题分析：根据有理数的减法法则，减去一个数等于加上这个数的相反数，然后根据加法法则求解即可.试题解析：（1）-2-（+10）=-2+（-10）=-12.（2）0-（-3.6）=0+3.6=3.6．（3）（-30）-（-6）-（+6）-（-15）=（-30）+（+6）+（-6）+（+15）=-30+0+15=-15．（4）（-323）-（-234）-（-123）-（+1.75）=-323+234+123+（-134）=（-323+123）+ [（+234）+（-134）]=-2+1 =-1．10．（1）原式=514；（2）原式＝3.【解析】【分析】（1）运用加法的运算律，把小数与小数相加，整数与整数相加，分数与分数相加；（2）把带分数化为假分数，除法转化为乘法，再按有理数的混合运算法则计算.【详解】（1）原式=3.587+5-512+7-314-1.587=（3.587-1.587）+（5+7）+（-512-314）=2+12-83 4=51 4 .（2）原式＝-1×{[-143÷4+0.5]÷（-19）-9}＝-1×[（-23）÷（-19）-9]＝-1×（6-9）＝-1×（-3）＝3.11．（1）52-．（2）1-．（3）10-．【解析】试题分析：（1）化简，利用加法结合律计算.(2)利用乘法分配律计算.(3)先算乘方，再算乘除，最后计算加减.试题解析：（1）3131.75613848⎛⎫⎛⎫+----- ⎪ ⎪⎝⎭⎝⎭7515274848=--+ 22448=- 52=-．（2）()31122.525 2.5485⎛⎫⨯--⨯+⨯- ⎪⎝⎭310122.5 2.5 2.5485=⨯+⨯-⨯35122.5445⎛⎫=⨯+- ⎪⎝⎭22.55⎛⎫=⨯- ⎪⎝⎭1=-．（3）()()222017213313⎛⎫-⨯-+-÷- ⎪⎝⎭()19919=-⨯+÷-()19=-+-10=-．点拨：计算题中的一些运算技巧（1）熟练掌握常用分数和小数的互化：10.52=，10.254=，10.25=，10.1258=，10.110=, 20.45=,30.65=,340.3750.885==，. （2）利用带分数的性质，把复杂的数写成两个数的和，再用乘法分配律计算. (3)多个数相乘，负数是奇数个，最后符号为负；负数是偶数个，最后符号为正. (4) 带分数，统一成假分数的乘积形式，约分计算.（5）有理数的混合运算法则即先算乘方或开方,再算乘法或除法,后算加法或减法.有括号时、先算小括号里面的运算,再算中括号,然后算大括号.运算律：①加法的交换律：a+b=b+a ； ①加法的结合律：(a+b)+c=a+(b+c)； ①乘法的交换律：ab=ba ； ①乘法的结合律：(ab )c =a (bc )；①乘法对加法的分配律：a (b+c )=ab+ac ； 注：除法没有分配律. 12．3 【解析】【试题分析】根据绝对值、完全平方的非负性得，由题意可知80410830x y y z x -=⎧⎪-=⎨⎪-=⎩，解得21434x y z ⎧⎪=⎪⎪=⎨⎪⎪=⎪⎩，代入得：x ＋y ＋z ＝3.． 【试题解析】由题意可知80410830x y y z x -=⎧⎪-=⎨⎪-=⎩，解得21434x y z ⎧⎪=⎪⎪=⎨⎪⎪=⎪⎩，所以x ＋y ＋z ＝3.．【方法点拨】绝对值的非负性与平方的非负性可以和许多数学知识相结合进行考查． 13．150【解析】 【分析】先计算括号内的，然后再根据多个有理数相乘的运算法则进行求解即可. 【详解】112⎛⎫- ⎪⎝⎭ ×113⎛⎫- ⎪⎝⎭ ×114⎛⎫- ⎪⎝⎭×…×(1－149)×(1－150 )=1234484923454950⨯⨯⨯⨯⨯⨯ =150. 【点拨】本题考查了有理数的加、乘混合运算，熟练掌握运算顺序以及运算法则是解题的关键. 14．112n-【分析】把一个面积为1的正方形分成两个面积为12的长方形，接着把面积为12的长方形分成两个面积为14的正方形，再把面积为14的正方形分成两个面积为18的三角形，…，由图形揭示的规律进行解答即可得. 【详解】 由图可知11122=-， 221111222+=-，233111112222++=-， …2111112222n n +++=-， 所以234n n 1111111222222++++⋅⋅⋅+=-.【点拨】本题考查了规律题——图形的变化类，认真观察，通过计算从中发现规律是解题的关键. 15．119992001【分析】根据有理数的混合运算法则计算即可． 【详解】因为1+2+3+…+n =12{（1+2+…+n ）+[n +（n -1）+（n -2）+…+1]} = 12 [（1+n ）+（2+n -1）+（3+n -2）+…+（n +1）]= 12n （n +1），所以()12112123?··11n n n n n ⎛⎫==- ⎪++++++⎝⎭．所以原式=1+2（12-13）+2（13-14）+…+2（1111)1222000200122001-=+⨯-⨯=119992001【点拨】本题考查的是有理数的混合运算，掌握有理数的混合运算法则是解题的关键，解答时，注意正确找出规律． 16．（1）14-（2）124-【分析】（1）根据例子将每项的整数部分相加，分数部分相加即可解答； （2）根据例子将每项的整数部分相加，分数部分相加即可解答. 【详解】（1）115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭104⎛⎫=+- ⎪⎝⎭14=-（2）原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭124⎛⎫=-+- ⎪⎝⎭124=-【点拨】此题考察新计算方法，正确理解题意是解题的关键，根据例子即可仿照计算. 17．（1）①>；①=；①>；（2）||||||a b a b ++；（3）0x ，10或10-或5或5-【分析】（1）根据有理数绝对值的化简方法分别化简、计算后进行比较即可；（2）根据（1）的规律即可得到答案；（3）根据（2）的规律即可得到答案.【详解】（1）①因为|3||2|5,|32|1+-=-=，所以|3||2||32|+->-.①因为11112323+=+， 所以11112323+=+. ①因为|6||3|9,|63|3+-=-=，所以|6||3||63|+->-.故答案为>，=，>；（2）当a ，b 异号时，||||||a b a b +>+，当a ，b 同号时，||||||a b a b +=+，所以||||||a b a b ++；（3）由（2）中得出的结论可知，x 与2015-同号，所以x 的取值范围是0x . 因为1234123415,5a a a a a a a a +++=+++=，所以12a a +与34a a +异号，则1210a a +=或10-或5或5-，故答案为0x ，10或10-或5或5-.【点拨】此题考查了有理数绝对值的化简：正数的绝对值等于它本身，零的绝对值是零，负数的绝对值等于它的相反数，以及绝对值的化简方法的应用.18．101312-.先仿照已知条件给的设设S=1+3+2333++…+1003，然后再将等式的两边同时乘以3，就可得出另外一个式子，然后两式相减，即可求出.【详解】解：设S=1+3+2333++…+1003（1），3S=3+2333++…+1003+1013（2）（2）-（1）得：2S=1013-1 ①S=101312- ①1+3+2333++…+1003=101312- 19．（1）0.22万人（2）这7天的游客总人数是3.42万人【分析】(1)根据表格确定出七天内游客人数最多与最少的，求出之差即可；；(2) 根据9月30日的人数，以及表格，求出这7天的游客总人数即可．【详解】解：7天中游客人数最多的是10月3日，最少的是10月7日，它们相差0.58-0.36=0.22(万人).(2) (1) 1日游客人数为0.3+0.16=0.46(万人)；2日游客人数为0.46+0.08=0.54(万人)；3日游客人数为0.54+0.04=0.58(万人)；4日游客人数为0.58-0.04=0.54(万人)；5日游客人数为0.54-0.08=0.46(万人)；6日游客人数为0.46+0.02=0.48(万人)；7日游客人数为0.48-0.12=0.36(万人).0.46+0.54+0.58+0.54+0.46+0.48+0.36=3.42(万人).答：这7天的游客总人数是3.42万人20．(1) 右边幂的底数等于左边各个幂的底数的和；(2)2 5050．【分析】（1）通过观察可知,右边幂的底数等于左边各个幂的底数的和,（2）利用规律即可解决问题．【详解】()1右边幂的底数等于左边各个幂的底数的和,（2）333331234...100+++++,2(123...100)=++++,21100[100]2+=⨯, 25050=．【点拨】本题主要考查数字变化类规律型,解决本题的关键是要熟练掌握学会观察并归纳规律. 21．（1）见解析（2）40332 【分析】（1）按照运算法则运算即可；（2）按照（1）中计算方式，逐步写出第2017个代数式，由此可以写出第2017个数；【详解】(1)第1个数：12；第2个数：32；第3个数：52. (2)第2 017个数：2 017－23403240331(1)(1)(1)(1)1+)[1][1][1][1]23440334034-----++++（ =2017-14365403440332345640334034⨯⨯⨯⨯⨯⨯⨯ =2017-12=40332. 【点拨】题目考查了数字的变化规律，解决此类问题的关键是找出所求数字与序号的关系，题目整体难易适中，适合课后训练．22．114- 【解析】【分析】参考小红和小明的两种不同方法计算即可.【详解】解：法1：原式的倒数为()13221132242792812352114614374261437⎛⎫⎛⎫⎛⎫-+-÷-=-+-⨯-=-+-+=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ①113221426143714⎛⎫⎛⎫-÷-+-=- ⎪ ⎪⎝⎭⎝⎭； 法2：原式1123215111113426314742624234214⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-÷+-+=-÷-=-÷=-⨯=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦． 【点拨】灵活采用运算技巧能使计算简化.23．（1）111n n -+ ；（2）20042005 ；（3）1n n +；（4）10072015. 【解析】【分析】（1）根据题意确定出拆项规律，写出第n 个式子即可；（2）根据拆项规律，先拆项再抵消写即可求解；（3）根据拆项规律，先拆项再抵消写即可求解；（4）根据拆项规律，先拆项再抵消写即可求解．【详解】解：（1）111(1)1n n n n =-++（n 是正整数） （2）111111223344520042005++++⋯+⨯⨯⨯⨯⨯ =11111122320042005-+-+⋯+-=1﹣12005 =20042005． （3）1111112233445(1)n n ++++⋯+⨯⨯⨯⨯+ =1111112231n n -+-+⋯+-+ =111n -+ =1n n +． （4）111111335577920132015+++++⨯⨯⨯⨯⨯ =11111111123355720132015⎛⎫⨯-+-+-+⋯+- ⎪⎝⎭ =11122015⎛⎫⨯- ⎪⎝⎭=1201422015⨯=10072015． 故答案为：（1）111n n -+ ；（2）20042005 ；（3）1n n +；（4）10072015. 【点拨】 考查了有理数的混合运算，（4）的关键是将式子变形为11111111123355720132015⎛⎫⨯-+-+-+⋯+- ⎪⎝⎭进行计算． 24．4【分析】根据题意将小数和分数互相转化，将分数除法转变为分数乘法，然后根据分数的乘法运算法则和乘法分配律计算即可．【详解】原式1(6.910.091)33377.12 4.34711188.039.4211+-⨯⎛⎫=⨯-+ ⎪⎝⎭+-=22.78 205111.394111⎛⎫⨯-⎪⎝⎭-=22051.392 205111.3911⎡⎤⎛⎫⨯-⨯⎪⎢⎥⎝⎭⎣⎦-=22⨯=4故答案为4．【点拨】本题考查了含小数的分数乘除混合运算，关键是掌握分数除法的运算法则，并且要将小数转化为分数或分数转化为小数．。

专题1.8 有理数（满分100）学校:___________姓名：___________班级：___________考号：___________题号一二三总分得分评卷人得 分一．选择题（本大题共10小题，每小题3分，满分30分）1．（2022•黔东南州）下列说法中，正确的是（ ）A ．2与﹣2互为倒数B ．2与12互为相反数C ．0的相反数是0D ．2的绝对值是﹣22．（2021秋•滕州市月考）下列说法中正确的有（ ）个．①0是整数，也是正数：②﹣123是负分数；③3.2是正小数，不是正分数；④自然数一定是正数；⑤负分数一定是负有理数；⑥非负数就是正数和零．A ．0B ．1C ．2D ．33．（2022春•东台市月考）某种细胞开始分裂时有两个，1小时后分裂成4个并死去一个，2小时后分裂成6个并死去一个，3小时后分裂成10个并死去一个，按此规律，8小时后细胞存活的个数是（ ）A ．253B ．255C ．257D ．2594．（2021秋•新华区校级期中）若a ，b 互为相反数，且ab ≠0，c 、d 互为倒数，|m |＝2，则（a +b ）2021+（ba）3﹣3cd +2m 的值（ ）A ．0B ．0或﹣8C ．﹣2成6D ．2或﹣65．（2020秋•江阴市校级月考）电子跳蚤落在数轴上的某点K 0，第一步从K 0向左跳1个单位到K 1，第二步由K 1向右跳2个单位到K 2，第三步由K 2向左跳3个单位到K 3，第四步由K 3跳4个单位到K 4，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点K 100所表示的数恰是30，则电子跳蚤的初始位置K 0点所表示的数为（ ）A ．﹣26B ．﹣20C ．﹣30D ．306．（2022•钟山县模拟）计算：1+12+122+123+124+⋯⋯+1299+12100结果是（ ）A．1―12100B．1―12101C．2―12100D．2―121017．（2022春•岳麓区校级月考）在一次数学活动课上，某数学老师在4张同样的纸片上各写了一个正整数，从中随机取2张，并将它们上面的数相加，重复这样做，每次所得的和都是5，6，7，8中的一个数，并且这4个数都能取到，根据以上信息，下列判断正确的是（ ）A．四个正整数中最小的是1B．四个正整数中最大的是8C．四个正整数中有两个是2D．四个正整数中一定有38．（2022•平邑县一模）小云计划户外徒步锻炼，每天有“低强度”“高强度”“休息”三种方案，下表对应了每天不同方案的徒步距离（单位：km）．若选择“高强度”要求前一天必须“休息”（第一天可选择“高强度”）．则小云5天户外徒步锻炼的最远距离为（ ）km．日期第1天第2天第3天第4天第5天低强度86654高强度121315128休息00000A．35B．36C．37D．389．（2020秋•江夏区校级月考）观察下列等式：12＝1，22＝4，32＝9，42＝16，52＝25，…，若12+22+32+42+52+…+n2的个位数字是1（0＜n≤2020，且n为整数），则n的最大值是（ ）A．2001B．2006C．2011D．201910．（2021秋•江岸区校级月考）下列说法中，正确的个数是（ ）①若|1a |=1a，则a≥0；②若|a|＞|b|，则有（a+b）（a﹣b）是正数；③A、B、C三点在数轴上对应的数分别是﹣2、6、x，若相邻两点的距离相等，则x＝2；④若代数式2x+|9﹣3x|+|1﹣x|+2011的值与x无关，则该代数式值为2021；⑤a+b+c＝0，abc＜0，则b c|a|+a c|b|+a b|c|的值为±1．A．1个B．2个C．3个D．4个评卷人得 分二．填空题（本大题共5小题，每小题3分，满分15分）11．（2021秋•东城区期末）现把2021个连续整数1，2，3…2021的每个数的前面任意填上“+”号或者“﹣”号，然后将它们相加，则所得的结果绝对值的最小值为 ．12．（2021秋•公安县期末）小聪在纸上画了一条数轴后，折叠纸面，使数轴上表示﹣2的点与表示5的点重合，若数轴上A ，B 两点之间的距离为10，且A ，B 两点经上述折叠后重合，则B 点表示的数为 ．13．（2021秋•大田县期中）三个整数a ，b ，c 满足a ＜b ＜c ，且a +b +c ＝0．若|a |＜10，则|a |+|b |+|c |的最大值为 ．14．（2021春•杨浦区校级期末）已知a ，b ，c 为整数，且|a ﹣b |2021+|c ﹣a |2020＝1，则|a ﹣b |+|b ﹣c |+|c ﹣a |＝ ．15．（2020秋•鄞州区期末）已知整数a ，b ，c ，d 的绝对值均小于5，且满足1000a +100b 2+10c 3+d 4＝2021，则abcd 的值为 ．评卷人得 分三．解答题（本大题共8小题，满分55分）16．（8分）（2021秋•随县期末）计算：①﹣2×3﹣|﹣4|；②﹣32+（―12）×（﹣8）+（﹣6）2；③（134―78―712）×（﹣117）；④8÷（﹣6）﹣[﹣3+116×（―27）]．17．（4分）（2022春•南岸区校级月考）我国约有9600000平方千米的土地，平均1平方千米的土地一年从太阳得到的能量相当于燃烧150000吨煤所产生的能量．（1）一年内我国土地从太阳得到的能量相当于燃烧多少吨煤所产生的能量？（2）若1吨煤大约可以发出8000度电，那么（1）中的煤大约发出多少度电？（结果用科学记数法表示）18．（6分）（2021秋•邹城市期中）已知下列各有理数：a ，b ，c 的大小关系为a ＜﹣1＜b ＜0＜1＜c ．（1）画出数轴，在数轴上标出这些数表示的点；（2）在横线上填上合适的符号（＞或＜或＝）：①a +c b +c ；②a ﹣c a ﹣b ；③ab ac ；④ab ac ；（3）化简：|a +b |﹣|b ﹣c |﹣|1﹣c |．19．（6分）（2022•义安区模拟）观察以下算式：①1×11×5=18×(1+31×5)；②2×35×9=18×(1+35×9)；③3×59×13=18×(1+39×13)．（1）请写出第④个算式： ．（2）请用n （n 是正整数）表示出第n 个算式，并计算1×11×5+2×35×9+3×59×13+⋯+9×1733×37+10×1937×41．20．（6分）（2021秋•汝阳县期末）某批发商于上周日买进某产品10000kg，每千克2.4元，进入批发市场后共占5个摊位，每个摊位最多能容纳2000kg该品种的产品，每个摊位的市场管理价为每天20元．如表为本周内该产品每天的批发价格比前一天的涨跌情况．（涨记为正，跌记为负，上周日当天的售价刚好为每千克2.4元）星期一二三四五+0.3﹣0.1+0.25+0.2﹣0.5与前一天相比价格的涨跌情况/元当天的交易量/kg25002000300015001000（1）星期四该产品价格为每千克多少元？（2）本周内该产品的最高价格为每千克多少元？最低价格为每千克多少元？（3）该批发商在销售过程中采用逐步减少摊位个数（每天减少一个）的方法来降低成本，增加收益，请你帮他算一算，这样他在本周的买卖中共赚了多少钱？21．（8分）（2021秋•嘉鱼县期末）数轴是一个非常重要的数学工具，它使数和数轴上的点建立起一一对应的关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．我们知道|4|＝|4﹣0|，它的几何意义是数轴上表示4的点与原点（即表示0的点）之间的距离，又如式子|7﹣3|，它的几何意义是数轴上表示数7的点与表示数3的点之间的距离．也就是说，在数轴上，如果点A表示的数记为a，点B表示的数记为b，则A，B两点间的距离就可记作|a﹣b|．回答下列问题：（1）几何意义是数轴上表示数2的点与数﹣3的点之间的距离的式子是 ；式子|a+5|的几何意义是 ；（2）根据绝对值的几何意义，当|m﹣2|＝3时，m＝ ；（3）探究：|m+1|+|m﹣9|的最小值为 ，此时m满足的条件是 ；（4）|m+1|+|m﹣9|+|m﹣16|的最小值为 ，此时m满足的条件是 ．22．（8分）（2021秋•江北区校级期中）已知数轴上两点A，B对应的数分别为﹣8和4，点P为数轴上一动点，若规定：点P到A的距离是点P到B的距离的3倍时，我们就称点P是关于A→B的“广益点”．（1）若点P到点A的距离等于点P到点B的距离时，求点P表示的数是多少；（2）若点P以每秒1个单位的速度从原点O开始向右运动，当点P是关于A→B的“广益点”时，求点P的运动时间；（3）若点P在原点的左边（即点P对应的数为负数），且点P，A，B中，其中有一个点是关于其它任意两个点的“广益点”，请直接写出所有符合条件的点P表示的数．23．（9分）（2022春•房山区期中）现将偶数个互不相等的有理数分成个数相同的两排，需满足第一排中的数越来越大，第二排中的数越来越小．例如，轩轩将“1，2，3，4”进行如下分组： 第一列　第二列　第一排　1　2　第二排4 3然后把每列两个数的差的绝对值进行相加，定义为该分组方式的“M值”．例如，以上分组方式的“M值”为M＝|1﹣4|+|2﹣3|＝4．（1）另写出“1，2，3，4”的一种分组方式，并计算相应的“M值”；（2）将4个自然数“a，6，7，8”按照题目要求分为两排，使其“M值”为6，则a的值为 ．（3）已知有理数c，d满足c+d＝2，且c＜d．将6个有理数“c，d，﹣5，﹣2，2，4”按照题目要求分为两排，使其“M值”为18，求d的值．。

2013届高三第一学期理科数学综合训练题一一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． ⒈已知集合{}是虚数单位 , , )1(|2i R a i a a x x A ∈-+==，若R A ⊆，则=aA ．1B ．1-C ．1±D ．0⒉若四边形ABCD 满足 0=+CD AB ，0)(=⋅-AC AD AB ，则该四边形一定是 A ．直角梯形 B ．菱形 C ．矩形 D ．正方形⒊某社区现有480个住户，其中中等收入家庭200户、低收入家庭160户，其他为高收入家庭．在建设幸福广东的某次分层抽样调查中，高收入家庭被抽取了6户，则该社区本次被抽取的总户数为A ．20B ．24C ．30D ．36 ⒋直线3π=x ，2π=x 都是函数) , 0)(sin()(πϕπωϕω≤<->+=x x f 的对称轴，且函数)(x f 在区间]2, 3[ππ上单调递减，则A ．6=ω，2πϕ= B ．6=ω，2πϕ-= C ．3=ω，2πϕ=D ．3=ω，2πϕ-=⒌一个底部水平放置的几何体，下半部分是圆柱， 上半部分是正四棱锥，其三视图如图1所示， 则这个几何体的体积=V A ．3054+π B ．π69C ．π66D ．2454+π⒍a 、b 、0>c ，“a ln 、b ln 、c ln 成等差数列”是“a2A ．充分不必要条件B ．必要不充分条件C ．充要条件⒎在平面直角坐标系xOy 中，0=++c by ax 与c by ax =+22所 表示的曲线如图2所示，则常数a 、b 、c 之间的关系可能是 A ．0<<a c 且0>b B ．0<<a c 且0<b C ．0>>c a 且0<b D ．A 或C⒏已知平面区域{}21 , 21|) , (≤≤-≤≤-=y x y x D ，y ax z +=（a 是常数），D y x P ∈∀) , (00，记2500≥+=y ax z 为事件A ，则使81)(=A p 的常数a 有D二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． (一)必做题（9～13题）⒐已知) , (~2σμN X ，68.0)(=+≤<-σμσμX P ，95.0)22(=+≤<-σμσμX P ，某次全市20000人参加的考试，数学成绩大致服从正态分布)100 , 100(N ， 则本次考试120分以上的学生约有 人． ⒑图3是讨论三角函数某个性质的程序框图，若输入)( 11sin+∈=N i i a i π，则输出=i ．⒒设抛物线C ：x y 42=的准线与对称轴相交于点P ， 过点P 作抛物线C 的切线，切线方程是 ．⒓在平面直角坐标系中，四边形ABCD 在映射f ：)1 , 2() , (x y y x -→作用下的象集为四边形////D C B A ，若ABCD 的面积1=S ，则////D C B A 的面积=/S ． ⒔以下命题中，真命题的序号是 （请填写所有真命题的序号）．①回归方程x y5.12ˆ+-=表示变量x 增加一个单位时，y 平均增加5.1个单位． ②已知平面α、β和直线m ，若α//m 且βα⊥，则β⊥m ．③“若12<x ，则11<<-x ”的逆否命题是“若1-<x 或1>x ，则12>x ”．④若函数)(x f y =与函数)(x g y =的图象关于直线x y =对称，b a f =)(，若2)(/=a f ，则21)(/=b g ．(二)选做题（14、15题，考生只能从中选做一题）⒕（坐标系与参数方程选做题）若直线⎩⎨⎧=-=t y t x 21（Rt ∈为参数）与圆⎩⎨⎧+==a y x θθsin cos （πθ20<≤，θ为参数，a 为常数且0>a ）相切，则=a ．⒖（几何证明选讲选做题）如图4，P 是圆O 外 一点，直线PO 与圆O 相交于C 、D ，PA 、PB 是圆O 的切线，切点为A 、B ．若1==CD PC ， 则四边形PADB 的面积=S ．ABCDEF1A 1B 1C 1D三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．⒗（本小题满分14分）如图5，一架飞机原计划从空中A 处直飞相距km 680的空中B 处，为避开直飞途中的雷雨云层，飞机在A 处沿与原飞行方向成θ角的方向飞行，在中途C 处转向与原方向线成o 45角的方向直飞到达B 处．已知135sin =θ．⑴在飞行路径ABC ∆中，求C tan ； ⑵求新的飞行路程比原路程多多少km ．（参考数据：414.12=，732.13=）⒘（本小题满分12分）某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛：答对3题者直接进入决赛，答错3题者则被淘汰．已知选手甲答对每个问题的概率相同，并且相互之间没有影响，答题连续两次答错的概率为91． ⑴求选手甲可进入决赛的概率；⑵设选手甲在初赛中答题的个数为ξ，试求ξ的分布列，并求ξ的数学期望．⒙（本小题满分14分）如图6，1111D C B A ABCD -是棱长为6的正方体，E 、F 分别是棱AB 、BC上的动点，且BF AE =．⑴求证：E C F A 11⊥；⑵当1A 、E 、F 、1C 共面时，求： ①1D 到直线E C 1的距离；②面DE A 1与面DF C 1所成二面角的余弦值．⒚（本小题满分14分）已知圆锥曲线C 上任意一点到两定点)0 , 1(1-F 、)0 , 1(2F 的距离之和为常数，曲线C 的离心率21=e ．⑴求圆锥曲线C 的方程；⑵设经过点2F 的任意一条直线与圆锥曲线C 相交于A 、B ，试证明在x 轴上存在一个定点⒛（本小题满分12分）已知数列{})(+∈N n a n ，01=a ，n n n n a a 221⨯+=+)1(≥n ． ⑴求数列{}n a 的通项；⑵设数列{}n a 的前n 项和为n S ，试用数学归纳法证明2)43(221-+-⨯=-n n S n n ．21（本小题满分14分）设)(x f y =是定义在区间) , (b a （a b >）上的函数，若对1x ∀、) , (2b a x ∈，都有|||)()(|2121x x x f x f -≤-，则称)(x f y =是区间) , (b a 上的平缓函数．⑴试证明对R k ∈∀，1)(2++=kx x x f 都不是区间)1 , 1(-上的平缓函数；⑵若)(x f 是定义在实数集R 上的、周期为2=T 的平缓函数，试证明对1x ∀、R x ∈2，1|)()(|21≤-x f x f ．2013届高三第一学期理科数学训练题一答题卷一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．______________；10．______________；11．______________；12．______________；13．______________；14．______________；15．______________．三、解答题：本大题共6小题，共80分．16．（本小题满分14分）18．（本小题满分14分）20．（本小题满分12分）理科数学评分参考一、选择题 CBBA DDAC二、填空题 ⒐500 ⒑22 ⒒01=+±y x （对一个3分，全对5分） ⒓2⒔①④（正确选项一个3分，全对5分；错误选项一个扣3分，2个扣5分，扣完为止） ⒕52+（答52±给3分，其他0分） ⒖322三、解答题 ⒗⑴135sin =θ，θ是锐角，所以125tan =θ，)45tan()]45(tan[tan 0+-=+-=θθπC ，0045tan tan 145tan tan ⋅-+-=θθ，717112511125-=⨯-+-=．⑵26217)45sin(sin 0=+=θC ，由正弦定理θsin 45sin sin 0BC AC CAB ==，得52045sin sin 0=⨯=CAB AC ，2200=BC ，新的飞行路程比原路程多)(8.1226802200520km AB BC AC =-+=-+． ⒘⑴设选手甲任答一题，正确的概率为p ，依题意91)1(2=-p ，32=p ，甲选答3道题目后进入决赛的概率为278)32(3=，甲选答4道、5道题目后进入决赛的概率分别为27831)32(323=⋅C 、8116)31()32(2324=C ，所以选手甲可进入决赛的概率81648116278278=++=P ．⑵ξ可取3，4，5，依题意31271278)3(=+==ξP ，27103132)31(3231)32()4(223223=⋅⋅+⋅⋅==C C P ξ，27831)32()31(32)31()32()5(22242224=⋅⋅+⋅⋅==C C P ξ，所以，ξ的分布列为：27107278527104313=⨯+⨯+⨯=ξE ．⒙⑴以D 为原点，DA 、DC 、1DD 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，则)6 , 0 , 6(1A 、)6 , 6 , 0(1C ，设m AE =，则)0 , , 6(m E ，)0 , 6 , 6(m F -，从而、，直接计算知，所以．⑵①当1A 、E 、F 、1C 共面时，因为底面1111//D C B A ABCD ，所以EF C A //11，所以AC EF //，从而E 、F 分别是AB 、BC 的中点，设1D 到直线E C 1的距离为h ，在E D C 11∆中，93662221=++=E C ，221111BC D C hE C ⨯=⨯，解得24=h ．②由①得，)0 , 3 , 6(E 、 )0 , 6 , 3(F ，设平面DE A 1的一个法向量为) , , (1c b a n =，依题意⎪⎩⎪⎨⎧=+=⋅=+=⋅066036111c a DA n b a DE n ，所以)1 , 2 , 1(1-=n ，同理平面DF C 1的一个法向量为)1 , 1 , 2(2-=n ，由图，面DE A 1与面DF C 1所成二面角的余弦值21||cos 21=⋅=n n θ．⒚⑴依题意，设曲线C 的方程为12222=+b y a x （0>>b a ），1=c ，21==a c e ，2=a ，322=-=c a b ，所求方程为13422=+yx．⑵当直线AB 不与x 轴垂直时，设其方程为)1(-=x k y ，由⎪⎩⎪⎨⎧-==+)1(13422x k y yx ，得0)3(48)43(2222=-+-+k x k x k ，从而22438kkx x B A +=+，2243)3(4kkx x B A +-=⋅，设)0 , (t P ，则B A B A y y t x t x PB PA +--=⋅))((2222222243)485(123)())(()1(kkt t t t kx x k t x x kB A B A ++--+-=++++-+=，当4485312322tt t +--=-，811=t 时，对R k ∈∀，64135-=⋅PB PA ；当x AB ⊥轴时，直线AB 的方程为1=x ，1==B A x x ，23)(±=B A y y ，对811=t ，6413549649))((-=-=+--=⋅B A B A y y t x t x PB PA ，即存在x 轴上的点)0 , 811(P ，使PBPA ⋅的值为常数64135-．⒛⑴由nn n n a a 221⨯+=+得n a a n n nn =--+1122，122211-=----n a a n n n n ，所以101232212111)22()22()22(2a a a a a a a a n n n n n n n n n n +-++-+-=-------- 1)2()1(++-+-= n n 2)1(-=n n ，高三理科数学综合训练题一（第 11 页 共 11 页）⑵1=n 时，左边011==a S ，右边02)431(12)43(221=-+-⨯=-+-⨯-n n n ，左边=右边，命题成立；设)(+∈=N k k n 时，命题成立，即2)43(221-+-⨯=-k k S k k ，则11+++=k k k a S S ，2)2(2)1(22)43(22121-+-=+⨯+-+-⨯=--k kk k k kk k k2]4)1(3)1[(22-++-+⨯k k k ，从而1+=k n 时，命题成立．综上所述，数列{}n a 的前n 项和2)43(221-+-⨯=-n n S n n ．21.⑴1x ∀、)1 , 1(2-∈x ，|||||)()(|212121x x k x x x f x f -⨯++=-．若0≥k ，则当1x 、)1 , 21(2∈x 时，121>++k x x ……2分，从而|||)()(|2121x x x f x f ->-；若0<k ，则当1x 、)21, 1(2--∈x 时，121-<++k x x ，1||21>++k x x ，从而|||)()(|2121x x x f x f ->-，所以对任意常数k ，1)(2++=kx x x f 都不是区间)1 , 1(-上的平缓函数．⑵若1x 、]2 , 0[2∈x ，①当1||21≤-x x 时，1|||)()(|2121≤-≤-x x x f x f ；②当1||21>-x x 时， 不妨设2021≤<≤x x ，根据)(x f 的周期性，)2()0(f f =，|)()2(||)0()(||)()2()0()(||)()(|212121x f f f x f x f f f x f x f x f -+-≤-+-=- 1)(22|2|||122121<--=-+=-+≤x x x x x x ，所以对1x ∀、]2 , 0[2∈x ，都有1|)()(|21≤-x f x f ．对1x ∀、R x ∈2，根据)(x f 的周期性（且2=T ），存在1p 、]2 , 0[2∈p ，使)()(11p f x f =、)()(22p f x f =，从而1|)()(||)()(|2121≤-=-p f p f x f x f ．。

§4.4函数y＝A sin(ωx＋φ)的图像及应用1.y＝A sin(ωx＋φ)的有关概念2.用五点法画y＝A sin(ωx＋φ)(A>0，ω>0，x∈R)一个周期内的简图时，要找五个特征点3.函数y＝sin x的图像经变换得到y＝A sin(ωx＋φ)(A>0，ω>0)的图像的两种途径概念方法微思考1.怎样从y ＝sin ωx 的图像变换得到y ＝sin(ωx ＋φ)(ω>0，φ>0)的图像？ 提示 向左平移φω个单位长度.2.函数y ＝sin(ωx ＋φ)图像的对称轴是什么？ 提示 x ＝k πω＋π2ω－φω(k ∈Z ).题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)y ＝sin ⎝⎛⎭⎫x －π4的图像是由y ＝sin ⎝⎛⎭⎫x ＋π4的图像向右平移π2个单位长度得到的.( √ ) (2)将函数y ＝sin ωx 的图像向右平移φ(φ>0)个单位长度，得到函数y ＝sin(ωx －φ)的图像.( × )(3)函数y ＝A cos(ωx ＋φ)的最小正周期为T ，那么函数图像的两个相邻对称中心之间的距离为T2.( √ ) (4)函数y ＝sin x 的图像上各点纵坐标不变，横坐标缩短为原来的12，所得图像对应的函数解析式为y ＝sin 12x .( × )题组二 教材改编2.为了得到函数y ＝2sin ⎝⎛⎭⎫2x －π3的图像，可以将函数y ＝2sin 2x 的图像向 平移 个单位长度. 答案 右 π63.y ＝2sin ⎝⎛⎭⎫12x －π3的振幅、频率和初相分别为 . 答案 2，14π，－π34.如图，某地一天从6～14时的温度变化曲线近似满足函数y ＝A sin(ωx ＋φ)＋b ，则这段曲线的函数解析式为 .答案 y ＝10sin ⎝⎛⎭⎫π8x ＋3π4＋20，x ∈[6,14] 解析 从题图中可以看出，从6～14时的是函数 y ＝A sin(ωx ＋φ)＋b 的半个周期， 所以A ＝12×(30－10)＝10，b ＝12×(30＋10)＝20， 又12×2πω＝14－6， 所以ω＝π8.又π8×10＋φ＝2π＋2k π，k ∈Z ，取φ＝3π4， 所以y ＝10sin ⎝⎛⎭⎫π8x ＋3π4＋20，x ∈[6,14]. 题组三 易错自纠5.要得到函数y ＝sin ⎝⎛⎭⎫4x ＋π3的图像，只需将函数y ＝sin 4x 的图像( ) A.向左平移π12个单位长度B.向右平移π12个单位长度C.向左平移π3个单位长度D.向右平移π3个单位长度答案 A解析 ∵y ＝sin ⎝⎛⎭⎫4x ＋π3＝sin ⎣⎡⎦⎤4⎝⎛⎭⎫x ＋π12， ∴要得到y ＝sin ⎝⎛⎭⎫4x ＋π3的图像，只需将函数y ＝sin 4x 的图像向左平移π12个单位长度. 6.将函数y ＝2sin ⎝⎛⎭⎫2x ＋π6的图像向右平移14个周期后，所得图像对应的函数为 . 答案 y ＝2sin ⎝⎛⎭⎫2x －π3 解析 函数y ＝2sin ⎝⎛⎭⎫2x ＋π6的周期为π，将函数y ＝2sin ⎝⎛⎭⎫2x ＋π6的图像向右平移14个周期，即π4个单位长度，所得函数为y ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4＋π6＝2sin ⎝⎛⎭⎫2x －π3. 7.y ＝cos(x ＋1)图像上相邻的最高点和最低点之间的距离是 . 答案π2＋4解析 相邻最高点与最低点的纵坐标之差为2，横坐标之差恰为半个周期π，故它们之间的距离为π2＋4.8.若函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，0<φ<π)的部分图像如图所示，则f ⎝⎛⎭⎫π4的值为 .答案3解析 由题干图像可知A ＝2，34T ＝11π12－π6＝3π4，∴T ＝π，∴ω＝2，∵当x ＝π6时，函数f (x )取得最大值，∴2×π6＋φ＝π2＋2k π(k ∈Z )，∴φ＝π6＋2k π(k ∈Z )，又0<φ<π，∴φ＝π6，∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6， 则f ⎝⎛⎭⎫π4＝2sin ⎝⎛⎭⎫π2＋π6＝2cos π6＝ 3.题型一 函数y ＝A sin(ωx ＋φ)的图像及变换例1 (2018·合肥模拟)已知函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A >0，ω>0，－π2<φ<π2的最小正周期是π，且当x ＝π6时，f (x )取得最大值2.(1)求f (x )的解析式；(2)作出f (x )在[0，π]上的图像(要列表).解 (1)因为函数f (x )的最小正周期是π，所以ω＝2. 又因为当x ＝π6时，f (x )取得最大值2.所以A ＝2，同时2×π6＋φ＝2k π＋π2，k ∈Z ，φ＝2k π＋π6，k ∈Z ，因为－π2<φ<π2，所以φ＝π6，所以f (x )＝2sin ⎝⎛⎭⎫2x ＋π6. (2)因为x ∈[0，π]，所以2x ＋π6∈⎣⎡⎦⎤π6，13π6， 列表如下：描点、连线得图像：引申探究在本例条件下，若将函数f (x )的图像向右平移m (m >0)个单位长度后得到函数y ＝g (x )的图像，且y ＝g (x )是偶函数，求m 的最小值.解 由已知得y ＝g (x )＝f (x －m )＝2sin ⎣⎡⎦⎤2(x －m )＋π6＝2sin ⎣⎡⎦⎤2x －⎝⎛⎭⎫2m －π6是偶函数，所以2m －π6＝π2(2k ＋1)，k ∈Z ，m ＝k π2＋π3，k ∈Z ，又因为m >0，所以m 的最小值为π3.思维升华 (1)y ＝A sin(ωx ＋φ)的图像可用“五点法”作简图得到，可通过变量代换z ＝ωx ＋φ计算五点坐标.(2)由函数y ＝sin x 的图像通过变换得到y ＝A sin(ωx ＋φ)的图像有两条途径：“先平移后伸缩”与“先伸缩后平移”.跟踪训练1 (1)若把函数y ＝sin ⎝⎛⎭⎫ωx －π6的图像向左平移π3个单位长度，所得到的图像与函数y ＝cos ωx 的图像重合，则ω的一个可能取值是( ) A.2 B.32 C.23 D.12答案 A解析 y ＝sin ⎝⎛⎭⎫ωx ＋ω3π－π6和函数y ＝cos ωx 的图像重合，可得ω3π－π6＝π2＋2k π，k ∈Z ，则ω＝6k ＋2，k ∈Z .∴2是ω的一个可能值.(2)已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π6(0<ω<2)满足条件：f ⎝⎛⎭⎫－12＝0，为了得到函数y ＝f (x )的图像，可将函数g (x )＝cos ωx 的图像向右平移m (m >0)个单位长度，则m 的最小值为( ) A.1 B.12 C.π6 D.π2答案 A解析 由题意得sin ⎝⎛⎭⎫－12ω＋π6＝0，即－12ω＋π6＝k π(k ∈Z )，则ω＝π3－2k π(k ∈Z )，结合0<ω<2，得ω＝π3，所以f (x )＝sin ⎝⎛⎭⎫π3x ＋π6＝cos ⎝⎛⎭⎫π2－π3x －π6＝cos ⎣⎡⎦⎤π3(x －1)，所以只需将函数g (x )＝cos π3x 的图像向右至少平移1个单位长度，即可得到函数y ＝f (x )的图像，故选A. 题型二 由图像确定y ＝A sin(ωx ＋φ)的解析式例2 (1)若函数y ＝A sin(ωx ＋φ)的部分图像如图所示，则y ＝ .答案 2sin ⎝⎛⎭⎫2x －π6解析 由题图可知，A ＝2，T ＝2⎣⎡⎦⎤π3－⎝⎛⎭⎫－π6＝π，所以ω＝2，由五点作图法可知2×π3＋φ＝π2，所以φ＝－π6，所以函数的解析式为y ＝2sin ⎝⎛⎭⎫2x －π6. (2)已知函数f (x )＝sin(ωx ＋φ) ⎝⎛⎭⎫ω>0，|φ|<π2的部分图像如图所示，则y ＝f ⎝⎛⎭⎫x ＋π6取得最小值时x 的集合为 .答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k π－π3，k ∈Z 解析 根据题干所给图像，周期T ＝4×⎝⎛⎭⎫7π12－π3＝π，故π＝2πω，∴ω＝2， 因此f (x )＝sin(2x ＋φ)，另外图像经过点⎝⎛⎭⎫7π12，0，代入有2×7π12＋φ＝π＋2k π(k ∈Z )， 再由|φ|<π2，得φ＝－π6，∴f (x )＝sin ⎝⎛⎭⎫2x －π6， ∴f ⎝⎛⎭⎫x ＋π6＝sin ⎝⎛⎭⎫2x ＋π6， 当2x ＋π6＝－π2＋2k π(k ∈Z )，即x ＝－π3＋k π(k ∈Z )时，y ＝f ⎝⎛⎭⎫x ＋π6取得最小值. 思维升华 y ＝A sin(ωx ＋φ)中φ的确定方法(1)代入法：把图像上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图像的最高点或最低点代入.(2)五点法：确定φ值时，往往以寻找“五点法”中的特殊点作为突破口.跟踪训练2 已知函数f (x )＝A sin(ωx ＋φ)＋B ⎝⎛⎭⎫A >0，ω>0，|φ|<π2的部分图像如图所示，将函数f (x )的图像向左平移m (m >0)个单位长度后，得到函数g (x )的图像关于点⎝⎛⎭⎫π3，32对称，则m的值可能为( )A.π6B.π2C.7π6D.7π12答案 D解析 依题意得⎩⎨⎧A ＋B ＝332，－A ＋B ＝－32，解得⎩⎪⎨⎪⎧A ＝3，B ＝32，T 2＝πω＝2π3－π6＝π2， 故ω＝2，则f (x )＝3sin(2x ＋φ)＋32. 又f ⎝⎛⎭⎫π6＝3sin ⎝⎛⎭⎫π3＋φ＋32＝332， 故π3＋φ＝π2＋2k π(k ∈Z )，即φ＝π6＋2k π(k ∈Z ). 因为|φ|<π2，故φ＝π6，所以f (x )＝3sin ⎝⎛⎭⎫2x ＋π6＋32. 将函数f (x )的图像向左平移m 个单位长度后得到g (x )＝3sin ⎝⎛⎭⎫2x ＋π6＋2m ＋32的图像，又函数g (x )的图像关于点⎝⎛⎭⎫π3，32对称，即h (x )＝3sin ⎝⎛⎭⎫2x ＋π6＋2m 的图像关于点⎝⎛⎭⎫π3，0对称，故3sin ⎝⎛⎭⎫2π3＋π6＋2m ＝0，即5π6＋2m ＝k π(k ∈Z )，故m ＝k π2－5π12(k ∈Z ).令k ＝2，则m ＝7π12.题型三 三角函数图像、性质的综合应用命题点1 图像与性质的综合问题例3 已知函数f (x )＝2sin(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2的部分图像如图所示，若f (0)＝3，且AB →·BC →＝π28－8，B ，C 分别为最高点与最低点.(1)求函数f (x )的递增区间；(2)若将f (x )的图像向左平移π6个单位长度，得到函数g (x )的图像，求函数g (x )在区间⎣⎡⎦⎤0，π2上的最大值和最小值.解 (1)由f (0)＝3，可得2sin φ＝3，即sin φ＝32. 又∵|φ|<π2，∴φ＝π3.由题意可知，AB →＝⎝⎛⎭⎫14T ，2，BC →＝⎝⎛⎭⎫12T ，－4， 则AB →·BC →＝T28－8＝π28－8，∴T ＝π.故ω＝2，∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π3. 由－π2＋2k π≤2x ＋π3≤π2＋2k π，k ∈Z ，解得－5π12＋k π≤x ≤π12＋k π，k ∈Z ，∴函数f (x )的递增区间为⎣⎡⎦⎤－5π12＋k π，π12＋k π，k ∈Z . (2)由题意将f (x )的图像向左平移π6个单位长度，得到函数g (x )的图像，∴g (x )＝f ⎝⎛⎭⎫x ＋π6 ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋π3 ＝2sin ⎝⎛⎭⎫2x ＋2π3. ∵x ∈⎣⎡⎦⎤0，π2， ∴2x ＋2π3∈⎣⎡⎦⎤2π3，5π3，sin ⎝⎛⎭⎫2x ＋2π3∈⎣⎡⎦⎤－1，32. ∴当2x ＋2π3＝2π3，即x ＝0时，sin ⎝⎛⎭⎫2x ＋2π3＝32，g (x )取得最大值3， 当2x ＋2π3＝3π2，即x ＝5π12时，sin ⎝⎛⎭⎫2x ＋2π3＝－1，g (x )取得最小值－2.命题点2 函数零点(方程根)问题例4 已知关于x 的方程2sin 2x －3sin 2x ＋m －1＝0在⎝⎛⎭⎫π2，π上有两个不同的实数根，则m 的取值范围是 . 答案 (－2，－1)解析 方程2sin 2x －3sin 2x ＋m －1＝0可转化为 m ＝1－2sin 2x ＋3sin 2x ＝cos 2x ＋3sin 2x ＝2sin ⎝⎛⎭⎫2x ＋π6，x ∈⎝⎛⎭⎫π2，π. 设2x ＋π6＝t ，则t ∈⎝⎛⎭⎫76π，136π， ∴题目条件可转化为m2＝sin t ，t ∈⎝⎛⎭⎫76π，136π有两个不同的实数根. ∴y ＝m2和y ＝sin t ，t ∈⎝⎛⎭⎫76π，136π的图像有两个不同交点，如图：由图像观察知，m2的取值范围是⎝⎛⎭⎫－1，－12， 故m 的取值范围是(－2，－1). 引申探究本例中，若将“有两个不同的实数根”改成“有实根”，则m 的取值范围是 . 答案 [－2,1)解析 由上例题知，m2的取值范围是⎣⎡⎭⎫－1，12， ∴－2≤m <1，∴m 的取值范围是[－2,1). 命题点3 三角函数模型例5 据市场调查，某种商品一年内每件出厂价在7千元的基础上，按月呈f (x )＝A sin(ωx ＋φ)＋B ⎝⎛⎭⎫A >0，ω>0，|φ|<π2的模型波动(x 为月份)，已知3月份达到最高价9千元，9月份价格最低，为5千元，则7月份的出厂价格为 元. 答案 6 000解析 作出函数简图如图：三角函数模型为y ＝A sin(ωx ＋φ)＋B ，由题意知A ＝12(9 000－5 000)＝2 000，B ＝7 000，T ＝2×(9－3)＝12， ∴ω＝2πT ＝π6.将(3,9 000)看成函数图像的第二个特殊点， 则有π6×3＋φ＝π2，∴φ＝0，故f (x )＝2 000sin π6x ＋7 000(1≤x ≤12，x ∈N ＋).∴f (7)＝2 000×sin7π6＋7 000＝6 000(元). 故7月份的出厂价格为6 000元.思维升华 (1)研究y ＝A sin(ωx ＋φ)的性质时可将ωx ＋φ视为一个整体，利用换元法和数形结合思想进行解题.(2)方程根的个数可转化为两个函数图像的交点个数.跟踪训练3 (1)已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，－π2≤φ≤π2的图像上的两个相邻的最高点和最低点的距离为22，且过点⎝⎛⎭⎫2，－12，则函数f (x )的解析式为 . 答案 f (x )＝sin ⎝⎛⎭⎫πx 2＋π6解析 根据已知两个相邻最高点和最低点的距离为22， 可得⎝⎛⎭⎫T 22＋(1＋1)2＝22，解得T ＝4，故ω＝2πT ＝π2，即f (x )＝sin ⎝⎛⎭⎫πx 2＋φ. 又函数图像过点⎝⎛⎭⎫2，－12， 故f (2)＝sin ⎝⎛⎭⎫π2×2＋φ＝－sin φ＝－12，又－π2≤φ≤π2，解得φ＝π6，故f (x )＝sin ⎝⎛⎭⎫πx 2＋π6. (2)若函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π6(ω>0)满足f (0)＝f ⎝⎛⎭⎫π3，且函数在⎣⎡⎦⎤0，π2上有且只有一个零点，则f (x )的最小正周期为 . 答案 π解析 ∵f (0)＝f ⎝⎛⎭⎫π3，∴x ＝π6是f (x )图像的一条对称轴，∴f ⎝⎛⎭⎫π6＝±1， ∴π6×ω＋π6＝π2＋k π，k ∈Z ， ∴ω＝6k ＋2，k ∈Z ， ∴T ＝π3k ＋1(k ∈Z ).又f (x )在⎣⎡⎦⎤0，π2上有且只有一个零点， ∴π6<T 4≤π2－π6， ∴2π3<T ≤4π3， ∴2π3<π3k ＋1≤4π3(k ∈Z )， ∴－112≤k <16，又∵k ∈Z ，∴k ＝0，∴T ＝π.三角函数图像与性质的综合问题例 (12分)已知函数f (x )＝23sin ⎝⎛⎭⎫x 2＋π4·cos ⎝⎛⎭⎫x 2＋π4－sin(x ＋π). (1)求f (x )的最小正周期；(2)若将f (x )的图像向右平移π6个单位长度，得到函数g (x )的图像，求函数g (x )在区间[0，π]上的最大值和最小值. 规范解答解 (1)f (x )＝23sin ⎝⎛⎭⎫x 2＋π4cos ⎝⎛⎭⎫x 2＋π4－sin(x ＋π)＝3cos x ＋sin x [3分] ＝2sin ⎝⎛⎭⎫x ＋π3，[5分] 于是T ＝2π1＝2π.[6分](2)由已知得g (x )＝f ⎝⎛⎭⎫x －π6＝2sin ⎝⎛⎭⎫x ＋π6，[8分] ∵x ∈[0，π]，∴x ＋π6∈⎣⎡⎦⎤π6，7π6， ∴sin ⎝⎛⎭⎫x ＋π6∈⎣⎡⎦⎤－12，1，[10分] ∴g (x )＝2sin ⎝⎛⎭⎫x ＋π6∈[－1,2].[11分] 故函数g (x )在区间[0，π]上的最大值为2，最小值为－1.[12分]解决三角函数图像与性质的综合问题的一般步骤 第一步：(化简)将f (x )化为a sin x ＋b cos x 的形式； 第二步：(用辅助角公式)构造f (x )＝a 2＋b 2· ⎝⎛⎭⎪⎫sin x ·a a 2＋b 2＋cos x ·b a 2＋b 2； 第三步：(求性质)利用f (x )＝a 2＋b 2sin(x ＋φ)研究三角函数的性质.1.为了得到函数y ＝sin ⎝⎛⎭⎫2x －π6的图像，可以将函数y ＝sin 2x 的图像( ) A.向右平移π6个单位长度B.向右平移π12个单位长度C.向左平移π6个单位长度D.向左平移π12个单位长度答案 B解析 y ＝sin ⎝⎛⎭⎫2x －π6＝sin 2⎝⎛⎭⎫x －π12，故将函数y ＝sin 2x 的图像向右平移π12个单位长度，可得y ＝sin ⎝⎛⎭⎫2x －π6的图像.2.(2018·洛阳统考)若将函数f (x )＝sin 2x ＋cos 2x 的图像向右平移φ个单位长度，所得图像关于y 轴对称，则φ的最小正值是( ) A.π8 B.π4 C.3π8 D.5π4答案 C解析 f (x )＝sin 2x ＋cos 2x ＝2cos ⎝⎛⎭⎫2x －π4，将函数f (x )的图像向右平移φ个单位长度后所得图像对应的函数为y ＝2cos ⎝⎛⎭⎫2x －π4－2φ，且该函数为偶函数， 故2φ＋π4＝k π(k ∈Z )，所以φ的最小正值为3π8.3.(2019·合肥模拟)函数f (x )＝cos ⎝⎛⎭⎫ωx ＋π6(ω>0)的最小正周期是π，则其图像向右平移π3个单位长度后对应函数的递减区间是( ) A.⎣⎡⎦⎤－π4＋k π，π4＋k π(k ∈Z ) B.⎣⎡⎦⎤π4＋k π，3π4＋k π(k ∈Z ) C.⎣⎡⎦⎤π12＋k π，7π12＋k π(k ∈Z ) D.⎣⎡⎦⎤－5π12＋k π，π12＋k π(k ∈Z ) 答案 B解析 由题意知ω＝2ππ＝2，将函数f (x )的图像向右平移π3个单位长度后得到函数g (x )＝cos ⎣⎡⎦⎤2⎝⎛⎭⎫x －π3＋π6＝cos ⎝⎛⎭⎫2x －π2＝sin 2x 的图像，由2k π＋π2≤2x ≤2k π＋3π2(k ∈Z )，解得所求函数的递减区间为⎣⎡⎦⎤k π＋π4，k π＋3π4 (k ∈Z ). 4.函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2的部分图像如图所示，则f (x )的递增区间为( )A.[－1＋4k π，1＋4k π](k ∈Z )B.[－3＋8k π，1＋8k π](k ∈Z )C.[－1＋4k ，1＋4k ](k ∈Z )D.[－3＋8k ，1＋8k ](k ∈Z ) 答案 D解析 由题图知，T ＝4×(3－1)＝8，所以ω＝2πT ＝π4，所以f (x )＝sin ⎝⎛⎭⎫π4x ＋φ.把(1,1)代入，得sin ⎝⎛⎭⎫π4＋φ＝1，即π4＋φ＝π2＋2k π(k ∈Z )，又|φ|<π2，所以φ＝π4，所以f (x )＝sin ⎝⎛⎭⎫π4x ＋π4.由2k π－π2≤π4x ＋π4≤2k π＋π2(k ∈Z )，得8k －3≤x ≤8k ＋1(k ∈Z )，所以函数f (x )的递增区间为[8k －3,8k ＋1](k ∈Z ).5.将函数f (x )＝3sin x －cos x 的图像沿着x 轴向右平移a (a >0)个单位长度，所得函数图像关于y 轴对称，则a 的最小值是( ) A.π6 B.π3 C.π2 D.2π3 答案 B解析 依题意得f (x )＝2sin ⎝⎛⎭⎫x －π6， 因为函数f (x －a )＝2sin ⎝⎛⎭⎫x －a －π6的图像关于y 轴对称， 所以sin ⎝⎛⎭⎫－a －π6＝±1，a ＋π6＝k π＋π2，k ∈Z ， 即a ＝k π＋π3，k ∈Z ，又a >0，所以a ＝k π＋π3，k ∈N .因此正数a 的最小值是π3，故选B.6.将函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎫|φ|<π2的图像向左平移π6个单位长度后关于原点对称，则函数f (x )在⎣⎡⎦⎤0，π2上的最小值为( )A.－32B.－12C.12D.32答案 A解析 将函数f (x )＝sin(2x ＋φ)的图像向左平移π6个单位长度得到y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋φ＝sin ⎝⎛⎭⎫2x ＋π3＋φ的图像，该图像关于原点对称，即为奇函数，则π3＋φ＝k π(k ∈Z )，又|φ|<π2，所以φ＝－π3，即f (x )＝sin ⎝⎛⎭⎫2x －π3.当x ∈⎣⎡⎦⎤0，π2时，2x －π3∈⎣⎡⎦⎤－π3，2π3，所以当2x －π3＝－π3，即x ＝0时，f (x )取得最小值，最小值为－32. 7.已知函数f (x )＝A tan(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2的部分图像如图所示，则f ⎝⎛⎭⎫π24＝ .答案3解析 由题干图像知πω＝2×⎝⎛⎭⎫3π8－π8＝π2， 所以ω＝2.因为2×π8＋φ＝k π＋π2(k ∈Z )，所以φ＝k π＋π4(k ∈Z )，又|φ|<π2，所以φ＝π4，这时f (x )＝A tan ⎝⎛⎭⎫2x ＋π4. 又函数图像过点(0,1)，代入上式得A ＝1，所以f (x )＝tan ⎝⎛⎭⎫2x ＋π4. 所以f ⎝⎛⎭⎫π24＝tan ⎝⎛⎭⎫2×π24＋π4＝ 3. 8.已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2的部分图像如图所示，又x 1，x 2∈⎝⎛⎭⎫－π6，π3，且f (x 1)＝f (x 2)，则f (x 1＋x 2)＝ .答案32解析 由题图可知，T 2＝π3－⎝⎛⎭⎫－π6＝π2，则T ＝π，ω＝2，又－π6＋π32＝π12，所以f (x )的图像过点⎝⎛⎭⎫π12，1， 即sin ⎝⎛⎭⎫2×π12＋φ＝1， 所以2×π12＋φ＝π2＋2k π，k ∈Z ，又|φ|<π2，可得φ＝π3，所以f (x )＝sin ⎝⎛⎭⎫2x ＋π3. 由f (x 1)＝f (x 2)，x 1，x 2∈⎝⎛⎭⎫－π6，π3， 可得x 1＋x 2＝－π6＋π3＝π6，所以f (x 1＋x 2)＝f ⎝⎛⎭⎫π6＝sin ⎝⎛⎭⎫2×π6＋π3 ＝sin 2π3＝32.9.(2018·洛阳模拟)已知函数f (x )＝cos ⎝⎛⎭⎫3x ＋π3，其中x ∈⎣⎡⎦⎤π6，m ，若f (x )的值域是⎣⎡⎦⎤－1，－32，则m 的取值范围是 . 答案 ⎣⎡⎦⎤2π9，5π18解析 画出函数的图像如图所示.由x ∈⎣⎡⎦⎤π6，m ，可知5π6≤3x ＋π3≤3m ＋π3， 因为f ⎝⎛⎭⎫π6＝cos 5π6＝－32且f ⎝⎛⎭⎫2π9＝cos π＝－1，要使f (x )的值域是⎣⎡⎦⎤－1，－32，只要2π9≤m ≤5π18，即m ∈⎣⎡⎦⎤2π9，5π18. 10.已知函数f (x )＝sin ωx ＋cos ωx (ω>0)，x ∈R .若函数f (x )在区间(－ω，ω)内是增加的，且函数y ＝f (x )的图像关于直线x ＝ω对称，则ω的值为 . 答案π2解析 f (x )＝sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π4， 因为f (x )在区间(－ω，ω)内是增加的，且函数图像关于直线x ＝ω对称， 所以f (ω)必为一个周期上的最大值， 所以有ω·ω＋π4＝2k π＋π2，k ∈Z ，所以ω2＝π4＋2k π，k ∈Z .又ω－(－ω)≤2πω2，即ω2≤π2，即ω2＝π4，所以ω＝π2. 11.已知函数f (x )＝2sin ⎝⎛⎭⎫2ωx ＋π6(其中0<ω<1)，若点⎝⎛⎭⎫－π6，0是函数f (x )图像的一个对称中心. (1)求ω的值，并求出函数f (x )的递增区间； (2)先列表，再作出函数f (x )在区间[－π，π]上的图像. 解 (1)因为点⎝⎛⎭⎫－π6，0是函数f (x )图像的一个对称中心， 所以－ωπ3＋π6＝k π(k ∈Z )，ω＝－3k ＋12(k ∈Z )，因为0<ω<1，所以当k ＝0时，可得ω＝12.所以f (x )＝2sin ⎝⎛⎭⎫x ＋π6. 令2k π－π2≤x ＋π6≤2k π＋π2(k ∈Z )，解得2k π－2π3≤x ≤2k π＋π3(k ∈Z )，所以函数的递增区间为⎣⎡⎦⎤2k π－2π3，2k π＋π3(k ∈Z ). (2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫x ＋π6，x ∈[－π，π]，列表如下：作出函数部分图像如图所示：12.(2017·山东)设函数f (x )＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2，其中0<ω<3.已知f ⎝⎛⎭⎫π6＝0. (1)求ω；(2)将函数y ＝f (x )的图像上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图像向左平移π4个单位长度，得到函数y ＝g (x )的图像，求g (x )在⎣⎡⎦⎤－π4，3π4上的最小值. 解 (1)因为f (x )＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2， 所以f (x )＝32sin ωx －12cos ωx －cos ωx ＝32sin ωx －32cos ωx ＝3⎝⎛⎭⎫12sin ωx －32cos ωx＝3sin ⎝⎛⎭⎫ωx －π3. 由题设知f ⎝⎛⎭⎫π6＝0， 所以ωπ6－π3＝k π，k ∈Z ，故ω＝6k ＋2，k ∈Z .又0<ω<3， 所以ω＝2.(2)由(1)得f (x )＝3sin ⎝⎛⎭⎫2x －π3，所以g (x )＝3sin ⎝⎛⎭⎫x ＋π4－π3＝3sin ⎝⎛⎭⎫x －π12. 因为x ∈⎣⎡⎦⎤－π4，3π4， 所以x －π12∈⎣⎡⎦⎤－π3，2π3， 当x －π12＝－π3，即x ＝－π4时，g (x )取得最小值－32.13.将函数f (x )＝sin(2x ＋θ)⎝⎛⎭⎫－π2<θ<π2的图像向右平移φ(0<φ<π)个单位长度后，得到函数g (x )的图像，若f (x )，g (x )的图像都经过点P ⎝⎛⎭⎫0，32，则φ的值为 . 答案5π6解析 g (x )＝sin [2(x －φ)＋θ]＝sin(2x －2φ＋θ)， 若f (x )，g (x )的图像都经过点P ⎝⎛⎭⎫0，32， 所以sin θ＝32，sin(－2φ＋θ)＝32， 又－π2<θ<π2，所以θ＝π3，sin ⎝⎛⎭⎫π3－2φ＝32. 又0<φ<π，所以－5π3<π3－2φ<π3，所以π3－2φ＝－4π3.即φ＝5π6.14.(2018·郑州模拟)已知函数f (x )＝3sin ωx ＋cos ωx (ω>0)，x ∈R .在曲线y ＝f (x )与直线y ＝1的交点中，若相邻交点距离的最小值为π3，则f (x )的最小正周期为 .答案 π解析 f (x )＝3sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π6(ω>0). 由2sin ⎝⎛⎭⎫ωx ＋π6＝1， 得sin ⎝⎛⎭⎫ωx ＋π6＝12， ∴ωx ＋π6＝2k π＋π6或ωx ＋π6＝2k π＋5π6(k ∈Z ). 令k ＝0，得ωx 1＋π6＝π6，ωx 2＋π6＝5π6， ∴x 1＝0，x 2＝2π3ω. 由|x 1－x 2|＝π3， 得2π3ω＝π3，∴ω＝2. 故f (x )的最小正周期T ＝2π2＝π.15.已知函数y ＝M sin(ωx ＋φ)(M >0，ω>0,0<φ<π)的图像关于直线x ＝13对称.该函数的部分图像如图所示，AC ＝BC ＝22，C ＝90°，则f ⎝⎛⎭⎫12的值为 .答案 34解析 依题意知，△ABC 是直角边长为22的等腰直角三角形，因此其边AB 上的高是12，函数f (x )的最小正周期是2，故M ＝12，2πω＝2，ω＝π，f (x )＝12sin(πx ＋φ). 又f (x )的图像关于直线x ＝13对称， ∴f ⎝⎛⎭⎫13＝12sin ⎝⎛⎭⎫π3＋φ＝±12. ∴π3＋φ＝k π＋π2，k ∈Z ，又0<φ<π， ∴φ＝π6，∴f (x )＝12sin ⎝⎛⎭⎫πx ＋π6，∴f ⎝⎛⎭⎫12＝12sin ⎝⎛⎭⎫π2＋π6＝34.16.已知函数f (x )＝A sin(2x ＋φ)－12⎝⎛⎭⎫A >0，0<φ<π2的图像在y 轴上的截距为1，且关于直线x ＝π12对称，若存在x ∈⎣⎡⎦⎤0，π2，使m 2－3m ≥f (x )成立，则实数m 的取值范围为 . 答案 (－∞，1]∪[2，＋∞)解析 ∵函数f (x )＝A sin(2x ＋φ)－12⎝⎛⎭⎫A >0，0<φ<π2的图像在y 轴上的截距为1， ∴A sin φ－12＝1， 即A sin φ＝32. ∵函数f (x )＝A sin(2x ＋φ)－12的图像关于直线x ＝π12对称， ∴2×π12＋φ＝k π＋π2，k ∈Z ， 又0<φ<π2，∴φ＝π3， ∴A ·sin π3＝32， ∴A ＝3，∴f (x )＝3sin ⎝⎛⎭⎫2x ＋π3－12. 当x ∈⎣⎡⎦⎤0，π2时，2x ＋π3∈⎣⎡⎦⎤π3，4π3， ∴当2x ＋π3＝4π3， 即x ＝π2时，f (x )min ＝－32－12＝－2. 令m 2－3m ≥－2，解得m ≥2或m ≤1.。

图1高三理科数学综合训练题（2014.2）一、选择题：本大题共8个小题；每小题5分，共40分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1.已知集合{2,0,1,4}A =，{04,R}=<≤∈B x x x ，C A B = ．则集合C 可表示为A ．{2,0,1,4}B ． {1,2,3,4}C ．{1,2,4}D ． {04,R}x x x <≤∈2.复数z 满足(1i)1z -=（其中i 为虚数单位），则z =A ．11i 22- B ．11i 22+ C ．11i 22-+ D ．11i 22--3．下列函数中，为奇函数的是A ．122x x y =+B ．{},0,1y x x =∈C ．sin y x x =⋅D ．1,00,01,0x y x x <⎧⎪==⎨⎪->⎩4．“1ω=”是“ 函数()cos f x x ω=在区间[]0,π上单调递减”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．执行如图1所示的程序框图，则输出的a 的值为 （注：“2a =”，即为“2a ←”或为“:2a =”．） A ．2 B ．13C ．12- D ．3-6．412x x -(的展开式中常数项为A ．12B ．12-C ．32D ．32-7．如图2，在矩形OABC 内：记抛物线21y x =+与直线1y x =+ 围成的区域为M （图中阴影部分）．随机往矩形OABC 内投一点P ，则点P 落在区域M 内的概率是 A ．118 B ．112C ．16 D ．1311+8.在平面直角坐标系中，定义两点11(,)P x y 与22(,)Q x y 之间的“直角距离”为1212(,)d P Q x x y y =-+-．给出下列命题：（1）若(1,2)P ，(sin ,2cos )()Q R ααα∈，则(,)d P Q的最大值为3 （2）若,P Q 是圆221x y +=上的任意两点，则(,)d P Q的最大值为 (3) 若(1,3)P ，点Q 为直线2y x =上的动点，则(,)d P Q 的最小值为12． 其中为真命题的是 A ．（1）（2）（3） B ．（1）（2） C ．（1）(3) D ． (2)(3)二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．本大题分为必做题和选做题两部分．（一）必做题：第9、10、11、12、13题为必做题，每道试题考生都必须作答． 9．函数f x ()的定义域为 ．10．某几何体的三视图如图3所示，其正视图是边长为2的正方形，侧视图和俯视图都是等腰直角三角形，则此几何体的体积是 ．11.已知双曲线2222:1x y C a b -=与椭圆22194x y +=有相同的焦点，且双曲线C 的渐近线方程为2y x =±，则双曲线C 的方程为 ．12. 设实数,x y 满足,102,1,x y y x x ≤⎧⎪≤-⎨⎪≥⎩向量2,x y m =-()a ，1,1=-()b ．若// a b ，则实数m 的最大值为 ．13.在数列{}n a 中，已知24a =， 315a =，且数列{}n a n +是等比数列，则n a = ． （二）选做题：第14、15题为选做题，只能选做一题，两题全答的，只计算前一题的得分． 14.（坐标系与参数方程选做题）在直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．若曲线1C 的参数方程为,x t y =⎧⎪⎨=⎪⎩（t 为参数），曲线2C 的极坐标方程为sin cos 1ρθρθ-=-．则曲线1C 与曲线2C 的交点个数为________个．图415．（几何证明选讲选做题）如图4，已知AB 是⊙O 的直径，TA是⊙O 的切线，过A 作弦//AC BT ，若4AC =，AT =，则AB = ．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分12分）已知函数()sin(2)(0π)f x x ϕϕ=+<<的图像经过点π(,1)12． （1）求ϕ的值；（2）在ABC ∆中，A ∠、B ∠、C ∠所对的边分别为a 、b 、c ，若222a b c ab +-=，且π()2122A f +=．求sin B ． 17.（本小题满分12分）某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天60名网友的网购金额情况，得到如下数据统计表（如图5（1））：若网购金额超过2千元的顾客定义为“网购达人”，网购金额不超过2千元的顾客定 义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为3:2．（1）试确定x ，y ，p ，q 的值，并补全频率分布直方图（如图5(2)）．（2）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购 达人”中用分层抽样的方法确定10人，若需从这10人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．图5(1) (2)18．（本小题满分14分）如图6所示，平面ABCD ⊥平面BCEF ，且四边形ABCD 为矩形，四边形BCEF 为直角梯形，//BF CE ， BC CE ⊥，4DC CE ==，2BC BF ==．（1）求证：//AF 平面CDE ； （2）求平面ADE 与平面BCEF 所成锐二面角的余弦值； （3）求直线EF 与平面ADE 所成角的余弦值．19.（本小题满分14分）已知数列{}n a 的前n 项和为n S ，且满足24(1)(1)(2)(N )n n n S n a n *++=+∈． （1）求1a ，2a 的值； （2）求n a ； （3）设1n nn b a +=，数列{}n b 的前n 项和为n T ，求证：34n T <．AD BC FE图620.（本小题满分14分）如图7，直线:(0)l y x b b =+>，抛物线2:2(0)C y px p =>，已知点(2,2)P 在抛物线C 上，且抛物线C 上的点到直线l 的距离的最小（1）求直线l 及抛物线C 的方程；（2）过点(2,1)Q 的任一直线（不经过点P ）与抛物线C 交于A 、B 两点，直线AB 与直线l 相交于点M ，记直线PA ，PB ，PM 的斜率分别为1k ，2k ， 3k ．问：是否存在实数λ，使得123k k k λ+=？若存在，试求出λ的值；若不存在，请说明理由．21．（本小题满分14分）已知函数2901xf x a ax =>+()() ．（1）求f x ()在122[,]上的最大值；（2）若直线2y x a =-+为曲线y f x =()的切线，求实数a 的值；（3）当2a =时，设1214122x x x ,⎡⎤∈⎢⎥⎣⎦…,,, ，且121414x x x =…+++ ，若不等式1214f x f x +f x λ≤…()+()+()恒成立，求实数λ的最小值．图7yM PBQxAOl参考答案一、选择题：本大题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案CBDADCBA二、填空题：本大题共6小题，每小题5分，共30分．9．{2}x x ≥；10．83；11．2214y x -=；12．6；13．123n n -⋅-；14．1；15．．三、解答题：本大题共6小题，共80分．16．（本小题满分12分） （1）由题意可得π()112f =，即πsin()16ϕ+=．……………………………2分 0πϕ<< ，ππ7π666ϕ∴<+<， ππ62ϕ∴+=， π3ϕ∴=．……………5分 （2）222a b c ab +-= ， 2221cos 22a b c C ab +-∴==，………………………7分sin C ∴==．………………………………8分 由（1）知π()sin(2)3f x x =+，π(+)sin()cos 2122A f A A π∴=+==()0,A π∈ ，sin 2A ∴==，……………………10分 又sin sin(π())sin()B A C A C =-+=+ ，1sin sin cos cos sin 22224B AC A C ∴=+=+=．…………12分 17．（本小题满分12分）（1）根据题意，有39151860,182.39153x y y x +++++=⎧⎪⎨=⎪+++⎩+解得9,6.x y =⎧⎨=⎩………………2分0.15p ∴=，0.10q =．补全频率分布直方图如图所示．………………4分（2）用分层抽样的方法，从中选取10人，则其中“网购达人”有210=45⨯人，“非网购达人”有310=65⨯人．……………6分 故ξ的可能取值为0，1，2，3；03463101(0)6C C P C ξ=== ， 12463101(1)2C C P C ξ===，21463103(2)10C C P C ξ===，30463101(3)30C C P C ξ===．……………10分所以ξ的分布列为：01236210305E ξ∴=⨯+⨯+⨯+⨯=．……………………………12分18．（本小题满分14分）（解法一）（1）取CE 中点为G ，连接DG 、FG ， //BF CG 且BF CG =，∴四边形BFGC 为平行四边形，则//BC FG 且BC FG =． ……………2分 四边形ABCD 为矩形， //BC AD ∴且BC AD =，//FG AD ∴且FG AD =，∴四边形AFGD 为平行四边形，则//AF DG ．DG ⊂ 平面CDE ，AF ⊄平面CDE ， //AF ∴平面CDE ．…………………………4分（2）过点E 作CB 的平行线交BF 的延长线于P ，连接FP ，EP ，AP ，////EP BC AD ， ∴A ，P ，E ，D 四点共面．四边形BCEF 为直角梯形，四边形ABCD 为矩形，∴EP CD ⊥，EP CE ⊥，又 CD CE C = ，EP ∴⊥平面CDE ，∴EP DE ⊥， 又 平面ADE 平面BCEF EP =，∴DEC ∠为平面ADE 与平面BCEF 所成锐二面角的平面角．……………7分4DC CE ==，∴cos CE DEC DE ∠==．即平面ADE 与平面BCEF 9分 （3）过点F 作FH AP ⊥于H ，连接EH ，根据（2）知A ，P ，E ，D 四点共面，////EP BC AD ，∴BC BF ⊥，BC AB ⊥， 又 AB BF B = ， BC ∴⊥平面ABP ，∴BC FH ⊥，则FH EP ⊥． 又 FH AP ⊥， FH ∴⊥平面ADE ．∴直线EF 与平面ADE 所成角为HEF ∠．……11分4DC CE ==，2BC BF ==，∴0sin 45FH FP ==EF =HE ，∴cos HE HEF EF ∠===．即直线EF 与平面ADE 14分 （解法二）（1） 四边形BCEF 为直角梯形，四边形ABCD 为矩形，∴BC CE ⊥，BC CD ⊥，又 平面ABCD ⊥平面BCEF ，且平面ABCD 平面BCEF BC =，DC ∴⊥平面BCEF ．以C 为原点，CB 所在直线为x 轴，CE 所在直线为y 轴，CD 所在直线为z 轴建立坐标系．根据题意我们可得以下点的坐标：(2,0,4)A ，(2,0,0)B ，(0,0,0)C ，(0,0,4)D ，(0,4,0)E ，(2,2,0)F ， 则(0,2,4)AF =- ，(2,0,0)CB =．………………………2分BC CD ⊥ ，BC CE ⊥， CB ∴为平面CDE 的一个法向量．又0220(4)00AF CB ⋅=⨯+⨯+-⨯=，//AF ∴平面CDE ． ……………4分（2）设平面ADE 的一个法向量为1111(,,)n x y z = ，则110,0.AD n DE n ⎧⋅=⎪⎨⋅=⎪⎩(2,0,0)AD =- ，(0,4,4)DE =- ，∴11120440x y z -=⎧⎨-=⎩，取11z =，得1(0,1,1)n =． ……6分DC ⊥ 平面BCEF ，∴平面BCEF 一个法向量为(0,0,4)CD =，设平面ADE 与平面BCEF 所成锐二面角的大小为α，则11cos CD n CD n α⋅===⋅ ． 因此，平面ADE 与平面BCEF……………9分 （3）根据（2）知平面ADE 一个法向量为1(0,1,1)n =，(2,2,0)EF =-，1111cos ,2EF n EF n EF n ⋅∴<>===-⋅， ……………………12分 设直线EF 与平面ADE 所成角为θ，则1cos sin ,EF n θ=<>=因此，直线EF 与平面ADE． ……………14分 19．（本小题满分14分）（1）当=1n 时，有2114(11)(+1=1+2a a ⨯+）（），解得1=8a ．当=2n 时，有21224(21)(1)(22)a a a ⨯+++=+，解得2=27a ．………………2分（2）（法一）当2n ≥时，有2(2)4(1)1nn n a S n ++=+, ……………①211(1)4(1)n n n a S n--++=． …………………② ①—②得：221(2)(1)41n n n n a n a a n n -++=-+，即：331(1)=n n a n a n-+．……………5分 ∴1223333===1(1)(1)3n n n a a a a n n n --==+-…．∴ 3=(1)n a n +(2)n ≥． ……………8分 另解：33333121333121(1)42(1)(1)3n n n n n a a a n n a a n a a a n n ---+=⋅⋅⋅⋅=⋅⋅⋅⋅=+- ． 又 当=1n 时，有1=8a ， ∴3=(1)n a n +．………………………8分（法二）根据1=8a ，2=27a ，猜想：3=(1)n a n +． ……………………………3分用数学归纳法证明如下：（Ⅰ）当1n =时，有318(11)a ==+，猜想成立． （Ⅱ）假设当n k =时，猜想也成立，即：3=(1)k a k +．那么当1n k =+时，有2114(11)(1)(12)k k k S k a +++++=++，即：211(12)4(1)11k k k a S k +++++=++，………………………①又 2(2)4(1)1kk k a S k ++=+， …………………………②①-②得：22223111(3)(2)(3)(2)(1)4=2121k k k k k a k a k a k k a k k k k ++++++++=--++++，解得33+1(2)(11)k a k k =+=++．∴当1n k =+时，猜想也成立．因此，由数学归纳法证得3=(1)n a n +成立．………………………………8分 （3） 211111=(1(11n n n b a n n n n n +=<=-+++))， …………………………10分 ∴1231=n n n T b b b b b -+++++…2222211111=234(1)n n ++++++…211111<22323(1)(1)n n n n +++++⨯⨯-+ (11111)1111=()()()()4233411n n n n +-+-++-+--+ (1113)=4214n +-<+．…………14分 20．（本小题满分14分）（1）（法一） 点(2,2)P 在抛物线C 上， 1p ∴=． …………………2分设与直线l 平行且与抛物线C 相切的直线l '方程为y x m =+，由2,2,y x m y x =+⎧⎨=⎩ 得22(22)0x m x m +-+=， 22(22)448m m m ∆=--=- ， ∴由0∆=，得12m =，则直线l '方程为12y x =+．两直线l 、l '间的距离即为抛物线C 上的点到直线l 的最短距离，∴4=，解得2b =或1b =-（舍去）．∴直线l 的方程为2y x =+，抛物线C 的方程为22y x =． ………………6分（法二） 点(2,2)P 在抛物线C 上， 1p ∴=，抛物线C 的方程为22y x =．…2分设2(,))2t M t t R ∈（为抛物线C 上的任意一点，点M 到直线l 的距离为d =根据图象，有202t t b -+>，21)21]d t b ∴=-+-，t R ∈ ，d ∴4=，解得2b =． 因此，直线l 的方程为2y x =+，抛物线C 的方程为22y x =．……………6分 （2） 直线AB 的斜率存在，∴设直线AB 的方程为1(2)y k x -=-，即21y kx k =-+，由221,2,y kx k y x =-+⎧⎨=⎩ 得22420ky y k --+=， 设点A 、B 的坐标分别为11(,)A x y 、22(,)B x y ，则122y y k +=，1224k y y k-=， 11121112222222y y k y x y --===-+- ，2222k y =+， ……………………9分 121212121222+82()82242242222()4324y y k k k k k y y y y y y k k⋅+++∴+=+===-++++++⋅+.……10分 由21,2,y kx k y x =-+⎧⎨=+⎩ 得211M k x k +=-，411M k y k -=-，∴341221121321k k k k k k --+-==+--， ………13分 1232k k k ∴+=．因此，存在实数λ，使得123k k k λ+=成立，且2λ=．……14分21．（本小题满分14分）（1）2222229[1(1)2]9(1)()(1)(1)ax x ax ax f x ax ax ⋅+-⋅-'==++，………………………………2分 令()0f x '=，解得x =（负值舍去），由122<<，解得144a <<．（ⅰ）当104a <≤时，由1[,2]2x ∈，得()0f x '≥，∴()f x 在1[,2]2上的最大值为18(2)41f a =+．………………………3分（ⅱ）当4a ≥时，由1[,2]2x ∈，得()0f x '≤，∴()f x 在1[,2]2上的最大值为118()24f a =+．…………………4分（ⅲ）当144a <<时， 在12x a <<时，()0f x '>，在2x a<<时，()0f x '<，∴()f x 在1[,2]2上的最大值为=2f a a（）5分 （2）设切点为(,())t f t ，则()1,()2.f t f t t a '=-⎧⎨=-+⎩…………………………………6分由()1f t '=-，有2229[1]1(1)at at -=-+，化简得2427100a t at -+=， 即22at =或25at =， ……………………………① 由()2f t t a =-+，有2921ta t at=-+，……………②由①、②解得2a =或4a =． ………………………9分（3）当2a =时，29()12xf x x =+，由（2）的结论直线4y x =-为曲线()y f x =的切线，(2)2f = ，∴点(2,(2))f 在直线4y x =-上，根据图像分析，曲线()y f x =在直线4y x =-下方． ……………10分 下面给出证明：当1[,2]2x ∈时，()4f x x ≤-．3222928104()(4)41212x x x x f x x x x x -+---=-+=++ 2221(2)12x x x --=+（），∴当1[,2]2x ∈时，()(4)0f x x --≤，即()4f x x ≤-．………………12分∴12141214()()()414()f x f x f x x x x +++≤⨯-+++ ，121414x x x +++= ， 1214()()()561442f x f x f x ∴+++≤-= ．∴要使不等式1214()()()f x f x f x λ+++≤ 恒成立，必须42λ≥．…………13分又 当12141x x x ==== 时，满足条件121414x x x +++= ，且1214()()()42f x f x f x +++= ，因此，λ的最小值为42．………………14分。

2013届高三第一学期理科数学综合训练题四一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1.若复数2(32)(1)a a a i -++-是纯虚数，则实数a 的值为( )A. 1B. 2C. 1或2D. -1 2.已知向量(1,1),2(4,2)=+=a a b ，则向量,a b 的夹角的余弦值为( )B. -2D. 2-3．若110lg lg lg lg 1092=++++x x x x ，则x x x x 1092lg lg lg lg ++++ 的值是( ) A ．1022 B ．1024C ．2046D ．20484．圆C 关于直线:210l x y -+=对称且圆心在x 轴上，圆C 与y 轴相切，则圆C 的方程为( ) A ．1)1(22=+-y x B ．1)1(22=++y xC ．41)21(22=-+y x D ．41)21(22=++y x5．若m 、n 为两条不重合的直线，α、β为两个不重合的平面，则下列命题中的真命题个数是( )①若m 、n 都平行于平面α，则m 、n 一定不是相交直线； ②若m 、n 都垂直于平面α，则m 、n 一定是平行直线； ③已知α、β互相垂直，m 、n 互相垂直，若α⊥m ，则β⊥n ； ④m 、n 在平面α内的射影互相垂直，则m 、n 互相垂直．A ．1B ．2C ．3D ．46．已知函数2221,0()21,0x x x f x x x x ⎧+-≥=⎨--<⎩，则对任意12,x x R ∈，若120x x <<，下列不等式成立的是( )A. 12()()0f x f x +<B. 12()()0f x f x +>C. 12()()0f x f x ->D. 12()()0f x f x -<7．学校准备从5位报名同学中挑选3人，分别担任2011年世界大学生运动会田径、游泳和球类3个不同项目比赛的志愿者，已知其中同学甲不能担任游泳比赛的志愿者，则不同的安排方法共有( )A ．24种B ．36种C ．48种D ．60种8.设},,20,20|),{(R ∈<<<<=c a c a c a A ，则任取A c a ∈),(，关于x 的方程022=++c x ax 有实根的概率为( )A ．22ln 1+ B ．22ln 1- C ．42ln 21+ D ．42ln 23-二、填空题：本大题共6小题，每小题5分，满分30分．9.已知命题“,|||1|2x R x a x ∃∈-++≤”是假命题，则实数a 的取值范围是____ ____. 10．在等比数列{}n a 中，首项=1a 32，()44112a x dx =+⎰，则公比q 为 ．11．如图1，已知一个锥体的正视图（也称主视图），左视图（也称侧视图）和俯视图均为直角三角形， 且面积分别为3，4，6，则该锥体的体积是 ．12.在二项式52a x x ⎛⎫- ⎪⎝⎭的展开式中， x 的一次项系数是10-，则实数a 的值为 ．13．定义在R 上的奇函数()f x 满足(3)(f x f x -=+，且(1)f =，则(2011)(f f -= ． 14. 给出如图所示的程序框图，那么输出的数是________．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 15．（本小题满分12分）某种项目的射击比赛，开始时在距目标100m 处射击，如果命中记6分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已经在150m 处，这时命中记3分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已经在200m 处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分，且不再继续射击．已知射手甲在100m 处击中目标的概率为12，他的命中率与其距目标距离的平方成反比，且各次射击是否击中目标是相互独立的．（1）分别求这名射手在150m 处、200m 处的命中率；（2）设这名射手在比赛中得分数为ξ，求随机变量ξ的分布列和数学期望．正视图 左视图图116.（本题满分12分）已知函数()sin()f x A x ωϕ=+(0,0,,)2A x ωϕπ>><∈R 的图象的一部分如下图所示.（1）求函数()f x 的解析式;（2）当2[6,]3x ∈--时,求函数()(2)y f x f x =++的最大值与最小值及相应的x 的值.17.（本题满分14分）已知椭圆C ：)0( 12222>>=+b a by ax的离心率为23，过坐标原点O 且斜率为21的直线l 与C 相交于A 、B ，102||=AB ．（1）求a 、b 的值；（2）若动圆1)(22=+-y m x 与椭圆C 和直线 l 都没有公共点，试求m 的取值范围．18、（本小题满分14分）如图，AC 是圆O 的直径，点B 在圆O 上，︒=∠30BAC ，AC BM ⊥交AC 于点M ，⊥EA 平面ABC ，EA FC //，134===FC EA AC ，，． （1）证明：BF EM ⊥；（2）求平面BEF 与平面ABC 所成的锐二面角的余弦值．E19．（本小题满分14分）平面直角坐标系中，已知直线l :4=x ，定点)0,1(F ，动点),(y x P 到直线l 的距离是到定点F 的距离的2倍.（1）求动点P 的轨迹C 的方程；（2）若M 为轨迹C 上的点，以M 为圆心，MF 长为半径作圆M ，若过点)0,1(-E 可作圆M 的两条切线EA ,EB （A ，B 为切点），求四边形EAMB 面积的最大值．20．（本题满分14分）已知三次函数()()32,,f x ax bx cx a b c R =++∈.（1）若函数()f x 过点(1,2)-且在点()()1,1f 处的切线方程为20y +=，求函数()f x 的解析式；（2）在（Ⅰ）的条件下，若对于区间[]3,2-上任意两个自变量的值12,x x 都有12()()f x f x t -≤，求实数t 的最小值；（3）当11x -≤≤时，1)(≤'x f ，试求a 的最大值，并求a 取得最大值时()f x 的表达式.班级：__________ 座号：__________ 姓名：__________2013届高三第一学期理科数学训练题四答题卷一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．______________；10．______________；11．______________；12．______________；13．______________；14．______________．三、解答题：本大题共6小题，共80分．15．（本小题满分12分）16．（本小题满分12分）17．（本小题满分14分）18．（本小题满分14分）19．（本小题满分14分）ABC EFMO20．（本小题满分14分）。

第4讲 数列求和与综合问题高考统计·定方向题型1 数列中的a n 与S n 的关系■核心知识储备·1．数列{a n }中，a n 与S n 的关系 a n ＝⎩⎨⎧S 1(n ＝1)，S n －S n －1(n ≥2).2．求数列{a n }通项的方法 (1)叠加法形如a n －a n －1＝f (n )(n ≥2)的数列应用叠加法求通项公式，a n ＝a 1＋(a 2－a 1)＋…＋(a n －a n －1)＝a 1＋f (2)＋…＋f (n )(和可求)．(2)叠乘法 形如a n a n －1＝f (n )(n ≥2)的数列应用叠乘法求通项公式，a n ＝a 1·a 2a 1·a 3a 2·…·a na n －1＝a 1·f (2)·f (3)…f (n )(积可求)．(3)待定系数法形如a n ＝λa n －1＋μ(n ≥2，λ≠1，μ≠0)的数列应用待定系数法求通项公式，a n ＋μλ－1＝λ⎝ ⎛⎭⎪⎫a n －1＋μλ－1⎝ ⎛⎭⎪⎫构造新数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n ＋μλ－1为等比数列.■高考考法示例·【例1】 (1)(2018·巴蜀适应性月考)数列{a n }中，a 1＝1，a n ＋1＝S n ＋3n (n ∈N *，n ≥1)，则数列{S n }的通项公式为________．(2)(2018·锦州市模拟)已知数列{a n }的前n 项和为S n ，a n ≠0，a 1＝1，且2a n a n＋1＝4S n －3(n ∈N *)．①求a 2的值并证明：a n ＋2－a n ＝2； ②求数列{a n }的通项公式．(1)S n ＝3n －2n [∵a n ＋1＝S n ＋3n ＝S n ＋1－S n ， ∴S n ＋1＝2S n ＋3n ， ∴S n ＋13n ＋1＝23·S n 3n ＋13， ∴S n ＋13n ＋1－1＝23⎝ ⎛⎭⎪⎫S n 3n －1，又S 13－1＝13－1＝－23，∴数列⎩⎨⎧⎭⎬⎫S n 3n －1是首项为－23，公比为23的等比数列， ∴S n 3n －1＝－23×⎝ ⎛⎭⎪⎫23n －1＝－⎝ ⎛⎭⎪⎫23n ，∴S n ＝3n －2n .](2)[解] ①令n ＝1得2a 1a 2＝4a 1－3， 又a 1＝1， ∴a 2＝12.由2a n a n ＋1＝4S n －3， 得2a n ＋1a n ＋2＝4S n ＋1－3. 即2a n ＋1(a n ＋2－a n )＝4a n ＋1.∵a n ≠0，∴a n ＋2－a n ＝2.②由①可知：数列a 1，a 3，a 5，…，a 2k －1，…为等差数列，公差为2，首项为1，∴a 2k －1＝1＋2(k －1)＝2k －1，即n 为奇数时，a n ＝n .数列a 2，a 4，a 6，…，a 2k ，…为等差数列，公差为2，首项为12， ∴a 2k ＝12＋2(k －1)＝2k －32， 即n 为偶数时，a n ＝n －32. 综上所述，a n ＝⎩⎪⎨⎪⎧n ，n 为奇数，n －32，n 为偶数.1．数列{a n }中，a 1＝1，对任意n ∈N *，有a n ＋1＝1＋n ＋a n ，令b i ＝1a i(i ∈N *)，则b 1＋b 2＋…＋b 2 018＝( )A ．2 0171 009 B ．2 0172 018 C ．2 0182 019D ．4 0362 019D [∵a n ＋1＝n ＋1＋a n ，∴a n ＋1－a n ＝1＋n ， ∴a n －a n －1＝n ，∴a n ＝a 1＋(a 2－a 1)＋…＋(a n －a n －1) ＝1＋2＋…＋n ＝n (n ＋1)2， ∴b n ＝2n (n ＋1)＝2⎝ ⎛⎭⎪⎫1n －1n ＋1，∴b 1＋b 2＋…＋b 2 018＝21－12＋12－13＋…＋12 018－12 019＝4 0362 019，故选D ．] 2．数列{a n }满足，12a 1＋122a 2＋123a 3＋…＋12n a n ＝2n ＋1，则数列{a n }的通项公式为________．a n ＝⎩⎨⎧6，n ＝12n ＋1，n ≥2 [因为12a 1＋122a 2＋123a 3＋…＋12n a n ＝2n ＋1，所以12a 1＋122a 2＋123a 3＋…＋12n －1a n －1＝2(n －1)＋1，两式相减得12n a n ＝2， 即a n ＝2n ＋1，n ≥2. 又12a 1＝3， 所以a 1＝6，因此a n ＝⎩⎨⎧6，n ＝1，2n ＋1，n ≥2.]题型2 求数列{a n }的前n 项和■核心知识储备·1．分组求和法：将数列通项公式写成c n ＝a n ＋b n 的形式，其中{a n }与{b n }是等差(比)数列或一些可以直接求和的数列．2．裂项相消法：把数列与式中的各项分别裂开后，某些项可以相互抵消从而求和的方法，主要适用于⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n ＋1或⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n ＋2(其中{a n }为等差数列)等形式的数列求和．3．错位相减法：形如{a n ·b n }(其中{a n }为等差数列，{b n }为等比数列)的数列求和，一般分六步：①S n ；②qS n ；③差式；④和式；⑤整理；⑥结论．■高考考法示例· ►角度一 分组求和法【例2－1】 (2018·昆明市教学质量检查)已知数列{a n }中，a 1＝3，{a n }的前n 项和S n 满足：S n ＋1＝a n ＋n 2.(1)求数列{a n }的通项公式；(2)设数列{b n }满足：b n ＝(－1)n ＋2a n ，求{b n }的前n 项和T n . [解] (1)由S n ＋1＝a n ＋n 2 ① 得S n ＋1＋1＝a n ＋1＋(n ＋1)2②则②－①得a n ＝2n ＋1.当a 1＝3时满足上式， 所以数列{a n }的通项公式为a n ＝2n ＋1. (2)由(1)得b n ＝(－1)n ＋22n ＋1， 所以T n ＝b 1＋b 2＋…＋b n＝[](－1)＋(－1)2＋…＋(－1)n＋(23＋25＋…＋22n ＋1)＝(－1)×[1－(－1)n ]1－(－1)＋23×(1－4n )1－4＝(－1)n －12＋83(4n－1)．【教师备选】(2018·石家庄三模)已知等差数列{a n }的首项a 1＝2，前n 项和为S n ，等比数列{b n }的首项b 1＝1，且a 2＝b 3，S 3＝6b 2，n ∈N *.(1)求数列{a n }和{b n }的通项公式；(2)数列{c n }满足c n ＝b n ＋(－1)n a n ，记数列{c n }的前n 项和为T n ，求T n . [解] (1)设数列{a n }的公差为d ，数列{b n }的公比为q . ∵a 1＝2，b 1＝1，且a 2＝b 3，S 3＝6b 2，∴⎩⎪⎨⎪⎧2＋d ＝q 2，3(2＋2＋2d )2＝6q .解得⎩⎨⎧d ＝2，q ＝2.∴a n ＝2＋(n －1)×2＝2n ，b n ＝2n －1.(2)由题意：c n ＝b n ＋(－1)n a n ＝2n －1＋(－1)n 2n .∴T n ＝(1＋2＋4＋…＋2n －1)＋[－2＋4－6＋8－…＋(－1)n ·2n ]， ①若n 为偶数：T n ＝1－2n 1－2＋{(－2＋4)＋(－6＋8)＋…＋[－2(n －1)＋2n ]}＝2n －1＋n 2×2＝2n＋n －1.②若n 为奇数：T n ＝1－2n 1－2＋{(－2＋4)＋(－6＋8)＋…＋[－2(n －2)＋2(n －1)]－2n }＝2n －1＋2×n －12－2n ＝2n －n －2.∴T n ＝⎩⎨⎧2n＋n －1，n 为偶数，2n －n －2，n 为奇数.►角度二 裂项相消法求和【例2－2】 (2015·全国卷Ⅰ)S n 为数列{a n }的前n 项和．已知a n ＞0，a 2n ＋2a n ＝4S n ＋3.(1)求{a n }的通项公式； (2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和． [解] (1)由a 2n ＋2a n ＝4S n ＋3，可知a 2n ＋1＋2a n ＋1＝4S n ＋1＋3.两式相减可得a 2n ＋1－a 2n ＋2(a n ＋1－a n )＝4a n ＋1， 即2(a n ＋1＋a n )＝a 2n ＋1－a 2n ＝(a n ＋1＋a n )(a n ＋1－a n )．由于a n >0，可得a n ＋1－a n ＝2.又a 21＋2a 1＝4a 1＋3，解得a 1＝－1(舍去)或a 1＝3.所以{a n }是首项为3，公差为2的等差数列，通项公式为a n ＝2n ＋1. (2)由a n ＝2n ＋1可知b n ＝1a n a n ＋1＝1(2n ＋1)(2n ＋3)＝12⎝ ⎛⎭⎪⎫12n ＋1－12n ＋3.设数列{b n }的前n 项和为T n ，则 T n ＝b 1＋b 2＋…＋b n＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫12n ＋1－12n ＋3＝12⎝ ⎛⎭⎪⎫13－12n ＋3＝n3(2n ＋3). 【教师备选】(2018·郑州第三次质量预测)已知数列{a n }的前n 项和为S n ，a 1＝－2，且满足S n ＝12a n ＋1＋n ＋1(n ∈N *)．(1)求数列{a n }的通项公式；(2)若b n ＝log 3(－a n ＋1)，设数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1b n b n ＋2的前n 项和为T n ，求证：T n ＜34.[解] (1)由S n ＝12a n ＋1＋n ＋1(n ∈N *)，得S n －1＝12a n ＋n (n ≥2，n ∈N *)， 两式相减，并化简，得a n ＋1＝3a n －2，即a n ＋1－1＝3(a n －1)，又a 1－1＝－2－1＝－3≠0， 所以{a n －1}是以－3为首项，3为公比的等比数列， 所以a n －1＝(－3)·3n －1＝－3n . 故a n ＝－3n ＋1.(2)证明：由b n ＝log 3(－a n ＋1)＝log 33n ＝n ， 得1b n b n ＋2＝1n (n ＋2)＝12⎝⎛⎭⎪⎫1n －1n ＋2， T n ＝121－13＋12－14＋13－15＋…＋1n －1－1n ＋1＋1n －1n ＋2＝121＋12－1n ＋1－1n ＋2＝34－2n ＋32(n ＋1)(n ＋2)＜34.►角度三 错位相减法求和【例2－3】 (2018·合肥教学质量检测)已知等比数列{a n }的前n 项和S n 满足4S 5＝3S 4＋S 6，且a 3＝9.(1)求数列{a n }的通项公式；(2)设b n ＝(2n －1)·a n ，求数列{b n }的前n 项的和T n . [解] (1)设等比数列{a n }的公比为q . 由4S 5＝3S 4＋S 6，得S 6－S 5＝3S 5－3S 4， 即a 6＝3a 5，∴q ＝3，∴a n ＝9×3n －3＝3n －1. (2)由(1)得b n ＝(2n －1)·a n ＝(2n －1)·3n －1， ∴T n ＝1×30＋3×31＋5×32＋…＋(2n －1)×3n －1，① ∴3T n ＝1×31＋3×32＋…＋(2n －3)×3n －1＋(2n －1)×3n ， ②①－②得－2T n ＝1＋2(31＋32＋…＋3n －1)－(2n －1)·3n ＝1＋2×3(1－3n －1)1－3－(2n －1)·3n ＝－2－2(n －1)·3n ，∴T n ＝(n －1)·3n ＋1.【教师备选】(2018·石家庄教学质量检测)已知数列{a n }满足：a 1＝1，a n ＋1＝n ＋1n a n ＋n ＋12n . (1)设b n ＝a nn ，求数列{b n }的通项公式； (2)求数列{a n }的前n 项和S n .[解] (1)由a n ＋1＝n ＋1n a n ＋n ＋12n 可得a n ＋1n ＋1＝a n n ＋12n .又∵b n ＝a n n ，∴b n ＋1－b n ＝12n ，由a 1＝1，得b 1＝1， 累加可得：(b 2－b 1)＋(b 3－b 2)＋…＋(b n －b n －1)＝121＋122＋…＋12n －1，化简并代入b 1＝1得：b n ＝2－12n －1.(2)由(1)可知a n ＝2n －n2n －1，设数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫n 2n －1的前n 项和为T n ，则T n ＝120＋221＋322＋…＋n2n －1① 12T n ＝121＋222＋323＋…＋n 2n ②①－②得12T n ＝120＋121＋122＋…＋12n －1－n 2n ＝120－12n1－12－n2n ＝2－n ＋22n ，∴T n ＝4－n ＋22n －1.又∵数列{2n }的前n 项和为n (n ＋1)， ∴S n ＝n (n ＋1)－4＋n ＋22n －1.已知等差数列{a n}的前n项和为S n，且a1＝1，S3＋S4＝S5.(1)求数列{a n}的通项公式；(2)令b n＝(－1)n－1a n a n＋1，求数列{b n}的前2n项和T2n.[解](1)设等差数列{a n}的公差为d，由S3＋S4＝S5，可得a1＋a2＋a3＝a5，即3a2＝a5，故3(1＋d)＝1＋4d，解得d＝2.∴a n＝1＋(n－1)×2＝2n－1.(2)由(1)可得b n＝(－1)n－1·(2n－1)·(2n＋1)＝(－1)n－1·(4n2－1)．∴T2n＝(4×12－1)－(4×22－1)＋(4×32－1)－(4×42－1)＋…＋(－1)2n－1·[4×(2n)2－1]＝4[12－22＋32－42＋…＋(2n－1)2－(2n)2]＝－4(1＋2＋3＋4＋…＋2n－1＋2n)＝－4×2n(2n＋1)2＝－8n2－4n.题型3数列中的创新与交汇问题近几年新课标高考对该知识的命题主要体现在以下两方面：一是新信息情境下的数列问题，此类问题多以新定义、新运算或实际问题为背景，主要考查学生的归纳推理解决新问题的能力；二是创新命题角度考迁移能力，题目常与函数、向量、三角、解析几何等知识交汇结合，考查数列的基本运算与应用．■高考考法示例·►角度一新信息情境下的数列问题【例3－1】(2017·全国卷Ⅰ)几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16，…，其中第一项是20，接下来的两项是20,21，再接下来的三项是20,21,22，依此类推．求满足如下条件的最小整数N ：N ＞100且该数列的前N 项和为2的整数幂．那么该款软件的激活码是( )A ．440B ．330C ．220D ．110[思路点拨] 阅读题干―――――→提取数据数据分组―――――――→联想数列知识推理论证得出结论A [设首项为第1组，接下来的两项为第2组，再接下来的三项为第3组，依此类推，则第n 组的项数为n ，前n 组的项数和为n (1＋n )2.由题意知，N >100，令n (1＋n )2>100⇒n ≥14且n ∈N *，即N 出现在第13组之后．第n 组的各项和为1－2n 1－2＝2n －1，前n 组所有项的和为2(1－2n )1－2－n ＝2n ＋1－2－n .设N 是第n ＋1组的第k 项，若要使前N 项和为2的整数幂，则N －n (1＋n )2项的和即第n ＋1组的前k 项的和2k －1应与－2－n 互为相反数，即2k －1＝2＋n (k ∈N *，n ≥14)，k ＝log 2(n ＋3)⇒n 最小为29，此时k ＝5，则N ＝29×(1＋29)2＋5＝440.故选A ．]►角度二 交汇类创新问题【例3－2】 (2018·长沙联考)已知正项数列{a n }，{b n }满足：对于任意的n ∈N *，都有点(n ，b n )在直线y ＝22(x ＋2)上，且b n ，a n ＋1，b n ＋1成等比数列，a 1＝3.(1)求数列{a n }，{b n }的通项公式；(2)设S n ＝1a 1＋1a 2＋…＋1a n ，如果对任意的n ∈N *，不等式2aS n <2－b n a n恒成立．求实数a 的取值范围．[思路点拨] (1)点(n ，b n )在直线y ＝22(x ＋2)上――→满足方程求b n ―――――――→b n ，a n ＋1，b n ＋1成等比数列求a n ； (2)裂项，求S n ―――――――→2aS n ＜2－b n a n 分离变量建立a 的不等式―――――――→数列的单调性求实数a 的取值范围[解] (1)∵点(n ，b n )在直线y ＝22(x ＋2)上，∴b n ＝22(n ＋2)，即b n ＝(n ＋2)22.又∵b n ，a n ＋1，b n ＋1成等比数列，∴a 2n ＋1＝b n ·b n ＋1＝(n ＋2)2(n ＋3)24， ∴a n ＋1＝(n ＋2)(n ＋3)2， ∴n ≥2时，a n ＝(n ＋1)(n ＋2)2， a 1＝3适合上式，∴a n ＝(n ＋1)(n ＋2)2. (2)由(1)知，1a n ＝2(n ＋1)(n ＋2)＝2⎝ ⎛⎭⎪⎫1n ＋1－1n ＋2， ∴S n ＝2⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12－13＋⎝ ⎛⎭⎪⎫13－14＋…＋⎝ ⎛⎭⎪⎫1n ＋1－1n ＋2 ＝2⎝ ⎛⎭⎪⎫12－1n ＋2＝n n ＋2. 故2aS n <2－b n a n可化为： 2an n ＋2<2－(n ＋2)22(n ＋1)(n ＋2)2＝2－n ＋2n ＋1＝n n ＋1， 即a <n ＋22(n ＋1)＝12⎝ ⎛⎭⎪⎫1＋1n ＋1对任意的n ∈N *恒成立，令f (n )＝n ＋22(n ＋1)＝12⎝ ⎛⎭⎪⎫1＋1n ＋1，显然f (n )随n 的增大而减小，且f (n )>12恒成立，故a ≤12. 综上知，实数a 的取值范围是⎝ ⎛⎦⎥⎤－∞，12.1．若数列{a n }满足：对任意的n ∈N *，只有有限个正整数m 使得a m <n 成立，记这样的m 的个数为(a n )*，则得到一个新数列{(a n )*}．例如，若数列{a n }是1,2,3，…，n ，…，则数列{(a n )*}是0,1,2，…，n －1，….已知对任意的n ∈N *，a n ＝n 2，则(a 5)*＝________，((a n )*)*＝________.2 n 2 [因为a m <5，而a n ＝n 2，所以m ＝1,2，所以(a 5)*＝2.因为(a 1)*＝0，(a 2)*＝1，(a 3)*＝1，(a 4)*＝1，(a 5)*＝2，(a 6)*＝2，(a 7)*＝2，(a 8)*＝2，(a 9)*＝2，(a 10)*＝3，(a 11)*＝3，(a 12)*＝3，(a 13)*＝3，(a 14)*＝3，(a 15)*＝3，(a 16)*＝3， 所以((a 1)*)*＝1，((a 2)*)*＝4，((a 3)*)*＝9，((a 4)*)*＝16，猜想((a n )*)*＝n 2.]2．(2014·全国卷Ⅱ)已知数列{a n }满足a 1＝1，a n ＋1＝3a n ＋1.(1)证明：⎩⎨⎧⎭⎬⎫a n ＋12是等比数列，并求{a n }的通项公式； (2)证明：1a 1＋1a 2＋…＋1a n<32. [证明] (1)由a n ＋1＝3a n ＋1得a n ＋1＋12＝3⎝ ⎛⎭⎪⎫a n ＋12. 又a 1＋12＝32，所以⎩⎨⎧⎭⎬⎫a n ＋12是首项为32，公比为3的等比数列．所以a n ＋12＝3n 2，因此{a n }的通项公式为a n ＝3n －12.(2)由(1)知1a n ＝23n －1. 因为当n ≥1时，3n －1≥2×3n －1，所以13n－1≤12×3n －1. 于是1a 1＋1a 2＋…＋1a n ≤1＋13＋…＋13n －1 ＝32⎝ ⎛⎭⎪⎫1－13n <32. 所以1a 1＋1a 2＋…＋1a n<32.[高考真题]1.(2016·全国卷Ⅲ)定义“规范01数列”{a n }如下：{a n }共有2m 项，其中m 项为0，m 项为1，且对任意k ≤2m ，a 1，a 2，…，a k 中0的个数不少于1的个数．若m ＝4，则不同的“规范01数列”共有( )A ．18个B ．16个C ．14个D ．12个C [由题意知：当m ＝4时，“规范01数列”共含有8项，其中4项为0,4项为1，且必有a 1＝0，a 8＝1.不考虑限制条件“对任意k ≤2m ，a 1，a 2，…，a k 中0的个数不少于1的个数”，则中间6个数的情况共有C 36＝20(种)，其中存在k ≤2m ，a 1，a 2，…，a k 中0的个数少于1的个数的情况有：①若a 2＝a 3＝1，则有C 14＝4(种)；②若a 2＝1，a 3＝0，则a 4＝1，a 5＝1，只有1种；③若a 2＝0，则a 3＝a 4＝a 5＝1，只有1种．综上，不同的“规范01数列”共有20－6＝14(种)．故共有14个．故选C ．]2.(2018·全国卷Ⅰ)记S n 为数列{a n }的前n 项和．若S n ＝2a n ＋1，则S 6＝________.－63 [法一：因为S n ＝2a n ＋1，所以当n ＝1时，a 1＝2a 1＋1，解得a 1＝－1； 当n ＝2时，a 1＋a 2＝2a 2＋1，解得a 2＝－2；当n ＝3时，a 1＋a 2＋a 3＝2a 3＋1，解得a 3＝－4；当n ＝4时，a 1＋a 2＋a 3＋a 4＝2a 4＋1，解得a 4＝－8；当n ＝5时，a 1＋a 2＋a 3＋a 4＋a 5＝2a 5＋1，解得a 5＝－16；当n ＝6时，a 1＋a 2＋a 3＋a 4＋a 5＋a 6＝2a 6＋1，解得a 6＝－32.所以S 6＝－1－2－4－8－16－32＝－63.法二：因为S n ＝2a n ＋1，所以当n ＝1时，a 1＝2a 1＋1，解得a 1＝－1， 当n ≥2时，a n ＝S n －S n －1＝2a n ＋1－(2a n －1＋1)，所以a n ＝2a n －1，所以数列{a n }是以－1为首项，2为公比的等比数列，所以a n ＝－2n －1，所以S 6＝－1×(1－26)1－2＝－63.] 3.(2017·全国卷Ⅱ)等差数列{a n }的前n 项和为S n ，a 3＝3，S 4＝10，则∑nk ＝1 1S k ＝________.2n n ＋1[设等差数列{a n }的首项为a 1，公差为d ，则 由⎩⎪⎨⎪⎧ a 3＝a 1＋2d ＝3，S 4＝4a 1＋4×32d ＝10，得⎩⎨⎧a 1＝1，d ＝1. ∴S n ＝n ×1＋n (n －1)2×1＝n (n ＋1)2，1S n ＝2n (n ＋1)＝2⎝ ⎛⎭⎪⎫1n －1n ＋1.∴∑nk ＝11S k ＝1S 1＋1S 2＋1S 3＋…＋1S n＝2⎝ ⎛⎭⎪⎫1－12＋12－13＋13－14＋…＋1n －1n ＋1 ＝2⎝⎛⎭⎪⎫1－1n ＋1＝2n n ＋1.] 4.(2016·全国卷Ⅱ)S n 为等差数列{a n }的前n 项和，且a 1＝1，S 7＝28.记b n ＝[lg a n ]，其中[x ]表示不超过x 的最大整数，如[0.9]＝0，[lg 99]＝1.(1)求b 1，b 11，b 101；(2)求数列{b n }的前1 000项和．[解] (1)设{a n }的公差为d ，据已知有7＋21d ＝28，解得d ＝1.所以{a n }的通项公式为a n ＝n .b 1＝[lg 1]＝0，b 11＝[lg 11]＝1，b 101＝[lg 101]＝2.(2)因为b n ＝⎩⎨⎧ 0，1≤n ＜10，1，10≤n ＜100，2，100≤n ＜1 000，3，n ＝1 000，所以数列{b n }的前1 000项和为1×90＋2×900＋3×1＝1 893.[最新模拟]5．(2018·昆明教学质量检查)数列{a n }满足a n ＋1＋a n ＝(－1)n ·n ，则数列{a n }的前20项的和为( )A ．－100B ．100C ．－110D ．110A [由a n ＋1＋a n ＝(－1)n n ，得a 2＋a 1＝－1，a 3＋a 4＝－3，a 5＋a 6＝－5，…，a 19＋a 20＝－19，∴a n 的前20项的和为a 1＋a 2＋…＋a 19＋a 20＝－1－3－…－19＝－1＋192×10＝－100，故选A ．] 6．(2018·安阳模拟)设等差数列{a n }的前n 项和为S n ，点(n ，S n )在函数f (x )＝x 2＋Bx ＋C －1(B ，C ∈R )的图象上，且a 1＝C ．(1)求数列{a n }的通项公式；(2)记数列b n ＝a n (a 2n －1＋1)，求数列{b n }的前n 项和T n .[解] (1)设数列{a n }的公差为d ，则S n ＝na 1＋n (n －1)2d ＝d 2n 2＋⎝ ⎛⎭⎪⎫a 1－d 2n ，又S n ＝n 2＋Bn ＋C －1，两式对照得⎩⎪⎨⎪⎧ d 2＝1，C －1＝0，⎩⎨⎧d ＝2，a 1＝C ＝1，所以数列{a n }的通项公式为a n ＝2n －1.(2)b n ＝(2n －1)(2·2n －1－1＋1)＝(2n －1)2n ，则T n ＝1×2＋3×22＋…＋(2n －1)·2n ，2T n ＝1×22＋3×23＋…＋(2n －3)·2n ＋(2n －1)·2n ＋1， 两式相减得T n＝(2n－1)·2n＋1－2(22＋…＋2n)－2＝(2n－1)·2n＋1－2×22(1－2n－1)1－2－2＝(2n－3)·2n＋1＋6.。