数学实验实验二

数学实验二实验内容：学习matlab的m文件编写和函数的编写，体会matlab编程特点，掌握matlab 的编程基本方法。

要求：一．学习ppt教案的例题代码，能正确的输入、运行代码；二．写出如下各段代码的作用，将以下各段循环执行的代码，改为不需要循环的矩阵和数组运行，并使用tic,toc测试不同代码的执行时间：%程序1,文件名：ex2_2_1.mticdx = pi/30;nx = 1 + 2*pi/dx;for i = 1:nxx(i) = (i-1)*dx;y(i) = sin(3*x(i));endtoc以上程序实现将[0,2*pi]间隔pi/30分成60等分，x和y分别为61个元素的数组，y为计算sin(3x)的值。

以上程序可以使用简单的matlab数组计算实现：x2=0:pi/30:2*pi;y2=sin(3*x2);大家可以比较一下，x1和x2完全相同，y和y2也完全相同。

%程序2，文件名：ex2_2_2.mticA=round(2+rand(50,60)*6); 生成一个在[2,8]上均匀分布的50*60随机数组[X,Y]=size(A); 求出其大小；X=50,Y=60minA=A(1,1); 设最小值为矩阵A的第1行1列的元素for i=1:Xfor j=1:Yif A(i,j)<minAminA=A(i,j);minX=i;minY=j;endendend 以上程序按行、列搜索矩阵A的最小值，若当前值A(I,j)小，则将最小值设为当前值；[minA ,minX,minY] 输出矩阵最小值minA及矩阵最小值所在的行minX、列minY。

toc上述程序可以使用find函数及min函数实现；此时只需： minA=min(A(:));[minX,minY]=find(A ’==minA,1);%注意此处需将矩阵A 转置，因为matlab 中是按列优先搜索的，而题目的程序是按行有限搜索。

实验二： 微分方程模型Matlab 求解与分析一、实验目的[1] 掌握解析、数值解法，并学会用图形观察解的形态和进行解的定性分析； [2] 熟悉MATLAB 软件关于微分方程求解的各种命令；[3] 通过范例学习建立微分方程方面的数学模型以及求解全过程； [4] 熟悉离散 Logistic 模型的求解与混沌的产生过程。

二、实验原理1. 微分方程模型与MATLAB 求解解析解用MATLAB 命令dsolve(‘eqn1’,’eqn2’, ...) 求常微分方程（组）的解析解。

其中‘eqni'表示第i 个微分方程，Dny 表示y 的n 阶导数,默认的自变量为t 。

（1） 微分方程 例1 求解一阶微分方程 21y dxdy+= (1) 求通解 输入：dsolve('Dy=1+y^2')输出：ans =tan(t+C1)（2）求特解 输入：dsolve('Dy=1+y^2','y(0)=1','x')指定初值为1，自变量为x 输出：ans =tan(x+1/4*pi)例2 求解二阶微分方程 221()04(/2)2(/2)2/x y xy x y y y πππ'''++-=='=-原方程两边都除以2x ，得211(1)04y y y x x'''++-= 输入:dsolve('D2y+(1/x)*Dy+(1-1/4/x^2)*y=0','y(pi/2)=2,Dy(pi/2)=-2/pi','x')ans =- (exp(x*i)*(pi/2)^(1/2)*i)/x^(1/2) +(exp(x*i)*exp(-x*2*i)*(pi/2)^(3/2)*2*i)/(pi*x^(1/2))试试能不用用simplify 函数化简 输入: simplify(ans)ans =2^(1/2)*pi^(1/2)/x^(1/2)*sin(x) （2）微分方程组例3 求解 d f /d x =3f +4g ; d g /d x =-4f +3g 。

2 微积分实验2.1 基础训练1. 已知)cos(mx e y nx=，利用符号运算函数求y ''. 编写函数文件返回求导结果（1个参数）. 解：function d=myfun syms m n xy=exp(n*x)*cos(m*x); d = diff(y,x,2);2. 已知函数22xa ae y x +=，求解该函数在x =5处的一阶导数值.编写本问题的函数文件第一行格式如下（函数名、文件名自己设定）： function r=myfun %变量r 存储导数值 解：function r=myfun syms a xy=a*exp(x)/sqrt(a^2+x^2); f=diff(y,x); r=subs(f,x,5);3. 使用符号工具箱计算函数211xy +=的6阶麦克劳林多项式. 要求编写一个function 文件返回该结果. 解：function f=fun syms xf = taylor(1/(1+x^2),x, 'order',7); f = simplify(f);4. 求不定积分dx x x ⎰2ln 和定积分dx xex ⎰∞-12。

syms xint(log(x)^2*x) f=x*exp(-x^2);int(f,x,1,inf)5. 求解方程组求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧=+++=++-=-++=+-+159326282310262113654d z y x d z y x d z y x d z y x .编程调用solve 函数求解方程组；编写函数返回4个参数：依次为x ，y ，z ，d 所得结果。

编写本问题的函数文件第一行格式如下（函数名、文件名自己设定）： function [x,y,z,d]=myfun % x,y,z,d 为题目所求的解 解：function [x,y,z,d]=myfun % x,y,z,d 为题目所求的解[x,y,z,d]=solve('4*x+5*y-6*z+3*d=11','2*x+6*y+2*z-d=10',... '3*x-2*y+8*z+2*d=6','x+2*y+3*z+9*d=15')2.2 实验任务问题来源全国数学建模竞赛1997年A 题 一件产品由若干零件组装而成，标志产品性能的某个参数取决于这些零件的参数。

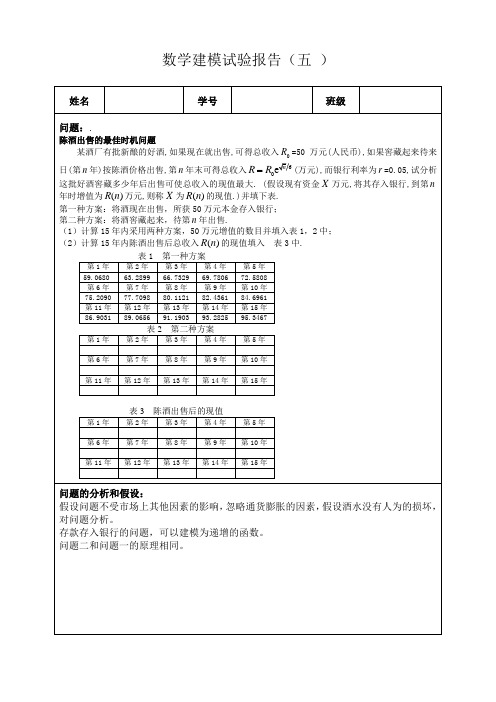
数学建模试验报告（五 ）姓名 学号 班级问题：.陈酒出售的最佳时机问题某酒厂有批新酿的好酒,如果现在就出售,可得总收入0R =50万元(人民币),如果窖藏起来待来日(第n 年)按陈酒价格出售,第n 年末可得总收入60en R R (万元),而银行利率为r =0.05,试分析这批好酒窖藏多少年后出售可使总收入的现值最大. (假设现有资金X 万元,将其存入银行,到第n 年时增值为()R n 万元,则称X 为()R n 的现值.)并填下表. 第一种方案：将酒现在出售，所获50万元本金存入银行； 第二种方案：将酒窖藏起来，待第n 年出售.（1）计算15年内采用两种方案，50万元增值的数目并填入表1，2中； （2）计算15年内陈酒出售后总收入()R n 的现值填入 表3中.表1 第一种方案第1年 第2年 第3年 第4年 第5年 59.0680 63.2899 66.7329 69.7806 72.5808 第6年 第7年 第8年 第9年 第10年 75.2090 77.7098 80.1121 82.4361 84.6961 第11年 第12年 第13年 第14年 第15年 86.9031 89.0656 91.1903 93.2825 95.3467 表2 第二种方案第1年 第2年第3年第4年第5年第6年第7年第8年第9年第10年第11年第12年第13年第14年第15年表3 陈酒出售后的现值第1年 第2年第3年第4年第5年第6年第7年第8年第9年第10年第11年第12年第13年第14年第15年问题的分析和假设：假设问题不受市场上其他因素的影响，忽略通货膨胀的因素，假设酒水没有人为的损坏， 对问题分析。

存款存入银行的问题，可以建模为递增的函数。

问题二和问题一的原理相同。

建模：第一种方案，过n年出售：设第n年的收益为bn，则根据题目，写出运算公式为：r=50bn=r*exp(sqrt(n)/6)第二种方案，立即出售，存款存入银行：可以设存入银行的年收入为r，初始值为r0=50（万元）则，第n年的时候r=r0*（1+0.05）^nr0=50求解的Matlab程序代码：第一种方案，过n年出售：在m文件种编辑：输入为，for n=1:15b(n)=50*exp(sqrt(n)/6);endbb =用来计算1-15年的收益。

引言：离散数学是一门基础性的数学学科，广泛应用于计算机科学、电子信息等领域。

本文是《离散数学实验报告（二）》，通过对离散数学实验的深入研究和实践，总结了相关的理论知识和应用技巧，希望能够对读者对离散数学有更加深入的理解。

概述:本实验主要涉及离散数学中的集合、关系、图论等基本概念及其应用。

通过对离散数学的实验学习，深入掌握了这些概念和应用，对于在实际问题中的应用和拓展具有重要的意义。

正文内容：一、集合相关概念及应用1.定义：集合是由元素组成的无序的整体。

介绍了集合的基本概念、集合的表示法以及集合的运算。

2.集合的应用：介绍了集合在数学、计算机科学中的应用，如数据库的查询、关系代数等。

二、关系相关概念及应用1.定义：关系是一个元素与另一个元素之间的对应关系。

介绍了关系的基本概念、关系的表示方法及其运算。

2.关系的应用：介绍了关系在图像处理、社交网络分析等领域的应用，如图像中的像素点之间的关系、社交网络中用户之间的关系等。

三、图论基础知识及应用1.定义：图是由顶点和边组成的抽象的数学模型。

介绍了图的基本概念、图的表示方法和图的运算。

2.图论的应用：介绍了图论在路由算法、电子商务等领域的应用，如路由器的路由选择、电子商务中的商品推荐等。

四、布尔代数的概念及应用1.定义：布尔代数是一种基于集合论和逻辑学的代数系统。

介绍了布尔代数的基本概念、布尔表达式及其化简方法。

2.布尔代数的应用：介绍了布尔代数在电路设计、开关控制等方面的应用，如逻辑门电路的设计、开关控制系统的建模等。

五、递归的概念及应用1.定义：递归是一种通过调用自身来解决问题的方法。

介绍了递归的基本原理、递归的应用技巧。

2.递归的应用：介绍了递归在算法设计、树的遍历等方面的应用，如快速排序算法、树结构的遍历等。

总结：通过本次离散数学的实验学习，我深入掌握了集合、关系、图论等基本概念与应用。

集合的应用在数据库查询、关系代数等方面起到了重要的作用。

关系的应用在图像处理、社交网络分析等领域有广泛的应用。

班级 学号 姓名高等数学实验2 微分、积分一. 用MA TLAB 计算下列导数：diff 函数（1）已知2xy e =，求y '、y ''、(10)y 。

（2）已知nx y e =，求y '''。

（3）已知210x y xe-=,求y '、y ''与(8)y 。

(4)设2sin ()43x f x x x =++，求()f x '、()f x ''及()6f π''。

二．用MA TLAB 解方程。

solve 函数1．一元方程与线性方程（组）（1） 解方程 062=--x x（2）解方程组⎪⎩⎪⎨⎧=-+=-+060622x y y x （3）解方程组⎪⎪⎩⎪⎪⎨⎧=+++=++=++-=++012412324543213214321431x x x x x x x x x x x x x x2．非线性方程（组）（4）解非线性方程组⎩⎨⎧=+-=--0sin 3.0cos 5.00cos 3.0sin 5.0212211x x x x x x 三。

用MA TLAB 计算极值：(1)已知销售额R 是价格P 的函数，且200184R P P ⎛⎫=-⎪+⎝⎭。

当价格P 为何值时， 销售额R 有最大值，且求此最大值。

(2)已知某公司收益函数210xR xe -=，成本函数32(1085)/100C x x =++，其中x 为产（销）量，求最大收益、最低平均成本和最大利润。

四．用MATLAB 计算下列不定积分 int 函数1．ln xdx ⎰； 2。

321x x e dx -⎰； 3． 42(31)sin(21)x x x dx -++⎰； 4．(sin sin cos )ax bx cx dx ⨯⨯⎰； 5．（练习）5(4)ln(32)x x x dx --⎰； 6．（练习）4sin(25)x x e dx +⎰；五．用MATLAB 计算下列定积分 int 函数1．120(1)x xe dx x +⎰ 2。

数学实验课后习题解答配套教材：王向东戎海武文翰编著数学实验王汝军编写实验一曲线绘图【练习与思考】画出下列常见曲线的图形。

以直角坐标方程表示的曲线：1.立方曲线3x y=clear;x=-2:0.1:2; y=x.^3; plot(x,y)2.立方抛物线3x y=clear;y=-2:0.1:2; x=y.^3; plot(x,y) grid on3.高斯曲线2xe y-=clear;x=-3:0.1:3;y=exp(-x.^2); plot(x,y); grid on%axis equal以参数方程表示的曲线4. 奈尔抛物线)(,3223x y t y t x ===clear;t=-3:0.05:3; x=t.^3;y=t.^2; plot(x,y) axis equal grid on5. 半立方抛物线2323,()x t y t y x ===clear;t=-3:0.05:3; x=t.^2;y=t.^3; plot(x,y) %axis equal grid on6.迪卡尔曲线2332233,(30)11at at x y x y axy t t==+-=++ clear;a=3;t=-6:0.1:6; x=3*a*t./(1+t.^2); y=3*a*t.^2./(1+t.^2); plot(x,y)7.蔓叶线233222,()11at at x x y y t t a x===++- clear;a=3;t=-6:0.1:6;x=3*a*t.^2./(1+t.^2); y=3*a*t.^3./(1+t.^2); plot(x,y)8. 摆线)cos 1(),sin (t b y t t a x -=-=clear;clc; a=1;b=1;t=0:pi/50:6*pi; x=a*(t-sin(t)); y=b*(1-cos(t)); plot(x,y); axis equal grid on9. 内摆线（星形线）)(sin ,cos 32323233a y x t a y t a x =+==clear;a=1;t=0:pi/50:2*pi; x=a*cos(t).^3; y=a*sin(t).^3; plot(x,y)10. 圆的渐伸线（渐开线）)cos (sin ),sin (cos t t t a y t t t a x -=+=clear; a=1;t=0:pi/50:6*pi;x=a*(cos(t)+t.*sin(t)); y=a*(sin(t)+t.*cos(t)); plot(x,y) grid on11. 空间螺线ct z t b y t a x ===,sin ,coscleara=3;b=2;c=1; t=0:pi/50:6*pi; x=a*cos(t); y=b*sin(t); z=c*t;plot3(x,y,z) grid on以极坐标方程表示的曲线：12. 阿基米德线0,≥=r a rϕclear; a=1;phy=0:pi/50:6*pi; rho=a*phy;polar(phy,rho,'r-*')13. 对数螺线ϕa e r =clear; a=0.1;phy=0:pi/50:6*pi; rho=exp(a*phy); polar(phy,rho) 14. 双纽线))()((2cos 22222222y x a y x a r -=+=ϕclear; a=1;phy=-pi/4:pi/50:pi/4; rho=a*sqrt(cos(2*phy)); polar(phy,rho)hold onpolar(phy,-rho)15. 双纽线)2)((2sin 222222xy a y x a r =+=ϕclear; a=1;phy=0:pi/50:pi/2;rho=a*sqrt(sin(2*phy)); polar(phy,rho) hold onpolar(phy,-rho)16. 四叶玫瑰线0,2sin ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(2*phy); polar(phy,rho)17. 三叶玫瑰线0,3sin ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*sin(3*phy); polar(phy,rho)18. 三叶玫瑰线0,3cos ≥=r a r ϕclear;close a=1;phy=0:pi/50:2*pi; rho=a*cos(3*phy); polar(phy,rho)实验二 极限与导数【练习与思考】1． 求下列各极限（1）nn n)11(lim -∞→ （2）n nn n 3lim 3+∞→ （3）)122(lim n n n n ++-+∞→clear;syms ny1=limit((1-1/n)^n,n,inf)y2=limit((n^3+3^n)^(1/n),n,inf)y3=limit(sqrt(n+2)-2*sqrt(n+1)+sqrt(n),n,inf)y1 =1/exp(1) y2 =3 y3 =0（4）)1112(lim 21---→x x x （5）x x x 2cot lim 0→ （6）)3(lim 2x x x x -+∞→clear; syms x ;y4=limit(2/(x^2-1)-1/(x-1),x,1) y5=limit(x*cot(2*x),x,0)y6=limit(sqrt(x^2+3*x)-x,x,inf)y4 =-1/2 y5 =1/2 y6 =3/2（7）x x x m )(cos lim ∞→ （8）)111(lim 1--→x x e x （9）x x x 11lim30-+→ clear;syms x my7=limit(cos(m/x),x,inf)y8=limit(1/x-1/(exp(x)-1),x,1) y9=limit(((1+x)^(1/3)-1)/x,x,0)y7 =1y8 =(exp(1) - 2)/(exp(1) - 1) y9 =1/32． 考虑函数22),sin(3)(32<<-=x x x x f作出图形，并说出大致单调区间；使用diff 求)('x f ，并求)(x f 确切的单调区间。

云南大学数学与统计学实验教学中心实验报告
数学实验（二）
一、实验目的：练习用数值迭代逼近法解非线性方程。

1.区间迭代法：对分法和黄金分割法
2.点的迭代法：简单迭代法
二、实验内容：用二分法（即对分法）编程求解方程。

0123=---x x x
三、实验环境：MATLAB.
四.实验方法：
程序代码：
function X=fan(a,b)
e=1e-2;
ep=1;
x0=a;
xn=b;
x=0;
k=0;
N=100;
while (ep>e)
x=(x0+xn)/2;
f1=x^3-x^2-x-1;
f2=x0^3-x0^2-x0-1;
f3=xn^3-xn^2-xn-1;
if f1*f2<0
x0=a;
xn=x;
elseif f1*f3<0
x0=x;
xn=b;
end
ep=abs(f1);
k=k+1;
if k>N
break;
end
x
ep
实验结果：
fan(a,b)
x =
1.8572
ep =
0.0993
五、实验过程
1实验步骤
2 关键代码及其解释
3 调试过程
六、实验总结
1．遇到的问题及解决过程
2．产生的错误及原因分析
3．体会和收获。

数学实验第二次测验题及参考答案（09级）数学实验第二次测验题及参考答案一、写出下列MATLAB指令的运算结果.1. A=[1;2;3]; transpose(A)1 2 31 2 32. A=[1, 2, 3 ; 4, 5, 6 ]; B=A([1 2], [1,3]) , d=size(A)B =1 34 6d =2 33. a=1:3; b=linspace(1,3,3); x=sum(a.*b), y=cross(a, b)x = 14y = 0 0 04. A=[1,2, 3; 4,5,6; 7,8,9]; B=ones(3); C=A-BC =0 1 23 4 56 7 85. v=[1, 2, 3]; A=diag(v); E=eig(A), D=det(A)E=123D =66. x=[1,2,3,4,5]; [mean(x), median(x), range(x),sum(x), prod(x)]3 34 15 1207. x=[2,3,4]; a=cumsum(x) ,b=sort(x)a =2 5 9b =2 3 48．format rat; v=[1, 2, 3]; A=diag(v); inv(A)ans =1 0 00 1/2 00 0 1/39. [m,v]=normstat(1,4) % 求参数为1,4的正态分布的均值与方差m =1, v =16二、写出下列MATLAB指令的实验目的.1. dsolve('x*Dy+y-exp(-x)=0', 'y(1)=2*exp(1)', 'x')求微分方程0=-+'-x e y y x 在初始条件e y x 2|1==下的特解.2. u=[1,2,3],v=[0,3,2], w=[5, 2, 1]; dot(w, cross(u, v))计算向量u, v, w 的混合积.3. A=[1 2 3; 2 2 5; 3 5 1]; b=[1;2;3]; det(A); inv(A)*b利用逆矩阵解线性方程组=++=++=++3532522132321 321321x x x x x x x x x .4. A=[0 0 1; 0 1 1; 1 1 1; 1 0 0]; rref(A)求向量组)1,0,0(1=α,)1,1,0(2=α,)1,1,1(3=α,)0,0,1(4=α的秩.或对矩阵A 做行初等变换。