常微分方程图文 (6)
- 格式:ppt
- 大小:1.20 MB
- 文档页数:59

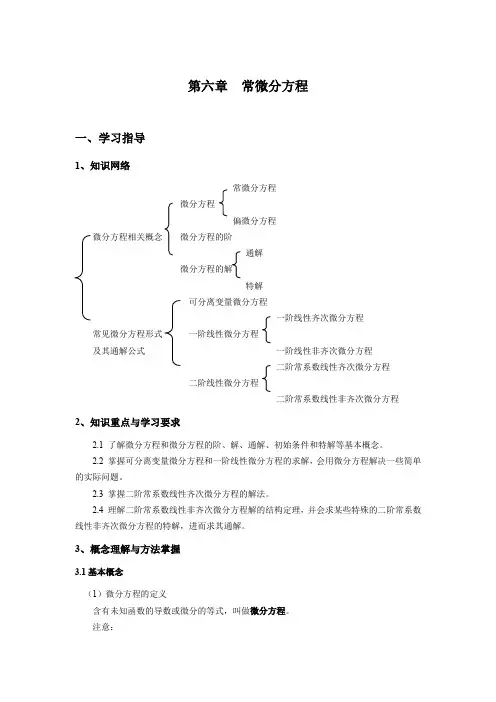
第六章常微分方程一、学习指导1、知识网络常微分方程微分方程偏微分方程微分方程相关概念微分方程的阶通解微分方程的解特解可分离变量微分方程一阶线性齐次微分方程常见微分方程形式一阶线性微分方程及其通解公式一阶线性非齐次微分方程二阶常系数线性齐次微分方程二阶线性微分方程二阶常系数线性非齐次微分方程2、知识重点与学习要求2.1 了解微分方程和微分方程的阶、解、通解、初始条件和特解等基本概念。
2.2 掌握可分离变量微分方程和一阶线性微分方程的求解,会用微分方程解决一些简单的实际问题。
2.3 掌握二阶常系数线性齐次微分方程的解法。
2.4 理解二阶常系数线性非齐次微分方程解的结构定理,并会求某些特殊的二阶常系数线性非齐次微分方程的特解,进而求其通解。
3、概念理解与方法掌握3.1基本概念(1)微分方程的定义含有未知函数的导数或微分的等式,叫做微分方程。
注意:① 在微分方程中,自变量及未知函数可以不出现,但未知函数的导数(或微分)必须出现。
② 在微分方程中,如果未知函数是一元函数,则为常微分方程;如果未知函数是多元函数,则为偏微分方程。
本章只讨论常微分方程。
(2)微分方程的阶微分方程中出现的未知函数的导数的最高阶数,称为微分方程的阶。
(3)微分方程的解如果把一个函数代入微分方程中,能使方程变为恒等式,那么这个函数就称为微分方程的解;如果微分方程的解中含有任意常数,并且相互独立的任意常数的个数与微分方程的阶数相同,这样的解则称为微分方程的通解,不含任意常数的解叫做微分方程的特解。
(4)初始条件初始条件是用来确定通解中任意常数的条件,通常是由系统(微分方程)在初始时刻所处的状态给出。
3.2 几种常见类型微分方程的解法注意:微分方程特定类型有其特定的解法,故在解微分方程之前,一定要准确判断出它的类型。
1、可分离变量的微分方程 (1)方程形式 形如()()dyf xg y dx= 的微分方程叫做可分离变量的微分方程。
其中(),()f x g y 在其定义的某个范围内为连续函数,且()0g y ≠。



第一章 绪论什么是线性微分方程:形如)()()()(y 1)1(1)(x f y x a y x a y x a n n n n =+'+++--Λ的微分方程,即y 及y 的各阶导数都是一次有理整式,即不含y 及y 的各阶导数的乘积的微分方程叫:线性微分方程。
第二章 一阶微分方程的初等解法§ 2.1 变量分离方程1、形式:)()(y x f dxdy ϕ= 做题步骤:① 0)(≠y ϕ 可将方程改写为:dx x f y dy )()(=ϕ,这样对两边积分:⎰⎰+=c dx x f y dy )()(ϕ,得出方程的通解,但c 要保证积分式有意义 ② 0)(=y ϕ时,求出0y y = 也是方程的解2、y x P dxdy )(=得dx x P ce y ⎰=)( (2.4) 而0=y 也是方程的解,而若(2.4)允许c=0,则y=0也在(2.4)中,故(2.4)是原方程的通解,其中c=0。
3、齐次方程:)(xy g dx dy = (2.5) 做变量变换x y u =,即ux y =,则u dx du x dx dy +=,整理后为:x u u g dx du -=)(,即为变量分离方程。
同时要注意:将一个方程转化为齐次方程求解时,两个方程是否同解(c 的范围是否相同)4、222111c y b x a c y b x a dx dy ++++= (2.13) 做题步骤:①k c c b b a a ===212121(常数),通解:c kx y += (c 为任意常数) ② 212121c c k b b a a ≠==,令y b x a u 22+=,有212222c u c ku b a dx dy b a dx du ++++=+=,为变量分离方程 ③ 2121b b a a ≠,如果没有常数21c c 、,则很容易变成齐次方程做,(体会:)让分子分母都为零,则为两条曲线⎩⎨⎧=++=++00222111c y b x a c y b x a (2.14),两条曲线相交的交点为),(βα,而没有那两个常数时方程为都过原点的形式,因此过原点的这两直线可视为原坐标系平移后原直线在新坐标系下的坐标,令⎩⎨⎧-=-=βαy Y x X ,(2.14) 变为⎩⎨⎧=+=+002211Y b X a Y b X a ,从而 (2.13) 变为)(2211X Y g Y b X a Y b X a dX dY =++=,§ 2.2 线性微分方程与常数变易法1、)()(x Q y x P dxdy += (2.28) 做题步骤:① 考虑y x P dxdy )(=,求出它的通解为:⎰=dx x P ce y )(;② 常数变易变为:⎰=dx x P e x c y )()((2.29) ③ 求微分得:⎰+⎰=dx x P dx x P e x P x c e dxx dc dx dy )()()()()( (2.30) ,④ 将(2.29)和(2.30)代入(2.28),得到: ⎰=-dx x P e x Q dx x dc )()()(,⑤ 积分后得到⎰'+⎰=-c dx e x Q x c dx x P )()()(,于是得到方程(2.28)的通解为: ))(()()(⎰'+⎰⎰=-c dx e x Q e y dx x P dx x P2、伯努利微分方程n y x Q y x P dxdy )()(+= 做题步骤:① 两边同除以n y ,得到)()(1x Q x P y dx dy yn n +=--,② 设n y z -=1,得dx dy y n dx dz n --=)1( ③ 于是原方程变为:)()1()()1(x Q n z x P n dxdz -+-=,即为线性微分方程 § 2.3 恰当微分方程与积分因子1、恰当方程形式:0),(),(=+dy y x N dx y x M (M 、N 在已知区域上连续且具有一阶连续偏导数)推理过程:① 若已知此微分方程是恰当方程能推出什么?先设原函数为),(y x u yx u y N x y u y M ∂∂∂=∂∂∂∂∂=∂∂22、 由条件得:yx u x y u ∂∂∂=∂∂∂22即x N y M ∂∂=∂∂ ② 那么反过来若由它俩相等能否推出方程是恰当方程? 从x u M ∂∂=出发,两边同时求积分:⎰⎰∂∂==x u Mdx u +c ,但c 若是常数那么?则应为:⎰⎰+=∂∂=)(y Mdx dx x u u ϕ ③ 对u 关于y 求偏导:),()(y x N y Mdx y y u ='+∂∂=∂∂⎰ϕ,如何证明等式左边等于右边(方程有意义),即右边也与x 无关即只与y 有关? 对右边关于x 求偏导0=∂∂-∂∂=∂∂∂∂-∂∂⎰y M x N dx y M x x N (因为证充分,则y M x N ∂∂=∂∂为已知)④ 两端积分:dy Mdx y N y ⎰⎰∂∂-=)()(ϕ,于是⎰⎰⎰∂∂-+=)(dy y M N Mdx u 做题步骤:① 先设u(x,y),② 证明xN y M ∂∂=∂∂,③ 从M 出发对方程两端同时求积分得)(),(),(y dx y x M y x u ϕ+=⎰,④ 对u 求偏导:),()(y x N y Mdx y y u ='+∂∂=∂∂⎰ϕ,⑤ 两边积分得dy dx y M N y ⎰⎰∂∂-=)()(ϕ,⑥ 得⎰⎰⎰∂∂-+=dy dx y M N Mdx u )(。

115§6常微分方程的求解一、知识背景常微分方程在物理学,工程技术中运用非常广泛,相当重要。
许多物质运动的过程用常微分方程来描述,如:质点的加速运动、谐振动、电容充放电过程及电感通电断电等过程,因此,求解常微分方程成为很多物理问题求解的一种常用方法。
而有时很难求出解析解,但可求出常微分方程的数值解以逼近解析解,以完成对摸型的研究。
求解常微分方程数值解通常有欧拉法和龙格-贝塔法。
欧拉法解法的基本思想是在小区间上用差商代替导数,并通过把小区间不断地划分求极限,从而最终得到数值解。
龙格-贝塔方法基本思想也是用差商代替导数,但是该方法是在小区间内运用了微分中值定理,在小区间内多取点,再取加权平均值来构造精度更高的计算式。
在MATLAB 系统中,主要采用龙格-贝塔法来计算常微分方程的数值解。
图 6-10d d =+c q tq R或 cqt q R-=d d 我们也可写成右面方程组形式:),(d d t q f tq =,00)(q t q =这即是一阶常微分方程初值问题的一般形式。
二、 计算指令 —— ode23,ode45语句格式(以ode23为例):[ t, y ] = ode23 (‘f ’,tspan,y0,tol )语句中各符号意义如下f :求解的常微分方程的文件名,把方程写成函数形式并存储于m 文件中。
方程形式为y'=f(t,y)。
举例:如图6-1中所示电路,先将开关k 掷向“1”端,待电容器c 充完电后,将开关k 掷向“2”端,电容器开始放电。
放电过程满足下面方程:116tspan :输入[t0,tf],分别为自变量的初始值和最终值,为单调递增(减)的积分区间。
y0:函数的初始值矢量。
Tol :误差范围,(缺省值为0.000001)[t,f]:t 是输出的时间列矢量,矩阵y 的每个列矢量是解的一个分量。
例1:用求数值解方法,求解常微分方程:3'x x -=,初始值x(0)=1。


第六讲 常微分方程 一 知识点详解(一)常微分方程的概念 1内容展开(1) 定义:含有未知一元函数及其导数和自变量的方程称为常微分方程,简称微分方程 (2) 微分方程的阶:微分方程中含有的未知函数的导数色最高阶称为微分方程的阶 (3) 微分方程的解:1) 解得定义:将()y f x =带入微分方程,使方程称为恒等式,则称()y f x =是微分方程的解 2) 通解:微分方程的解中含有自由常数,且含独立自由常数的个数等于微风方程的阶数,则称该解为通解3) 特届:不含任意常数的解称为微分方程的特解。
求特解时,初始条件的个数等于微分方程的阶数 (二)一介微分方程 1 内容展开(1)变量可分离微分方程 1)方程形式()()'y f x g y =2) 解法 当()0g y ≠时,()()()()'dyy f x g y f x dx g y =⇔= 两边求不定积分()()dy f x dx C g y =+⎰⎰其中拨C 为任意常数,其中()dyg y ⎰表示函数()1g y 的一个原函数,()f x dx ⎰表示函数()f x 的一个原函数若0y 使()00g y =,则0y y =也是原方程的一个特解注:①尽可能把y 写成x 的函数,也尽可能把y 从对数中“解脱”出来 ②不要漏掉()00g y =这种常数解 (2)齐次微分方程 1)方程形式 'y y f x ⎛⎫=⎪⎝⎭2)解法 令y u x =由于''y u xu =+,所以微分方程'y y f x ⎛⎫= ⎪⎝⎭变为()()'1u f u u x =-,这是关于未知函数u 的一个变量可微分方程,由此方程解得未知函数()u u x =,进而得到微分方程的解()()y x xu x =(3)一阶线性微分方程 1)方程形式 ()()'y p x yq x +=当右端项()q x 恒为零时称其为一阶齐次线性微分方程,否则称其为一阶非齐次线性微分方程 2)解法()()()p x dx p x dy y e q x e dx C -⎛⎫⎰⎰=+ ⎪⎝⎭⎰ (4)伯努利方程1)方程形式 形如()()()',0,1n y p x y q x y n +=≠2)解法 令1n u y -=,则伯努利方程变为()()()()'11u n p x u n q x +-=-,这是关于未知函数()u u x =的一个一阶线性微分方程 (5)全微分方程1)方程形式 ()(),,0p x y d x Q x y d y+=,若P Qy x∂∂=∂∂,该方程称为全微分方程 2)解法()()()()00,,,,x y x y P x y dx Q x y dy C +=⎰2 记忆方法(1)齐次微分方程和一阶齐次线性微分方程最终都要化为变量可分离微分方程求解 (2) 齐次微分方程的基本方法是:令y u x=; (3) 一阶非齐次线性微分方程的求解就是记公式 3 例题讲解【例6.1】微分方程()'1y x y x-=的通解是() 解析:可分离变量微分方程()()11,y x x dy dy dx dx x y x--== 1,dy dx dx y x =-⎰⎰⎰即ln ln y x x C =-+所以xy Cxe -=【例6.2】微分方程'2ln xy y x x +=满足()119y =-的解为() 解析: 将'2ln xy y x x +=化为'2ln y y x x+=带入通解公式得 222ln 2ln ln ln dx dxx x x x y e x e C e x e dx C --⎡⎤⎰⎰⎡⎤=⋅+=⋅+⎢⎥⎣⎦⎣⎦⎰⎰221ln x xdx C x ⎡⎤=+⎣⎦⎰ 2ln 39x x C x x=-+由()119y =-求得0C =所以1ln 33x y x ⎛⎫=- ⎪⎝⎭【例6.3】 微分方程312dy y y dx x x ⎛⎫=- ⎪⎝⎭满足11x y==的特解为y=()解析:令y ux =,有dy du u x dx dx =+原方程化为312du u x u u dx +=-即 32du dx u x =-,积分得21ln x C u =+即22ln x y x C=+ 由于1,1,x y ==得C=1,所以得解y =(三)可降阶微分方程 1内容展开 (1) 方程()()n yf x =求n 次定积分得解(2) 方程()''',y f x y =这类方程的特点是不显含未知函数y ,显含自变量x ,令()'p x y =,则微分方程()''',y f x y =变为()',p f x p =,这是关于()p p x =的一个一阶微分方程(3) 方程()''',y f y y =这类方程的特点是不显含自变量x ,显含未知函数y ,令()'p y y =,则2'2d y d p d p d y p p d x dx dy dx===,因此微分方程()''',y f y y =变为()',p p f y p =这是一个以y 为自变量,()p y 为未知函数的一阶微分方程2记忆方法1) 方程形如()''',y f x y =时,令()'p x y = 2) 方程形如()''',y f y y =时,令()'p y y =3例题讲解【例6.4】微分方程()2'''0yy y+=满足初始条件'011,2x x yy ====的特解是() 解析:令''',d p d p d y d p y p y p d x d y d x d y ===⋅=原方程化为:20dp yp p dy+=得00dpp yp dy=+=或 0p =不满足初始条件'01x y ==舍弃0dpyp dy +=按分离变量法解之得1C p y=由初始条件'012x y ==解得112C =于是得12dy dx y=解之得22y x C =+以'01x y ==带入,得21C =且取+号所以y =(四)二阶线性微分方程解得性质1内容展开()()()'''y p x y q x y f x ++= ①非齐次()()'''0y p x y q x y ++= ②齐次(1) 若12,y y 是②得解,则123c y c y +也是②的解,其中12,c c 为任意常数 (2) 若12,y y 是②得两个线性无关的解12y c y ⎛⎫≠⎪⎝⎭,则1122yc y c y =+ 是②的通解 (3) 若12,y y 是①的解,则12y y -为②得解(4) 若y是②的通解,*y 是①的特解,则*y y y =+ 是①的通解 (5) 若*1y 是()()()'''1y p x y q x y f x ++=得解,*2y 是()()()'''2y p x y q x y f x ++=的解,则**12y y +是()()()()'''12y p x y q x y f x f x ++=+得解 2记忆方法与线性代数中方程组得解的理论是类似的 3例题讲解 无(五) 高阶常系数线性微分方程 1 内容展开(1) 二阶常系数齐次线性微分方程1) 方程形式 '''0y ay by ++=,其中a,b 是常数 2) 解法(特征方程法)方程20a b λλ++=称为它的特征方程,特征方程的根12,λλ称为它的特征根 ①当12λλ≠且均为实数时,微分方程的通解是()1212xxy x C e C eλλ=+②当12λλ=时,微分方程的通解是()1112xxy x C e C xe λλ=+③当1,2i λαβ=±时,微分方程的通解是()()12cos sin x y x e C x C x αββ=+ (2) 高于二阶常系数齐次线性微分方程方法和二阶常系数线性微分方程类似(3) 二阶常系数非齐次线性微分方程 1) 方程形式()'''y ay by f x ++=2) 解法:由解得性质知,需找到对应齐次方程的通解和非齐次方程的一个特解,下找特解: ①右端项为()xn f x Pe μ=其中()n P x 为n 次多项式设方程的特解形式为()()*k x n yx x Q x e μ=,其中A) ()1110nn n n n Q x a x a xa x a --=++++ ,为n 次多项式的一般形式;B) k 的取值:当μ不是'''0y ay by ++=的特征根时,k=0 当μ是'''0y ay by ++=的单特征根时,k=1 当μ是'''0y ay by ++=的复特征根时,k=2 将()()*k x n yx x Q x e μ=代入微分方程()'''xn y a y b y P x e μ++=求出特定系数(),0,1,2,3,k a k n =②右端项为()()cos xn f x e P x x αβ=的方程,其中()n P x 为n 次多项式设方程的特解形式为()()()*cos sin k x n n yx x e Q x x W x x αββ=+⎡⎤⎣⎦其中“A )()1110,nn n n n Q x a x a x a x a --=++++ ()1110,n n n n n W x b x b x b x b --=++++B)k 的取值:当i αβ±不是'''0y ay by ++=的特征根时,k=0 当i αβ±是'''0y ay by ++=的特征根时,k=1 将()()()*cos sin k x n n y x x e Q x x W x x αββ=+⎡⎤⎣⎦代入()'''c o s x n y a y b y eP xαβ++=求出待定系数(),0,1,2k k a b k n =注:数三只要求自由项为多项式函数,指数函数,正炫函数,余弦函数的二阶常系数非齐次方程 2记忆方法(1) 方程右端含有三角函数时,所设特解中有与微分方程右端项中最高次幂相同的多项式函数,相同的指数函数和kx (k 的取值取决于右端项中的指数函数x e μ中的μ的作为特征根的重数)(2) 方程右端含有三角函数时,所设特解中有与微分方程右端项中最高次幂相同的多项式函数,相同的指数函数,相同系数正炫函数与余弦函数,和k x (k 的取值取决于右端项中的指数函数x e μ和三角函数()cos sin x x ββ和中的i αβ±是否为特征根)3例题讲解【例6.5】求微分方程'''2432x y y y e -+=的通解解析:与所给方程对应的齐次线性微分方程为'''430y y y -+=它的特征方程为2430r r -+=得特征根121,3r r ==所以,对应齐次线性微分方程的通解为312x x Y C e C e =+由于2不是特征方程的根,故设该非齐次线性微分方程的特解为*2xy Ae=,将()()'''*2*2*2,2,4x x xy Ae y Ae y Ae ===带入原方程,有222244232x x x x Ae Ae Ae e -⋅+=解得2A =-所以*22x y e =-所以,原方程通解为*32122x x x y Y y C e C e e =+=+- (六) 欧拉方程 1内容展开(1) 方程形式 形如()2'''x y axy by f x ++=的微分方程称为2阶欧拉方程,其中a ,b是常数(2) 解法,当0x >时,令'x e =,欧拉方程变为()2'2(1)d y dya by f e dt dt+-+=,这时一个以t 为自变量,y 为未知函数的2阶线性常系数微分方程当0x <时,作变量代换'x e =-,可类似求解 2记忆方法当0x >时令'x e =;当0x <时,令'x e =- 3例题讲解 无 (七) 差分方程 1内容展开 (1)定义一阶常系数齐次线性差分方程 10t t y ay ++=一阶常系数非齐次线性差分方程 ()1t t y ay f t ++=其中()f t 为已知常数,a 为非零常数 (2)其次差分方程的通解通过迭代,并由数学归纳法可得一阶常系数齐次线性差分方程的通解为:()()tC y t C a =⋅-其中C 为任意常数(3) 非齐次差分方程的解得性质1) 若*y 是非齐次差分方程的一个特解,()C y t 是齐次差分方程的通解,则非齐次差分方程的通解为()*t C t y y t y =+2) 若1t y y 和分别是差分方程()11t t y ay f t ++=和()12t t y ay f t ++=的解,则1t y y +是差分方程()()112t t y ay f t f t ++=+得解 (4) 非齐次差分方程的特解形式非齐次差分方程()1t t y ay f t ++=的特解*t y 形式的设定如下表2记忆方法其次差分方程1t t y ay ++的通解为()()tC y t C a =⋅- 非齐次差分方程()1t t y ay f t ++=的特解*t y 形式设定如下3例题讲解【例6.6】差分方程121050t t y y t ++-=的通解为() 解析:原方程的一般形式为1552t t y y t ++=对应的其次差方程为150t t y y ++=,其通解为()()'5C y t C =-(C 为任意常数)()52f t t =是t 的一次多项式且51a =≠-,故设原方程的特解*t y At B =+带入原方程得()()5152A t B At B t ++++=即5662At A B t ++=比较系数知 55,1272A B ==-故*51126t y t ⎛⎫=- ⎪⎝⎭从而原差分方程的通解为()()'*515126t C t y y t y C t ⎛⎫=+=-+- ⎪⎝⎭三 典型例题【例6.7】设函数()y x 连续,求解方程:()()2012xy s ds y x x +=⎰1) 分析:题目中遇到变项积分一般都是要求导数的 2) 解析:易判断()y x 可导,等式两端对x 求导得:()()'122y x y x x +=在原方程中令()000x y ==得从而得初值问题()'2400y y xy ⎧+=⎪⎨=⎪⎩这是含初始条件时的一阶非齐次线性微分方程,由公式有:222421dx dx xy e xe C x Ce --⎛⎫⎰⎰=+=-+ ⎪⎝⎭⎰代入初始条件()001y C =⇒=所以221x y x e -=-+3) 备注:变限积分与微分方程综合考察时,注意确定初始条件,方法—令积分上下限取值相同 【例6.8】求微分方程''cos y y x x +=+1) 分析:自由项是函数之和时二阶常系数非齐次线性微分方程的特解利用解得叠加原理 2) 解析:原方程对应的 齐次方程''0y y +=的特征方程为210λ+=,特征根1,2,i λ=±故齐次方程的通解为12cos sin yC x C x =+ 设非齐次方程''y y x +=的特解为1y Ax B =+代入方程,得A=1,B=0所以1y x = 设非齐次方程''cos y y x +=的特解为2c o s s i n y Ex x Dx x =+代入方程得10,2E D ==所以21sin 2y x x = 由于12y y +为原方程''cos y y x x +=+的一个特解,所以原方程的通解为12121cos sin sin 2y yy y C x C x x x x =++=+++ 3)备注:数学三不要求自由项是函数之和时二阶常系数非齐次线性微分方程,但大家要学会自由项为一项时的二阶常系数非齐次线性微分方程,即数学三考生要学会解微分方程''y y x +=和''cos y y x +=。

常微分方程数值解-图文一只小船度过宽为d的河流,目标是起点A正对着的另一岸B点,已知河水流速v1与船在静水中的中的速度v2之比为k(1)建立描述小船航线的数学模型,求其解析解;(2)设d=100m,v1=1m/,v2=2m/,用数值解法求渡河所需时间,任何时刻小船的位置及航行曲线,作图,并与解析解比较;(3)若流速v1=0,0.5,1.5,2m/结果将如何;解题过程(1)以B为原点,沿河岸向右为某轴正向,垂直河岸向下为y轴正向,建立坐标系。
设在t时刻,船在某方向上的位移是某(t),在Y方向上的位移是y(t)。
在t时刻,船在某方向上的速度是某'(t),在y方向上的速度是y'(t),将船的速度v和水度v1在某,y轴方向上分解,可得:v某v1v2in及vyv2co又tan某y故in某某y22cov2yy某22y某y22则有vydy=dt以及v某(2)d某=v1dtv2某y某22数值解:下面将用龙格-库塔方法对微分方程和微分方程组进行近似求解function某dot=fun(t,某,v1,v2)d=100;v1=1;v2=2;if(norm(某)>1e-5)某dot=[v1-v2某某(1)/qrt(某(1).^2+某(2).^2),-v2某某(2)/qrt(某(1).^2+某(2).^2)];ele某dot=[0,0];endholdoff;某0=[0,-d];[t,某(:,1),某(:,2)];eta=linpace(-pi/2,0,100);d=100;v1=1;v2=2;rou=d某(ab(tan(eta/2))).^(v2/v1)/in(eta);某p=-rou.某co(eta);yp=-rou.某in(eta);plot(某p,yp,'r某');得到v1=1m/时的渡河路线,所用时间为:66.7秒解析解:令某rin;yrco,将直角坐标化为极坐标,由导数的的链式法则,我们可以得到d某indrrcoddycodrrind又d某v某dt;dyvydtdtanm()2其中mv2解得rv1in编程如下:a=pi/2:-0.01某pi:0;d=100;m=2;r=d某ab(tan(a/2).^m./in(a));polar(a,r,'.')运行轨迹如下:(3)依次修改参数V1,运行结果如下如图左一上所示v1=0时的渡河路线,在静水中,船沿直线到达B点,渡河时间为50秒。