函数的图像及应用

五个重要的初等函数的图像和性质：一、羊角线：y=|x-a|（1）图像性质：单调性，对称性，（2）应用：①方程|x-2|=2a-1有两个不等实根，求a 的取值范围；②|x-2|=(1/2)x+a 有两个不等实根，求a 的取值范围；③若y=|x-2a+1|是偶函数，求a 的取值范围；二、槽形线：y=|x-a|+|x-b|（1）图像：值域，单调性，对称性（2）应用：①方程|x-2|+|x-3|=2a-1有2个不等实根，求a 的取值范围；②|x-2|+|x-3|> 2a+1恒成立，求a 的取值范围；③若y=|x-2a|+|x-3a+1|是偶函数，求a 的值；④若|x-2|+|x-3|> 3，求a 的取值范围.三、Z 形线：y=|x-a|-|x-b|（1）图像：值域，单调性，对称性（2）应用：①方程|x-2|+|x-3|=2a-1仅有一个实根，求a 的取值范围；②若|x-2|-|x-3|> 2a+1恒成立，求a 的取值范围；③若y=|x-2a|-|x-3a+1|是奇函数，求a 的值；④若|x+2|-|x-3|> 3，求a 的取值范围.引申：无解问题，有解问题 四、最简分式函数：bc)ad 0,(c dcx b ax y ≠≠++= （1）图像：定义域、值域、单调性、对称性、对称中心原式化为：dcx c a d cx b d cx y c ad bc c ad ca ++=++-+=-)(，移项整理则有：)(c d cad bc c ad bc x d cx c a y --=+=---故有： ⅰ⎪⎪⎪⎩⎪⎪⎪⎨⎧≠⎪⎩⎪⎨⎧=-=-≠≠++=;)2(),,()1(),0(的一切实数值域为渐近线为双曲线中心为c a y c a y c d x c a c d bc ad c d cx b ax y ； ⅱ当02>-cad bc 即ad bc >时，函数由反比例函数将对称中心按向量),(c a c d -=ξ平移，再经过横向的伸缩变换（102<-<c ad bc 时横向伸长，21cad bc -<时横向缩短）而得； ⅲ当20cad bc -<即ad bc <时，函数由反比例函数将对称中心按向量),(c a c d -=ξ平移，然后做关于X 轴的对称变换，再经过横向的伸缩变换而得（1||02<-<c ad bc 时横向伸长，||12cad bc -<时横向缩短）而得。

二次函数图像的变化规律及应用引言：二次函数是高中数学中的重要内容之一，它的图像呈现出一种独特的形态，具有丰富的变化规律和广泛的应用。

本文将从图像的变化规律和应用两个方面，对二次函数进行深入的探讨。

一、图像的变化规律1. 平移变换二次函数的图像可以通过平移变换而得到不同的形态。

平移变换是指在坐标平面上将图像整体向左、右、上、下平移的操作。

对于二次函数y=ax^2+bx+c，当平移向右时，a保持不变，b不变，c减小；当平移向左时，a保持不变，b不变，c增大；当平移向上时，a增大，b不变，c增大；当平移向下时，a减小，b不变，c减小。

通过平移变换，我们可以观察到二次函数图像在平面上的移动轨迹，进而掌握其变化规律。

2. 缩放变换缩放变换是指在坐标平面上将图像整体放大或缩小的操作。

对于二次函数y=ax^2+bx+c，当缩放因子为k时，a不变，b不变，c增大（或减小）k倍。

缩放变换可以改变二次函数图像的大小和形状，通过观察不同缩放因子下的图像，我们可以总结出二次函数图像的缩放规律。

3. 翻折变换翻折变换是指在坐标平面上将图像关于某一直线进行对称的操作。

对于二次函数y=ax^2+bx+c，当翻折轴为x轴时，a不变，b变号，c不变；当翻折轴为y轴时，a变号，b不变，c不变；当翻折轴为直线x=k时，a不变，b变号，c变号。

翻折变换可以改变二次函数图像的位置和形状，通过观察不同翻折轴下的图像，我们可以总结出二次函数图像的翻折规律。

二、图像的应用1. 最值问题二次函数的图像呈现出一个开口朝上或朝下的抛物线形态，通过观察图像的顶点，我们可以得出二次函数的最值。

当抛物线开口朝上时，顶点为最小值；当抛物线开口朝下时，顶点为最大值。

最值问题在实际应用中有广泛的应用，例如在物理学中，我们可以通过最值问题求解物体的最高点或最低点。

2. 零点问题二次函数的图像与x轴的交点称为零点，也叫根或解。

通过观察图像与x轴的交点，我们可以求解二次函数的零点。

函数的图像及其性质研究与应用函数是数学中一个非常重要的概念，它描述了两个集合之间的一种对应关系。

在实际应用中，函数的图像是我们研究和分析函数性质的重要工具之一。

本文将从几个方面来探讨函数的图像及其性质的研究与应用。

一、函数的图像函数的图像是指函数在坐标系中的表示形式。

通常我们用平面直角坐标系来表示函数的图像，其中横轴表示自变量，纵轴表示因变量。

函数的图像可以通过绘制函数的关系式来得到。

例如，对于一元函数y=f(x)，我们可以通过给定自变量x的值，计算相应的因变量y的值，然后在坐标系中绘制这些点，最终得到函数的图像。

函数的图像可以帮助我们直观地理解函数的性质。

通过观察函数的图像，我们可以了解函数的增减性、奇偶性、周期性等特征。

例如，对于增函数来说，函数的图像随着自变量的增大而上升；对于周期函数来说，函数的图像在一个周期内重复出现。

二、函数的性质研究函数的性质研究是数学中的一个重要分支，它帮助我们深入理解函数的行为规律。

函数的性质包括但不限于增减性、奇偶性、周期性、单调性等。

1. 增减性函数的增减性描述了函数在定义域内的增减趋势。

对于一元函数来说，如果函数在某个区间内的导数大于零，则函数在该区间内是增函数；如果函数在某个区间内的导数小于零，则函数在该区间内是减函数。

通过研究函数的增减性，我们可以确定函数的极值点和拐点，进而帮助解决最优化问题。

2. 奇偶性函数的奇偶性描述了函数的对称性。

对于一元函数来说，如果函数满足f(-x)=-f(x)，则函数是奇函数；如果函数满足f(-x)=f(x)，则函数是偶函数。

奇函数的图像关于原点对称，而偶函数的图像关于纵轴对称。

奇偶性的研究有助于简化函数的运算和化简复杂的表达式。

3. 周期性周期函数是一类具有重复性质的函数。

对于周期函数来说，存在一个正数T，使得对于任意的x，函数满足f(x+T)=f(x)。

周期函数的图像在一个周期内重复出现，因此我们只需要研究一个周期内的行为即可。

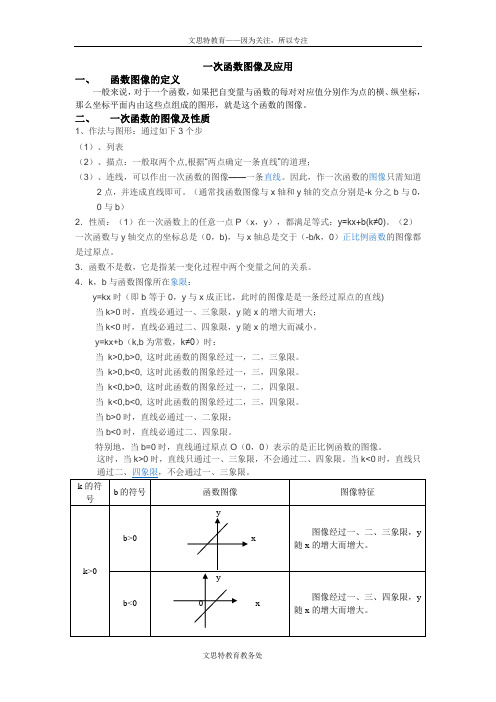
一次函数图像及应用一、函数图像的定义一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图像。

二、一次函数的图像及性质三、小试身手1、画出函数y=2x-1与y=-0.5x+1的图象2、直线y=2x-3与x轴交点坐标为_______，与y轴交点坐标为_________，•图象经过第________象限，y随x增大而_________．3、分别说出满足下列条件的一次函数的图象过哪几个象限？（1）k>0 b>0 （2）k>0 b<0（3）k<0 b>0 （4）k<0 b<04、在同一直角坐标系中画出下列函数图象，并归纳y=kx+b（k、b是常数，k≠0）中b对函数图象的影响．１．y=x-1 y=x y=x+1２．y=-2x+1 y=-2x y=-2x-1练习巩固1、例1 小芳以200米／分的速度起跑后，先匀加速跑5分钟，每分提高速度20米／分，又匀速跑10分钟．试写出这段时间里她跑步速度y（米／分）随跑步时间x（分）变化的函数关系式，并画出图象．2、Ａ城有肥料200吨，Ｂ城有肥料300吨，现要把这些肥料全部运往Ｃ、Ｄ两乡．从Ａ城往Ｃ、Ｄ两乡运肥料费用分别为每吨20元和25元；从Ｂ城往Ｃ、Ｄ两乡运肥料费用分别为每吨15元和24元．现Ｃ乡需要肥料240吨，Ｄ乡需要肥料260吨．怎样调运总运费最少？3、从Ａ、Ｂ两水库向甲、乙两地调水，其中甲地需水15万吨，乙地需水13万吨，Ａ、Ｂ两水库各可调出水14万吨．从Ａ地到甲地50千米，到乙地30千米；从Ｂ地到甲地60千米，到乙地45千米．设计一个调运方案使水的调运量（万吨·千米）最少．4、某单位急需用车，但又不准备买车，他们准备和一个体车主或一国有出租车公司其中一家签让合同．设汽车每月行驶x千米，应付给个体车主的月费用是y 1元，应付给出租车公司的月费用是y2元，y1、y2分别是x之间函数关系如下图所示．每月行驶的路程等于多少时，租两家车的费用相同，是多少元？四、课后习题1.当x <0时,函数y =-2x 的图象在A.第一象限B.第二象限C.第三象限D.第四象限2.直线x y 3-=过点(0,0)和点A.(1,-3)B.(1,3)C.(-1,-3)D.(3,-1)3.函数x y 2=与x y 3-=的共同特点是A.图象经过一､三象限B.图象经过二､四象限C.图象经过原点D.y 随着x 的增大而增大4.函数y =-x 21+1和y =x 21+1的图象交于一点,这点的坐标是A.(1,21) B.(-1,23) C.(1,0) D.(0,1)5.函数x m y )1(-=(1≠m ),y 随着x 的增大而增大,则A.m <0B.m >0C.m <1D.m >19.下面图象中,不可能是关于x 的一次函数y =mx -(m -3)的图象的是10.在同一个直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是A.通过点(-1,0)的是①和③B.交点在y轴上的②和④C.相互平行的是①和③D.关于x轴对称的是②和③32.某公司市场营业员销部的营销人员的个人收入与其每月的销售量成一次函数关系,其图象如图所示.由图中给出的信息可知,营销人员没有销售时的收入是A.310B.300C.290D.28033.如图,OA,BA分别表示甲､乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快A.2.5米B.2米C.1.5米D.1米34.一游泳池长90米,甲､乙二人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲､乙与游泳池一边的距离随游泳时间的变化而变化图象.若不计转向时间,则从开始起到3分钟止他们相遇的次数为A.2次B.3次C.4次D.5次。

指数函数的图像及应用教案指数函数是数学中的一种重要的函数类型，其函数表达式为y = a^x，其中a为常数且大于0且不等于1，x为自变量，y为函数的值。

指数函数的特点是随着自变量x的增大，函数的值也会呈现出快速增长或快速减小的情况。

在本文中，我们将重点介绍指数函数的图像和应用。

一、指数函数的图像1. 当a大于1时，指数函数的图像呈现出递增的趋势。

例如，当a=2时，指数函数y = 2^x的图像如下：x -2 -1 0 1 2y 1/4 1/2 1 2 4从图中可以看出，随着自变量x的增大，函数的值y也会呈现出较快的增长，形成一个逐渐向上的曲线。

2. 当a介于0和1之间时，指数函数的图像呈现出递减的趋势。

例如，当a=1/2时，指数函数y = (1/2)^x的图像如下：x -2 -1 0 1 2y 4 2 1 1/2 1/4从图中可以看出，随着自变量x的增大，函数的值y会呈现出较快的减小，形成一个逐渐向下的曲线。

3. 当a等于1时，指数函数的图像为一条水平直线y=1，因为任何数的1次方都等于1，所以函数的值始终为1。

二、指数函数的应用指数函数在数学中有许多重要的应用，以下是其中一些常见的应用示例：1. 经济增长模型在经济学中，指数函数常被用于描述经济增长的过程。

例如，人口增长模型中经常使用指数函数来描述人口随时间的增长。

指数函数的特性使得人口在某些情况下会呈现出爆炸式增长，这对于制定政府的人口政策和规划社会资源分配具有重要的指导意义。

2. 化学反应速率模型在化学中，许多反应速率都符合指数函数的模型。

指数函数可以描述反应物浓度与反应速率之间的关系。

例如，放射性衰变过程中的半衰期可以通过指数函数来描述。

3. 财务管理与复利计算复利是指每期的利息还会产生新的利息，所以总金额并不是简单地原始金额加上利息，而是以指数函数的形式增长。

复利计算在财务管理中十分常见，可以用来计算投资的回报率、贷款的利息等。

4. 生物学模型在生物学中，指数函数可以用来描述生物种群的生长模式。

函数sin的图像及应用sin函数是三角函数中最常见的一种函数，它表示的是一个周期性的波动曲线。

sin(x)的图像是一条振荡于y=0附近的曲线，周期为2π。

首先，让我们来看一下sin(x)函数的图像。

我们知道sin(0)=0，因此函数图像会经过原点(0,0)。

而当x取π/2、π、3π/2等值时，sin(x)函数的值会达到最大值1；而当x取5π/2、3π、7π/2等值时，sin(x)函数的值会达到最小值-1。

因此，sin(x)的图像会在这些点上有拐点。

另外，sin(x)函数是奇函数，即满足sin(-x)=-sin(x)，因此它在y轴上是关于原点对称的。

sin(x)的图像可以被用于描述各种自然现象和科学问题。

以下是一些常见的应用：1. 声音和音乐：在声音和音乐的领域中，我们可以用sin(x)函数来描述声波的振动。

不同频率的声波振动会产生不同的音调，而sin(x)函数的周期性特点可以用来演示各种音调的波动。

2. 电信号：在电工学和通信领域中，sin(x)函数用于描述交流电信号的变化。

交流电信号的周期性特点和振幅可以用sin(x)函数来表示，这样可以更好地理解电信号的变化和输送过程。

3. 光和光学：在光学研究中，我们可以用sin(x)函数来描述光波的传播和干涉现象。

例如，当光通过狭缝时，会形成干涉条纹，这些条纹的分布可以通过sin(x)函数来描述和解释。

4. 天文学：在天文学中，sin(x)函数也有广泛的应用。

例如，我们可以用sin(x)函数来解释地球的季节变化和日晷的行为。

地球围绕太阳的运动可以用sin(x)函数来模拟，这样我们可以预测太阳的升起和落下时间。

5. 振动和波动：在物理学研究中，sin(x)函数常常用来描述振动和波动的现象。

例如，弹簧振子、钟摆以及水波等都可以通过sin(x)函数来描述它们的运动规律。

总之，sin函数是一种周期性的函数，可以用来描述各种自然现象和科学问题中的振动和波动现象。

我们可以通过观察和分析sin(x)的图像来理解这些现象的变化规律，进而应用到实际的科学研究和工程问题中。

函数图像的应用归纳总结在数学中，函数图像是一种重要的工具，它在各个领域具有广泛的应用。

通过观察和分析函数图像，我们可以得出许多有用的结论和推论。

本文将对函数图像的应用进行归纳总结，并探讨其在实际问题中的应用。

一、函数图像的形态通过观察函数图像的形态，我们可以了解函数的性质和变化趋势。

比如，当函数图像呈现上升趋势时，我们可以判断该函数是递增的；当函数图像呈现下降趋势时，我们可以判断该函数是递减的。

另外，函数图像的凹凸性也是我们关注的重点。

当函数图像呈现向上的凹状时，我们可以判断函数具有凹性；当函数图像呈现向下的凸状时，我们可以判断函数具有凸性。

这些凹凸性的特点对于优化问题的求解和最值点的确定具有重要的指导作用。

二、函数图像的交点和零点观察函数图像的交点和零点可以帮助我们解决方程和不等式问题。

当两个函数图像相交时，我们可以通过寻找交点的横坐标和纵坐标来求解方程。

当函数图像与x轴相交时，我们可以通过寻找零点的横坐标来求解方程或不等式。

例如，当我们需要求解方程“f(x) = g(x)”时，我们可以将两个函数图像绘制在同一坐标系上，通过观察交点的横坐标来得到方程的解。

同样地，当我们需要求解不等式“f(x) > g(x)”时，我们可以观察函数图像与x轴的交点和函数图像的上升或下降趋势，从而确定不等式的解集。

三、函数图像的极值点和最值点函数图像的极值点和最值点对于优化问题的求解非常重要。

当函数图像在某一点具有极值时，该点的横坐标和纵坐标可以帮助我们确定极值点的位置和值。

当函数图像在某一段区间上具有最值时，该区间的两个端点和函数图像的变化趋势可以帮助我们确定最值点的位置和值。

例如，当我们需要求解函数的极值问题时，我们可以通过观察函数图像的变化趋势和拐点的位置来确定极值点的值和位置。

同样地，当我们需要求解函数在一段区间上的最值问题时，我们可以观察函数图像在该区间上的变化趋势和端点的值，从而确定最值点的位置和值。