第七章_机电能量转换原理
- 格式:ppt
- 大小:1.39 MB
- 文档页数:53
第一章机电能量转换的基本原理现代人类的生产和生活中,最主要的动力能源是电能。
实现机械能与电能转换的装置统称为机电能量转换装置........,以下简称机电装置。
它们大小不一,品种繁多,按其功能的不同可分为三大类:(1)机电信号变换器.......。
它们是实现机电信号变换的装置,是在功率较小的信号下工作的传感器,通常应用于测量和控制装置中。
例如拾音器、扬声器、旋转变压器等;(2)动铁换能器.....。
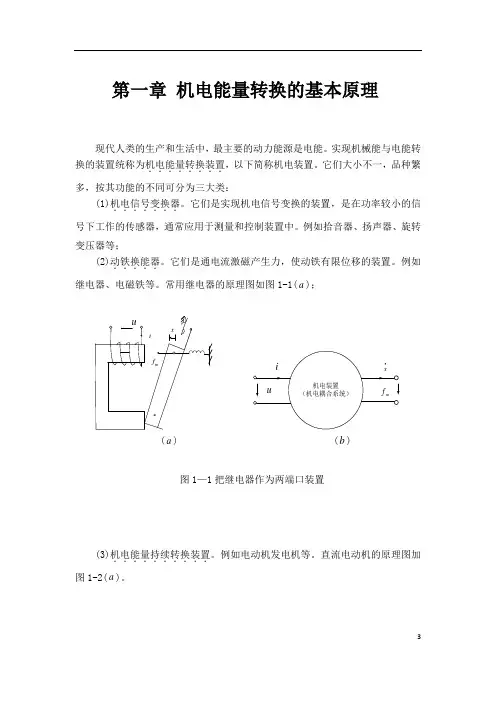
它们是通电流激磁产生力,使动铁有限位移的装置。
例如继电器、电磁铁等。
常用继电器的原理图如图1-1(a);(a) (b)图1—1把继电器作为两端口装置(3)机电能量持续转换装置..........。
例如电动机发电机等。
直流电动机的原理图加图1-2(a)。
4uf(a) (b)图1-2把直流电动机作为三端口装置机电装置实现机电能量转换的形式,大体有四种:①电致伸缩与压电效应:②磁致伸缩;③电场力;④电磁力。
前两种功率很小,又是不可逆的。
应用第三种形式——电场力来实现机电能量转换的装置称为静电式机电装置.......,只能得到不大的力和功率。
实用上绝大多数的机电装置是应用第四种形式——电磁力来实现机电能量转换的,称为电磁式机电装......置.。
本书以电磁式机电装置作为主要研究对象。
下面不加说明的机电装置仅指电磁式机电装置,或是电磁式与静电式两种机电装置。
它们都是由载流的电系统,可动的机械系统和作为耦合媒介与储存能量的电磁场三部分组成;队总体看,它们每个又都有固定的和可动的两大部件。
严格说,耦合电磁场应该是电场和磁场的综合体。
但在机电装置中,电频率较低,可动部件的运动速度大大低于光速,这样不仅可以忽略不计电磁辐射,认为机电装置是质量守恒的物理系统;而且可以把电场和磁场分别考虑,认为它们是彼此独立的。
因此在电磁式机电装置中耦合电磁场仅是磁场,但在静电式机电装置中耦合场仅是电场。
在分析研究时,机电装置总可以归纳成具有若干个电端5口和机械端口的装置。






第一章磁路与变压器§1-1 磁路的概念与计算P15(一)磁路的概念磁路:磁通经过的路径把导线绕成线圈,在套装或置放在铁芯上,当线圈内通有电流时,由于铁芯的导磁能力较好,大部分磁通被约束在铁芯内部,并按照一定的路径构成磁路。
另一方面,在构成磁路的铁芯和铁芯之间的工作气隙内,将会得到较强的磁场。
激磁电流(励磁电流):载流线圈中通过的用以产生(激励)磁路的电流。
激磁电流为直流,磁路中磁通恒定不随时间变化,成为直流磁路/恒定磁通磁路。
激磁电流为交流,磁通随时间而变化,称为交流磁路。
主磁通:线圈中通有激磁电流时,铁芯磁路(包括工作气隙)中通过较多的磁通。
漏磁通:围绕着载流线圈,在部分铁芯和铁芯周围的空间,产生的一些分散的较弱的磁通。
(二)安培环路定律安培环路定律:沿着任何一条闭合回线L,磁场强度H的线积分值∮H·dl恰好等于被该闭合回线所包围的总电流值Σi(亦称为全电流)∮H·dl=Σi(若电流与闭合回线.................)........L.的循环方向符合右手螺旋关系,取正值若沿着长度l,磁场强度H处处相等,且闭合回路所包围的总电流是由通有电流i的N匝线圈(或导体)所产生,则Hl=Ni磁路的欧姆定律:穿过某一截面积的磁通量φ等于磁通密度B的面积分φ=∫B·dA若闭合铁芯磁路中,磁通均匀地通过各个截面,却磁通密度B垂直于各个截面,则φ= B·A or B=φ/A磁场强度H与磁通密度B之间有下列关系B=μH(μ为介质的磁导率,空气μ0≈4π*10-7H/mF=Ni=(B/μ)*l =φ*l /(μ*A)F=Ni 作用在磁路上的安匝数,磁路的磁通势,磁势R =l /(μ*A)磁路的磁阻作用在磁路上的磁通势等于磁路内的磁通量乘以磁路的磁阻。
F=φ* RE=I*R (磁势F对应于电路中电势E,磁通量φ对应于电流I,磁阻对应于电阻R)磁阻的倒数称为磁导..匝数越多,激磁电流越大,磁势就越大。


