2020小升初数学公式大全

【导语】孩⼦的奥数成绩⽆法提⾼，是因为不适合学奥数呢?还是因为没有掌握住好的⽅法?以下整理的⼩升初常见的数学公式，希望对⼤家有所帮助。

1、每份数×份数=总数 总数÷每份数=份数 总数÷份数=每份数 2、1倍数×倍数=⼏倍数 ⼏倍数÷1倍数=倍数 ⼏倍数÷倍数=1倍数 (1-2不必涉及，不⽤讲也不提，让孩⼦⾃悟就可以了) 3、速度×时间=路程 路程÷速度=时间 路程÷时间=速度 4、单价×数量=总价 总价÷单价=数量 总价÷数量=单价 5、⼯作效率×⼯作时间=⼯作总量 ⼯作总量÷⼯作效率=⼯作时间 ⼯作总量÷⼯作时间=⼯作效率 (3-5功夫放在理解量的概念和感念间的关系上，不必背公式) 6、正⽅形 C周长，S⾯积，a边长 周长=边长×4，C=4a ⾯积=边长×边长，S=a×a 7、正⽅体 V：体积，a：棱长 表⾯积=棱长×棱长×6S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a 8、长⽅形 C周长，S⾯积，a边长 周长=(长+宽)×2C=2(a+b) ⾯积=长×宽S=ab 9、长⽅体 V：体积s：⾯积a：长b：宽h：⾼ (1)表⾯积(长×宽+长×⾼+宽×⾼)×2 S=2(ab+ah+bh) (2)体积=长×宽×⾼ V=abh 10、三⾓形 s⾯积，a底，h⾼ ⾯积=底×⾼÷2 s=ah÷2 三⾓形⾼=⾯积×2÷底 三⾓形底=⾯积×2÷⾼述题，抓住最后的两三分。

11、平⾏四边形 s⾯积，a底，h⾼ ⾯积=底×⾼ s=ah 12、梯形 s⾯积a上底b下底h⾼ ⾯积=(上底+下底)×⾼÷2 s=(a+b)×h÷2 13、圆形 S⾯积，C周长，∏(pai)，d=直径，r=半径 (1)周长=直径×∏=2×∏×半径 C=∏d=2∏r (2)⾯积=半径×半径×∏ 14、圆柱体 v：体积h：⾼s;底⾯积r：底⾯半径c：底⾯周长 (1)侧⾯积=底⾯周长×⾼ (2)表⾯积=侧⾯积+底⾯积×2 (3)体积=底⾯积×⾼ (4)体积=侧⾯积÷2×半径 15、圆锥体 v：体积h：⾼s;底⾯积r：底⾯半径 体积=底⾯积×⾼÷3 总数÷总份数=平均数 16、扇形 圆⼼⾓n度，半径r 弧长L=n/180×∏×r ⾯积S=n/360×∏×r×r =1/2×L×r 圆锥侧⾯积S侧=∏×r×l 圆锥表⾯积S=∏×r×l+∏×r×r (6-16，周长让孩⼦们⾃悟，⾯积统⼀为平均累线乘累⾼，理解了⾯积是线段的积累，OK，⾄于说体积，⽤平均累⾯乘累⾼即可) 17、和差问题的公式 (和+差)÷2=⼤数 (和-差)÷2=⼩数 18、和倍问题 和÷(倍数-1)=⼩数 ⼩数×倍数=⼤数 (或者和-⼩数=⼤数) 19、差倍问题 差÷(倍数-1)=⼩数 ⼩数×倍数=⼤数 (或⼩数+差=⼤数) 20、植树问题 (A)⾮封闭线路上的植树问题主要可分为以下三种情形： ⑴如果在⾮封闭线路的两端都要植树，那： 株数=段数+1=全长÷株距-1 全长=株距×(株数-1) 株距=全长÷(株数-1) ⑵如果在⾮封闭线路的⼀端要植树，另⼀端不要植树，那就这样： 株数=段数=全长÷株距 全长=株距×株数 株距=全长÷株数 ⑶如果在⾮封闭线路的两端都不要植树，那么： 株数=段数-1=全长÷株距-1 全长=株距×(株数+1) 株距=全长÷(株数+1) (B)封闭线路上的植树问题的数量关系如下： 株数=段数=全长÷株距 全长=株距×株数 株距=全长÷株数 21、盈亏问题 (盈+亏)÷两次分配量之差=参加分配的份数 (⼤盈-⼩盈)÷两次分配量之差=参加分配的份数 (⼤亏-⼩亏)÷两次分配量之差=参加分配的份数 (17、18、19、21不记公式，领悟各个量之间的关系就OK了，提前学⽅程，在四年级上学期就学，20参照⼿指头就⾏了) 22、相遇问题 相遇路程=速度和×相遇时间 相遇时间=相遇路程÷速度和 速度和=相遇路程÷相遇时间 23、追及问题 追及距离=速度差×追及时间 追及时间=追及距离÷速度差 速度差=追及距离÷追及时间 24、流⽔问题 顺流速度=静⽔速度+⽔流速度 逆流速度=静⽔速度-⽔流速度 静⽔速度=(顺流速度+逆流速度)÷2 ⽔流速度=(顺流速度-逆流速度)÷2 (相遇问题，追及问题，流⽔问题，⼯程问题，⽜吃草问题，⽔龙头问题，等是⼀个问题) 25、浓度问题 溶质的重量+溶剂的重量=溶液的重量 溶质的重量÷溶液的重量×100%=浓度 溶液的重量×浓度=溶质的重量 溶质的重量÷浓度=溶液的重量 (浓度问题其实是个平均问题，理解了就迎刃⽽解了，何必背公式) 26、利润与折扣问题 利润=售出价-成本 利润率=利润÷成本×100%=(售出价÷成本-1)×100% 涨跌⾦额=本⾦×涨跌百分⽐ 折扣=实际售价÷原售价×100%(折扣<1) 税后利息=本⾦×利率×时间×(1-利息税) (利润问题重在理解概念，弄清关系，不需记公式。

小升初数学公式汇总当准备参加小升初数学考试时，掌握一些重要的数学公式是至关重要的。

下面是一些常见的小升初数学公式的汇总，以便你更好地理解和记忆。

1. 直角三角形的勾股定理：在一个直角三角形中，直角边的平方等于两个其他边的平方之和。

即a^2 + b^2 = c^2，其中a和b为直角三角形的两条直角边，c为斜边。

2. 面积公式：- 矩形的面积为长乘以宽，即A = l * w。

- 正方形的面积为边长的平方，即A = s^2。

- 三角形的面积为底边乘以高的一半，即A = 1/2 * b * h。

- 圆的面积为半径的平方乘以π，即A = π* r^2。

3. 周长公式：- 矩形的周长为长和宽之和的两倍，即P = 2 * (l + w)。

- 正方形的周长为边长的四倍，即P = 4s。

- 三角形的周长为三条边的和，即P = a + b + c。

- 圆的周长为直径乘以π，即P = π* d。

4. 速度公式：速度等于路程除以时间，即v = s / t，其中v为速度，s为路程，t为时间。

5. 百分比公式：百分比等于所占比例乘以100，即百分数= （所占比例/ 总量）* 100。

6. 等比数列求和公式：等比数列是指每一项与前一项的比等于同一个常数。

等比数列的前n项和公式为Sn = a * (1 - r^n) / (1 - r)，其中Sn为前n项和，a 为首项，r为公比，n为项数。

7. 二次方程求根公式：对于二次方程ax^2 + bx + c = 0，其求根公式为x = (-b ±√(b^2 - 4ac)) / (2a)。

其中±表示两个根，√表示开根号。

8. 三角函数公式：- 正弦定理：在一个三角形中，任意一边的长度与对应的角的正弦值成比例。

即a/sinA = b/sinB = c/sinC，其中a、b、c为三角形的边长，A、B、C为三角形的角度。

- 余弦定理：在一个三角形中，任意一边的平方等于其他两边的平方之和减去两倍它们的乘积再乘以对应角的余弦值。

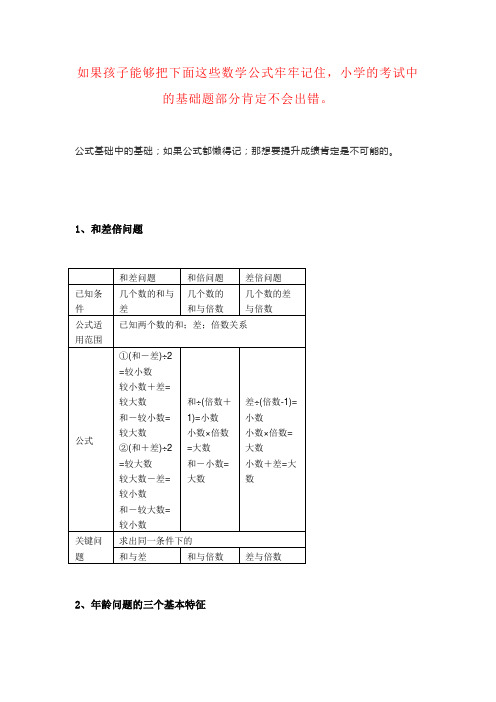
如果孩子能够把下面这些数学公式牢牢记住，小学的考试中的基础题部分肯定不会出错。

公式基础中的基础；如果公式都懒得记；那想要提升成绩肯定是不可能的。

1、和差倍问题2、年龄问题的三个基本特征①两个人的年龄差是不变的；②两个人的年龄是同时增加或者同时减少的；③两个人的年龄的倍数是发生变化的；3、归一问题的基本特点问题中有一个不变的量；一般是那个“单一量”；题目一般用“照这样的速度”……等词语来表示。

关键问题：根据题目中的条件确定并求出单一量；4、植树问题5、鸡兔同笼问题基本概念：鸡兔同笼问题又称为置换问题、假设问题；就是把假设错的那部分置换出来；基本思路：①假设；即假设某种现象存在（甲和乙一样或者乙和甲一样）：②假设后；发生了和题目条件不同的差；找出这个差是多少；③每个事物造成的差是固定的；从而找出出现这个差的原因；④再根据这两个差作适当的调整；消去出现的差。

基本公式：①把所有鸡假设成兔子：鸡数＝（兔脚数×总头数－总脚数）÷（兔脚数－鸡脚数）②把所有兔子假设成鸡：兔数＝（总脚数一鸡脚数×总头数）÷（兔脚数一鸡脚数）关键问题：找出总量的差与单位量的差。

6、盈亏问题基本概念：一定量的对象；按照某种标准分组；产生一种结果：按照另一种标准分组；又产生一种结果；由于分组的标准不同；造成结果的差异；由它们的关系求对象分组的组数或对象的总量。

基本思路：先将两种分配方案进行比较；分析由于标准的差异造成结果的变化；根据这个关系求出参加分配的总份数；然后根据题意求出对象的总量。

基本题型：①一次有余数；另一次不足；基本公式：总份数＝（余数＋不足数）÷两次每份数的差②当两次都有余数；基本公式：总份数＝（较大余数一较小余数）÷两次每份数的差③当两次都不足；基本公式：总份数＝（较大不足数一较小不足数）÷两次每份数的差基本特点：对象总量和总的组数是不变的。

关键问题：确定对象总量和总的组数。

小升初数学和差公式汇总机差倍问题小升初数学和差公式汇总
(和+差)÷2=大数
(和-差)÷2=小数
和倍问题
和÷(倍数-1)=小数
小数×倍数=大数
(或者和-小数=大数)
小升初数学和差倍问题公式
差÷(倍数-1)=小数
小数×倍数=大数
(或小数+差=大数)
植树问题
1.非封闭线路上的植树问题主要可分为以下三种情形:
⑴如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距-1
全长=株距×(株数-1)
株距=全长÷(株数-1)
⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+1)
2.封闭线路上的植树问题的数量关系如下
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数。

小升初数学追及问题公式小升初数学追及问题公式两个运动物体在不同地点同时出发(或者在同一地点而不是同时出发，或者在不同地点又不是同时出发)作同向运动，在后面的，行进速度要快些，在前面的，行进速度较慢些，在一定时间之内，后面的追上前面的物体。

这类应用题就叫做追及问题。

追及时间=追及路程÷(快速-慢速)追及路程=(快速-慢速)某追及时间简单的题目直接利用公式，复杂的题目变通后利用公式。

例1、好马每天走120千米，劣马每天走75千米，劣马先走12天，好马几天能追上劣马?解：(1)劣马先走12天能走多少千米? 75某12=900(千米)(2)好马几天追上劣马? 900÷(120-75)=20(天)列成综合算式 75某12÷(120-75)=900÷45=20(天)答：好马20天能追上劣马。

例2、小明和小亮在200米环形跑道上跑步，小明跑一圈用40秒，他们从同一地点同时出发，同向而跑。

小明第一次追上小亮时跑了500米，求小亮的速度是每秒多少米。

解：小明第一次追上小亮时比小亮多跑一圈，即200米，此时小亮跑了(500-200)米，要知小亮的速度，须知追及时间，即小明跑500米所用的时间。

又知小明跑200米用40秒，则跑500米用[40某(500÷200)]秒，所以小亮的速度是(500-200)÷[40某(500÷200)]=300÷100=3(米)答：小亮的.速度是每秒3米。

例3、我人民解放军追击一股逃窜的敌人，敌人在下午16点开始从甲地以每小时10千米的速度逃跑，解放军在晚上22点接到命令，以每小时30千米的速度开始从乙地追击。

已知甲乙两地相距60千米，问解放军几个小时可以追上敌人?解：敌人逃跑时间与解放军追击时间的时差是(22-16)小时，这段时间敌人逃跑的路程是[10某(22-6)]千米，甲乙两地相距60千米。

由此推知追及时间=[10某(22-6)+60]÷(30-10)=220÷20=11(小时)答：解放军在11小时后可以追上敌人。

小升初数学公式范文一、四则运算1.加法公式：a+b=b+a2.减法公式：a-b≠b-a3.乘法公式：a×b=b×a4.除法公式：a÷b≠b÷a二、整数运算1.正整数的乘法：(a+b)×c=a×c+b×c2.正整数的除法：(a+b)÷c=a÷c+b÷c3.正整数的乘方：a^m×a^n=a^(m+n)4.正整数的连乘：a ×b ×c × ... × n = a^(x1 + x2 + x3 + ... + xn)5.正整数的连除：a ÷b ÷c ÷ ... ÷ n = a^(x1 - x2 - x3 - ... - xn)三、分数运算1.分数的加法：a/b + c/d = (ad + bc)/(bd)2.分数的减法：a/b - c/d = (ad - bc)/(bd)3.分数的乘法：a/b × c/d = ac/bd4.分数的除法：a/b ÷ c/d = (ab)/(cd)5.分数的乘方：(a/b)^m=a^m/b^m6.分数的比较大小：a/b < c/d ： ad < bca/b > c/d ： ad > bc四、小数运算1.小数的加法：a+b=c2.小数的减法：a-b=c3.小数的乘法：a×b=c4.小数的除法：a÷b=c五、平方根与立方根1.平方根的性质：√a×√a=a（a≥0）2.立方根的性质：³√a׳√a׳√a=a（a≥0）六、速算技巧1.乘11的技巧：将一个两位数的十位数和个位数之和写在中间，即十位数、十位数与个位数之和、个位数。

例如：32×11=3522.乘99的技巧：将一个两位数的个位数减1，再用个位数到9的差补齐百位和个位。

小升初数学必背知识点及公式归纳（一览）一、整数的基本概念•整数的定义：正整数、负整数、零。

•整数的大小比较：同号比大小，异号比符号。

•整数的加减法：同号相加、异号相减。

•整数的乘法：同号得正，异号得负。

•整数的除法：不含零的除法，同号得正，异号得负。

二、分数的基本概念•分数的定义：分子、分母，真分数、假分数、带分数。

•分数的化简：约分、通分。

•分数的加减法：通分后，分子加减，分母不变。

•分数的乘法：分子相乘，分母相乘。

•分数的除法：分母取倒数，分子相乘。

•分数的比较：通分后，分子比较大小。

三、小数的基本概念•小数的定义：整数部分，小数部分，小数点。

•小数的读法和写法。

•小数的加减法：小数点对齐，相加减。

•小数的乘法和除法：按数学定义计算。

四、比例和比例的应用•比例的定义：同比例、反比例。

•比例的性质：比例代表相等的关系。

•比例的计算方法：已知三者求第四者，单位比例法。

•比例的应用：线段的等比分割，图形的相似性，百分数。

五、图形的基本概念和计算•角度的概念：角的定义，角的表示，角的度量。

•三角形的基本概念：三角形的定义，三角形的分类，三角形的性质。

•四边形的基本概念：四边形的定义，四边形的分类，四边形的性质。

•圆的基本概念：圆的定义，圆周率，圆的面积和周长。

六、代数式和方程的基本概念•代数式的定义：字母、系数、指数，同类项、合并同类项。

•方程的定义：等式和未知数。

•解一元一次方程：加减消元法，分离系数法，代入法。

•方程式的应用：问题转化成方程的形式，解方程。

七、平面直角坐标系和图形的位置关系•平面直角坐标系的基本概念：横纵坐标，平面直角坐标系。

•图形的位置关系：平移、旋转、对称。

•坐标系中的图形：点、线、圆。

小升初34个小学数学必考公式计算问题通常在前几个题目中出现概率较高，主要考察两个方面，一个是基本的四则运算能力，同时，一些速算巧算及裂项换元等技巧也经常成为考察的重点。

小编在这里整理了相关知识，快来学习学习吧!小升初34个小学数学必考公式1、和差倍问题：和差问题和倍问题差倍问题已知条件几个数的和与差几个数的和与倍数几个数的差与倍数公式适用范围已知两个数的和，差，倍数关系公式①(和－差)÷2=较小数较小数＋差=较大数和－较小数=较大数②(和＋差)÷2=较大数较大数－差=较小数和－较大数=较小数和÷(倍数＋1)=小数小数×倍数=大数和－小数=大数差÷(倍数-1)=小数小数×倍数=大数小数＋差=大数关键问题求出同一条件下的和与差和与倍数差与倍数2、年龄问题的三个基本特征：①两个人的年龄差是不变的;②两个人的年龄是同时增加或者同时减少的;③两个人的年龄的倍数是发生变化的;3、归一问题的基本特点：问题中有一个不变的量，一般是那个“单一量”，题目一般用“照这样的速度”……等词语来表示。

关键问题：根据题目中的条件确定并求出单一量;4、植树问题：基本类型在直线或者不封闭的曲线上植在直线或者不封闭的曲线上植在直线或者不封闭的曲线上植树，只封闭曲线上植树，两端都植树树，两端都不植树有一端植树树基本公式棵数=段数＋1棵距×段数=总长棵数=段数－1棵距×段数=总长棵数=段数棵距×段数=总长关键问题确定所属类型，从而确定棵数与段数的关系5、鸡兔同笼问题：基本概念：鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来;基本思路：①假设，即假设某种现象存在(甲和乙一样或者乙和甲一样)：②假设后，发生了和题目条件不同的差，找出这个差是多少;③每个事物造成的差是固定的，从而找出出现这个差的原因;④再根据这两个差作适当的调整，消去出现的差。

小升初数学必考的34个数学重难点公式_中考数学1、和差倍问题2、年龄问题的三个基本特征①两个人的年龄差是不变的；②两个人的年龄是同时增加或者同时减少的；③两个人的年龄的倍数是发生变化的；3、归一问题的基本特点问题中有一个不变的量，一般是那个，题目一般用......等词语来表示。

关键问题：根据题目中的条件确定并求出单一量；4、植树问题5、鸡兔同笼问题基本概念：鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来；基本思路：①假设，即假设某种现象存在（甲和乙一样或者乙和甲一样）：②假设后，发生了和题目条件不同的差，找出这个差是多少；③每个事物造成的差是固定的，从而找出出现这个差的原因；④再根据这两个差作适当的调整，消去出现的差。

基本公式：①把所有鸡假设成兔子：鸡数＝（兔脚数&times;总头数－总脚数）&divide;（兔脚数－鸡脚数）②把所有兔子假设成鸡：兔数＝（总脚数一鸡脚数&times;总头数）&divide;（兔脚数一鸡脚数）关键问题：找出总量的差与单位量的差。

6、盈亏问题基本概念：一定量的对象，按照某种标准分组，产生一种结果：按照另一种标准分组，又产生一种结果，由于分组的标准不同，造成结果的差异，由它们的关系求对象分组的组数或对象的总量。

基本思路：先将两种分配方案进行比较，分析由于标准的差异造成结果的变化，根据这个关系求出参加分配的总份数，然后根据题意求出对象的总量。

基本题型：①一次有余数，另一次不足；基本公式：总份数＝（余数＋不足数）&divide;两次每份数的差②当两次都有余数；基本公式：总份数＝（较大余数一较小余数）&divide;两次每份数的差③当两次都不足；基本公式：总份数＝（较大不足数一较小不足数）&divide;两次每份数的差基本特点：对象总量和总的组数是不变的。

关键问题：确定对象总量和总的组数。

7、牛吃草问题基本思路：假设每头牛吃草的速度为份，根据两次不同的吃法，求出其中的总草量的差；再找出造成这种差异的原因，即可确定草的生长速度和总草量。