高二数学期末考试复习专题四

2020-2021学年高二数学下学期期末考试试题 (IV)本试卷满分150分，考试时间120分钟一、选择题（每小题5分，共60分）1．若集合{}{}084|,51|<+-=<-=x x B x x A ，则=B A （ ） A ．{}6|<x x B ．{}2|>x x C ．{}62|<<x x D ． ∅ 2．函数)4(log 3-=x y 的定义域为 （ ）A ．RB ．),4()4,(+∞-∞C ．)4,(-∞D ． ),4(+∞3．某电视台在娱乐频道节目播放中，每小时播放广告20分钟，那么随机打开电视机观看这个频道看到广告的概率为 （ ）A ．12 B ．13 C ．14D ．164．在等比数列{}n a 中，*0()n a n N >∈且,16,464==a a 则数列{}n a 的公比q 是（ ）A ．1B ．2C ．3D ．45．已知3(,sin ),2a α=1(cos ,)3b α=且//,a b 则锐角α的大小为 （ ） A ．4πB ．3πC ．6πD ．125π6．按照程序框图(如右图)执行， 第3个输出的数是( ).A ．3B ．4C ．5D ．67．如图所示，一个空间几何体的正视图和侧视图都是边长为2的正方形，俯视图 是一个圆，那么这个几何体的体积为 （ ） A ．2πB ．πC ．2πD ．4π8．已知函数b x x x f +-=2)(2在区间)4,2(内有唯一零点，则b 的取值范围是（ ） A ． R B ．)0,(-∞ C ．),8(+∞- D ．)0,8(-9.若实数,x y 满足约束条件222x y x y ≤⎧⎪≤⎨⎪+≥⎩，则目标函数2z x y =+的最大值为（ ）A. 6B. 5C. 4D. 3 10.已知长方体的相邻三个侧面面积分别为6,3,2,则它的体积是( )A ．5B ．6 C.5 D ．611．三个数21log ,)21(,33321===c b a 的大小顺序为 （ ）A ．a c b <<B ．a b c <<C ．b a c <<D ．c a b <<12．设函数x x f 6sin )(π=，则)2009()3()2()1(f f f f ++++ 的值等于( )A ．21B ．23C ．231+ D ．32+二、填空题（每小题5分，共20分）13．已知函数1322(),log (21)2x xe xf x x -⎧<=⎨-≥⎩则=))2((f f ．14．在⊿ABC 中，已知====c C b a 则,3,4,3π．15. 已知5sin =5α则44sin cos αα-的值是 . 16．某厂生产A 、B 、C 三种不同型号的产品，产品数量之比依次为2：3：5．现用分层抽样的方法抽取一个容量为n 的样本，样本中A 种型号产品有16件，则样本容量n ＝ ． 三、解答题：(共70分)解答应写出文字说明、证明过程或演算步骤。

1高二数学期末复习题四1．如果等差数列{}n a 中，34512a a a ++=，那么127...a a a +++=（ ）（A ）28 （B ）21 （C ）14 （D ）35 2．在△ABC 中，a ＝32，b ＝22，B ＝45°，则A 等于（）A ．30°B ．60°C ．60°或120°D ． 30°或1503．满足线性约束条件23,23,0,0x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩的目标函数z x y =+的最大值是（ ）（A ）1. （B ）32. （C ）2. （D ）3.4．设'()f x 是函数()f x 的导数，'()y f x =所示，则()y f x =的图像最有可能的是（5．不等式2601x x x ---＞的解集为（ ）．（A ）{}2,3x x x -＜或＞ （B ）{}213x x x -＜，或＜＜（C ） {}213x x x -＜＜，或＞ （D ）{}2113x x x -＜＜，或＜＜ 6．已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）．(B) (C) (D) 347．已知命题"0cos 2cos ,2.0:"=-+⎥⎦⎤⎢⎣⎡∈∃m x x x p π的否定为假命题，实数m 的取值范围（ ） A 、⎥⎦⎤⎢⎣⎡--1,89 B 、⎥⎦⎤⎢⎣⎡-2,89 C 、[]2,1- D 、⎪⎭⎫⎢⎣⎡+∞-,898．已知椭圆2222:1(0)x y C a b a b +=＞＞F 且斜率为(0)k k ＞的直线与C 相交于A B 、两点．若3AF FB =，则k = （ ）（A ）1 （B （C （D ）29．设n S 为等比数列{}n a 的前n 项和，已知3432S a =-，2332S a =-，则公比q =（ ） （A ）3（B ）4（C ）5（D ）610、函数f （x ）的定义域为R ，f （-1）=2，对任意x R ∈，f （x ）＞2，则f(x)＞2x+4的解集为（ ）（A ）(-1,1) (B)(-1，+∞) (C)(-∞,-1) (D)(-∞,+∞) 二、填空题：11．已知抛物线的顶点为坐标原点，对称轴为x 轴，且过点P （-2，22），则抛物线的方程为 。

2013-2014学年度品尚学校高二数学复习 4考试范围：--；考试时间：100分钟；命题人：万财文考号：___________一、单选题(注释)1、已知向量，若，则实数m等于( )D．0A．－B．C．－或【答案】C【解析】试题分析：∵，∴．考点：平面向量共线的坐标表示．2、不等式的解集是（）A．B．D．C．【答案】B【解析】试题分析：∵，∴，即，∴不等式的解集为．考点：分式不等式转化为一元二次不等式．3、执行如图所示的程序框图，如果输入，那么输出的a值为（）A．B．C．D．【答案】C【解析】试题分析：根据程序框图的描述，是求使成立的最小a值，故选C．考点：程序框图．4、等腰直角三角形中，是斜边的中点，若，则=( )A．B．C．D．【答案】A【解析】试题分析：如图建立平面直角坐标系，则A(0,0),B(2,0),C(0,2),又∵D是BC的中点，∴D(1,1),∴．考点：平面向量数量积的坐标表示．5、下列命题正确的是（）A．B．C．当且时，D．【答案】D【解析】试题分析：A:当c<0时，错误；B：，∴；C:当即时不成立；D：正确．考点：不等式的性质．6、若变量x，y满足约束条件，则z＝5y－x的最大值是( )A．16 B．30 C．24 D．8 【答案】A试题分析：画出如下图可行域，易得A(4,4),B(0,2),C(8,0),又∵z=5y-x，即，∴问题等价于求直线在可行域内在y轴上的最大截距，显然当x=4，y=4时，．考点：线性规划求目标函数最值．7、设△ABC的内角A, B, C所对的边分别为a, b, c, 若, 则△ABC的形状是 ( )A．锐角三角形B．直角三角形C．钝角三角形D．不确定【答案】B【解析】试题分析：∵，由正弦定理，∴，即，又∵,∴，∴△ABC是直角三角形．考点：1、正弦定理；2、三角恒等变形．8、已知均为非零实数，不等式与不等式的解集分别为集合M和集合N，那么“”是“”的（）A．充分非必要条件B．既非充分又非必要条件C．充要条件D．必要非充分条件【解析】试题分析：取，则可得M=，N=，因此不是充分条件，而由M=N,显然可以得到，∴是必要条件．考点：1、不等式的基本性质；2、简易逻辑．9、在分别是角A、B、C的对边,若,则的周长的取值范围是（）A． B． C．D．【答案】C【解析】试题分析：∵，∴，化简后可得：，∴，又∵，∴，即周长的范围为．考点：1、余弦定理；2、基本不等式．10、对任意正数x，y不等式恒成立，则实数的最小值是 ( )A．1 B．2 C．3 D．4【答案】A【解析】试题分析：∵，两边同除，得，要使不等式恒成立，则，，∴，∴k的最小值是1．考点：基本不等式．分卷II分卷II 注释(注释)11、已知等差数列前15项的和=30，则=___________．【答案】6 【解析】试题分析：∵等差数列的前15项的和,∴，而．考点：等差数列的性质．12、下面框图所给的程序运行结果为S ＝28，如果判断框中应填入的条件是 “”,则整数_______．【答案】7【解析】试题分析：∵程序运行结果为S=28,而1+10+9+8=28，∴程序应该运行到k=7的时候停止，因此整数a=7． 考点：程序框图．13、已知非零向量满足，则向量与的夹角为 ．【答案】【解析】试题分析：∵，∴，又∵，∴，∴，∴，∴．考点：平面向量的数量积．14、已知数集，记和中所有不同值的个数为．如当时，由，，，，，得．若，则= ．【答案】2n-3【解析】试题分析：根据题意分析，A中最小的两个不同元素的和为1+2=3，最大的为n-1+n=2n-1，显然可以取遍从3到2n-1的所有整数，∴M(A)=2N-3．考点：新定义问题15、设实数满足：,则取得最小值时，．【答案】121【解析】试题分析：∵，∴，上述等号成立的条件依次为：，∴a=1，b=c=10，d=100，a+b+c+d=121．考点：1、基本不等式；2、不等式的放缩．(注释)16、在中，角所对的边分别为，且满足，．(1)求的面积；(2)若，求的值．【答案】（1）；（2）．【解析】试题分析：（1）根据满足，，可以求得bc=5，sinA=，利用三角形的面积计算公式可得；（2）由（1），bc=5，结合b+c=6，易得b=1，c=5或b=5，c=1，从而根据余弦定理,即可求得．（1）∵，∴，又由,得，；（2）对于，又，或，由余弦定理得，．考点：1、平面向量的数量积；2、三角形面积计算；3、余弦定理．17、已知关于的不等式的解集为．(1)．求实数a，b的值；(2)．解关于的不等式(c为常数）．【答案】（1）a=1，b=2；（2）当c>2时解集为{x|x>c或x<2}；当c＝2时解集为{x|x≠2，x R}；当c<2时解集为{x|x>2或x<c}．【解析】试题分析：（1）根据一元二次方程与一元二次不等式的关系，根据题意可以得到1，b为方程的两根且a>0，根据韦达定理可以得到方程组，从而求得a=1，b=2；（2）原不等式等价于(x－c)(x－2)>0，根据一元二次不等式的解法，对c进行分类讨论，即可得到当c>2时解集为{x|x>c或x<2}；当c＝2时解集为{x|x≠2，x R}；当c<2时解集为{x|x>2或x<c}．（1）由题知1，b为方程的两根且a>0，即，∴a＝1，b＝2；（2）不等式等价于(x－c)(x－2)>0，∴当c>2时解集为{x|x>c或x<2}；当c＝2时解集为{x|x≠2，x R}；当c<2时解集为{x|x>2或x<c}．考点：1、一元二次不等式；2、分式不等式转化为一元二次不等式．18、在分别是角A、B、C的对边，，且．(1)．求角B的大小；(2)．求sin A＋sin C的取值范围．【答案】（1）B=；（2）．【解析】试题分析：（1）由，可得，等式中边角混在了一起，需要进行边角的统一，根据正弦定理可得，进一步变形化简可得，∴B；（2）由（1）可得，即，因此可以将sinA+sinC进行三角恒等变形转化为关于A的函数，即，从而可以得到sinA+sinC取值范围是．（1）由，得由正弦定理得：，又又又；∵，∴，∴，∵，∴，∴，∴．故sin A＋sin C的取值范围是．考点：1、平面向量垂直的坐标表示；2、三角恒等变形．19、已知数列，设数列满足．(1)求数列的前项和为；(2)若数列，若对一切正整数恒成立，求实数的取值范围．【答案】（1）；（2）或．【解析】试题分析：（1）根据题意可以得到等比数列的通项公式为，∵，∴，因此是1为首项3为公差的等差数列，从而可以求得的前n 项和；（2）对一切正整数n恒成立，等价于，可以得到数列从第二项起是递减的，而，因此问题等价于求使不等式成立的m的取值范围，从而得到或．（1）由题意知，，又∵，∴∴，∴；（2）由（1）知，∴当n=1时，；当时，，即；∴当n=1时，取最大值是．又对一切正整数恒成立，∴；即．考点：1、等差、等比数列的前n项和；2、数列单调性的判断；3、恒成立问题的处理方法．20、如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．(1)．设AD=x（x≥0），DE=y，求用x表示y的函数关系式,并求函数的定义域；(2)．如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应在哪里？如果DE是参观线路，则希望它最长，DE的位置又应在哪里？请予证明．【答案】（1）；（2）如果DE是水管，DE的位置在AD=AE=处，如果DE是参观路线，则DE为AB中线或AC中线时，DE最长，证明过程详见解析．【解析】试题分析：（1）在△ADE中，利用余弦定理可得，又根据面积公式可得，消去AE后即可得到y与x的函数关系式，又根据可以得到x的取值范围；（2）如果DE是水管，则问题等价于当时，求的最小值，利用基本不等式即可求得当时，y有最小值为，如果DE是参观路线，则问题等价于问题等价于当时，求的最小值，根据函数在[1,2]上的单调性，可得当x=1或2时，y有最小值．（1）在△ADE中，由余弦定理：①又∵②②代入①得（y＞0）, ∴，由题意可知，所以函数的定义域是，；（2）如果DE是水管,当且仅当，即x＝时“＝”成立，故DE∥BC，且DE＝．如果DE是参观线路，记，可知函数在[1，]上递减，在[，2]上递增，故∴y max＝．即DE为AB中线或AC中线时，DE 最长．考点：1、平面向量的数量积；2、三角形面积计算．21、设正项数列的前项和为，向量，（）满足．(1)求数列的通项公式；(2)设数列的通项公式为（），若，，（）成等差数列，求和的值；(3)．如果等比数列满足，公比满足，且对任意正整数，仍是该数列中的某一项，求公比的取值范围．【答案】（1）；（2）；（3）．【解析】试题分析：（1）由可以得到，即，利用，可得，即是以1为首项，2为公差的等差数列，从而求得通项公式；（2）由是等差数列可得，即，整理得，根据m,t是正整数，所以t-1只可能是1,2,4，从而解得；（3）易知，因为仍是该数列中的某一项，所以是该数列中的某一项，又是q的几次方的形式，所以也是q的几次方的形式，而，所以，所以只有可能是q，，所以，所以．（1）∵，∴，∴①当n=1，有，是正项数列，∴当，有②，①-②，得，，∴，∴数列以，公差为2的等差数列，；（2）易知，∵是等差数列，即，∴，整理得，∵m,t是正整数，所以t只可能是2,3,5，∴；易知，∵仍是该数列中的某一项，记为第t项，∴，即，∵，∴，，又∵，∴只有t-k=1，即，解得考点：1、数列的通项公式；2、数列综合．。

2021年高二数学第二学期期末复习试卷文（四）（含解析）一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的1．复数（i是虚数单位）=（）A． 2 B．﹣2 C． 2i D．﹣2i2．若集合M={x|x﹣2＜0}，N={x|x2﹣4x+3＜0}，则M∩N=（） A． {x|﹣2＜x＜2} B． {x|x＜2} C． {x|1＜x＜2} D． {x|1＜x＜3} 3．函f（x）=2x﹣2﹣x在定义域上是（）A．偶函数 B．奇函数C．既是奇函数又是偶函数 D．既不是奇函数也不是偶函数4．已知等差数列{an }中，a3+a7﹣a10=8，a11﹣a4=4，记Sn=a1+a2+…+an，则S13=（）A． 78 B． 152 C． 156 D． 1685．如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的表面积为（） A． B． C． D．6．已知，则2x+y的最大值是（）A． 3 B． C． 0 D．﹣37．△ABC的三个内角A、B、C成等差数列，，则△ABC一定是（）A．直角三角形 B．等边三角形 C．锐角三角形 D．钝角三角形8．北京xx年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为米（如图所示），则旗杆的高度为（）A． 10米 B． 30米 C． 10米 D．米9．下列说法正确的是（）A．“x2=1”是“x=1”的充分不必要条件B．“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C．命题“∃x∈R，使得x2+x+1＜0”的否定是：“∀x∈R，均有x2+x+1＜0”D．命题“若α=β，则sinα=sinβ”的逆否命题为真命题10．已知函数，正实数a、b、c满足f（c）＜0＜f（a）＜f（b），若实数d是函数f（x）的一个零点，那么下列四个判断：①d＜a；②d＞b；③d＜c；④d＞c．其中可能成立的个数为（）A． 1 B． 2 C． 3 D． 4二.填空题（每小题5分，共20分.）11．中心在坐标原点，一个焦点为（5，0），且以直线为渐近线的双曲线方程为．12．如图，是一程序框图，则输出结果为K= ，S=（说明，M=N是赋值语句，也可以写成M←N，或M：=N）13．以下四个命题：①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样②在回归分析模型中，残差平方和越小，说明模型的拟合效果越好③在回归直线方程中，当解释变量x每增加一个单位时，预报变量增加0.1个单位④在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．其中正确的序号是．选做题：在下面两道小题中选做一题，两题都选只计算前一题的得分.【参数方程与极坐标】14．（参数方程与极坐标）已知F是曲线（θ∈R）的焦点，，则|MF|的值是．【几何证明选讲】15．如图，P是圆O外的一点，PD为切线，D为切点，割线PEF经过圆心O，PF=6，PD=2，则∠DFP= °．三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）16．如图，设A是单位圆和x轴正半轴的交点，P，Q是单位圆上两点，O是坐标原点，且，∠AOQ=α，α∈[0，π）．（Ⅰ）若点Q的坐标是，求的值；（Ⅱ）设函数，求f（α）的值域．17．某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示（1）求甲、乙两名运动员得分的中位数；（2）你认为哪位运动员的成绩更稳定？（3）如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分，求甲的得分大于乙的得分的概率．18．如图，在等腰梯形PDCB中，PB=3，DC=1，PD=BC=，A为PB边上一点，且PA=1，将△PAD沿AD折起，使平面PAD⊥平面ABCD．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）若M是侧棱PB中点，截面AMC把几何体分成的两部分，求这两部分的体积之比．19．从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，打算本年度投入800万元，以后每年投入将比上年平均减少20%，本年度旅游收入为400万元，由于该项建设对旅游的促进作用，预计今后的旅游业收入每年会比上年平均增加25%．（Ⅰ）设第n年（本年度为第一年）的投入为a n万元，旅游业收入为b n万元，写出a n，b n 的表达式；（Ⅱ）至少经过几年旅游业的总收入超过总投入？20．如图，已知圆C：x2+y2=2与x轴交于A1、A2两点，椭圆E以线段A1A2为长轴，离心率．（Ⅰ）求椭圆E的标准方程；（Ⅱ）设椭圆E的左焦点为F，点P为圆C上异于A1、A2的动点，过原点O作直线PF的垂线交直线x=﹣2于点Q，判断直线PQ与圆C的位置关系，并给出证明．21．如图，在直角坐标系中，正方形ABCD的四个顶点分别为A（0，0），B（1，0），C（1，1），D（0，1）．（Ⅰ）已知函数（其中），过f（x）图象是任意一点R的切线l将正方形ABCD截成两部分，设R点的横坐标为t，S（t）表示正方形ABCD被切线l所截的左下部分的面积，求S（t）的解析式；（Ⅱ）试问S（t）在定义域上是否存在最大值和最小值？若存在，求出S（t）的最大值和最小值；若不存在，请说明理由．xx学年广东省深圳市罗湖区翠圆中学高二（下）期末数学复习试卷（文科）（四）参考答案与试题解析一、选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的1．复数（i是虚数单位）=（）A． 2 B．﹣2 C． 2i D．﹣2i考点：复数代数形式的乘除运算．专题：计算题．分析：先利用完全平方差公式计算分子的值，再计算分式的值，注意虚数单位i注意 i2=﹣1．解答：解：复数===﹣2，故选 B．点评：本题考查复数代数形式的乘法和除法法则．2．若集合M={x|x﹣2＜0}，N={x|x2﹣4x+3＜0}，则M∩N=（）A． {x|﹣2＜x＜2} B． {x|x＜2} C． {x|1＜x＜2} D． {x|1＜x＜3}考点：交集及其运算．专题：集合．分析：利用交集定义和不等式性质求解．解答：解：∵集合M={x|x﹣2＜0}={x|x＜2}，N={x|x2﹣4x+3＜0}={x|1＜x＜3}，∴M∩N={x|1＜x＜2}．故选：C．点评：本题考查交集的求法，是基础题，解题时要认真审题．3．函f（x）=2x﹣2﹣x在定义域上是（）A．偶函数 B．奇函数C．既是奇函数又是偶函数 D．既不是奇函数也不是偶函数考点：函数奇偶性的判断．专题：综合题．分析：先看函数的定义域是否关于原点对称，否则是非奇非偶函数，在定义域关于原点对称时，考查f（x）与f（﹣x）的关系，依据奇偶函数的定义，做出判断．解答：解：函数的定义域为R，关于原点对称，f（﹣x）=2﹣x ﹣2x=﹣（2x﹣2﹣x）=﹣f（x），故函数f（x）=2x﹣2﹣x在定义域上是奇函数，故选 B．点评：本题考查奇偶函数的定义和判断方法，一定要先看函数的定义域是否关于原点对称，然后考查f（x）与f（﹣x）的关系．4．已知等差数列{a n}中，a3+a7﹣a10=8，a11﹣a4=4，记S n=a1+a2+…+a n，则S13=（）A． 78 B． 152 C． 156 D． 168考点：等差数列的前n项和．专题：等差数列与等比数列．分析：两式相加结合等差数列的性质可得a7=12，而S13=13a7，代值计算可得．解答：解：∵等差数列{a n}中，a3+a7﹣a10=8，a11﹣a4=4，∴（a3+a7﹣a10）+（a11﹣a4）=（a3+a11）﹣（a4+a10）+a7=8+4=12，由等差数列的性质可得a3+a11=a4+a10，∴a7=12，∴S13===13a7=13×12=156故选：C．点评：本题考查等差数列的性质和前n项和公式，属基础题．5．如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的表面积为（）A． B． C． D．考点：由三视图求面积、体积．专题：计算题．分析：由题意可知三视图复原的几何体是三棱锥，正方体的一个角，根据三视图的数据，求出三棱锥的表面积即可．解答：解：由题意可知三视图复原的几何体是三棱锥，正方体的一个角，所以几何体的表面积为：3个等腰直角三角形与一个等边三角形的面积的和，即：3×=．故选A．点评：本题是基础题，考查三视图的视图能力，空间想象能力，计算能力，送分题．6．已知，则2x+y的最大值是（）A． 3 B． C． 0 D．﹣3考点：简单线性规划．专题：计算题．分析：先根据条件画出可行域，设z=2x+y，再利用几何意义求最值，将最大值转化为y轴上的截距，只需求出直线z=2x+y，过可行域内的点A（1，1）时的最大值，从而得到z最大值即可解答：解：先根据约束条件画出可行域，设z=2x+y，∵直线z=2x+y过可行域内点A（1，1）时z最大，最大值为3，故选A．点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．7．△ABC的三个内角A、B、C成等差数列，，则△ABC一定是（）A．直角三角形 B．等边三角形 C．锐角三角形 D．钝角三角形考点：平面向量数量积的运算；等差数列的性质．专题：计算题．分析：由，结合等腰三角形三线合一的性质，我们易判断△ABC为等腰三角形，又由△ABC 的三个内角A、B、C成等差数列，我们易求出B=60°，综合两个结论，即可得到答案．解答：解：∵△ABC的三个内角A、B、C成等差数列∴2B=A+C又∵A+B+C=180°∴B=60°设D为BC边上的中点则=2又∵∴=0∴即△ABC为等腰三角形，故△ABC为等边三角形，故选：B点评：本题考查的知识点是平面向量的数量积运算和等差数列的性质，其中根据平面向量的数量积运算，判断△ABC为等腰三角形是解答本题的关键．8．北京xx年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为米（如图所示），则旗杆的高度为（）A． 10米 B． 30米 C． 10米 D．米考点：解三角形的实际应用．专题：计算题；数形结合．分析：先画出示意图，根据题意可求得∠AEC和∠ACE，则∠EAC可求，然后利用正弦定理求得AC，最后在Rt△ABC中利用AB=AC•sin∠ACB求得答案．解答：解：如图所示，依题意可知∠AEC=45°，∠ACE=180°﹣60°﹣15°=105°∴∠EAC=180°﹣45°﹣105°=30°由正弦定理可知=，∴AC=•sin∠CEA=20米∴在Rt△ABC中，AB=AC•sin∠ACB=20×=30米答：旗杆的高度为30米故选B．点评：本题主要考查了解三角形的实际应用．此类问题的解决关键是建立数学模型，把实际问题转化成数学问题，利用所学知识解决．9．下列说法正确的是（）A．“x2=1”是“x=1”的充分不必要条件B．“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C．命题“∃x∈R，使得x2+x+1＜0”的否定是：“∀x∈R，均有x2+x+1＜0”D．命题“若α=β，则sinα=sinβ”的逆否命题为真命题考点：命题的真假判断与应用．专题：阅读型．分析：根据常用逻辑用语中有关充要条件的判断方法、特称命题否定的叙述、原命题与其否命题真假之间的关系、三角函数运算相关知识进行各命题真假的判断．解答：解：当x=1成立时有x2=1成立，∴“x2=1”是“x=1”的必要不充分条件，故A错；当“x=﹣1”成立时有（1）2﹣（﹣1）×5﹣6=0即“x2﹣5x﹣6=0”成立当x2﹣5x﹣6=0成立时，不一定有x=﹣1成立故“x=﹣1”是“x2﹣5x﹣6=0”的充分不必要条件，故B错；命题“∃x∈R，使得x2+x+1＜0”的否定应为：“∀x∈R，均有x2+x+1≥0”，故C错误；命题“若α=β，则sinα=sinβ”的逆否命题为“若sinα≠sinβ，则α≠β”是正确的，故D正确；故选D．点评：本题考查命题真假的判断，考查常用逻辑用语的基本知识，考查三角函数的运算，解决该类问题的关键是逐一对各个说法进行辨析，考查学生的转化与化归能力．10．已知函数，正实数a、b、c满足f（c）＜0＜f（a）＜f（b），若实数d是函数f（x）的一个零点，那么下列四个判断：①d＜a；②d＞b；③d＜c；④d＞c．其中可能成立的个数为（）A． 1 B． 2 C． 3 D． 4考点：函数零点的判定定理．专题：数形结合．分析：利用零点就是两函数图象的交点，再利用图象得结论．解答：解：因为函数在（0，+∞）上是减函数，又因为f（c）＜0＜f（a）＜f（b），所以a＜b＜c，又因为零点就是两函数图象的交点，在同一坐标系内画出函数y=与y=lnx的图象，如图a、b、c，d的位置如图所示只有②③成立．故可能成立的有两个．故选B．点评：本题考查函数零点的判定的应用和数形结合思想的应用，数形结合的应用大致分两类：一是以形解数，即借助数的精确性，深刻性来讲述形的某些属性；二是以形辅数，即借助与形的直观性，形象性来揭示数之间的某种关系，用形作为探究解题途径，获得问题结果的重要工具．二.填空题（每小题5分，共20分.）11．中心在坐标原点，一个焦点为（5，0），且以直线为渐近线的双曲线方程为．考点：双曲线的标准方程．专题：待定系数法．分析：设双曲线方程为 +=1，由5= ①，和 = ②，解方程组求得 a2，b2的值．解答：解：设双曲线方程为 +=1，由题意得 c=5= ①，= ②，由①②得 a2=16，b2=9，故所求的双曲线方程为﹣=1，故答案为：﹣=1．点评：本题考查利用待定系数法求双曲线的标准方程的方法，以及双曲线的简单性质得应用．12．如图，是一程序框图，则输出结果为K= 11 ，S=（说明，M=N是赋值语句，也可以写成M←N，或M：=N）考点：程序框图．专题：图表型．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知该程序的作用是输出满足条件S=++…++的值．解答：解：根据题意，本程序框图为求和运算第1次循环：S=0+，K=3第2次循环：S=+，K=5第3次循环：S=++，K=7第4次循环：S=++…+，K=9第5次循环：S=++…++，K=11此时，K＞10输出K=11，S=++…++=．故答案为：11，．点评：本题主要考查程序框图，通过对程序框图的认识和理解按照程序框图的顺序进行执行，属于基础题．13．以下四个命题：①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样②在回归分析模型中，残差平方和越小，说明模型的拟合效果越好③在回归直线方程中，当解释变量x每增加一个单位时，预报变量增加0.1个单位④在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．其中正确的序号是②④．考点：独立性检验；分层抽样方法；线性回归方程．专题：计算题．分析：从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样系统抽样；在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；在回归直线方程中，当解释变量x每增加一个单位时，预报变量平均增加0.1个单位；k2=13.079，其两个变量间有关系的可能性是90%以上．解答：解：①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样不是分层抽样，故①不正确，②在回归分析模型中，残差平方和越小，说明模型的拟合效果越好，故②正确，③在回归直线方程中，当解释变量x每增加一个单位时，预报变量平均增加0.1个单位，故③不正确，④在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．④正确故答案为：②④点评：本题考查独立性检验，考查分层抽样方法，考查线性回归方程，考查判断两个相关变量之间的关系，是一个综合题目，这种题考查的知识点比较多，需要认真分析．选做题：在下面两道小题中选做一题，两题都选只计算前一题的得分.【参数方程与极坐标】14．（参数方程与极坐标）已知F是曲线（θ∈R）的焦点，，则|MF|的值是．考点：椭圆的参数方程．专题：计算题．分析：先利用二倍角公式进行化简，然后消去参数θ得到曲线方程，求出抛物线的焦点坐标，根据两点的距离公式求出|MF|的值即可．解答：解：y=1+cos2θ=2cos2θ=2•化简得x2=2y∴F（0，）而，∴|MF|=故答案为：点评：本题主要考查了抛物线的参数方程，以及两点的距离公式的应用等有关基础知识，属于基础题．【几何证明选讲】15．如图，P是圆O外的一点，PD为切线，D为切点，割线PEF经过圆心O，PF=6，PD=2，则∠DFP= 30 °．考点：圆的切线的性质定理的证明．专题：计算题；压轴题．分析：根据切割线定理写出比例式，代入已知量，得到PE的长，在直角三角形中，根据边长得到锐角的度数，根据三角形角之间的关系，得到要求的角的大小．解答：解：连接OD，则OD垂直于切线，根据切割线定理可得PD2=PE•PF，∴PE=2，∴圆的直径是4，在直角三角形POD中，OD=2，PO=4，∴∠P=30°，∴∠DEF=60°，∴∠DFP=30°，故答案为：30°点评：本题考查圆的切线的性质和证明，考查直角三角形角之间的关系，是一个基础题，题目解答的过程比较简单，是一个送分题目．三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）16．如图，设A是单位圆和x轴正半轴的交点，P，Q是单位圆上两点，O是坐标原点，且，∠AOQ=α，α∈[0，π）．（Ⅰ）若点Q的坐标是，求的值；（Ⅱ）设函数，求f（α）的值域．考点：正弦函数的定义域和值域；平面向量数量积的运算；单位圆与周期性；两角和与差的余弦函数．专题：三角函数的求值．分析：（Ⅰ）根据三角函数的定义和题意求出cosα，sinα的值，再由两角差的余弦公式展开后代入求值；（Ⅱ）根据向量的数量积坐标运算和条件代入，利用两角和正弦公式进行化简，根据α的范围和正弦函数的性质求出值域．解答：解：（Ⅰ）∵点Q的坐标是，∴．∴=．（Ⅱ）===．∵α∈[0，π），则，∴．故f（α）的值域是．点评：本题是由关三角函数的综合题，考查了三角函数的定义，两角和差的正弦（余弦）公式，正弦函数的性质的应用，三角函数是高考的重点，必须掌握和理解公式以及三角函数的性质，并会应用．17．某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示（1）求甲、乙两名运动员得分的中位数；（2）你认为哪位运动员的成绩更稳定？（3）如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分，求甲的得分大于乙的得分的概率．考点：茎叶图；极差、方差与标准差．分析：（1）由茎叶图中茎表示十位数，叶表示个数数，我们可以列出甲、乙两名篮球运动员各场的得分，进而求出甲、乙两名运动员得分的中位数；（2）由表中数据，我们易计算出甲、乙两名篮球运动员各场的得分的方差S甲2与S乙2，，然后比较S甲2与S乙2，根据谁的方差小谁的成绩稳定的原则进行判断．（3）我们计算出从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数，然后再计算出其中甲的得分大于乙的基本事件个数，代入古典概率计算公式，即可求解．解答：解：（1）运动员甲得分的中位数是22，运动员乙得分的中位数是23（2分）（2）∵（3分）（4分）（5分）∴S甲2＜S乙2，从而甲运动员的成绩更稳定（8分）（3）从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为49其中甲的得分大于乙的是：甲得（14分）有3场，甲得（17分）有3场，甲得（15分）有3场甲得2（4分）有4场，甲得2（2分）有3场，甲得2（3分）有3场，甲得3（2分）有7场，共计26场（11分）从而甲的得分大于乙的得分的概率为（12分）点评：本题考查的知识点是茎叶图，中位数，方差的计算及应用，古典概型等知识点，解题的关键是根据茎叶图的茎是高位，叶是低位，列出茎叶图中所包含的数据，再去根据相关的定义和公式进行求解和计算．18．如图，在等腰梯形PDCB中，PB=3，DC=1，PD=BC=，A为PB边上一点，且PA=1，将△PAD沿AD折起，使平面PAD⊥平面ABCD．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）若M是侧棱PB中点，截面AMC把几何体分成的两部分，求这两部分的体积之比．考点：直线与平面垂直的判定；棱柱、棱锥、棱台的体积．专题：证明题；综合题；转化思想．分析：（Ⅰ）依题意通过计算，以及平面PAD⊥平面ABCD，由面面垂直的性质定理，证明CD⊥平面PAD．（Ⅱ）设N是AB的中点，连接MN，依题意，证明PA⊥面ABCD，MN⊥面ABCD，计算与，得到V PADCM=V PADCB﹣V MACB，求出V PADCM：V MACB=两部分体积比．解答：证明：（Ⅰ）依题意知PA=1，∴AD⊥AB，又CD∥AB∴CD⊥AD（3分）又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，由面面垂直的性质定理知，CD⊥平面PAD（6分）（Ⅱ）解：设N是AB的中点，连接MN，依题意，PA⊥AD，PA⊥AB，所以，PA⊥面ABCD，因为MN∥PA，所以MN⊥面ABCD．（8分）（10分）（11分）所以，（12分）V PADCM：V MACB=两部分体积比为2：1（14分）点评：本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是中档题．19．从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业，打算本年度投入800万元，以后每年投入将比上年平均减少20%，本年度旅游收入为400万元，由于该项建设对旅游的促进作用，预计今后的旅游业收入每年会比上年平均增加25%．（Ⅰ）设第n年（本年度为第一年）的投入为a n万元，旅游业收入为b n万元，写出a n，b n 的表达式；（Ⅱ）至少经过几年旅游业的总收入超过总投入？考点：函数模型的选择与应用．专题：函数的性质及应用；等差数列与等比数列．分析：（Ⅰ）依题意每年投入构成首项为800万元，公比为的等比数列，每年旅游业收入组织首项为400万元，公比为的等比数列，进而求出a n，b n的表达式．（Ⅱ）先设至少经过n年旅游业的总收入才能超过总投入，由b n﹣a n＞0，解得n的取值范围即可．解答：（Ⅰ）解，依题意每年投入构成首项为800万元，公比为的等比数列，每年旅游业收入组织首项为400万元，公比为的等比数列．所以，，（Ⅱ）解，经过n年，总收投入，经过n年，总收入，设经过n年，总收入超过总投入，由此，T n﹣S n＞0，＞0，化简得，设代入上式整理得，5x2﹣7x+2＞0，解得，，或x＞1（舍去），由，n=4时，=，n=5，=，因为在定义域上是减函数，所以 n≥5，答：至少经过5年旅游业的总收入超过总投入．点评：本小题主要考查数列的基本应用、数列求和、不等式等基础知识；考查综合运用数学知识解决实际问题的能力，属于中档题．20．如图，已知圆C：x2+y2=2与x轴交于A1、A2两点，椭圆E以线段A1A2为长轴，离心率．（Ⅰ）求椭圆E的标准方程；（Ⅱ）设椭圆E的左焦点为F，点P为圆C上异于A1、A2的动点，过原点O作直线PF的垂线交直线x=﹣2于点Q，判断直线PQ与圆C的位置关系，并给出证明．考点：圆与圆锥曲线的综合；直线与圆的位置关系；椭圆的标准方程．专题：计算题；数形结合．分析：（Ⅰ）直接求出a再利用离心率求出c即可求出椭圆E的标准方程；（Ⅱ）先设出点P的坐标，利用条件求出点Q的坐标，再求出k OP和k PQ的表达式，利用点P 在圆上，可以得直线PQ与圆C保持相切．解答：解：（Ⅰ）因为，所以c=1（2分）则b=1，即椭圆E的标准方程为（4分）（Ⅱ）当点P在圆C上运动时，直线PQ与圆C保持相切（6分）证明：设P（x0，y0）（），则y02=2﹣x02，所以，，所以直线OQ的方程为（9分）所以点Q（﹣2，）（11分）所以（13分）又，所以k OP⊥k PQ=﹣1，即OP⊥PQ，故直线PQ始终与圆C相切（14分）点评：本题是对圆和椭圆的综合考查．在做这一类型题目时，一定要画出图象，利用图象来分析问题．21．如图，在直角坐标系中，正方形ABCD的四个顶点分别为A（0，0），B（1，0），C（1，1），D（0，1）．（Ⅰ）已知函数（其中），过f（x）图象是任意一点R的切线l将正方形ABCD截成两部分，设R点的横坐标为t，S（t）表示正方形ABCD被切线l所截的左下部分的面积，求S（t）的解析式；（Ⅱ）试问S（t）在定义域上是否存在最大值和最小值？若存在，求出S（t）的最大值和最小值；若不存在，请说明理由．考点：定积分在求面积中的应用．专题：导数的综合应用．分析：（Ⅰ）讨论切点位置，得到不同的切点位置对应的面积解析式；注意讨论要全面；（Ⅱ）由（Ⅰ）的解析式分析各段的单调性，全等最值．解答：解：（Ⅰ）设R（t，f（t））（其中），f（x）图象上的两端点为又，所以过点R（t，f（t））的切线l的方程为：…（2分）（ⅰ）当切点为时，，切线l为：，切线l与CD的交点坐标为．当切线过点D（0，1）时，…（4分）故当时，切线l与CD相交，此时正方形ABCD被切线l所截的左下部分是直角梯形，S（t）=…（6分）（ⅱ）当切线过点B（1，0）时，当时，切线l与AD，AB都相交，正方形ABCD被切线l所截的左下部分是直角三角形，S（t）=…（7分）（ⅲ）当切点为时，切线l为：，切线l与BC的交点坐标为故当时，切线l与AD，BC都相交，正方形ABCD被切线l所截的左下部分是直角梯形，S（t）=…（9分）综上所述：…（10分）（Ⅱ）解：当，，故S（t）在上递增，S（t）最大无限接近，S（t）无最大值和最小值…（11分）当时，，S（t）在上递减，S（t）最大无限接近，S（t）无最大值和最小值…（12分）故当，成立…（13分）综上所述：S（t）在定义域上存在最大值，不存在最小值．…（14分）．点评：本题考查了分段函数进行是求法与函数的最值求法；借助于导数的几何意义、利用单调性求最值；考查了学生的计算能力；属于难题．*228394 6EEA 滪UNh'25630 641E 搞<)39110 98C6 飆24375 5F37 強-33667 8383 莃。

江苏省泰兴中学2015-2016学年高二数学下学期期末复习4（无答案）苏教版【复习目标】1. 理解二项式定理及其展开式的特点，二项开展式的通项公式及二项式系数的性质；2. 能灵活运用通项公式、组合数的性质解题，提高应用意识和分析问题、解决问题的 能力.【课前温习】一.回归课本，知识梳理1．二项式定理的有关概念(1)二项式定理：(a ＋b )n ＝C 0n a n ＋C 1n an －1b 1＋…＋C r n a n －r b r ＋…＋C n n b n (n ∈N *)， 这个公式叫做_____ _____． ①二项展开式：右边的多项式叫做 (a ＋b )n 的二项展开式．②项数：二项展开式中共有____ ____项．③二项式系数：在二项展开式中_____ _____(r ＝____________)叫做二项式系数． ④通项：在二项展开式中的____________________叫做二项展开式的通项，用T r ＋1表示，即通项为展开式的第r ＋1项：T r ＋1＝____________________________. 2．二项式系数的性质(1)C m n ＝C n －m n ；(2)C m n ＋C m －1n ＝C m n ＋1；(3)当r <n －12时，______________________；当r >n －12时，C r ＋1n <C rn ； (4)当n 是偶数时，中间的一项二项式系数________________________________取得最大值；当n 为奇数时，中间的两项二项式系数______________________________、__________________________相等，且同时取得最大值；(5)各二项式系数和：C 0n ＋C 1n ＋C 2n ＋…＋C nn ＝______，C 0n ＋C 2n ＋C 4n ＋…＝C 1n ＋C 3n ＋C 5n ＋…＝______.二.基础训练1. (1＋2x )5的展开式中，x 2的系数等于________．2．(4x －2－x )6(x ∈R )展开式中的常数项是________． 3．已知n 为正偶数，且⎝⎛⎭⎪⎫x 2－12x n 的展开式中第4项的二项式系数最大，则第4项的系数是______．(用数字作答)4. 12323...n nn n n n C C C C ++++= 5. 若多项式21091001910(1)(1)(1)x x a a x a x a x +=+++++++，则=9a .【典型例题】例1已知在⎝⎛⎭⎪⎪⎫3x －123x n 的展开式中，第6项为常数项．(1)求n ；(2)求含x 2的项的系数； (3)求展开式中所有的有理项．例2 在(2x －3y )10的展开式中，求：(1)二项式系数的和；(2)各项系数的和；(3)奇数项的二项式系数和与偶数项的二项式系数和；(4)奇数项系数和与偶数项系数和；(5)x 的奇次项系数和与x 的偶次项系数和；(6)求展开式中二项式系数最大的项；(7)求展开式中系数最大的项．例3 求证：(1)32n ＋2－8n －9能被64整除(n ∈N *)；(2)3n >(n ＋2)·2n －1 (n ∈N *，n >2)【课时小结】江苏省泰兴中学高二(理科)数学复习作业（4） 班级: 姓名: 学号： 1.在⎝ ⎛⎭⎪⎫x 2－2x 6的二项展开式中，x 2的系数为________. 2.若二项式⎝ ⎛⎭⎪⎫x －2x n 的展开式中第5项是常数项，则自然数n 的值为________.3.在⎝⎛⎭⎪⎪⎫x 2－13x n 的展开式中，只有第5项的二项式系数最大，则展开式中常数项是 ________.4.(1－x )20的二项展开式中，x 的系数与x 9的系数之差为________.5.⎝ ⎛⎭⎪⎫ax －1x 8的展开式中x 2的系数为70，则a ＝________. 6.若(2x ＋3)3＝a 0＋a 1(x ＋2)＋a 2(x ＋2)2＋a 3(x ＋2)3，则a 0＋a 1＋2a 2＋3a 3＝________.7.在(x ＋43y )20的展开式中，系数为有理数的项共有____项.8. (1＋x ＋x 2)(x －1x)6的展开式中的常数项为________. 9. 若a 4(x ＋1)4＋a 3(x ＋1)3＋a 2(x ＋1)2＋a 1(x ＋1)＋a 0＝x 4，则a 3－a 2＋a 1＝______.10.对于n ∈N *，将n 表示为n ＝a 0×2k ＋a 1×2k －1＋a 2×2k －2＋…＋a k －1×21＋a k ×20，当i ＝0时，a i ＝1，当1≤i ≤k 时，a i 为0或1.记I (n )为上述表示中a i 为0的个数(例如：1＝1×20,4＝1×22＋0×21＋0×20，故I (1)＝0，I (4)＝2)，则(1)I (12)＝____ __；(2)12712()n I n =∑＝____ __. 11. 设,0>a 若12(1)n ax +的展开式中含2x 项的系数等于含x 项的系数的9倍,且展开式中第3项等于135x ,求a 的值.12. (1)设(3x－1)4＝a0＋a1x＋a2x2＋a3x3＋a4x4.①求a0＋a1＋a2＋a3＋a4；②求a0＋a2＋a4；③求a1＋a2＋a3＋a4.(2)求证：32n＋2－8n－9能被64整除(n∈N*)．13.已知(3x＋x2)2n的展开式的二项式系数和比(3x－1)n的展开式的二项式系数和大992，求⎝ ⎛⎭⎪⎫2x －1x 2n 的展开式中： (1)二项式系数最大的项；(2)系数的绝对值最大的项.欢迎您的下载，资料仅供参考！。

常熟市浒浦高级中学 高二数学期末复习（4）选修2-2 导数及其应用 6/10姓名：____________1．函数x e x f x -=)(在]1,1[-上的最小值是 .2．曲线()321f x x x =++在点()()1,1f 处的切线方程为 ．3．已知函数f(x)＝mx 2＋lnx －2x 在定义域内是增函数，则实数m 的取值范围为________． 4．函数f(x)＝13x 3－x 2－3x －1的图象与x 轴的交点个数是________． 5．函数12ln y x x=+的单调减区间为___________. 6．设m R ∈，若函数2()xy e mx x R =+∈有大于零的极值点，则m 的取值范围是________．7．已知()f x 为定义在(0，+∞)上的可导函数，且()'()f x xf x >恒成立，则不等式0)()1(2>-x f xf x 的解集为______ _____．8．若不等式29ln bx c x x ++≤对任意的()0+x ∈∞，，()03b ∈，恒成立，则实数c 的取值范围是 ． 9．已知函数f(x)=x 2+,g(x)=-m.若∀x 1∈[1,2],∃x 2∈[-1,1]使f(x 1)≥g(x 2),则实数m 的取值范围是__________. 10．设f(x)＝－13x 3＋12x 2＋2ax ，若f(x)在(23，＋∞)上存在单调递增区间，则a 的取值范围为________． 11．定义在R 上的函数()f x 满足：(1)1f =，且对于任意的x R ∈,都有1'()2f x <，则不等式22log 1(log )2x f x +>的解集为 __________________. 12．已知函数)(x f 的定义域［-1，5］，部分对应值如表，)(x f 的导函数)('x f y =的图象如图所示，下列关于函数)(x f 的命题正确的是_______________.（填序号）①函数)(x f 的值域为［1，2］；②函数)(x f 在［0，2］上是减函数；③如果当],1[t x -∈时，)(x f 的最大值是2，那么t 的最大值为4；④当21<<a 时，函数a x f y -=)(最多有4个零点.13．已知曲线 y = x 3+ x －2 在点 P 0 处的切线 1l 平行于直线4x －y －1=0，且点 P 0 在第三象限,⑵若直线 1l l ⊥ , 且 l 也过切点P 0 ,求直线l 的方程.14．已知函数R x x x x f ∈-=,sin 21)(． （1）试求函数)(x f 的递减区间；（2）试求函数)(x f 在区间[]ππ,-上的最值．15．某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品需向总公司交3元的管理费，预计当每件产品的售价为x 元(117≤≤x )时，一年的销售量为2)12(x -万件．（1）求该分公司一年的利润L (万元)与每件产品的售价x 的函数关系式； （2）当每件产品的售价为多少元时，该分公司一年的利润L 最大？并求出L 的最大值．16．设P 1，P 2，P 3，…，P n ，…是曲线y=x 上的点列，Q 1，Q 2，Q 3， …，Q n ，…是x 轴正半轴上的点列，且△OQ 1P 1，△Q 1Q 2P 2，…，△Q n －1Q n P n ，…都是正三角形，设它们的边长为a 1，a 2，…，a n ，…，求证：a 1+a 2+…+a n =31n （n+1）.17．已知椭圆C ：2222x y a b＋＝1(a>b>0)，点A 、B 分别是椭圆C 的左顶点和上顶点，直线AB 与圆G ：x 2＋y 2＝24c (c 是椭圆的半焦距)相离，P 是直线AB 上一动点，过点P 作圆G 的两切线，切点分别为M 、N. (1)若椭圆C经过两点1,3⎛ ⎝⎭、2⎛⎫⎪ ⎪⎝⎭，求椭圆C 的方程； (2)当c 为定值时，求证：直线MN 经过一定点E ，并求OP ·OE 的值(O 是坐标原点)；(3)若存在点P 使得△PMN 为正三角形，试求椭圆离心率的取值范围．.18．已知函数()ln ,()xf x ax xg x e =+=．（2）若不等式()g x<有解，求实数m 的取值菹围； （3）证明：当a=0时，()()2f x g x ->．参考答案1．1 【解析】试题分析：因为()1x f x e '=-，()00,()00f x x f x x ''>⇒><⇒<，所以()f x 在[1,0]-单调递减，在[0,1]单调递增，从而函数x e x f x -=)(在]1,1[-上的最小值是0(0)01f e =-=.考点：函数的最值与导数. 2．52y x =- 【解析】试题分析：因为2()32f x x x '=+，所以所求切线的斜率(1)325k f '==+=，而(1)1113f =++=，故所求的切线方程为35(1)y x -=-即52y x =-. 考点：导数的几何意义. 3．1,2⎡⎫+∞⎪⎢⎣⎭【解析】f′(x)＝2mx ＋1x －2，根据题意得f′(x)≥0在x ∈(0，＋∞)上恒成立，所以2m≥2x－21x ，求出2x －21x在x ∈(0，＋∞)上的最大值为1，则m≥12.检验：当m ＝12时满足题意．4．3【解析】f′(x)＝x 2－2x －3＝(x ＋1)(x －3)，函数在(－∞，－1)和(3，＋∞)上是增函数，在(－1,3)上是减函数，由f(x)极小值＝f(3)＝－10<0，f(x)极大值＝f(－1)＝23>0知函数f(x)的图象与x 轴的交点个数为3. 5．1(0,)2【解析】试题分析：因为2120,0x y x x '>=-+<，解得02x <<，因此函数12ln y x x=+的单调减区间为1(0,)2. 考点：导数求单调区间 6．12m <- 【解析】试题分析：由题意得，20xy e m '=+=有大于零的解，即,(0)2xe m x =->有解，因此01.22e m <-=-考点：函数极值 7．{1}x x > 【解析】试题分析：由()'()f x xf x >可得()()'0f x x <.即函数()()f x g x x=在(0，+∞)上递减.由0)()1(2>-x f x f x 可得1()()1f f x x x x>.所以1,10,1x x x x <∴-<<>.又因为0x >.所以1x >即{1}x x >.考点：1.函数导数.2.构建新函数的思维.3.函数的单调性. 8．(]9ln3-∞-， 【解析】试题分析：根据题意，得关于b 的函数：2()(9ln )f b xb x x c =+-+，这是一个一次函数，要使()0f b ≤对任意的(0,3),(0,)b x ∈∈+∞恒成立，则：(3)0f ≤，即有：239ln 0x x x c +-+≤对任意的(0,)x ∈+∞恒成立，则有：239ln c x x x ≤--+，可令函数2()39ln g x x x x =--+，求导可得：29239(23)(3)'()32x x x x g x x x x x--+-=--+==，发现有：min ()(3)99ln399ln3g x g ==--+=-，故有：9ln 3c ≤-．考点：1.恒成立问题;2.一次函数的性质;3.函数与导数的运用 9．【解析】要使∀x 1∈[1,2],∃x 2∈[-1,1],使f(x 1)≥g(x 2),只需f(x)=x 2+在[1,2]上的最小值大于等于g(x)=-m 在[-1,1]上的最小值,因为f ′(x)=2x-=≥0在[1,2]上成立,且f ′(1)=0,所以f(x)=x 2+在[1,2]上单调递增, 所以f(x)min =f(1)=12+=3. 因为g(x)=-m 是单调递减函数,所以g(x)min =g(1)=-m, 所以-m ≤3,即m ≥-. 10．(－19，＋∞) 【解析】由f′(x)＝－x 2＋x ＋2a ＝－(x －12)2＋14＋2a ，得当x ∈[23，＋∞)时，f′(x)的最大值为f′(23)＝29＋2a.令29＋2a>0，得a>－19.所以a>－19时，f(x)在(23，＋∞)上存在单调递增区间．11．(0,2)【解析】12．①②④ 根据已知的对应值表及表格画出③根据以上知识可得：当x [1t ]∈-，时，)(x f 的最大值是2，则t=0，或4．故③不正确；④由图象可以看出：当1.5＜a ＜2时，函数a x f y -=)(有4个零点；当a=2时，函数a x f y -=)(有2个零点；当a=1.5时，函数a x f y -=)(有3个零点；当1≤a ＜1.5时，函数a x f y -=)(有4个零点；∴当1＜a ＜2时，函数a x f y -=)(最多有4个零点．故④正确． 综上可知①②④正确． 故答案为①②④．考点：应用导数研究函数的单调性、极值，函数的零点. 13．(1) (－1,－4);(2) 14(1)4y x +=-+即4170x y ++=.试题解析：解:⑴由y=x 3+x －2，得y ′=3x 2+1，由已知得3x 2+1=4，解之得x =±1.当x=1时，y=0;当x=－1时，y=－4. 又∵点P 0在第三象限,∴切点P 0的坐标为 (－1,－4) .5分 ⑵∵直线1l l ⊥,1l 的斜率为4,∴直线l 的斜率为14-, ∵l 过切点P 0,点P 0的坐标为 (－1,－4) ∴直线l 的方程为14(1)4y x +=-+即4170x y ++= 10分 考点：1.导数在切线中的应用；2.直线的方程. 14．（I ）Z k k k ∈++-),23,23(ππππ；（2）最大值为2)(ππ=f ，最小值为2)(ππ-=-f ．【解析】 试题分析：（1）首先求导函数()f x '，然后再通过解不等式()0f x '<的符号确定单调区间；（2）利用（1）求得极值，然后与()f π、()f π-的值进行比较即可求得最值． （I ）求导数得：,cos 21)(x x f -=' 令,0)(<'x f 即,0cos 21<-x 得：Z k k x k ∈+<<+-,2323ππππ，∴函数)(x f 在每个区间Z k k k ∈++-),23,23(ππππ上为减函数．（2）由（I ）知，函数)(x f 在区间),3(),3,(ππππ--上为增函数，在区间)3,3(ππ-上为减函数，∴函数)(x f 在3π-=x 处取极大值623)3(ππ-=-f ，在3π=x 处取极小值236)3(-=ππf ，∵2)(ππ-=-f ，2)(ππ=f ∴函数()f x 在区间[]ππ,-上的最大值为2)(ππ=f ，最小值为2)(ππ-=-f ．考点：1、导函数与函数的单调性；2、利用导数研究函数的最值；3、简单三角函数的解法．15．（1）3230288864L x x x =-+-，]11,7[∈x ；（2）当每件产品的售价8=x 时，该分公司一年的利润最大，且最大利润32max =L 万元.【解析】试题分析：（1）解实际应用题，关键是正确理解题意，正确列出等量关系或函数关系式.本题中利润=每件产品的利润⨯销售量，进而根据已知即可得出该分公司一年的利润L 与每件产品的售价x 的函数关系式；（2）根据（1）中确定的函数关系式，由函数的最值与函数的导数的关系，求出该函数的最大值即可.（1）分公司一年的利润L (万元)与售价x 的函数关系式为2)12)(33(x x L ---=86428830)24144)(6(232-+-=-+-=x x x x x x ，]11,7[∈x 6分（2）)8)(12(3)9620(3288603'22--=+-=+-=x x x x x x L令0'=L ，得8=x 或12=x (不合题意，舍去) 8分 当]8,7[∈x 时，0'>L ，L 单调递增；当]11,8[∈x 时，0'<L ，L 单调递减 10分 于是：当每件产品的售价8=x 时，该分公司一年的利润最大，且最大利润32max =L 万元 12分考点：导数的实际应用. 【答案】证明：（1）当n=1时，点P 1是直线y=3x 与曲线y=x 的交点，∴可求出P 1（31，33）.∴a 1=|OP 1|=32.而31×1×2=32，命题成立.（6分）（2）假设n=k （k ∈N*）时命题成立，即a 1+a 2+…+a k =31k （k+1），则点Q k 的坐标为（31k （k+1），0），∴直线Q k P k+1的方程为y=3[x －31k （k+1）].代入y=x ，解得P k+1点的坐标为)).1(33,3)1((2++k k∴a k+1=|Q k P k+1|=33（k+1）·32=32（k+1）.∴a 1+a 2+…+a k +a k+1=31k （k+1）+32（k+1）=31（k+1）（k+2）.∴当n=k+1时，命题成立. 由（1）（2）可知，命题对所有正整数都成立.（13分） 【解析】略17．（1）2294x y ＋＝1.（2）见解析（3e ≤ 【解析】(1)解：令椭圆mx 2＋ny 2＝1，其中m ＝21a ，n ＝21b ，得32 1927 1.4m n m n ⎧⎪⎪⎨⎪⎪⎩＋＝，＋＝所以m ＝19，n ＝14，即椭圆方程为2294x y ＋＝1.(2)证明：直线AB ：x y a b ＋-＝1，设点P(x 0，y 0)，则OP 的中点为00,22x y ⎛⎫⎪⎝⎭，所以点O 、M 、P 、N 所在的圆的方程为220022x y x ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭＋y-＝22004x y +，化简为x 2－x 0x ＋y 2－y 0y ＝0，与圆x 2＋y 2＝24c 作差，即直线MN ：x 0x ＋y 0y ＝24c .因为点P(x 0，y 0)在直线AB 上，得00x ya b＋-＝1， 所以x 0 b x y a ⎛⎫ ⎪⎝⎭＋＋24c by ⎛⎫ ⎪⎝⎭－＝0，即2004b x y ac by ⎧⎪⎪⎨⎪⎪⎩＋＝，－＝，得x ＝－24c a ，y ＝24c b ，故定点E 2244c c a b ⎛⎫ ⎪⎝⎭-，，OP ·OE ＝220044b c c x x b a a b ⎛⎫⎛⎫⋅ ⎪ ⎪⎝⎭⎝⎭，＋-，＝24c . (3)解：由直线AB 与圆G ：x 2＋y 2＝24c (c 是椭圆的焦半距)相离，＞2c ，即4a 2b2＞c 2(a 2＋b 2)，4a 2(a 2－c 2)＞c 2(2a 2－c 2)，得e 4－6e 2＋4＞0.因为0＜e ＜1，所以0＜e 2＜3①.连结ON 、OM 、OP ，若存在点P 使△PMN 为正三角形，则在Rt △OPN 中，OP ＝2ON ＝2r ＝c ，≤c ，a 2b 2≤c 2(a 2＋b 2)，a 2(a 2－c 2)≤c 2(2a 2－c 2)，得e 4－3e 2＋1≤0.因为0＜e＜1e 2＜1≤e 2＜3e ≤ 18．（1） 参考解析；（2）0m <；（3）参考解析【解析】 试题分析：（1）由于 ()ln f x ax x =+，(0,)x ∈+∞．需求()f x 的单调区间，通过对函数()f x 求导，在讨论a 的范围即可得函数()f x 的单调区间．（2）本小题可等价转化为，求实数m的取值菹围，使得(0,)m x e x <-∈+∞有解，等价于m小于函数()h x x e =-(0,)x ∈+∞的最小值．所以对函数()h x 求导，由导函数的解析式，通过应用基本不等式，即可得到函数()h x 的单调性，从而得到最小值．即可得到结论．（3）由于当0a =时，()()l n x f x g x e x-=-．本小题解法通过构造()()(ln )x f x g x e x x x -=---．即两个函数()x m x e x =-与()ln n x x x =-的差，通过等价证明函数()m x 的最小值与函数()n x 的最大值的差大于2．所以对两个函数分别研究即可得到结论．（1） ()f x 的定义域是(0,)+∞，1'(),(0)f x a x x=+>01当0a =时，'()0f x >，所以在(0,)+∞单调递增；02当0a <时，由'()0f x =，解得1x a =-．则当1(0,)x a∈-时． '()0f x >，所以()f x 单调递增．当1(,)x a∈-+∞时，'()0f x <，所以()f x 单调递减．综上所述：当0a =时，()f x 在(0,)+∞单调递增；当0a <时，()f x 在1(0,)a-上单调递增，在1(,)a-+∞单调递减．（2）由题意：x e <e x m <-有解，因此只需(0,)m x e x <-∈+∞有解即可，设()h x x e =-，'()11x x h x e e =-=-，因为- 11 - 1≥>，且(0,)x ∈+∞时1x e >，所以10x e -<，即'()0h x <．故()h x 在[0,)+∞上递减，所以()(0)0h x h <=故0m <．（3）当0a =时，()l n f x x =，()f x 与()g x 的公共定义域为(0,)+∞，()()ln ln (ln )x x x f x g x x e e x e x x x -=-=-=---，设()x m x e x =-，x ∈(0,)+∞．因为'()10x m x e =->，()m x 在(0,)+∞单调递增． ()(0)1m x m >=．又设()ln n x x x =-，x ∈(0,)+∞，1'()1n x x=-．当(0,1)x ∈时，'()0n x >，()n x 单调递增，当(1,)x ∈+∞时，'()0n x <，()n x 单调递减．所以1x =为()n x 的极大值点，即()(1)1n x n ≤=-．故()()()()1(1)2f xg x m x n x -=->--=． 考点：1．函数的单调性．2．含不等式的证明．3．构建新的函数问题．4．运算能力．5．数学知识综合应用．。

2020年高二数学（文）下学期 期末复习试卷四第Ⅰ卷（选择题）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1.已知集合U R =，集合{}2|40M x x =-≤，则U C M =A. {}|22x x -<<B. {}|22x x -≤≤C. {}|22x x x <->或D.{}|22x x x ≤-≥或2.设复数z 满足()()225z i i --=，则z =A. 23i +B. 23i -C. 32i +D.32i -3.为了判断两个分类变量X 与Y 之间是否有关系，应用独立性检验法算得2K 的观测值为6，附：临界值表如下：则下列说法正确的是A. 有95%的把握认为X 与Y 有关系B. 有99%的把握认为X 与Y 有关系C.有99.5%的把握认为X 与Y 有关系D. 有99.9%的把握认为X 与Y 有关系4.设x R ∈，向量()()1,,2,6a x b ==-r r，且//a b r r ，则a b ⋅=r rA. -4B. 10C.255.下列四个结论：①若“p q ∧”是真命题，则p ⌝可能是真命题；②命题“2000,10x R x x ∃∈--<”的否定是“2,10x R x x ∃∈--≥”；③“5a >且5b >-”是“0a b +>”的充要条件；④当0a <时，幂函数ay x =在区间()0,+∞上单调递减.其中正确的结论个数是A.0个B.1个C. 2个D. 3个 6.已知函数()133xxf x ⎛⎫=- ⎪⎝⎭，则()f x A. 是偶函数，且在R 上是增函数 B. 是奇函数，且在R 上是增函数 C.是偶函数，且在R 上是减函数 D. 是奇函数，且在R 上是减函数7. 在单调递减等差数列{}n a 中，若32431,4a a a==，则1a = A. 1 B. 2 C. 32D. 38.已知()f x 是定义在R 上的奇函数，且当()0,x ∈+∞时，()20182018log xf x x =+， 则函数()f x 的零点的个数是 A. 1 B. 2 C. 3 D. 49.函数22sin 33,00,1441x y x xππ⎛⎫⎡⎫⎛⎤=∈-⎪ ⎪⎢⎥⎣⎭⎝⎦⎝⎭+U 的图象大致是10.若将函数sin 3y x x =+的图象向右平移()0ϕϕ>个单位长度得到函数sin 3y x x =-的图象，则ϕ的最小值为A. 6πB. 2πC. 3πD.23π11.如果函数()f x 在区间D 上是增函数，且()f x x在区间上是减函数，则称函数()f x 在区间D 上是缓增函数，区间D 叫做缓增区间.若函数()21322f x x x =-+在区间D 上是缓增函数，则缓增区间D 是A.[)1,+∞B. 3⎡⎣C. []0,1D.3⎡⎤⎣⎦12.已知函数()22ln x e f x k x x x ⎛⎫=-+ ⎪⎝⎭，若2x =是函数()f x 的唯一极值点，则实数k 的取值范围是A. (],e -∞B. []0,eC. (),e -∞D.[)0,e二、填空题：本大题共4小题，每小题5分，共20分.13.已知()f x 的定义域为[]1,1-，则()2log f x 的定义域为 . 14.若曲线ln y x =的切线过原点，则此切线的斜率为 .15.已知()f x 是R 上的偶函数，()g x 是R 上的奇函数，且()()1g x f x =-，若()22f -=，则()2018f = .16.已知函数()f x A,不等式()21log a x x -<在x A ∈时恒成立，则实数a 的取值范围为 .三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程. 17.（本题满分12分）设函数()()22280f x x ax aa =-->，记不等式()0f x ≤的解集为A.（1）当1a =时，求集合A;（2）若()1,1A -⊆，求实数a 的取值范围.18.（本题满分12分）若二次函数()()2,f x ax bx c a b R =++∈满足()()12f x f x x +-=，且()0 1.f = （1）求()f x 的解析式；（2）若在区间[]1,1-上，不等式()2f x x m >+恒成立，求实数m 的取值范围.19.（本题满分12分） 如图，在长方体1111ABCD A B C D -中，,E F 分别为111,DD C D 的中点.（1）证明：平面11ADC B ⊥平面1A BE ； （2）证明：1//B F 平面1A BE ；（3）若正方体棱长为1，求四面体11A B BE -的体积.20.（本题满分12分）已知椭圆C 的中心在原点，一个焦点为()2,0F -，且长轴与短轴长的比是2 3.（1）求椭圆C 的方程；（2）设点(),0M m 在 椭圆C 的长轴上，点P 是椭圆上任意一点，当PM 最小时，点P 恰好落在椭圆的右顶点上，求实数m 的取值范围.21.（本题满分12分）已知()()2ln , 3.f x x x g x x ax ==-+-（1）求函数()f x 在区间[](),20t t t +>上的最小值；（2）对一切实数()()()0,,2x f x g x ∈+∞≥恒成立，求实数a 的取值范围.22.（本题满分10分）选修4-4：参数方程与极坐标系在平面直角坐标系xoy 中，直线1l 的参数方程为2x t y kt =+⎧⎨=⎩（t 为参数），直线2l 的参数方程为2x m m y k =-+⎧⎪⎨=⎪⎩（m 为参数），设直线1l ，2l 的交点为P,当变化时，P 的轨迹为曲线.（1）写出曲线C 的普通方程；（2）以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系， 设()3:cos sin 0l ρθθ+，M 为3l 与C 的交点，求M 的极径.23.（本题满分10分）选修4-5：不等式选讲 已知函数()()24,1 1.f x x ax g x x x =-++=++- （1）当1a =时，求不等式()()f x g x ≥的解集；（2）若不等式()()f x g x ≥的解集包含，求实数a 的取值范围.高二数学(文)答案一、选择题1.C2.A3.A4.D5.B6.B7.B8.C9.A 10.D 11.D 12.A1．C 【解析】因为{}240M x x =-≤{}22x x =-≤≤，全集U R =，所以U C M ={}22x x x <->或，故选C.2．A 【解析】利用方程思想求解复数并化简.由(z －2i)(2－i)＝5，得z ＝2i ＋52－i＝2i ＋ 5(2＋i)(2－i)(2＋i)＝2i ＋2＋i ＝2＋3i.3．A 【解析】依题意，K 2＝6，且P (K 2≥3．841)＝0．05，因此有95%的把握认为“X 和Y 有关系”，选A ．4．D 【解析】∵a ＝(1，x )，b ＝(2，－6)且a ∥b ，∴－6－2x ＝0，x ＝－3，∴a ＝(1，－3)，a ·b ＝20，故选D ．5．B 【解析】①若p q ∧是真命题，则p 和q 同时为真命题，p ⌝必定是假命题；②命题“2000,10x R x x ∃∈--<”的否定是“2,10x R x x ∀∈--≥”；③“5a >且5b >-”是“0a b +>”的充分不必要条件；④ay x =1'a y a x-⇒=⋅，当0a <时，'0y <，所以在区间()0+∞，上单调递减. 选B ．6．B 【解析】()()113333xxx xf x f x --⎛⎫⎛⎫-=-=-=- ⎪ ⎪⎝⎭⎝⎭，所以函数是奇函数，并且3x 是增函数，13x⎛⎫ ⎪⎝⎭ 是减函数，根据增函数-减函数=增函数，所以函数是增函数，故选A.7．B 【解析】由题知，a 2＋a 4＝2a 3＝2，又∵a 2a 4＝34，数列{a n }单调递减，∴a 4＝12，a 2＝32．∴公差d ＝a 4－a 22＝－12．∴a 1＝a 2－d ＝2．8．C 【解析】作出函数y ＝2 018x和y ＝－log 2 018x 的图象如图所示，可知函数f (x )＝2 018x＋log 2 018x 在x ∈(0，＋∞)上存在一个零点，又f (x )是定义在R 上的奇函数，所以f (x )在x ∈(－∞，0)上只有一个零点，又f (0)＝0，所以函数f (x )的零点个数是3，故选C.9．A 【解析】因为函数22sin ()11xy f x x==+可化简为222sin ()1x x f x x =+可知函数为奇函数关 于原点对称，可排除答案C ；同时有42224sin 2cos 2cos ''()(1)x x x x x xy f x x ++==+3222(2sin cos cos )(1)x x x x x x x ++=+，则当(0,)2x π∈ '()0f x >,可知函数在2x π=处附近单调递增，排除答案B 和D ，故答案选A ．10．D 【解析】因为y ＝sin x ＋3cos x ＝2sin ⎝ ⎛⎭⎪⎫x ＋π3，y ＝sin x －3cos x ＝2sin ⎝⎛⎭⎪⎫x －π3，所以把y ＝2sin ⎝ ⎛⎭⎪⎫x ＋π3的图象至少向右平移2π3个单位长度可得y ＝2sin ⎝ ⎛⎭⎪⎫x －π3的图象．所以选D 。

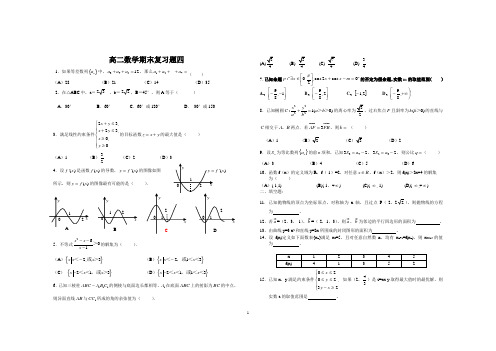
高二数学期末考试复习专题四《不等式》第二课时深圳市新安中学 吕正军【知识要点】（Ⅰ）其他不等式1.分式不等式的解法：①移项（使右边为 ）；② ；③因式分解（使最高次项系数为 ）；④转化为整式不等式__________________0)()(⇔ x g x f ⎩⎨⎧⇔≥_________________________________________0)()(x g x f __________________0)()(⇔ x g x f ⎩⎨⎧⇔≤_________________________________________0)()(x g x f 2、高次不等式的解法：_____________________（画出近似的函数图像）步骤：①因式分解（使x 的系数为正）；②标根（注意空心圈、实心圈，穿根的口诀是___ __________________）3、其他可转化为一元二次不等式的不等式，如：1）6-≥x x 2）51-≥+x x 3） 642-≥x x 4）62-≥x x5） 0)(2>+⋅+⋅C a B a A x x 6）0log )(log 2>+⋅+⋅C x B x A a a上述不等式都可利用______________________法转化为一元二次不等式求解。

（Ⅱ）含参数的不等式，对参数分类讨论的原则如下：当二次项系数含参数时，按参数符号进行分类讨论：二次项系数000 ，，=； 否则，若能因式分解（可求根），但两根大小无法判断时，按 进行讨论： ，，=；若又不能因式分解时，按 进行讨论：000 ∆∆=∆，，；不论哪类讨论，最后一定要（Ⅲ）一元二次不等式恒成立情况小结：20ax bx c ++>（0a ≠）恒成立⇔20ax bx c ++<（0a ≠）恒成立⇔ ．a x f <)(恒成立⇔a x f >)(恒成立⇔（IV ）不等式的证明1． 步骤：①作差；②将差式化简变形；③确定符号2． 以一个显然成立的不等式为基础，利用不等式的性质不断恒等变形得到。

高二数学期末模拟四一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1、函数的单调递减区间是（）A ．（﹣2，3）B ．（﹣∞，﹣2）∪（3，+∞）C ．（3，+∞）D ．（0，3）2、设集合M ＝{x |0<x <4}，N |13≤x ≤M ∩N ＝()A |0<x B |13≤x C ．{x |4≤x <5}D ．{x |0<x ≤5}3、设a ∈R ，则“a >1”是“a 2>a ”的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4、已知随机变量ξ服从正态分布()22,N σ，且()020.4P ξ<<=，则()0P ξ>=（）A ．0.9B ．0.8C ．0.4D ．0.15．（x +1）（2x +1）（3x +1）…（nx +1）（n ∈N *）展开式中的一次项系数为（）A ．B ．C ．D ．6．某中学从4名男生和4名女生中推荐4人参加社会公益活动，若选出的4人中既有男生又有女生，则不同的选法共有（）A ．68种B ．70种C ．240种D ．280种7.某单位选派一支代表队参加市里的辩论比赛，现有“初心”“使命”两支预备队.选哪支队是随机的，其中选“初心”队获胜的概率为0.8，选“使命”队获胜的概率为0.7，单位在比赛中获胜的条件下，选“使命”队参加比赛的概率为（）A.29B.25 C.815D.7158、某高校为研究学生每周平均体育运动时间进行了一次抽样调查，已知被抽取的男、女生人数相同．调查显示：抽取的男生中每周平均体育运动时间超过4小时的人数占比为45，抽取的女生中每周平均体育运动时间超过4小时的人数占比为35，若在犯错误的概率不超过1%的前提下，可以认为该校学生每周平均体育运动时间与性别有关，则被抽取的男生人数至少为（）附：()2P k χ≥0.0500.0100.0050.001k3.8416.6357.87910.828()()()()()22n ad bc a b c d a c b d χ-=++++A ．60B ．65C ．70D ．75二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分。

2023高二数学选修四期末复习题及答案1. 题目一题目描述：某公司的销售额可以表示为线性函数：y = 2x + 5，其中x代表销售量 (单位：件)，y代表销售额 (单位：万元)。

请求当销售量为10件时，销售额是多少？解答：将x代入线性函数，得到：y = 2(10) + 5 = 25 (万元)2. 题目二题目描述：已知函数f(x) = 3x^2 - 2x + 1，求f(-1)的值。

解答：将x代入函数，得到：f(-1) = 3(-1)^2 - 2(-1) + 1 = 3 - (-2) + 1 = 63. 题目三题目描述：已知函数g(x) = √(x + 2)，求g(4)的值。

解答：将x代入函数，得到：g(4) = √(4 + 2) = √64. 题目四题目描述：一辆汽车以恒定的速度行驶，行驶了2小时后，行驶的距离是120公里。

求这辆汽车的速度。

解答：速度定义为单位时间内行驶的距离，即速度 = 距离 ÷时间。

已知行驶120公里，时间2小时，代入公式可得：速度 = 120公里 ÷ 2小时 = 60公里/小时5. 题目五题目描述：已知等差数列的公式为an = a1 + (n - 1)d，其中an代表第n项，a1代表首项，d代表公差。

若a1 = 2，d = 3，求a5的值。

解答：代入公式可得：a5 = 2 + (5 - 1)3 = 2 + 12 = 146. 题目六题目描述：已知等比数列的公式为an = a1 * r^(n - 1)，其中an代表第n项，a1代表首项，r代表公比。

若a1 = 4，r = 2，求a3的值。

解答：代入公式可得：a3 = 4 * 2^(3 - 1) = 4 * 4 = 16以上为2023高二数学选修四期末复习题及答案。

希望对你的复习有所帮助！。