2015北京八中初二(上)期中数学

2015北京八中百万庄校区初二（上）期中数 学本试题共5页，共八道大题，满分100分，考试时长90分钟。

一、.精心选一选 (每小题3分,共30分)1．计算3)71(--的结果是（）A ．3431-B ．211-C ．－343D ．－212．将201)3(,)2(,)61(---这三个数按从小到大的顺序排列为（ ）A ．210)3()61()2(-<<-- B ．201)3()2()61(-<-<- C ．102)61()2()3(-<-<-D ．120)61()3()2(-<-<-3.下列各式中，从左到右的变形是因式分解的是（ ）.A. a 2－4ab+4b 2=(a －2b )2B.1)(122--=--y x xy xy y xC. 224)2)(2(y x y x y x -=-+D. ax+ay+a=a (x+y )4．如图2 所示，AB = AC ，要说明△ADC ≌△AEB ，需添加的条件不能．．是（ )A ．∠B ＝∠C B. DC = BE C ．∠ADC ＝∠AEBD. AD = AE5、在下列图案中，不是．．轴对称图形的是（ ）A. B. C. D.6．如图9－1，若OP 平分∠AOB ，PC ⊥OA ，PD ⊥OB ，垂足分别是C 、D ，则下列结论中错误的是 （ ） A ．PC ＝PD B ．OC ＝PCC ．∠CPO ＝∠DPOD ．OC ＝ODB CED F图9－17．下列等式成立的是A ．632x x x = B ．x m m x n n +=+ C ．1x y x y-+=-- D ．22x y x y x y +=++8. 如图，△ABC ≌△BAD ，点A 和点B ，点C 和点D 是对应点，如果 AB =6cm ，BD =5cm ，AD =4cm ，那么BC 的长是 （ ）A ．4cmB ．5cmC ．6cmD ．无法确定9.如图，正方形ABCD 的边长为4，将一个足够大的直角三角板的直角顶点放于点A 处，该三角板的两条直角边与CD 交于点F ，与CB 延长线交于点E ．四边形AECF 的面积是（ ）． Ａ. 12 Ｂ．16 Ｃ．8 Ｄ．4 10.如图所示,将一张正方形纸片经过两次对折,并剪出一个小洞后展开铺平,得到的图形是（ ）二.细心填一填(每小题2分,共20分)11. 一种细菌的半径为0.000407m ，用科学记数法表示为__________m.12．当x ＝_____时，分式13-x x 没有意义;当x ＝_____时，分式112--x x 的值为0.13. 计算 232)4()2(ba ba -÷-的结果是____________． 14. 计算aa -+-329122的结果是____________．15. 如果162++mx x 是一个完全平方式，则 m = ______．FD BCEA CA DDC B A16. 如图，在△ABC 和△DEF 中，AB =DE ，AC =DF . 请再添加一个条件，使△ABC和△DFE 全等.添加 的条件是（填写一个即可）：，理由是17. 如图，把△ABC 绕C 点顺时针旋转30°，得到△A ’B ’C ， A ’B ’交AC 于点D ， 若∠A ’DC=80°,则∠A= °.18. 如图，在ABC △中，90C ∠=，AD 平分CAB ∠，BC =9cm ，，BD =6cm ，那么点D 到直线AB 的距离是 cm ．19. 如图，ΔABC 中，AB ＝AC ，AB 的垂直平分线交AC 于P 点．（1）若∠A ＝35°，则∠BPC ＝_____；（2）若AB ＝5 cm ，BC ＝3 cm ，则ΔPBC 的周长＝_____．20．探究：观察下列各式211211-=⨯，3121321-=⨯，4131431-=⨯，……请你根据以上式子的规律填写：111111223344520102011+++++⨯⨯⨯⨯⨯…=______； 1111_____133557(21)(21)n n ++⋯+=⨯⨯⨯-+．三.精心解一解：(21,22每小题2分,23,24,25每小题4分,共16分)B'A A'BDDB C A FEDCBA21. 因式分解：=+-m mx mx 2422．22. 因式分解：y y x 92-=_______________.23．化简：244222x x x x x -+---24. 先化简，再求值：)11(x -÷11222-+-x x x ，其中x =2.25. 解分式方程：2316111x x x +=+--四.耐心想一想：(本小题6分)26.应用题 2010年4月14日我国青海玉树地区发生强烈地震，急需大量赈灾帐篷。

北京八中2023—2024学年度第一学期期中练习题年级：初二科目：数学一、选择题（每题2分，共20分）在下列各题的四个备选答案中，只有一个．．．．是正确的．1.下面四个图形中，是轴对称图形的是（）A. B. C. D.2.下列运算正确的是（）A.336x x x += B.2510x x x ⋅= C.()3666x x = D.()22422x x =3.如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画出了一个与书上完全一样的三角形，那么小明画图的依据是（）A.ASAB.AASC.SASD.SSS4.下列说法错误．．的是（）A.直角三角形两锐角互余B.直角边、斜边分别相等的两个直角三角形全等C.如果两个三角形全等，则它们一定是关于某条直线成轴对称D.与线段两个端点距离相等的点在这条线段的垂直平分线上5.如图，已知DBE BCA ≌△△，85DBE C =∠=︒∠，55BDE ∠=︒，则EBC ∠的度数等于（）A.30︒B.25︒C.35︒D.40︒6.使()()2x p x -+展开整理后不含x 项，则p 的值为（）A.1B.2C.3D.47.如图是战机在空中展示的轴对称队形．以飞机B ，C 所在直线为x 轴、队形的对称轴为y 轴，建立平面直角坐标系．若飞机E 的坐标为(40，a )，则飞机D 的坐标为（）A.(40,)a -B.(40,)a -C.(40,)a -- D.(,40)a -8.已知2x a ab =-，2y ab b =-，x 与y 的大小关系是（）A.x y≥ B.x y≤ C.x y< D.x y>9.在ABC 中，5AC =，中线4=AD ，那么边AB 的取值范围为（）A .19AB << B.313AB << C.513AB << D.913AB <<10.甲、乙两位同学进行一种数学游戏．游戏规则是：两人轮流ABC 及A B C ''' 对应的边或角添加等量条件（点A '，B '，C '分别是点A ，B ，C 的对应点），某轮添加条件后，若能判定ABC 与A B C ''' 全等，则当轮添加条件者失败，另一人获胜．轮次行动者添加条件1甲2cmAB A B ''==2乙4cmBC B C ''==3甲…上表记录了两人游戏的部分过程，则下列说法正确的是（）①若第3轮甲添加5cm AC A C ''==，则乙获胜；②若甲想获胜，第3轮可以添加条件30C C '==︒∠∠：③若乙想获胜，可修改第2轮添加条件为90A A '∠=∠=︒．A.①②B.①③C.②③D.①②③二、填空题（每题3分，共24分）11.计算：()01π-=_____．12.若一个多边形的内角和等于1260°，它是_____边形，从这个多边形的一个顶点出发共有_____条对角线．13.已知3m a =，4n a =，则2m n a +的值是_________．14.如图，将一把含有45︒角的三角尺的直角顶点放在一张宽3cm 的纸带边沿上，另一个顶点放在纸带的另一边沿上，测得三角尺的一直角边与纸带的一边所在的直线成30︒，则三角尺的直角边的长为______cm ．15.等腰三角形的一个内角为50︒，则它的顶角的度数为___________．16.如图，6cm AB AC ==，DB DC =，若60ABC ∠=︒，则BE =______cm ．17.如图，在ABC 中，,||AB AC AB CD =，过点B 作BE AC ⊥于E ，BD CD ⊥于D ，8,3,CD BD ABE == 的周长为_________．18.已知在长方形纸片ABCD 中，6AB =，5AD =，现将两个边长分别为a 和b 的正方形纸片按图1、图2两种方式放置（图1、图2中两张正方形纸片中均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为1S ，图2中阴影部分的面积为2S ；若213-=S S 时，则1b -值为______．三、解答题（19题每题4分，共16分；20，21，23每题6分，22题5分；24题8分；25题9分；解答题共56分）．19.计算（1）()22124a babc -⋅；（2）()()325n n -+；（3）()()22x y x y ----；（4）()()32222362x y x y xy xy -+÷．20.先化简，再求值：2(21)6(1)(32)(32)a a a a a -++-+-，其中2220230a a +-=．21.如图，在△ABC 和△CED 中，AB ∥CD ，AB =CE ，AC =CD .求证：∠B =∠E .22.作图并填空．在ABC 中，（1）利用尺规作出BC 的垂直平分线，交BC 于D ，连接AD ；（2）画出ADC △的高CH ，CH 与BD 的大小关系为______；（3）画出ADC △的角平分线DM 交AC 点M ，若60ABC S =△，10DCM S =△，设AD a =，DC b =，则:a b =______．23.如图，在平面直角坐标系xOy 中，ABC 三个顶点分别为()2,6A -，()5,1B -，()3,1C ．点B 与点C 关于直线l 对称（1）画出直线l ，写出点A 关于l 的对称点A '坐标；（2）则A BC ' 的面积为______；（3）若点P 在直线l 上，90BPC ∠=︒，直接写出点P 坐标．24.如图，ABC 是等边三角形，D 为BC 的中点，BE AB ⊥交AD 的延长线于点E ，点F 在AE 上，且AF BE =，连接CF 、CE ．求证：（1）ACF BCE ∠=∠：（2）CF EF =．25.如图，在ABC 中，120180BAC ︒<<︒，AB AC =．AD BC ⊥于点D ．以AC 为边作等边ACE △，直线BE 交直线AD 于点F ．连接CF 交AE 于M ．（1）求证：FEA FCA ∠=∠：（2）探索FE ，FA ，FC 之间的数量关系，并证明你的结论．四、附加题（26题4分，27题6分，共10分）26.小明同学用四张长为x ，宽为y 的长方形卡片，拼出如图所示的包含两个正方形的图形（任意两张相邻的卡片之间没有重叠，没有空隙）．（1）通过计算小正方形面积，可推出()2x y +，xy ，()2x y -三者之间的等量关系式为______；（2）利用（1）中的结论，试求：当()()3002001996x x --=时，求()22500x -的值．27.在平面直角坐标系xOy 中，若点P 和点1P 关于y 轴对称，点1P 和点2P 关于直线l 对称，则称点2P 是点P 关于y 轴、直线l 的“二次对称点”．（1）已知点()A 3,5，直线l 是经过()0,2且平行于x 轴的一条直线，点A '为点A 关于y 轴，直线l 的“二次对称点”，则点A '的坐标为______；（2）如图1，正方形ABCD 的顶点坐标分别是()0,1A ，()0,3B ，()2,3C ，()2,1D ；点E 的坐标为()1,1，若点M 为正方形ABCD （不含边界）内一点，点M '为点M 关于y 轴，直线OE 的“二次对称点”，则点M '的横坐标x 的取值范围是______；（3）如图2，(),0T t （0t ≥）是x 轴上的动点，线段RS 经过点T ，且点R 、点S 的坐标分别是(),1R t ，(),1S t -，直线l 经过()0,1且与x 轴夹角为60︒，在点T 的运动过程中，若线段RS 上存在点N ，使得点N '是点N 关于y 轴，直线l 的“二次对称点”，且点N '在y 轴上，则点N '纵坐标y 的取值范围是______．北京八中2023—2024学年度第一学期期中练习题年级：初二科目：数学一、选择题（每题2分，共20分）在下列各题的四个备选答案中，只有一个．．．．是正确的．1.下面四个图形中，是轴对称图形的是（）A. B. C. D.【答案】D【分析】根据轴对称图形的定义判断即可．【详解】∵不是轴对称图形，∴A 不符合题意；∵不是轴对称图形，∴B 不符合题意；∵不是轴对称图形，∴C 不符合题意；∵是轴对称图形，∴D 符合题意；故选D ．【点睛】本题考查了轴对称图形即沿直线折叠，直线两旁的部分能够完全重合的图形，熟记定义是解题的关键．2.下列运算正确的是（）A.336x x x +=B.2510x x x ⋅= C.()3666x x = D.()22422x x =【答案】C【分析】本题考查了合并同类项，幂的乘方，同底数幂的乘法，积的乘方．根据合并同类项法则，同底数幂的乘法法则，幂的乘方法则，积的乘方法则进行判断即可．【详解】解：A 、33362x x x x +=≠，选项错误，不符合题意；B 、21075x x x x ⋅=≠，选项错误，不符合题意；C 、()3666x x =，选项正确，符合题意；D 、()2244242x x x =≠，选项错误，不符合题意．故选：C ．3.如图，小明书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画出了一个与书上完全一样的三角形，那么小明画图的依据是（）A.ASAB.AASC.SASD.SSS【答案】A【分析】根据图形可知两角及夹边是已知条件即可判断．【详解】解：由图可知，左下角和右下角可测量，为已知条件，两角的夹边也可测量，为已知条件，故可根据ASA 得到与原图形全等的三角形，故选：A ．【点睛】本题考查全等三角形的的判定定理，掌握全等三角形的的判定定理是关键．4.下列说法错误．．的是（）A.直角三角形两锐角互余B.直角边、斜边分别相等的两个直角三角形全等C.如果两个三角形全等，则它们一定是关于某条直线成轴对称D.与线段两个端点距离相等的点在这条线段的垂直平分线上【答案】C【分析】本题考查了直角三角形的性质，全等三角形的判定和性质，垂直平分线的判定．根据直角三角形的性质，全等三角形的判定和性质，垂直平分线的判定等知识，一一判断即可．【详解】解：A 、直角三角形两锐角互余，故A 不符合题意；B 、直角边、斜边分别相等的两个直角三角形全等，故B 不符合题意；C 、如果两个三角形全等，则它们不一定是关于某条直线成轴对称，故C 符合题意；D 、与线段两个端点距离相等的点在这条线段的垂直平分线上，故D 不符合题意．故选：C ．5.如图，已知DBE BCA ≌△△，85DBE C =∠=︒∠，55BDE ∠=︒，则EBC ∠的度数等于（）A.30︒B.25︒C.35︒D.40︒【答案】A【分析】本题考查三角形全等的性质、三角形内角和的应用，根据DBE BCA ≌△△可得55ABC BDE ∠=∠=︒，再根据DBE ABC EBC =∠-∠∠即可求解．【详解】解：∵DBE BCA ≌△△，∴55ABC BDE ∠=∠=︒，∵85DBE C =∠=︒∠，∴30DB EBC E ABC -∠=︒∠=∠，故选：A ．6.使()()2x p x -+展开整理后不含x 项，则p 的值为（）A.1B.2C.3D.4【答案】B【分析】本题主要考查多项式乘多项式．根据多项式乘多项式的运算法则可进行把含x 的多项式进行展开，然后再根据题意可求解．【详解】解：()()()2222222x p x x px x p x p x p -+=-+-=+--，∵展开后不含x 项，∴20p -=，解得：2p =；故选：B ．7.如图是战机在空中展示的轴对称队形．以飞机B ，C 所在直线为x 轴、队形的对称轴为y 轴，建立平面直角坐标系．若飞机E 的坐标为(40，a )，则飞机D 的坐标为（）A.(40,)a -B.(40,)a -C.(40,)a --D.(,40)a -【答案】B【分析】直接利用关于y 轴对称，纵坐标相同，横坐标互为相反数，进而得出答案．【详解】解：根据题意，点E 与点D 关于y 轴对称，∵飞机E 的坐标为(40，a )，∴飞机D 的坐标为(-40，a )，故选：B ．【点睛】此题主要考查了关于y 轴对称点的性质，正确记忆横纵坐标的符号关系是解题关键．8.已知2x a ab =-，2y ab b =-，x 与y 的大小关系是（）A.x y ≥B.x y≤ C.x y< D.x y>【答案】A【分析】本题主要考查完全平方公式、比较大小．利用作差法即可比较大小关系．【详解】解：已知2x a ab =-，2y ab b =-，则()22a a x yb ab b-=---22a ab ab b =-+-()20a b =-≥，所以x y ≥．故选：A ．9.在ABC 中，5AC =，中线4=AD ，那么边AB 的取值范围为（）A.19AB <<B.313AB << C.513AB << D.913AB <<【答案】B【分析】作辅助线（延长AD 至E ，使4DE AD ==，连接BE ）构建全等三角形BDE ADC △≌△，然后由全等三角形的对应边相等知5BE AC ==；而三角形的两边之和大于第三边、两边之差小于第三边，据此可以求得AB 的取值范围．【详解】解：延长AD 至E ，使4DE AD ==，连接BE ，则8AE =，∵AD 是边BC 上的中线，D 是中点，∴BD CD =，又∵,DE AD BDE ADC =∠=∠，∴()BDE ADC SAS ≌，∴5BE AC ==，由三角形三边关系，得AE BE AB AE BE -<<+，即8585AB -<<+，∴313AB <<．故选：B ．【点睛】本题主要考查了全等三角形的判定与性质、三角形三边关系等知识，解题关键是正确作出辅助线构造全等三角形，运用全等三角形的性质判定对应线段相等．10.甲、乙两位同学进行一种数学游戏．游戏规则是：两人轮流ABC 及A B C ''' 对应的边或角添加等量条件（点A '，B '，C '分别是点A ，B ，C 的对应点），某轮添加条件后，若能判定ABC 与A B C ''' 全等，则当轮添加条件者失败，另一人获胜．轮次行动者添加条件1甲2cm AB A B ''==2乙4cm BC B C ''==3甲…上表记录了两人游戏的部分过程，则下列说法正确的是（）①若第3轮甲添加5cm AC A C ''==，则乙获胜；②若甲想获胜，第3轮可以添加条件30C C '==︒∠∠：③若乙想获胜，可修改第2轮添加条件为90A A '∠=∠=︒．A.①②B.①③C.②③D.①②③【答案】B 【分析】本题考查全等三角形的判定定理．根据全等三角形的判定定理逐一分析判断即可．【详解】解：①∵如果甲添加5cm AC A C ''==，又∵2cm AB A B ''==，4cm BC B C ''==，∴()SSS ABC A B C '''△≌△，∴乙获胜，故结论①正确；②∵如果甲添加30C C '==︒∠∠，又12AB BC =，反证法，假设90CAB ∠≠︒，那么在AC 上存在另一点D ，使得∠90CDB =︒，则在Rt CDB △中30︒角的对边为斜边的一半，即是12cm 2BD BC ==，又因为一点到直线的垂直线段长度最短，且交点唯一，那么A 与D 应重合，90CDB CAB ∠=∠=︒，∴ABC 是直角三角形，且90A ∠=︒，∴这两个三角形的三边长度就确定下来，且必然对应相等，∴这两个三角形全等，故甲会输，故结论②错误，③如果第二轮条件修改为90A A '∠=∠=︒，则第3轮甲无论添加任何对应的边或角的等量条件，都能判定A ABC B C '''≌△△，则甲失败，乙获胜，故说法正确，符合题意．故选：B ．二、填空题（每题3分，共24分）11.计算：()01π-=_____．【答案】1【分析】根据零指数幂的意义即可求出答案．【详解】∵10π-≠，∴()011π-=，故答案为1.【点睛】本题考查零指数幂的意义，解题的关键是熟练运用零指数幂的意义，本题属于基础题型．12.若一个多边形的内角和等于1260°，它是_____边形，从这个多边形的一个顶点出发共有_____条对角线．【答案】①.九②.27【分析】根据多边形内角和公式得到多边形边数，根据多边形对角线的条数的计算公式进行计算即可得到答案.【详解】设这个多边形的边数为n ，∴（n ﹣2）×180°＝1260°，解得n ＝9，∴这个多边形为九边形；∴对角线的条数＝(93)92-⨯＝27条．故答案为九；27【点睛】本题考查多边形内角和、多边形对角线的条数，解题的关键是掌握多边形内角和、多边形对角线的条数的计算.13.已知3m a =，4n a =，则2m n a +的值是_________．【答案】36【分析】根据()222m n m n mn a a a a a +==g g 求解即可得到答案．【详解】解：∵3m a =，4n a =∴()()22223436m n m n mn a a a a a +===⨯=g g ，故答案为：36．【点睛】本题主要考查了幂的乘方的逆运算，同底数幂乘法的逆运算，解题的关键在于能够熟练掌握相关计算法则进行求解．14.如图，将一把含有45︒角的三角尺的直角顶点放在一张宽3cm 的纸带边沿上，另一个顶点放在纸带的另一边沿上，测得三角尺的一直角边与纸带的一边所在的直线成30︒，则三角尺的直角边的长为______cm ．【答案】6【分析】本题考查了含30度角的直角三角形的性质．如图，作AH CD ⊥于H ，根据含30度角的直角三角形的性质求解即可．【详解】解：如图，作AH CD ⊥于H ，∵三角板的一边与纸带的一边所在的直线成30︒角，即30ACH ∠=︒，3cm AH =，∴等腰直角三角形的直角边()26cm BC AC AH ===，故答案为：6．15.等腰三角形的一个内角为50︒，则它的顶角的度数为___________．【答案】80︒或50︒【分析】分50︒的内角是等腰三角形的底角或顶角两种情况，利用三角形内角和定理求解．【详解】解：当50︒的内角是等腰三角形的底角时，它的顶角的度数为：180505080︒-︒-︒=︒；当50︒的内角是等腰三角形的顶角时，它的底角的度数为：()118050652⨯︒-︒=︒，符合要求；故答案为：80︒或50︒．【点睛】本题考查等腰三角形的定义、三角形内角和定理，解题的关键是注意分情况讨论，避免漏解．16.如图，6cm AB AC ==，DB DC =，若60ABC ∠=︒，则BE =______cm ．【答案】3【分析】本题考查了垂直平分线的判定与性质、等边三角形的判定与性质；先根据AB AC =，DB DC =，得AD 是BC 的垂直平分线，进而证明ABC 是等边三角形，即可求解．【详解】解：∵AB AC =，DB DC =，∴AD 是BC 的垂直平分线，∴AD BC ⊥，BE CE =，∵60ABC ∠=︒，AB AC =，∴60ACB ∠=︒，∴60BAC ∠=︒，∴ABC 是等边三角形，∴6cm BC AB AC ===，∴13cm 2BE BC ==，故答案为：3．17.如图，在ABC 中，,||AB AC AB CD =，过点B 作BE AC ⊥于E ，BD CD ⊥于D ，8,3,CD BD ABE == 的周长为_________．【答案】11【分析】根据角平分线的性质得出BE BD =，再证明Rt Rt (HL)BEC BDC ≌，得出CE CD =即可求解．【详解】解：∵AB AC =，∴A ABC CB =∠∠，∵||AB CD ，∴ABC BCD ∠=∠，∴BCD ACB ∠=∠，∴CB 平分ACD ∠，∵BD CD ⊥，BE AC ⊥，∴BE BD =，∵BC BC =，∴Rt Rt (HL)BEC BDC ≌，∴CE CD =，∵ABE 的周长AE BE AB =++，∵AB AC =，即ABE 的周长=CA AE BE CE BE CD ++=+=8311BD +=+=，故答案为：11．【点睛】本题考查了全等三角形的判定与性质，角平分线的性质，熟练掌握角平分线的性质是解题的关键．18.已知在长方形纸片ABCD 中，6AB =，5AD =，现将两个边长分别为a 和b 的正方形纸片按图1、图2两种方式放置（图1、图2中两张正方形纸片中均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为1S ，图2中阴影部分的面积为2S ；若213-=S S 时，则1b -值为______．【答案】2【分析】本题主要考查整式的混合运算的实际应用．利用面积的和差关系，分别表示出1S 和2S ，再表示出21S S -，结合213-=S S ，即可求解．【详解】∵四边形ABCD 是长方形，∴6AB CD ==，5AD BC ==，∵2216(5)()(6)30666306S a a b a a a b a ab b a ab =-+--=-+--+=--+，225(6)()(5)30555S a a b a a a b a ab =-+-⋅-=-+--+，∵213-=S S ，∴()212230555306S b S -+--=----++2230555306a a b a ab b a ab=-+--+-++-b =，∵213-=S S ，∴3b =，∴12-=b ．故答案是：2．三、解答题（19题每题4分，共16分；20，21，23每题6分，22题5分；24题8分；25题9分；解答题共56分）．19.计算（1）()22124a b abc -⋅；（2）()()325n n -+；（3）()()22x y x y ----；（4）()()32222362x y x y xy xy -+÷．【答案】（1）53a b c（2）231310n n +-（3）2244x xy y ++（4）2332x y xy -+【分析】本题考查了整式的混合运算．（1）先计算积的乘方，再计算单项式的乘法即可；（2）利用多项式乘多项式的运算法则即可求解．（3）利用完全平方公式计算即可；（4）利用多项式除单项式的运算法则即可求解．【小问1详解】解：()22124a b abc -⋅24144a b abc =⋅53a b c =；【小问2详解】解：()()325n n -+2321510n n n -+-=231310n n =+-；【小问3详解】解：()()22x y x y ----()22x y =--2244x xy y =++；【小问4详解】解：()()32222362x y x y xy xy -+÷()()()3222223262x y xy x y xy xy xy =÷-÷+÷2332x y xy =-+．20.先化简，再求值：2(21)6(1)(32)(32)a a a a a -++-+-，其中2220230a a +-=．【答案】225a a ++，2028【分析】此题主要考查了整式的混合运算－化简求值．直接利用乘法公式以及整式的混合运算法则化简，再利用已知变形代入即可．【详解】解：2(21)6(1)(32)(32)a a a a a -++-+-2224416694a a a a a =-+++-+，225a a =++，∵2220230a a +-=，∴222023a a +=，∴原式202352028=+=．21.如图，在△ABC 和△CED 中，AB ∥CD ，AB =CE ，AC =CD .求证：∠B =∠E .【答案】证明见解析.【详解】试卷分析：根据AB//CD 得出∠DCA=∠CAB ，结合AB=CE ，AC=CD 得出△CAB ≌△DCE ，从而得出答案.试卷解析：∵AB//CD ，∴∠DCA=∠CAB 又∵AB=CE ，AC=CD ，∴△CAB ≌△DCE ∴∠B=∠E.考点：（1）平行线的性质；（2）三角形全等的判定与性质22.作图并填空．在ABC 中，（1）利用尺规作出BC 的垂直平分线，交BC 于D ，连接AD ；（2）画出ADC △的高CH ，CH 与BD 的大小关系为______；（3）画出ADC △的角平分线DM 交AC 点M ，若60ABC S =△，10DCM S =△，设AD a =，DC b =，则:a b =______．【答案】（1）见解析（2）CH BD<（3）2:1【分析】本题考查了作图−基本作图，角平分线的性质．（1）利用基本作图，作BC 的垂直平分线；（2）根据斜边大于直角边以及线段中点的意义即可求解；（3）作ME CD ⊥于点E ，MF AD ⊥于点F ，利用角平分线的性质求得ME MF =，利用面积法即可求解．【小问1详解】解：如图，直线l 为所作；【小问2详解】解：ADC △的高CH 如图所示，∵CH DH ⊥，∴90H ∠=︒，∴CH CD <，∵BC 的垂直平分线，交BC 于D ，∴BD CD =，∴CH BD <，故答案为：CH BD <；【小问3详解】解：ADC △的角平分线DM 如图所示，作ME CD ⊥于点E ，MF AD ⊥于点F，∵BD CD =，60ABC S =△，∴1302ADC ABC S S == ，∵10DCM S =△，∴20ADM S =△，∵DM 是ADC ∠的角平分线，ME CD ⊥，MF AD ⊥，∴ME MF =，∵12022a AD MF MF ⨯=⨯=，11022b CD MF MF ⨯=⨯=，∴40220a MF b ME ==，∴:2:1a b =故答案为：2:1．23.如图，在平面直角坐标系xOy 中，ABC 三个顶点分别为()2,6A -，()5,1B -，()3,1C ．点B 与点C 关于直线l 对称（1）画出直线l ，写出点A 关于l 的对称点A '坐标；（2）则A BC ' 的面积为______；（3）若点P 在直线l 上，90BPC ∠=︒，直接写出点P 坐标．【答案】（1）直线l 见解析，点A 关于l 的对称点A '坐标为()06，；（2）20（3）点P 的坐标为()1,5-和()1,3--．【分析】本题主要考查了坐标与图形，等腰直角三角形的性质和判定，垂直平分线的性质．（1）根据点B 与点C 的坐标求出中点坐标D ，然后过点D 作BC 的垂线即可得出直线l ；（2）根据三角形面积公式求出结果即可；（3）分两种情况：当P 在直线BC 上方时，当P 在直线BC 下方时，分别求出结果即可．【小问1详解】解：∵()5,1B -，()3,1C ，∴中点D 的坐标为()1,1-，过点D 作BC 的垂线，即为所求作的直线l ，如图所示：；∴点A 关于l 的对称点A '坐标为()06，；【小问2详解】解：如图，()1861202A BC S '=⨯⨯-= ；故答案为：20；【小问3详解】解：∵B 与点C 关于直线l 对称，∴直线l 垂直平分BC ，∵点P 在直线l 上，∴BP CP =，∵PD BC ⊥，∴PD 平分BPC ∠，∵90BPC ∠=︒，∴190452BPD CPD ∠=∠=⨯︒=︒，∴BPD △为等腰直角三角形，∴142PD BD BC ===，当P 在直线BC 上方时，如图所示：此时点P 的纵坐标为：145+=，∴此时点P 的坐标为()15-，；当P 在直线BC 下方时，如图所示：此时点P 的纵坐标为：143-=-，∴此时点P 的坐标为()1,3--；综上分析可知，点P 的坐标为()1,5-和()1,3--．24.如图，ABC 是等边三角形，D 为BC 的中点，BE AB ⊥交AD 的延长线于点E ，点F 在AE 上，且AF BE =，连接CF 、CE ．求证：（1）ACF BCE ∠=∠：（2）CF EF =．【答案】（1）见解析（2）见解析【分析】（1）先根据条件得到AD 是ABC 的中线，同时是角平分线，高线，再结合BE AB ⊥利用角之间的变换得到EBD CAD ∠=∠，从而证明()SAS CAF CBE ≌，即可得到结论；（2）先根据垂直平分线的性质得到CE BE =，进而得到CE CF =，再根据三角形外角的性质得到60CFD CAF ACF ∠=∠+∠=︒即可证明CFE 是等边三角形，即可得到结论．【小问1详解】证明：∵ABC 是等边三角形，D 为BC 的中点，∴AD 是ABC 的中线，同时是角平分线，高线，AC BC =，∴AD BC ⊥，CAD BAD ∠=∠，∴90DBA BAD ∠+∠=︒，∵BE AB ⊥，∴90DBA EBD ∠+∠=︒，∴EBD BAD ∠=∠，∴EBD CAD ∠=∠，∵AF BE =，AC BC =，∴()SAS CAF CBE ≌，∴ACF BCE ∠=∠；【小问2详解】证明：∵ABC 是等边三角形，∴AC AB =，∴AD 是BC 的垂直平分线，∵点E 在AD 的延长线上，∴CE BE =，由（1）得：()SAS CAF CBE ≌，∴CF BE =，CF AF =，∴CE CF =，∵ABC 是等边三角形，D 为BC 的中点，∴AD 是ABC 的中线，同时是角平分线，高线，∴1302CAD CAB ACF ∠=∠=︒=∠，∴60CFD CAF ACF ∠=∠+∠=︒，∴CFE 是等边三角形，∴CF EF =；【点睛】本题考查了等边三角形的判定与性质，垂直平分线的性质，三角形全等的判定与性质，三角形外角性质，看到等边三角形要想到三线合一，一般证明两个角相等都会用到三角形全等．25.如图，在ABC 中，120180BAC ︒<<︒，AB AC =．AD BC ⊥于点D ．以AC 为边作等边ACE △，直线BE 交直线AD 于点F ．连接CF 交AE 于M ．（1）求证：FEA FCA ∠=∠：（2）探索FE ，FA ，FC 之间的数量关系，并证明你的结论．【答案】（1）见解析（2）2FE FA FD +=，见解析【分析】（1）由等边三角形的性质及等腰三角形的性质，求得FEA FBA ∠=∠，根据线段垂直平分线的性质求得ABE ACF ∠=∠，据此可得出答案；（2）在FC 上截取FN ，使FN FE =，连接EN ，根据等边三角形的性质得出60EFM ∠=︒，根据等边三角形的判定得出EFN 是等边三角形，求出60FEN ∠=︒，EN EF =，求出AEF CEN ∠=∠，根据SAS 推出EFA ENC △≌，根据全等得出FA NC =，求出2FC FD =，即可得出答案．【小问1详解】证明：AD 为边BC 的垂直平分线，AB AC ∴=，ACE Q V 为等边三角形，AC AE ∴=，AB AE =∴，FEA FBA ∴∠=∠；∵直线AD 垂直平分BC ，AB AC ∴=，FB FC =，ABC ACB FBC FCB ∴∠=∠∠=∠，，FBC ABC FCB ACB ∴∠-∠=∠-∠，即ABE ACF ∠=∠，ABE AEF ∠=∠ ，∴FEA FBA ∠=∠；【小问2详解】解：2FE FA FD +=，证明：在FC 上截取FN ，使FN FE =，连接EN ，如图2，由（1）得：AEF ACF ∠=∠，FME CMA ∠=∠ ，EFC CAE ∴∠=∠，等边三角形ACE 中，60CAE ∠=︒，60EFC ∴∠=︒．FN FE = ，EFN ∴ 是等边三角形，60FEN ∴∠=︒，EN EF =，ACE Q V 为等边三角形，60AEC ∴∠=︒，EA EC =，FEN AEC ∴∠=∠，FEN MEN AEC MEN ∴∠-∠=∠-∠，即AEF CEN ∠=∠，在EFA △和ENC ∠中，EF EN AEF CEN EA EC =⎧⎪∠=∠⎨⎪=⎩，()SAS EFA ENC ∴ ≌，FA NC ∴=，FE FA FN NC FC ∴+=+=，60EFC FBC FCB ∠=∠+∠=︒ ，FBC FCB ∠=∠，160302FCB ∴∠=⨯︒=︒，AD BC ⊥ ，90FDC ∴∠=︒，2FC FD ∴=，2FE FA FD ∴+=．【点睛】本题是三角形综合题，考查了等腰三角形的性质，等边三角形的性质和判定，含30︒角的直角三角形的性质，全等三角形的性质和判定的应用，能综合运用知识点进行推理是解此题的关键．四、附加题（26题4分，27题6分，共10分）26.小明同学用四张长为x ，宽为y 的长方形卡片，拼出如图所示的包含两个正方形的图形（任意两张相邻的卡片之间没有重叠，没有空隙）．（1）通过计算小正方形面积，可推出()2x y +，xy ，()2x y -三者之间的等量关系式为______；（2）利用（1）中的结论，试求：当()()3002001996x x --=时，求()22500x -的值．【答案】（1）()()224x y x y xy-=+-（2）()22500x -的值是2016．【分析】本题主要考查几何图形与整式乘法．（1）直接利用图象面积得出答案；（2）利用多项式乘法将已知条件变形，即可求出答案．【小问1详解】解：由题意得，小正方形的面积=大正方形的面积4-个长方形的面积和，()()224x y x y xy ∴-=+-，故答案为：()()224x y x y xy -=+-；【小问2详解】解：设300A x =-，200B x =-，∴100A B +=-，2500A B x -=-，1996AB =，∴22()()4A B A B AB -=+-，∴()()222500100419962016x -=--⨯=，故()22500x -的值是2016．27.在平面直角坐标系xOy 中，若点P 和点1P 关于y 轴对称，点1P 和点2P 关于直线l 对称，则称点2P 是点P 关于y 轴、直线l 的“二次对称点”．（1）已知点()A 3,5，直线l 是经过()0,2且平行于x 轴的一条直线，点A '为点A 关于y 轴，直线l 的“二次对称点”，则点A '的坐标为______；（2）如图1，正方形ABCD 的顶点坐标分别是()0,1A ，()0,3B ，()2,3C ，()2,1D ；点E 的坐标为()1,1，若点M 为正方形ABCD （不含边界）内一点，点M '为点M 关于y 轴，直线OE 的“二次对称点”，则点M '的横坐标x 的取值范围是______；（3）如图2，(),0T t （0t ≥）是x 轴上的动点，线段RS 经过点T ，且点R 、点S 的坐标分别是(),1R t ，(),1S t -，直线l 经过()0,1且与x 轴夹角为60︒，在点T 的运动过程中，若线段RS 上存在点N ，使得点N '是点N 关于y 轴，直线l 的“二次对称点”，且点N '在y 轴上，则点N '纵坐标y 的取值范围是______．【答案】（1）()3,1--（2）13x <<（3）31N y '-≤≤【分析】（1）根据“二次对称点”的定义求解即可；（2）由题意，直线OE 的解析式为y x =，点M 关于y 轴对称的点的轴坐标的取值范围为13y <<，由直线OE 的解析式为y x =，得M 关于y 轴，直线OE 的“二次对称点”点M '的横坐标即是关于y 轴的纵坐标，，由此可得结论；（3）如图2中，当点N 与S 重合，且N '在y 轴上时，连接SN ''交直线于点K ，交y 轴于点J ，连接KN '，设直线l 交x 轴于点D ，交y 轴于点C ，如图3中，当点T 与原点重合，N 与()01，重合时，N '和N ''都与()01，重合，此时()01N '，．求出这两种特殊位置N '的坐标，可得结论．【小问1详解】解∶点()A 3,5关于y 轴的对称点为()13,5A -，∵直线l 是经过()0,2且平行于x 轴的一条直线，∴点()13,5A -关于直线l 的对称点为()3,1A '--；故答案为：()3,1--【小问2详解】解∶如图，设直线OE 的解析式为y kx =，∵点E 的坐标为()1,1，∴1k =，∴直线OE 的解析式为y x =，∵()0,1A ，()0,3B ，()2,3C ，()2,1D ,∴点M 关于y 轴对称的点的轴坐标的取值范围为13y <<，∴点M 关于y 轴，直线OE 的“二次对称点”点M '的横坐标x 的取值范围是13x <<，故答案为：13x <<；【小问3详解】解∶如图2，设点N 关于y 轴的对称点为点N ''当点N 与S 重合，且N '在y 轴上时，连接SN ''交直线于点K ，交y 轴于点J ，连接KN '，设直线l 交x 轴于点D ，交y 轴于点C ，∵,60CDO ∠=︒OD KJ ∥，OD OC ⊥，∴60CKJ CDO ∠=∠=︒，30KCJ ∠=︒∵N '和N ''关于直线l 对称，∴18060120CKN CKN ︒'''∠=∠=︒-︒=，∴1801203030KN J KCJ '∠=︒-︒-︒=︒=∠，∴KC KN '=，∵KJ CN '⊥，∴2CJ JN '==，∴3ON '=，∴此时点()0,3N '-，如图3，当点T 与原点重合，N 与()01，重合时，N '和N ''都与()01，重合，此时()01N '，．根据题意得：0t ≥，观察图象得：满足条件的N '的纵坐标为31N y '-≤≤．故答案为：31N y '-≤≤【点睛】本题属于四边形综合题，考查了正方形的性质，轴对称变换，一次函数的性质等知识，解题的关键是学会寻找特殊位置，解决问题，属于中考压轴题．。

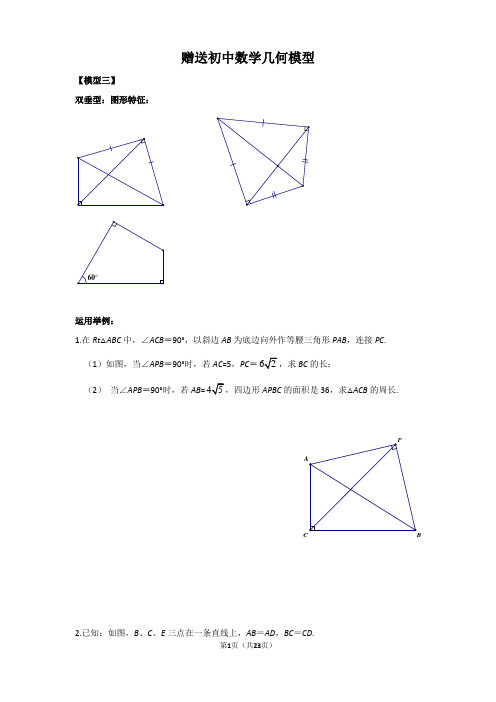
赠送初中数学几何模型【模型三】双垂型：图形特征：60°运用举例：1.在Rt△ABC中，∠ACB＝90°，以斜边AB为底边向外作等腰三角形PAB，连接PC. （1）如图，当∠APB＝90°时，若AC=5，PC＝62，求BC的长；（2）当∠APB＝90°时，若AB=45APBC的面积是36，求△ACB的周长.P 2.已知：如图，B、C、E三点在一条直线上，AB＝AD，BC＝CD.（1）若∠B＝90°，AB＝6，BC＝23，求∠A的值；（2）若∠BAD＋∠BCD＝180°，cos∠DCE＝35，求ABBC的值.3.如图，在四边形ABCD中，AB=AD，∠DAB=∠BCD=90°，（1）若AB=3，BC+CD=5，求四边形ABCD的面积（2）若p= BC+CD，四边形ABCD的面积为S，试探究S与p之间的关系。

DBC2015-2016学年北京市教院附中八年级（上）期中数学试卷一．用心选一选：（每小题3分，共30分）1．（3.00分）下列各式是因式分解且完全正确的是（）A．ab+ac+d=a（b+c）+d B．x3﹣x=x（x2﹣1）C．（a+2）（a﹣2）=a2﹣4 D．a2﹣1=（a+1）（a﹣1）2．（3.00分）医学研究发现一种新病毒的直径约为0.000043毫米，则这个数用科学记数法表示为（）A．0.43×10﹣4B．0.43×104C．4.3×10﹣5D．0.43×1053．（3.00分）下列各式（1﹣x），，，+x，，其中分式共有（）个．A．2 B．3 C．4 D．54．（3.00分）多项式9a2x2﹣18a3x3﹣36a4x4各项的公因式是（）A．a2x2 B．a3x3C．9a2x2D．9a4x45．（3.00分）如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）A．SSS B．SAS C．AAS D．HL6．（3.00分）甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等．如果设甲每小时做x个零件，那么下面所列方程中正确的是（）A．=B．=C．=D．=7．（3.00分）如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（）A．只有乙B．甲和乙C．只有丙D．乙和丙8．（3.00分）下列各式中，正确的是（）A．=B．+=C．=D．=9．（3.00分）如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（）A．16 B．12 C．8 D．410．（3.00分）在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（）A．35°B．45°C．55°D．65°二．细心填一填：（每小题3分，共24分）．11．（3.00分）计算：20042﹣20032=．12．（3.00分）40==（2a﹣1b）3=．13．（3.00分）如果分式的值为0，那么x的值为．14．（3.00分）将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为．15．（3.00分）计算：﹣=．16．（3.00分）如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是．17．（3.00分）如图点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是．18．（3.00分）在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标．三.用心做一做（19、20题每题3分，21、22、23题每题4分，共26分）19．（3.00分）因式分解：4a2﹣32a+64．20．（3.00分）计算：（ab﹣2）﹣2•（a﹣2）3（结果写成分式）21．（4.00分）计算：（1）（2）（+）÷．22．（4.00分）解分式方程：（1）（2）．23．（4.00分）先化简，，并任选一个你喜欢的数x代入求值．四．应用题（本题5分）24．（5.00分）列方程解应用题：甲乙两站相距1200千米，货车与客车同时从甲站出发开往乙站，已知客车的速度是货车速度的2.5倍，结果客车比货车早6小时到达乙站，求客车与货车的速度分别是多少？五、作图题（本题2分）25．（2.00分）画图（不用写作法，要保留作图痕迹）尺规作图：求作∠AOB的角平分线OC．六、解答题：（28题5分，其他每题4分，共17分）26．（4.00分）已知，如图，在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，DF=BE，AD=CB．求证：AD∥BC．27．（4.00分）已知：如图，AB=AD，AC=AE，且BA⊥AC，DA⊥AE．求证：（1）∠B=∠D．（2）AM=AN．28．（5.00分）如图，已知∠1=∠2，P为BN上的一点，PF⊥BC于F，PA=PC．求证：∠PCB+∠BAP=180°．29．（4.00分）已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x 轴上，且∠ACB=90°，AC=BC．（1）如图1，当A（0，﹣2），C（1，0），点B在第四象限时，则点B的坐标为；（2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断与哪一个是定值，并说明定值是多少？请证明你的结论．四、附加题30．（3.00分）以如图方格纸中的3个格点为顶点，有多少个不全等的三角形（）A．6 B．7 C．8 D．9八、填空题（共1小题，每小题1分，满分1分）31．（1.00分）考察下列命题：（1）全等三角形的对应边上的中线、高线、角平分线对应相等；（2）两边和其中一边上的中线对应相等的两个三角形全等；（3）两边和第三边上的中线对应相等的两个三角形全等；（4）两角和其中一角的角平分线对应相等的两个三角形全等；（5）两角和第三角的角平分线对应相等的两个三角形全等；（6）两边和其中一边上的高线对应相等的两个三角形全等；（7）两边和第三边上的高线对应相等的两个三角形全等；其中正确的命题是（填写序号）．九、解答题（共1小题，满分0分）32．我们知道假分数可以化为带分数．例如：．在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．例如：，这样的分式就是假分式；，这样的分式就是真分式．类似的，假分式也可以化为带分式（即整式与真分式和的形式）．例如：；．（1）将分式化为带分式；（2）若分式的值为整数，求x的整数值．2015-2016学年北京市教院附中八年级（上）期中数学试卷参考答案与试题解析一．用心选一选：（每小题3分，共30分）1．（3.00分）下列各式是因式分解且完全正确的是（）A．ab+ac+d=a（b+c）+d B．x3﹣x=x（x2﹣1）C．（a+2）（a﹣2）=a2﹣4 D．a2﹣1=（a+1）（a﹣1）【解答】解：A、没把多项式转化成几个整式积的形式，故A错误；B、还可以再分解，故B错误；C、整式的乘法，故C错误；D、把一个多项式转化成几个整式积的形式，故D正确；故选：D．2．（3.00分）医学研究发现一种新病毒的直径约为0.000043毫米，则这个数用科学记数法表示为（）A．0.43×10﹣4B．0.43×104C．4.3×10﹣5D．0.43×105【解答】解：将0.000 043用科学记数法表示为4.3×10﹣5．故选：C．3．（3.00分）下列各式（1﹣x），，，+x，，其中分式共有（）个．A．2 B．3 C．4 D．5【解答】解：中的分母含有字母是分式．故选A．4．（3.00分）多项式9a2x2﹣18a3x3﹣36a4x4各项的公因式是（）A．a2x2 B．a3x3C．9a2x2D．9a4x4【解答】解：9a2x2﹣18a3x3﹣36a4x4中∵系数的最大公约数是9，相同字母的最低指数次幂是a2x2，∴公因式是9a2x2．故选：C．5．（3.00分）如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）A．SSS B．SAS C．AAS D．HL【解答】解：∵OM=ON，OP=OP，∠OMP=∠ONP=90°∴△OPM≌△OPN所用的判定定理是HL．故选：D．6．（3.00分）甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等．如果设甲每小时做x个零件，那么下面所列方程中正确的是（）A．=B．=C．=D．=【解答】解：设甲每小时做x个零件，则乙每小时做（x﹣6）个零件，由题意得，=．故选：D．7．（3.00分）如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（）A．只有乙B．甲和乙C．只有丙D．乙和丙【解答】解：在△ABC和乙三角形中，有两边a、c分别对应相等，且这两边的夹角都为50°，由SAS可知这两个三角形全等；在△ABC和丙三角形中，有一边a对应相等，和两组角对应相等，由AAS可知这两个三角形全等，所以在甲、乙、丙三个三角形中和△ABC全等的是乙和丙，故选：D．8．（3.00分）下列各式中，正确的是（）A．=B．+=C．=D．=【解答】解：A、，不能再化简，故本选项错误；B、+=+=，故本选项错误；C、=，故本选项错误；D、=，故本选项正确；故选：D．9．（3.00分）如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（）A．16 B．12 C．8 D．4【解答】解：∵四边形ABCD为正方形，∴∠D=∠ABC=90°，AD=AB，∴∠ABE=∠D=90°，∵∠EAF=90°，∴∠DAF+∠BAF=90°，∠BAE+∠BAF=90°，∴∠DAF=∠BAE，在△AEB和△AFD中∴△AEB≌△AFD（ASA），∴S=S△AFD，△AEB∴它们都加上四边形ABCF的面积，可得到四边形AECF的面积=正方形的面积=16．故选：A．10．（3.00分）在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（）A．35°B．45°C．55°D．65°【解答】解：过点E作EF⊥AD，∵DE平分∠ADC，且E是BC的中点，∴CE=EB=EF，又∠B=90°，且AE=AE，∴△ABE≌△AFE，∴∠EAB=∠EAF．又∵∠CED=35°，∠C=90°，∴∠CDE=90°﹣35°=55°，即∠CDA=110°，∠DAB=70°，∴∠EAB=35°．故选：A．二．细心填一填：（每小题3分，共24分）．11．（3.00分）计算：20042﹣20032=4007．【解答】解：原式=（2004+2003）×（2004﹣2003）=4007．故答案为：4007．12．（3.00分）40=1=4（2a﹣1b）3=．【解答】解：40=1；===4；（2a﹣1b）3=8a﹣3b3=．故答案为：1；4；．13．（3.00分）如果分式的值为0，那么x的值为2．【解答】解：由题意得：x2﹣4=0，且x+2≠0，解得：x=2，故答案为：2．14．（3.00分）将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为90°．【解答】解：∵一张长方形纸片沿BC、BD折叠，∴∠ABC=∠A′BC，∠EBD=∠E′BD，而∠ABC+∠A′BC+∠EBD+∠E′BD=180°，∴∠A′BC+∠E′BD=180°×=90°，即∠CBD=90°．故答案为：90°．15．（3.00分）计算：﹣=2．【解答】解：﹣，=，=，=2．故答案为：2．16．（3.00分）如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是AO=DO或AB=DC或BO=CO．【解答】解：添加AO=DO或AB=DC或BO=CO后可分别根据ASA、AAS、AAS判定△AOB≌△DOC．故填AO=DO或AB=DC或BO=CO．17．（3.00分）如图点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是3．【解答】解：∵P是∠BAC的平分线AD上一点，PE⊥AC于点E，PE=3，∴点P到AB的距离=PE=3．故答案为：3．18．（3.00分）在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标（1，5）或（1，﹣1）或（5，﹣1）．【解答】解：如图所示：有3个点，当E在E、F、N处时，△ACE和△ACB全等，点E的坐标是：（1，5），（1，﹣1），（5，﹣1），故答案为：（1，5）或（1，﹣1）或（5，﹣1）．三.用心做一做（19、20题每题3分，21、22、23题每题4分，共26分）19．（3.00分）因式分解：4a2﹣32a+64．【解答】解：4a2﹣32a+64=4（a2﹣8a+16）=4（a﹣4）2．20．（3.00分）计算：（ab﹣2）﹣2•（a﹣2）3（结果写成分式）【解答】解：（ab﹣2）﹣2•（a﹣2）3（结果=a﹣2b4•a﹣6=a﹣8b4=．21．（4.00分）计算：（1）（2）（+）÷．【解答】解：（1）原式=••，=﹣2；（2）原式=•=．22．（4.00分）解分式方程：（1）（2）．【解答】解：（1）去分母得：x+3=4x，移项合并得：3x=3，解得：x=1；（2）去分母得：x2+2x+1﹣4=x2﹣1，解得：x=1，经检验x=1是增根，分式方程无解．23．（4.00分）先化简，，并任选一个你喜欢的数x代入求值．【解答】解：原式=…（2分）=…（3分）=x﹣1．…（4分）任选一个非﹣1，1，﹣2的数代入求值，给（1分）．当x=2，原式=x﹣1=1．四．应用题（本题5分）24．（5.00分）列方程解应用题：甲乙两站相距1200千米，货车与客车同时从甲站出发开往乙站，已知客车的速度是货车速度的2.5倍，结果客车比货车早6小时到达乙站，求客车与货车的速度分别是多少？【解答】解：设货车速度为x千米/小时，则客车速度为2.5x千米/小时，根据题意得：=+6，解得x=120，经检验：x=120是原方程的解且符合实际．2.5×120=300（千米/小时），答：货车速度为120千米/小时，客车速度为300千米/小时．五、作图题（本题2分）25．（2.00分）画图（不用写作法，要保留作图痕迹）尺规作图：求作∠AOB的角平分线OC．【解答】解：如图所示：．六、解答题：（28题5分，其他每题4分，共17分）26．（4.00分）已知，如图，在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，DF=BE，AD=CB．求证：AD∥BC．【解答】解：∵AE=CF，∴AE+EF=CF+EF，即AF=CE，在△ADF和△CBE中，，∴△ADF≌△CBE（SSS），∴∠A=∠C，则AD∥BC．27．（4.00分）已知：如图，AB=AD，AC=AE，且BA⊥AC，DA⊥AE．求证：（1）∠B=∠D．（2）AM=AN．【解答】证明：（1）∵BA⊥AC，DA⊥AE，∴∠BAC=∠DAE=90°，在△ABC与△ADE中，，∴△ABC≌△ADE（SAS），∴∠B=∠D；（2）∵△ABC≌△ADE，∴AB=AD，∵∠BAC=∠DAE，∴∠BAM=∠DAN，在△ABM与△ADN中，，∴△ABM≌△ADN（ASA），∴AM=AN．28．（5.00分）如图，已知∠1=∠2，P为BN上的一点，PF⊥BC于F，PA=PC．求证：∠PCB+∠BAP=180°．【解答】证明：如图，过点P作PE⊥BA于E，∵∠1=∠2，PF⊥BC于F，∴PE=PF，∠PEA=∠PFB=90°，在Rt△PEA与Rt△PFC中，∴Rt△PEA≌Rt△PFC（HL），∴∠PAE=∠PCB，∵∠BAP+∠PAE=180°，∴∠PCB+∠BAP=180°．29．（4.00分）已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x 轴上，且∠ACB=90°，AC=BC．（1）如图1，当A（0，﹣2），C（1，0），点B在第四象限时，则点B的坐标为（3，﹣1），；（2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断与哪一个是定值，并说明定值是多少？请证明你的结论．【解答】（1）解：过B作BE⊥x轴于E，则∠BEC=∠ACB=∠AOC=90°，∴∠1+∠2=90°，∠1+∠OAC=90°，∴∠2=∠OAC，在△AOC和△CEB中∵，∴△AOC≌△CEB（AAS），∴OA=CE，OC=BE，∵A（0，﹣2），C（1，0），∴OA=CE=2，OC=BE=1，∴OE=1+2=3，∴点B的坐标为（3，﹣1 ）；（2）结论：，证明：作BE⊥x轴于E，∴∠1=90°=∠2，∴∠3+∠4=90°，∵∠ACB=90°，∴∠5+∠3=90°，∴∠5=∠4，在△CEB和△AOC中，∵∴△CEB≌△AOC，∴AO=CE，∵BE⊥x轴于E，∴BE∥y轴，∵BD⊥y轴于点D，EO⊥y轴于点O，∴BD∥OE，∴四边形OEBD是矩形，∴EO=BD，∴OC﹣BD=OC﹣EO=CE=AO，∴．四、附加题30．（3.00分）以如图方格纸中的3个格点为顶点，有多少个不全等的三角形（）A．6 B．7 C．8 D．9【解答】解：如图所示：△ABC、△BFD、△BFE、△BHC、△BHD、△BOC、△BOD、△BOE故选：C．八、填空题（共1小题，每小题1分，满分1分）31．（1.00分）考察下列命题：（1）全等三角形的对应边上的中线、高线、角平分线对应相等；（2）两边和其中一边上的中线对应相等的两个三角形全等；（3）两边和第三边上的中线对应相等的两个三角形全等；（4）两角和其中一角的角平分线对应相等的两个三角形全等；（5）两角和第三角的角平分线对应相等的两个三角形全等；（6）两边和其中一边上的高线对应相等的两个三角形全等；（7）两边和第三边上的高线对应相等的两个三角形全等；其中正确的命题是1，2，3，4，5（填写序号）．【解答】解：（1）全等三角形的对应边上的中线、高线、角平分线对应相等，正确；（2）两边和其中一边上的中线对应相等的两个三角形全等，正确；（3）两边和第三边上的中线对应相等的两个三角形全等，正确；（4）两角和其中一角的角平分线对应相等的两个三角形全等，正确；（5）两角和第三角的角平分线对应相等的两个三角形全等，正确；（6）两边和其中一边上的高线对应相等的两个三角形全等，错误；（7）两边和第三边上的高线对应相等的两个三角形全等，正确；故答案为：1，2，3，4，5．九、解答题（共1小题，满分0分）32．我们知道假分数可以化为带分数．例如：．在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．例如：，这样的分式就是假分式；，这样的分式就是真分式．类似的，假分式也可以化为带分式（即整式与真分式和的形式）．例如：；．（1）将分式化为带分式；（2）若分式的值为整数，求x的整数值．【解答】解：（1）==1﹣；（2）==2﹣，当为整数时，也为整数，∴x+1可取得的整数值为±1，±3，∴x的可能整数值为0，﹣2，2，﹣4．。

北京八中怡海分校2014~2015学年度第一学期期中练习初二数学试卷说明：1、本试卷共七页，计六道大题，31道小题；2、本试卷卷面分值104分，考试时间为100分钟；3、不要在密封线内答题。

一、精心选一选（每小题3分，共30分） 1. 下列交通标志是轴对称图形的是（ ）A ．B ．C ．D ．2. 下列各式从左到右的变形属于因式分解的是（ ）A ．(2)(3)(3)(2)m m m m --=--B ． 2223(1)2a a a -+=-+ C ．2(1)(1)1x x x +-=- D ． 21(1)(1)a a a -=+- 3. 已知图中的两个三角形全等，则∠1等于（）A ． 72°B ． 60°C ． 50°D ． 58°4. 如图，将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去左边的小三角形，将纸片展开，得到的图形是( )EDCBA第5题图cc72°50°1bba a5. 如图，已知AD AE =,添加下列条件仍无法证明ABE ACD ∆≅∆的是（ ） A ．AB AC = B ． BE CD = C ． B C ∠=∠ D ． ADC AEB ∠=∠6. 已知一个等腰三角形两边长分别为5，6，则它的周长为( ) A ．16B ．17C ．16或17D ．10或127. 在平面直角坐标系xOy 中，点P （2，1）关于y 轴对称的点的坐标是（ ） A ．（－2 ，1 ） B ．（ 2 ，1 ） C ．（－2 ，－1） D ．（2 ，－1） 8. 从边长为a 的大正方形纸板中挖去一个边长为b 的小正方形后，将其裁成四个相同的等腰梯形（如图(1)），然后拼成一个平行四边形（如图(2)），那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）A ．222()a b a b -=-B ．222()2a b a ab b +=++C ．222()2a b a ab b -=-+D ． 22()()a b a b a b -=+-9. 如图, 在△ABC 中, AD 是它的角平分线, AB = 8cm , AC = 6cm , 则S △ABD : S △ACD =( )A ．4 : 3B ． 3 : 4C ．16 : 9D ． 9 : 1610. 如图，AB=AC ，AB 的垂直平分线交AB 于D ，交AC 于E ，BE 恰好平分ABC ∠，有以下结论：（1）ED =EC （2）BEC ∆的周长等于2AE +EC (3)图中共有3个等腰三角形 （4）36A ∠=，其中正确的共有（ ）A ．4个B ．3个C ．2个D ．1个二、细心填一填（每小题2分，共20分）11. 将0.000103用科学记数法表示为 ． 12. 当x 时，分式12x x -+有意义． 13. 已知等腰三角形的一个内角为50，则顶角为 度．14. 已知一个等腰三角形一个外角等于120，腰长为4cm ，则该三角形的周长为 cm .第10题图DCBA第8题图图（1） 图（2）第9题图EDCBA15. 若210,1x x -=+则x = ．16. 计算222⎪⎭⎫⎝⎛÷a b b a = ．17. 因式分解234x x --= ．18. 若20,x y -=则223x yx y+=- ．19. 一等腰三角形一腰上的高与另一腰的夹角为30，这个等腰三角形的顶角为 度. 20. 如图，Rt ABC ∆中，90,30C CBA ∠=∠=,AE 平分CAB ∠交BC 于D ，BE AE ⊥于E ，给出下列结论，其中正确的有 ．（填序号）①2BD CD = ②3AE DE = ③AB AC BE =+ ④整个图形(不计图中字母)不是轴对称图形．三、作图题（3分）21. 如图，已知△ABC ，求作一点P ，使P 到∠A 的两边的距离相等，且P A ＝PB ．要求：尺规．．作图，并保留作图痕迹．（不要求写作法）四、耐心算一算（共25分）22.计算：011(6π)()|15--+- （4分）23. 因式分解：（每小题2分，共6分） （1）2249ax ay - （2）22363m mn n -+-第20题图C BAEDCBA（3）2(2)2mx m x ---24. 先化简，再求值：21121a aa a a ⎛⎫-÷ ⎪+++⎝⎭，其中2a =-． （5分）25. 解方程：3111x x x -=-+．（5分）26. 列方程解应用题：小马自驾私家车从A 地到B 地，驾驶原来的燃油汽车所需油费108元，驾驶新购买的纯电动车所需电费27元，已知每行驶1千米，原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元，求新购买的纯电动汽车每行驶1千米所需的电费．（5分）五、认真证一证（共22分）27. 如图，点B 在线段AD 上，BC DE ∥，AB ED =，BC DB =.求证：A E ∠=∠．（5分）28. 如图，已知△ABC 和△ADE 均为等边三角形，连接CD 、BE ，作AF CD ⊥于点F ，AG BE ⊥于点G ，求证：△AFG 为等边三角形．（5分）E C BADGFEDCBA29. 如图，已知AD 是BAC ∆的角平分线，AC =AB +BD , 31C ∠=,求B ∠的度数．（5分）30. 如图，已知等腰ABC ∆中，30BAC ,AB AC,PAB α∠==∠=,点B 关于直线AP 的对称点为点D ，连接AD ，连接BD 交AP 于点G ，连接CD 交AP 于点E ，交AB 于点F 。

北京市西城区北京八中20XX 一一20XX 学年度第一学期期中练习题年级：初二 科目：数学 班级： __________ 姓名： ________不管"、为任何实数，/+/?6. + 1% + 35的值总是（一、选择题（每题3分，共30分，每题只有一个正确答案） 以下各式中，从左到右的变形是因式分解的是（ A. （x + 2y ）（x 2y ） = x 2 4y 2 C. a 2 —4ab+4b 2=（ct —2b ）2计算一 3"的结果是（）.1. )・B. x 2y-xy 2 - I = xy(x-y)-\D. ax+ay+a=a(x+y)2.A. -9B. 91D.——93. 根据以下条件， A. AR=3, BC=4, B. /W=4, 8C=3,C.—9不能啡：顾是ZMBC 的大小和形状的是（AC=5 NA = 30°4.C. Z4=60°, Zfl=45°, A8=4D. ZC=9O°. AB=6, 4C=5 以下变形正确的选项是(a + \ aA. ---- ---- =—b + \ b“一 1 6/-1-b b a-b 1 C ・ a 2 -b 2a-h D.二］(a + h)25. 6.7.假设（X-4）（x + 7）是二次三项式/ + 6M-28的因式分解结果， A. 3 B. -3 C. 11 D. -11 假设分式2土的值是零，那么工的值是（x + 2 A. x = 0 B. A - = ±2 C. x = —2 巳知"=1，那么的值为（ A. 4 那么a 的值是（8.A.非负数B.恒为正数C.恒为负数D.不等于（）12. 在多项式一1七油％一8"%中应提取的公因式足 _________ .13. 如图，AB1BD, AB//ED, AB=ED,要说明 MBC 竺AEDG 假设以“S/IU 为依据，还要添加的条件为 _____________ :假设添加条件AC=EC ，那么可以用 _________ 公理（或 定理）判定全等.x。

2016 2017 学年度第一学期期中练习题年级：初二科目：数学班级：_______ 姓名： ___________1．本试卷共 6 页，共 5 道大题， 26 个小题，满分100 分，附加题在答题纸上，满考．．．．．分 20 分。

考试时间 100 分钟 .生须2．在试卷和答题纸上准确填写班级、姓名、学号.知3．答案一律填写在答题纸上，在试卷上作答无效.4．考试结束，将试卷和答题纸一并交回.一．选择题（ 1— 9 题每小题 3 分，第 10 题画图 2 分，答案 2 分，共 31 分）1．剪纸艺术是我国文化宝库中的优秀遗产，在民间广泛流传．下面四幅剪纸作品中，属于轴对称图形的是．A ．B ． C． D ．2．点 A（- 2， 1）关于 x 轴的对称点是 .A ．（ - 1， 2） B.（ - 2， - 1） C.（2， - 1） D.（ 2，1）3.下列等式从左到右的变形，属于因式分解的是.A ． a(x－ y)=ax－ ay B． x3－ x=x(x+1)( x－ 1)C．( x+1)( x+3)= x2+4x+3D ．x2 +2x+1= x(x+2)+14.为了了解我校八年级600名学生的体重情况，从中抽查了100 名学生的体重进行统计分析，在这个问题中，下列说法错误的是A ． 600 名学生的体重是总体B ．被抽取的100 名学生的体重是样本C．样本的容量是100D．被抽取的 100 名学生是样本5.要测量河两岸相对的两点 A,B 的距离，先在 AB 的垂线 BF 上取两点 C,D，使 CD=BC，再作出BF 的垂线 DE，使 A,C,E 在一条直线上（如图所示），可以说明△EDC ≌△ ABC，得 ED=AB，因此测得 ED 的长就是 AB 的长，判定△EDC ≌△ ABC 最恰当的理由是A. 边角边B.角边角C.边边边D.边边角则 EDF 的度数为 .A. 50B. 45C. 40D. 357. 如图，已知 AD=AE,添加下列条件仍无法证明ABE ≌ACD 的是 .A ．AB=ACB ． B=C C ． BE=CDD ． ADC = AEBAADEEDBFC第 5 题第 6 题BC第 7 题8 题图8．为了了解本校八年级学生的体能情况，随机抽查了其中 30 名学生，测试了 1 分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在 25～30 次的频率为 .AA ．0.1B ． 0.2C ． 0.3D ． 0.4P .9.若分式x 21的值为 0，则 x 的值为 .Bx1OA ． 1B ．0C ． 1D ． 1第 10 题10. 已知：如图，∠ AOB=40 ，点 P 为∠ AOB 内一点， P ,P 分别是点 P 关于 OA 、OB 的对称点，连接 P P ，分别交 OA 于 M 、OB 于 N. 如果 P P =5cm ，△ PMN 的周长为 l ， P OP 的度数为 ，请根据以上信息 完成作图 ，并指出 l 和 的值 .．．．．A. l=5cm, =80B. l=5cm, =85C. l=6cm, =80D. l = 6cm , =85二．填空题（每题 3 分，共 24 分）1有意义，则 x 应满足的条件是 .11.要使分式 x - 212. 已知关于 x 的二次式 x 2 + mx+n ，当 m=_____, n=______时 (写出一组满足条件的整数值即可 )，它在有理数范围内能够进行因式分解.13. 已知 : 等腰三角形的两边长分别为6cm, 3cm, 则此等腰三角形的周长是_________ cm.14．如图的扇形图反映了世界七大洲的面积占全球陆地面积的百分比， 在这个统计图中， 洲的面积最大，表示它占全球陆地面积百分比的扇形的圆心角的度数是°．15. 如图，在 Rt △ ABC 中，∠ C=90 °， AB 的垂直平分线交 BC 边于点 E.连接 AE,若∠ B =15°则∠ EAC=.ABDAEACDC EBC D第 15 题B第 16 题第 17 题16. 如图，△ ABC ≌△ DEC 且 AED=120 , B, C, D 三点在一条直线上， CD = 2 3 cm, AB=4cm,则∠ D= °； AE=cm.17.如图，已知线段 AB=3 ，线段 AC=6， AB 绕点 A 旋转一周，连接 BC ，并取 BC 中点 D ，连接AD ，则 AD 的最大值为；最小值为.18. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线 OB ，另一把直尺压住射线OA 并且与第一把直尺交于点 P ，小明说：“射线 OP 就是∠ BOA 的角平分线． ”小明的做法，其理论依据是 .三．解答题（每小题5 分，共 20 分）19. 将下列各式因式分解(1) a 32a 2b ab2(2) x 2 2 x 820．先化简，再求值：(x 1)(x 1) ( x2) 2，其中x=3.21. 如图，点E，F 在 BC 上， BE＝ CF，∠ A＝∠ D，∠ B＝∠ C， AF 与 DE 交于点 O．(1)求证： AB＝ DC ；(2)试判断△ OEF 的形状，并说明理由．A DOB E F C四．作图题：（每题 5 分，共 10 分）22.如图 1 是 4×4 正方形网格，其中已有 3 个小方格涂成了黑色。

2015-2016学年度第一学期期中考试年级：初二 科目：数学 班级： 姓名：_________1．下列图形中，是轴对称图形的是A B C D2．下列各式从左边到右边的变形中，是因式分解的是A ．ay ax y x a +=+)(B ．4)4(442+-=+-x x x xC ．)12(55102-=-x x x x D ．x x x x x 3)4)(4(3162+-+=+- 3．下列运算中，正确的是 A ． B ．x x x 236⋅= C ．()x x 238= D ．222)(y x y x +=+4．已知：如图，D 、E 分别在AB 、AC 上，若AB=AC ，AD=AE ， ∠A =60°，∠B =35°，则∠BDC 的度数是A ．95°B ．90°C ．85°D ．80° 5．如图，OP 平分∠MON ，P A ⊥ON 于点A ，点Q 是射线OM 上的一个动点，若P A =2，则PQ 的最小值为A ．1B ．2C ．3D ．4 6．下列各式中，正确的是A ．3355x x y y --=- B ．a b a b c c +-+-=C ．aa ba ab -=-- D．a b a b c c ---=-222235x x x +=AO7．如图，已知△ABC 的六个元素，则下列甲、乙、丙三个三角形中和△ABC 全等的图形是A ．甲B ．乙C ．丙D ．乙与丙 8．如图，把△ABC 沿EF 对折，叠合后的图形如图所示．若60A ∠=︒，195∠=︒，则∠2的度数为A ．24°B ．25°C ．30°D ．35°二、填空题（9、10 题2分，11至16题每题3分，共22分） 9．当__________时，分式11x-有意义． 10．在解分式方程1113122-=--+x x x 时，小兰的解法如下： 解：方程两边同乘以)1)(1(-+x x ，得 13)1(2=--x ． ① 1312=--x ． ② 解得 25=x ． 检验：25=x 时，0)1)(1(≠-+x x ， ③ 所以，原分式方程的解为25=x ． ④ 如果假设基于上一步骤正确的前提下，你认为小兰在哪些步骤中出现了错误 （只填序号）．11．如图，将△ABC 绕点A 旋转到△ADE ，∠BAC =75°，∠DAC =25°，则∠CAE =______°．ABCB'C'EF 1212．如图，已知AB ⊥BD , AB ∥ED ，AB =ED ，要说明ΔABC ≌ΔEDC ，若以“SAS ”为依据，还要添加的条件 为______________；若添加条件AC =EC ，则可以用 _______判定全等．13．如图，在ABC ∆中，分别以点A 和点B 为圆心，大于12AB 的长为半径画弧，两弧相交于点M 、N ，作直线MN ，交BC 于点D ，连接AD ．若ADC ∆的周长为16，AB =12，则ABC ∆的周长为 ．14．若关于x 的二次三项式2x +kx b +因式分解为(1)(3)x x --，则k+b 的值为__________．15．计算：313--2x x y -÷（）（）=____________．16．在平面直角坐标系中，已知点A （1，2），B （5，5），C （5，2），存在点E ，使△ACE 和△ACB 全等，写出所有满足条件的E 点的坐标 ．三、解答题 (18至20题每题4分， 21、22题每题5分，共30分) 17．因式分解：（1） （2） 33312a b ab -18． 因式分解： 19．计算：211(1)m m m-+÷． 20．如图，点B ，E ，F ，C 在一条直线上，AB ＝DC ，BE ＝CF ，∠B652--x x 2296y x x -+-CE CDABF求证：∠A ＝∠D ．21．已知0342=--x x ，求代数式()()()2232y y x y x x --+--的值．22．先化简，再对a 取一个适当的数，代入求值．221369324a a a a a a a +--+-÷-+-四、作图题（本题5分）23．电信部门要在．P ．区域内．．．修建一座电视信号发射塔．如图， 按照设计要求，发射塔到两个城镇A 、B 的距离必须 相等，到两条高速公路m 和n 的距离也必须相等．发射 塔应修建在什么位置？在图中标出它的位置．（要求：尺规作图，不写作法，但要保留作图痕迹，并写出结论）五、解答题（24、25题每题6分，26题7分，共19分） 24．已知：△ABC 中，AC ⊥BC ，CE ⊥AB 于E ，AF 平分∠CAB交CE 于F ，过F 作FD ∥BC 交AB 于D ．求证：AC =AD ．25．赵老师为了响应市政府“绿色出行”的号召，上下班由自驾车方式改为骑自行车方式．已知赵老师家距学校20千米，上下班高峰时段，自驾车的速度是自行车速度的2倍，骑自行车所用时间比自驾车所用时间多95小时．求自驾车速度和自行车速度各是多少？ 26．在ABC ∆中，（1）如图1，BP 为ABC ∆的角平分线，PM AB ⊥于M ，PN BC ⊥于N ，50,60AB BC ==，请补全图形，并直接写出ABP ∆与BPC ∆面积的比值；（2）如图2，分别以ABC ∆的边AB 、AC 为边向外作等边三角形ABD 和ACE ，CD 与BEnB相交于点O ，求证：BE=CD ；（3）在（2）的条件下判断AOD ∠与AOE ∠的数量关系，并加以证明．（注：可以直接应用等边三角形每个角为60°）2015-2016学年度第一学期初二数学期中考试答案一、选择题二、填空题9．1x ≠ 10． ①② 11． 50 ° 12． BC=DC ， HL13．28 14．-1 15．y27x16． （1,5）（1，-1）（5,1） C三、解答题 17．因式分解：（1） +1)(6)x x -（ （2） 32)(2)ab a b a b +-（ 18.（3） 19．1-1m ． 21. 18 22．33a -25．设自行车速度为x 千米/时， 则2020529x x -= x =18附加题1．因式分解（每题3分，共6分）：（1）1)12(2-+-+k x k kx （2） =+1)(1kx k x -+（） 2．5 3. （1）312x -+；（2）0，-2,2，-4；（3）0，-8,1，-9(3)(3)x y x y -+--222222(2)2=2(1)2(1)x x x x x x x x x x --+--=--（）（）。

2024-2025学年度第一学期期中练习题年级：初二 科目：数学 班级：_______ 姓名：________一、选择题（每题2分，共20分）在下列各题的四个备选答案中，只有一个．．．．是正确的. 1．如图所示的4组图形中，成轴对称的是( )A.B.C.D.2．下列计算正确的是( )A. 336a a a +=B. 235a a a +=C. 326()a a =D. 339a a a ⋅= 3． 在平面直角坐标系中，点(3,2)关于x 轴对称的点的坐标为( )A. ()3,2-B. ()2,3-C. ()3,2-D. ()2,3-4．下列是最简分式的是( )A. 2xy xB. 2x y x y ++C. 22x y x y-+ D. 22x y x y --5．如图，修建房屋时，为了使木门框不变形，建筑工人在木门框上斜着加了一根木条，这样做的道理是( ) A. 三角形具有稳定性 B.两点之间，线段最短 C. 垂线段最短 D. 两直线平行，内错角相等第5题图6．如图，点C 在∠AOB 的OB 边上，用尺规作出了CN ∥OA ，连接EN ，△ODM ≌△CEN 根据的是( ) A. SASB. SSSC. ASAD. AAS第6题图易水小寒转发7．如图，在△ABC 中，AD 是BC 边上的高，BE 平分∠ABC 交AC 边于点E ，∠BAC =55°，∠ABE =25°，则∠CAD 的度数是 ( ) A. 15°B. 20°C. 25°D. 30°第7题图 第8题图 第9题图8．如图，将两块大小相同的三角板（∠B ＝∠C ＝30°的直角三角形）按图中所示的位置摆放．若BE 交CF 于点D ，交AC 于点M ，AB 交CF 于点N ，则下列结论中： ①∠EAM ＝∠F AN ；②△ACN ≌△ABM ；③∠EAF +∠BAC ＝120°；④EM ＝FN . 正确的有( )A ．1个B ．2个C ．3个D ．4个9．如图，大正方形的边长为a ，小正方形的边长为b ，若a+b =7，ab =11，则阴影部分的面积为( ) A. 8 B. 7C. 6D. 510．如图，点E 在等边△ABC 的边BC 上，BE =4，射线CD ⊥BC ，垂足为点C ，点P 是射线CD 上一动点，点F 是线段AB 上一动点， 当EP +FP 的值最小时，BF =5，则AB 的长为( )A. 6.5B. 7C.8.5D. 10二、填空题（每题2分，共16分） 11．若分式12-x 有意义，则x 的取值范围是 ． 第10题图 12．因式分解：xy 2-x =________．13．n 边形从一个顶点出发最多引5条对角线，则n =_____． 14．26x x k ++是一个完全平方式，那么k =_____． 15．如图，△ABC 中，∠BAC =90°，AC =8cm ，DE 是BC 边上的垂直平分线，△ABD 的周长为14cm ，则△ABC 的面积是______cm 2．16．若等腰三角形一腰上的高与另一腰的夹角为42°，则这个等腰三角形顶角的度数为 ．17．已知1020a =，10050b =，则2a b +=________．A a C DP易水小寒转发18．如图AB =AC ，AF =AE ，∠EAF =∠BAC ，点C ，D ，E ，F 共线，有如下结论：①△AFB ≌△AEC ；②BF =CE ；③∠BFC =∠EAF ； ④AB =BC ．正确的结论有________．第18题图三、解答题(19题16分，20题8分，21题4分，22题6分，23题5分，24-26每题6分，27题7分，共64分) 19．计算:（1）3225()x x x ⋅÷； （2）3x 2 (x 2 + 2x − 3)； （3）()()312x x +-； （4）2(2)2(2)(2)a b a b a b +-+-．20. 因式分解： （1）234ma ma m --； （2）22(2)m n m +-． 22．如图，在△ABC 中，∠C =90°，∠ABC =60°．（1）尺规作图：在AC 上找一点D ，使得点D 到A 、B 的距离相等； （保留作图痕迹，不用写作法和证明）（2）若AC =9，求点D 到AB 的距离．23．请根据条件进行推理，完成下面的证明，并在括号内注明理由．如图，AB=AC ，BD=CD ，DE ⊥AB 于E ，DF ⊥AC 于F ． 求证：DE=DF ．证明：在△ABD 和△ACD 中，AB=AC ，AD=______， BD=CD ，∴△ABD ≌△ACD ( ) ． ∴∠________=∠_______． ∴AD 是∠BAC 的角平分线． 又∵DE ⊥AB 于E ，DF ⊥AC 于F ，F易水小24．如图，∠A =∠D =90°，AC 与BD 相交于点E ，BE CE ．求证：△ABC ≌△DCB ．25．在日历上，我们可以发现其中某些数满足一定的规律．（1）图①是2024年8月份的月历，我们用如图所示的“Z”字型框架任意框住月历中的5个数（如图①中的阴影部分），将位置B ，D 上的数相乘，位置A ，E 上的数相乘，再相减． 例如：5×19－4×20，2×16－1×17，不难发现，结果都等于______．（请完成填空）“Z”字型框架图① 图②（2）设“Z”字型框架中位置C 上的数为x ，请利用整式的运算对（1）中的规律加以证明.（3）如图②，在某月历中，正方形方框框住部分（阴影部分）9个位置上的数，如果最小的数和最大的数的乘积为57，那么中间位置上的数a ＝_____．26．在等边△ABC 中，点D 在AC 边上（不与A ，C 重合），延长BC 至点E ，使AD=CE ，连接DE ．（1）如图1，当点D 是AC 边中点时，线段DB 与DE 的数量关系是 ； （2）如图2，当点D 是AC 边上任意一点时，（1）中线段DB 与DE 的数量关系是否成立？若成立，请证明；若不成立，请说明理由．图1 图2B易水小寒转发27．已知，如图1，四边形ABCD ，∠B =90°，AB ＞BC ，AC 平分∠BAD ，点E 是边AB 上的一点，且EC =CD ．（1） 若AB =6，AE =4，则AD = ；（2） 若∠BAD =m °，则∠ECD 的度数为 (用含m 的式子表示)；（3）如图2，连接ED ，过点B 作BH ⊥AC ，垂足为点G ，交ED 于点H ，判断EH 与HD 的数量关系并证明．图1 图2E AE易水小寒转四、附加题（28题2分，第29题8分，共10分）28. 已知a ，b ，c 为△ABC 的三边，且满足a+b =3c -2，a -b =2c -6，则c 的取值范围是____________．29. 小聪和小明在学习了平面直角坐标系后，产生了强烈的兴趣，于是尝试定义了平面直角坐 标系xOy 中任意两点()111,P x y 与()222,P x y 的一种新距离： 小聪定义了1P 与2P 的“倍分解距离”，如下：在平面直角坐标系x O y 中，任意两点()111,P x y 与()222,P x y ，任意给定0m ＞都有如下定义： 若1212x x y y -≥-，则()1212,m d P P m x x =-； 若1212x x y y --＜，则()12121,m d P P y y m=-． 例如，点M （1，2），N （3，1），Q （2，4），当m =1时：(),132m d M N =-=，(),143m d N Q =-=．小明定义了1P 与2P 的“和距离”，如下：在平面直角坐标系xOy 中，任意两点()111,P x y 与()222,P x y ． 点1P 与2P 的“和距离”为：()121212,d P P x x y y =-+-和． 例如，点M （1，2），N （3，1），(),13213d M N =-+-=和． 根据以上材料解决如下问题： 在平面直角坐标系xOy 中：（1）m =1时，已知点()3,1A ，则(),m d A O = ，(),d A O =和 ；（2）若点()(),0,0C x y x y ≥≥，且点(),3d C O =和，请写出符合题意的三个点C 的坐 标，证明这些点在一条直线上；（3）当m =2， n ＞0时，若点E ，F 满足(),3m d E O =, (),d F O n =和，当所有符合条 件的点E 所组成的图形和点F 所组成的图形有四个交点时，直接写出n 的取值范围．易水小寒转发。

2015年北师大版八年级（上）期中数学常考试题60题一、选择题（共20小题）1．（常考指数：63）二次根式的值是（）都是直角三角形．若正方形A，B，C，D的边长分别是3，5，2，3，则最大正方形E的面积是（）是2的平方根±6．（常考指数：66）在实数：，0，，π，中，无理数有（）7．（常考指数：42）若x，y为实数，且|x+2|+=0，则（）2009的值为（）．）9．（常考指数：59）实数a，b在数轴上对应点的位置如图所示，则必有（）＜011．（常考指数：45）若代数式有意义，则x的取值范围是（）12．（常考指数：94）下列根式中属最简二次根式的是（）CC14．（常考指数：66）如图，四边形ABCD为矩形纸片，把纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF，若CD=6，则AF等于（）CC20．（常考指数：17）如图，OA，BA分别表示甲、乙两名学生运动的一次函数图象，图中s和t分别表示运动的路程和时间，根据图象判断，甲的速度与乙的速度相比，下列说法中正确的是（）二、填空题（共20小题）21．（常考指数：40）一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是_________．22．（常考指数：45）已知|a+1|+=0，则a﹣b=_________．23．（常考指数：47）定义运算“@”的运算法则为：x@y=，则（2@6）@8=_________．24．（常考指数：50）已知直角三角形的两边的长分别是3和4，则第三边长为_________．25．（常考指数：51）如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是_________．26．（常考指数：116）的算术平方根是_________．27．（常考指数：122）如图所示，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了_________步路（假设2步为1米），却踩伤了花草．28．（常考指数：24）已知|x﹣12|+（y﹣13）2与z2﹣10z+25互为相反数，则以x，y，z为边的三角形是_________三角形．29．（常考指数：46）若一个正数的两个平方根是2a﹣1和﹣a+2，则a=_________，这个正数是_________．30．（常考指数：39）计算：（+1）（﹣1）=_________．31．（常考指数：19）计算：=_________．32．（常考指数：17）要使一个菱形ABCD成为正方形，则需增加的条件是_________．（填一个正确的条件即可）33．（常考指数：42）三角形的三边长分别为，，，则这个三角形的周长为_________cm．34．（常考指数：19）49的平方根是_________，36的算术平方根是_________，﹣8的立方根是_________．35．（常考指数：74）在平面直角坐标系中，点P（2，﹣3）关于原点对称点P′的坐标是_________．36．（常考指数：16）点A（﹣6，8）到x轴的距离为_________，到y轴的距离为_________，到原点的距离为_________．37．（常考指数：23）函数y=的自变量x的取值范围是_________．38．（常考指数：37）已知一次函数y=（k﹣1）x|k|+3，则k=_________．39．（常考指数：20）如图，一次函数图象经过点A，且与正比例函数y=﹣x的图象交于点B，则该一次函数的表达式为_________．40．（常考指数：36）已知一次函数y=ax+b（a、b为常数），x与y的部分对应值如右表：那么方程ax+b=0的解是_________，不等式ax+b＞0的解是_________．三、解答题（共20小题）41．（常考指数：31）如图，∠AOB=90°，OA=45cm，OB=15cm，一机器人在点B处看见一个小球从点A出发沿着AO 方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？42．（常考指数：34）如图，一艘帆船由于风向的原因，先向正东方航行了160千米，然后向正北方航行了120千米，这时它离出发点有多远？43．（常考指数：40）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米．一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？44．（常考指数：44）计算：．45．（常考指数：70）如图所示，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，∠A=90°，求四边形ABCD 的面积．46．（常考指数：75）“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70km/h．如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处，过了2s后，测得小汽车与车速检测仪间距离为50m，这辆小汽车超速了吗？（参考数据转换：1m/s=3.6km/h）47．（常考指数：14）求下列各式中x的值：①（x﹣2）2=25；②﹣8（1﹣x）3=27．48．（常考指数：47）先化简，再求值：，其中．49．（常考指数：21）已知a、b、c 满足．（1）求a、b、c的值；（2）试问以a、b、c为边能否构成三角形？若能构成三角形，请求出三角形的周长，若不能，请说明理由．50．（常考指数：42）观察下列等式：①；②；③；…回答下列问题：（1）利用你观察到的规律，化简：；（2）计算：．51．（常考指数：63）如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：（1）△ACE≌△BCD；（2）AD2+DB2=DE2．52．（常考指数：13）已知：在平面直角坐标系中，点A、B的坐标分别是（a，0），（b，0）且+|b﹣2|=0．（1）求a、b的值；（2）在y轴上是否存在点C，使三角形ABC的面积是12？若存在，求出点C的坐标；若不存在，请说明理由．（3）已知点P是y轴正半轴上一点，且到x轴的距离为3，若点P沿x轴负半轴方向以每秒1个单位长度平移至点Q，当运动时间t为多少秒时，四边形ABPQ的面积S为15个平方单位？写出此时点Q的坐标．53．（常考指数：15）已知一次函数y=（6+3m）x+n﹣4．（1）当m、n为何值时，函数的图象过原点？（2）当m、n满足什么条件时，函数的图象经过第一、二、三象限？54．（常考指数：17）如图，已知正比例函数y=kx（k≠0）经过点P（2，4），（1）求这个正比例函数的解析式；（2）该直线向上平移4个单位，求平移后所得直线的解析式．55．（常考指数：13）一次函数y=kx+b的图象经过点M（8，﹣3），且当x=4时，y=0．（1）求函数的解析式；（2）求函数图象与坐标轴围成的三角形的面积．56．（常考指数：19）现行固定网通电话的通话收费标准为：前3分钟（不足3分钟按3分钟计）0.22元，3分钟后每分钟按0.11元（不足1分钟按1分钟计）．（2）上述变化中，自变量和因变量分别是什么？（3）通话10.5分钟时的话费是多少元？57．（常考指数：22）如图，在直角坐标平面内，已知点A的坐标（﹣5，0），（1）图中B点的坐标是_________；（2）点B关于原点对称的点C的坐标是_________；点A关于y轴对称的点D的坐标是_________；（3）△ABC的面积是_________；（4）在直角坐标平面上找一点E，能满足S△ADE=S△ABC 的点E有_________个；（5）在y轴上找一点F，使S△ADF=S △ABC，那么点F 的所有可能位置是_________；（用坐标表示，并在图中画出）58．（常考指数：20）（1）﹣72+2×（﹣3）2+（﹣6）÷（﹣）2（2）2﹣6﹣（）﹣1．59．（常考指数：14）（1）计算：•（÷）；（2）已知实数x、y满足：+（y﹣）2=0，求的值．60．（常考指数：12）（1）根据两点确定一条直线，画出函数y1=5x+4的图象；（2）再画出函数y2=2x+10的图象；（3）写出它们交点的坐标；（4）当y1＜y2时，写出x的取值范围．本题考查二次根式的化简，=二次根式时，时，2．（常考指数：64）如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A ，B ，C ，D 的边长分别是3，5，2，3，则最大正方形E 的面积是（ ）是2的平方根、、±，故± 解：∵6．（常考指数：66）在实数：，0，，π，中，无理数有（），，，无理数有7．（常考指数：42）若x，y为实数，且|x+2|+=0，则（）2009的值为（）|x+2|+）．），故（、9．（常考指数：59）实数a，b在数轴上对应点的位置如图所示，则必有（）＜0＜＜＜＜11．（常考指数：45）若代数式有意义，则x的取值范围是（）．、，可化简；、=2、=3．9、根据=|a|14．（常考指数：66）如图，四边形ABCD 为矩形纸片，把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ，若CD=6，则AF 等于（ ）． FAE=（，2×．．20．（常考指数：17）如图，OA ，BA 分别表示甲、乙两名学生运动的一次函数图象，图中s 和t 分别表示运动的路程和时间，根据图象判断，甲的速度与乙的速度相比，下列说法中正确的是（ ）二、填空题（共20小题）21．（常考指数：40）一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A 点沿纸箱爬到B 点，那么它所行的最短路线的长是 10 ．=1022．（常考指数：45）已知|a+1|+=0，则a ﹣b= ﹣9 ．|a+1|+23．（常考指数：47）定义运算“@”的运算法则为：x@y=，则（2@6）@8= 6 ．@8=@8=4@8==624．（常考指数：50）已知直角三角形的两边的长分别是3和4，则第三边长为 5或 ．第三边的长为：=第三边的长为：或或25．（常考指数：51）如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是 n 2+2n ．26．（常考指数：116）的算术平方根是 2 ．的值，然后再利用算术平方根的定义即可求出结果．解：∵的算术平方根是=2=427．（常考指数：122）如图所示，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了 4 步路（假设2步为1米），却踩伤了花草．=5m 28．（常考指数：24）已知|x ﹣12|+（y ﹣13）2与z 2﹣10z+25互为相反数，则以x ，y ，z 为边的三角形是 直角 三角形．29．（常考指数：46）若一个正数的两个平方根是2a ﹣1和﹣a+2，则a= ﹣1 ，这个正数是 9 ．30．（常考指数：39）计算：（+1）（﹣1）= 1 ．+1（）计算：+263．32．（常考指数：17）要使一个菱形ABCD 成为正方形，则需增加的条件是 ∠A=90°或AC=BD ．（填一个正确的条件即可）33．（常考指数：42）三角形的三边长分别为，，，则这个三角形的周长为 5 cm ．三角形的三边长的和为三角形的周长，所以这个三角形的周长为+解：这个三角形的周长为+=2+3=5+2+2（34．（常考指数：19）49的平方根是 ±7 ，36的算术平方根是 6 ，﹣8的立方根是 ﹣2 ． 35．（常考指数：74）在平面直角坐标系中，点P （2，﹣3）关于原点对称点P ′的坐标是 （﹣2，3） ． 到原点的距离为=1037．（常考指数：23）函数y=的自变量x 的取值范围是 x ≤0.5且x ≠﹣1 ．38．（常考指数：37）已知一次函数y=（k ﹣1）x |k|+3，则k= ﹣1 ． 39．（常考指数：20）如图，一次函数图象经过点A ，且与正比例函数y=﹣x 的图象交于点B ，则该一次函数的表达式为 y=x+2 ．，；三、解答题（共20小题）41．（常考指数：31）如图，∠AOB=90°，OA=45cm，OB=15cm，一机器人在点B处看见一个小球从点A出发沿着AO 方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？44．（常考指数：44）计算：．=45．（常考指数：70）如图所示，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，∠A=90°，求四边形ABCD的面积．=×（=2047．（常考指数：14）求下列各式中x的值：①（x﹣2）2=25；②﹣8（1﹣x）3=27．﹣x=，其中=649．（常考指数：21）已知a 、b 、c 满足．（1）求a 、b 、c 的值；（2）试问以a 、b 、c 为边能否构成三角形？若能构成三角形，请求出三角形的周长，若不能，请说明理由． =0﹣=2=3a+b+c=2+5+3=5+550．（常考指数：42）观察下列等式：①；②；③；…回答下列问题：（1）利用你观察到的规律，化简：； （2）计算：．==2中的根号去掉，要用（（52．（常考指数：13）已知：在平面直角坐标系中，点A 、B 的坐标分别是（a ，0），（b ，0）且+|b ﹣2|=0． （1）求a 、b 的值；（2）在y 轴上是否存在点C ，使三角形ABC 的面积是12？若存在，求出点C 的坐标；若不存在，请说明理由．（3）已知点P 是y 轴正半轴上一点，且到x 轴的距离为3，若点P 沿x 轴负半轴方向以每秒1个单位长度平移至点Q ，当运动时间t 为多少秒时，四边形ABPQ 的面积S 为15个平方单位？写出此时点Q 的坐标．的面积积的面积53．（常考指数：15）已知一次函数y=（6+3m ）x+n ﹣4． （1）当m 、n 为何值时，函数的图象过原点？（2）当m 、n 满足什么条件时，函数的图象经过第一、二、三象限？ 54．（常考指数：17）如图，已知正比例函数y=kx （k ≠0）经过点P （2，4）， （1）求这个正比例函数的解析式；（2）该直线向上平移4个单位，求平移后所得直线的解析式．55．（常考指数：13）一次函数y=kx+b 的图象经过点M （8，﹣3），且当x=4时，y=0． （1）求函数的解析式；（2）求函数图象与坐标轴围成的三角形的面积． 解得，函数解析式：）知，一次函数的解析式是：三角形的面积为：×56．（常考指数：19）现行固定网通电话的通话收费标准为：前3分钟（不足3分钟按3分钟计）0.22元，3分钟后每分钟按0.11元（不足1分钟按1分钟计）．（3）通话10.5分钟时的话费是多少元？y=57．（常考指数：22）如图，在直角坐标平面内，已知点A的坐标（﹣5，0），（1）图中B点的坐标是（﹣3，4）；（2）点B关于原点对称的点C的坐标是（3，﹣4）；点A关于y轴对称的点D的坐标是（5，0）；（3）△ABC的面积是20；（4）在直角坐标平面上找一点E，能满足S△ADE=S△ABC的点E有无数个；（5）在y轴上找一点F，使S△ADF=S△ABC，那么点F的所有可能位置是（0，4）或（0，﹣4）；（用坐标表示，并在图中画出），AB×（﹣﹣﹣（），）先把根式化成最简二次根式，同时求出=4×﹣﹣﹣﹣）计算：•÷+的值．，再求÷•；）由）可知，）解得所以=。