高中数学第一章三角函数章末分层突破学案新人教A版必修4

1.4.2 正弦函数、余弦函数的性质(二)学习目标 1.掌握y ＝sin x ，y ＝cos x 的最大值与最小值，并会求简单三角函数的值域和最值(重点).2.掌握y ＝sin x ，y ＝cos x 的单调性，并能利用单调性比较大小(重、难点).3.会求函数y ＝A sin(ωx ＋φ)及y ＝A cos(ωx ＋φ)的单调区间(重点)．知识点 正弦函数、余弦函数的图象和性质(表中k ∈Z ))【预习评价】1．在下列区间中，使y ＝sin x 为增函数的是( ) A ．[0，π] B ．[π2，3π2]C ．[－π2，π2]D ．[π，2π]解析 因为函数y ＝sin x 的单增区间是[－π2＋2k π，π2＋2k π]，k ∈Z ，故当k ＝0时，即为[－π2，π2]，故选C ．答案 C2．函数y ＝2－sin x 取得最大值时x 的值为________．解析 当sin x ＝－1，即x ＝－π2＋2k π(k ∈Z )时，函数y ＝2－sin x 的最大值为3．答案 －π2＋2k π(k ∈Z )题型一 正弦函数、余弦函数的单调性【例1】 (1)下列函数，在[π2，π]上是增函数的是( )A ．y ＝sin xB ．y ＝cos xC ．y ＝sin 2xD ．y ＝cos 2x解析 对于函数y ＝cos 2x ，令π＋2k π≤2x ≤2π＋2k π，(k ∈Z )， 即π2＋k π≤x ≤π＋k π (k ∈Z )， 故y ＝cos 2x 的单增区间是[π2＋k π，π＋k π](k ∈Z )，则当k ＝0时单增区间为[π2，π]，故选D ．答案 D(2)求函数y ＝1＋sin ⎝ ⎛⎭⎪⎫－12x ＋π4，x ∈[－4π，4π]的单调减区间． 解 y ＝1＋sin ⎝ ⎛⎭⎪⎫－12x ＋π4＝－sin ⎝ ⎛⎭⎪⎫12x －π4＋1． 由2k π－π2≤12x －π4≤2k π＋π2(k ∈Z )．解得4k π－π2≤x ≤4k π＋32π(k ∈Z )．又∵x ∈[－4π，4π]，∴函数y ＝1＋sin(－12x ＋π4)的单调减区间为[－4π，－5π2]，[－π2，3π2]，[7π2，4π]．规律方法 单调区间的求法求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)的函数的单调区间，要先把ω化为正数， (1)当A >0时，把ωx ＋φ整体放入y ＝sin x 或y ＝cos x 的单调增区间内，求得的x 的范围即函数的增区间；放入y ＝sin x 或y ＝cos x 的单调减区间内，可求得函数的减区间．(2)当A <0时，把ωx ＋φ整体放入y ＝sin x 或y ＝cos x 的单调增区间内，求得的x 的范围即函数的减区间；放入y ＝sin x 或y ＝cos x 的单调减区间内，可求得函数的增区间．提醒 求函数y ＝A sin(ωx ＋φ)的单调区间时，把ωx ＋φ看作一个整体，借助y ＝sinx 的单调区间来解决．当A <0或ω<0时，要注意原函数的单调性与y ＝sin x 的单调性的关系．【训练1】 求函数f (x )＝2cos(2x －π6)的单调增区间．解 令－π＋2k π≤2x －π6≤2k π，k ∈Z ，解得－5π12＋k π≤x ≤π12＋k π，k ∈Z ，所以函数f (x )的单调增区间是[－5π12＋k π，π12＋k π](k ∈Z )．题型二 利用正弦函数、余弦函数的单调性比较大小 【例2】 利用三角函数的单调性，比较下列各组数的大小． (1)sin 49π45与cos 39π45；(2)cos ⎝ ⎛⎭⎪⎫－235π与cos ⎝ ⎛⎭⎪⎫－174π. 解 (1)sin 49π45＝sin(π＋4π45)＝－sin 4π45，cos 39π45＝cos(π－6π45)＝－cos 6π45＝－sin 11π30，∵0＜4π45＜11π30＜π2，且y ＝sin x 在[0，π2]上是增函数∴sin 4π45<sin 11π30；从而－sin 4π45>－sin 11π30，即sin 49π45>cos 39π45.(2)cos ⎝ ⎛⎭⎪⎫－235π＝cos 235π＝cos(4π＋35π)＝cos 35π， cos ⎝ ⎛⎭⎪⎫－174π＝cos 174π＝cos ⎝ ⎛⎭⎪⎫4π＋π4＝cos π4．∵0<π4<35π<π，且y ＝cos x 在[0，π]上是减函数，∴cos 35π<cos π4，即cos ⎝ ⎛⎭⎪⎫－235π<cos ⎝ ⎛⎭⎪⎫－174π． 规律方法 比较三角函数值的大小的步骤 (1)依据诱导公式把几个三角函数化为同名函数． (2)依据诱导公式把角化到属于同一个单调增(减)区间． (3)依据三角函数的单调性比较大小后写出结论． 【训练2】 比较下列各组数的大小：(1)sin ⎝ ⎛⎭⎪⎫－376π与sin ⎝ ⎛⎭⎪⎫493π； (2)cos 870°与sin 980°．解 (1)sin ⎝ ⎛⎭⎪⎫－376π＝sin ⎝ ⎛⎭⎪⎫－6π－π6＝sin ⎝ ⎛⎭⎪⎫－π6，sin ⎝ ⎛⎭⎪⎫493π＝sin ⎝⎛⎭⎪⎫16π＋π3＝sin π3， ∵y ＝sin x 在⎣⎢⎡⎦⎥⎤－π2，π2上是增函数，∴sin ⎝ ⎛⎭⎪⎫－π6<sin π3，即sin ⎝ ⎛⎭⎪⎫－376π<sin 493π． (2)cos87π18＝cos(4π＋5π6)＝cos 5π6，sin 49π9＝sin(4π＋13π9)＝sin 13π9＝sin(π2＋17π18)＝cos 17π18，∵0＜5π6＜17π18＜π，且y ＝cos x 在[0，π]上是减函数，∴cos 5π6>cos 17π18，即cos 8π18>sin 49π9.方向1 正弦函数、余弦函数的值域问题【例3-1】 函数f (x )＝2cos(2x ＋π4)，x ∈[－π2，0]的值域为________．解析 ∵－π2≤x ≤0，∴－3π4≤2x ＋π4≤π4，∴－22≤cos(2x ＋π4)≤1， 故－1≤2cos(2x ＋π4)≤2，即f (x )的值域是[－1，2]． 答案 [－1，2]方向2 与正、余弦函数有关的复合函数的值域问题【例3-2】 函数f (x )＝sin 2x ＋3cos x －34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π2的最大值是________．解析f (x )＝sin 2x ＋3cos x －34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π2，f (x )＝1－cos 2x ＋3cos x －34，令cos x ＝t 且t ∈[0，1]，则y ＝－t 2＋3t ＋14＝－⎝ ⎛⎭⎪⎫t －322＋1，则当t ＝32时，f (x )取最大值1. 答案1方向3 含参数的最值问题【例3-3】 若函数y ＝a －b cos x (b >0)的最大值为32，最小值为－12，求函数y ＝【例3-4】 －4a cos bx 的最值和最小正周期． 解 ∵y ＝a －b cos x (b >0)， ∴y max ＝a ＋b ＝32，y min ＝a －b ＝－12．由⎩⎪⎨⎪⎧a ＋b ＝32，a －b ＝－12，解得⎩⎪⎨⎪⎧a ＝12，b ＝1.∴y ＝－4a cos bx ＝－2cos x ，所以函数y=－4a cos bx 的最大值为2，最小值为-2,最小正周期为2π. 规律方法 求三角函数值域或最值的常用方法(1)可化为单一函数y ＝A sin(ωx ＋φ)＋k 或y ＝A cos(ωx ＋φ)＋k ，其最大值为|A |＋k ，最小值－|A |＋k (其中A ，ω，k ，φ为常数，A ≠0，ω≠0)．(2)可化为y ＝A sin 2x ＋B sin x ＋C 或y ＝A cos 2x ＋B cos x ＋C (A ≠0)，最大值、最小值可利用二次函数在定义域上的最大值、最小值的求法来求(换元法)．课堂达标1．y ＝2sin(3x ＋π3)的值域是( )A ．[－2,2]B ．[0,2]C ．[－2,0]D ．[－1,1]解析 因为sin(3x ＋π3)∈[－1,1]，所以y ∈[－2,2]．答案 A2．下列关系式中正确的是( )A ．sin 11°<cos 10°<sin 168°B．sin 168°<sin 11°<cos 10°C ．sin 11°<sin 168°<cos 10°D．sin 168°<cos 10°<sin 11°解析 因为sin 168°＝sin 12°，cos 10°＝sin 80°，又因为函数y ＝sin x 在[0，π2]上单调递增，所以sin 11°<sin 12°<sin 80°，即sin 11°<sin 168°<cos 10°． 答案 C3．函数f (x )＝2cos(2x －π4)的单减区间是________．解析 令2k π≤2x －π4≤π＋2k π，k ∈Z ，得π8＋k π≤x ≤5π8＋k π，k ∈Z ， 即f (x )的单减区间是[π8＋k π，5π8＋k π](k ∈Z )．答案 [π8＋k π，5π8＋k π](k ∈Z )4．函数y ＝cos(x ＋π6)，x ∈[0，π2]的值域是________．解析 ∵0≤x ≤π2，∴π6≤x ＋π6≤2π3， ∴cos 2π3≤cos(x ＋π6)≤cos π6．∴－12≤y ≤32，即值域为[－12，32]．答案 [－12，32]5．求函数y ＝3－2sin 12x 的最值及取到最值时的自变量x 的集合．解 ∵－1≤sin 12x ≤1，∴当sin 12x ＝－1，12x ＝2k π－π2，k ∈Z ，即x ＝4k π－π，k ∈Z 时，y max ＝5，此时自变量x 的集合为{x |x ＝4k π－π，k ∈Z }； 当sin 12x ＝1，12x ＝2k π＋π2，k ∈Z ，即x ＝4k π＋π，k ∈Z 时，y min ＝1，此时自变量x 的集合为{x |x ＝4k π＋π，k ∈Z }．课堂小结1．求函数y ＝A sin(ωx ＋φ)(A >0，ω>0)单调区间的方法把ωx ＋φ看成一个整体，由2k π－π2≤ωx ＋φ≤2k π＋π2 (k ∈Z )解出x 的范围，所得区间即为增区间，由2k π＋π2≤ωx ＋φ≤2k π＋3π2(k ∈Z )解出x 的范围，所得区间即为减区间．若ω<0，先利用诱导公式把ω转化为正数后，再利用上述整体思想求出相应的单调区间．2．比较三角函数值的大小，先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较，再利用单调性作出判断．3．求三角函数值域或最值的常用方法：将y 表示成以sin x (或cos x )为元的一次或二次等复合函数，再利用换元或配方或利用函数的单调性等来确定y 的范围．基础过关1．函数y ＝sin 2x 的单调减区间是( ) A ．⎣⎢⎡⎦⎥⎤π2＋2k π，32π＋2k π(k ∈Z ) B ．⎣⎢⎡⎦⎥⎤k π＋π4，k π＋34π(k ∈Z ) C ．[]π＋2k π，3π＋2k π(k ∈Z ) D ．⎣⎢⎡⎦⎥⎤k π－π4，k π＋π4(k ∈Z ) 解析 令π2＋2k π≤2x ≤3π2＋2k π，k ∈Z ，得π4＋k π≤x ≤3π4＋k π，k ∈Z ， 则y ＝sin 2x 的单减区间是[π4＋k π，3π4＋k π](k ∈Z )．答案 B2．下列函数中，周期为π，且在⎣⎢⎡⎦⎥⎤π4，π2上为减函数的是( )A ．y ＝sin ⎝⎛⎭⎪⎫2x ＋π2B ．y ＝cos ⎝⎛⎭⎪⎫2x ＋π2C ．y ＝sin ⎝ ⎛⎭⎪⎫x ＋π2D ．y ＝cos ⎝⎛⎭⎪⎫x ＋π2解析 因为函数周期为π，所以排除C ，D ．又因为y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π2＝－sin 2x 在⎣⎢⎡⎦⎥⎤π4，π2上为增函数，故B 不符合．故选A ．答案 A3．函数f (x )＝15sin ⎝ ⎛⎭⎪⎫x ＋π3＋cos ⎝ ⎛⎭⎪⎫x －π6的最大值为( )A.65B ．1 C.35D.15解析 cos ⎝ ⎛⎭⎪⎫x －π6＝cos ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫x ＋π3＝sin ⎝ ⎛⎭⎪⎫x ＋π3，则f (x )＝15sin ⎝ ⎛⎭⎪⎫x ＋π3＋sin ⎝⎛⎭⎪⎫x ＋π3＝65sin ⎝ ⎛⎭⎪⎫x ＋π3，函数的最大值为65.答案 A4．函数y ＝sin(x 2－π3)取最大值时自变量的取值集合是________．解析 当x 2－π3＝π2＋2k π，k ∈Z ，即x ＝5π3＋4k π，k ∈Z 时，函数取最大值．答案 {x |x ＝5π3＋4k π，k ∈Z }5．sin 1，sin 2，sin 3按从小到大排列的顺序为________________________． 解析 ∵1<π2<2<3<π，sin(π－2)＝sin 2，sin(π－3)＝sin 3．y ＝sin x 在⎝⎛⎭⎪⎫0，π2上递增，且0<π－3<1<π－2<π2，∴sin(π－3)<sin 1<sin(π－2)， 即sin 3<sin 1<sin 2． 答案 sin 3<sin 1<sin 26．已知函数f (x )＝2cos ⎝ ⎛⎭⎪⎫3x ＋π4． (1)求f (x )的单调递增区间(k ∈Z )；(2)求f (x )的最小值及取得最小值时相应的x 值(k ∈Z )． 解 (1)令－π＋2k π≤3x ＋π4≤2k π，可得－5π12＋23k π≤x ≤－π12＋23k π，故f (x )的单调递增区间是[－5π12＋23k π，－π12＋23k π](k ∈Z )．(2)当3x ＋π4＝－π＋2k π，即x ＝－5π12＋23k π(k ∈Z )时，f (x )的最小值为－2．7．求函数y ＝cos 2x －sin x 的值域． 解 y ＝cos 2x －sin x ＝－sin 2x －sin x ＋1 ＝－⎝ ⎛⎭⎪⎫sin x ＋122＋54． ∵sin x ∈[－1,1]，∴当sin x ＝－12时，y max ＝54；当sin x ＝1时，y min ＝－1．∴函数y ＝cos 2x －sin x 的值域为⎣⎢⎡⎦⎥⎤－1，54．能力提升8．若函数y ＝sin(π＋x )，y ＝cos(2π－x )都是减函数，则x 的集合是( )A ．⎩⎨⎧⎭⎬⎫x |2k π≤x ≤2k π＋π2，k ∈ZB ．⎩⎨⎧⎭⎬⎫x |k π≤x ≤2k π＋π2，k ∈ZC ．⎩⎨⎧⎭⎬⎫x |2k π－π2≤x ≤2k π＋π2，k ∈ZD ．⎩⎨⎧⎭⎬⎫x |2k π＋π2≤x ≤2k π＋3π2，k ∈Z解析 y ＝sin(π＋x )＝－sin x ，y ＝cos(2π－x )＝cos x ，对y ＝－sin x 在⎣⎢⎡⎦⎥⎤－π2＋2k π，π2＋2k π(k ∈Z)上单调递减．对y ＝cos x 在[2k π，π＋2k π](k ∈Z)上单调递减． 取两集合的交集，故选A ． 答案 A9．函数y ＝sin x 的定义域为[a ，b ]，值域为⎣⎢⎡⎦⎥⎤－1，12，则b －a 的最大值和最小值之和等于( )A ．4π3B ．8π3C ．2πD ．4π解析 作出y ＝sin x 的一个简图， 如图所示，∵函数的值域为[－1，12]，且sin π6＝sin 5π6＝12，sin 3π2＝－1，∴定义域[a ，b ]中b －a 的最小值为3π2－5π6＝2π3，定义域[a ，b ]中b －a 的最大值为2π＋π6－5π6＝4π3，故可得，最大值与最小值之和为2π． 答案 C10．已知α，β为锐角三角形的两个内角，则cos α与sin β的大小关系是________． 解析 因为α，β是锐角三角形的两个内角，故α＋β>π2，∴α>π2－β，α∈(0，π2)，π2－β∈(0，π2)， 所以cos α<cos(π2－β)＝sin β．答案 cos α<sin β11．若f (x )＝2sin ωx (0<ω<1)在区间⎣⎢⎡⎦⎥⎤0，π3上的最大值是2，则ω＝________．解析 ∵x ∈⎣⎢⎡⎦⎥⎤0，π3，即0≤x ≤π3，且0<ω<1，∴0≤ωx ≤ωπ3<π3．∵f (x )max ＝2sin ωπ3＝2，∴sin ωπ3＝22，ωπ3＝π4，即ω＝34． 答案 3412．求下列函数的单调增区间：(1)y ＝1－sin x 2；(2)y ＝log 12cos(π3－x 2)． 解 (1)由2k π＋π2≤x 2≤2k π＋32π，k ∈Z ， 得4k π＋π≤x ≤4k π＋3π，k ∈Z ．∴y ＝1－sin x 2的增区间为[4k π＋π，4k π＋3π] (k ∈Z )． (2)要求函数y ＝log 12cos ⎝ ⎛⎭⎪⎫π3－x 2的增区间，即求使y ＝cos ⎝ ⎛⎭⎪⎫x 2－π3>0且单调递减的区间．为此，x 满足：2k π≤x 2－π3<2k π＋π2，k ∈Z ． 整理得4k π＋2π3≤x <4k π＋5π3，k ∈Z ． ∴函数y ＝log 12cos ⎝ ⎛⎭⎪⎫π3－x 2的增区间为 ⎣⎢⎡⎭⎪⎫4k π＋2π3，4k π＋5π3，k ∈Z ． 13．(选做题)已知函数f (x )＝sin(2x ＋φ)，其中φ为实数，且|φ|<π.若f (x )≤|f ⎝ ⎛⎭⎪⎫π6|对x ∈R 恒成立．且f ⎝ ⎛⎭⎪⎫π2>f (π)，求f (x )的单调递增区间． 解 由f (x )≤|f ⎝ ⎛⎭⎪⎫π6|对x ∈R 恒成立知， 2·π6＋φ＝2k π±π2(k ∈Z )． ∴φ＝2k π＋π6或φ＝2k π－5π6(k ∈Z )． ∵|φ|<π，得φ＝π6或φ＝－5π6， 又∵f ⎝ ⎛⎭⎪⎫π2>f (π)， ∴φ＝－5π6，故f (x )=2sin(2x －5π6)由2k π－π2≤2x －5π6≤2k π＋π2(k ∈Z )． 得f (x )的单调递增区间是[k π＋π6，k π＋2π3](k ∈Z )．。

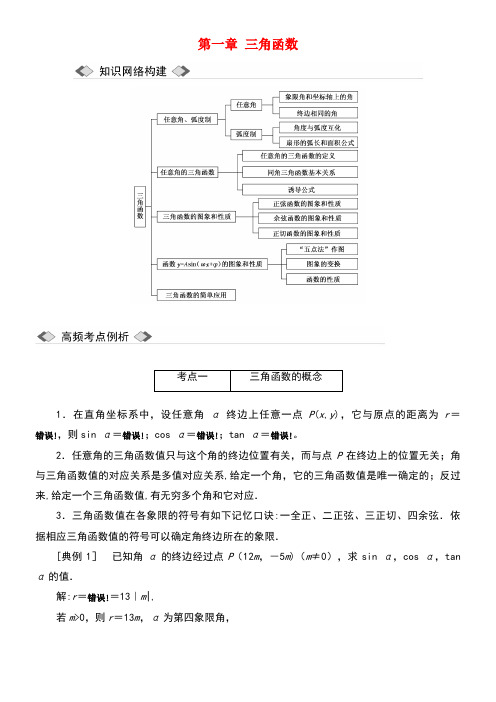
第一章三角函数考点一三角函数的概念1．在直角坐标系中，设任意角α终边上任意一点P(x,y)，它与原点的距离为r＝错误!，则sin α＝错误!；cos α＝错误!；tan α＝错误!。

2．任意角的三角函数值只与这个角的终边位置有关，而与点P在终边上的位置无关；角与三角函数值的对应关系是多值对应关系,给定一个角，它的三角函数值是唯一确定的；反过来,给定一个三角函数值,有无穷多个角和它对应．3．三角函数值在各象限的符号有如下记忆口诀:一全正、二正弦、三正切、四余弦．依据相应三角函数值的符号可以确定角终边所在的象限．[典例1］已知角α的终边经过点P（12m，－5m)（m≠0），求sin α，cos α，tan α的值．解:r＝错误!＝13｜m|,若m>0，则r＝13m，α为第四象限角，sin α＝错误!＝错误!＝－错误!，cos α＝错误!＝错误!＝错误!，tan α＝错误!＝错误!＝－错误!.若m〈0，则r＝－13m,α为第二象限角，sin α＝错误!＝错误!＝错误!，cos α＝错误!＝错误!＝－错误!，tan α＝错误!＝错误!＝－错误!。

［对点训练]1．（1)α是第四象限角，P（错误!，x）为其终边上一点，且sin α＝错误!x，则cos α的值为( )A.错误!B.错误! C。

错误! D．－错误!（2)若－错误!〈α〈0，则点P（tan α，cos α)位于( ）A．第一象限 B．第二象限 C．第三象限 D．第四象限解析：(1）由定义可得sin α＝错误!＝错误!x，x〈0，可得x＝－错误!，∴cos α＝错误!＝错误!.(2)∵－错误!〈α<0，∴tan α〈0,cos α〉0,∴点P(tan α，cos α）位于第二象限．答案：(1）A （2）B三角函数式的化简、求值与证明问题的依据主要是同角三角函数的关系式及诱导公式．化简的顺序是：(1）先用诱导公式化为同角三角函数．(2)再用同角三角函数关系化简．用同角三角函数关系化简时，有两种思路:①化弦法：当切函数的项比较少时，常常化弦达到化简的目的；②化切法：当弦函数的项比较少或者正、余弦的表达式是齐次式时，常常化切，便于化简．[典例2］已知错误!＝－4，求(sin θ－3cos θ）·（cos θ－sin θ)的值．解：错误!＝错误!＝－4，解得tan θ＝2。

2018版高中数学第一章三角函数1.4.2 正弦函数、余弦函数的性质学案新人教A版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018版高中数学第一章三角函数1.4.2 正弦函数、余弦函数的性质学案新人教A版必修4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018版高中数学第一章三角函数1.4.2 正弦函数、余弦函数的性质学案新人教A版必修4的全部内容。

1.4。

2 正弦函数、余弦函数的性质1.掌握y＝sin x（x∈R)，y＝cos x(x∈R）的周期性、奇偶性、单调性和最值。

（重点）2。

会求函数y＝A sin(ωx＋φ)及y＝A cos(ωx＋φ)的周期，单调区间及最值。

(难点)3.了解周期函数、周期、最小正周期的含义。

(易混点）[基础·初探]教材整理1 函数的周期性阅读教材P34～P35“例2”以上部分,完成下列问题.1.函数的周期性(1）对于函数f（x），如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f（x),那么函数f(x）就叫做周期函数，非零常数T叫做这个函数的周期。

（2)如果在周期函数f（x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f（x）的最小正周期.2.两种特殊的周期函数（1)正弦函数是周期函数，2kπ(k∈Z且k≠0）都是它的周期,最小正周期是2π.（2）余弦函数是周期函数，2kπ（k∈Z且k≠0）都是它的周期，最小正周期是2π。

函数y＝2cos x＋5的最小正周期是________。

【解析】函数y＝2cos x＋5的最小正周期为T＝2π.【答案】2π教材整理2 正、余弦函数的奇偶性阅读教材P37“思考”以下至P37第14行以上内容,完成下列问题.1.对于y＝sin x，x∈R恒有sin（－x）＝－sin x，所以正弦函数y＝sin x是奇函数，正弦曲线关于原点对称.2。

1 第1课时 任意角的三角函数的定义 学习目标：1.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义．(重点、难点)2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号．(易错点)3.掌握公式——并会应用． [自 主 预 习·探 新 知] 1．单位圆 在直角坐标系中，我们称以原点O为圆心，以单位长度为半径的圆为单位圆． 2．任意角的三角函数的定义 (1)条件在平面直角坐标系中，设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么：

图1­2­1 (2)结论 ①y叫做α的正弦，记作sin_α，即sin α＝y； ②x叫做α的余弦，记作cos_α，即cos α＝x；

③yx叫做α的正切，记作tan_α，即tan α＝yx(x≠0)． (3)总结 正弦、余弦、正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们将它们统称为三角函数．

3．正弦、余弦、正切函数在弧度制下的定义域 三角函数 定义域 sin α R cos α R

tan α 

x∈R x≠kπ＋π2，k∈Z

4．正弦、余弦、正切函数值在各象限内的符号 (1)图示： 2

图1­2­2 (2)口诀：“一全正，二正弦，三正切，四余弦”． 5．诱导公式一

[基础自测] 1．思考辨析 (1)sin α表示sin与α的乘积．( )

(2)设角α终边上的点P(x，y)，r＝|OP|≠0，则sin α＝yr，且y越大，sin α的值越大．( ) (3)终边相同的角的同一三角函数值相等．( ) (4)终边落在y轴上的角的正切函数值为0.( ) [解析] (1)错误．sin α表示角α的正弦值，是一个“整体”．

(2)错误．由任意角的正弦函数的定义知，sin α＝yr.但y变化时，sin α是定值． (3)正确． (4)错误．终边落在y轴上的角的正切函数值不存在． [答案] (1)× (2)× (3)√ (4)× 2．已知sin α＞0，cos α＜0，则角α是( ) A．第一象限角 B．第二象限角 C．第三象限角 D．第四象限角 B [由正弦、余弦函数值在各象限内的符号知，角α是第二象限角．]

第一章 三角函数章末复习课 新人教A 版必修4课时目标 1.复习三角函数的基本概念、同角三角函数基本关系式及诱导公式.2.复习三角函数的图象及三角函数性质的运用． 知识结构一、选择题1．c os 330°等于( ) A.12 B ．－12 C.32 D ．－322．已知cos(π＋x )＝35，x ∈(π，2π)，则tan x 等于( )A ．－34B ．－43 C.34 D.433．已知集合M ＝⎩⎨⎧⎭⎬⎫x |x ＝k π2＋π4，k ∈Z ，N ＝{x |x ＝k π4＋π2，k ∈Z }．则( )A ．M ＝NB ．M NC ．N MD ．M ∩N ＝∅4．为得到函数y ＝cos ⎝⎛⎭⎪⎫2x ＋π3的图象，只需将函数y ＝sin 2x 的图象( ) A ．向左平移5π12个单位长度B ．向右平移5π12个单位长度C ．向左平移5π6个单位长度D ．向右平移5π6个单位长度5．若sin 2x >cos 2x ，则x 的取值范围是( )A ．{x |2k π－3π4<x <2k π＋π4，k ∈Z }B ．{x |2k π＋π4<x <2k π＋5π4，k ∈Z }C ．{x |k π－π4<x <k π＋π4，k ∈Z }D ．{x |k π＋π4<x <k π＋3π4，k ∈Z }6．如图所示，一个大风车的半径为8 m ，每12 min 旋转一周，最低点离地面2 m ．若风车翼片从最低点按逆时针方向开始旋转，则该翼片的端点P 离地面的距离h (m)与时间t (min)之间的函数关系是( )A ．h ＝8cos π6t ＋10B ．h ＝－8cos π3t ＋10C ．h ＝－8sin π6t ＋10D ．h ＝－8cos π6t ＋107．已知sin α＝55，则sin 4α－cos 4α的值为________．8．已知函数f (x )＝sin(ωx ＋φ)(ω>0)的图象如图所示，则ω＝________.9．函数f (x )＝|sin x |的单调递增区间是__________．10．函数f (x )＝3sin ⎝ ⎛⎭⎪⎫2x －π3的图象为C ， ①图象C 关于直线x ＝1112π对称；②函数f (x )在区间⎝ ⎛⎭⎪⎫－π12，5π12内是增函数； ③由y ＝3sin 2x 的图象向右平移π3个单位长度可以得到图象C .以上三个论断中，正确论断的序号是________．三、解答题11．已知tan α＝2，求下列代数式的值． (1)4sin α－2cos α5cos α＋3sin α； (2)14sin 2α＋13sin αcos α＋12cos 2α.12．已知函数f (x )＝－sin 2x －a sin x ＋b ＋1的最大值为0，最小值为－4，若实数a >0，求a 、b 的值．能力提升13．若0<x <π2，则2x 与πsin x 的大小关系是( )A ．2x >πsin xB ．2x <πsin xC ．2x ＝πsin xD ．与x 的取值有关14．对于函数f (x )＝⎩⎪⎨⎪⎧sin x ，sin x ≥cos x ，cos x ，sin x <cos x .给出下列四个命题：①该函数的图象关于x ＝2k π＋π4(k ∈Z )对称；②当且仅当x ＝k π＋π2(k ∈Z )时，该函数取得最大值1；③该函数是以π为最小正周期的周期函数；④当且仅当2k π＋π<x <2k π＋3π2 (k ∈Z )时，－22≤f (x )<0.其中正确的是________．(填序号)三角函数的性质是本板块复习的重点，在复习时，要充分利用数形结合思想把图象与性质结合起来，即利用图象的直观性得到函数的性质，或由单位圆中三角函数线表示的三角函数值来获得函数的性质，同时也能利用函数的性质来描述函数的图象，这样既有利于掌握函数的图象与性质，又能熟练运用数形结合的思想方法．章末复习课答案作业设计 1．C2．D [cos(π＋x )＝－cos x ＝35，∴cos x ＝－35<0，∵x ∈(π，2π)，∴x ∈(π，32π)，∴sin x ＝－45，∴tan x ＝43.]3．B [M ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝2k ＋14π，k ∈Z ，N ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝k ＋24π，k ∈Z .比较两集合中分式的分子，知前者为奇数π，后者是整数π.再根据整数分类关系，得M N .选B.]4．A [∵y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π3＝sin ⎣⎢⎡⎦⎥⎤π2＋⎝⎛⎭⎪⎫2x ＋π3＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋5π12＝sin ⎝ ⎛⎭⎪⎫2x ＋5π6. 由题意知要得到y ＝sin ⎝⎛⎭⎪⎫2x ＋5π6的图象只需将y ＝sin 2x 向左平移5π12个单位长度．] 5．D [sin 2x >cos 2x ⇔|sin x |>|cos x |.在直角坐标系中作出单位圆及直线y ＝x ，y ＝－x ，根据三角函数线的定义知角x 的终边应落在图中的阴影部分，故应选D.] 6．D [据题意可设y ＝10－8cos ωt (t ≥0)．由已知周期为12 min ，可知t ＝6时到达最高点，即函数取最大值，知18＝10－8cos 6ω，即cos 6ω＝－1.∴6ω＝π，得ω＝π6.∴y＝10－8cos π6t (t ≥0)．]7．－35解析 sin 4α－cos 4α＝sin 2α－cos 2α＝2sin 2α－1＝2×15－1＝－35.8.32解析 由图象可知三角函数的周期为T ＝4×π3＝2πω，∴ω＝32.9.⎣⎢⎡⎦⎥⎤k π，k π＋π2，k ∈Z 解析 f (x )＝|sin x |的周期T ＝π，且f (x )在区间[0，π2]上单调递增，∴f (x )的单调增区间为[k π，k π＋π2]，k ∈Z .10．①②解析 ①f ⎝ ⎛⎭⎪⎫11π12＝3sin ⎝ ⎛⎭⎪⎫116π－π3＝3sin 32π＝－3，∴x ＝1112π为对称轴；②由－π12<x <5π12⇒－π2<2x －π3<π2，由于函数y ＝3sin x 在⎝ ⎛⎭⎪⎫－π2，π2内单调递增，故函数f (x )在⎝ ⎛⎭⎪⎫－π12，5π12内单调递增； ③∵f (x )＝3sin2⎝⎛⎭⎪⎫x －π6，∴由y ＝3sin 2x 的图象向右平移π3个单位长度得到函数f (x )＝3sin2⎝⎛⎭⎪⎫x －π3的图象，得不到图象C .11．解 (1)原式＝4tan α－23tan α＋5＝611.(2)原式＝14sin 2α＋13sin αcos α＋12cos 2αsin 2α＋cos 2α＝14tan 2α＋13tan α＋12tan 2α＋1＝14×4＋13×2＋125＝1330. 12．解 令t ＝sin x ，则g (t )＝－t 2－at ＋b ＋1＝－⎝ ⎛⎭⎪⎫t ＋a 22＋a24＋b ＋1，且t ∈[－1,1]．下面根据对称轴t 0＝－a2与区间[－1,1]的位置关系进行分类讨论．(1)当－a2≤－1，即a ≥2时，⎩⎪⎨⎪⎧y max ＝g －＝a ＋b ＝0，y min ＝g ＝－a ＋b ＝－4.解之得⎩⎪⎨⎪⎧a ＝2，b ＝－2.(2)当－1<－a2<0，即0<a <2时，⎩⎪⎨⎪⎧y max ＝g ⎝ ⎛⎭⎪⎫－a 2＝a 24＋b ＋1＝0，y min ＝g＝－a ＋b ＝－4.解得⎩⎪⎨⎪⎧a ＝2，b ＝－2或⎩⎪⎨⎪⎧a ＝－6，b ＝－10.都不满足a 的范围，舍去． 综上所述，a ＝2，b ＝－2. 13．B[在同一坐标平面内作出函数y ＝2x 与函数y ＝πsin x 的图象，如图所示． 观察图象易知：当x ＝0时，2x ＝πsin x ＝0；当x ＝π2时，2x ＝πsin x ＝π；当x ∈⎝⎛⎭⎪⎫0，π2时，函数y ＝2x 是直线段，而曲线y ＝πsin x 是上凸的．所以2x <πsin x ．故选B.]14．① 解析f (x )＝max{sin x ，cos x }，在同一坐标系中画出y ＝sin x 与y ＝cos x 的图象易知f (x )的图象为实线关于x ＝2k π＋π4(k ∈Z )对称，故①对；线所表示的曲线．由曲＝2k π＋π2(k ∈Z )时，f (x )max ＝1，故②错；当x ＝2k π (k ∈Z )或x 该函数以2π为最小正周期，故③错；观察曲线易知，当2k π＋时，－22≤f (x )<0，反之不成立，故④错． π<x <2k π＋3π2(k ∈Z )。

2018-2019学年高中数学第一章三角函数1.2.1 任意角的三角函数（1）学案新人教A版必修4编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第一章三角函数1.2.1 任意角的三角函数（1）学案新人教A版必修4）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第一章三角函数1.2.1 任意角的三角函数（1）学案新人教A 版必修4的全部内容。

1.2.1 任意角的三角函数(一)学习目标 1.借助单位圆理解任意角的三角函数定义(重点）.2。

掌握正弦、余弦、正切函数在各象限内的符号。

3.通过对任意角的三角函数的定义理解终边相同的角的同一三角函数值相等（难点)．知识点1 三角函数的概念1．任意角的三角函数的定义前提如图，设α是一个任意角,它的终边与单位圆交于点P(x，y)定义正弦y叫做α的正弦，记作sin α，即sin α＝y余弦x叫做α的余弦,记作cos α，即cos α＝x正切错误!叫做α的正切，记作tan α，即tan α＝错误!(x≠0）三角函数正弦、余弦、正切都是以角为自变量，以单位圆上的点的坐标或坐标的比值为函数值的函数，将它们统称为三角函数2三角函数定义域sin αRcos αRtan α{α｜α∈R且α≠kπ＋π2，k∈Z}【预习评价】已知角α的终边经过点(－错误!，－错误!），则sin α＝________，cos α＝________，tan α＝________．解析因为（－错误!）2＋（－错误!)2＝1,所以点(－错误!,－错误!)在单位圆上，由三角函数的定义知sin α＝－错误!，cos α＝－错误!，tan α＝错误!．答案－错误!－错误!错误!知识点2 三角函数值在各象限的符号口诀概括为：一全正、二正弦、三正切、四余弦(如图)．【预习评价】三角函数在各象限的符号由什么决定？提示三角函数值的符号是根据三角函数定义和各象限内坐标符号推导出的．从原点到角的终边上任意一点的距离r总是正值．因此，三角函数在各象限的符号由角α的终边所在象限决定．知识点3 诱导公式一1．语言表示：终边相同的角的同一三角函数的值相等．2．式子表示：错误!【预习评价】计算：sin(2π＋错误!）＝________，cos错误!＝________．解析sin（2π＋错误!）＝sin错误!＝错误!，cos错误!＝cos(6π＋错误!)＝cos错误!＝错误!．答案12错误!考查方向题型一任意角的三角函数的定义及应用方向1 三角函数定义的直接应用【例1-1】在平面直角坐标系中，角α的终边与单位圆交于点A，点A的纵坐标为错误!，求tan α．解由题意，设点A的坐标为（x，错误!），所以x2＋(错误!）2＝1，解得x＝错误!或－错误!．当x＝错误!时，角α在第一象限,tan α＝错误!＝错误!；当x＝－错误!时，角α在第二象限，tan α＝错误!＝－错误!．方向2 含参数的三角函数定义问题【例1—2】已知角α的终边过点P（－3a,4a）(a≠0），求2sin α＋cos α的值．解r＝错误!＝5｜a|，①若a>0,则r＝5a，角α在第二象限．sin α＝yr＝错误!＝错误!，cos α＝错误!＝错误!＝－错误!,所以2sin α＋cos α＝错误!－错误!＝1．②若a<0，则r＝－5a，角α在第四象限，sin α＝错误!＝－错误!,cos α＝错误!＝错误!．所以2sin α＋cos α＝－错误!＋错误!＝－1．方向3 已知三角函数值求参数值【例1-3】已知角α的终边经过点P（5m,12)，且cos α＝－错误!，则m＝________．解析cos α＝－错误!<0,则α的终边在第二或三象限，又点P的纵坐标是正数，所以α是第二象限角，所以m<0，由错误!＝－错误!,解得m＝－1．答案－1规律方法由角α终边上任意一点的坐标求其三角函数值的步骤（1）已知角α的终边在直线上时，常用的解题方法有以下两种：①先利用直线与单位圆相交,求出交点坐标，然后再利用正弦、余弦函数的定义求出相应三角函数值；②在α的终边上任选一点P(x,y），P到原点的距离为r（r〉0)，则sin α＝错误!，cos α＝xr。

1.1.1 任意角(建议用时：45分钟)[学业达标]一、选择题1．已知A ＝{第二象限角}，B ＝{钝角}，C ＝{大于90°的角}，那么A ，B ，C 的关系是( )A ．B ＝A ∩CB ．B ∪C ＝C C ．A CD ．A ＝B ＝C【解析】 钝角大于90°，小于180°，故B ⊆C ，选项B 正确．【答案】 B2．下列是第三象限角的是( )A ．－110°B ．－210°C ．80°D ．－13°【解析】 －110°是第三象限角，－210°是第二象限角，80°是第一象限角，－13°是第四象限角．故选A.【答案】 A3．终边与坐标轴重合的角α的集合是( )A ．{α|α＝k ·360°，k ∈Z }B ．{α|α＝k ·180°＋90°，k ∈Z }C ．{α|α＝k ·180°，k ∈Z }D ．{α|α＝k ·90°，k ∈Z }【解析】 终边在坐标轴上的角为90°或90°的倍数角，所以终边与坐标轴重合的角的集合为{α|α＝k ·90°，k ∈Z }．故选D.【答案】 D4．若α是第一象限角，则下列各角中属于第四象限角的是( )A ．90°－αB ．90°＋αC ．360°－αD ．180°＋α 【解析】 因为α是第一象限角，所以－α为第四象限角，所以360°－α为第四象限角．【答案】 C5．若φ是第二象限角，那么φ2和90°－φ都不是( ) A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角【解析】 ∵φ是第二象限角，∴k ·360°＋90°<φ<k ·360°＋180°，k ∈Z ，∴k ·180°＋45°<φ2<k ·180°＋90°，k ∈Z ， ∴φ2是第一或第三象限角，而－φ是第三象限角， ∴90°－φ是第四象限角，故选B.【答案】 B二、填空题6．在0°～360°范围内，与角－60°的终边在同一条直线上的角为________.【解析】 根据终边相同角定义知，与－60°终边相同角可表示为β＝－60°＋k ·360°(k ∈Z )，当k ＝1时β＝300°与－60°终边相同，终边在其反向延长线上且在0°～360°范围内角为120°.故填120°，300°.【答案】 120°，300°7．自行车大链轮有48齿，小链轮有20齿，当大链轮转过一周时，小链轮转过的角度应该是________(齿轮大小相等)．【解析】 当大链轮转过一周48齿时，小链轮也必须转过48齿，即转过4820＝2.4周，所以小链轮转过的角度应该为360°×2.4＝864°.【答案】 864°三、解答题8．在与530°终边相同的角中，求满足下列条件的角．(1)最大的负角；(2)最小的正角；(3)－720°到－360°的角. 【导学号：70512002】【解】 与530°终边相同的角为k ·360°＋530°，k ∈Z .(1)由－360°＜k ·360°＋530°＜0°且k ∈Z ，可得k ＝－2，故所求的最大负角为－190°.(2)由0°＜k ·360°＋530°＜360°且k ∈Z ，可得k ＝－1，故所求的最小正角为170°.(3)由－720°≤k ·360°＋530°≤－360°且k ∈Z ，可得k ＝－3，故所求的角为－550°.9．若角β的终边落在直线y ＝－33x 上，写出角β的集合；当－360°＜β＜360°时，求角β.【解】∵角β的终边落在直线y＝－33x上，∴在0°到360°范围内的角为150°和330°，∴角β的集合为{x|x＝k·180°＋150°，k∈Z}，当－360°＜β＜360°时，角β为－210°，－30°，150°，330°.[能力提升]1．如图1­1­4，终边落在直线y＝±x上的角α的集合是( )图1­1­4A．{α|α＝k·360°＋45°，k∈Z}B．{α|α＝k·180°＋45°，k∈Z}C．{α|α＝k·180°－45°，k∈Z}D．{α|α＝k·90°＋45°，k∈Z}【解析】终边落在直线y＝±x上，在[0°，360°)内的角有45°，135°，225°和315°共四个角，相邻2角之间均相差90°，故终边落在直线y＝±x上的角的集合为{α|α＝k·90°＋45°，k∈Z}．【答案】 D2．已知，如图1­1­5所示．(1)分别写出终边落在OA，OB位置上的角的集合；图1­1­5(2)写出终边落在阴影部分(包括边界)的角的集合．【解】(1)终边落在OA位置上的角的集合为{α|α＝90°＋45°＋k·360°，k∈Z}＝{α|α＝135°＋k·360°，k∈Z}，终边落在OB位置上的角的集合为{β|β＝－30°＋k·360°，k∈Z}．(2)由题图可知，阴影部分角的集合是由所有介于[－30°，135°]之间的所有与之终边相同的角组成的集合，故该区域可表示为{α|－30°＋k·360°≤α≤135°＋k·360°，k∈Z}．。