01.3梁板结构——1.3、整体式双向板梁板结构(课件)
- 格式:docx
- 大小:501.08 KB
- 文档页数:15





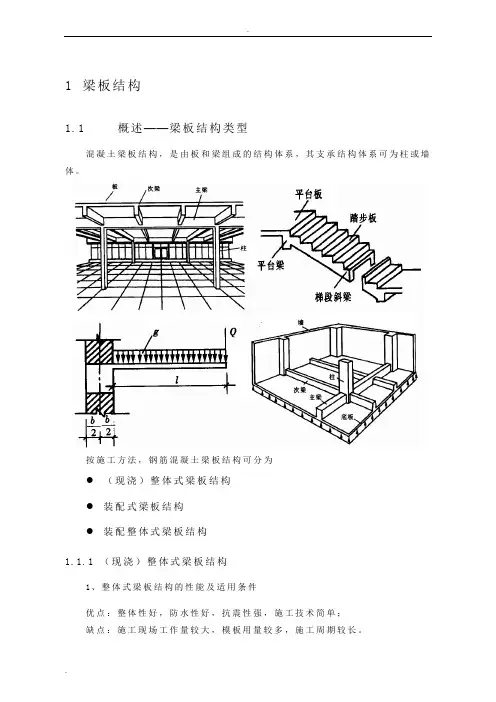
.1 梁板结构1.1 概述——梁板结构类型混凝土梁板结构,是由板和梁组成的结构体系,其支承结构体系可为柱或墙体。
按施工方法,钢筋混凝土梁板结构可分为● (现浇)整体式梁板结构 ● 装配式梁板结构 ● 装配整体式梁板结构 1.1.1 (现浇)整体式梁板结构1、整体式梁板结构的性能及适用条件优点:整体性好,防水性好,抗震性强,施工技术简单; 缺点:施工现场工作量较大,模板用量较多,施工周期较长。
一般适用于下列情况:●楼面荷载较大、平面形状复杂或布置上有特殊要求的建筑物;●对防渗、防漏或抗震要求较高的建筑物;●有震动荷载的楼面;●高层建筑2、整体式梁板结构的结构分类及应用按结构组成,整体式梁板结构可分为:●梁板结构(或肋梁楼盖):有板有梁,图1.1.1。
●板柱结构(或无梁楼盖):有板无梁,图1.1.2。
按楼板的传力方式和支撑条件,整体式梁板结构分为●单向板梁板结构(单向板肋梁楼盖)2.● 双向板梁板结构(双向板肋梁楼盖)● 密肋梁板结构(密肋楼盖)● 井式梁板结构(井式楼盖)4无梁楼盖3、整体式梁板结构的板与梁整体式梁板结构中的板,通常为承受均布荷载的四边支承矩形板(大板中的一个单元),短边的长度为1l ,长边的长度为2l ,计算简图见图1.1.3。
.在板的中央部位,取出两个单位宽度的正交板带,将作用在板上的均布荷载q ,分解到正交板带上,分别为1q 和2q 。
两个方向的板带所承受的分配荷载1q 和2q ,与各个方向板带长度的对应关系挠度:41111q l v EI a =、42222q l v EIa =荷载分配:4221441122l q q l l a a a =+、4112441122l q q l l a a a =+ 4421111222q l l q l l a a 骣骣骣鼢?珑?鼢?=?珑?鼢?珑?鼢?桫桫桫其中,125384a a ==(板带支承条件和板厚相同) 上述公式表明,两个方向板带所分配的荷载1q 、2q ,仅与板带的跨度比12l l 骣÷ç÷ç÷ç÷桫有关,或者,仅与其线刚度比21i i 骣÷ç÷ç÷ç÷桫相关(11EI i l =,22EI i l =)。




---------------------------------------------------------------最新资料推荐------------------------------------------------------01.3梁板结构——1.3、整体式双向板梁板结构(课件)1.3 整体式双向板梁板结构由两个方向板带共同承受荷载,在纵横两个方向上发生弯曲且都不能忽略的四边支承板,称为双向板。
双向板的支承形式:四边支承、三边支承、两边支承或四点支承。
双向板的平面形状:正方形、矩形、圆形、三角形或其他形状。
双向板梁板结构。
又称为双向板肋形楼盖。
图 1.3.1。
双重井式楼盖或井式楼盖。
我国《混凝土结构设计规范》(GB50010-2019)规定:对于四边支承的板,当长边与短边长度之比小于或等于 2 时,应按双向板计算;当长边与短边长度之比大于 2,但小于 3 时,宜按双向板计算;若按沿短边方向受力的单向板计算时,应沿长边方向布置足够数量的构造钢筋;当长边与短边长度之比大于或等于 3 时,可按沿短边方向受力的单向板计算。
1.3.1 双向板的受力特点 1、四边支承双向板弹性工作阶段的受力特点整体式双向梁板结构中的四边支承板,在荷载作用下,板的荷载由短边和长边两个方向板带共同承受,各1 / 14个板带分配的荷载,与长跨和短跨的跨度比值( )02 01l l 相关。
当跨度比值 ( )02 01l l 接近时,两个方向板带的弯矩值较为接近。
随着 ( )02 01l l 的增大,短向板带弯矩值逐渐增大,最大正弯矩出现在中点;长向板带弯矩值逐渐减小。
而且,最大弯矩值不发生在跨中截面,而是偏离跨中截面,图 1.3.2。
这是因为,短向板带对长向板带具有一定的支承作用。
2、四边支承双向板的主要试验结果位移与变形双向板在荷载作用下,板的竖向位移呈碟形,板的四角处有向上翘起的趋势。
裂缝与破坏对于均布荷载作用下的正方形平面四边简支双向板:在裂缝出现之前,基本处于弹性工作阶段;随着荷载的增加,由于两个方向配筋相同(正方形板),第一批裂缝出现在板底中央部位,该裂缝沿对角线方向向板的四角扩展,直至因板底部钢筋屈服而破坏。

1.3 整体式双向板梁板结构由两个方向板带共同承受荷载,在纵横两个方向上发生弯曲且都不能忽略的四边支承板,称为双向板。
双向板的支承形式:四边支承、三边支承、两边支承或四点支承。
双向板的平面形状:正方形、矩形、圆形、三角形或其他形状。
双向板梁板结构。
又称为双向板肋形楼盖。
图1.3.1® 1X1整棒式取阿极卑扳结构布冒双重井式楼盖或井式楼盖。
我国《混凝土结构设计规范》(GB50010-2002 )规定:对于四边支承的板,当长边与短边长度之比小于或等于2时,应按双向板计算;当长边与短边长度之比大于2,但小于3时,宜按双向板计算;若按沿短边方向受力的单向板计算时,应沿长边方向布置足够数量的构造钢筋;当长边与短边长度之比大于或等于3时,可按沿短边方向受力的单向板计算。
1.3.1 双向板的受力特点1、四边支承双向板弹性工作阶段的受力特点■vj-i-tF* ■■■■■■E«4・・------- F 八i I O- .-i 王十王P_VT&■■■■■€整体式双向梁板结构中的四边支承板,在何载作用下,板的何载由短边和长边两个方向板带共同承受,各个板带分配的荷载,与长跨和短跨的跨度比值(l02 1 01 )相关。
当跨度比值(|02101)接近时,两个方向板带的弯矩值较为接近。
随着(102101)的增大,短向板带弯矩值逐渐增大,最大正弯矩出现在中点;长向板带弯矩值逐渐减小。
而且,最大弯矩值不发生在跨中截面,而是偏离跨中截面,图1.3.2。
这是因为,短向板带对长向板带具有一定的支承作用。
2、四边支承双向板的主要试验结果位移与变形艸边简支取向叛在均布荷裁阵月节申央处轨带航弯矩分布双向板在荷载作用下,板的竖向位移呈碟形,板的四角处有向上翘起的趋势。
裂缝与破坏对于均布荷载作用下的正方形平面四边简支双向板:在裂缝出现之前,基本处于弹性工作阶段;随着荷载的增加,由于两个方向配筋相同(正方形板),第一批裂缝出现在板底中央部位,该裂缝沿对角线方向向板的四角扩展,直至因板底部钢筋屈服而破坏。
当接近破坏时,板顶面靠近四角附近,出现垂直于对角线方向、大体呈圆弧形的环状裂缝。
这些裂缝的出现,又促进了板底对角线方向裂缝的发展。
图1.3.3a。
对于均布荷载作用下的矩形平面四边简支双向板:在裂缝出现之前,也基本处于弹性工作阶段;随着荷载的增加,第一批裂缝出现在板底中央部位,且平行于板的长边方向,该裂缝向板角处延伸,与板边大体呈45°角,在接近破坏时,板四角处顶面也出现圆弧形裂缝,最终由于跨中及45。
角方向裂缝处截面的受拉钢筋达到屈服,混凝土达到抗压强度而导致双向板破坏,图1.3.3b。
® 1- 3, 3啊筋覘矗土双向慑的徙坏裂菱塑性铰线双向板裂缝处截面的钢筋,从开始屈服到截面即将破坏这个阶段,截面处于第川工作阶段,与前面所讨论的塑性铰的概念相同,此处因钢筋达到屈服所形成的临界裂缝,称为塑性铰线。
塑性铰线的出现,使结构被裂缝分割的若干板块,称为几何可变体系,结构达到承载力极限状态。
&双向板的内力分析方法有两种理论:按弹性理论的分析方法求解板的内力与变形,并配筋; 按塑性理论的分析方法求解板的内力与变形,并配筋。
1.3.2双向板按弹性理论的分析方法1、单区格双向板的内力及变形计算当板厚远小于板短边,且板的挠度远小于板的厚度时,双向板可按弹性薄板 理论计算。
均布荷载作用下的单区格双向矩形板的边界条件,有六种不同的情况,计算 简图见图1.3.4。
不同情况下,单区格双向矩形板的内力及变形计算结果(弯矩和挠度系数), 见附录8。
表中列出了双向板,计算时,只需要根据实际支承情况和短跨与长跨 的比值,直接查出弯矩系数和挠度系数,即可计算得到各种单区格双向矩形板最 大弯矩值和最大挠度值,即m=表中系数?(g q )l 0x u=表中系数?(g+认 B c其中符号见P50。
需要说明的是,附录8中的表中系数,是根据材料的泊松比m= 0制定的,当 ml 0时,如,混凝土, m= 0.2,尚应考虑双向弯曲对两个方向板带弯矩值的相 互影响,可按下式计算= m x + mm ym y m = m y + mri x其中符号见P50 。
对于支座截面弯矩值,由于另外一个方向板带的弯矩等于零,所以,不存在 两个方向板带弯矩的相互影响问题。
T® 1 3.4职向板的计算衢圈◎2、多区格等跨连续双向板的内力及变形计算计算假定:采用单区格双向矩形板的内力及变形计算为基础的实用计算方法,将多区格等跨连续双向板的内力分析问题,转化为单区格双向矩形板的内力计算问题。
该方法假定:双向板支承梁的受弯线刚度很大,其竖向位移可忽略不计;双向板支承梁的受扭线刚度很小,可以自由转动;双向板沿同一方向相邻跨度的相对差值,小于20%。
在上述假定条件下,支承梁可看作为双向板的不动铰支座,从而使内力计算得到简化,并且计算误差大为降低。
结构控制截面的确定:取各支座截面和跨内截面作为结构的控制截面;结构控制截面产生最危险内力的最不利荷载组合:根据结构的弹性变形曲线确定活荷载的最不利布置方式。
(1)、多区格板跨内截面最大正弯矩计算最不利活荷载布置:按棋盘式布置,图135a。
活荷载的棋盘式布置,可以使所有活荷载布置区格板内的跨内双向正弯矩达到最大值。
计算多区格等跨连续双向板跨内截面最大正弯矩时,采用近似内力分析方法:将棋盘式布置的活荷载分解为:各区格板满布的对称活荷载q和区2格板棋盘式布置的反对称活荷载土q,图1.3.5b、c。
2■b'于是,对于恒荷载和活荷载共同作用的多区格等跨连续双向板上,有对称荷载g殊口反对称荷载q 《即,对称荷载反对称荷载q 0=?q2多区格等跨连续双向板在对称荷载g色g+q作用下,2四边支承条件:中间区格板所有中间支座均可视为固定支座;中间区格板均可视为四边固定的单区格双向板;角区格板可视为两邻边为简支,另外两边为固定支座的单区格双向板;边区格板可视为三边固定、一边简支的单区格双向板,图1.3.4。
计算方法:根据各单区格板的四边支承条件,分别求出多区格等跨连续双向板中的各区格板,在对称荷载g^= g + q作用下的跨内截面正弯矩。
2多区格等跨连续双向板在反对称荷载q 作用下,2四边支承条件:中间区格板所有中间支座均可视为铰支座;中间区格板均可视为四边简支的单区格双向板;边区格板和角区格板均可视为四边简支的单区格双向板,如1.3.4。
计算方法:根据各单区格板的四边支承条件,分别求出多区格等跨连续双向板中的各区格板,在反对称荷载q 0= ? q作用下的跨内截面正弯矩。
2同理,可求多区格板跨内截面最大负弯矩。
最后,将各区格板在上述两种荷载作用下,求得的板跨内截面正、负弯矩值(绝对值)加以叠加,即可得到各区格板的跨内截面最大正、负弯矩值。
(2)、各区格板支座截面最大负弯矩计算支座最大负弯矩可近似按满布活荷载时求得,这时,中间区格板所有中间支座均可视为固定支座,边区格板和角区格板的外边界支承条件, 按实际情况确定。
根据各区格板的四边支承条件,可分别求出各区格板在满布荷载g+q作用下,支座截面的最大负弯矩值(绝对值)。
但对于某些相邻区格板,当单区格板跨度或边界条件不同时,两区格板之间的支座截面最大负弯矩值(绝对值),可能不相同,一般可取其平均值,作为该支座截面的负弯矩设计值。
1.3.3 双向板按塑性理论的分析方法——极限平衡法(塑性铰线法)1、极限平衡法(塑性铰线法)塑性铰与塑性铰线(1)、基本假定结构达到承载力极限状态时,在最大弯矩处形成塑性铰线,将整体双向板分割成若干板块,成为几何可变体系。
双向板中的塑性铰线是直线。
塑性铰线的位置与板的形状、尺寸、边界条件、荷载形式、配筋位置及数量有关。
一般将裂缝出现在板底的称为正塑性铰线,它发生在板底的正弯矩处,通过相邻板块转动轴的交点。
图1.3.6 ;裂缝出现在板面的称为负塑性铰线, 它发生在板上部的固定边界的负弯矩处。
将塑性铰线所分割的各个板块视为平面刚体,所有的变形都集中在塑性铰线上,当结构达到承载力极限状态时,各板块均可绕塑性铰线转动。
双向板的破坏机构形式可能不止一个,在所有可能的破坏机构形式中,必定有一个是最危险的,其极限荷载值最小。
塑性铰线是由钢筋屈服而产生的,沿塑性铰线上的弯矩为常数,它等于相应配筋板的极限弯矩值,板在正塑性铰线处的扭矩和剪力很小,可忽略不计。
(2)、极限平衡法的基本方程以均布荷载作用下的四边为固定支座(或连续)的双向板为例。
双向板在极限荷载p的作用下,在正常配筋条件下,塑性铰线将双向板分害V 为四个板块,斜向的正塑性铰线与板边的夹角大约成45°角,图1.3.7。
根据上述假设,每个板块均应满足力的平衡条件和力矩平衡条件,由此可得到极限平衡法的基本方程,并求得板的极限荷载p。
凶⑷ <0 <0图1-1.6板块的壘性校线图1.3.7四边囲定口廊粧班限平茹埜的汁算模丈一止境性代就.....假设:板跨内承受正弯矩的钢筋,沿l °x 、l 0y 方向塑性铰线上单位板宽内的 极限弯矩,分别为:m x 、m y ;板支座上承受负弯矩的钢筋,沿l ox 、l oy 方向塑性铰线上单位板宽内 的极限弯矩,分别为:m x©mxii、m yQ m yii ;于是:板跨内塑性铰线上沿l ox 、l oy 方向的总极限正弯矩,分别为:Mx 二l oy m x 、M y = l ox m y ;板支座塑性铰线上沿l ox 、l oy 方向的总极限负弯矩,分别为:M xi = l oy m x 、M x x = l oy m x xM y x l ox m y 、M y X l ox m yii 。
取梯形板块ABFE (即,板块①)为脱离体,其受力状态如图 在该板块上的所有力对板支座塑性铰线AB 取力矩,即,? M ABM x +M x ® pl 0x 箱同理,对板块CDEF (即,板块②),可得又取三角形板块ADE (即,板块③)为脱离体,其受力状态如图1.3.7c ,将 作用在该板块上的所有力对板支座塑性铰线AD 取力矩,即,? MAD= 0,可得,l l 3 l0x l0x —=P —2 24l3M y +M yd P JM y + M yi =1.3.7b ,将作用=o ,可得,l oy m x + l oy m x ©= p (l oy -l ox )知 7 24 l 0x2l 0xM x +M严 P l ox 材 12二ox同理,对板块BCD (即,板块④) ,可得将以上四个公式相叠加,即可得到四边固定支承的双向板,在均布荷载作用 下,按极限平衡法计算的基本方程,即2M x + 2M y + M xi + M x # M y + M yi =皿(3l °y - l °x )12 \ /当四边为简支时,M x @ M x i M y0 M yii 等于零,于是,埶yd )这个公式就是四边简支双向板按极限平衡法计算的基本方程,它表明双向板塑性铰线上截面总极限弯矩与极限荷载p 之间的关系。