统计建模与R软件第六章习题

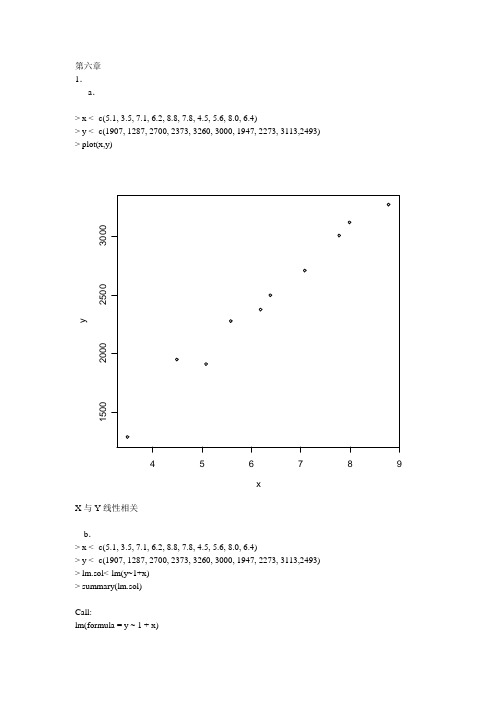
第六章 1． a ．> x <- c(5.1, 3.5, 7.1, 6.2, 8.8, 7.8, 4.5, 5.6, 8.0, 6.4)> y <- c(1907, 1287, 2700, 2373, 3260, 3000, 1947, 2273, 3113,2493) > plot(x,y)456789150020002500300xyX 与Y 线性相关b ．> x <- c(5.1, 3.5, 7.1, 6.2, 8.8, 7.8, 4.5, 5.6, 8.0, 6.4)> y <- c(1907, 1287, 2700, 2373, 3260, 3000, 1947, 2273, 3113,2493) > lm.sol<-lm(y~1+x) > summary(lm.sol) Call:lm(formula = y ~ 1 + x)Residuals:Min 1Q Median 3Q Max-128.591 -70.978 -3.727 49.263 167.228Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 140.95 125.11 1.127 0.293x 364.18 19.26 18.908 6.33e-08 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 96.42 on 8 degrees of freedomMultiple R-Squared: 0.9781, Adjusted R-squared: 0.9754F-statistic: 357.5 on 1 and 8 DF, p-value: 6.33e-08回归方程为Y=140.95+364.18X，极为显著d．> new <- data.frame(x=7)> lm.pred <- predict(lm.sol,new,interval="prediction",level=0.95)> lm.predfit lwr upr[1,] 2690.227 2454.971 2925.484Y(7)= 2690.227, [2454.971,2925.484]2．> out<-data.frame(+ x1 <- c(0.4,0.4,3.1,0.6,4.7,1.7,9.4,10.1,11.6,12.6,10.9,23.1,23.1,21.6,23.1,1.9,26.8,29.9), + x2 <- c(52,34,19,34,24,65,44,31,29,58,37,46,50,44,56,36,58,51),+ x3 <- c(158,163,37,157,59,123,46,117,173,112,111,114,134,73,168,143,202,124),+ y <- c(64,60,71,61,54,77,81,93,93,51,76,96,77,93,95,54,168,99)+ )> lm.sol<-lm(y~x1+x2+x3,data=out)> summary(lm.sol)Call:lm(formula = y ~ x1 + x2 + x3, data = out)Residuals:Min 1Q Median 3Q Max-27.575 -11.160 -2.799 11.574 48.808Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 44.9290 18.3408 2.450 0.02806 *x1 1.8033 0.5290 3.409 0.00424 **x2 -0.1337 0.4440 -0.301 0.76771x3 0.1668 0.1141 1.462 0.16573---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 19.93 on 14 degrees of freedomMultiple R-Squared: 0.551, Adjusted R-squared: 0.4547F-statistic: 5.726 on 3 and 14 DF, p-value: 0.009004回归方程为y=44.9290+1.8033x1-0.1337x2+0.1668x3由计算结果可以得到，回归系数与回归方程的检验都是显著的3．a．> x<-c(1,1,1,1,2,2,2,3,3,3,4,4,4,5,6,6,6,7,7,7,8,8,8,9,11,12,12,12)> y<-c(0.6,1.6,0.5,1.2,2.0,1.3,2.5,2.2,2.4,1.2,3.5,4.1,5.1,5.7,3.4,9.7,8.6,4.0,5.5,10.5,17.5,13.4,4.5, + 30.4,12.4,13.4,26.2,7.4)> lm.sol <- lm(y ~ 1+x)> summary(lm.sol)Call:lm(formula = y ~ 1 + x)Residuals:Min 1Q Median 3Q Max-9.84130 -2.33691 -0.02137 1.05921 17.83201Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) -1.4519 1.8353 -0.791 0.436x 1.5578 0.2807 5.549 7.93e-06 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 5.168 on 26 degrees of freedomMultiple R-Squared: 0.5422, Adjusted R-squared: 0.5246F-statistic: 30.8 on 1 and 26 DF, p-value: 7.931e-06线性回归方程为y=-1.4519+1.5578x，并且未通过t检验和F检验> plot(x,y)> abline(-1.4519,1.5578)>246810120510********xyc ．> x<-c(1,1,1,1,2,2,2,3,3,3,4,4,4,5,6,6,6,7,7,7,8,8,8,9,11,12,12,12)> y<-c(0.6,1.6,0.5,1.2,2.0,1.3,2.5,2.2,2.4,1.2,3.5,4.1,5.1,5.7,3.4,9.7,8.6,4.0,5.5,10.5,17.5,13.4,4.5, + 30.4,12.4,13.4,26.2,7.4)> y.res<-resid(lm.sol);y.fit<-predict(lm.sol) > plot(y.res~y.fit)> y.rst<-rstandard(lm.sol) > plot(y.rst~y.fit) >普通残差051015-10-5051015y.fity .r e s标准化残差051015-2-10123y.fity .r s td ． （4）> lm.new<-update(lm.data3,sqrt(.)~.);coef(lm.new) (Intercept) x 0.7665018 0.29136202x 0.084890650.4466549x 0.58752220.2913620x0.7665018 ++=+=∧∧y y> plot(x,y)> lines(x,y=0.5875222+0.08489065*x^2+0.4466549*x) > y.res<-resid(lm.new);y.fit<-predict(lm.new) > plot(y.res~y.fit)> y.rst<-rstandard(lm.new)> plot(y.rst~y.fit)4．> lm.sol<-lm(Y~X1+X2,data=toothpaste)> summary(lm.sol)Call:lm(formula = Y ~ X1 + X2, data = toothpaste)Residuals:Min 1Q Median 3Q Max-0.497785 -0.120312 -0.008672 0.110844 0.581059Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 4.4075 0.7223 6.102 1.62e-06 ***X1 1.5883 0.2994 5.304 1.35e-05 ***X2 0.5635 0.1191 4.733 6.25e-05 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.2383 on 27 degrees of freedomMultiple R-squared: 0.886, Adjusted R-squared: 0.8776F-statistic: 105 on 2 and 27 DF, p-value: 1.845e-13> source("Reg_Diag.R");Reg_Diag(lm.sol)residual s1 standard s2 student s3 hat_matrix s4 DFFITS1 -0.047231639 -0.21248023 -0.20868284 0.13012303 -0.080711402 -0.098070223 -0.42151698 -0.41500522 0.04704358 -0.092207713 0.074288624 0.33492116 0.32934525 0.13385955 0.129473814 -0.006645926 -0.03003380 -0.02947287 0.13797634 -0.011791395 0.581059204 * 2.55701395 * 2.88236603 * 0.09091719 0.911528866 -0.107785364 -0.46031439 -0.45349258 0.03475104 -0.086046747 0.300758350 1.31532456 1.33418993 0.07955382 0.392237398 0.424810360 2.05723960 * 2.19842345 * 0.24932956 * 1.266991129 -0.027532493 -0.12804079 -0.12568545 0.18600211 -0.0600803310 -0.026629932 -0.11546376 -0.11333335 0.06356511 -0.0295276111 -0.497785364 -2.12587089 * -2.28622467 * 0.03475104 -0.4337935912 0.061913782 0.26540305 0.26078220 0.04194215 0.0545641513 0.112816344 0.48968055 0.48267493 0.06556908 0.1278588114 -0.150249714 -0.65395500 -0.64687388 0.07069034 -0.1784101015 0.104927089 0.45112292 0.44436784 0.04761107 0.0993549316 0.154341375 0.66319490 0.65616401 0.04652075 0.1449372917 0.057639541 0.25360011 0.24915642 0.09056633 0.0786266818 -0.146012230 -0.64156026 -0.63442169 0.08813106 -0.1972315219 -0.124487198 -0.53776150 -0.53055795 0.05659354 -0.1299471720 -0.040713930 -0.18584177 -0.18248454 0.15505538 -0.0781727521 -0.199843357 -0.88485598 -0.88118586 0.10202733 -0.2970258322 -0.359558498 -1.59386063 -1.64328265 0.10408399 -0.5601064823 -0.387785364 -1.65609855 -1.71455446 0.03475104 -0.3253235524 -0.010697936 -0.04979066 -0.04886215 0.18729463 -0.0234568025 -0.283315771 -1.25181018 -1.26568782 0.09823492 -0.4177465226 0.017855655 0.08230563 0.08077720 0.17144488 0.0367443327 0.279286070 1.27482211 1.29043074 0.15505538 0.5527948628 0.022483501 0.09864705 0.09682047 0.08548985 0.0296026229 0.174895100 0.76513625 0.75910825 0.08017207 0.2241103830 0.147269942 0.66281470 0.65578162 0.13089383 0.25449685s5 cooks_distance s6 COVRATIO s71 2.251190e-03 1.28095242 2.923723e-03 1.15211573 5.778631e-03 1.27690564 4.812656e-05 1.29899825 * 2.179654e-01 0.5361673 *6 2.542824e-03 1.13309647 4.984335e-02 0.99745488 * 4.685683e-01 * 0.89452379 1.248734e-03 1.373272210 3.016556e-04 1.194126111 5.423517e-02 0.669681912 1.027897e-03 1.159781213 5.608624e-03 1.166813514 1.084362e-02 1.148706415 3.391268e-03 1.149474316 7.153137e-03 1.118050417 2.134879e-03 1.222624518 1.326021e-02 1.172800619 5.782640e-03 1.149323820 2.112633e-03 1.320308321 2.965359e-02 1.141740222 9.837757e-02 0.929311223 3.291392e-02 0.841337024 1.904437e-04 1.377585325 5.690208e-02 1.037953426 4.672410e-04 1.350588127 9.941147e-02 1.100173228 3.032306e-04 1.223243929 1.700877e-02 1.139997330 2.205512e-02 1.2266609> toothpaste<-data.frame(+ X1=c(-0.05, 0.25,0.60,0,0.20, 0.15,-0.15, 0.15,+ 0.10,0.40,0.45,0.35,0.30, 0.50,0.50, 0.40,-0.05,+ -0.05,-0.10,0.20,0.10,0.50,0.60,-0.05,0, 0.05, 0.55), + X2=c( 5.50,6.75,7.25,5.50,6.50,6.75,5.25,6.00,+ 6.25,7.00,6.90,6.80,6.80,7.10,7.00,6.80,6.50,+ 6.25,6.00,6.50,7.00,6.80,6.80,6.50,5.75,5.80,6.80), + Y =c( 7.38,8.51,9.52,7.50,8.28,8.75,7.10,8.00,+ 8.15,9.10,8.86,8.90,8.87,9.26,9.00,8.75,7.95,+ 7.65,7.27,8.00,8.50,8.75,9.21,8.27,7.67,7.93,9.26) + )>> lm.sol<-lm(Y~X1+X2,data=toothpaste)> summary(lm.sol)Call:lm(formula = Y ~ X1 + X2, data = toothpaste)Residuals:Min 1Q Median 3Q Max-0.37130 -0.10114 0.03066 0.10016 0.30162Coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) 4.0759 0.6267 6.504 1.00e-06 ***X1 1.5276 0.2354 6.489 1.04e-06 ***X2 0.6138 0.1027 5.974 3.63e-06 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.1767 on 24 degrees of freedom Multiple R-squared: 0.9378, Adjusted R-squared: 0.9327F-statistic: 181 on 2 and 24 DF, p-value: 3.33e-155．XX<-cor(cement[1:4])kappa(XX,exact=TRUE)[1] 1376.881> eigen(XX)$values[1] 2.235704035 1.576066070 0.186606149 0.001623746$vectors[,1] [,2] [,3] [,4][1,] -0.4759552 0.5089794 0.6755002 0.2410522[2,] -0.5638702 -0.4139315 -0.3144204 0.6417561[3,] 0.3940665 -0.6049691 0.6376911 0.2684661[4,] 0.5479312 0.4512351 -0.1954210 0.6767340删去了X3,X4> cement<-data.frame(+ X1=c( 7, 1, 11, 11, 7, 11, 3, 1, 2, 21, 1, 11, 10),+ X2=c(26, 29, 56, 31, 52, 55, 71, 31, 54, 47, 40, 66, 68),+ Y =c(78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5, + 93.1,115.9, 83.8, 113.3, 109.4)+ )> XX<-cor(cement[1:2])> kappa(XX,exact=TRUE)[1] 1.592620复共线性消失了。

r软件课后答案【篇一：统计建模与r软件课后答案】> x-c(1,2,3);y-c(4,5,6)e-c(1,1,1)z-2*x+y+e;z[1] 7 10 13z1-crossprod(x,y);z1[,1][1,]32z2-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 81012[3,]1215182.2(1) a-matrix(1:20,ow=4);b-matrix(1:20,ow=4,byrow=t) c-a+b;c(2) d-a%*%b;d(3) e-a*b;e(4) f-a[1:3,1:3](5) g-b[,-3]x-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4h-matrix(ow=5,ncol=5)for (i in 1:5)+ for(j in 1:5)+ h[i,j]-1/(i+j-1)（1） det(h)（2） solve(h)（3） eigen(h)2.5studentdata-data.frame(姓名=c(张三,李四,王五,赵六,丁一) + ,性别=c(女,男,女,男,女),年龄=c(14,15,16,14,15),+ 身高=c(156,165,157,162,159),体重=c(42,49,41.5,52,45.5))2.6write.table(studentdata,file=student.txt)write.csv(studentdata,file=student.csv)2.7count-function(n){if (n=0)print(要求输入一个正整数)repeat{if (n%%2==0)n-n/2elsen-(3*n+1)if(n==1)break}print(运算成功)}}第三章3.1首先将数据录入为x。

利用data_outline函数。

如下 data_outline(x)3.2hist(x,freq=f)lines(density(x),col=red)y-min(x):max(x)lines(y,dnorm(y,73.668,3.9389),col=blue)plot(ecdf(x),verticals=t,do.p=f)lines(y,pnorm(y,73.668,3.9389))qqnorm(x)qqline(x)3.3stem(x)boxplot(x)fivenum(x)3.4shapiro.test(x)ks.test(x,pnorm,73.668,3.9389)one-sample kolmogorov-smirnov testdata: xd = 0.073, p-value = 0.6611alternative hypothesis: two-sidedwarning message:in ks.test(x, pnorm, 73.668, 3.9389) :ties should not be present for the kolmogorov-smirnov test这里出现警告信息是因为ks检验要求样本数据是连续的，不允许出现重复值3.5x1-c(2,4,3,2,4,7,7,2,2,5,4);x2-c(5,6,8,5,10,7,12,12,6,6);x3-c(7,11,6,6,7,9,5,5,10,6,3,10)boxplot(x1,x2,x3,names=c(x1,x2,x3),vcol=c(2,3,4))windows()plot(factor(c(rep(1,length(x1)),rep(2,length(x2)),rep(3,length(x3) ))),c(x1,x2,x3))3.6rubber-data.frame(x1=c(65,70,70,69,66,67,68,72,66,68),+x2=c(45,45,48,46,50,46,47,43,47,48),x3=c(27.6,30.7,31.8,32.6,31 .0,31.3,37.0,33.6,33.1,34.2))plot(rubber)【篇二：r软件课后习题第五章】> ####写出求正态总体均值检验的r程序（程序名：mean.test1.r） mean.test1-function(x, mu=0, sigma=-1, side=0){source(p_value.r)n-length(x); xb-mean(x)if (sigma0){z-(xb-mu)/(sigma/sqrt(n))p-p_value(pnorm, z, side=side)data.frame(mean=xb, df=n, z=z, p_value=p)}else{t-(xb-mu)/(sd(x)/sqrt(n))p-p_value(pt, t, paramet=n-1, side=side)data.frame(mean=xb, df=n-1, t=t, p_value=p)}}####写出求p值的r程序（程序名：p_value.r）p_value-function(cdf, x, paramet=numeric(0), side=0){n-length(paramet)p-switch(n+1,cdf(x),cdf(x, paramet),cdf(x, paramet[1], paramet[2]),cdf(x, paramet[1], paramet[2], paramet[3]))if (side0) pelse if (side0) 1-pelseif (p1/2) 2*pelse 2*(1-p)}####输入数据，再调用函数mean.test1()x-c(220,188,162,230,145,160,238,188,247,113,126,245,164,231,256 ,183,190,158,224,175) source(mean.test1.r)a-mean.test1(x, mu=225,side=0)a得到：mean dft p_value1 192.15 19 -3.478262 0.002516436可知，p值小于0.05,故与正常值存在差异5.2####输入数据，再调用函数mean.test1()x-c(1067,919,1196,785,1126,936,918,1156,920,948)source(mean.test1.r)mean.test1(x, mu=1000,side=1)得到：mean df tp_value1 997.1 9 -0.06971322 0.5270268所以灯泡寿命为1000小时以上的概率是0.47297325.3####写出两总体均值检验的r程序（程序名：mean.test2.r）mean.test2-function(x, y,sigma=c(-1, -1), var.equal=false, side=0){source(p_value.r)n1-length(x); n2-length(y)xb-mean(x); yb-mean(y)if (all(sigma0)){z-(xb-yb)/sqrt(sigma[1]^2/n1+sigma[2]^2/n2)p-p_value(pnorm, z, side=side)data.frame(mean=xb-yb, df=n1+n2, z=z, p_value=p)}else{if (var.equal == true){sw-sqrt(((n1-1)*var(x)+(n2-1)*var(y))/(n1+n2-2))t-(xb-yb)/(sw*sqrt(1/n1+1/n2))nu-n1+n2-2}else{s1-var(x); s2-var(y)nu-(s1/n1+s2/n2)^2/(s1^2/n1^2/(n1-1)+s2^2/n2^2/(n2-1)) t-(xb-yb)/sqrt(s1/n1+s2/n2)}p-p_value(pt, t, paramet=nu, side=side)data.frame(mean=xb-yb, df=nu, t=t, p_value=p)}}####输入数据，再调用函数mean.test2()x-c(113,120,138,120,100,118,138,123)y-c(138,116,125,136,110,132,130,110)source(mean.test2.r)mean.test2(x, y, var.equal=true, side=0)得到：mean df tp_value1 -3.375 14 -0.5659672 0.5803752p值大于0.05,故接受原假设5.4####写出均值已知和均值未知两种情况方差比检验的r程序（程序名：var.test2.r）var.test2-function(x, y,mu=c(inf,inf),side=0){source(p_value.r)n1-length(x); n2-length(y)if (all(all(muinf)){sx2-sum((x-mu[1])^2)/n1;sy2-sum((y-mu[2])^2)/n2df1=n1;df2=n2}else{sx2-var(x); sy2-var(y);df1=n1-1;df2=n2-1}r-sx2/sy2p-p_value(pf, r, paramet=c(df1,df2), side=side)data.frame(rate=r, df1=df1, df2=df2,f=f, p_value=p)}}####输入数据x-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00,0.40,4.50,4.60,2.50,6.00,-1.40)a-shapiro.test(x)ashapiro-wilk normality testdata: xw = 0.9699, p-value = 0.75270.05y-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3.10,1.70,-2.00)b-shapiro.test(y)bshapiro-wilk normality testdata: yw = 0.971, p-value = 0.77540.05由以上可知，两组数据均为正态分布####输入数据，再调用函数mean.test2()x-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00,0.40,4.50,4.60,2.50,6.00,-1.40)y-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3.10,1.70,-2.00)source(mean.test2.r)a-mean.test2(x, y, var.equal=true, side=0);amean dftp_value1 -0.56 38 -0.641872 0.5248097b-mean.test2(x, y, var.equal=false, side=0);bmean dft p_value1 -0.56 36.08632 -0.641872 0.525013c-t.test(x-y, alternative = two.sided);cone sample t-testdata: x - yt = -0.6464, df = 19, p-value = 0.5257alternative hypothesis: true mean is not equal to 095 percent confidence interval:-2.373146 1.253146sample estimates:mean of x-0.56以上p值均大于0.05，故均值无差异。

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13> z1<-crossprod(x,y);z1[,1][1,] 32> z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1)> A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) > C<-A+B;C(2)> D<-A%*%B;D(3)> E<-A*B;E(4)> F<-A[1:3,1:3](5)> G<-B[,-3]> x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4> H<-matrix(nrow=5,ncol=5)> for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)（1）> det(H)（2）> solve(H)（3）> eigen(H)2.5> studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一')+ ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6> write.table(studentdata,file='student.txt')> write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。

第二章2.1> x<-c(1,2,3);y<-c(4,5,6)> e<-c(1,1,1)> z<-2*x+y+e;z[1] 7 10 13>z1<-crossprod(x,y);z1[,1][1,] 32>z2<-outer(x,y);z2[,1] [,2] [,3][1,] 4 5 6[2,] 8 10 12[3,] 12 15 182.2(1) > A<-matrix(1:20,nrow=4);B<-matrix(1:20,nrow=4,byrow=T) >C<-A+B;C(2) > D<-A%*%B;D(3) > E<-A*B;E(4) > F<-A[1:3,1:3](5) > G<-B[,-3]2.3>x<-c(rep(1,5),rep(2,3),rep(3,4),rep(4,2));x2.4>H<-matrix(nrow=5,ncol=5)>for (i in 1:5)+ for(j in 1:5)+ H[i,j]<-1/(i+j-1)（1）> det(H)（2）> solve(H)（3）> eigen(H)2.5>studentdata<-data.frame(姓名=c('张三','李四','王五','赵六','丁一') + ,性别=c('女','男','女','男','女'),年龄=c('14','15','16','14','15'),+ 身高=c('156','165','157','162','159'),体重=c('42','49','41.5','52','45.5')) 2.6>write.table(studentdata,file='student.txt')>write.csv(studentdata,file='student.csv')2.7count<-function(n){if (n<=0)print('要求输入一个正整数')else{ repeat{if (n%%2==0)n<-n/2elsen<-(3*n+1)if(n==1)break}print('运算成功')}}第三章3.1首先将数据录入为x。

统计建模与R语言习题6.6答案Homework6.6 P333解：设抗生素为x1（有用抗生素为1，没有为0）危险因子为x2（有危险因子为1，没有为0）计划为x3（事先有计划为1，临时决定为0）感染为Y整个R语言计算过程：doc<-data.frame(x1<-c(1,1,1,1,0,0,0,0),x2<-c(1,1,0,0,1,1,0,0),x3<-c(1,0,1,0,1,0,1,0) ,success<-c(1,11,0,0,28,23,8,0),fail<-c(17,87,2,0,30,3,32,9))doc$Ymat<-cbind(doc$success,doc$fail)glm.sol<-glm(Ymat~x1+x2+x3,family=binomial,data=doc) summary(glm.sol)pre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=0))p<-exp(pre)/(1+exp(pre));ppre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=1))p<-exp(pre)/(1+exp(pre));ppre<-predict(glm.sol,data.frame(x1=0,x2=1,x3=1))p<-exp(pre)/(1+exp(pre));ppre<-predict(glm.sol,data.frame(x1=1,x2=0,x3=1))p<-exp(pre)/(1+exp(pre));p回归模型输出结果如下：Call:glm(formula = Ymat ~ x1 + x2 + x3, family = binomial, data = doc)Deviance Residuals:1 2 3 4 5 6 7 8 0.26470 -0.07162 -0.15231 0.00000 -0.785201.49623 1.21563 -2.56229 Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -0.8207 0.4947 -1.659 0.0971 .x1 -3.2544 0.4813 -6.761 1.37e-11 ***x2 2.0299 0.4553 4.459 8.25e-06 ***x3 -1.0720 0.4254 -2.520 0.0117 *---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 83.491 on 6 degrees of freedomResidual deviance: 10.997 on 3 degrees of freedomAIC: 36.178Number of Fisher Scoring iterations: 5从上述结果即有常数项以及x项的系数β分别为-0.8207，-3.2544, 2.0299，-1.0720，并且回归方程通过检验得到回归模型：P=exp（-0.8207-3.2544x1+2.0299x2-1.0720x3）/(1+exp(-0.8207-3.2544x1+2.0299x2-1.0720x3))假设医生需要对一产妇进行剖腹手术，令x1=1,x2=1,x3=0即在手术中是用抗生素且有危险因子和临时决定进行手术，那么pre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=0))p<-exp(pre)/(1+exp(pre));p10.1145421即11.4521%，也就是说在临时决定进行手术的感染率为11.4521% 那么当x3=1时pre<-predict(glm.sol,data.frame(x1=1,x2=1,x3=1))> p<-exp(pre)/(1+exp(pre));p10.04240619即4.240619%，也就是说在事先有计划进行手术的感染率为4.240619%。

统计建模与R软件第六章习题（回归分析）下篇#6.6剖腹产后感染> data<-data.frame(+ x1=rep(c(1,1,1,1,1,0,0,0,0,0,0,0),c(1,17,2,11,87,28,30,23,3,9,8,32)),+ x2=rep(c(1,1,0,1,1,1,1,1,1,0,0,0),c(1,17,2,11,87,28,30,23,3,9,8,32)),+ x3=rep(c(1,1,1,0,0,1,1,0,0,0,1,1),c(1,17,2,11,87,28,30,23,3,9,8,32)),+ y=rep(c(1,0,0,1,0,1,0,1,0,0,1,0),c(1,17,2,11,87,28,30,23,3,9,8,32))+ )#x1表⽰是否使⽤了抗⽣素，x2表⽰是否有危险因⼦，x3表⽰是否有事先准备剖腹产，y表⽰是否有感染> glm.sol<-glm(y~x1+x2+x3,family=binomial,data=data)> summary(glm.sol)Call:glm(formula = y ~ x1 + x2 + x3, family = binomial, data = data)Deviance Residuals:Min 1Q Median 3Q Max-1.7149 -0.5298 -0.4933 0.7227 2.5141Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -0.8207 0.4947 -1.659 0.0971 .x1 -3.2544 0.4813 -6.761 1.37e-11 ***x2 2.0299 0.4553 4.459 8.25e-06 ***x3 -1.0720 0.4254 -2.520 0.0117 *---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 299.01 on 250 degrees of freedomResidual deviance: 226.52 on 247 degrees of freedomAIC: 234.52Number of Fisher Scoring iterations: 5#logistic回归模型为：P=exp(-0.8207-3.2544x1+2.0299x2-1.0720x3)/(1+exp(-0.8207-3.2544x1+2.0299x2-1.0720x3))#⽤上述回归模型作观测，使⽤抗⽣素，⽆危险因⼦，有剖腹产计划的感染概率为：> pre<-predict(glm.sol,data.frame(x1=1,x2=0,x3=1))> p<-exp(pre)/(1+exp(pre));p10.005783046 #感染概率为0.578%，⾮常⾮常低#不使⽤抗⽣素，有危险因⼦，⽆剖腹产计划的感染率为：> pre1<-predict(glm.sol,data.frame(x1=0,x2=1,x3=0))> p<-exp(pre1)/(1+exp(pre1));p10.7701639 #感染概率为77%，相当⾼了，回归⽅程中是否使⽤抗⽣素的回归系数绝对值最⼤，这个剖腹产还是要使⽤抗⽣素的=_=#6.7肺癌病⼈> cancer<-data.frame(+ x1=c(70,60,70,40,40,70,70,80,60,30,80,40,60,40,20,50,50,40,80,70,+ 60,90,50,70,20,80,60,50,70,40,30,30,40,60,80,70,30,60,80,70),+ x2=c(64,63,65,69,63,48,48,63,63,53,43,55,66,67,61,63,66,68,41,53,+ 37,54,52,50,65,52,70,40,26,44,54,59,69,50,62,68,39,49,64,67),+ x3=c(5,9,11,10,58,9,11,4,14,4,12,2,25,23,19,4,16,12,12,8,+ 13,12,8,7,21,28,13,13,22,36,9,87,5,22,4,15,4,11,10,18),+ x4=rep(c(1,2,3,0,1,2,3,0),c(7,7,2,4,8,4,3,5)),+ x5=rep(c(1,0),c(21,19)),+ y=rep(c(1,0,1,0,1,0,1,0,1,0,1),c(1,11,1,5,2,1,3,1,1,12,2))+ )#x1表⽰⽣活⾏动能⼒评分，x2表⽰病⼈年龄，x3表⽰由诊断到直⼊研究时间（⽉），x4表⽰肿瘤类型（0是磷癌，1是⼩型细胞癌，2是腺癌，3是⼤型细胞癌），x5表⽰两种化疗⽅法（1是常规，0是试验新法），y表⽰病⼈的⽣存时间（0是⽣存时间短，⼩于200天；1是⽣存时间长，⼤于等于200天）6.7.1logistic回归模型> glm.c<-glm(y~x1+x2+x3+x4+x5,family=binomial,data=cancer)> summary(glm.c)Call:glm(formula = y ~ x1 + x2 + x3 + x4 + x5, family = binomial,data = cancer)Deviance Residuals:Min 1Q Median 3Q Max-1.73402 -0.64522 -0.22773 0.09734 2.21941Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -7.22297 4.39926 -1.642 0.1006x1 0.10048 0.04322 2.325 0.0201 *x2 0.01716 0.04417 0.389 0.6976x3 0.01828 0.05405 0.338 0.7353x4 -1.07233 0.58653 -1.828 0.0675 .x5 -0.62473 0.96204 -0.649 0.5161---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)Null deviance: 44.987 on 39 degrees of freedomResidual deviance: 28.329 on 34 degrees of freedomAIC: 40.329Number of Fisher Scoring iterations: 6#模型不显著，肿瘤类型x4与化疗⽅法x5应该是主要的影响因素#计算各病⼈⽣存时间⼤于等于200天的概率估计值> n=c(cancer$y==1)> n[1] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE[14] FALSE FALSE FALSE FALSE FALSE TRUE TRUE FALSE TRUE TRUE TRUE FALSE TRUE[27] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE[40] TRUE> pre=glm.c$fitted[n];pre1 13 19 20 22 23 240.33257413 0.08518899 0.75283057 0.56015746 0.86922215 0.09686322 0.4315437926 39 400.75903351 0.89058079 0.78407564> p=exp(pre)/(1+exp(pre));p1 13 19 20 22 23 24 260.5823856 0.5212844 0.6797952 0.6364890 0.7045838 0.5241969 0.6062422 0.681143939 400.7090100 0.68655786.7.2逐步回归法选取⾃变量> ew<-step(glm.c)Start: AIC=40.33y ~ x1 + x2 + x3 + x4 + x5Df Deviance AIC- x3 1 28.430 38.430- x2 1 28.484 38.484- x5 1 28.750 38.75028.329 40.329- x4 1 32.483 42.483- x1 1 38.297 48.297Step: AIC=38.43y ~ x1 + x2 + x4 + x5Df Deviance AIC- x2 1 28.564 36.564- x5 1 28.955 36.95528.430 38.430- x4 1 32.563 40.563- x1 1 38.474 46.474Step: AIC=36.56y ~ x1 + x4 + x5Df Deviance AIC- x5 1 29.073 35.07328.564 36.564- x4 1 32.892 38.892- x1 1 38.478 44.478Step: AIC=35.07y ~ x1 + x4Df Deviance AIC29.073 35.073- x4 1 33.535 37.535- x1 1 39.131 43.131#剩下x1与x4⾃变量> summary(ew)Call:glm(formula = y ~ x1 + x4, family = binomial, data = cancer) Deviance Residuals:Min 1Q Median 3Q Max-1.4825 -0.6617 -0.1877 0.1227 2.2844Coefficients:Estimate Std. Error z value Pr(>|z|)(Intercept) -6.13755 2.73844 -2.241 0.0250 *x1 0.09759 0.04079 2.393 0.0167 *x4 -1.12524 0.60239 -1.868 0.0618 .---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1)Null deviance: 44.987 on 39 degrees of freedomResidual deviance: 29.073 on 37 degrees of freedomAIC: 35.073Number of Fisher Scoring iterations: 6#模型显著性提⾼#计算逐步回归后新模型各病⼈⽣存时间⼤于等于200天的概率估计值> pre1=ew$fitted[n];pre11 13 19 20 22 23 240.39371565 0.07358866 0.84149409 0.66674959 0.82054044 0.08444317 0.3937156526 39 400.63277649 0.84149409 0.66674959> p1=exp(pre1)/(1+exp(pre1));p11 13 19 20 22 23 24 260.5971768 0.5183889 0.6987798 0.6607750 0.6943510 0.5210983 0.5971768 0.653118839 400.6987798 0.6607750#6.8⾃动咖啡售货机与咖啡销售> x<-c(0,0,1,1,2,2,3,3,4,4,5,5,6,6) #咖啡机数量> y<-c(508.1,498.4,568.2,577.3,651.7,657,713.4,697.5,755.3,758.9,787.6,792.1,841.4,831.8) #咖啡销量6.8.1线性回归模型> lm.coffee<-lm(y~x)> summary(lm.coffee)Call:lm(formula = y ~ x)Residuals:Min 1Q Median 3Q Max-25.400 -11.484 -3.779 14.629 24.921Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 523.800 8.474 61.81 < 2e-16 ***x 54.893 2.350 23.36 2.26e-11 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 17.59 on 12 degrees of freedomMultiple R-squared: 0.9785, Adjusted R-squared: 0.9767F-statistic: 545.5 on 1 and 12 DF, p-value: 2.265e-11#线性回归⽅程为y=523.800+54.893x6.8.2多项式回归模型> plot(x,y)#从散点图上看，⽤⼆次曲线拟合更好> lm.coffee1<-lm(y~x+I(x^2))> summary(lm.coffee1)Call:lm(formula = y ~ x + I(x^2))Residuals:Min 1Q Median 3Q Max-10.6643 -5.6622 -0.4655 5.5000 10.6679Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 502.5560 4.8500 103.619 < 2e-16 ***x 80.3857 3.7861 21.232 2.81e-10 ***I(x^2) -4.2488 0.6063 -7.008 2.25e-05 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 7.858 on 11 degrees of freedomMultiple R-squared: 0.9961, Adjusted R-squared: 0.9953F-statistic: 1391 on 2 and 11 DF, p-value: 5.948e-14#多项式回归⽅程为：y=502.5560+80.3857x-4.2488x^2 相⽐线性回归，残差标准误降低，R平⽅达到0.99616.8.3画出散点图与拟合曲线> plot(x,y)> xfit<-seq(0,6,0.01)> yfit<-predict(lm.coffee1,data.frame(x=xfit))> lines(xfit,yfit)#6.9重伤病⼈出院后恢复情况> x<-c(2,5,7,10,14,19,26,31,34,38,45,52,53,60,65) #住院天数> y<-c(54,50,45,37,35,25,20,16,18,13,8,11,8,4,6) #预后指数6.9.1内在线性模型⽅法> plot(x,y)> lm.patient<-lm(log(y)~x)> summary(lm.patient)Call:lm(formula = log(y) ~ x)Residuals:Min 1Q Median 3Q Max-0.37241 -0.07073 0.02777 0.05982 0.33539Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 4.037159 0.084103 48.00 5.08e-16 ***x -0.037974 0.002284 -16.62 3.86e-10 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.1794 on 13 degrees of freedomMultiple R-squared: 0.9551, Adjusted R-squared: 0.9516F-statistic: 276.4 on 1 and 13 DF, p-value: 3.858e-10#线性回归⽅程为：lny=4.037159-0.037974x#计算估计值> yev=exp(4.037159)*exp(-0.037974*x);yev[1] 52.520890 46.865838 43.438277 38.761171 33.298855 27.540372 21.111861 17.460916 [9] 15.580856 13.385165 10.260781 7.865696 7.572604 5.804996 4.8011196.9.2⽤⾮线性⽅法计算估计值> nls.patient<-nls(y~a*exp(b*x),start=list(a=10,b=-0.01))> summary(nls.patient)Formula: y ~ a * exp(b * x)Parameters:Estimate Std. Error t value Pr(>|t|)a 58.606568 1.472160 39.81 5.70e-15 ***b -0.039586 0.001711 -23.13 6.01e-12 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 1.951 on 13 degrees of freedomNumber of iterations to convergence: 6Achieved convergence tolerance: 5.107e-07#⾮线性模型为：y=58.606568 * exp(-0.039586 * x)#计算估计值> yev=58.606568 * exp(-0.039586 * x);yev[1] 54.145495 48.082427 44.422441 39.448135 33.671197 27.624768 20.938944 17.178881 [9] 15.255236 13.021200 9.869772 7.481062 7.190702 5.450388 4.471647#使⽤nlm( )函数> fn<-function(p,X,Y)+ {+ f<-Y-p[1]*exp(p[2]*X)+ res<-sum(f^2)+ f1<-exp(p[2]*X)+ f2<-p[1]*exp(p[2]*X)*X+ J<-cbind(f1,f2)+ res+ }> nlm(fn,p=c(50, -0.01),x,y,hessian=TRUE)$minimum[1] 49.4593$estimate[1] 58.60712251 -0.03958742$gradient[1] -1.774625e-05 -9.522651e-03$hessian[,1] [,2][1,] 7.022561 4285.646[2,] 4285.646407 5161077.388$code[1] 2$iterations[1] 33#计算估计值> yev=58.60712251*exp(-0.03958742*x);yev[1] 54.145853 48.082541 44.422420 39.447948 33.670846 27.624284 20.938369 17.178287 [9] 15.254644 13.020620 9.869235 7.480580 7.190229 5.449975 4.471276#来看下估计值与实际值的差> y-yev[1] -0.14585337 1.91745922 0.57758014 -2.44794812 1.32915418 -2.62428435[7] -0.93836901 -1.17828719 2.74535642 -0.02062025 -1.86923491 3.51941952[13] 0.80977134 -1.44997507 1.52872352。

第二章R软件的使用1.求解非线性方程组一般用Newton法.Newton法的迭代格式为：其中J(x)为函数f(x)的Jacobi矩阵.请补全以下程序：Newtons = function (fun, x, ep=1e-5, it_max=100)(index = 0; k = 1while (k<=it_max)(x1 = x; obj = fun(x);x = x -(obj$J, obj$f);norm = sqrt((x-x1) %*% (x-x1))if (norm<ep)(index = 1;}k = k+1}obj = fun(x);list(root=, it=, index=index, FunVal=)}funs = function(x)(f = c(x[1]A2+x[2]A2-5, (x[1]+1)*x[2]-(3*x[1]+1))J = matrix(c(2*x[1], 2*x[2], x[2]-3, x[1]+1),nrow=2, byrow=T)list(f=f, J=J)}n 0,那么中止运算,并输出一句话：2.编写一个R程序(函数).输入一个整数n,如果“要求输入一个正整数〞；否那么,如果n是偶数,那么将n除以2,并赋给n;否那么,将3 n + 1赋给n.不断循环,只到n = 1 ,才停止计算,并输出一句话："运算成功〞.这个例子是为了检验数论中的一个简单的定理.请补全以下程序：fn = function(n)(if(n<=0)list(fail="要求输入一个正整数")else(i=0;(if(n 2==0)n =n = (3*n+1) if(n==1) breaki=i+1(result="运算成功", n=n, iter=i)}}##运行得到如下结果：fn(1)$result[1]"运算成功"$n[1] 1$iter[1] 2第三章数据描述性分析3.data_outline.R计算样本的各种描述性统计量.请补全该程序. data_outline = function(x){n = length(x)m =(x)v =(x)s = sd(x)me =(x)cv = 100*s/mcss = sum((x-m)A2)uss = sum(xA2)R =R1 = quantile(x,3/4)-quantile(x,1/4)sm =g1 = n/((n-1)*(n-2))*sum((x-m)A3)/sA3g2 = ((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)A4)/sA4-(3*(n-1)A2)/((n-2)*(n-3)))data.frame(N=n, Mean=m, Var=v, std_dev=s, Median=me, std_mean=sm, CV=cv, CSS=css, USS=uss, R=R, R1=R1, Skewness=g1, Kurtosis=g2, s=1) }第四章参数估计4.请写出正态均值、方差区间估计及假设检验,非正态均值区间估计的函数名(共23个程序)正态均值区间估计及假设检验正态方差区间估计及假设检验非正态均值区间估计：interval_estimate3〔双〕5.单个正态总体均值四的区间估计函数是interval_estimate1.R,请补全此程序.interval_estimate1 = function(x, sigma=-1, alpha=0.05)(n = length(x); xb = mean(x)if ()(tmp = sigma/sqrt(n)*; df = n}else(tmp =*qt(1-alpha/2,n-1); df =}(mean=xb, df=df, a=xb-tmp, b=xb+tmp)6.单个正态总体方差的区间估计函数是interval_var1.R,请补全此程序.interval_var1 = function(x,, alpha=0.05)(n = length(x)if ()(S2 = ; df = nelse(S2 = var(x); df =a = df*S2/qchisq(1-alpha/2,df)b = df*S2/qchisq(alpha/2,df)data.frame(var=, df=df, a=a, b=b) }第五章假设检验7.P_value.R为求P值的R程序,请补全它.P_value = function(cdf, x,, side=0)(n = length(paramet)P =(,cdf(x),cdf(x, paramet),cdf(x, paramet[1], paramet[2]),cdf(x, paramet[1], paramet[2], paramet[3]))if ()Pelse if (side>0)elseif (P<1/2)2*Pelse2*(1-P)}8.mean.test1.R是求单个正态总体均值检验的R程序,请补全它. mean.test1 = function(x, mu=0,, side=0)(source("")n = length(x); xb = mean(x)if ()(z = (xb-mu)/(sigma/sqrt(n))P = P_value(, z, side=side)data.frame(mean=xb, df=n, Z=z, P_value=P)}else(t = (xb-mu)/(sd(x)/sqrt(n))P = P_value(, t, paramet=n-1, side=side)data.frame(mean=xb, df=n-1, T=t, P_value=P)}}9.var.test1.R是求单个正态总体方差检验的R程序,请补全它. var.test1 = function(x, sigma2=1,, side=0)(source("P_value.R")n = length(x)if ()(S2 =; df=nelse(S2 = var(x); df=n-1}chi2 = df*S2/sigma2;P = P_value(, chi2, paramet=, side=side)data.frame(var=S2, df=df, chisq2=chi2, P_value=P)}第六章回归分析12下面是利用R软件中的lm()求解回归参数的计算过程.请补全结果,在横线上填统计量, 而不是具体的数值.>x = c(0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.20, 0.21,0.23)>y = c(42.0, 43.5, 45.0, 45.5, 45.0, 47.5, 49.0, 53.0, 50.0, 55.0, 55.0, 60.0)>lm.sol = lm(y ~ 1+x)>summary(lm.sol)Call:lm(formula = y ~ 1 + x)Residuals:Min 1Q Median 3Q Max-2.0431 -0.7056 0.1694 0.6633 2.2653Coefficients:(Intercept) Estimate Std. Error t valuePr(>|t|)5.88e-09 ***x 130.835 9.683 13.51 9.50e-08 *** Signif. codes: 0' *** ' 0.001' ** ' 0.01' *' 0.05'. '0.1' ' 1Residual standard error:on 10 degrees of freedomMultiple R-Squared:, Adjusted R-squared: 0.9429F-statistic: 182.6 on 1 and 10 DF, p-value: 9.505e-08第七章方差分析14请补全单因素方差分析表._方差来源自由度平方和均方F比p值因素Ar-1S A MSA= F= p误差n-rMSE=总和第八章应用多元分析⑴1.请补全以下程序.discriminiant.distance = function(TrnXI, TrnX2,= NULL, var.equal = FALSE){if (is.null(TstX) = = TRUE) TstX = rbind(TrnX1,TrnX2)if (is.vector(TstX) = = TRUE) TstX =else if (is.matrix(TstX) != TRUE)TstX = as.matrix(TstX)if (is.matrix(TrnX1) != TRUE) TrnX1 = as.matrix(TrnX1)if (is.matrix(TrnX2) != TRUE) TrnX2 = as.matrix(TrnX2)nx = nrow(TstX)blong = matrix(rep(0, nx), nrow=1, byrow=TRUE,dimnames=list("blong〞, 1:nx))mu1 = colMeans(TrnX1); mu2 = colMeans(TrnX2)if (){S =(rbind(TrnX1,TrnX2))w = mahalanobis(TstX, mu2, S)-mahalanobis(TstX, mu1, S)}else{S1 = var(TrnX1); S2 = var(TrnX2)w = mahalanobis(TstX, mu2, S2)-mahalanobis(TstX, mu1, S1)}for (i in 1:nx){if (w[i]>0)blong[i] = 1elseblong[i] = 2}}2.请补全以下程序.distinguish.distance = function(TrnX,, TstX = NULL, var.equal = FALSE){ if (== FALSE)( mx = nrow(TrnX); mg = nrow(TrnG) TrnX = rbind(TrnX, TrnG) TrnG = factor(rep(1:2, c(mx, mg)))}if (is.null(TstX) = = TRUE) TstX = TrnXif (is.vector(TstX) = = TRUE) TstX = t(as.matrix(TstX)) else if (is.matrix(TstX) != TRUE) TstX = as.matrix(TstX)if (is.matrix(TrnX) != TRUE) TrnX = as.matrix(TrnX)nx = nrow(TstX)blong = matrix(rep(0, nx), nrow=1, dimnames=list("blong", 1:nx)) g = length(levels(TrnG)) mu = matrix(0, nrow=g, ncol=ncol(TrnX)) for (i in 1:g)mu[i,] = colMeans(TrnX[TrnG= =i,])D = matrix(0, nrow=g, ncol=nx) if ()(for (i in 1:g)D[i,] =}else( for (i in 1:g)D[i,] = mahalanobis(TstX, mu[i,], var(TrnX[TrnG= =i,])) }for (j in 1:nx)(for (i in 1:g)if (D[i,j]<dmin)(dmin = D[i,j]; blong[j] = i}}blong}3.请补全以下程序.discriminiant.bayes = function(TrnX1, TrnX2,, TstX = NULL, var.equal = FALSE)(if (is.null(TstX) = = TRUE) TstX = rbind(TrnX1,TrnX2)if (is.vector(TstX) = = TRUE) TstX = t(as.matrix(TstX))else if (is.matrix(TstX) != TRUE)TstX = as.matrix(TstX)if (is.matrix(TrnX1) != TRUE) TrnX1 = as.matrix(TrnX1)if (is.matrix(TrnX2) != TRUE) TrnX2 = as.matrix(TrnX2) nx = nrow(TstX)blong = matrix(rep(0, nx), nrow=1, byrow=TRUE, dimnames=list("blong〞, 1:nx))mu1 = colMeans(TrnX1); mu2 = colMeans(TrnX2)if (){S = var(rbind(TrnX1,TrnX2)); beta =w =}else{S1 = var(TrnX1); S2 = var(TrnX2)beta = 2*log(rate)+log(det(S1)/det(S2))w = mahalanobis(TstX, mu2, S2)-mahalanobis(TstX, mu1, S1) }for (i in 1:nx){if ()blong[i] = 1elseblong[i] = 2}blong}第九章应用多元分析(II)4.下面是主成分法的R程序,请补全它. factor.analyl = function(S, m){p = nrow(S); diag_S = diag(S); sum_rank = sum(diag_S)rowname = paste("X", 1:p, sep="")colname = paste("Factor", 1:m, sep="")A = matrix(0, nrow=p, ncol=m,dimnames=list(rowname, colname))eig =for (i in 1:m)A[,i] =*eig$vectors[,i]h = diag()rowname = c("SS loadings", "Proportion Var", "Cumulative Var")B = matrix(0, nrow=3, ncol=m,dimnames=list(rowname, colname))for (i in 1:m){B[1,i] =B[2,i] = B[1,i]/sum_rankB[3,i] = sum(B[1,1:i])/sum_rank}method = c("Principal Component Method")list(method=method, loadings=A, var=(common=h, spcific=diag_S-h), B=B) }5.下面是主因子法的R程序,请补全它.factor.analy2 = function(){p = nrow(R); diag_R = diag(R); sum_rank = sum(diag_R)rowname = paste("X〞, 1:p, sep="")colname = paste("Factor", 1:m, sep="")A = matrix(0, nrow=p, ncol=m,dimnames=list(rowname, colname))kmax=20; k = 1; h ={diag(R) = h; h1 = h; eig = eigen(R)for (i in 1:m)A[,i] = sqrt(eig$values[i])*eig$vectors[,i]h = diag(A %*% t(A))if ((<1e-4)|k==kmax) breakk = k+1}rowname = c("SS loadings", "Proportion Var", "Cumulative Var")B = matrix(0, nrow=3, ncol=m,dimnames=list(rowname, colname))for (i in 1:m){B[1,i] = sum(A[,i]A2)B[2,i] = B[1,i]/sum_rankB[3,i] = sum(B[1,1:i])/sum_rank}= c("Principal Factor Method")list(method=method, loadings=A,var=cbind(common=h, spcific=diag_R-h), B=B, iterative=k) }6.下面是将因子分析的三种估计方法结合在一起的R程序,请补全它.factor.analy = function(S, m=0,d=, method=""){if (){p = nrow(S); eig = eigen(S)sum_eig = sum(diag(S))for (i in 1:p)(if (/sum_eig>0.70)( m = i; break}}}source("factor.analy1.R")source("factor.analy2.R")source("factor.analy3.R") (method,princomp=factor.analy1(S, m), factor=factor.analy2(S, m, d), likelihood=factor.analy3(S, m, d) ) }程序填空题题库答案第二章R软件的使用1.求解非线性方程组一般用Newton法.Newton法的迭代格式为：…日=坤_ (坤}「丫印、=■T其中J(x)为函数f(x)的Jacobi矩阵.请补全以下程序：Newtons = function (fun, x, ep=1e-5, it_max=100)(index = 0; k = 1while (k<=it_max)(x1 = x; obj = fun(x);x = x - solve(obj$J, obj$f);norm = sqrt((x-x1) %*% (x-x1))if (norm<ep)(index = 1; break}k = k+1}obj = fun(x);list(root= x, it= k, index=index, FunVal= obj$f)}n 0,那么中止运算,并输出一句话：2.编写一个R程序(函数).输入一个整数n,如果“要求输入一个正整数〞；否那么,如果n是偶数,那么将n除以2,并赋给n;否那么,将3 n + 1赋给n.不断循环,只到n = 1,才停止计算,并输出一句话：“运算成功〞.这个例子是为了检验数论中的一个简单的定理.请补全以下程序：fn = function(n)(if(n<=0)list(fail="要求输入一个正整数")else(i=0;repeat (if(n %%2==0) n = n/2else ## 或者是else if(n%%2>0)n = (3*n+1)if(n==1) break i=i+1 }list (result="运算成功", n=n, iter=i)}}第三章数据描述性分析3. data_outline.R计算样本的各种描述性统计量.请补全该程序. data_outline = function(x)(n = length(x) m = mean (x) v = var (x) s = sd(x) me = median (x) cv = 100*s/m css = sum((x-m)A2) uss = sum(xA2) R = max(x)-min(x) R1 = quantile(x,3/4)-quantile(x,1/4) sm = s/sqrt(n)g1 = n/((n-1)*(n-2))*sum((x-m)A3)/sA3g2 = ((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)A4)/sA4-(3*(n-1)A2)/((n-2)*(n-3)))data.frame(N=n, Mean=m, Var=v, std_dev=s, Median=me, std_mean=sm, CV=cv, CSS=css, USS=uss, R=R, R1=R1, Skewness=g1, Kurtosis=g2, s=1) }第四章参数估计4.请写出正态均值、方差区间估计及假设检验,非正态均值区间估计的函数名〔共23个程序〕正态均值区间估计及假设检验正态方差区间估计及假设检验非正态均值区间估计：interval_estimate3〔双〕5.单个正态总体均值□的区间估计函数是interval_estimate1.R,请补全此程序.interval_estimate1 = function〔x, sigma=-1, alpha=0.05〕｛n = length〔x〕; xb = mean〔x〕if 〔sigma>=0〕｛tmp = sigma/sqrt〔n〕* qnorm〔1-alpha/2〕 ; df = nelse(tmp = sd(x)/sqrt(n) *qt(1-alpha/2,n-1); df = n-1}data.frame (mean=xb, df=df, a=xb-tmp, b=xb+tmp)}6.单个正态总体方差〃的区间估计函数是interval_var1.R,请补全此程序. interval_var1 = function(x, mu=Inf , alpha=0.05){n = length(x)if (mu<Inf ){S2 = sum((x-mu)^2)/n ; df = n}else{S2 = var(x); df = n-1}a = df*S2/qchisq(1-alpha/2,df)b = df*S2/qchisq(alpha/2,df)data.frame(var=S2, df=df, a=a, b=b)}第五章假设检验7.P_value.R为求P值的R程序,请补全它.P_value = function(cdf, x, paramet=numeric(0) , side=0){n = length(paramet)P = switch (n+1 ,cdf(x),cdf(x, paramet),cdf(x, paramet[1], paramet[2]),cdf(x, paramet[1], paramet[2], paramet[3]))if (side<0) Pelse if (side>0) 1Pelseif (P<1/2)2*Pelse2*(1-P)}8.mean.test1.R是求单个正态总体均值检验的R程序,请补全它.mean.test1 = function(x, mu=0, sigma=-1 , side=0){source(" P_value R ")n = length(x); xb = mean(x)if (sigma>=0){z = (xb-mu)/(sigma/sqrt(n))P = P value(pnorm , z, side=side)data.frame(mean=xb, df=n, Z=z, P_value=P)}else{t = (xb-mu)/(sd(x)/sqrt(n))P = P_value(pt, t, paramet=n-1, side=side)data.frame(mean=xb, df=n-1, T=t, P_value=P)}}9.var.test1.R是求单个正态总体方差检验的R程序,请补全它.var.test1 = function(x, sigma2=1, mu=Inf , side=0){ source("P_value.R") n = length(x) if (mu<Inf ){ S2 = sum((x-mu)^2)/n ; df=n}else{S2 = var(x); df=n-1}chi2 = df*S2/sigma2;P = P value(pchisq , chi2, paramet=df, side=side)data.frame(var=S2, df=df, chisq2=chi2, P_value=P)}第六章回归分析10.下面是利用R软件中的lm()求解回归参数的计算过程.请补全结果,在横线上填统计量, 而不是具体的数值.>x = c(0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.20, 0.21,0.23)>y = c(42.0, 43.5, 45.0, 45.5, 45.0, 47.5, 49.0, 53.0, 50.0, 55.0, 55.0, 60.0)>lm.sol = lm(y ~ 1+x)>summary(lm.sol)Call:lm(formula = y ~ 1 + x)Residuals:Min 1Q Median 3Q Max-2.0431 -0.7056 0.1694 0.6633 2.2653Coefficients:Estimate Std. Error t valuePr(>|t|)__5.88e-09 ***(Intercept)国就偶)x130.8359.68313.519.50e-08 ***—Signif. codes: 0' *** ' 0.001' ** ' 0.01' *' 0.05Residual standard error: 三on 10 degrees of freedomMultiple R-Squared: 芋,Adjusted R-squared: 0.9429 F-statistic: 182.6 on 1 and 10 DF, p-value: 9.505e-08第七章方差分析11.请补全单因素方差分析表.方妾来源自由度平方和均方因素A r-1 MSA=)—L误差n-r S E MSE=—H — r总和n-1 &第八章应用多元分析⑴12.请补全以下程序.discriminiant.distance = function(TrnX1, TrnX2, TstX = NULL, var.equal = FALSE){if (is.null(TstX) = = TRUE) TstX = rbind(TrnX1,TrnX2)if (is.vector(TstX) = = TRUE) TstX = t(as.matrix(TstX))else if (is.matrix(TstX) != TRUE)TstX = as.matrix(TstX)if (is.matrix(TrnX1) != TRUE) TrnX1 = as.matrix(TrnX1)if (is.matrix(TrnX2) != TRUE) TrnX2 = as.matrix(TrnX2)nx = nrow(TstX)blong = matrix(rep(0, nx), nrow=1, byrow=TRUE, dimnames=list("blong", 1:nx))mu1 = colMeans(TrnX1); mu2 = colMeans(TrnX2)if (var.equal = = TRUE ){S = va£(rbind(TrnX1,TrnX2))w = mahalanobis(TstX, mu2, S)-mahalanobis(TstX, mu1, S)}else{S1 = var(TrnX1); S2 = var(TrnX2)w = mahalanobis(TstX, mu2, S2)-mahalanobis(TstX, mu1, S1) for (i in 1:nx)(if (w[i]>0)blong[i] = 1elseblong[i] = 2}blong}13.请补全以下程序.distinguish.distance = function(TrnX, TrnG , TstX = NULL, var.equal = FALSE){if ( is.factor(TrnG) == FALSE){mx = nrow(TrnX); mg = nrow(TrnG)TrnX = rbind(TrnX, TrnG)TrnG = factor(rep(1:2, c(mx, mg)))}if (is.null(TstX) = = TRUE) TstX = TrnXif (is.vector(TstX) = = TRUE) TstX = t(as.matrix(TstX))else if (is.matrix(TstX) != TRUE)TstX = as.matrix(TstX)if (is.matrix(TrnX) != TRUE) TrnX = as.matrix(TrnX)nx = nrow(TstX)blong = matrix(rep(0, nx), nrow=1, dimnames=list("blong", 1:nx)) g = length(levels(TrnG)) mu = matrix(0, nrow=g, ncol=ncol(TrnX))for (i in 1:g)mu[i,] = colMeans(TrnX[TrnG= =i,])D = matrix(0, nrow=g, ncol=nx)if (var.equal = = TRUE ){for (i in 1:g)D[i,] = mahalanobis(TstX, mu[i,], var(TrnX))}else{for (i in 1:g)D[i,] = mahalanobis(TstX, mu[i,], var(TrnX[TrnG= =i,])) }for (j in 1:nx){dmini = Inffor (i in 1:g)if (D[i,j]<dmin){dmin = D[i,j]; blong[j] = i} blong}14.请补全以下程序.discriminiant.bayes = function(TrnXI, TrnX2, rate=1 , TstX = NULL, var.equal = FALSE){if (is.null(TstX) = = TRUE) TstX = rbind(TrnX1,TrnX2)if (is.vector(TstX) = = TRUE) TstX = t(as.matrix(TstX))else if (is.matrix(TstX) != TRUE)TstX = as.matrix(TstX)if (is.matrix(TrnX1) != TRUE) TrnX1 = as.matrix(TrnX1)if (is.matrix(TrnX2) != TRUE) TrnX2 = as.matrix(TrnX2)nx = nrow(TstX)blong = matrix(rep(0, nx), nrow=1, byrow=TRUE, dimnames=list("blong", 1:nx))mu1 = colMeans(TrnX1); mu2 = colMeans(TrnX2)if (var.equal = = TRUE ){S = var(rbind(TrnX1,TrnX2)); beta = 2*log(rate)w = mahalanobis(TstX, mu2, S)-mahalanobis(TstX, mu1, S) } else{S1 = var(TrnX1); S2 = var(TrnX2)beta = 2*log(rate)+log(det(S1)/det(S2))w = mahalanobis(TstX, mu2, S2)-mahalanobis(TstX, mu1, S1) }for (i in 1:nx){if (w[i]>beta )blong[i] = 1elseblong[i] = 2}blong}第九章应用多元分析(II)15.下面是主成分法的R程序,请补全它.factor.analy1 = function(S, m){p = nrow(S); diag_S = diag(S); sum_rank = sum(diag_S) rowname = paste("X", 1:p, sep="") colname = paste("Factor〞, 1:m, sep="")A = matrix(0, nrow=p, ncol=m, dimnames=list(rowname, colname)) eig = eigen(S) for (i in 1:m)A[,i] = sqrt(eig$values[i]) *eig$vectors[,i] h = diag(A%*%t(A))rowname = c("SS loadings", "Proportion Var", "Cumulative Var") B = matrix(0, nrow=3, ncol=m, dimnames=list(rowname, colname))for (i in 1:m)(B[1,i] = sum(A[,i]『2)B[2,i] = B[1,i]/sum_rankB[3,i] = sum(B[1,1:i])/sum_rank}method = c("Principal Component Method") list(method=method, loadings=A,var=cbind (common=h, spcific=diag_S-h), B=B)}16.下面是主因子法的R程序,请补全它.factor.analy2 = function( R, m, d) (p = nrow(R); diag_R = diag(R); sum_rank = sum(diag_R) rowname = paste("X", 1:p, sep="") colname = paste("Factor", 1:m, sep="")A = matrix(0, nrow=p, ncol=m, dimnames=list(rowname, colname))kmax=20; k = 1; h = diag R-d repeat {diag(R) = h; hl = h; eig = eigen(R) for (i in 1:m)A[,i] = sqrt(eig$values[i])*eig$vectors[,i] h = diag(A %*% t(A))if ((sqrt(sum((h-h1)A2)) <1e-4)|k==kmax) break k = k+1}rowname = c("SS loadings", "Proportion Var", "Cumulative Var") B = matrix(0, nrow=3, ncol=m,dimnames=list(rowname, colname))for (i in 1:m)(B[1,i] = sum(A[,i]A2)B[2,i] = B[1,i]/sum_rankB[3,i] = sum(B[1,1:i])/sum_rank}method = c("Principal Factor Method")list(method=method, loadings=A,var=cbind(common=h, spcific=diag_R-h), B=B, iterative=k)}17.下面是将因子分析的三种估计方法结合在一起的R程序,请补全它.factor.analy = function(S, m=0,d=1/diag(solve(S)) , method=" likelihood "){if (m==0){p = nrow(S); eig = eigen(S)sum_eig = sum(diag(S))for (i in 1:p){if (sum(eig$values[1:i]) /sum eig>0.70){m = i; break}}}source("factor.analy1.R")source("factor.analy2.R")source("factor.analy3.R")switch (method,princomp=factor.analy1(S, m),factor=factor.analy2(S, m, d),likelihood=factor.analy3(S, m, d)。

第七章1．a．> lamp<-data.frame(+ X=c(115,116,98,83,103,107,118,116,73,89,85,97),+ A=factor(rep(1:3,c(4,4,4)))+ )> lamp.aov<-aov(X ~ A, data=lamp)> source("anova.tab.R");anova.tab(lamp.aov)Df Sum Sq Mean Sq F value Pr(>F)A 2 1304.00 652.00 4.9228 0.03595 * Residuals 9 1192.00 132.44Total 11 2496.00---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘.’ 1 P值大于0.01，接受原假设。

没有显著差异b．> source("interval_estimatel.R")> x<-c(115,116,98,83)> interval_estimatel(x)mean df a b1 103 3 78.04264 127.9574均值为103，区间估计为（78.04264，127.9574）> source("interval_estimatel.R")> x<-c(103,107,118,116)> interval_estimatel(x)mean df a b1 111 3 99.59932 122.4007均值为111，区间估计为（99.59932，122.4007）> source("interval_estimatel.R")> x<-c(73,89,85,97)> interval_estimatel(x)mean df a b186 3 70.08777 101.9122均值为86，区间估计为（70.08777，101.9122）c．> pairwise.t.test(X, A, p.adjust.method = "none")Pairwise comparisons using t tests with pooled SD data: X and A1 22 0.351 -3 0.066 0.013> X=c(115,116,98,83,103,107,118,116,73,89,85,97)> A=factor(rep(1:3,c(4,4,4)))> pairwise.t.test(X, A, p.adjust.method = "holm")Pairwise comparisons using t tests with pooled SDdata: X and A1 22 0.35 -3 0.13 0.04P value adjustment method: holm> X=c(115,116,98,83,103,107,118,116,73,89,85,97)> A=factor(rep(1:3,c(4,4,4)))> pairwise.t.test(X, A, p.adjust.method = "bonferroni")Pairwise comparisons using t tests with pooled SDdata: X and A1 22 1.00 -3 0.20 0.04P value adjustment method: bonferroni2．> lamp<-data.frame(+ X=c(20,18,18,17,15,16,13,18,22,17,26,19,26,28,23,25,24,25,18,22,27,24,12,14), + A=factor(rep(1:4,c(10,6,6,2)))+ )> lamp.aov<-aov(X ~ A, data=lamp)> source("anova.tab.R");anova.tab(lamp.aov)Df Sum Sq Mean Sq F value Pr(>F)A 3 351.72 117.24 15.105 2.277e-05 ***Residuals 20 155.23 7.76Total 23 506.96---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1p值远远小于0.01，拒绝原假设。

统计建模与r软件课后习题答案统计建模与R软件课后习题答案在统计建模与R软件课程中，学生们经常需要完成一系列的习题来巩固所学知识。

这些习题涉及到统计建模的理论和实践，以及如何使用R软件来进行数据分析和建模。

在本文中，我们将给出一些常见的统计建模与R软件课后习题的答案，希望能够帮助学生更好地理解课程内容。

1. 线性回归模型习题：使用R软件对给定数据集进行线性回归分析，并给出回归方程和相关系数。

答案：在R软件中，可以使用lm()函数来进行线性回归分析。

例如，对于数据集data，可以使用以下代码进行线性回归分析：```model <- lm(y ~ x, data=data)summary(model)```其中，y和x分别表示因变量和自变量。

通过summary()函数可以得到回归方程和相关系数等信息。

2. 逻辑回归模型习题：使用R软件对给定数据集进行逻辑回归分析，并给出回归方程和模型拟合度。

答案：逻辑回归分析可以使用glm()函数来进行。

例如，对于数据集data，可以使用以下代码进行逻辑回归分析：```model <- glm(y ~ x, data=data, family=binomial)summary(model)```其中，y和x分别表示因变量和自变量，family=binomial表示使用二项分布进行逻辑回归分析。

通过summary()函数可以得到回归方程和模型拟合度等信息。

3. 方差分析习题：使用R软件对给定数据集进行方差分析，并给出各组之间的差异是否显著。

答案：在R软件中，可以使用aov()函数来进行方差分析。

例如，对于数据集data，可以使用以下代码进行方差分析：```model <- aov(y ~ group, data=data)summary(model)```其中，y和group分别表示因变量和自变量。

通过summary()函数可以得到各组之间的差异是否显著等信息。