2011八年级数学14章一次函数测试题周周清

新世纪教育网精选资料版权全部@新世纪教育网
练习 75（2012.03.15 ）
297.（2011浙江舟山）如，①②③④⑤五个平行四形拼成一个含30°内角
的菱形 EFGH （不重叠无隙）．若①②③④四个平行四形面的和 14cm2，四形 ABCD 面是 11cm2，①②③④四个平行四形周的和
（）
（A）48cm（B） 36cm（C） 24cm（D） 18cm
E A H
④
①
D
⑤
B③
②
F C G
（第 10 题）
298.（2011 山德州） 1 是一个 1 的等三角形和一个菱形的合形，菱形等三角形的一半，以此基本位，能够拼成一个形状同样但尺寸更大的形（如 2），依此
律拼下去（如 3），⋯⋯，第
n个形的周是
⋯⋯123
（ A）2n（B）4n（C）2n 1（ D）2n 2
299.（2011 山泰安）如， 6 的大正方形中有两个小正方形，若两个小正方形的面分 S1，S2， S1+S2的
第 3第 4
A.17
B.17
C.18
D.19
新世纪教育网精选资料版权全部@新世纪教育网
300.（2011 山东泰安）如图，点 O 是矩形 ABCD 的中心， E 是 AB 上的点，沿CE 折叠后，点 B 恰巧与点 O重合，若 BC=3，则折痕 CE 的长为
A.2 3
B.33
D.6
2 C. 3。

第十四章 一次函数测试题本卷贰O 贰贰年贰月捌日编写； 出题人：令狐学复；欧阳化语；令狐理总。

〔时间是：90分钟 总分120分〕一、相信你一定能填对！〔每一小题3分，一共30分〕 1．以下函数中，自变量x 的取值范围是x ≥2的是〔 〕A ．y=2x -B ．y=2x - C ．y=24x - D ．y=2x +·2x - 2．下面哪个点在函数y=12x+1的图象上〔 〕A ．〔2，1〕B ．〔-2，1〕C ．〔2，0〕D ．〔-2，0〕 3．以下函数中，y 是x 的正比例函数的是〔 〕 A ．y=2x-1 B ．y=3xC ．y=2x 2D ．y=-2x+1 4．一次函数y=-5x+3的图象经过的象限是〔 〕 A ．一、二、三 B ．二、三、四 C ．一、二、四 D ．一、三、四5．假设函数y=〔2m+1〕x 2+〔1-2m 〕x 〔m 为常数〕是正比例函数，那么m 的值是〔 〕 A ．m>12 B ．m=12 C ．m<12 D ．m=-126．假设一次函数y=〔3-k 〕x-k 的图象经过第二、三、四象限，那么k 的取值范围是〔 〕 A ．k>3 B ．0<k ≤3 C ．0≤k<3 D ．0<k<37．一次函数的图象与直线y=-x+1平行，且过点〔8，2〕，那么此一次函数的解析式为〔 〕A ．y=-x-2B ．y=-x-6C ．y=-x+10D ．y=-x-18．汽车开场行驶时，油箱内有油40升，假如每小时耗油5升，那么油箱内余油量y 〔升〕与行驶时间是t 〔时〕的函数关系用图象表示应为以下图中的〔 〕9．李教师骑自行车上班，最初以某一速度匀速行进，•中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李教师加快了速度，仍保持匀速行进，假如准时到校．在课堂上，李教师请学生画出他行进的路程y•〔千米〕与行进时间是t 〔小时〕的函数图象的示意图，同学们画出的图象如下图，你认为正确的选项是〔 〕10．一次函数y=kx+b 的图象经过点〔2，-1〕和〔0，3〕，•那么这个一次函数的解析式为〔 〕 A ．y=-2x+3 B ．y=-3x+2 C ．y=3x-2 D ．y=12x-3 二、你能填得又快又对吗？〔每一小题3分，一共30分〕11．自变量为x 的函数y=mx+2-m 是正比例函数，那么m=________，•该函数的解析式为_________． 12．假设点〔1，3〕在正比例函数y=kx 的图象上，那么此函数的解析式为________．13．一次函数y=kx+b 的图象经过点A 〔1，3〕和B 〔-1，-1〕，那么此函数的解析式为_________． 14．假设解方程x+2=3x-2得x=2，那么当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方．15．一次函数y=-x+a与y=x+b的图象相交于点〔m，8〕，那么a+b=_________．16．假设一次函数y=kx+b交于y•轴的负半轴，•且y•的值随x•的增大而减少，•那么k____0，b______0．〔填“>〞、“<〞或者“＝〞〕17．直线y=x-3与y=2x+2的交点为〔-5，-8〕，那么方程组30220x yx y--=⎧⎨-+=⎩的解是________．18．一次函数y=-3x+1的图象经过点〔a，1〕和点〔-2，b〕，那么a=________，b=______．19．假如直线y=-2x+k与两坐标轴所围成的三角形面积是9，那么k的值是_____．20．如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，那么此一次函数的解析式为__________，△AOC的面积为_________．三、认真解答，一定要细心哟！〔一共60分〕21．〔14分〕根据以下条件，确定函数关系式：〔1〕y与x成正比，且当x=9时，y=16；〔2〕y=kx+b的图象经过点〔3，2〕和点〔-2，1〕．22．〔12分〕一次函数y=kx+b的图象如下图：〔1〕求出该一次函数的表达式；〔2〕当x=10时，y的值是多少？〔3〕当y=12时，•x的值是多少？23．〔12分〕一农民带了假设干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数〔含备用零钱〕的关系如下图，结合图象答复以下问题：〔1〕农民自带的零钱是多少？〔2〕降价前他每千克土豆出售的价格是多少？〔3〕降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱〔含备用零钱〕是26元，问他一一共带了多少千克土豆？24．〔10分〕如下图的折线ABC•表示从甲地向乙地打长途所需的费y〔元〕与通话时间是t〔分钟〕之间的函数关系的图象．〔1〕写出y与t•之间的函数关系式．〔2〕通话2分钟应付通话费多少元？通话7分钟呢？25．〔12分〕雅美服装厂现有A种布料70米，B种布料52米，•现方案用这两种布料消费M、N两种型号的时装一共80套．做一套M型号的时装需用A种布料1.•1米，B种布料，可获利50元；做一套N型号的时装需用A种布料，B种布料0.•9米，可获利45元．设消费M型号的时装套数为x，用这批布料消费两种型号的时装所获得的总利润为y元．①求y〔元〕与x〔套〕的函数关系式，并求出自变量的取值范围；②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？答案:1．D 2．D 3．B 4．C 5．D 6．A 7．C 8．B 9．C 10．A11．2；y=2x 12．y=3x 13．y=2x+1 14．<2 15．1616．<；< 17．58xy=-⎧⎨=-⎩18．0；7 19．±6 20．y=x+2；421．①y=169x；②y=15x+7522．y=x-2；y=8；x=1423．①5元；②0.5元；③45千克24．①当0<t≤3时，y=2.4；当t>3时，y=t-0.6．②25．①y=50x+45〔80-x〕=5x+3600．∵两种型号的时装一共用A种布料[1.1x+0.•6〔80-x〕]米，一共用B种布料[0.4x+0.9〔80-x〕]米，∴解之得40≤x≤44，而x为整数，∴x=40，41，42，43，44，∴y与x的函数关系式是y=5x+3600〔x=40，41，42，43，44〕；②∵y随x的增大而增大，∴当x=44时，y最大=3820，即消费M型号的时装44套时，该厂所获利润最大，最大利润是3820元．本卷贰O贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

第十四章 一次函数测试题制卷人：打自企； 成别使； 而都那。

审核人：众闪壹； 春壹阑； 各厅…… 日期：2022年二月八日。

〔时间是：90分钟 总分120分〕一、相信你一定能填对！〔每一小题3分，一共30分〕 1．以下函数中，自变量x 的取值范围是x ≥2的是〔 〕A ．y=2x -B ．y=12x - C ．y=24x - D ．y=2x +·2x - 2．下面哪个点在函数y=12x+1的图象上〔 〕A ．〔2，1〕B ．〔-2，1〕C ．〔2，0〕D ．〔-2，0〕 3．以下函数中，y 是x 的正比例函数的是〔 〕 A ．y=2x-1 B ．y=3xC ．y=2x 2D ．y=-2x+1 4．一次函数y=-5x+3的图象经过的象限是〔 〕 A ．一、二、三 B ．二、三、四 C ．一、二、四 D ．一、三、四5．假设函数y=〔2m+1〕x 2+〔1-2m 〕x 〔m 为常数〕是正比例函数，那么m 的值是〔 〕 A ．m>12 B ．m=12 C ．m<12 D ．m=-126．假设一次函数y=〔3-k 〕x-k 的图象经过第二、三、四象限，那么k 的取值范围是〔 〕A ．k>3B ．0<k ≤3C ．0≤k<3D ．0<k<37．一次函数的图象与直线y=-x+1平行，且过点〔8，2〕，那么此一次函数的解析式为〔 〕 A ．y=-x-2 B ．y=-x-6 C ．y=-x+10 D ．y=-x-18．汽车开场行驶时，油箱内有油40升，假如每小时耗油5升，那么油箱内余油量y 〔升〕与行驶时间是t 〔时〕的函数关系用图象表示应为以下图中的〔 〕9．李教师骑自行车上班，最初以某一速度匀速行进，•中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李教师加快了速度，仍保持匀速行进，假如准时到校．在课堂上，李教师请学生画出他行进的路程y•〔千米〕与行进时间是t 〔小时〕的函数图象的示意图，同学们画出的图象如下图，你认为正确的选项是〔 〕10．一次函数y=kx+b 的图象经过点〔2，-1〕和〔0，3〕，•那么这个一次函数的解析式为〔 〕 A ．y=-2x+3 B ．y=-3x+2 C ．y=3x-2 D ．y=12x-3 二、你能填得又快又对吗？〔每一小题3分，一共30分〕11．自变量为x 的函数y=mx+2-m 是正比例函数，那么m=________，•该函数的解析式为_________．12．假设点〔1，3〕在正比例函数y=kx的图象上，那么此函数的解析式为________．13．一次函数y=kx+b的图象经过点A〔1，3〕和B〔-1，-1〕，那么此函数的解析式为_________．14．假设解方程x+2=3x-2得x=2，那么当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方．15．一次函数y=-x+a与y=x+b的图象相交于点〔m，8〕，那么a+b=_________．16．假设一次函数y=kx+b交于y•轴的负半轴，•且y•的值随x•的增大而减少，•那么k____0，b______0．〔填“>〞、“<〞或者“＝〞〕17．直线y=x-3与y=2x+2的交点为〔-5，-8〕，那么方程组30220x yx y--=⎧⎨-+=⎩的解是________．18．一次函数y=-3x+1的图象经过点〔a，1〕和点〔-2，b〕，那么a=________，b=______．19．假如直线y=-2x+k与两坐标轴所围成的三角形面积是9，那么k的值是_____．20．如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，那么此一次函数的解析式为__________，△AOC的面积为_________．三、认真解答，一定要细心哟！〔一共60分〕21．〔14分〕根据以下条件，确定函数关系式：〔1〕y与x成正比，且当x=9时，y=16；〔2〕y=kx+b的图象经过点〔3，2〕和点〔-2，1〕．22．〔12分〕一次函数y=kx+b的图象如下图：〔1〕求出该一次函数的表达式；〔2〕当x=10时，y的值是多少？〔3〕当y=12时，•x的值是多少？23．〔12分〕一农民带了假设干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数〔含备用零钱〕的关系如下图，结合图象答复以下问题：〔1〕农民自带的零钱是多少？〔2〕降价前他每千克土豆出售的价格是多少？〔3〕降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱〔含备用零钱〕是26元，问他一一共带了多少千克土豆？24．〔10分〕如下图的折线ABC•表示从甲地向乙地打长途所需的费y〔元〕与通话时间是t〔分钟〕之间的函数关系的图象．〔1〕写出y与t•之间的函数关系式．〔2〕通话2分钟应付通话费多少元？通话7分钟呢？25．〔12分〕雅美服装厂现有A种布料70米，B种布料52米，•现方案用这两种布料消费M、N两种型号的时装一共80套．做一套M型号的时装需用A种布料1.•1米，B种布料，可获利50元；做一套N型号的时装需用A种布料，B种布料0.•9米，可获利45元．设消费M型号的时装套数为x，用这批布料消费两种型号的时装所获得的总利润为y元．①求y〔元〕与x〔套〕的函数关系式，并求出自变量的取值范围；②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？答案:1．D 2．D 3．B 4．C 5．D 6．A 7．C 8．B 9．C 10．A11．2；y=2x 12．y=3x 13．y=2x+1 14．<2 15．1616．<；< 17．58xy=-⎧⎨=-⎩18．0；7 19．±6 20．y=x+2；421．①y=169x；②y=15x+7522．y=x-2；y=8；x=1423．①5元；②0.5元；③45千克24．①当0<t≤3时，y=2.4；当t>3时，y=t-0.6．②25．①y=50x+45〔80-x〕=5x+3600．∵两种型号的时装一共用A种布料[1.1x+0.•6〔80-x〕]米，一共用B种布料[0.4x+0.9〔80-x〕]米，∴解之得40≤x≤44，而x为整数，∴x=40，41，42，43，44，∴y与x的函数关系式是y=5x+3600〔x=40，41，42，43，44〕；②∵y随x的增大而增大，∴当x=44时，y最大=3820，即消费M型号的时装44套时，该厂所获利润最大，最大利润是3820元．制卷人：打自企；成别使；而都那。

第十四章 一次函数测试题 一、相信你一定能填对！（每小题3分，共30分）1．下列函数中，自变量x 的取值X 围是x ≥2的是（ ）A ．y=2x -B ．y=12x - C ．y=24x - D ．y=2x +·2x - 2．下面哪个点在函数y=12x+1的图象上（ ） A ．（2，1） B ．（-2，1） C ．（2，0） D ．（-2，0）3．下列函数中，y 是x 的正比例函数的是（ ）A ．y=2x-1B ．y=3x C ．y=2x 2 D ．y=-2x+1 4．一次函数y=-5x+3的图象经过的象限是（ ）A ．一、二、三B ．二、三、四C ．一、二、四D ．一、三、四6．若一次函数y=（3-k ）x-k 的图象经过第二、三、四象限，则k 的取值X 围是（ ）A ．k>3B ．0<k ≤3C ．0≤k<3D ．0<k<37．已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（ ）A ．y=-x-2B ．y=-x-6C ．y=-x+10D ．y=-x-18．汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量y （升）与行驶时间t （时）的函数关系用图象表示应为下图中的（ ）9．李老师骑自行车上班，最初以某一速度匀速行进，•中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．在课堂上，李老师请学生画出他行进的路程y•（千米）与行进时间t（小时）的函数图象的示意图，同学们画出的图象如图所示，你认为正确的是（）10．一次函数y=kx+b的图象经过点（2，-1）和（0，3），•那么这个一次函数的解析式为（）A．y=-2x+3 B．y=-3x+2 C．y=3x-2 D．y=12x-3二、你能填得又快又对吗？（每小题3分，共30分）11．已知自变量为x的函数y=mx+2-m是正比例函数，则m=________，•该函数的解析式为_________．12．若点（1，3）在正比例函数y=kx的图象上，则此函数的解析式为________．13．已知一次函数y=kx+b的图象经过点A（1，3）和B（-1，-1），则此函数的解析式为_________．14．若解方程x+2=3x-2得x=2，则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方．15．已知一次函数y=-x+a与y=x+b的图象相交于点（m，8），则a+b=_________．16．若一次函数y=kx+b交于y•轴的负半轴，•且y•的值随x•的增大而减少，•则k____0，b______0．（填“>”、“<”或“＝”）17．已知直线y=x-3与y=2x+2的交点为（-5，-8），则方程组30220x yx y--=⎧⎨-+=⎩的解是________．y234A18．已知一次函数y=-3x+1的图象经过点（a，1）和点（-2，b），则a=________，b=______．19．如果直线y=-2x+k与两坐标轴所围成的三角形面积是9，则k的值为_____．20．如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，则此一次函数的解析式为__________，△AOC的面积为_________．三、认真解答，一定要细心哟！（共60分）21．（14分）根据下列条件，确定函数关系式：（1）y与x成正比，且当x=9时，y=16；（2）y=kx+b的图象经过点（3，2）和点（-2，1）．23．（12分）一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图象回答下列问题：（1）农民自带的零钱是多少？（2）降价前他每千克土豆出售的价格是多少？（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？24．（10分）如图所示的折线ABC•表示从甲地向乙地打长途所需的费y（元）与通话时间t（分钟）之间的函数关系的图象（1）写出y与t•之间的函数关系式．（2）通话2分钟应付通话费多少元？通话7分钟呢？25．（12分）已知雅美服装厂现有A种布料70米，B种布料52米，•现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.•1米，B种布料，可获利50元；做一套N型号的时装需用A种布料，B种布料0.•9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．①求y（元）与x（套）的函数关系式，并求出自变量的取值X围；②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？3．B 4．C 5．D 6．A 7．C 8．B 9．C 10．A 11．2；y=2x 12．y=3x 13．y=2x+1 14．<2 15．1616．<；< 17．58xy=-⎧⎨=-⎩18．0；7 19．±6 20．y=x+2；421．①y=169x；②y=15x+7522．y=x-2；y=8；x=1423．①5元；②0.5元；③45千克24．①当0<t≤3时，y=2.4；当t>3时，y=t-0.6．②25．①y=50x+45（80-x）=5x+3600．∵两种型号的时装共用A种布料[1.1x+0.•6（80-x）]米，共用B种布料[0.4x+0.9（80-x）]米，∴解之得40≤x≤44，而x为整数，∴x=40，41，42，43，44，∴y与x的函数关系式是y=5x+3600（x=40，41，42，43，44）；②∵y随x的增大而增大，∴当x=44时，y最大=3820，即生产M型号的时装44套时，该厂所获利润最大，最大利润是3820元．。

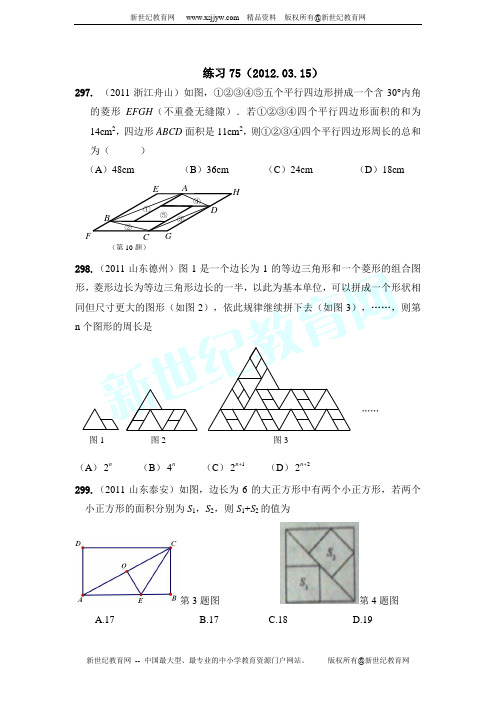
练习75（2012.03.15）
297. （2011浙江舟山）如图，①②③④⑤五个平行四边形拼成一个含30°内角
的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（ ）
（A ）48cm
（B ）36cm （C ）24cm （D ）18cm
298.（2011山东德州）图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n 个图形的周长是
（A ）2n （B ）4n （C ）12n + （D ）22n +
299.（2011山东泰安）如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2，则S 1+S 2的值为
第3题图
第4题图
A.17
B.17
C.18
D.19
（第10题） F A B C
D H E
G ①
② ③ ④ ⑤ 图1 图2 图3 ……
300.（2011山东泰安）如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为
A.2 3
B. 33
2 C.
3 D.6。

八年级 数学 第十四章一次函数 单元测试班级：____________姓名：____________座号：____________评分：____________一、填空题：(每空3分，共42分)1．已知函数：①y=0.2x+6；②y=-x-7；③y=4-2x ；④(1y x =；⑤y=4x ；⑥y=-(2-x)，其中，y 的值随x 的增大而增大的函数是_____________；y 的值随x 的增大而减小的函数是________________；图像经过原点的函数是_____________.（只填序号） 2. 在数学25+-=x y 中，K ＝ ，b=3.函数y=x -2自变量x 的取值范围是_________. 4.在432-=x y 中，当y=-6时，x ＝ 5. 若点P(a ，b)在第二象限内，则直线y ＝ax ＋b 不经过第_______限6.某商店出售一种瓜子，其售价y （元）与瓜子质量x （千克）之间的关系如下表由上表得y 与x 之间的关系式是 .7．已知直线y x a =-与2y x b =+的交点为（5，-8），则方程组020x y a x y b --=⎧⎨-+=⎩的解是____________．8.若直线y=kx+b 平行直线y=5x+3，且过点（2，-1），则k=______ ,b=______ . 9.已知y+2和x 成正比例，当x=2时，y=4，则y 与x 的函数关系式是_________________. 10.已知正比例函数y ＝（m －1）25m x -的图象在第二、四象限，则m的值为_________, 二、选择题：（每题3分，共18分） 11．函数y=2x+1的图象经过（ ） A ．(2 , 0)B ．(0 , 1)C. (1 , 0)D ．(12, 0) 12.下列各曲线中不能表示y 是x 的函数是（ ）。

13．已知一次函数y=kx+b 的图象如图所示,则k 、b 的符号是( )(A)k>0,b>0 (B)k>0,b<0 (C)k<0,b>0 (D)k<0,b<014. 如图，直线与y 轴的交点是（0，－3）,则当x<0时，（ ） A. y<0 B. y<－3 C. y>0 D. y>－315．已知点（-4，y 1），（2，y 2）都在直线y=- 12 x+2上，则y 1 、y 2大小关系是( )（A ）y 1 >y 2 （B ）y 1 =y 2 （C ）y 1 <y 2 （D ）不能比较16.一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度n(厘米)与燃烧 时间t(时)的函数关系的图象是( )三、解答题： 17．（本题10分）一次函数y=kx+4的图象经过点（－3，－2），则 （1）求这个函数表达式；（3）判断（－5，3）是否在此函数的图象上；（4）把这条直线向下平移4个单位长度后的函数关系式是________________．18．（本题10分）下图中，1l 反映了某公司产品的销售 收入与销售量的关系，2l 反映了该公司产品的销售成本 与销售量的关系，根据图中信息求出：①直线1l 对应的函数表达式是 ； ②直线2l 对应的函数表达式是 。

八年级（上）数学第十四章《一次函数》单元测试题（时间：120分钟 总分：120分）一．精心选一选：（本大题共10题，每小题3分，共30分）：相信自己有能力选得又快又准，每道小题四个选择支中只有惟一一个是正确的，请将正确答案的代号填入下表。

1．骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，自变量是 （ ）A.沙漠B.体温C.时间D.骆驼 2．下面两个变量是成正比例变化的是 ( )A ． 正方形的面积和它的边长．B ． 变量x 增加,变量y 也随之增加;C ． 矩形的一组对边的边长固定,它的周长和另一组对边的边长．D ． 圆的周长与它的半径．3． 下面哪个点不在函数y=－2x+3的图象上 （ ） A ．（-5，13） B ．（0.5，2） C ．（3，0） D ．（1，1） 4．在函数中，自变量x 的取值范围是 （ ）A.x ≥2 B ．x>2 C. x ≤2 D ．x<25．已知点（-4，y 1），（2，y 2）都在直线y= - 12x+2上，则y 1 、y 2大小关系是 ( )A ． y 1 > y 2B ． y 1 = y 2C ．y 1 < y 2D ． 不能比较6．下列各图给出了变量x 与y 之间的函数是（ ）7．直线y=kx ＋b 经过一、二、四象限,则k 、b 应满足 ( )A ． k>0, b<0B ． k>0, b>0C ． k<0, b<0;D ． k<0, b>08．关于函数12+-=x y ，下列结论正确的是 （ ）A ．图象必经过点（﹣2，1）B ．图象经过第一、二、三象限C ．当21>x 时，0<y D ．y 随x 的增大而增大9．已知一次函数y= ax+4与y = bx-2的图象在x 轴上相交于同一点,则ba的值是 ( ) A ．4 B ．-2 C ． 12 D ． - 12AB D2-x y =10．已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是 ( )A． B． C． D．11．小明骑自行车上学，开始以正常速度匀速行驶，但行至中途自行车出了故障，只好停下来修车。

第14章 一次函数单元测试题班级 学号 姓名 分数一、填空（30分）1. 已知函数y=(k –3)x k -8是正比例函数，则k=________.2. 函数y=x -1x -2自变量x 的取值范围是_________. 3. 已知一次函数经过点(–1 , 2)且y 随x 增大而减小，请写出一个满足上述条件的函数关系式 _________________.4. 已知y+2和x 成正比例，当x=2时，y=4，则y 与x 的函数关系式是_________________.5. 直线y=3x+b 与y 轴交点(0 ,–2)，则这条直线不经过第____象限.6. 直线y=x –1和y=x+3的位置关系是_________，由此可知方程组y =x -1y =x +3⎧⎨⎩解的情况为________.7. 已知点A(a ,–2) , B(b ,–4)在直线y=–x+6上，则a 、b 的大小关系是a____b. 8. 一次函数y= 2x -4的图象与x 轴交点坐标是 ，与y 轴交点坐标是 .9. 从A 地向B 地打长途，不超3分钟，收费2.4元，以后每超一分超加收一元，若通话时间为t 分钟（t ≥3且t 是整数），则付话费y 元与t 分钟函数关系式是__________________.10.某商店出售货物时，要在进价的基础上增加一定的利润，下表体现了其数量x （个）与售价y （元）的对应关系，根据表中提供的信息可知y 与x 之间的关系式是____________ ___。

数量x （个） 1 2 3 4 5 售价y （元） 8+0.216+0.424+0.632+0.840+1.0二、 选择（30分）11. 下列各图给出了变量x 与y 之间的函数是：（ ）12.下列函数，y 随x 增大而减小的是（ ） A ．y=x B ．y=x –1 C ．y=x+1D ．y=–x+113.y=kx+b 图象如图则（ ） A ．k>0 , b>0 B ．k>0 , b<0C ．k<0 , b<0D ．k<0 , b>014.已知直线y=(k –2)x+k 不经过第三象限，则k 的取值范围是（ ）A ．k ≠2B ．k>2C ．0<k<2D ．0≤k<2xyoAxyoB xyo D xyoC15.y=kx+k的大致图象是（）A B C D16.函数y=kx+2，经过点(1 , 3)，则y=0时，x=（）A．–2B．2C．0D．±2 17.直线y=x+1与y=–2x–4交点在（）A．第一象限B．第二象限C．第三象限D．第四象限18.函数y=2x+1的图象经过（）A．(2 , 0)B．(0 , 1) C. (1 , 0)D．(12, 0)19.正确反映，龟兔赛跑的图象是（）A B C D20、三峡工程在2003年6月1日至2003年6月10日下闸蓄水期间，水库水位由106米升至135米，高峡平湖初现人间，假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是：（）三、解答题（60分）21.（10分）已知函数y=(2m–2)x+m+1(1)m为何值时，图象过原点.(2)已知y随x增大而增大，函数图象与y轴交点在x轴上方，求m取值范围.22.（10分）已知一次函数图象经过点(3 , 5) , (–4，–9)两点.(1)求一次函数解析式.(2)求图象和坐标轴围成三角形面积.23、（10分）直线y=2x+m和直线y=3x+3的交点在第二象限，求m的取值范围.24、(10分)等腰三角形周长40cm.（1）写出底边长ycm与腰xcm的函数关系式.并写出自变量取值范围.(2)画出函数图象25、(10分)甲、乙两人分别骑自行车和摩托车从甲地到乙地（1）谁出发较早，早多长时间？谁到达乙地早？早多长时间?（2）两人行驶速度分别是多少？（3）分别求出自行车和摩托车行驶过程的函数解析式？26、(10分)某地拔号入网有两种收费方式，A计时制:3元/时; B月租制:54元/月，另加通信费1.2元/时，问选择哪种上网方式省钱？。

第14章一次函数一、选择题1.下列各关系中，符合正比例关系的是（）A. 正方形的周长P和它的一边长a B. 距离s一定时，速度v和时间t C. 圆的面积S和圆的半径r D. 正方体的体积V和棱长a2.已知x轴上的点P到y轴的距离为3，则点P的坐标为（）A. （3，0）B. （0，3）C. （0，3）或（0，﹣3）D. （3，0）或（﹣3，0）3.某种签字笔的单价为2元，购买这种签字笔x支的总价为y元．则y与x之间的函数关系式为（）A. B.C. y=-2xD. y=2x4.点P（m+3，m﹣1）在x轴上，则点P的坐标为（）A. （0，﹣2）B. （2，0） C. （4，0） D. （0，﹣4）5.如果点P（m，1-2m）在第四象限，那么m的取值范围是A. 0＜m＜B. -＜m＜0 C. m＜0 D. m＞6.在三角形面积公式S=ah，a=2cm中，下列说法正确的是（）A. S，a是变量，h是常量 B. S，h是变量，是常量C. S，h是变量，a是常量 D. S，h，a是变量，是常量7.一次函数y=kx+b的图象如图所示，不等式kx+b＞0的解集是（）A. x＞2B. x＞4 C. x＜2 D. x＜48.一次函数y=kx+b经过第一、三、四象限，则下列正确的是（）A. k＞0，b＞0B. k＞0，b＜0 C. k＜0，b＞0 D. k＜0，b＜09.函数y=中，自变量x的取值范围是（）A. x＞5B. x＜5 C. x≥5D. x≤510.已知和是二元一次方程ax+by+3=0的两个解，则一次函数y=ax+b（a≠0）的解析式为（）A. y=﹣2x﹣3 B. y=x+C. y=﹣9x+3 D. y=-x-11.函数y=x+的图象如图所示，下列对该函数性质的论述正确的是（）A. 该函数的图象是轴对称图形 B. 在每个象限内，y的值随x值的增大而减小C. 当x＞0时，该函数在x=1时取得最小值2D. y的值可能为112.将函数y=﹣3x的图象沿y轴向下平移2个单位长度后，所得图象对应的函数关系式为（）A. y=3x+2B. y=﹣3x﹣2 C. y=﹣3（x+2） D. y=﹣3（x﹣2）二、填空题13.直线y=2x﹣6向上平移3个单位后得到的直线是________ ．14.若函数y= -2x m+2是正比例函数，则m的值是________.15.点（a，a+2）在第二象限，则a的取值范围是________．16.“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，________ 随________ 变化而变化，其中自变量是________ ，因变量是________ ．17.已知一次函数y=kx+b（k、b为常数，且k≠0），x、y的部分对应值如下表：18.某通讯公司推出了①②两种收费方式，收费y1， y2（元）与通讯时间x（分钟）之间的函数关系如图所示，则使不等式kx+30＜x成立的x的取值范围是________19.长方形的周长是24cm，其中一边长为xcm（x＞0），面积为y，则这个长方形面积y与边长x之间的关系可以表示为________20.甲、乙两车分别从A，B两地同时相向匀速行驶，当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过15小时后两车同时到达距A地300千米的C地（中途休息时间忽略不计）．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数关系如图所示，则当甲车到达B地时，乙车距A地________千米．21. 如图，这是台州市地图的一部分，分别以正东、正北方向为x轴、y轴的正方向建立直角坐标系，规定一个单位长度表示1km，甲、乙两人对着地图如下描述路桥区A处的位置．则椒江区B处的坐标是________ ．22. 运动员在400m一圈的跑道上训练，他跑一圈所用的时间t（s）与跑步速度v（m/s）之间的函数关系式为t=________ ．三、解答题23.如图是边长为4的正方形，请你建立适当的直角坐标系，并写出点A，B，C，D的坐标．24.直线y=kx+1经过点A（1，3），求关于x的不等式kx+1≥3的解集．25.若x，m都为非负数，x﹣y﹣m=﹣1，2x+m=3．求y与x的函数关系式，并画出此函数的图象．26.公交公司的某路公交车每月运营总支出的费用为4000元，乘客乘车的票价为2元/人次．设每月的乘客量为x（人次），每月的赢利额为y（元）．（赢利额=总收入﹣总支出）（1）y（元）与x（人次）之间的关系式为________；（x为正整数）（2）根据关系式填表：27.如图，在直角坐标系中，直线y=kx+4与x轴正半轴交于一点A，与y轴交于点B，已知△OAB的面积为10，（1）求这条直线的解析式；（2）若将这条直线沿x轴翻折，求翻折后得到的直线的解析式．参考答案一、选择题A D D C D C CBCD C B二、填空题13. y=2x﹣3 14. -1 15. ﹣2＜a＜016. 温度；时间；时间；温度 17. x＜﹣2 18. x＞30019. y=（12﹣x）x 20. 100 21. （） 22.三、解答题23.解：根据题意，建立的平面直角坐标系如右图所示，则点A的坐标是（0，4），点B的坐标是（4，4），点C的坐标是（0，0），点D的坐标是（4，0）．24. 解：把A（1，3）代入y=kx+1得：k+1=3，解得：k=2，则不等式是2x+1≥3，解得：x≥1．25. 解：∵2x+m=3，∴m=3﹣2x．∵x，m都为非负数，∴3﹣2x≥0，x≥0，∴0≤x≤．把m=3﹣2x代入x﹣y﹣m=﹣1得，y=3x﹣2，其函数图象如图．26. （1）y=2x﹣4000（2）3000；﹣2000；﹣1000；0；1000；2000；（3）200027. （1）解：当y=0时，kx+4=0，解得x=﹣，则A（﹣，0），当x=0时，y=kx+4=4，则B（0，4），因为△OAB的面积为10，所以•（﹣）•4=10，解得k=﹣，所以直线解析式为y=﹣x+4（2）解：若将直线y=﹣x+4沿x轴翻折，翻折后得到的直线的解析式为﹣y=﹣x+4，即y=x﹣4。

周周清3（函数的基本性质与待定系数法）一、选择题：（20）1、若一次函数b kx y +=的图象经过一、二、三象限,则b k ,应满足的条件是:A.0,0>>b kB.0,0<>b kC.0,0><b kD.0,0<<b k2、已知：)2()2(122+++=-+m x m y m m 是正比例函数,则m 的值是：A.m =1B. m =-2C. m =1或m =-2D. m ≠03. 在下列四个函数中，y 的值随x 值的增大而减小的是（ ）Ａ．2y x = Ｂ．36y x =- Ｃ．25y x =-+ Ｄ．37y x =+4. 正比例函数y=(2k-3)x 的图像过点(-3,5),则k 的值为 ( ) A. 95- B. 37 C. 35 D. 32 5. 已知正比例函数y=(2m-1)x 的图像上两点A(x 1,y 1),B(x 2,y 2),当x 1<x 2时,有y 1>y 2,那么m 的取值范围是 ( ) A. m<21 B. m>21 C. m<2 D. m>0 6. 如图所示，OA ，BA 分别表示甲、乙两名学生运动的一次函数图象，图中s 和t 分别表示运动路程和时间，根据图象可知，快者的速度比慢者的速度每秒快（ ）（A ）2.5米 （B ）2米 （C ）1.5米 （D ）1米二、填空题（20）7．y =x 的取值范围是 。

8. 已知函数y kx b y =+的图象与轴交点的纵坐标为5-，且当12x y ==时，，则此函数的解析式为 ．9. 已知一次函数35y x =+与一次函数6y ax =-，若它们的图象是两条互相平等的直线，则a = ．10. 若一次函数y=kx+b 交于y 轴的正半轴,且y 的值随x 的增大而减小,则k____0,b___0.(填”>””=””<”号)三，简答题（60）11. 作出函数41y x =-的图象，并回答下列问题：（1）y 的值随x 值的增大而（2）图象与x 轴的交点A 的坐标 、与y 轴的交点B 的坐标是（3）⊿AOB 的面积是12. 已知一次函数的图像经过(-3,5),(1,37)两点,求此一次函数的解析式.13. 如图所示，直线m 是一次函数y =kx +b 的图象．（1）求该一次函数解析式。