5-Simulink_子系统与模块封装

simulink中的子系统模块使用介绍
simulink中的子系统模块是将多个模块组合成一个单独的模块，以便更好地组织和管理复杂的模型。

在simulink中，子系统模块可
以包含一组输入和输出端口，并且可以与其他模块一样进行信号连接。

本文将介绍如何使用子系统模块。

1. 创建子系统模块
要创建子系统模块，可以从simulink库中选择“子系统”模块，并将其拖动到模型中。

然后，可以双击该模块以打开子系统编辑器。

在编辑器中，可以添加输入和输出端口，以及其他需要的模块。

2. 使用子系统模块
一旦创建了子系统模块，就可以将其用作模型中的模块。

在模型中连接其他模块时，可以将子系统模块视为单个模块，并将其输入和输出端口连接到其他模块的输入和输出端口。

3. 子系统模块的优点
使用子系统模块可以使模型更易于理解和维护。

通过将多个模块组合成一个子系统模块，可以隐藏模型的复杂性，并使其更易于组织和管理。

此外，子系统模块还可以在多个模型之间重复使用。

4. 总结
子系统模块是simulink中的重要功能之一，可用于组织和管理
复杂的模型。

使用子系统模块可以使模型更易于理解和维护，并且可以在多个模型之间重复使用。

- 1 -。

simulink封装如何写介绍
Simulink封装可以通过以下步骤来写介绍：
1.确定封装的功能和用途：在介绍中首先需要明确封装的功能和
用途，包括模块的输入、输出以及实现的功能等。

2.描述封装的具体操作步骤：介绍中需要详细描述封装的操作步
骤，包括如何导入模块、如何设置参数、如何进行初始化等。

3.强调封装的优点和特点：介绍中需要强调封装的优点和特点，
包括使用方便、易于维护、可扩展性强等。

4.给出封装的实例和效果：在介绍中可以给出封装的实例和效
果，包括使用封装的模块实现的算法逻辑、性能指标等。

5.给出封装的参考文献和联系方式：在介绍中可以给出封装的参
考文献和联系方式，方便用户进行深入了解和使用。

需要注意的是，Simulink封装介绍需要简洁明了，让用户能够快速了解封装的功能和用途。

同时，需要注意表达清晰、准确，避免使用过于专业或难以理解的术语。

simulink中subsystem模块Simulink是一个基于MATLAB的图形编程环境，用于模拟、分析和设计动态系统。

在Simulink中，子系统（Subsystem）模块是一种重要的组件，允许用户将多个模块封装在一起，形成一个单独的、可重用的模块，类似于编程中的函数或方法。

子系统不仅可以帮助管理大型模型的复杂性，还能促进模型的模块化设计和重用。

一、子系统模块的特点1．封装性：子系统可以将一组有逻辑联系的模块封装成一个单元，从而隐藏内部实现的细节，仅通过输入和输出与外部世界交互。

2．重用性：创建的子系统可以在同一个模型中多次使用，也可以在不同的Simulink模型中重用。

3．层次性：子系统可以嵌套使用，即一个子系统内部可以包含其他子系统，这有助于建立分层和结构化的模型设计。

4．可维护性：子系统简化了模型的结构，使得对模型的修改、调试和维护更为方便。

二、创建和使用子系统创建子系统：1．可以通过选择模型中的一部分组件，然后使用Simulink的“创建子系统”功能将它们封装为一个子系统。

2．也可以从Simulink库中直接拖拽一个空的子系统模块到模型中，然后向其中添加组件。

配置输入和输出：1．子系统的输入和输出通过特殊的模块（如Inport和Outport）来实现。

2．每个Inport模块代表子系统的一个输入，每个Outport模块代表子系统的一个输出。

编辑子系统：1．双击子系统模块可以进入其内部，对子系统内部的模块进行编辑和配置。

2．子系统内部可以包含各种Simulink模块，如数学运算、逻辑判断、信号处理等。

参数化子系统：1．子系统可以有自己的参数，这些参数可以在子系统的掩码（Mask）中定义和配置。

2．掩码技术允许为子系统创建一个用户界面，用户可以通过这个界面输入参数值，这些参数值可以影响子系统内部模块的行为。

三、子系统的类型1．虚拟子系统：默认的子系统类型，不对信号进行缓存，信号直接通过子系统。

学院电气信息工程学院学号姓名课程通信系统仿真日期2013年11月7日一、实验项目：构建SIMULINK子系统和模块的封装二、实验目的：1、学习构建SIMULINK子系统，模块的封装；2、传递函数模块的应用。

三、实验设备：计算机四、实验内容及步骤：1、学习信号与系统中的传递函数的应用：拉氏变换和Z变换。

a.通过仿真求出H(s)=5/(2S+1)的阶跃响应和冲击响应。

构建模型得出波形。

对比采用默认仿真参数以及采用仿真步长为1/1000秒两种情况的波形。

你能解释吗？b.将200Hz的锯齿波通过1000次每秒的采样保持器之后得到时间离散信号，观察采样保持器前后波形额变化，解释为什么。

然后将时间离散信号通过传递函数H(z)=4/(z+0.3)的系统，求出响应波形。

仿真步长为1/1000秒。

需要设置所以模块额参数，特别是采样率一定要设置为1/1000秒。

2、学习构建SIMULINK子系统：构建一个子系统，使得它具有将输入信号m(t)和一个常数C相加后再和一个1000Hz的幅度为A的正弦波相乘的功能。

即输出信号：事实上，这就是个幅度调制子系统。

y(t)=A(m(t)+C)sin(2*pi*f*t)其中f=1000Hz。

参数A，C，f要求在Matlab命令空间中用语句进行设置。

3、对子系统进行封装：请对2所建立子系统进行封装（Mask），编写参数输入对话框和帮助文档。

并将模块放在一个自己的库中。

五、实验结果与总结：1、- 1 -学院 电气信息工程学院 学号 姓名 课程通信系统仿真日期 2013年11月7日 - 2 -a.设置参数如下图：采用默认仿真参数得到的波形：学院电气信息工程学院学号姓名课程通信系统仿真日期2013年11月7日- 3 -设置仿真步长为1/1000秒，以及得到的波形：b.学院 电气信息工程学院 学号 姓名 课程通信系统仿真日期 2013年11月7日 - 4 -参数设置如下图：在命令空间中用语句进行设置A,C,f学院 电气信息工程学院 学号 姓名 课程通信系统仿真 日期 2013年11月7日 - 5 -实验结果如下图：2、学院电气信息工程学院学号姓名课程通信系统仿真日期2013年11月7日- 6 -参数设置如下图：学院 电气信息工程学院 学号 姓名 课程通信系统仿真 日期 2013年11月7日 - 7 -实验结果如下图：3、学院 电气信息工程学院 学号 姓名 课程通信系统仿真 日期 2013年11月7日- 8 -六、拟完成的思考题目：1、 说明封装子系统的过程。

Simulink S-Function 编程（C语言）与模块封装技术1．S-Function概念S-Function（System function）是Simulink模块的计算机语言描述。

可以用M、C/C++、Ada、Fortran 语言以MEX（Matlab Executable，MATLAB可执行文件，在Windows系统中就是其为DLL）文件的形式编写。

S-Function以特殊的方式与Simulink方程求解器交互。

这种交互和Simulink内建模块的做法非常相似。

S-Function模块可以是连续、离散或者混合系统。

通过S-Function，用户可以将自己的模块加入Simulink模型中。

从而可以实现用户自定义的算法或者与硬件设备交互等。

2．S-Function工作机制2.1 Simulink模块的数学描述Simulink模块包括一系列输入、状态和输出。

输出是采样时间、输入、模块状态的函数。

下面的方程描述了输入、输出和状态的数学关系。

2.2 仿真过程Simulink模型的执行按下述几个步骤。

首先是初始化阶段。

在这一阶段Simulink将库模块集合到模型，传播宽度、数据类型和采样时间，评估模块参数，确定模块执行顺序，分配内存。

然后是仿真阶段。

此时Simulink进入一个仿真循环，循环的每次执行对应一个仿真步。

在每个仿真步，Simulink按初始化阶段确定的顺序执行各个模块。

对每个模块，Simulink计算模块在当前采样时间的状态、微分和输出。

这将持续到仿真结束。

图1描述了Simulink的仿真过程。

图1 Simulink执行仿真的步骤2.3 S-function的回调（Callback）方法S-function包括一系列的回调方法，用以执行每个仿真步骤所需的任务。

在一个模型的仿真过程中，每个仿真步骤，Simulink将调用各S-function的适当方法。

S-function执行的方法包括：●初始化：在首次仿真循环中执行。

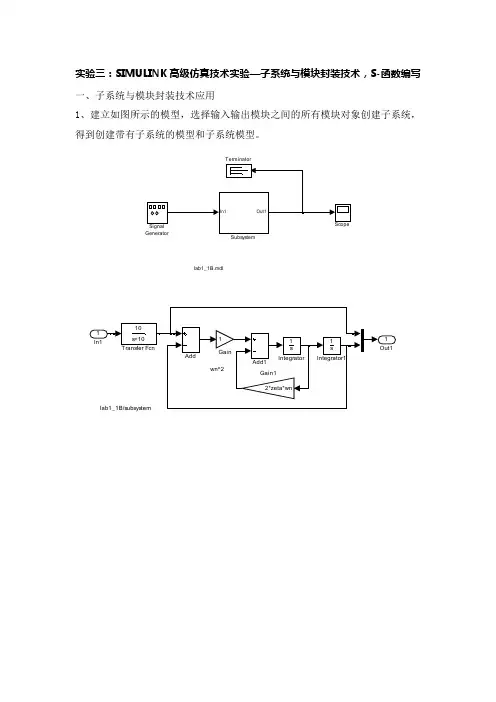
实验三：SIMULINK高级仿真技术实验—子系统与模块封装技术，S-函数编写一、子系统与模块封装技术应用1、建立如图所示的模型，选择输入输出模块之间的所有模块对象创建子系统，得到创建带有子系统的模型和子系统模型。

lab1_1B.mdl Terminator2、线性系统由下列微积分方程组成：1122231312322123535x x x x x x u x x x x u y x u u=-+⎧⎪=--+⎪⎨=---+⎪⎪=-+-⎩（1） 采用积分器方法在SIMULINK 上建立模型。

（2）对上述模型进行子系统封装，要求子系统的输入信号两个u1和u2，输出信号有四个x1，x2，x3和y 。

lab1_2B.mdl二、基于SIMULINK 的微分方程求解： 1、考虑下面给出的微分代数方程：11231222122321230.20.325210x x x x x x x x x x x x x x x =-++⎧⎪=--⎨⎪++-=⎩已知初始条件为123(0)0.8,(0)(0)0.1x x x ===。

在SIMULINK 上搭建微分代数方程的仿真模型，利用MATLAB 的函数模块进行编程，并对系统进行仿真。

-0.4-0.20.20.40.60.812、延迟微分方程的SIMULINK 求解。

考虑下面给出的延迟微分方程式：3()13()(1)0.2(0.5)(0.5)()3()2()4()x t x t y t x t x t y t y t y t x t =-------⎧⎨++=⎩要求：（1）建立延迟微分方程的SIMULINK 模型（2） 在阶跃输入下的系统状态变量和输出响应曲线，并在图上标注(),()x t y t 。

0123456789100.050.10.150.20.250.30.350.4tx &y三、双输入双输出系统的状态方程表示为：2.255 1.250.5462.25 4.25 1.250.25240.250.5 1.251221.25 1.750.250.75020001022x x u y x ---⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=+⎢⎥⎢⎥---⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦输入信号分别是sin(),cos()t t ，要求：（1） 在SIMULINK 搭建上述多变量系统仿真模型，并利用MATLAB 语言绘制系统的输出曲线和状态曲线。