(完整word版)matlab绘制温度场

Matlab图形绘制技巧与实例展示一、介绍Matlab是一种功能强大的计算机软件，常用于科学计算和数据可视化分析。

其中，图形绘制是Matlab的一项重要功能，能够直观地展示数据和结果。

本文将探讨一些Matlab图形绘制的技巧，并通过实例展示其应用。

二、基础图形绘制Matlab提供了多种基础图形绘制函数，如plot、scatter、bar等。

这些函数可以用来绘制折线图、散点图、柱状图等常见图形。

例如我们可以使用plot函数绘制一个简单的折线图：```matlabx = 1:10;y = [1, 2, 3, 4, 5, 4, 3, 2, 1, 0];plot(x, y);```运行以上代码，就可以得到一个由点连接而成的折线图。

通过修改x和y的取值，可以得到不同形状和样式的折线图。

三、图形修饰在绘制图形时，我们通常需要添加标题、坐标轴标签、图例等进行修饰。

Matlab提供了相应的函数，如title、xlabel、ylabel、legend等。

下面是一个例子：```matlabx = 1:10;y = [1, 4, 9, 16, 25, 16, 9, 4, 1, 0];plot(x, y);title('Parabolic Curve');xlabel('X-axis');ylabel('Y-axis');legend('Curve');```执行以上代码，我们得到一个带有标题、坐标轴标签和图例的折线图。

四、子图绘制有时候，我们希望在一幅图中同时显示多个子图，以便比较它们之间的关系。

Matlab提供了subplot函数来实现这个功能。

下面是一个例子：```matlabx = 1:10;y1 = [1, 2, 3, 4, 5, 4, 3, 2, 1, 0];y2 = [0, 1, 0, 1, 0, 1, 0, 1, 0, 1];subplot(2, 1, 1);plot(x, y1);title('Subplot 1');subplot(2, 1, 2);plot(x, y2);title('Subplot 2');通过subplot函数，我们将一幅图分为两个子图，并在每个子图中绘制不同的折线图。

第28卷　第11期2006年11月武　汉　理　工　大　学　学　报JOURNA L OF WUHAN UNIVERSIT Y OF TECHN OLOG Y Vol.28　No.11　Nov.2006MA T LAB 与VB 接口编程实现磨削温度场的仿真汪心立,张建华,任升峰,段彩云,董春杰(山东大学机械工程学院,济南250061)摘　要:　将MA TLAB 的强大数学运算功能和图形绘制功能与VB 在用户界面开发方面的优势结合起来,通过混合编程实现了磨削温度场的仿真研究。

在仿真系统的前端界面输入计算温度场的命令语句或者是直接输入磨削用量后经过调用MA TLAB 软件计算可以得到相应条件下的温度场模型,同时该仿真系统除了应用温度场仿真外还可扩充到其他物理量如磨削力,表面粗糙度等的仿真研究。

关键词:　磨削;　温度场;　MA TLAB ;　VB ;　计算机仿真中图分类号:　TP 391.9文献标志码:　A 文章编号:167124431(2006)1120111203Simulation of G rinding T emperature Field B ased on the Applicationof MAT LAB and VBW A N G Xi n 2li ,ZHA N G Jian 2hua ,R EN S heng 2f eng ,DUA N Cai 2yun ,DON G Chun 2jie(School of Mechanical Engineering ,Shandong University ,Jinan 250061,China )Abstract :　This paper introduced the research of simulation in grinding temperature field based on the hybrid programming between MA TLAB and VB.The simulation integrates their advantages ,which were powerful mathematic calculation capacity and graphic capacity of MA TLAB ,and VB ’s friendly visual interface.When inputting programmed command of temperature pattern or grinding parameters directly ,the temperature distribution could be gained through calculating by MA TLAB ,and be 2sides ,it could also be applied to other physical quantity simulation ,for example grinding force ,surface roughness and so on.K ey w ords :　grinding ;　temperature fields ;　MA TLAB ;　VB ;　computer simulation 收稿日期:2006205220.基金项目:国家自然科学基金(50275087).作者简介:汪心立(19802),男,硕士.E 2mail :wangxinli @在磨削温度场的仿真研究中,应用数学模型和计算机仿真技术能够得出比较准确的温度分布图,可以分析磨削用量对温度场的影响,进而发现磨削温度场的变化规律,通过优化磨削用量,使温度场的温度变化趋向于合理[1],最终能够达到在磨削过程中减少磨削烧伤发生的效果。

MATLAB 中⽮量场图的绘制 (quiver/quiver3/dfield/pplane) Plot the vector field with MATLABMATLAB 中⽮量场图的绘制（q...1.quiver 函数⼀般⽤于绘制⼆维⽮量场图，函数调⽤⽅法如下：该函数展⽰了点(x,y)对应的的⽮量(u,v)。

其中，x 的长度要求等于u 、v 的列数，y 的长度要求等于u 、v 的⾏数。

在绘制图像的过程中，通常⽤ meshgrid 来⽣成所需的⽹格采样点。

下⾯举⼏个例⼦：例1：⼀个最简单的例⼦，该⼆维⽮量场图中的⽮量皆从(0,0)出发，分别指向(1,0) 、(-1,0) 、(0,1) 、(0,-1)。

画出下图但我们发现箭头并没有完全指到(1,0) 、(-1,0) 、(0,1) 、(0,-1) 。

如果需要箭头完全指到(1,0) 、(-1,0) 、(0,1) 、(0,-1)，我们需要改变scale 参数，将其设为1。

参考⽅法如下： 画出图像如下 ：当然，也可以改变颜⾊。

改变颜⾊可以参考LineSpec 的设置，参考代码如下： 画出图像如下：例2：(参考MathWorks )：已知u=ycosx" role="presentation" style="margin: 0px; padding: 0px; display: inline; line-height: normal; font-size: 13.3333px; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border:0px; position: relative;">u=ycosx, v=ysinx" role="presentation" style="margin: 0px; padding: 0px; display: inline; line-height: normal; font-size:13.3333px; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">v=ysinx 画出下图:2.quiver3函数⽤法与quiver 类似，⽤于三维⽮量场图的绘制。

matlab微分方程方向场在MATLAB中，可以使用方向场来可视化微分方程的解。

方向场是一个图形工具，用于显示微分方程在不同点上的斜率或者梯度。

通过观察方向场，我们可以获得微分方程解的大致行为和趋势。

要绘制微分方程的方向场，可以按照以下步骤进行操作：1. 定义微分方程，首先，需要将微分方程转化为MATLAB可识别的形式。

例如，如果有一个一阶微分方程dy/dx = f(x, y)，则需要定义一个函数f(x, y)，该函数返回斜率的值。

2. 创建方向场，使用meshgrid函数创建一个网格，该网格覆盖了所关注的x和y的范围。

可以通过指定x和y的范围以及步长来调整网格的精细度。

3. 计算斜率，在网格上计算微分方程的斜率。

对于每个网格点，使用定义的微分方程函数f(x, y)计算斜率的值。

4. 绘制方向场，使用quiver函数绘制方向场。

quiver函数接受x和y的坐标网格以及对应的斜率值，并在每个网格点上绘制箭头表示斜率的方向和大小。

下面是一个简单的示例代码，用于绘制微分方程 dy/dx = x y 的方向场：matlab.% 定义微分方程函数。

f = @(x, y) x y;% 创建网格。

x = linspace(-5, 5, 20);y = linspace(-5, 5, 20);[X, Y] = meshgrid(x, y);% 计算斜率。

slope = f(X, Y);% 绘制方向场。

quiver(X, Y, ones(size(slope)), slope);xlabel('x');ylabel('y');title('Direction Field of dy/dx = x y');运行以上代码，即可绘制出微分方程 dy/dx = x y 的方向场。

方向场可以帮助我们观察微分方程的解在不同点上的行为，例如确定稳定点、不稳定点、周期解等。

通过调整定义微分方程的函数f(x, y)，可以绘制不同微分方程的方向场。

MATLAB图形绘制技巧与实例介绍：MATLAB是一种功能强大，广泛应用于科学计算和工程领域的软件平台。

它拥有丰富的图形绘制功能，可以用于可视化数据和传达研究成果。

本文将探讨一些MATLAB图形绘制的技巧和提供一些实例，让读者了解如何高效地利用MATLAB 绘制各种类型的图形。

一、基本绘图函数MATLAB中最基本的绘图函数是plot，它可以绘制二维图形。

可以通过指定x和y向量作为输入参数，将数据点连线绘制出来。

除了plot函数，还有其他一些常用的绘图函数，如scatter用于绘制散点图，bar用于绘制条形图，hist用于绘制直方图等。

这些函数具有丰富的参数选项，可以根据需要进行调整，以得到满意的图形效果。

二、自定义图形样式在MATLAB中，可以通过一些简单的命令实现图形样式的自定义。

例如，可以通过修改线型、颜色和点标记等属性，使得图形更加美观和易读。

除了利用内置的属性选项，还可以使用一些自定义的方法，如在plot函数中添加字符串参数来自定义线型和颜色。

三、多图绘制在某些情况下，需要在一个图形窗口中展示多个图形。

MATLAB提供了subplot函数，可以将图形窗口划分为多个小的绘图区域，并在每个区域中绘制不同的图形。

这对于比较不同数据集之间的关系或展示多个实验结果非常有用。

另外，还可以使用hold on和hold off命令，以在同一个图形窗口中绘制多个图形，并在绘制后保持图形的可编辑性。

四、3D图形绘制除了二维图形，MATLAB还支持绘制三维图形。

可以使用plot3函数将数据点绘制成三维曲线或散点图。

也可以使用mesh和surf函数绘制三维表面图，这在可视化函数和曲面的形状时非常有用。

通过调整视角和添加颜色映射等设置，可以使得3D图形更加生动和具有立体感。

五、图形标注和注释为了更好地传达和解释图形的含义，MATLAB提供了一些标注和注释功能。

可以使用xlabel、ylabel和title函数添加坐标轴标签和标题。

MATLAB主要命令汇总MATLAB函数参考附录1.1 管理用命令函数名功能描述函数名功能描述addpath 增加一条搜索路径 rmpath 删除一条搜索路径demo 运行Matlab演示程序 type 列出.M文件doc 装入超文本文档 version 显示Matlab的版本号help 启动联机帮助 what 列出当前目录下的有关文件lasterr 显示最后一条信息 whatsnew 显示Matlab的新特性lookfor 搜索关键词的帮助 which 造出函数与文件所在的目录path 设置或查询Matlab路径附录1.2管理变量与工作空间用命令函数名功能描述函数名功能描述clear 删除内存中的变量与函数 pack 整理工作空间内存disp 显示矩阵与文本 save 将工作空间中的变量存盘length 查询向量的维数 size 查询矩阵的维数load 从文件中装入数据 who,whos 列出工作空间中的变量名附录1.3文件与操作系统处理命令函数名功能描述函数名功能描述cd 改变当前工作目录 edit 编辑.M文件delete 删除文件 matlabroot 获得Matlab的安装根目录diary 将Matlab运行命令存盘 tempdir 获得系统的缓存目录dir 列出当前目录的内容 tempname 获得一个缓存(temp)文件! 执行操作系统命令附录1.4窗口控制命令函数名功能描述函数名功能描述echo 显示文件中的Matlab中的命令 more 控制命令窗口的输出页面format 设置输出格式附录1.5启动与退出命令函数名功能描述函数名功能描述matlabrc 启动主程序 quit 退出Matlab环境startup Matlab自启动程序附录2 运算符号与特殊字符附录2.1运算符号与特殊字符函数名功能描述函数名功能描述+ 加 ... 续行标志- 减 , 分行符(该行结果不显示)* 矩阵乘 ; 分行符(该行结果显示).* 向量乘 % 注释标志^ 矩阵乘方 ! 操作系统命令提示符.^ 向量乘方矩阵转置kron 矩阵kron积 . 向量转置\ 矩阵左除 = 赋值运算/ 矩阵右除 == 关系运算之相等.\ 向量左除 ~= 关系运算之不等./ 向量右除 < 关系运算之小于: 向量生成或子阵提取 <= 关系运算之小于等于() 下标运算或参数定义 > 关系运算之大于[] 矩阵生成 >= 关系运算之大于等于{} & 逻辑运算之与. 结构字段获取符 | 逻辑运算之或. 点乘运算,常与其他运算符联合使用(如.\) ~ 逻辑运算之非xor 逻辑运算之异成附录2.2逻辑函数函数名功能描述函数名功能描述all 测试向量中所用元素是否为真 is*(一类函数) 检测向量状态.其中*表示一个确定的函数(isinf)any 测试向量中是否有真元素 *isa 检测对象是否为某一个类的对象exist 检验变量或文件是否定义 logical 将数字量转化为逻辑量find 查找非零元素的下标附录3 语言结构与调试附录3.1编程语言函数名功能描述函数名功能描述builtin 执行Matlab内建的函数 global 定义全局变量eval 执行Matlab语句构成的字符串 nargchk 函数输入输出参数个数检验feval 执行字符串指定的文件 script Matlab语句及文件信息function Matlab函数定义关键词附录3.2控制流程函数名功能描述函数名功能描述break 中断循环执行的语句 if 条件转移语句case 与switch结合实现多路转移 otherwise 多路转移中的缺省执行部分else 与if一起使用的转移语句 return 返回调用函数elseif 与if一起使用的转移语句 switch 与case结合实现多路转移end 结束控制语句块 warning 显示警告信息error 显示错误信息 while 循环语句for 循环语句附录3.3交互输入函数名功能描述函数名功能描述input 请求输入 menu 菜单生成keyboard 启动键盘管理 pause 暂停执行附录3.4面向对象编程函数名功能描述函数名功能描述class 生成对象 isa 判断对象是否属于某一类double 转换成双精度型 superiorto 建立类的层次关系inferiorto 建立类的层次关系 unit8 转换成8字节的无符号整数inline 建立一个内嵌对象附录3.5调试函数名功能描述函数名功能描述dbclear 清除调试断点 dbstatus 列出所有断点情况dbcont 调试继续执行 dbstep 单步执行dbdown 改变局部工作空间内存 dbstop 设置调试断点dbmex 启动对Mex文件的调试 sbtype 列出带命令行标号的.M文件dbquit 退出调试模式 dbup 改变局部工作空间内容dbstack 列出函数调用关系附录4 基本矩阵与矩阵处理附录4.1基本矩阵函数名功能描述函数名功能描述eye 产生单位阵 rand 产生随机分布矩阵linspace 构造线性分布的向量 randn 产生正态分布矩阵logspace 构造等对数分布的向量 zeros 产生零矩阵ones 产生元素全部为1的矩阵 : 产生向量附录4.2特殊向量与常量函数名功能描述函数名功能描述ans 缺省的计算结果变量 non 非数值常量常由0/0或Inf/Inf获得computer 运行Matlab的机器类型 nargin 函数中参数输入个数eps 精度容许误差(无穷小) nargout 函数中输出变量个数flops 浮点运算计数 pi 圆周率i 复数单元 realmax 最大浮点数值inf 无穷大 realmin 最小浮点数值inputname 输入参数名 varargin 函数中输入的可选参数j 复数单元 varargout 函数中输出的可选参数附录4.3时间与日期函数名功能描述函数名功能描述calender 日历 eomday 计算月末clock 时钟 etime 所用时间函数cputime 所用的CPU时间 now 当前日期与时间date 日期 tic 启动秒表计时器datenum 日期(数字串格式) toc 读取秒表计时器datestr 日期(字符串格式) weekday 星期函数datevoc 日期(年月日分立格式)附录4.4矩阵处理函数名功能描述函数名功能描述cat 向量连接 reshape 改变矩阵行列个数diag 建立对角矩阵或获取对角向量 rot90 将矩阵旋转90度fliplr 按左右方向翻转矩阵元素 tril 取矩阵的下三角部分flipud 按上下方向翻转矩阵元素 triu 取矩阵的上三角部分repmat 复制并排列矩阵函数附录5 特殊矩阵函数名功能描述函数名功能描述compan 生成伴随矩阵 invhilb 生成逆hilbert矩阵gallery 生成一些小的测试矩阵 magic 生成magic矩阵hadamard 生成hadamard矩阵 pascal 生成pascal矩阵hankel 生成hankel矩阵 toeplitz 生成toeplitz矩阵hilb 生成hilbert矩阵 wilkinson 生成wilkinson特征值测试矩阵附录6 数学函数附录6.1三角函数函数名功能描述函数名功能描述sin/asin 正弦/反正弦函数 sec/asec 正割/反正割函数sinh/asinh 双曲正弦/反双曲正弦函数 sech/asech 双曲正割/反双曲正割函数cos/acos 余弦/反余弦函数 csc/acsc 余割/反余割函数cosh/acosh 双曲余弦/反双曲余弦函数 csch/acsch 双曲余割/反双曲余割函数tan/atan 正切/反正切函数 cot/acot 余切/反余切函数tanh/atanh 双曲正切/反双曲正切函数 coth/acoth 双曲余切/反双曲余切函数atan2 四个象限内反正切函数附录6.2指数函数函数名功能描述函数名功能描述exp 指数函数 log10 常用对数函数log 自然对数函数 sqrt 平方根函数附录6.3复数函数函数名功能描述函数名功能描述abs 绝对值函数 imag 求虚部函数angle 角相位函数 real 求实部函数conj 共轭复数函数附录6.4数值处理函数名功能描述函数名功能描述fix 沿零方向取整 round 舍入取整floor 沿-∞方向取整 rem 求除法的余数ceil 沿+∞方向取整 sign 符号函数附录6.5其他特殊数学函数函数名功能描述函数名功能描述airy airy函数 erfcx 比例互补误差函数besselh bessel函数(hankel函数) erfinv 逆误差函数bessili 改进的第一类bessel函数 expint 指数积分函数besselk 改进的第二类bessel函数 gamma gamma函数besselj 第一类bessel函数 gammainc 非完全gamma函数bessely 第二类bessel函数 gammaln gamma对数函数beta beta函数 gcd 最大公约数betainc 非完全的beta函数 lcm 最小公倍数betaln beta对数函数 log2 分割浮点数elipj Jacobi椭圆函数 legendre legendre伴随函数ellipke 完全椭圆积分 pow2 基2标量浮点数erf 误差函数 rat 有理逼近erfc 互补误差函数 rats 有理输出附录7 坐标转换函数名功能描述函数名功能描述cart2pol 笛卡儿坐标到极坐标转换 pol2cart 极坐标到笛卡儿坐标转换cart2sph 笛卡儿坐标到球面坐标转换 sph2cart 球面坐标到笛卡儿坐标转换附录8 矩阵函数附录8.1矩阵分析函数名功能描述函数名功能描述cond 求矩阵的条件数 rcond LINPACK倒数条件估计det 求矩阵的行列式 rref 矩阵的行阶梯型实现norm 求矩阵的范数 rrefmovie 消元法解方程演示null 右零空间 subspace 子空间orth 正交空间 trace 矩阵的迹rank 求矩阵的秩附录8.2线性方程函数名功能描述函数名功能描述/,\ 线性方程求解 nnls 非零最小二乘chol Cholesky分解 pinv 求伪逆矩阵inv 矩阵求逆 qr 矩阵的QR分解lscov 最小二乘方差 qrdelete QR分解中删除一行lu 矩阵的LU三角分解 qrinsert QR分解中插入一行附录8.3特征值与奇异值函数名功能描述函数名功能描述banlance 改进特征值精度的均衡变换 qz QZ算法求矩阵特征值cdf2rdf 复块对角阵到实块对角阵转换 rdf2cdf 实块对角阵到复块对角阵转换eig 求矩阵的特征值和特征向量 schur Schur分解hess 求Hessenberg矩阵 svd 奇异值分解poly 求矩阵的特征多项式附录8.4矩阵函数函数名功能描述函数名功能描述expm 矩阵指数函数 logm 矩阵对数函数funm 矩阵任意函数 sqrtm 矩阵平方根附录9 数据分析与Fourier变换函数附录9.1基本运算函数名功能描述函数名功能描述cumprod 向量累积 prod 对向量中各元素求积cumsum 向量累加 sort 对向量中各元素排序max 求向量中最大元素 sortrows 对矩阵中各行排序min 求向量中最小元素 std 求向量中各元素标准差mean 求向量中各元素均值 sum 对向量中各元素求和median 求向量中中间元素 trapz 梯形法求数值积分附录9.2微分计算函数名功能描述函数名功能描述del2 离散Laplace变换 gradient 梯度计算diff 差分于近视微分附录9.3滤波与卷积函数名功能描述函数名功能描述Conv 卷给与多项式乘法 filter 一维数字滤波conv2 二维卷积 filter2 二维数字滤波Deconv 因式分解与多项式乘法附录9.4方差处理函数名功能描述函数名功能描述corrcoef 相关系数计算 cov 协方差计算附录9.5Fourier变换函数名功能描述函数名功能描述abs 绝对值函数 fftshift fft与fft2输出重排angle 相角函数 ifft 离散Fourier逆变换cplxpair 依共轭复数对重新排序 ifft2 二维离散Fourier逆变换fft 离散Fourier变换 unwrap 相角矫正fft2 二维离散Fourier变换附录10 多项式处理函数附录10.1多项式处理函数名功能描述函数名功能描述conv 卷机与多项式乘法 polyfit 数据的多项式拟合deconv 因式分解与多项式乘法 polyval 多项式求值poly 求矩阵的特征多项式 polyvalm 多项式矩阵求值polyder 多项式求导 residue 部分分式展开polyeig 多项式特征值 roots 求多项式的根附录10.2数据插值函数名功能描述函数名功能描述griddata 数据网络的插值生成 interpft 一维插值（FFT方法）interp1 一维插值（查表） interpn 多维插值（查表）interp2 二维插值（查表） meshgrid 构造三维图形用x，y阵列interp3 三维插值（查表） spline 三次样条插值附录11 非线性数值方法函数名功能描述函数名功能描述dblquad 双重积分 odeget 获得微分方程求解的可选参数fmin 单变量最优化函数 odeset 设置微分方程求解的可选参数fmins 多变量最优化函数 quad 低阶数值积分方法ode45，ode23，ode113，ode15s，ode23s 微分方程数值解法 quad8 高阶数值积分方法odefile 对文件定义的微分方程求解附录12 稀疏矩阵函数附录12.1基本稀疏矩阵函数名功能描述函数名功能描述spdiags 稀疏对角矩阵 sprandn 稀疏正态分布随机矩阵speye 稀疏单位矩阵 sprandsym 稀疏对称随机矩阵sprand 稀疏均匀分布随机矩阵附录12.2稀疏矩阵转换函数名功能描述函数名功能描述find 查找非零元素下标 sparse 常规矩阵转换为稀疏矩阵full 稀疏矩阵转换为常规矩阵 spconvert 由外部格式引入稀疏矩阵附录12.3处理非零元素函数名功能描述函数名功能描述issparse 判断元素是否为稀疏矩阵 nzmax 允许的非零元素空间mmz 稀疏矩阵的非零元素个数 spalloc 为非零元素定位存储空间nonzeros 稀疏矩阵的非零元素 spfun 为非零元素定义处理函数附录12.4稀疏矩阵可视化函数名功能描述函数名功能描述gplot 绘制图论图形 spy 绘制稀疏矩阵结构附录12.5排序算法函数名功能描述函数名功能描述colmmd 列最小度排序 randperm 产生随机置换向量colperm 由非零元素的个数排序各列 symmd 对称最小度排序dmperm Dulmage-Mendelsohn分解 symrcm 反向Cuthill-McKee排序附录12.6范数、条件数函数名功能描述函数名功能描述condest 估算||*||1范数 normest 估算||*||2范数sprank 计算结构秩附录12.7特征值与奇异值函数名功能描述函数名功能描述eigs 求稀疏矩阵特征值和特征向量 svds 稀疏矩阵奇异值分解附录12.8其他函数名功能描述函数名功能描述spaugment 最小二乘算法形成 symbact 符号因子分解spparms 设置稀疏矩阵参数附录13 图形绘制附录13.1基本二维图形函数名功能描述函数名功能描述fill 填充二维多边形 polar 极坐标图形绘制loglog 全对数二维坐标绘制 semilogx x轴半对数坐标图形绘制plot 线性坐标图形绘制 semilogy y轴半对数坐标图形绘制附录13.2基本三维图形函数名功能描述函数名功能描述fill3 三维多边形填充 plot3 三维线或点型图绘制mesh 三维网格图形绘制 surf 三维表面图形绘制附录13.3三维颜色控制函数名功能描述函数名功能描述brighten 图形亮度调整 hidden 网格图的网格线开关设置caxis 坐标轴伪彩色设置 shading 设置渲染模式colormap 调色板设置附录13.4三维光照模型函数名功能描述函数名功能描述diffuse 图象漫射处理 surf1 带光照的三维表面绘制lighting 光照模式设置 surfnorm 曲面法线specular 设置镜面反射附录13.5标准调色板设置函数名功能描述函数名功能描述bone 带有蓝色调的灰色的调色板 hot 以黑红黄白为基色的调色板cool 以天蓝粉色为基色的调色板 hsv 色度饱和度亮度调色板copper 线性铜色调的调色板 pink 粉色色调的调色板flag 以红白蓝黑为基色的调色板 prism 光谱颜色表gray 线性灰度调色板附录13.6三维视点控制函数名功能描述函数名功能描述rotate3d 设置三维旋转开关 viewmtx 求视转换矩阵view 设置视点附录13.7坐标轴控制函数名功能描述函数名功能描述axis 坐标轴标度设置 hold 设置当前图形保护模式axes 坐标轴位置设置 subplot 将图形窗口分成几个区域box 坐标轴盒状显示 zoom 二维图形缩放grid 坐标网格线开关设置附录13.8图形注解函数名功能描述函数名功能描述colorbar 颜色条设置 xlabel 给图形的x轴加文字说明gtext 在鼠标位置加文字说明 ylabel 给图形的y轴加文字说明text 在图形上加文字说明 zlabel 给图形的z轴加文字说明title 给图形加标题附录13.9拷贝与打印函数名功能描述函数名功能描述print 打印图形或将图形存盘 orient 设置纸的方向orintopt 设置打印机为默认值附录14 特殊图形附录14.1特殊二维图形函数名功能描述函数名功能描述area 区域填充 feather 羽状条形图绘制bar 条形图绘制 fplot 给定函数绘制barh 水平条形图绘制 hist 直方图绘制bar3 3维条形图绘制 pareto pareto图绘制bar3h 3维水平条形图绘制 pie 饼状图绘制comet 彗星状轨迹绘制 stem 离散序列图形绘制errorbar 误差条形图绘制 stairs 梯形图绘制附录14.2等高线及其他二维图形函数名功能描述函数名功能描述contour 等高线绘制 pcolor 伪色绘制contourf 等高线填充绘制 quiver 有向图（箭头）绘制contour3 三维等高线绘制 voronoil voronoi图绘制clabel 等高线高程标志附录14.3特殊三维图形函数名功能描述函数名功能描述comet3 三维彗星状轨迹绘制 slice 切片图meshc 带等高线的三维网格绘制 surfc 带等高线的三维表面绘制meshz 带零平面的三维网格绘制 trisurf 表面图形的三角绘制stem2 杆图绘制 trimesh 网格图形的三角绘制quiver3 三维箭头（有向图）绘制 waterfall 瀑布型图形的绘制附录14.4图象显示与文件I/O函数名功能描述函数名功能描述brighten 图形色调亮化 image 图像显示colorbar 颜色条设置 imfinfo 图形文件信息colormap 调色板设置 imread 从文件读取图形contrast 灰度对比度设置 imwrite 保存图像附录14.5动画处理函数名功能描述函数名功能描述capture 屏幕抓取 movie 播放动画帧getframe 获取动画帧附录14.6实体模型函数名功能描述函数名功能描述cylinder 圆柱体生成 sphere 球体生成附录15 图形处理附录15.1图形窗口生成与控制函数名功能描述函数名功能描述clf 清除当前图形窗口 gcf 获取当前图形的窗口句柄close 关闭图形窗口 refresh 图形窗口刷新figure 生成图形窗口 shg 显示图形窗口附录15.2坐标轴建立与控制函数名功能描述函数名功能描述axes 坐标轴标度设置 gca 获得当前坐标轴句柄axis 坐标轴位置设置 hold 设置当前图形保护模式box 坐标轴盒状显示 ishold 返回hold的状态caxis 为彩色坐标轴刻度 subplot 将图形窗口分为几个区域cla 清除当前坐标轴附录15.3处理图形对象函数名功能描述函数名功能描述axes 坐标轴生成 surface 表面生成figure 图形窗口生成 text 文本生成image 图像生成 unicontrol 生成一个用户接口控制light 光源生成 uimenu 菜单生成line 线生成附录15.4图形函数名功能描述函数名功能描述copyobj 图像对象拷贝 gcbo 获得当前回调对象的句柄delete 对象删除 gco 获得当前对象的句柄drawnow 消除未解决的图像对象事件 get 获得对象属性findobj 查找对象 reset 重新设置对象属性gebf 获得当前回调窗口的句柄 set 设置对象属性附录16 GUI(图形用户接口)附录16.1GUI函数函数名功能描述函数名功能描述ginput 获取鼠标输入 uiresume 继续执行selectmoveresize 对象的选择、移动、大小设置、拷贝 uiwait 中断执行uicontrol 生成图形用户接口对象 waitgorbutterpress 等待按钮输入uimenu 生成菜单对象 waitfor 中断执行附录16.2GUI设计工具函数名功能描述函数名功能描述align 坐标轴与用户接口控制的对齐工具 menuedit 菜单编辑器cbedit 回调函数编辑器 propedit 属性编辑器guide GUI设计工具附录16.3对话框函数名功能描述函数名功能描述dialog 对话框生成 printdlg 打印对话框axlimdig 坐标轴设限对话框 questdlg 请求对话框errordlg 错误对话框 uigetfile 标准的打开文件对话框helpdlg 帮助对话框 uiputfile 标准的保存文件对话框inputdlg 输入对话框 uisetcolor 颜色选择对话框listdlg 列表选择对话框 uisetfont 字体选择对话框msgdlg 消息对话框 waitbar 等待条显示pagedlg 页位置对话框 warndlg 警告对话框附录16.4菜单函数名功能描述函数名功能描述makemenu 生成菜单结构 umtoggle 菜单对象选中状态切换menubar 设置菜单条属性 wimenu 生成window菜单项的子菜单附录16.5组按钮函数名功能描述函数名功能描述btndown 组按钮中的按钮按下 btnstate 查询按钮中的按钮状态btngroup 组按钮生成 btnup 组按钮中的按钮弹起btnpress 组按钮中的按钮按下管理附录16.6自定义窗口属性函数名功能描述函数名功能描述clruprop 清除用户自定义属性 setuprop 设置用户自定义属性getuprop 获取用户自定义属性附录16.7其他应用函数名功能描述函数名功能描述allchild 获取所有子对象 popupstr 获取弹出式菜单选中项的字符串edtext 坐标轴文本对象编辑 remapfig 改变窗口中对象的位置findall 查找所有对象 setptr 设置窗口指针getptr 获得窗口指针 setstatus 设置窗口中文本传状态getstatus 获取窗口中文本状态附录17 声音处理函数名功能描述函数名功能描述soond 将向量转换成声音 wavread 读。

哈佛大学能源与环境学院课程作业报告作业名称：传热学大作业——利用matlab程序解决热传导问题院系：能源与环境学院专业：建筑环境与设备工程学号：姓名：盖茨比2015年6月8日一、题目及要求1.原始题目及要求2.各节点的离散化的代数方程3.源程序4.不同初值时的收敛快慢5.上下边界的热流量（λ=1W/(m℃））6.计算结果的等温线图7.计算小结题目：已知条件如下图所示：二、各节点的离散化的代数方程各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12 三、源程序【G-S迭代程序】【方法一】函数文件为：function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为：A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]';[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746 【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为：function [y,n]=jacobi(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为：A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746四、不同初值时的收敛快慢1、[方法1]在Gauss 迭代和Jacobi 迭代中，本程序应用的收敛条件均为norm(y-x0)>=eps ，即使前后所求误差达到e 的-6次方时，跳出循环得出结果。

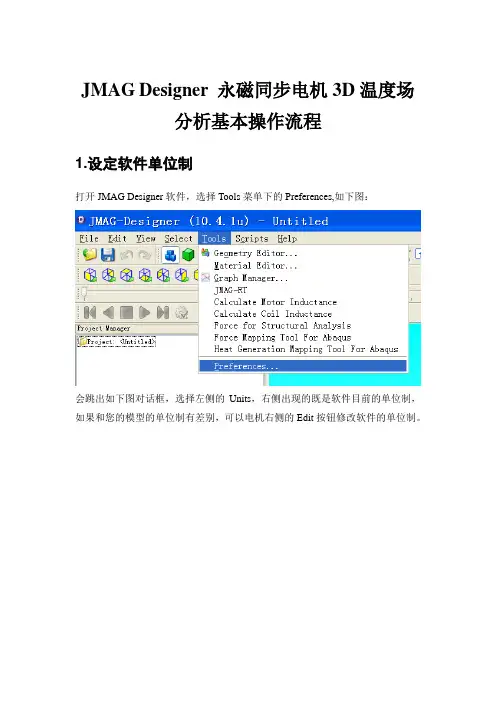
JMAG Designer 永磁同步电机3D温度场分析基本操作流程1.设定软件单位制打开JMAG Designer软件，选择Tools菜单下的Preferences,如下图：会跳出如下图对话框，选择左侧的Units，右侧出现的既是软件目前的单位制，如果和您的模型的单位制有差别，可以电机右侧的Edit按钮修改软件的单位制。

2.建模用户可以在JMAG Designer软件自带的Geometry Editor中建模，也支持多种3D 格式的图形直接导入，本例采用直接从外部导入.sat格式3D图形的方式。

选择File菜单下的Open，如下图：或者直接点击下图中所示的快捷键，如下图：会弹出如下图对话框，在文件类型中选择ACIS SAT Files(.sat)，选中要导入的图形文件。

图形导入后效果，如下图：在上方菜单栏中点击Save，保存。

如下图：3.前处理在左侧树形图中右键点击Solid Model，选择New Study下的Steady State Analysis，建立一个稳态温度场分析的Study。

如下图：赋材料属性在右侧的Toolbox栏下Materials里是软件的材料库，在做温度场分析时，需要用户自己创建材料，左键点击Create New Material。

如下图：此时会弹出材料编辑对话框，如下图：修改名字为steel_thermal，点击Thermal Properties，在Thermal Conductivity下的Constant中填入23，在Specific Heat下的Constant中填入460，点击OK。

如下图：此时在右侧的Toolbox栏下Materials下Customer Material中会出现刚刚创建的steel_thermal，如下图：左键按住steel_thermal，拖动鼠标到电机定子上松开，如下图：左侧会出现条件设置界面如下图，不需要任何改动，直接点击OK。

如下图：将定子其他部分及转子和轴都赋予同样材料，按住Ctrl键，鼠标左键单击选中定子其他部分及转子和轴，在左侧树形图中Materials下右键点击steel_thermal，选择Apply to Selected。

1.1 文件的打开和关闭1.1.1 文件的打开fopen ('filename', 'mode')mode格式有：‘r’：只读方式打开文件（默认的方式），该文件必须已存在。

‘r+’：读写方式打开文件，打开后先读后写。

该文件必须已存在。

‘w’：打开后写入数据。

该文件已存在则更新；不存在则创建。

‘w+’：读写方式打开文件。

先读后写。

该文件已存在则更新；不存在则创建。

‘a’：在打开的文件末端添加数据。

文件不存在则创建。

‘a+’：打开文件后，先读入数据再添加数据。

文件不存在则创建。

如果rt表示该文件以文本方式打开，如果添加的是“b”，则以二进制格式打开，这也是fopen函数默认的打开方式。

Fopen函数两个返回值:1、一个是返回一个文件标识(file Identifier)，它会作为参数被传入其他对文件进行读写操作的命令，通常是一个非负的整数，可用此标识来对此文件进行各种处理。

（如果返回的文件标识是–1，则代表fopen无法打开文件，其原因可能是文件不存在，或是用户无法打开此文件权限）；2、另一个返回值就是message，用于返回无法打开文件的原因；例：1-1[f,message]=fopen('fileexam1', 'r')if f==-1disp(message); %显示错误信息end(若文件fileexam1不存在，则显示如下信息。

Cannot open file.existence?permissions?memory?)例：1-2[f,message]=fopen('fileexam2', 'r');if f==-1disp (message); %显示错误信息elsedisp(f);end若文件fileexam2存在，则返回f值。

1.1.2文件的关闭Fclose(f)F为打开文件的标志，若若fclose函数返回值为0，则表示成功关闭f标志的文件；若返回值为–1，则表示无法成功关闭该文件。

MATLAB软件基础介绍MATLAB软件的一般命令,数组操作和运算函数;绘图命令,循环和选择结构;通过实例练习解决一些简单问题.2.1 引言MATLAB是MATrix LABoratory的缩写,由美国MathWorks公司开发的工程计算软件,迄今已推出了7.1版.当今数学类科技应用软件可分为两类,一类是数值计算型,如MATLAB,Xmath,Gauss等,这类软件擅长数值计算,对处理大批数据效率高;另一类是数学分析型软件,如Mathematica,Maple等,这类软件以符号计算见长,能给出解析解和任意精度解,其缺点是处理大量数据时效率高.现在, MATLAB已经发展为适合多学科,功能强大的大型软件,成为高级课程的基本教学工具.如MATLAB可以做:微积分:微分,积分,求极限,泰勒展开,级数求和;代数:求逆,特征值,行列式,代数方程解的简化,数学表达式的指定精度求值;数值分析:插值与拟合,数值微分与积分,函数逼近,代数方程和微分方程的数值解和符号解.统计计算:均值,方差,概率,参数估计,假设检验,相关性和回归分析,统计绘图,随机数产生器等.优化问题的求解:线性规划,非线性规划等问题的求解.动态系统模拟仿真等.它已成为大学生,研究生和博士生必须掌握的基本技能.同时, MATLAB也被研究单位和工业部门广泛应用,使科学研究和解决各种具体问题的效率大大提高.MATLAB集成环境主要包括五部分: MATLAB语言, MATLAB工作环境, 句柄图形,MATLAB数学函数库, MATLAB API (Application Program Interface).MATLAB主要有以下特点:1)运算符和库函数极其丰富,语言简洁,编程效率高. MATLAB除了提供和C语言一样的运算符外,还提供广泛的矩阵和向量运算符.2)图形功能强大.包括对二维和三维数据可视化,图像处理,动画制作等高低层次的绘图命令.3)功能强大的工具箱. 工具箱可分两类:功能性工具箱和学科性工具箱.前者主要用来扩充其符号计算功能,图示建模仿真,文字处理及与硬件实时交互的功能.而学科性工具箱是专业性较强的,如优化,统计,控制,小波,图像处理和通信工具箱等.4)易于扩充.除内部函数外,所有MATLAB的核心文件和工具箱文件都是可读可改的源文件,用户可修改文件和加入自己的文件,可与库文件一样被调用.2.1.1 安装(Windows操作平台)1.将源光盘插入光驱;2.在光盘的根目录下找到MATLAB的安装文件setup.exe;3.鼠标双击该安装文件,按提示逐步完成安装;4.安装完成后,在程序栏里便有了MATLAB选项.2.1.2 启动在”开始→程序→Matlab→MATLAB”中单击MATLAB.便会出现MATLAB Command Window(即命令窗口).2.2 MATLAB环境MATLAB既是一种语言,又是一个编程环境.2.2.1 命令窗口命令窗口是用户与Matlab进行交互的主要场所. Matlab语句的一般形式为:变量=表达式如:键入:x=4.5回车,将显示x=4.5再键入:y=sin(x*pi)回车,将显示:y=1…;‟ …,‟ …...‟的作用:1.表达式后面跟分号…;‟,将不显示结果;2.跟…,‟或不跟任何符号,将显示表达式的计算结果;3.当一个表达式没写完就需换行时,应在该行末键入…...‟之后再回车换行.如:s=1-1/2+1/3+1/4+sin(3*x*y)-cos(x)...-1/8+1/10+1/20…;‟ …,‟ …...‟的作用:用于命令行编辑的控制键和方向键1.按‟↑‟键,会显示刚才键入的命令行;2.反复按‟↑‟键,可以回调以前键入的所有命令行;3.…↓,‟键可以移动光标;←,→4.还有‟Home‟,‟End‟,‟Esc‟键等. ‟Esc‟清除一行.变量1.以字母开头,后面可跟字母,数字和下短线;2.大小写字母有区别,不超过31个字母.特殊变量名ans 用于结果的缺省变量名; pi 圆周率eps 计算机的最小数; inf 无穷大; NaN 不定量i或j -1的开方; realmin 最小可用正实数 realmax 最大可用正实数工作区接受Matlab命令的内存区域,存储着命令编辑区输入的命令和创建的所有变量值.查看或保存工作区变量:who 或whos 显示当前工作区中的所有变量clear 清除工作区中的所有变量clear(变量名) 清除指定工作区的变量save(文件名) 将当前工作区的变量储存在一个MAT-文件中load(文件名) 调出一个MAT-文件quit回车或单击右上角的‟ ‟,退出工作区.2.2.2 程序编辑器M文件:命令文件和函数文件1. M文件的建立1) 进入程序编辑器(MATLAB Editor/Debug):从‟File‟菜单中选择‟New‟及‟M-file‟项.2) 输入程序3) 保存程序:单击‟save‟按钮,出现一对话框,在文件名一框中键入一文件名,单击‟保存‟.2. 命令M文件及其运行命令M文件:一些命令行的组合,没有输入参数,也不返回输出参数.如: % 文件名exl.mx=4;y=6;z=2;items=x+y+zcost=x*25+y*22+z*99average_cost=cost/items1)在程序编辑窗口输入,以名为exl.m的M文件存磁盘.2)在Matlab命令编辑窗口输入exl,便会顺序执行该文件中的命令.3. 函数M文件及其调用函数M文件的形式为:fuction [输出变量列表]=函数名(输入变量列表)函数体语句;如:function f=f1(x)f=100*(x(2)-x(1)^2)^2-(1-x(1))^2;(注意函数M文件的文件名必须与其函数名相同)调用格式:x=[2 3];f=f1(x)结果为:f=992.2.3 文件管理what 返回当前目录下的M,MAT,MEX文件的列表dir 列出当前目录下的所有文件cd 显示当前的工作目录type test 在命令窗口下显示test.m的内容delete test 删除M文件test.mwhich test 显示M文件test.m所在的目2.3 数组和函数2.3.1 数组的运算1) 数组的简单构造:数组常采用‟:‟和函数‟linspace‟两种输入方式,如:x=1:5 (从1到5公差为1的等差数组)x=0:0.1:1 (从0到1,公差为0.1)x=linspace(0,pi,11) (11个从0到pi的等间隔数) 2) 数组的运算设a=[a1 a2 a3],b=[b1 b2 b3],c=标量标量加法a+b=[ a1+c a2+c a3+c]乘法 a*c=[ a1*c a2*c a3*c]数组加法 a+b=[ a1+ b1 a2+ b2 a3+ b3]乘法 a.*b= [a1*b1 a2*b2 a3*b3]数组右除 a./b= [a1/b1 a2/b2 a3/b3]左除 a.\b= [b1 /a1 b2/ a2 b3/ a3]数组求幂 a.^c=[ a1^c a2^c a3^c]c. ^a=[ a1^c a2^c a3^c]a.^b= [a1^b1 a2^b2 a3^b3] sort(v) 按升序排列max(v) 求最大值 min(v) 求最小值 sum(v) 求和mean(v) 求平均2.3.2 矩阵的创建1) 矩阵的直接定义键入: A=[1 2 3;4 5 6]或键入:A=[1 2 34 5 6 ]2) 特殊矩阵zeros(m,n) ones(m,n) eye(n) rand(m,n) diag(v) triu(x)3) 矩阵的剪裁和拼接键入:A=[1 2 3 ;4 5 6; 7 8 9];A(3.:) %A的第三行输出:ans= 7 8 9键入:B=A(2:3,:) %A的第二,三行输出:B=4 5 67 8 9键入:A(:,1) %A的第一列输出:ans=147输入: C=[B,zeros(2,1)]输出: C=4 5 6 07 8 9 02.3.3 矩阵的运算+ 矩阵加法–矩阵减法 * 乘法 , 转置 ^ 乘幂 / 左除 \ 右除如:A是可逆矩阵,AX=B的解是A左除B,即X=A\B; XA=B的解X= B/A. rank(A) 矩阵秩 inv(A) 矩阵的逆 det(A) 行列式orth(A) 正交化 poly(A) 特征多项式2.3.4 数学函数sin(x) cos(x) tan(x) cot(x) exp(x) log(x) log10(x) sqrt(x) 平方根+方向取整朝零方向取整 fix(x); 朝∞-方向取整floor(x); 朝∞ceil(x); 四舍五入到最近的整数round(x); 符号函数sign(x).2.4 图形功能2.4.1 二维图形1) 基本绘图命令plot(x, y, …color-linestyle-marker‟)x, y------转折点; color-linestyle-marker-------连线颜色,线型,数据点图标.颜色:y黄 r红 g绿 b 蓝 w 白 k 黑 m紫 c 灰 -实线 :点线 --虚线数据点图标: . 小黑点 +加法 *星号 O(不是零！是o,p,q的o)小圆圈 pentagram 五角星x=1:8;y=sin(x);plot(x,y,'k : O')plot(x,y,' O')x=0:0.1:2*pi; y=sin(x); plot(x,y, 'r:o');plot(x,y, 'r :');2) 坐标系的控制axis([xmin xmax ymin ymax]) [ ]中分别给出X轴和Y轴的最小,最大值;axis equal X轴和Y轴的单位长度相同. axis squrare 图框呈方形 axis off 取消坐标轴3) 图形标注x=linspace(0,2*pi,30);y=[sin(x);cos(x)];plot(x,y);grid;xlabel('x');ylabel('y');title('sine and cosine curves');text(3*pi/4,sin(3*pi/4),'\leftarrowsinx');text(3*pi/2,cos(3*pi/2),'cosx\rightarrow',...'HorizontalAlignment','right');(以上命令行可以形成一个M文件).hold on 把新的图形画在原来图形上.grid 在图形上加网格 xlabel ylabel 对X,Y轴加注 title 给整个图形加标题text gtext 在图形中特定位置加字符串.若使用gtext('sinx')代替命令text,则在图形窗口会出现十字线,其交点是字符串位置.移动鼠标可移动交点,点击鼠标即可将字符串固定.输出结果如下图:4) 多幅图形在同一画面中的多幅不同坐标系的图形,如何作?x=linspace(0,2*pi,30);y=sin(x);z=cos(x);u=2*sin(x).*co s(x);v=sin(x)./cos(x);subplot(2,2,1),plot(x,y),title('sin(x)'); subplot(2,2,2),plot (x,z),title('cos(x)');subplot(2,2,3),plot (x,u),title('2sin(x)cos(x)'); subplot(2,2,4),plot (x,v),title('sin(x)/cos(x)');2.4.2 三维图形1) 空间曲线例:作螺旋线⎪⎩⎪⎨⎧===.,c os ,s i n t z t y t x 键入:t=0:pi/51:10*pi;plot3(sin(t),cos(t),t);2) 带网格的曲面 作曲面5.75.7,sin 2222≤≤-++=x y x y x z .键入:x=-7.5:0.5:7.5;y=x;[X,Y]=meshgrid(x,y); % 三维图形的X,Y 数组R=sqrt(X.^2+Y.^2)+eps; % +eps 是为防止出现0/0Z=sin(R)./R;mesh(X,Y,Z); % 三维网格表面3) 等高线4) 条形图和面积图: 某产品上半年的销售利润profit,每月份售出产品的产值expense.x=1:1:6;expense=[ 21 34 89 25 22 90];profit=[ 10 20 60 11 9 70] sale=[ expense; profit]; area(x,sale)2.5 M文件的编写2.5.1 M文件1) 命令M文件:一些命令行的组合. 函数M文件:定义函数的程序,具有一定的特定格式;如: 命令M文件:x=[2 3];f=cos(x)函数M文件:function f=cost(x)f=100*(x(2)-x(1)^2)^2…-(1-x(1))^2;2) 函数M文件的形式为:function [输出变量列表]=函数名(输入变量列表)函数体语句:2.5.2 四种循环和选择控制结构1) while关系表达式 { statements }ends=0;n=1while s<=100s=s+n^2;n=n+1;endn,s2) forfor x=x1:step:xn{ statements }end如: for k=1:4x(k)=1/k;endformat rat %设置输出格式为有理数x例:建立一个函数M文件求自然数n的阶乘. function f=jch(n)f=1;for i=1:nf=f*I;end3) switch 表达式(标量或字符串)case 值1,语句体1case {值2.1,值2.2,…}语句体2…otherwise,语句体nendfor x=x1:step:xn{ statements }endMATLAB绘图第5章 MATLAB绘图5.1 二维数据曲线图5.2 其他二维图形5.3 隐函数绘图5.4 三维图形5.5 图形修饰处理5.6 图像处理与动画制作5.1 二维数据曲线图5.1.1 绘制单根二维曲线plot函数的基本调用格式为：plot(x,y)其中x和y为长度相同的向量，分别用于存储x坐标和y坐标数据。

matlab一维非稳态导热-回复Matlab是一种常用的科学计算软件，广泛应用于工程、物理、数学等领域。

在热传导研究中，非稳态导热问题是一个重要课题。

本文将以Matlab 为工具，介绍一维非稳态导热问题的求解方法。

首先，我们需要了解非稳态导热问题的基本概念。

非稳态导热问题是指热传导过程中温度场随时间的变化，即瞬态问题。

一维非稳态导热问题可以用下面的热传导方程描述：∂T/∂t = α∂²T/∂x²其中，T是温度，t是时间，x是空间坐标，α是热扩散系数。

为了求解上面的偏微分方程，我们需要确定边界条件和初始条件。

假设热导体的两端为x=0和x=L，边界条件可以是温度固定、热流固定或边界绝热（无热量流入或流出）。

初始条件是指在t=0时刻的温度场分布。

首先，我们需要定义问题的参数，包括热扩散系数α、热导体的长度L、时间范围tspan等等。

在Matlab中，可以使用类似下面的语句进行定义：alpha = 0.1; 热扩散系数L = 1; 热导体长度tspan = [0 10]; 时间范围接下来，我们需要定义初始条件和边界条件。

假设在t=0时刻，热导体的温度分布是一个高斯函数，可以使用下面的语句定义初始条件：x = linspace(0, L, 100); 在空间范围内生成100个均匀分布的点T0 = exp(-(x-L/2).^2); 初始温度分布对于边界条件，我们可以选择温度固定的情况，即热导体的两端温度为固定值T1和T2。

可以使用下面的语句定义边界条件：T1 = 1; 左端温度T2 = 0; 右端温度然后，我们可以使用Matlab的pdepe函数来求解一维非稳态导热问题。

pdepe函数是用于求解偏微分方程组的函数，其中包含了默认的边界条件和初始条件设置。

可以使用下面的语句进行求解：sol = pdepe(0,pdefun,icfun,bcfun,x,tspan);在上面的语句中，pdefun是一个用于计算偏微分方程右端项的函数句柄，icfun是一个用于计算初始条件的函数句柄，bcfun是一个用于计算边界条件的函数句柄。

热力图（Heatmap）绘制（含Matlab源代码）作者：晚熟的小熊（WX）一、热力简介热力图（Heatmap）是一种数据可视化技术，根据需要用热力图显示的矩阵，可以用来显示区域内数据的相对密集程度或分布情况。

它通常通过使用色彩映射来表示数据的密度或值大小。

热力图是一种通过对色块(Color block)着色来显示数据的统计图表。

绘图时，需指定颜色映射的规则(Colormap)，该颜色值反映了该位置上的数据密集程度或数值大小。

例如，较大的值由较深的颜色表示，较小的值由较浅的颜色表示；较大的值由偏暖的颜色表示，较小的值由较冷的颜色表示，等等。

二、热力图绘图完整Matlab代码%%清空环境变量clear;close all;clc;warning off;%读取数据X=xlsread('数据.xlsx');%8*8%%定义X轴名字定义Y轴名字load colormap2;b=bar3(X,1);for i=1:length(b)zdata=b(i).ZData;b(i).CData=zdata;b(i).FaceColor='interp';endcolormap(mycolor);view(0,90);c=colorbar;axis tight;set(gcf,'color',[111]);hold on;plot3([0.58.5],[0.50.5],[00],'k','Linewidth',3);hold on;%%调整坐标区参数Xlabel_name={'1','2','3','4','5','6','7','8'};Ylabel_name={'一','二','三','四','五','六','七','八'};set(gca,'ygrid','on','color',[250227225]/255,'Gridalpha',1);set(gca,'xgrid','on','color',[250227225]/255,'Gridalpha',0.4);set(gca,'zgrid','off');set(gca,'Box','off');set(gca,'TickDir','out','Ticklength',[0.01,0.01]);set(gca,'Linewidth',3);set(gca,'Xticklabel',Xlabel_name,'XTickLabelRotation',90,'fontsize',17); set(gca,'Yticklabel',Ylabel_name,'YTickLabelRotation',0,'fontsize',17); title('cell-states','Fontsize',25,'position',[-2,4.45],'Rotation',90);%%设置colorbar的刻度与标签显示参数caxis([0,1]);set(c,'tickdir','out');set(c,'Ytick',0.0:0.2:1.2);set(c,'YtickLabel',{'0.0','0.2','0.4','0.6','0.8','1.0'});set(c,'Linewidth',1.5);set(c,'FontSize',20);set(c,'Box','on');三、热力图效果展示。

测量到不同坐标点的高度值,如何用matlab画三维图附上部分数据：A=[-210.6627 -33391.1192 5.0273-221.3052 -33387.7415 4.5969-210.9391 -33393.0068 5.5647-221.8901 -33390.7396 5.0077-211.384 -33394.7093 5.6505-222.6117 -33392.778 5.0554-212.7074 -33397.5459 5.7381-225.8973 -33397.5869 5.5587];解：代码在matlab2009a版以上均可运行。

A=[-210.6627 -33391.1192 5.0273-221.3052 -33387.7415 4.5969-210.9391 -33393.0068 5.5647-221.8901 -33390.7396 5.0077-211.384 -33394.7093 5.6505-222.6117 -33392.778 5.0554-212.7074 -33397.5459 5.7381-225.8973 -33397.5869 5.5587];xData = A(:,1);yData = A(:,2);zData = A(:,3);fitresult = fit( [xData, yData], zData, 'linearinterp');figure( 'Name', '三维图' );plot( fitresult, [xData, yData], zData );xlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid onview( -53, 50 );试一试：A=[-210.6627 -33391.1192 5.0273-221.3052 -33387.7415 4.5969-210.9391 -33393.0068 5.5647-221.8901 -33390.7396 5.0077 -211.384 -33394.7093 5.6505-222.6117 -33392.778 5.0554-212.7074 -33397.5459 5.7381 -225.8973 -33397.5869 5.5587];xData = A(:,1);yData = A(:,2);zData = A(:,3);minx = min(xData);maxx = max(xData);miny = min(yData);maxy = max(yData);tx = linspace(minx,maxx)';ty = linspace(miny,maxy);[XI,YI] = meshgrid(tx,ty);ZI = griddata(xData,yData,zData,XI,YI); mesh(XI,YI,ZI), holdplot3(xData,yData,zData,'o'), hold offxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid onview( -53, 50 );.................x=[7392 7392 7392 7392 5608 5608 5608 5608 80 00 5000 6500 6500 6500 6500 6500 6500 6500 6500 6500 6500];y=[476 404 476 404 476 404 476 404 440 440 440 440 500 380 440 440 440 440 440 44 0];z=[17.06 16.93 17.8 17.4 17.17 16.89 17.28 17.26 17.04 16.94 16.92 17.3 17.37 17.17 17.34 17.11 17.22 17.24 17.11 17.2];minx = min(x);maxx = max(x);miny = min(y);maxy = max(y);[X,Y,Z]=griddata(x,y,z,linspace(minx,maxx)',linspace(miny,maxy),'v4') ; %插值figure,surf(X,Y,Z) %三维曲面...%% Initialization.% Convert all inputs to column vectors.x = x(:);y = y(:);z = z(:);%% Fit: ' fit 1'.ft = 'linearinterp';opts = fitoptions( ft );opts.Weights = zeros(1,0);opts.Normalize = 'on';[fitresult, gof] = fit( [x, y], z, ft, opts );% Plot fit with data.figure( 'Name', 'untitled fit 1' );h = plot( fitresult, [x, y], z );% legend( h, ' fit 1', 'z vs. x, y', 'Location', 'NorthEast' );% Label axesxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid on.......................x=[7392 7392 7392 7392 5608 5608 5608 5608 80 00 5000 6500 6500 6500 6500 6500 6500 6500 6500 6500 6500];y=[476 404 476 404 476 404 476 404 440 440440 440 500 380 440 440 440 440 440 44 0];z=[17.06 16.93 17.8 17.4 17.17 16.89 17.28 17.26 17.04 16.94 16.92 17.3 17.37 17.17 17.34 17.11 17.22 17.24 17.11 17.2];% Convert all inputs to column vectors.x = x(:);y = y(:);z = z(:);%% Fit: ' fit 1'.ft = fittype( 'poly22' );opts = fitoptions( ft );opts.Lower = [-Inf -Inf -Inf -Inf -Inf -Inf];opts.Upper = [Inf Inf Inf Inf Inf Inf];opts.Weights = zeros(1,0);[fitresult, gof] = fit( [x, y], z, ft, opts );fitresult% Plot fit with data.figure( 'Name', 'z' );h = plot( fitresult, [x, y], z );% legend( h, 'z fit 1', 'z vs. x, y', 'Location', 'NorthEast' );% Label axesxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid onview( -57.5, 42 );.................A=[18467 17001 308 20177 17642 276 26852 16114 225 23785 17643 194 27823 14737 189 18906 16346 173 25981 18051 173 22046 17634 171 23238 6502 169 27696 11621 169 27700 11609 16516607 17365 155 23146 15382 153 14405 18032 152 27232 14482 150 27380 18202 136 26591 13715 126 14074 16516 124 15801 3966 115 21684 13101 114 15255 5110 110 24580 13319 107 23325 16701 105 24065 7353 104 25021 16290 104 15952 18397 103 27346 13331 100 24685 14278 98 17414 15476 97 12778 5799 93 17044 10691 93 17981 18449 93 20983 15862 93 22605 14301 93 5451 2757 92 19041 15769 90 24003 15286 90 7100 2449 89 18413 11721 88 21475 8540 85 19007 11488 84 17008 4775 82 17079 5894 81 13855 3345 79 13920 5354 79 22193 12185 79 16569 6055 78 18993 12371 78 22965 13535 78 15517 17034 77 24631 9422 76 4153 2299 73 11702 4480 71 24153 12450 71 15007 5535 7019569 7348 7015087 3512 6922846 9149 6925461 9834 6816823 4207 6721766 12348 6712625 16259 66];x=A(:,1);y=A(:,2);z=A(:,3);minx = min(x);maxx = max(x);miny = min(y);maxy = max(y);[X,Y,Z]=griddata(x,y,z,linspace(minx,maxx)',linspace(miny,maxy),'v4') ; %插值figure,surf(X,Y,Z) %三维曲面...%% Initialization.% Convert all inputs to column vectors.x = x(:);y = y(:);z = z(:);%% Fit: 'untitled fit 1'.ft = 'linearinterp';opts = fitoptions( ft );opts.Weights = zeros(1,0);opts.Normalize = 'on';[fitresult, gof] = fit( [x, y], z, ft, opts ); % Plot fit with data.figure( 'Name', ' fit 1' );h = plot( fitresult, [x, y], z );% legend( h, ' fit 1', 'z vs. x, y', 'Location', 'NorthEast' ); % Label axesxlabel( 'x' );ylabel( 'y' );zlabel( 'z' );grid on。

matlab温度控制系统课程设计一、课程目标知识目标：1. 理解并掌握MATLAB软件在温度控制系统中的应用；2. 学习温度控制系统的基本原理和数学模型；3. 掌握利用MATLAB进行温度控制系统建模、仿真和性能分析的方法。

技能目标：1. 能够运用MATLAB软件构建温度控制系统的数学模型；2. 能够运用MATLAB进行温度控制系统的仿真分析，并优化系统性能；3. 能够运用所学知识解决实际温度控制问题。

情感态度价值观目标：1. 培养学生对自动控制技术的兴趣和热情；2. 培养学生的团队协作精神，提高沟通和交流能力；3. 增强学生的创新意识和实践能力，使其具备解决实际工程问题的信心。

课程性质：本课程为应用实践性课程，旨在通过MATLAB软件在温度控制系统中的应用，使学生掌握自动控制技术的基本原理和方法。

学生特点：学生已具备一定的自动控制理论知识，对MATLAB软件有一定了解，但缺乏实际应用经验。

教学要求：结合课程性质和学生特点，注重理论与实践相结合，以项目为导向，培养学生的实际操作能力和创新能力。

通过课程学习，使学生能够独立完成温度控制系统的建模、仿真和性能分析任务，并具备解决实际问题的能力。

教学过程中，将目标分解为具体的学习成果，以便进行后续的教学设计和评估。

二、教学内容1. 温度控制系统基本原理：包括热传递原理、温度传感器和执行器的工作原理等。

相关教材章节：第一章 温度控制系统概述2. MATLAB软件基础：介绍MATLAB软件的基本操作、数据类型、矩阵运算和编程基础。

相关教材章节：第二章 MATLAB软件基础3. 温度控制系统建模：利用MATLAB建立温度控制系统的数学模型，包括传递函数和状态空间模型。

相关教材章节：第三章 系统建模与仿真4. 温度控制系统仿真：运用MATLAB进行温度控制系统的动态仿真，分析系统性能。

相关教材章节：第四章 控制系统仿真5. 温度控制系统设计：结合MATLAB优化工具箱，进行控制器设计和参数优化。