等截面等跨连续梁在常用荷载作用下的内力系数表

2 常用结构计算2—1 荷载与结构静力计算表2—1-1 荷载1．结构上的荷载结构上的荷载分为下列三类:（1）永久荷载如结构自重、土压力、预应力等.（2)可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。

（3）偶然荷载如爆炸力、撞击力等。

建筑结构设计时，对不同荷载应采用不同的代表值。

对永久荷载应采用标准值作为代表值。

对可变荷载应根据设计要求，采用标准值、组合值、频遇值或准永久值作为代表值。

对偶然荷载应按建筑结构使用的特点确定其代表值。

2．荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载，按承载能力极限状态和正常使用极限状态分别进行荷载（效应）组合，并应取各自的最不利的效应组合进行设计。

对于承载能力极限状态,应按荷载效应的基本组合或偶然组合进行荷载（效应）组合。

γ0S≤R （2-1）式中γ0——结构重要性系数；S—-荷载效应组合的设计值；R—-结构构件抗力的设计值。

对于基本组合,荷载效应组合的设计值S应从下列组合值中取最不利值确定:(1)由可变荷载效应控制的组合（2—2）式中γG——永久荷载的分项系数；γQi——第i个可变荷载的分项系数，其中Y Q1为可变荷载Q1的分项系数；S GK-—按永久荷载标准值G K计算的荷载效应值；S QiK——按可变荷载标准值Q ik计算的荷载效应值，其中S Q1K为诸可变荷载效应中起控制作用者；ψci--可变荷载Q i的组合值系数；n—-参与组合的可变荷载数。

（2）由永久荷载效应控制的组合（2—3)（3）基本组合的荷载分项系数1)永久荷载的分项系数当其效应对结构不利时：对由可变荷载效应控制的组合,应取1.2；对由永久荷载效应控制的组合，应取1。

35；当其效应对结构有利时：一般情况下应取1。

0；对结构的倾覆、滑移或漂浮验算,应取0.9。

2)可变荷载的分项系数一般情况下应取1。

4；对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。

常用结构计算荷载结构静力计算荷载1．结构上的荷载结构上的荷载分为下列三类：（1）永久荷载如结构自重、土压力、预应力等。

（2）可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。

（3）偶然荷载如爆炸力、撞击力等。

建筑结构设计时，对不同荷载应采用不同的代表值。

对永久荷载应采用标准值作为代表值。

对可变荷载应根据设计要求，采用标准值、组合值、频遇值或准永久值作为代表值。

对偶然荷载应按建筑结构使用的特点确定其代表值。

2．荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载，按承载能力极限状态和正常使用极限状态分别进行荷载（效应）组合，并应取各自的最不利的效应组合进行设计。

对于承载能力极限状态，应按荷载效应的基本组合或偶然组合进行荷载（效应）组合。

γ0S≤R（2-1）式中γ0——结构重要性系数；S——荷载效应组合的设计值；R——结构构件抗力的设计值。

对于基本组合，荷载效应组合的设计值S应从下列组合值中取最不利值确定：（1）由可变荷载效应控制的组合（2-2）式中γG——永久荷载的分项系数；γQi——第i个可变荷载的分项系数，其中Y Q1为可变荷载Q1的分项系数；S GK——按永久荷载标准值G K计算的荷载效应值；S QiK——按可变荷载标准值Q ik计算的荷载效应值，其中S Q1K为诸可变荷载效应中起控制作用者；ψci——可变荷载Q i的组合值系数；n——参与组合的可变荷载数。

（2）由永久荷载效应控制的组合（2-3）（3）基本组合的荷载分项系数1）永久荷载的分项系数当其效应对结构不利时：对由可变荷载效应控制的组合，应取1.2；对由永久荷载效应控制的组合，应取1.35；当其效应对结构有利时：一般情况下应取1.0；对结构的倾覆、滑移或漂浮验算，应取0.9。

2）可变荷载的分项系数一般情况下应取1.4；对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。

对于偶然组合，荷载效应组合的设计值宜按下列规定确定：偶然荷载的代表值不乘分项系数；与偶然荷载同时出现的其他荷载可根据观测资料和工程经验采用适当的代表值。

1。

单向板与双向板的定义:按受力特点，混凝土楼盖中的周边支撑板可分为单向板和双向板两类。

只在一个方向弯曲或者主要在一个方向弯曲的板，称为单向板；在两个方向完全，且不能忽略人一个方向弯曲的板称为双向板。

2. 现浇单向板肋梁楼盖的设计步骤：1、结构平面布置并初步拟定板厚和主、次梁的截面尺寸;2、确定梁、板得计算简图；3、梁、板得内力分析；4、截面配筋及构造措施；5、绘制施工图.3. 简化假定:1、支座可以自由转动，但没有竖向位移;2、不考虑薄膜相应对板内力的影响；3、在确定板传给次梁的荷载一级次梁传给主梁的荷载时，分别忽略板、次梁的连续性；4、跨熟超过五跨的连续梁、板,当各跨荷载相同,且跨度相差不超过10%时，可按五跨的等跨连续梁、板计算。

4. 假定支座处没有竖向位移，实际上忽略了次梁、主梁、柱的竖向变形对板、次梁、主梁的影响。

柱子的竖向位移主要由轴向变形引起，在通常的内力分析中都是可以忽略的。

忽略主梁变形，将导致次梁跨中弯矩偏小、主梁跨中弯矩偏大。

当主梁的线刚度比次梁的线刚度大得多时,主梁变形对次梁内力的影响才比较小。

次梁变形对板内力的影响也是这样，如果考虑这种影响，内力分析就相当复杂。

5。

计算单元：为减少计算工作量，结构内力分析时,常常不是对整个结构进行分析，而是从实际结构中选取有代表性的某一部分作为计算的对象，成为计算单元.6. 塑性内力重分布的过程，假定支座截面和跨内截面的截面尺寸和配筋相同.梁的手里全过程大致可以分为三个阶段：1、弹性内力阶段;2、截面间弯曲刚度比值改变阶段;3、塑性铰阶段。

7。

考虑塑性内力重分布是以形成塑性铰为前提的，因此下列情况不宜采用：1、在使用阶段不允许出现裂缝或对裂缝开展有校验过限制的结构，如水池池壁，自防水屋面，一级处于侵蚀性环境中的结构;2、直接承受动力和重复荷载的结构;3、预应力结构和二次受力叠合结构;4、要求有较高安全储备的结构。

8. 截面弯矩的调整幅度用弯矩调幅系数β来表示：β=(Me—Ma）/Me，式中Me安弹性理论算得的弯矩值;Ma 调幅后的弯矩值。

结构力学公式结构 静力计算目 录1、常用截面几何与力学特征表 (1)2、单跨梁的内力及变形表 (8)2.1 简支梁的反力、剪力、弯矩、挠度 (8)2.2 悬臂梁的反力、剪力、弯矩和挠度 (10)2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度 (12)2.4 两端固定梁的反力、剪力、弯矩和挠度 (14)2.5 外伸梁的反力、剪力、弯矩和挠度 (16)3．等截面连续梁的内力及变形表 (19)3.1 二跨等跨梁的内力和挠度系数 (19)3.2 三跨等跨梁的内力和挠度系数 (20)3.3 四跨等跨连续梁内力和挠度系数 (23)3.4 五跨等跨连续梁内力和挠度系数 (23)3.5 二不等跨梁的内力系数 (24)3.6 三不等跨梁内力系数 (25)4．双向板在均布荷载作用下的内力及变形系数表 (26)4.1 四边简支 (26)4.2 三边简支，一边固定 (27)4.3 两边简支，两边固定 (27)4.4 一边简支，三边固定 (28)4.4 四边固定 (29)4.5 两边简支，两边固定 (29)5．拱的内力计算表 (30)5.1各种荷载作用下双铰抛物线拱计算公式 (30)6．刚架内力计算表 (35)6.1 “┌┐”形刚架内力计算表（一） (35)6.2“┌┐”形刚架内力计算表（二） (37)6.3“”形刚架的内力计算表 (39)11、常用截面几何与力学特征表234567注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰∙=A dA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：max y IW =3．i 称截面回转半径（mm ），其基本计算公式如下：AI i = 4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

梁的受力分析以钢筋混凝土现浇梁为例，梁纵向受力钢筋伸入柱子中锚固，模型如下图所示：由于工程中梁两端的锚固，其对应的力学模型应为两端固结的杆件，如下图所示：在均布荷载作用下其弯矩图为（弯矩总是画在梁受拉一侧）：剪力图为：变形图如下：结合弯矩图与剪力图可以看出，单跨梁在均布荷载作用下跨中和支座处是整个梁中受力最大的部位。

在跨中处梁下部受拉，下部纵向钢筋为主要受力筋；在支座处梁上部受拉，上部钢筋为主要受力筋，故纵向钢筋不宜在这些地方设置接头。

对梁受剪力情况而言，梁跨中最小、支座最大，故箍筋常在支座处加密。

剪力是弯矩的导数，梁支座弯矩变化幅度大，所以支座处剪力值最大；而在梁跨中，弯矩变化趋势逐渐平缓，所以跨中剪力值最小。

同理，我们可以看到在梁跨中受到集中力的情况下，弯矩、剪力图如下所示。

请思考跨中受集中荷载作用时剪力图为何是这样的？在结构设计中，常把梁节点简化为铰接（如主次梁交点），这种梁称为简支梁。

简支梁受均布荷载作用下弯矩图如下：请思考剪力图应是什么样的？剪力在何处最大？板和连续梁楼板按其受力形式的不同，可分为单向板和双向板。

顾名思义，单向板仅有一个方向承受荷载（短边承受荷载），双向板两个方向均可承受荷载。

《混凝土结构设计规范》GB50010-2010第9.1.1条规定：沿两对边支承的板应按单向板计算；对于四边支承的板，当长边与短边比值大于3时，可按沿短边方向的单向板计算，但应沿长边方向布置足够数量的构造钢筋；当长边与短边比值介于2与3之间时，宜按双向板计算；当长边与短边比值小于2时，应按双向板计算。

根据单向板的定义可以看出，单向板的受力情况与梁类似，在均布荷载作用下，计算时可先假定一个计算宽度b，将宽度b上的面荷载转化为线荷载计算，计算方法与梁相同。

示意图如下：计算宽度b可取任意值，对单向板的弯曲应力没有影响。

为了方便计算通常可取1m或1000mm，注意此处计算宽度应与面荷载单位相对应。

请大家思考计算宽度的取值为何对单向板弯曲应力没有影响，在之后的推送中会给出解答。

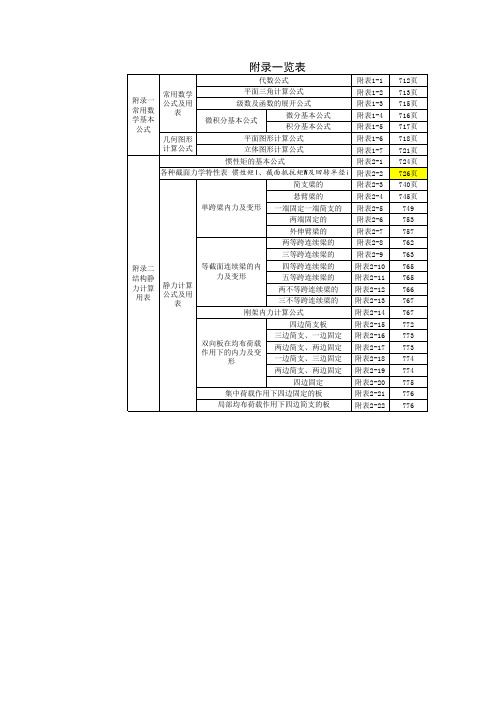
附录一等截面等跨连续梁在常用荷载作用下的内力系数表 1.在均布及三角形荷载作用下：皿=表中系数 V=表中系数2•在集中荷载作用下： 皿=表中系数 V=表中系数3.内力正负号规定： M —使截面上部受压、下部受拉为正；V —对临近截面所产生的力距沿顺时针方向者为正。

附表1-1 旳12（或旳12）;Xql （或XQI （或 XGl ）； XQ两跨梁0.203 -0.094 0.406 -0.594 0.0940.0940.222 0.222 -0.333 0.667 -1.333 -0.6671.3330.278 -0.167 0.833 -1.167 0.1670.167a.荷载图三跨梁跨内最大弯距附表1-2M20.080 0.025支座弯距M B M c V A-0.100 -0.100 0.400V BIV Br-0.6000.500剪力V clV er-0.5000.600V D-0.4000.101 -0.050 -0.050 0.450 -0.5500.550-0.4500.075 -0.050 -0.050 0.050 -0.0500.500-0.5000.0500.0500.073 0.054 -0.117 -0.033 0.383 -0.6170.5830.083-0.0170.094-0.017-0.067 0.017 0.433 -0.5670.0830.083-0.017-0.017 A----- A 0.0540.0680.0500.0630.1750.0210.0520.0380.100-0.063 -0.063 0.183 -0.313 -0.250 -0.1880.250 0.313-0.031-0.031-0.073-0.042-0.150-0.031-0.031-0.0210.010-0.1500.2190.0310.1770.2080.350-0.281-0.0310.250-0.3230.302-0.2920.052-0.6500.5000.281-0.2500.051-0.1980.0210.052-0.010-0.5000.650-0.2190.0310.021-0.010-0.350荷载图 0.077 四跨梁 跨内最大弯距 M 2 M 3 M 4 M B 0.036 0.036 0.077 -0.107 附表1-3 支座弯距 剪力 M e M D V A -0.071 -0.107 0.393 0.100 0.081 0.072 0.061 -0.054-0.036 -0.054 0.446 0.098 -0.121 -0.018 -0.058 0.380 V BI V Br -0.607 0.536 Vd V cr -0.464 0.464 V DI V Dr -0.536 0.607 V E -0.393 0.094 Z A0.056 0.056 0.062 0.067 0.049 A 0.071 0.028 -0.036 -0.067 -0.107 -0.036 -0.036 0.018 -0.004 0.433 0.042 0.028 0.055 0.052 0.066 -0.049 -0.054 0.013 -0.049 -0.554 0.018 -0.620 0.603 -0.036 0.429 -0.567 0.085 -0.049 0.496 0.018 0.482 -0.397 -0.040 -0.571 0.571 0.085 -0.022 -0.504 0.067 -0.518 0.054 -0.040 -0.558 -0.429 0.036 0.022 0.004 0.067 0.013 0.054 -0.442 0.036 0.004 -0.013 -0.067-0.045 -0.067 0.183 -0.317 0.272 -0.228 0.228 -0.272 0.317 -0.183 -0.084 -0.075 -0.022 -0.034 0.217 -0.234 0.011 0.011 0.239 -0.261 0.034 0.034 -0.011 -0.036 0.175 -0.325 0.314 -0.186 -0.025 -0.025 0.286 -0.214 0.040 0.040 -0.022-0.067 -0.022 -0.022 -0.022 0.205 -0.295 0.295 -0.205 0.022 0.0224 4u a A s s a 0.274 -0.178 0.048 -0.012 0.822 -1.1780.2260.226-0.060-0.0600.0120.0124 q 川0.198 -0.131 -0.143 0.036 -0.131 -0.1310.988-1.0120.1780.178-0.036-0.036附表1-4荷载图跨内最大弯距支座弯距剪力内力M2 M3 M B M e M D M E V A0.078 0.033 0.046 -0.105 -0.079 -0.079 -0.105 0.394 V BIV Br-0.6060.526V clV cr-0.4740.500V DIV Dr-0.5000.474V EIV Er-0.5260.606V F-0.3940.100 Ml M S M4M S0.085 -0.053 -0.040 -0.040 -0.053 0.447 -0.5530.0130.0130.500-0.500-0.013-0.0130.533-0.4470.079 -0.053 -0.040 -0.040 -0.053 -0.053 -0.0530.513-0.4870.487-0.5130.0530.0530.073(1) 0.0980.094 (2)0.0590.078-0.119 -0.022 -0.044 -0.051 0.3800.0550.0740.064 -0.035-0.067-0.111 -0.020 -0.057 0.0350.018 -0.005 0.001 0.433-0.6200.5980.0350.4240.5670.085-0.402-0.0230.5760.5910.0860.023-0.0230.493-0.409-0.0370.0230.006-0.5070.052-0.0370.5570.006-0.0010.052-0.4430.001-0.049 -0.054 0.014 -0.004 0.019 -0.0490.496-0.5050.0680.068-0.018-0.0180.0040.004。

常用结构计算荷载结构静力计算荷载1．结构上的荷载结构上的荷载分为下列三类：（1）永久荷载如结构自重、土压力、预应力等。

（2）可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。

（3）偶然荷载如爆炸力、撞击力等。

建筑结构设计时，对不同荷载应采用不同的代表值。

对永久荷载应采用标准值作为代表值。

对可变荷载应根据设计要求，采用标准值、组合值、频遇值或准永久值作为代表值。

对偶然荷载应按建筑结构使用的特点确定其代表值。

2．荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载，按承载能力极限状态和正常使用极限状态分别进行荷载（效应）组合，并应取各自的最不利的效应组合进行设计。

对于承载能力极限状态，应按荷载效应的基本组合或偶然组合进行荷载（效应）组合。

γ0S≤R （2-1）式中γ0——结构重要性系数；S——荷载效应组合的设计值；R——结构构件抗力的设计值。

对于基本组合，荷载效应组合的设计值S应从下列组合值中取最不利值确定：（1）由可变荷载效应控制的组合（2-2）式中γG——永久荷载的分项系数；γQi——第i个可变荷载的分项系数，其中Y Q1为可变荷载Q1的分项系数；S GK——按永久荷载标准值G K计算的荷载效应值；S QiK——按可变荷载标准值Q ik计算的荷载效应值，其中S Q1K为诸可变荷载效应中起控制作用者；ψci——可变荷载Q i的组合值系数；n——参与组合的可变荷载数。

（2）由永久荷载效应控制的组合（2-3）（3）基本组合的荷载分项系数1）永久荷载的分项系数当其效应对结构不利时：对由可变荷载效应控制的组合，应取1.2；对由永久荷载效应控制的组合，应取1.35；当其效应对结构有利时：一般情况下应取1.0；对结构的倾覆、滑移或漂浮验算，应取0.9。

2）可变荷载的分项系数一般情况下应取1.4；对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。

对于偶然组合，荷载效应组合的设计值宜按下列规定确定：偶然荷载的代表值不乘分项系数；与偶然荷载同时出现的其他荷载可根据观测资料和工程经验采用适当的代表值。

结构力学公式大全1、常用截面几何与力学特征表注：1．I称为截面对主轴（形心轴）的截面惯性矩（mm4）。

基本计算公式如下：2．W称为截面抵抗矩（mm3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：3．i称截面回转半径（mm），其基本计算公式如下：4．上列各式中，A为截面面积（mm2），y为截面边缘到主轴（形心轴）的距离（mm），I为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3．等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注：1．在均布荷载作用下：M＝表中系数×ql2；V＝表中系数×ql；。

2．在集中荷载作用下：M＝表中系数×Fl；V＝表中系数×F；。

[例1] 已知二跨等跨梁l＝5m，均布荷载q＝11.76kN/m，每跨各有一集中荷载F＝29.4kN，求中间支座的最大弯矩和剪力。

[解] MB支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN·mVB左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l＝6m，均布荷载q＝11.76kN/m，求边跨最大跨中弯矩。

[解] M1＝0.080×11.76×62＝33.87kN·m。

3.2 三跨等跨梁的内力和挠度系数注：1．在均布荷载作用下：M＝表中系数×ql2；V＝表中系数×ql；。