大学物理学-稳恒磁场教案
- 格式:doc
- 大小:2.25 MB
- 文档页数:20

第九章稳恒电流的磁场稳恒电流:导体中电流不随时间变化(也叫直流电)。
§9-1基本磁现象安培假说人们对磁现象的研究是很早的,而且开始时是与电现象分开研究的。
发现电、磁现象之间存在着相互联系的事实,首先应归功于丹麦物理学家奥斯特。
他在实验中发现,通有电流的导线(也叫载流导线)附近的磁针,会受力而偏转。
1820年7月21日,他在题为《电流对磁针作用的实验》小册子里,宣布了这个发现。
这个事实表明电流对磁铁有作用力,电流和磁铁一样,也产生磁现象。
1820年8月,奥斯特又发表了第二篇论文,他指出:放在马蹄形磁铁两极间的载流导线也会受力而运动。
这个实验说明了磁铁对运动的电荷有作用力。
1820年9月,法国人安培报告了通有电流的直导线间有相互作用的发现,并在1820年底从数字上给出了两平行导线相互作用力公式。
这说明了二者的作用是通过它们产生的磁现象进行的。
综上可知,电流是一切磁现象的根源。
为了说明物质的磁性,1822年安培提出了有关物质磁性的本性的假说,他认为一切磁现象的根源是电流,即电荷的运动,任何物体的分子中都存在着回路电流,成为分子电流。
分子电流相当于基元磁铁,由此产生磁效应。
安培假说与现代物质的电结构理论是符合的,分子中的电子除绕原子核运动外,电子本身还有自旋运动,分子中电子的这些运动相当于回路电流,即分子电流。
磁场的应用十分广泛。
如:电子射线、回旋加速器、质谱仪、真空开关等都利用了磁场。
§9-2 磁场磁感应强度磁力线磁通量一、磁场1、磁场:运动电荷或电流周围也有一种场,称为磁场。
2、磁场的主要表现(1)力的表现:磁场对运动电荷或载流导体有作用力。
(2)功的表现:磁场对载流导体能做功。
3、实验表明:磁场与电场一样,既有强弱,又有方向。
二、磁感应强度为了描述磁场的性质,如同在描述电场性质时引进电场 强度时一样,也引进一个描述磁场性质的物理量。
下面从磁场对运动电荷的作用力角度来定义磁感应强度。



稳恒电流的磁场内容:稳恒电流、电流密度、电动势磁场、磁感应强度毕奥-萨伐尔定律及应用磁场的高斯定理安培环路定理磁力、安培定律磁介质8.1 稳恒电流8.1.1电流在静电平衡条件下,导体内部场强为零,导体内的自由电子只有无规则的热运动而无宏观的定向运动。
如果在导体内建立一定的电场,则导体中的自由电子将在电场力作用下作定向运动。
大量电荷作有规则的定向运动形成电流。
带电粒子在导体中作有规则运动所形成的电流称为传导电流。
在金属中传导电流的载流子是自由电子;在电解液中传导电流的载流子是正、负离子和电子。
带电粒子及宏观带电体在空间作有规则机械运动所形成的电流称为运流电流。
产生电流一般需要两个条件:(1)存在可以自由运动的电荷(自由电荷);(2)存在电场。
通过导体任意一个横截面的电量的时间变化率称为电流强度I ,即dtq d I 电流的单位称安培,简称安,用A 表示。
1安=1库仑/秒8.1.2电流连续方程1.电流密度电流强度不能反映电流在截面上的分布,例如,电流在粗细不均匀的导线或大块导体中流动时,分布是不均匀的。
此外,在空间范围内,电流不再像在导线中只有正、负之分,而是具有方向。
为了能细致地描写导体中不同部位的电流大小和方向,引入电流密度矢量j ,其大小等于单位时间内通过该点垂直于电流方向的单位横截面积的电量,方向为该点电流的方向,即00n j dS dI = 0n 为沿电流方向的单位矢量,dS 0为垂直于0n 方向的面积元,电流密度矢量的单位是安培/米2。
电流密度矢量是导体中各点的点函数,是一个矢量场。
电流密度矢量场的场线称为电流线。
电流密度在某一面积S 上的通量就是通过S 的电流强度,即⎰•=Sd S J I电流I 是宏观量,它描述某特定导体的整体特征;电流密度矢量J 是微观量,它描述导体内部某一点的特征。
2.电流的连续性方程在有电流的区域中考察一个假想的封闭曲面S ,如图8-3所示,若单位时间内从曲面S 所围体积中有净电流流出,则由电荷守恒定律,电流量应等于该体积内电荷减少的速率,即dtdq dS I s -=⋅=⎰j 8.1.3 欧姆定律对于各向同性的良导体(金属或其他导电物质如电解液),其中有电流分布J 和电场强度分布E ,通常情况下遵守欧姆定律欧姆定律的微分形式:E E J e e ργ1==这里的e ρ为电阻率,请注意在不同场合与上面的电荷密度加以区别,这里的e γ为电导率1-=e e ργIU R =称为积分形式的欧姆定律 8.1.4电动势设在dt 时间内,电源迫使正电荷dp 从负极经电源内部移到正极所做的功为dA ,那么,电源的电动势ε可由下式定出:dpdA =ε 单位正电荷从电源负极B 移到电源正极A 时,“非静电力”所做的功,即⎰⋅=BA k d l E ε整个闭合电路中处处存在“非静电力”的情况,这时就无法区分“电源内部”和“电源外部”,于是,电动势可表示为“非静电性场强E k ”沿闭合电路上的环流,即⎰⋅=l E d k ε电动势的单位和电势的单位相同,也是伏特(V )。

大学物理稳恒磁场第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比。
§11-1 基本磁现象磁性,磁力,磁现象;磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
一、电流的磁效应1819年,丹麦科学家奥斯特发现电流的磁效应;1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B 的定义:(1)规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B 垂直的方向运动时,其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值,规定为磁场中某点磁感强度的大小。
即:qvF B max磁感强度B 是描写磁场性质的基本物理量。
若空间各点B 的大小和方向均相等,则该磁场为均匀磁场....;若空间各点B 的大小和方向均不随时间改变,称该磁场为稳恒磁场....。
磁感强度B 的单位:特斯拉(T )。
§11-3 毕奥-萨伐尔定律 一、毕-萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。
34rrlIdBd⨯=πμ式中μ0:真空磁导率,μ0=4π×10-7 NA2dB的大小:2sin4rIdldBθπμ=d B的方向:d B总是垂直于Id l与r组成的平面,并服从右手定则。
一段有限长电流的磁场:⎰⎰⨯==ll rrlIdBdB34πμ二、应用1。
一段载流直导线的磁场)cos(cos4210θθπμ-=rIB说明:(1)导线“无限长”:2rIBπμ=(2)半“无限长”:4221rIrIBπμπμ==2。
第七章 稳恒电流的磁场 风怡湘 辛卯年§7-1 磁场 磁感应强度 磁力线 磁通量一、磁感应强度大小:qVF B max=, 方向:沿V F ⨯max 方向(规定为沿磁场方向)。
二、磁力线(1)磁力线是闭合的。
这与静电场情况是截然不同的。
磁场为涡旋场。
(2)磁力线不能相交,因为各个场点B 的方向唯一。
三、磁通量定义:通过某一面的电力线数称为通过该面的磁通量,用m Φ表示。
(7-1)磁通量单位:SI 制中为Wb (韦伯)。
对于闭合曲面,因为磁力线是闭合的,所以穿入闭合面和穿出闭合面的磁力线条数相等,故0=Φm ,即闭合曲面7-2)此式是表示磁场重要特性的公式,称为磁场中高斯定理。
§7-2 毕奥——沙伐尔定律(矢量式)―――――――――――――――――――――――(7-3) 说明:(1)毕奥——沙伐尔定律是一条实验定律。
(2)l Id是矢量,方向沿电流流向。
(3)迭加原理对磁感应强度也适用。
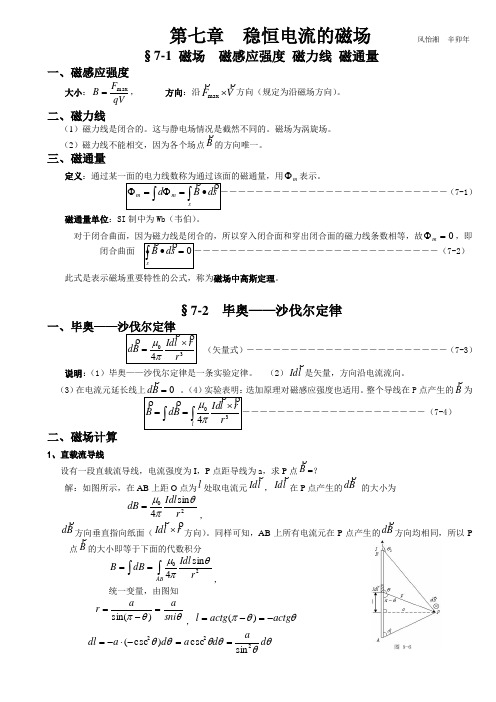
整个导线在P 点产生的B为7-4) 二、磁场计算1、直载流导线设有一段直载流导线,电流强度为I ,P 点距导线为a ,求P 点B=?解:如图所示,在AB 上距O 点为l 处取电流元l Id ,l Id 在P 点产生的B d的大小为20sin 4r Idl dB θπμ=, B d 方向垂直指向纸面(r l Id ⨯方向)。
同样可知,AB 上所有电流元在P 点产生的B d方向均相同,所以P点B的大小即等于下面的代数积分20sin 4r Idl dB B AB θπμ⎰⎰==, 统一变量,由图知θθπsni aar =-=)sin(,θθπactg actg l -=-=)(θθθθθθd ad a d a dl 222sin csc )csc (==-⋅-=⎰⎰=⋅=⇒2121sin 4sin sin sin 402220θθθθθθπμθθθθπμd a I a d aIB)cos (cos 4210θθπμ-=a I,B 垂直指向纸面。
第7章稳恒磁场前面我们研究了相对于观察者静止的电荷所激发的电场的性质与作用规律。
从本章起我们看到,在运动电荷周围,不仅存在着电场而且还存在着磁场。
磁场和电场一样也是物质的一种形态。
1820年,丹麦的奥斯特发现了电流的磁效应,当电流通过导线时,引起导线近旁的小磁针偏转,开拓了电磁学研究的新纪元,打开了电应用的新领域。
1837年惠斯通、莫尔斯发明了电动机,1876年美国的贝尔发明了电话。
……迄今,无论科学技术、工程应用、人类生活都与电磁学有着密切关系。
电磁学给人们开辟了一条广阔的认识自然、征服自然的道路。
7.1磁场磁感强度Fe O)能吸引铁。
十一磁现象的发现要比电现象早得多。
早在公元前人们知道磁石(34世纪我国发明了指南针。
但是,直到十九世纪,发现了电流的磁场和磁场对电流的作用以后,人们才逐渐认识到磁现象和电现象的本质以及它们之间的联系,并扩大了磁现象的应用范围。
到二十世纪初,由于科学技术的进步和原子结构理论的建立和发展,人们进一步认识到磁现象起源于运动电荷,磁场也是物质的一种形式,磁力是运动电荷之间除静电力以外的相互作用力。
7.1.1 基本磁现象磁场无论是天然磁石或是人工磁铁都有吸引铁、钴、镍等物质的性质,这种性质叫做磁性。
条形磁铁及其它任何形状的磁铁都有两个磁性最强的区域,叫做磁极。
将一条形磁铁悬挂起来,其中指北的一极是北极(用N表示),指南的一极是南极(用S表示)。
实验指出,极性相同的磁极相互排斥,极性相反的磁极相互吸引。
在相当长的一段时间内,人们一直把磁现象和电现象看成彼此独立无关的两类现象。
直到1820年,奥斯特首先发现了电流的磁效应。
后来安培发现放在磁铁附近的载流导线或载流线圈,也要受到力的作用而发生运动。
进一步的实验还发现,磁铁与磁铁之间,电流与磁铁之间,以及电流与电流之间都有磁相互作用。
上述实验现象导致了人们对“磁性本源”的研究,使人们进一步认识到磁现象起源于电荷的运动,磁现象和电现象之间有着密切的联系。
磁场和电场一样具有能量、动量和质量,是一种特殊的物质,叫场物质。
P是矢量,电流I 的方向m穿过磁场中某一曲面的磁力线总数,称为穿过该曲面的磁通量,用符号的磁通量为 d d m m S SB S ΦΦ==⋅⎰⎰ Wb ),1Wb =12m T ⋅。
SB dS ⋅=⎰在给定点P 所产生的磁感应强度称为真空的磁导率1-⋅m H )任意形状的载流导线在给定点P 产生的磁场的方向相同,则得LB dl ⋅⎰cos B dl θ=⎰0=⎰ 2002I d πμϕπ=⎰μ= 或电流方向反过来),则 ⎰⋅L l d B=-I 0μ0=l d0L B dl μ⋅=∑⎰的电流方向与回路L 的绕行方向符合右螺旋法则时,,则为0, 是所有电流产生.),sin(B l Id BIdl dF =B l Id F d ⨯=F =⎰F d =⎰⨯B l Id 真空中两条无限长的载流平行导线单位长度间相互作用力 a I I dl dF πμ2210=线圈磁矩的方向n与磁场B的方向成ϕ角(线圈平面与磁场的方向成θ角) 1F =θsin 1BIl 导线da 受力 1F '=)sin(1θπ-BIl = 2F =2BIl 导线cd 受力 2F '=2BIl载流导线电流保持不变,磁力所做的功等于电流强度乘以磁通量的增量.ΔP在外磁场作用下分子的附加磁矩mP的电子的进动轨道磁矩为m,e。
电子进动的方向是:0d (Lμ⋅=∑⎰B l 对于磁场,引入磁场强度矢量(辅助矢量),⎰(B μ即得有磁介质时的安培环路定理i LH dl I ⋅=∑⎰- H曲线与M - H曲线相似,可见B与H不成线性关系,即铁磁质的磁导率μ不再是常数、而是与H有关。
磁滞现象与磁滞回线时、磁介质反复磁化,分子振动加剧、温度升高,产生H的电流提供的热损曲线所围的面积等于反复磁化的一个周期中单位体积的。
授课章节第10章稳恒磁场教学目的掌握运用毕奥-萨伐尔定律计算磁感应强度的方法.理解磁场的高斯定理.掌握安培环路定理及求解磁场分布的方法.熟练使用安培定律计算载流导线或载流回路所受的磁力和磁力矩.掌握洛仑兹力公式,并能用此求解运动问题.了解顺磁质、抗磁质和铁磁质的特点及磁化机理.掌握有磁介质时的安培环路定理,并能用其求解磁场分布.教学重点、难点毕奥-萨伐尔定律;安培环路定理;洛仑兹力;顺磁质、抗磁质的磁化机理;教学内容备注§10.1磁场磁感应强度一、基本磁现象磁体有不可分割两个磁极,N极和S极;1820年丹麦物理学家奥斯特发现电流的磁效应。
磁场和电场一样具有能量、动量和质量,是一种特殊的物质,叫场物质。
二、磁感应强度磁场对外的重要表现是:(1)磁场对进入场中的运动电荷或载流导体有磁力的作用;(2)载流导体在磁场中移动时,磁场的作用力将对载流导体作功,表明磁场具有能量。
1.磁矩设线圈的面积为ΔS,线圈中电流为I,则线圈的磁矩定义为mP=IΔS n磁矩mP是矢量,电流I 的方向与n的方向成右手螺旋系.线圈的磁矩是表征线圈本身特性的物理量。
2.试验线圈在磁场中受到的磁力矩:当线圈转到一定位置时、线圈受到的磁力矩为零,这个位置叫平衡位置; 线圈从平衡位置转过90°时线圈受到的磁力矩最大;m P M ∝max在磁场中的一定点、比值m P M m ax 不变;在磁场中的不同点比值mP M m ax不同。
3.磁感应强度矢量B大小为 B=mP M m ax; B 的单位 特斯拉, (T).三、磁通量 磁场中的高斯定理 1.磁力线 磁场中作一系列曲线,曲线上每一点的切线方向为磁场B方向,垂直于该点B 矢量的单位面积的磁力线条数,为该点B矢量的量值.(1)磁力线都是环绕电流的闭合曲线,磁场是涡旋场.(2)任何两条磁力线在空间不相交.(3)磁力线的环绕方向与电流方向用右手定则.2.磁通量穿过磁场中某一曲面的磁力线总数,称为穿过该曲面的磁通量,用符号m Φ表示.m d Φ=S d B⋅ 而通过曲面S 的磁通量为m Φ=⎰⋅SS d B磁通量的单位: 韦伯(Wb ),1Wb =12m T ⋅。
四、磁场中的高斯定理对闭合曲面S⎰⋅SS d B =0称为磁场的高斯定理。
五、毕奥-萨伐尔定律任一电流元l Id 在给定点P 所产生的磁感应强度B d的大小与电流元的大小成正比,与电流元和由电流元到P 点的矢径r间的夹角的正弦成正比,而与电流元到P 点的距离r的平方成反比.B d 的方向垂直于l d 和r 所组成的平面,指向为由l Id 经小于180°的角转向r时右螺旋前进的方向.B d =k 3rrl Id⨯;其中k =πμ40,0μ称为真空的磁导率,0μ=17104--⋅⋅⨯A m T π(或1-⋅m H )因此,有 B d =304r rl Id ⨯πμ。
任意形状的载流导线在给定点P 产生的磁场 B=⎰⎰⨯=L L rr l Id B d 304 πμ。
运动电荷的磁场:(毕奥——萨伐尔定律的微观形式) 设在导体的单位体积内有n 个带电粒子,每个粒子带有电量q ,以速度v沿电表明磁场是无源场电流元在自身方向上不激发磁场流元l Id的方向作匀速运动而形成导体中的电流,电流元的横截面为S ,电流强度为:I=qnvS上式代入毕奥-萨伐尔定律,并注意到l Id 与v 的方向相同,则得dB =20),sin()(4r r v dl qNvSπμ 在电流元l Id 内,有nSdl dN =个带电粒子.运动的带电粒子产生的磁感应强度B 的大小为B =20),sin(4r r v qv dN dBπμ= B 的方向垂直于v 和电荷q 到场点的矢径r所决定的平面,运动电荷所产生的磁感应强度B 为B =304r rv q ⨯πμ 六、毕奥-萨伐尔定律的应用 略 §10.2安培环路定理一、安培环路定理 在无限长直电流产生的磁场中 ⎰⋅Ll d B =⎰dl B θcos =ϕπμπrd r I ⋅⎰2002=⎰πϕπμ2002d I =I 0μ1.如果使曲线积分的绕行方向反过来(或电流方向反过来),则⎰⋅Ll d B =-I 0μ2.如果闭合回路不包围载流导线,则0=⋅⎰Ll d B3.如果闭合曲线L 不在一个平面内,可以把每一段积分元l d分解为//l d 及⊥l d,则l d B ⋅=B·(⊥l d +//l d )= 90cos B ⊥l d +θcos B //l d=ϕπμrd r I 200±=ϕπμd I20± 式中“±”号取决于积分回路的绕行方向与电流方向的关系,则⎰⋅Ll d B=I 0μ以上讨论虽然是对长直载流导线而言,但其结论具有普遍性.在真空中的稳恒电流磁场中,磁感应强度B沿任意闭合曲线L 的线积分(也称B矢量的环流),等于穿过这个闭合曲线的所有电流强度的代数和的0μ倍.其数学表达式为⎰⋅Ll d B=0μi I ∑规定:当穿过回路L 的电流方向与回路L 的绕行方向符合右螺旋法则时,I 为正,反之,I 为负.如果I 不穿过回路L ,则为0,注意:场中各点的磁感应强度B是所有电流产生.磁场是有旋场(或涡旋场),是非保守力场.稳恒电流的磁场不存在标量势.二、安培环路定理的应用§10.3磁场对载流导线的作用一、安培定律磁场对载流导线的作用力也称安培力电流元的安培力),sin(BlIdBIdldF=写成矢量式为BlIdFd⨯=载流导线的安培力F=⎰L F d=⎰⨯LBlId二、无限长两平行载流直导线间的相互作用力电流单位“安培”的定义1. 平行载流直导线间的相互作用力两根相距为a的无限长平行直导线,通以同方向的电流1I和2I。
在导线2上电流元22dII在电流I1的磁场中所受安培力大小为2dF=),sin(122221BlIdIdlIB=2212dlaI Iπμ2Fd的方向指向导线1,单位长度所受安培力大小为22dldF=aI Iπμ221同理可得载流导线1每单位长度所受的安培力大小为11dldF=aI Iπμ2211Fd的方向指向导线2.2. “安培”的定义真空中两条无限长的载流平行导线单位长度间相互作用力aI IdldFπμ221=规定:真空中的两条无限长平行直导线,通有相等的稳恒电流I,当两导线相距1米,每一导线每米长度上受力为2×710-牛顿时,各导线中的电流强度为1安培.11041022127721=⨯⨯⋅=⋅===--ππμπdldfaIII(A)三、磁场对载流线圈的作用1.均匀磁场对载流线圈的作用线圈磁矩的方向n与磁场B的方向成ϕ角(线圈平面与磁场的方向成θ角)时,由安培定律导线bc受力1F=θsin1BIl导线da受力1F'=)sin(1θπ-BIl=θsin1BIl导线ab受力2F=2BIl导线cd受力2F'=2BIl1F和1F',2F和2F'方向相反,线圈在均匀磁场中受合力为零。
∑F =1F +'F1 +2F +'F2 =0但2F和2F'不在同一直线上.因此,载流线圈所受的磁力矩为M=θθcos2cos21212lFlF'+=θcos21lBIl=ϕsinBIS如果线圈有N匝M=ϕsinNBIS=ϕsinBPmM=Bpm⨯mP=NIS就是线圈磁矩,是矢量.上式对于在均匀磁场中任意形状的载流平面线圈也同样成立.讨论:(1)当ϕ=2π,mP与B垂直,M max=NBIS,磁力矩使ϕ有减少趋势.(2)当ϕ=0,m P与B同向,M=0,线圈处于稳定平衡状态.(3)当ϕ=π,m P与B反向,M=0,线圈处于非稳定平衡状态平面载流刚性线圈在均匀磁场中,只发生转动,不会发生整个线圈的平动.2.非均匀磁场对载流线圈的作用因为磁场不均匀,所以一般线圈受的合力0≠∑F ,合力指向磁场强的方向,所以线圈除转动外还要平动.四、磁力的功1.载流导线在磁场中运动时磁力所做的功设均匀磁场B中,有一载流的闭合回路abcda,ab长为l,可滑动,则磁力做的功为∆ΦIIBSaalBIaaFW=='⋅='⋅=载流导线电流保持不变,磁力所做的功等于电流强度乘以磁通量的增量.2.载流线圈在磁场中转动时磁力矩所做的功匀强磁场中, M作正功,使ϕ减少dW=ϕMd-=ϕϕdBIS sin-=)(cosϕBISd=ϕcos(BSId=ΦId磁力矩所做的总功为W=⎰ΦΦΦ21Id当电流I不变时W=)(12Φ-ΦI§10.4磁场对运动电荷的作用一、洛仑兹力电流元lId在磁场B中受力大小为dF=),sin(BlIdBIdl电流强度可写成I=qnvS且),sin(),sin(BlIdBv=写成dF=),sin(BvqvnSBdl导体线元l d内,带电粒子数目nSdldN=因此f=dNdF=),sin(BvqvB磁场对运动电荷作用的力f称为洛仑兹力.矢量式为f=Bv q⨯注意:(1) q 的正负影响洛伦兹力的方向。
(2)f·v=0,因此洛仑兹力不做功(3)同时存在电场和磁场时,则F=)(BvEq⨯+称为洛仑兹关系式。
二、带电粒子在匀强磁场中的运动(1) v与B平行或反平行F=Bv q⨯=0带电粒子仍作匀速直线运动.(2) v与B垂直洛仑兹力F的方向始终与速度v垂直带电粒子作匀速圆周运动.RvmqvB2=圆周运动半径(回旋半径)qBmvR=圆周运动周期qBmvRTππ22==回旋频率ν=T1=mqBπ2周期T和回旋频率ν只与磁感应强度及粒子质量m和电量q有关,而与粒子的速度及回旋半径无关.(3) v与B斜交成θ角v分解为⊥v=θsinv,//v=θcosv螺旋线的半径qBmvqBmvRθsin==⊥螺旋周期qBmvRTππ22==⊥螺距qBmvTvTvhθπθcos2cos//===带电粒子在磁场中的螺旋线运动,广泛地应用于“磁聚焦”技术.三、霍耳效应1.金属导体的霍耳效应霍耳在1879年发现匀强磁场B、金属导体板(宽a、厚b)与B垂直,电流I与B也垂直。
则在板上、下两面出现横向电势差,称为霍耳电势差。
HU=dIBRHHR是仅与导体材料有关的常数,称为霍耳系数.2.金属导体的霍耳效应的解释设在导体内载流子的电量为q,平均定向运动速度为v,它在磁场中所受的洛仑兹力大小为mf=qvB带电粒子所受的电场力大小为ef=qE=bUUq NM-由平衡条件有qvB=bUUq NM-则导体上、下两表面间的电势差为HU=MU-NU-=bvB因nqvbdI=,代入上式可得HU=dIBnq1比较,得霍耳系数HR=nq1上式表明,霍耳系数的数值决定于每个载流子所带的电q和载流子的浓度n,其正负取决于载流子所带电荷的正负.3.半导体的霍耳效应半导体有两种:1、空穴型的P型半导体、载流子是+e;2、电子型的N型半导体、载流子是-e。