八年级数学上册 《四边形性质探索》单元测试卷 北师大版

北师大版八年级上单元测试第1单元班级________姓名________一、单选题（每小题3分，共36分）1．下列各组数中，是勾股数的是（）A ．9，16，25B ．1，1C ．12D ．8，15，172．一个直角三角形两条直角边的长分别为6，8，则其斜边上的高为（）A ．6013B ．13C ．245D ．253．如图，在单位为1的正方形网格图中有a ，b ，c ，d 四条线段，从中任取三条线段所构成的三角形中恰好是直角三角形的个数为（）A ．1个B ．2个C ．3个D ．4个4．国庆假期中，小华与同学去玩探宝游戏，按照探宝图，他们从门口A 处出发先往东走8km ，又往北走2km ，遇到障碍后又往西走3km ，再向北走到6km 处往东拐，仅走了1km ，就找到了宝藏，则门口A 到藏宝点B 的直线距离是（）A ．20kmB ．14kmC ．11kmD ．10km5．如图所示，是用4个全等的直角三角形与1个正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直角边（x y >），下列四个说法：①2249x y +=，②2x y -=，③2449xy +=，④9x y +=．其中说法正确的是（）A．①②③B．①②④C．②③④D．①②③④6．如图长方体木箱的长、宽、高分别为12m，4m，3m，则能放进木箱中的木棒最长为（）A．19m B．24m C．13m D．15m7．本期，我们学习了用赵爽弦图证明勾股定理在如图所示的赵爽弦图中，在DH上取点M使得D的面积之差为=，连接AM、CM．若正方形EFGH的面积为6，则ADMDM GHD与CDM（）A．3B．2C3D．不确定8．如图，是一段楼梯，高BC是1.5m，斜边AC是2.5m，如果在楼梯上铺地毯，那么至少需要地毯（）A．2.5m B．3m C．3.5m D．4m9．《九章算术》是我国古代数学的经典著作，书中有一个“折竹抵地”问题：“今有竹高丈，末折抵地，问折者高几何？“意思是：一根竹子，原来高一丈（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？（）A．4尺B．4.55尺C．5.45尺D．5.55尺10．如图，一艘轮船以8nmile/h的速度从港口A出发，向东北方向航行，另一艘轮船以6nmile/h 的速度同时从港口A出发，向东南方向航行，出发2h后，两船的距离是（）A．20nmile B．15nmile C．12nmile D．10nmile11．如图，牧童在A处放牛，牧童家在B处，A、B处距河岸DC的距离AC、BD的长分别为500m和700m，且C，D两点的距离为500m，天黑前牧童从A处将牛牵到河边饮水再回家，那么牧童最少要走的距离为（）A．1000m B．1200m C．1300m D．1700m12．如图，是一种饮料的包装盒，长、宽、高分别为4cm、3cm、12cm，现有一长为16cm的吸管h cm的取值范围为（）插入到盒的底部，则吸管漏在盒外面的部分()A ．34h <<B ．34h ≤≤C ．24h ££D ．4h =二、填空题（每小题3分，共24分）13．如图，一只蚂蚁从长为2cm ，宽为2cm ，高为3cm 的长方形纸箱的A 点沿纸箱爬到B 点，那么它所行的最短路线长是___cm ．14．如图所示，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm ，正方形A ，B ，C 的面积分别是28cm ，210cm ，214cm ，则正方形D 的面积是___________2cm ．15．如图，在水池的正中央有一根芦，池底长10尺，它高出水面1尺，如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面则这根芦苇的长度是______．16．如图，有两棵树，一棵高8m ，另一棵高2m ，两树相距8m ，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少要飞______m ．17．如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上一点，测得BC＝60m，AC＝20m，则A，B两点间的距离为___m．18．如图所示的正方形网格内，点A，B，C，D，E是网格线交点，那么ECD EDCÐ+Ð=_____°．19．一艘帆船由于风向的原因先向正东方向航行了16km，然后向正北方向航行了12km，这时它离出发点有____________km.20．《九章算术》卷九“勾股”中记载：今有立木，系索其末，委地三尺，引索却行，去本八尺而索尽，问索长几何？译文：今有一竖立着的木柱，在木柱的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺，牵着绳索（绳索头与地面接触）退行，在距木柱根部8尺处时绳索用尽，则绳索长是____．三、解答题（本大题共40分）21．（6分）如图，在一棵大树AB的10m高的D处有两只猴子，它们同时发现地面上的点C 处有一根香蕉，一只猴子从点D处上爬到树顶点A处，利用拉在点A处的滑绳AC，滑到点C 处，另一只猴子从点D处滑到地面点B处，再由点B跑到点C，已知两只猴子所经过的路程都是15m，那么这棵树有多高？22．（6分）读诗求解“出水3尺一红莲，风吹花朵齐水面，水面移动有6尺，求水深几何请你算”．23．（6分）如图，某港口P位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后分别位于点Q，R处，且相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？24．（6分）如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC 的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D 的位置，问船向岸边移动了多少米．（假设绳子是直的）25．（8分）明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA 静止的时候，踏板离地高一尺（1AC =尺），将它往前推进两步（10EB =尺），此时踏板升高离地五尺（5BD =尺），求秋千绳索（OA 或OB ）的长度．26．（8分）如图，一架长2.5m 的梯子AB 斜靠在墙AC 上，∠C ＝90°，此时，梯子的底端B 离墙底C 的距离BC 为0.7m（1）求此时梯子的顶端A 距地面的高度AC ；（2）如果梯子的顶端A 下滑了0.9m ，那么梯子的底端B 在水平方向上向右滑动了多远？参考答案1．D2．C3．B4．D5．A6．C7．A8．C9．B10．A11．C12．B13．514．1715．13尺16．1017．18．9019．2020．73 6尺21．12m解：设树高AB为x m.由题意知BC=15-10=5(m)，AD=(x-10)m，AC=15-AD=15-x+10=(25-x)m.在Rt△ABC中，AB2+BC2=AC2，即x2+52=(25-x)2，解得x=12.答：这棵树有12m高．22．4.5尺解：设水深AP＝x尺，PB＝PC＝（x＋3）尺，根据勾股定理得：PA²＋AC²＝PC²，x²＋6²＝（x＋3）²．解得：x ＝4.5，答∶水深 4.5尺．23．北偏东45°（或西北）解：由题意可得：RP =18海里，PQ =24海里，QR =30海里，∵182+242=302，∴△RPQ 是直角三角形，∴∠RPQ =90°，∵“远航”号沿东北方向航行，即沿北偏东45°方向航行，∴∠RPS =45°，∴“海天”号沿北偏西45°（或西北）方向航行．24．船向岸边移动了9米．解：在Rt △ABC 中：∵∠CAB =90°，BC =17米，AC =8米，∴AB =（米），∵此人以1米每秒的速度收绳，7秒后船移动到点D 的位置，∴CD =17-1×7=10（米），∴AD =（米），∴BD =AB -AD =15-6=9（米），答：船向岸边移动了9米．25．秋千绳索的长度为14.5尺．解：设OA OB x ==尺，由题可知：5EC BD ==尺，1AC =尺，∴514EA EC AC =-=-=（尺），()4OE OA AE x =-=-尺，在Rt OEB 中，()4OE x =-尺，OB x =尺，10EB =尺，由勾股定理得：()222410x x =-+，解得：14.5x =，则秋千绳索的长度为14.5尺．26．（1）2.4米；（2）1.3m解：（1）∵∠C＝90°，AB＝2.5，BC＝0.7，=（米），∴AC 2.4答：此时梯顶A距地面的高度AC是2.4米；（2）∵梯子的顶端A下滑了0.9米至点A′，∴A′C＝AC−A′A＝2.4−0.9＝1.5（m），在Rt△A′CB′中，由勾股定理得：A′C2＋B′C2＝A′B′2，∴1.52＋B′C2＝2.52，∴B′C＝2（m），∴BB′＝CB′−BC＝2−0.7＝1.3（m），答：梯子的底端B在水平方向滑动了1.3m．。

2019年北师大版八下数学《第6章平行四边形》单元测试卷一．选择题（共10小题）1．若三角形的三条中位线长分别为2cm，3cm，4cm，则原三角形的周长为（）A．4.5cm B．18cm C．9cm D．36cm2．如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD＝8，则HE等于（）A．20B．16C．12D．83．如图，在▱ABCD中，AD＝8，点E，F分别是BD，CD的中点，则EF等于（）A．2B．3C．4D．54．如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，若△CEF的面积为12cm2，则S的值为（）△DGFA．4cm2B．6cm2C．8cm2D．9cm25．如图，△ABC中，已知AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（）A．4B．3C．D．26．从一个多边形的任何一个顶点出发都只有5条对角线，则它的边数是（）A．6B．7C．8D．97．一个多边形内角和是1080°，则这个多边形的对角线条数为（）A．26B．24C．22D．208．如图，在▱ABCD中，已知AD＝5cm，AB＝3cm，AE平分∠BAD交BC边于点E，则EC等于（）A．1 cm B．2 cm C．3 cm D．4 cm9．能够判定一个四边形是平行四边形的条件是（）A．一组对角相等B．两条对角线互相平分C．两条对角线互相垂直D．一对邻角的和为180°10．下列说法不正确的是（）A．有两组对边分别平行的四边形是平行四边形B．平行四边形的对角线互相平分C．平行四边形的对角互补，邻角相等D．平行四边形的对边平行且相等二．填空题（共5小题）11．如图，△ABC中，AB＝7，AC＝11，AD平分∠BAC，BD⊥AD，E是BC的中点，那么DE＝12．如图，在Rt△ABC中，∠C＝90°，CD是AB边上的中线，且CD＝5，则△ABC的中位线EF 的长是．13．已知△ABC中，D、E分别是AB、AC边的中点，则＝．14．若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是边形．15．若n边形的每个内角都等于150°，则n＝．三．解答题（共6小题）16．如图，在△ABC中，∠CAB＝90°，DE、DF是△ABC的中位线，连接EF、AD，求证：EF＝AD．17．如图，△ABC中，AB＝AC，E、F分别是BC、AC的中点，以AC为斜边作Rt△ADC．（1）求证：FE＝FD；（2）若∠CAD＝∠CAB＝24°，求∠EDF的度数．18．如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM＝MN；（2）∠BAD＝60°，AC平分∠BAD，AC＝2，求BN的长．19．在凸多边形中，四边形有2条对角线，五边形有5条对角线，经过观察、探索、归纳，你认为凸八边形的对角线条数应该是多少条？简单扼要地写出你的思考过程．20．如果多边形的每个内角都比它相邻的外角的4倍多30°，求这个多边形的内角和及对角线的总条数．21．如图，在▱ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．（1）求证：△AEB≌△CFD；（2）若四边形EBFD是菱形，求∠ABD的度数．2019年北师大版八下数学《第6章平行四边形》单元测试卷参考答案与试题解析一．选择题（共10小题）1．若三角形的三条中位线长分别为2cm，3cm，4cm，则原三角形的周长为（）A．4.5cm B．18cm C．9cm D．36cm【分析】根据三角形中位线定理可以求得三条边的长度，然后由三角形的周长公式可知原三角形的周长．【解答】解：∵三角形的三条中位线长分别为2cm，3cm，4cm，∴原三角形的三条边长分别为2cm×2＝4cm，3cm×2＝6cm，4cm×2＝8cm，∴原三角形的周长为：4cm+6cm+8cm＝18cm；故选：B．【点评】本题考查了三角形中位线定理，即三角形的中位线平行于第三边且等于第三边的一半．2．如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD＝8，则HE等于（）A．20B．16C．12D．8【分析】利用三角形中位线定理知DF＝AC；然后在直角三角形AHC中根据“直角三角形斜边上的中线等于斜边的一半”即可将所求线段EH与已知线段DF联系起来了．【解答】解：∵D、F分别是AB、BC的中点，∴DF是△ABC的中位线，∴DF＝AC（三角形中位线定理）；又∵E是线段AC的中点，AH⊥BC，∴EH＝AC，∴EH＝DF＝8．故选：D ．【点评】本题综合考查了三角形中位线定理、直角三角形斜边上的中线．三角形的中位线平行于第三边且等于第三边的一半．3．如图，在▱ABCD 中，AD ＝8，点E ，F 分别是BD ，CD 的中点，则EF 等于（ ）A ．2B ．3C ．4D ．5【分析】由四边形ABCD 是平行四边形，根据平行四边形的对边相等，可得BC ＝AD ＝8，又由点E 、F 分别是BD 、CD 的中点，利用三角形中位线的性质，即可求得答案．【解答】解：∵四边形ABCD 是平行四边形，∴BC ＝AD ＝8，∵点E 、F 分别是BD 、CD 的中点，∴EF ＝BC ＝×8＝4．故选：C ．【点评】此题考查了平行四边形的性质与三角形中位线的性质．此题比较简单，注意掌握数形结合思想的应用．4．如图，DE 是△ABC 的中位线，F 是DE 的中点，CF 的延长线交AB 于点G ，若△CEF 的面积为12cm 2，则S △DGF 的值为（ ）A ．4cm 2B ．6cm 2C ．8cm 2D ．9cm 2【分析】取CG 的中点H ，连接EH ，根据三角形的中位线定理可得EH ∥AD ，再根据两直线平行，内错角相等可得∠GDF ＝∠HEF ，然后利用“角边角”证明△DFG 和△EFH 全等，根据全等三角形对应边相等可得FG ＝FH ，全等三角形的面积相等可得S △EFH ＝S △DGF ，再求出FC ＝3FH ，再根据等高的三角形的面积比等于底边的比求出两三角形的面积的比，从而得解．【解答】解：如图，取CG 的中点H ，连接EH ，∴EH 是△ACG 的中位线，∴EH ∥AD ，∴∠GDF ＝∠HEF ，∵F 是DE 的中点，∴DF ＝EF ，在△DFG 和△EFH 中，，∴△DFG ≌△EFH （ASA ），∴FG ＝FH ，S △EFH ＝S △DGF ，又∵FC ＝FH +HC ＝FH +GH ＝FH +FG +FH ＝3FH ，∴S △CEF ＝3S △EFH ，∴S △CEF ＝3S △DGF ，∴S △DGF ＝×12＝4（cm 2）．故选：A ．【点评】本题考查了三角形的中位线定理，全等三角形的判定与性质，作辅助线，利用三角形的中位线进行解题是解题的关键．5．如图，△ABC 中，已知AB ＝8，∠C ＝90°，∠A ＝30°，DE 是中位线，则DE 的长为（ ）A ．4B ．3C ．D ．2【分析】先由含30°角的直角三角形的性质，得出BC ，再由三角形的中位线定理得出DE 即可．【解答】解：∵∠C ＝90°，∠A ＝30°，∴BC ＝AB ＝4，∴DE＝BC＝2．故选：D．【点评】本题考查了三角形的中位线定理，解答本题的关键是掌握含30°角的直角三角形的性质及三角形的中位线定理．6．从一个多边形的任何一个顶点出发都只有5条对角线，则它的边数是（）A．6B．7C．8D．9【分析】根据多边形的对角线的定义可知，从n边形的一个顶点出发，可以引（n﹣3）条对角线，由此可得到答案．【解答】解：设这个多边形是n边形．依题意，得n﹣3＝5，解得n＝8．故这个多边形的边数是8．故选：C．【点评】本题考查了多边形的对角线，如果一个多边形有n条边，那么经过多边形的一个顶点所有的对角线有（n﹣3）条，经过多边形的一个顶点的所有对角线把多边形分成（n﹣2）个三角形．7．一个多边形内角和是1080°，则这个多边形的对角线条数为（）A．26B．24C．22D．20【分析】先根据多边形的内角和公式求出边数，然后根据对角线的条数的公式进行计算即可求解．【解答】解：设多边形的边数是n，则（n﹣2）•180°＝1080°，解得n＝8，∴多边形的对角线的条数是：＝＝20．故选：D．【点评】本题考查了多边形的内角和定理与多边形的对角线的条数的公式，熟记公式是解题的关键．8．如图，在▱ABCD中，已知AD＝5cm，AB＝3cm，AE平分∠BAD交BC边于点E，则EC等于（）A．1 cm B．2 cm C．3 cm D．4 cm【分析】根据平行四边形的性质和角平分线的性质可以推导出等角，进而得到等腰三角形，推得AB＝BE，根据AD、AB的值，求出EC的长．【解答】解：∵AD∥BC，∴∠DAE＝∠BEA，∵AE平分∠BAD，∴∠BAE＝∠DAE，∴∠BAE＝∠BEA，∴BE＝AB＝3cm，∵BC＝AD＝5cm，∴EC＝BC﹣BE＝5﹣3＝2cm，故选：B．【点评】本题主要考查了平行四边形的性质，等腰三角形的判定；在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题．9．能够判定一个四边形是平行四边形的条件是（）A．一组对角相等B．两条对角线互相平分C．两条对角线互相垂直D．一对邻角的和为180°【分析】平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定方法选择即可．【解答】解：根据平行四边形的判定可知B正确．故选：B．【点评】本题考查了平行四边形的判定，在应用判定定理判定平行四边形时，应仔细观察题目所给的条件，仔细选择适合于题目的判定方法进行解答，避免混用判定方法．10．下列说法不正确的是（）A．有两组对边分别平行的四边形是平行四边形B．平行四边形的对角线互相平分C．平行四边形的对角互补，邻角相等D．平行四边形的对边平行且相等【分析】根据平行四边形的判定定理与性质进行判断．【解答】解：A、平行四边形的判定定理：有两组对边分别平行的四边形是平行四边形，故本选项正确；B、平行四边形的性质：平行四边形的对角线互相平分，故本选项正确；C、平行四边形的对角相等，邻角互补，故本选项错误；D、平行四边形的性质：平行四边形的对边平行且相等，故本选项正确；故选：C．【点评】本题考查了平行四边形的判定与性质．平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．二．填空题（共5小题）11．如图，△ABC中，AB＝7，AC＝11，AD平分∠BAC，BD⊥AD，E是BC的中点，那么DE＝2【分析】延长BD交AC于H，证明△ADB≌△ADH，得到AH＝AB＝7，BD＝DH，根据三角形中位线定理计算即可．【解答】解：延长BD交AC于H，在△ADB和△ADH中，，∴△ADB≌△ADH，∴AH＝AB＝7，BD＝DH，∴HC＝AC﹣AH＝4，∵BD＝DH，BE＝EC，∴DE＝CH＝2，故答案为：2．【点评】本题考查的是三角形中位线定理、全等三角形的判定和性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．12．如图，在Rt△ABC中，∠C＝90°，CD是AB边上的中线，且CD＝5，则△ABC的中位线EF 的长是5．【分析】根据直角三角形斜边上的中线等于斜边的一半的性质求出AB的长，再根据三角形的中位线平行于第三边并且等于第三边的一半即可求出EF的长．【解答】解：∵∠C＝90°，CD是AB边上的中线，∴AB＝2CD＝2×5＝10，∵EF是△ABC的中位线，∴EF＝AB＝×10＝5．故答案为：5．【点评】本题考查了三角形的中位线定理，直角三角形斜边上的中线等于斜边的一半的性质，熟记定理与性质是解题的关键．13．已知△ABC中，D、E分别是AB、AC边的中点，则＝．【分析】根据三角形的中位线定理求解．【解答】解：由D、E分别是AB、AC边的中点，可得DE为△ABC的中位线，所以＝．故答案为．【点评】本题考查了三角形的中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半．14．若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是十三边形．【分析】根据多边形的对角线的定义可知，从n边形的一个顶点出发，可以引（n﹣3）条对角线，由此可得到答案．【解答】解：设这个多边形是n边形．依题意，得n﹣3＝10，∴n＝13．故这个多边形是十三边形．故答案为：十三．【点评】多边形有n条边，则经过多边形的一个顶点所有的对角线有（n﹣3）条，经过多边形的一个顶点的所有对角线把多边形分成（n﹣2）个三角形．15．若n边形的每个内角都等于150°，则n＝12．【分析】根据多边形的内角和定理：180°•（n﹣2）求解即可．【解答】解：由题意可得：180°•（n﹣2）＝150°•n，解得n＝12．故多边形是12边形．故答案为：12．【点评】主要考查了多边形的内角和定理．n边形的内角和为：180°•（n﹣2）．此类题型直接根据内角和公式计算可得．三．解答题（共6小题）16．如图，在△ABC中，∠CAB＝90°，DE、DF是△ABC的中位线，连接EF、AD，求证：EF＝AD．【分析】根据三角形中位线定理得到DE∥AB，DF∥AC，得到四边形DEAF是平行四边形，得到四边形DEAF是矩形，根据矩形的性质证明即可．【解答】证明：∵DE、DF是△ABC的中位线，∴DE∥AB，DF∥AC，∴四边形DEAF是平行四边形，∵∠CAB＝90°，∴四边形DEAF是矩形，∴EF＝AD．【点评】本题考查的是三角形中位线定理、矩形的判定和性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．17．如图，△ABC中，AB＝AC，E、F分别是BC、AC的中点，以AC为斜边作Rt△ADC．（1）求证：FE＝FD；（2）若∠CAD＝∠CAB＝24°，求∠EDF的度数．【分析】（1）根据三角形的中位线定理得到FE＝AB，根据直角三角形的性质得到FD＝AC，等量代换即可；（2）根据平行线的性质得到∠EFC＝∠BAC＝24°，根据直角三角形的性质得到∠DFC＝48°，根据等腰三角形的性质计算即可．【解答】（1）证明：∵E、F分别是BC、AC的中点，∴FE＝AB，∵F是AC的中点，∠ADC＝90°，∴FD＝AC，∵AB＝AC，∴FE＝FD；（2）解：∵E、F分别是BC、AC的中点，∴FE∥AB，∴∠EFC＝∠BAC＝24°，∵F是AC的中点，∠ADC＝90°，∴FD＝AF．∴∠ADF＝∠DAF＝24°，∴∠DFC＝48°，∴∠EFD＝72°，∵FE＝FD，∴∠FED＝∠EDF＝54°．【点评】本题考查的是三角形中位线定理和直角三角形的性质的应用，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．18．如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM＝MN；（2）∠BAD＝60°，AC平分∠BAD，AC＝2，求BN的长．【分析】（1）根据三角形中位线定理得MN＝AD，根据直角三角形斜边中线定理得BM＝AC，由此即可证明．（2）首先证明∠BMN＝90°，根据BN2＝BM2+MN2即可解决问题．【解答】（1）证明：在△CAD中，∵M、N分别是AC、CD的中点，∴MN∥AD，MN＝AD，在RT△ABC中，∵M是AC中点，∴BM＝AC，∵AC＝AD，∴MN＝BM．（2）解：∵∠BAD＝60°，AC平分∠BAD，∴∠BAC＝∠DAC＝30°，由（1）可知，BM＝AC＝AM＝MC，∴∠BMC＝∠BAM+∠ABM＝2∠BAM＝60°，∵MN∥AD，∴∠NMC＝∠DAC＝30°，∴∠BMN＝∠BMC+∠NMC＝90°，∴BN2＝BM2+MN2，由（1）可知MN＝BM＝AC＝1，∴BN＝【点评】本题考查三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．19．在凸多边形中，四边形有2条对角线，五边形有5条对角线，经过观察、探索、归纳，你认为凸八边形的对角线条数应该是多少条？简单扼要地写出你的思考过程．【分析】首先从特殊四边形的对角线观察起，则四边形是2条对角线，五边形有5＝2+3条对角线，六边形有9＝2+3+4条对角线，则七边形有9+5＝14条对角线，则八边形有14+6＝20条对角线．【解答】解：凸八边形的对角线条数应该是20．理由：∵从一个顶点发出的对角线数目，它不能向本身引对角线，不能向相邻的两个顶点引对角线，∴从一个顶点能引的对角线数为（n﹣3）条；∵n边形共有n个顶点，∴能引n（n﹣3）条，但是考虑到这样每一条对角线都重复计算过一次，∴能引条．∴凸八边形的对角线条数应该是：＝20．【点评】能够从特殊中找到规律进行计算．20．如果多边形的每个内角都比它相邻的外角的4倍多30°，求这个多边形的内角和及对角线的总条数．【分析】首先外角为x°，则内角为（4x+30）°，根据内角与相邻的外角是互补关系可得x+4x+30＝180，解方程可得x的值，再利用外角和360°÷外角的度数可得边数．【解答】解：设外角为x°，x+4x+30＝180，解得：x＝30，360°÷30°＝12，∴（12﹣2）×180＝1800°，∴这个多边形的内角和是1800°，对角线的总条数＝＝54，答：这个多边形的内角和是1800°，对角线的总条数是54条．【点评】本题主要考查多边形内角与外角的知识点，此题要结合多边形的内角和公式寻求等量关系，构建方程求解即可．从n边形一个顶点可以引n﹣3条对角线．21．如图，在▱ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．（1）求证：△AEB≌△CFD；（2）若四边形EBFD是菱形，求∠ABD的度数．【分析】（1）根据平行四边形的性质和已知条件证明即可；（2）由菱形的性质可得：BE＝DE，因为∠EBD+∠EDB+∠A+∠ABE＝180°，所以∠ABD＝∠ABE+∠EBD＝×180°＝90°，问题得解．【解答】（1）证明：∵四边形ABCD是平行四边形，∴∠A＝∠C，AD＝BC，AB＝CD．∵点E、F分别是AD、BC的中点，∴AE＝AD，FC＝BC．∴AE＝CF．在△AEB与△CFD中，，∴△AEB≌△CFD（SAS）．（2）解：∵四边形EBFD是菱形，∴BE＝DE．∴∠EBD＝∠EDB．∵AE＝DE，∴BE＝AE．∴∠A＝∠ABE．∵∠EBD+∠EDB+∠A+∠ABE＝180°，∴∠ABD＝∠ABE+∠EBD＝×180°＝90°．【点评】本题考查了平行四边形的性质、全等三角形的判定和性质以及菱形的性质、等腰三角形的判断和性质，题目的综合性较强，难度中等．。

第一章 勾股定理一、基础题1。

下列说法正确的是（ d )A.若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2； B 。

若 a 、b 、c 是Rt △ABC 的三边，则a 2＋b 2＝c 2；C.若 a 、b 、c 是Rt △ABC 的三边, 90=∠A ,则a 2＋b 2＝c 2；D.若 a 、b 、c 是Rt △ABC 的三边， 90=∠C ，则a 2＋b 2＝c 2． 2. △ABC 的三条边长分别是a 、b 、c ,则下列各式成立的是( d ）A ．c b a =+ B. c b a >+ C 。

c b a <+ D 。

222c b a =+ 3．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（ b )A ．121B ．120C ．90D ．不能确定 4．△ABC 中，AB ＝15，AC ＝13，高AD ＝12,则△ABC 的周长为( ） A ．42 B ．32 C ．42 或 32 D ．37 或 33 5．斜边的边长为cm 17，一条直角边长为cm 8的直角三角形的面积是 ．6．假如有一个三角形是直角三角形，那么三边a 、b 、c 之间应满足 ，其中 边是直角所对的边;如果一个三角形的三边a 、b 、c 满足222b c a =+，那么这个三角形是 三角形，其中b 边是 边，b 边所对的角是 ． 7．一个三角形三边之比是6:8:10，则按角分类它是 三角形．8． 若三角形的三个内角的比是3:2:1,最短边长为cm 1，最长边长为cm 2，则这个三角形三个角度数分别是 ，另外一边的平方是 ．9．如图，已知ABC ∆中，︒=∠90C ，15=BA ，12=AC ，以直角边BC 为直径作半圆,则这个半圆的面积是 ．10． 一长方形的一边长为cm 3，面积为212cm ，那么它的一条对角线长是 ． 二、综合题11．如图，一个高4m 、宽3m 的大门,需要在对角线的顶点间加固一个木条，求木条的长．ACB3m 4m20m12。

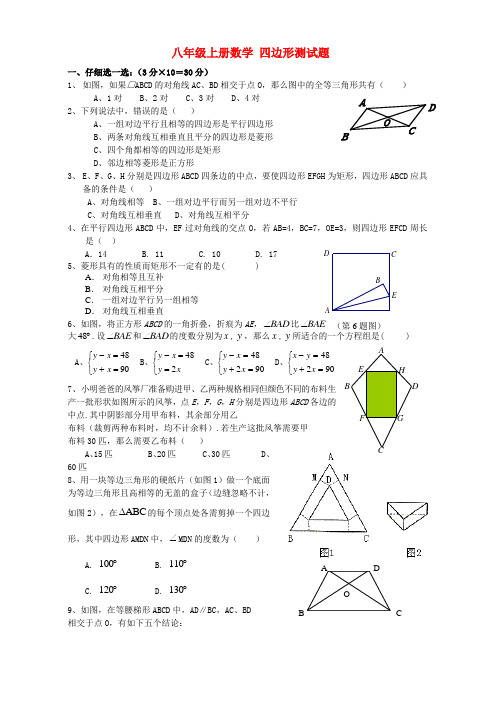
八年级上册数学 四边形测试题一、仔细选一选：（3分×10＝30分）1、 如图，如果□ABCD 的对角线AC 、BD 相交于点O ，那么图中的全等三角形共有（ ）A 、1对B 、2对C 、3对D 、4对2、下列说法中，错误的是（ ）A 、一组对边平行且相等的四边形是平行四边形B 、两条对角线互相垂直且平分的四边形是菱形C 、四个角都相等的四边形是矩形D 、邻边相等菱形是正方形3、 E 、F 、G 、H 分别是四边形ABCD 四条边的中点，要使四边形EFGH 为矩形，四边形ABCD 应具备的条件是（ ）A 、对角线相等B 、一组对边平行而另一组对边不平行C 、对角线互相垂直D 、对角线互相平分4、在平行四边形ABCD 中，EF 过对角线的交点O ，若AB=4，BC=7，OE=3，则四边形EFCD 周长是（ ）A ．14 B. 11 C. 10 D. 175、菱形具有的性质而矩形不一定有的是( )A ． 对角相等且互补B ． 对角线互相平分C ． 一组对边平行另一组相等D ． 对角线互相垂直6、如图，将正方形ABCD 的一角折叠，折痕为AE ，BAD ∠比BAE ∠ 大︒48.设BAE ∠和BAD ∠的度数分别为x ,y ，那么x ,y 所适合的一个方程组是( )A 、⎩⎨⎧=+=-9048x y x yB 、⎩⎨⎧==-x y x y 248C 、⎩⎨⎧=+=-90248x y x yD 、⎩⎨⎧=+=-90248x y y x7、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝，点E ，F ，G ，H 分别是四边形ABCD 各边的中点.其中阴影部分用甲布料，其余部分用乙 布料（裁剪两种布料时，均不计余料）.若生产这批风筝需要甲 布料30匹，那么需要乙布料（ ）A 、15匹B 、20匹C 、30匹D 、60匹8、用一块等边三角形的硬纸片（如图1）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图2），在∆ABC 的每个顶点处各需剪掉一个四边形，其中四边形AMDN 中，∠MDN 的度数为（ ） A. 100︒B. 110︒C. 120︒D. 130︒9、如图，在等腰梯形ABCD 中，AD ∥BC ，AC 、BD 相交于点O ，有如下五个结论：O A B D C（第6题图）ED C B A AE HF GB CAOC D① △AOD ∽△BOC ； ② ∠DAC ＝∠DCA ； ③梯形ABCD 是轴对称图形；④ △AOB ≌△AOD ； ⑤ AC ＝BD ．其中正确结论有 （ ） A.1个 B.2个 C.3个 D.4个10、有一张矩形纸片ABCD ，AB ＝2.5，AD ＝1.5，将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AC 与BC 交于点F （如下图），则CF 的长为（ ）A 、0.5B 、0.75C 、1D 、1.25 二、认真填一填：（3分×7＋4分＝25分）11、已知菱形的周长为40cm ，两条对角线的长度比为 3：4，那么两条对角线的长分别为 。

北师大版八年级上数学单元测试题 (四)姓名: ,班级: ,得分:一、填空题：（13⨯2=26分）1、在平行四边形ABCD 中∠A=500，BC=4cm ，则∠B= ，∠C= ，AD= 。

2、在平行四边形中周长为40cm ，两邻边之比为3∶5，则这个平行四边形四边分别为 ．３、在平行四边形ＡＢＣＤ中，周长为２０cm ，对角线ＡＣ、ＢＤ相交于点Ｏ，△ＡＯＢ的周长比△周长多4cm ，则ＡＢ＝ ＢＣ＝ 。

4、折叠式防盗门利用的是菱形的 性。

5、矩形的面积为2212b ab a -+，一边为b a 3-，则其周长是 .6、要使一个平行四边形成为一个正方形则需添加的条件是 。

7、矩形的一个角的平分线分矩形一边为1cm 和3cm 两部分，则这个矩形的面积为 。

8、如果边长分别为4cm 和5cm 的矩形与一个正方形的面积相等，那么这个正方形的边长为 cm.9、等腰梯形的一个内角为800，其它三个内角的度数为 。

10、等腰梯形上底、下底和腰分别为4cm 、10cm 、5cm ，则梯形的高为 。

11、直角梯形的两腰之比为1∶2，则它的锐角等于 。

12、过多边形的一个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形的边数为 。

13、两个多边形的边数相差1，则它们的内角和相差 。

二、选择题（10⨯2=20分） 1、由AB ∥CD ，AC ∥BD ，推出AC=BD ，下列理由不正确的是（ ）A 、平行线之间的平行线段相等；B 、平行四边形对边相等；C 、平行线之间距离相等；D 、平行四边形的一组对边平行且相等。

2、已知平行四边形的一条边长为14，下列各组数中能分别作它的两条对角线的长是（ ）A 、10与16B 、12与16C 、20与22D 、10与183、若A 、B 、C 三点不在同一直线上，则以其为顶点的平行四边形共有（ ）个A 、1B 、2C 、3D 、44、平行四边形一组对角的平分线（ ）A 、在同一直线上；B 、平行；C 、相交；D 、在同一直线上或平行。

北师大版八年级上册数学整理总结第一章 勾股定理1、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即222c b a =+2、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系222c b a =+，那么这个三角形是直角三角形。

3、勾股数：满足222c b a =+的三个正整数，称为勾股数。

第二章 实数一、实数的概念及分类1、实数的分类 正有理数有理数 零 有限小数和无限循环小数实数 负有理数正无理数无理数 无限不循环小数负无理数2、无理数：无限不循环小数叫做无理数。

在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数值，如sin60o 等二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数时一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a与b 互为相反数，则有a+b=0，a=—b，反之亦成立。

2、绝对值在数轴上，一个数所对应的点与原点的距离，叫做该数的绝对值。

（|a|≥0）。

零的绝对值是它本身，也可看成它的相反数，若|a|=a，则a≥0；若|a|=-a，则a≤0。

3、倒数如果a与b互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

4、数轴规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可）。

解题时要真正掌握数形结合的思想，理解实数与数轴的点是一一对应的，并能灵活运用。

5、估算三、平方根、算数平方根和立方根1、算术平方根：一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x就叫做a的算术平方根。

特别地，0的算术平方根是0。

表示方法：记作“a”，读作根号a。

CB 257第一章 勾股定理一、选择题1．等腰三角形的腰长为13cm ，底边长为10cm ，则面积为（ ）．A ．30 cm 2B ．130 cm 2C ．120 cm 2D ．60 cm 22．已知Rt △ABC 中，∠C ＝90°，若14=+b a cm ，10=c cm ，则Rt △ABC 的面积为（ ）．（A ）24cm 2 （B ）36cm 2 （C ）48cm 2 （D ）60cm 23．如图，分别以直角三角形的三边为边长向外作正方形，然后分别以三个正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为 S 1，S 2，S 3，则S 1，S 2，S 3之间的关系是（ ）． （A ）321S S S >+ （B ）321S S S =+（C ）321S S S <+ （D ）无法确定 4、以下列各组数为边长，能组成直角三角形的是（ ）A ．2，3，4B ．10，8，4C ．7，25，24D ．7，15，125、已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ）A ．25B ．14C ．7D ．7或256、以面积为9 cm 2的正方形对角线为边作正方形，其面积为（ ）A ．9 cm 2B ．13 cm 2C ．18 cm 2D ．24 cm 27、如图，直角△ABC 的周长为24，且AB:AC=5:3，则BC=（ ）A ．6B ．8C ．10D ．128、如图，一架云梯长25米，斜靠在一面墙上，梯子底端离墙7米，如果梯子的顶端下滑4米，那么梯子的底部在水平方向上滑动了（ ）A ．4米B ．6米C ．8米D ．10米9、将一根长24 cm 的筷子，置于底面直径为5cm 、高为12cm 的圆柱形水杯中，设筷子露在杯子外面的长为hcm ，则h 的取值范围是（ ）A ．5≤h ≤12B ．5≤h ≤24C ．11≤h ≤12D ．12≤h ≤2410、已知，如图，长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（ ）A ．6cm 2B ．8cm 2C ．10cm 2D ．12cm2 11、已知，如图，四边形ABCD 中，AB=3cm ，AD=4cm ，BC=13cm ，CD=12cm ，且∠A=90°，则四边形ABCD 的面积为（ ）A 、36，B 、22C 、18D 、1212．一个三角形的三边长分别是cm cm cm 25,20,15，则这个三角形的面积是（ ）A 250 2cmB 1502cmC 200 2cmD 不能确定13．将直角三角形的三边扩大相同的倍数后，得到的三角形是（ ）A 直角三角形B 锐角三角形 词C 钝角三角形D 不能确定二、填空题1．如图，小张为测量校园内池塘A ，B 两点的距离，他在池塘边选定一点 C ，使∠ABC ＝90°，并测得AC 长26m ，BC 长24m ，则A ，B 两点间的距离为 m ．2．如图，阴影部分是一个半圆，则阴影部分的面积为 ．（π不取近似值）321S S S3．底边长为16cm ，底边上的高为6cm 的等腰三角形的腰长为 cm ．4．一艘轮船以16km/h 的速度离开港口向东北方向航行，另一艘轮船同时离开港口以12km/h的速度向东南方向航行，它们离开港口半小时后相距 km ．5．一个长为10m 为梯子斜靠在墙上，梯子的顶端距地面的垂直高度为8m ，梯子的顶端下滑2m 后，底端滑动 m ．6．若△ABC 中，∠C=90°，（1）若a =5，b =12，则c = ；（2）若a =6，c =10，则b = ；（3）若a ∶b =3∶4，c =10，则a = ，b = .7．某农舍的大门是一个木制的矩形栅栏，它的高为2m ，宽为1.5m ，现需要在相对的顶点间用一块木棒加固，木板的长为 .8．直角三角形两直角边长分别为5cm ，12cm ，则斜边上的高为 .9、如图，从电线杆离地面６米处向地面拉一条长１０米的缆绳，这条缆绳在地面的固定点距离电线杆底部为 米。

四边形性质的探索 同步练习(二)班级_____________姓名______________学号______________成绩______________ 一．耐心填一填（2′×12=24′）1.已知：平行四边形ABCD 的周长为30cm,AB ：BC=2：3，则AB= ；2.若一个多边形的内角和是外角和的5倍，则这个多边形是 边形；3.在梯形ABCD 中，两底AB=14cm ，DC=6Ccm ，两底角∠A=30°，∠B=60°，则腰 BC= ；4.菱形两条对角线分别长4cm ，8cm ，则菱形边长为 ；5.如图，把边长为AD=12cm ，AB=8cm 的矩形沿着AE 为折痕对折使点D 落在BC 上点F 处，则DE= cm; 6.一个正正多边形每一个内角都等于它相邻的外角的 一半，这是一个正 边形； 7.如图，在⊿ABC 中，AD ⊥BC 于D ，E 、F 分别是AB 、AC 的中点，当⊿ABC 满足条件 时， AEDF 是菱形； 8.在四边形ABCD 中，若AB ∥CD ，AD=BC ，则四边形ABCD 是 ；9.对角线 的四边形是平行四边形；对角线 的平行四边形是矩形；对角线 的 平行四边形是菱形；10.如图,在矩形ABCD 中,BF ∥DE,若AD=12cm,AB=7cm ,且AE ：EB=5：2,则S 四边形EBFD = 。

二．精心选一选（2×14=28′） 11.已知平行四边形ABCD ，AC 、BD 是对角线，下列 结论中不一定正确的是（ ）； （A ） AB=CD ； （B ）AC=BD ；（C ） AC ⊥BD 时，它是菱形；（D ）当∠ABC=90°时，它是矩形。

12.能够找到一点，使该点到各边距离都相等的是（ ）① 平行四边形 ②菱形 ③矩形 ④正方形 ⑤三角形（A ）①② （B ）②③④⑤ （C ） ②④ （D ） ②④⑥13.已知一个四边形ABCD 的边长分别为a 、b 、c 、d ，其中a 、c 为对边，且a 2+b 2+c 2+d 2=2ac+2bd ，则四边形是（ ）（A ） 任意四边形；（B ）梯形；FCE D BA5题图7题图FC E DB A FC ED BA 10题图QB（B）行四边形；（D）对角线互相垂直的四边形；14.如图，正方形ABCD的边长为3，以CD为一边向CD两旁作等边⊿PCD和等边⊿QCD。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、如图，在四边形ABCD中，∠ABC=∠ACB=∠ADC= ，若AD=4，CD=2，则BD的长为（）A.6B.C.5D.2、如图，∠B=30°，线段BC=2，点E、F分别是线段BC和射线BA上的动点，设，则的最小值是（）A.1B.2C.3D.43、如图，四边形ABDC中，∠ABD＝120°，AB⊥AC，BD⊥CD，AB＝8，CD＝，则该四边形的面积是_______.A. B. C. D.4、如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）A.5B.25C.10 +5D.355、如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（）A.4B.3C.2D.56、在正方形网格中，△ABC的位置如图所示，则cosB的值为（）A. B. C. D.7、如图，在，则的面积是（）A. B. C. D.8、在下列长度的各组线段中，能组成直角三角形的是（）A.5，6，7B.5，12，13C.1，4，9D.5，11，129、直角三角形的一条直角边是另一条直角边的，斜边长为10，则它的面积为（）A.10B.15C.20D.3010、如图，在Rt△ABC中，∠B=90°，AB=BC，AC= .四边形BDEF是△ABC的内接正方形（点D，E，F在三角形的边上）.则此正方形的面积为( )A.25.B. .C.5.D.10.11、如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=，则EF＋CF的长为（）A.5B.4C.6D.12、如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD 于F点，若CF=1，FD=2，则BC的长为A. B. C. D.13、如图，菱形ABCD的周长为16，若∠BAD=60°，E是AB的中点，则点E的坐标为（）A.(1，1)B.C.D.14、已知的两直角边分别是，，则的斜边上的高是（）A. B. C. D.15、三边长分别为5cm，4cm，3cm的三角形的面积是（）A.6cm 2B.10cm 2C.12cm 2D.15 cm 2二、填空题(共10题，共计30分)16、如图，若与都是正方形网格中的格点三角形（顶点在格点上），则与的周长比为________.17、若圆的一条弦长为12，其弦心距等于8，则该圆的半径等于________．18、如图，▱ABCD的对角线AC与BD交于点O，BD⊥AD，AB＝10，AD＝6，则AC的长为________.19、如图，在四边形ABCD中，连接AC，DE⊥AC于点 E，∠ACB=90°，，AC=DE，AB=6，CD=5，则线段DE的长为________．20、已知双曲线与直线交于A、B两点（点A在点B的左侧）．如图，点P 是第一象限内双曲线上一动点，BC⊥AP于C，交x轴于F，PA交y轴于E，则的值是________．21、直角三角形纸片的两直角边BC、AC的长分别为6、8，现将如图那样折叠，使点与点重合，折痕为，则的长为________．22、若△ABC的三边长分别为3cm、4cm、5cm，则△ABC的外接圆半径为________.23、把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为________．24、如图，直线l1、l2、l3分别过正方形ABCD的三个顶点A，B，D，且相互平行，若l1与l2的距离为1，l2与l3的距离为1，则该正方形的面积是________．25、已知在△ABC中，∠C＝90°，AC＝3，BC＝4，分别以AC、BC、AB为直径作半圆，如图所示，则阴影部分的面积是________.三、解答题(共5题，共计25分)26、如图，方格纸上每个小正方形的面积为1．⑴在方格纸上，以线段AB为边画正方形ABCD，并计算所画正方形ABCD的面积．⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A2B2C2D2，正方形的各个顶点都在方格纸的格点上．27、在数轴上作出表示的点．28、如图，AB=4，BC=3，CD=13，AD=12，∠B=90°，求四边形ABCD的面积.29、如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD 的面积．30、如图，，平分，，，求的面积．参考答案一、单选题(共15题，共计45分)2、C3、C4、B5、A6、B7、A8、B9、B10、A11、A12、B13、B14、A15、A二、填空题(共10题，共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、29、30、。