12第十二章 立体几何【讲义】

立体几何专题讲义立体几何专题讲义一、考点分析基本图形1.棱柱——有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

斜棱柱底面是正多边形的棱柱正棱柱★直棱柱其他棱柱2.棱锥——有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

正棱锥3.球——球的性质：球心与截面圆心的连线垂直于截面；r=R2-d2（其中，球心到截面的距离为d、球的半径为R、截面的半径为r）球与多面体的组合体：球与正四面体，球与长方体，球与正方体等的内接与外切。

平行垂直基础知识网络★★★平行与垂直关系可互相转化1.平行关系a⊥α,b⊥α⇒a//ba⊥α,a//b⇒b⊥αa⊥α,a⊥β⇒α//βα//β,a⊥α⇒a⊥βα//β,γ⊥α⇒γ⊥β2.垂直关系线线平行判定线线垂直性质线线垂直判定面面垂直定义面面垂直线面平行面面平行线面垂直异面直线所成的角，线面角，二面角的求法★★★1.求异面直线所成的角θ∈(0,90°):解题步骤：找（作）：利用平移法找出异面直线所成的角；（1）可固定一条直线平移另一条与其相交；（2）可将两条一面直线同时平移至某一特殊位置。

常用中位线平移法证：证明所找（作）的角就是异面直线所成的角（或其补角）。

常需要证明线线平行；计算：通过解三角形，求出异面直线所成的角；2.求直线与平面所成的角θ∈[0,90°]:关键找“两足”：垂足与斜足二、典型例题考点一：三视图1.一个空间几何体的三视图如图1所示，则该几何体的体积为______。

2.若某空间几何体的三视图如图2所示，则该几何体的体积是______。

3.一个几何体的三视图如图3所示，则这个几何体的体积为______。

4.若某几何体的三视图（单位：cm）如图4所示，则此几何体的体积是______。

5.如图5是一个几何体的三视图，若它的体积是33，则a=______。

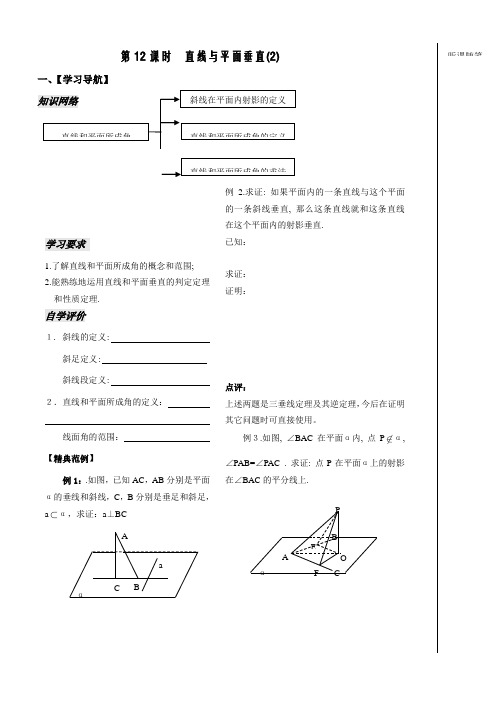
第12课时直线与平面垂直(2)一、【学习导航】学习要求1.了解直线和平面所成角的概念和范围;2.能熟练地运用直线和平面垂直的判定定理和性质定理.自学评价１. 斜线的定义: 斜足定义:斜线段定义: ２．直线和平面所成角的定义：线面角的范围：【精典范例】例1：.如图，已知AC，AB分别是平面α的垂线和斜线，C，B分别是垂足和斜足，aα，求证：a⊥BC 例 2.求证: 如果平面内的一条直线与这个平面的一条斜线垂直, 那么这条直线就和这条直线在这个平面内的射影垂直.已知：求证：证明：点评：上述两题是三垂线定理及其逆定理，今后在证明其它问题时可直接使用。

例３.如图, ∠BAC在平面α内, 点Pα,∠PAB=∠PAC . 求证: 点P在平面α上的射影在∠BAC的平分线上.BCαa听课随笔AAPOC EFBα思考：你能设计一个四个面都是直角的四面体吗?思维点拨：要证线面垂直，通常是从线线垂直来证明，而要证明线面垂直，通常又是从线线垂直来证明，即线线垂直和线面垂直互相转化．追踪训练1.如图，∠BCA=90°，PC⊥面ABC，则在三角形ABC，三角形PAC的边所在的直线中：(1)与PC垂直的直线有(2)与AP垂直的直线有2.若直线a与平面α不垂直，那么在平面内α与直线a垂直的直线 ( )A.只有一条B.有无数条C.是平面α内的所有直线D.不存在3.从平面外一点向平面引斜线段，如果斜线段长相等，那么它们在平面内的射影相等吗？4.在正方体ABCD-A1B1C1D1中，Ｐ为DD１的中点，O为底面ABCD的中心，求证：B１O⊥平面PAC点拨：使B１O垂直与平面ABC内的两条相交直线．【选修延伸】Ｒt△ABC的斜边ＢＣ在平面Ｍ内，两直角边和平面Ｍ所成的角分别是４５°和３０°，求斜边的高ＡＤ和平面Ｍ所成的角C BPA 听课随笔总结：要求斜线AD与平面M所成的角，找出斜线ＡＤ在平面Ｍ内的射影是关键．解题步骤：①作，②证，③求。

立体几何中的轨迹问题在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与求平面轨迹类似，应注意几何条件，善于基本轨迹转化．对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可转化为平面问题．对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性．立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题．其一般方法有：1、几何法：通过证明或几何作图，确定图形中取得最值的特殊位置，再计算它的值；2、代数方法：分析给定图形中的数量关系，选取适当的自变量及目标函数，确定函数解析式，利用函数的单调性、有界性，以及不等式的均值定理等，求出最值．轨迹问题【例1】如图，在正四棱锥S－ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE AC．则动点P的轨迹与△SCD组⊥成的相关图形最有可能的是( )D DA．B．C．解析：如图，分别取CD、SC的中点F、G，连结EF、EG、FG、BD．设AC与BD的交点为O，连结SO，则动点P的轨迹是△SCD的中位线FG．由正四棱锥可得SB⊥AC，EF⊥AC．又∵EG∥SB ∴EG⊥AC∴AC⊥平面EFG，∵P∈FG，E∈平面EFG，∴AC⊥PE．另解：本题可用排除法快速求解．B中P在D点这个特殊位置，显然不满足PE AC；C中P点所在的轨⊥迹与CD平行，它与CF成角，显然不满足PE AC；D于中P点所在的轨迹与CD平行，它与CF所成的角π4⊥为锐角，显然也不满足PE AC．⊥评析：动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形．不但考查了立体几何点线面之间的位置关系，而且又能巧妙地考查求轨迹的基本方法，是表现最为活跃的一种创新题型．这类立体几何中的相关轨迹问题，如“线线垂直”问题，很在程度上是找与定直线垂直的平面，而平面间的交线往往就是动点轨迹．【例2】(1)如图，在正四棱柱ABCD —A1B1C1D1中，E、F、G、H分别是CC1、C1D1、DD1、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足时，有MN∥平面B1BDD1．(2)正方体ABCD—A1B1C1D1中，P在侧面BCC1B1及其边界上运动，且总保持AP⊥BD1，则动点P的轨迹是线段B1C．(3)正方体ABCD —A1B1C1D1中，E、F分别是棱A1B1，BC上的动点，且A1E=BF，P为EF的中点，则点P的轨迹是线段MN(M、N分别为前右两面的中心)．(4)已知正方体ABCD—A1B1C1D1的棱长为1，在正方体的侧面BCC1B1上到点A距离为的点的集合形成一条曲线，那么这条曲线的形状是，它的长度是．1ACC1AE1AA1A1(1)(2)(3)(4)若将“在正方体的侧面BCC1B1上到点A距离为的点的集合”改为“在正方体表面上与点A距离为的点的集合”那么这条曲线的形状又是，它的长度又是．A【例3】(1)(04北京)在正方体ABCD -A 1B 1C 1D 1中，P 是侧面BB 1C 1C 内一动点，若P 到直线BC 与直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是 ( D )A ．A 直线B ．圆C ．双曲线D ．抛物线变式：若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1：2(或2：1)”， 则动点P 的轨迹所在的曲线是 椭圆 (双曲线)．(2)(06北京)平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是 (A )A ．一条直线B ．一个圆C ．一个椭圆D ．双曲线的一支解：设l 与l 是其中的两条任意的直线，则这两条直线确定一个平面，且斜线AB 垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内，故动点C 都在这个平面与平面α的交线上，故选A ．(3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1，M 在棱AB 上，且AM =，点P 到直13线A 1D 1的距离与点P 到点M 的距离的平方差为1，则点P 的轨迹为 抛物线 ．(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3，长为2的线段MN 点一个端点M 在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 ．π6【例4】(04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与△ABC 组成图形可能是：( D )BAB CD 【例5】四棱锥P -ABCD ，AD ⊥面PAB ，BC ⊥面PAB ，底面ABCD 为梯形，AD =4，BC =8，AB =6，∠APD =∠CPB ，满足上述条件的四棱锥的顶点P 的轨迹是()A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分分析：∵AD ⊥面PAB ，BC ⊥平面PAB ∴AD ∥BC 且AD ⊥PA ，CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴=AD PA CBPB ∴PB =2PA在平面APB 内，以AB 的中点为原点，AB 所在直线为x 轴建立平面直角坐标系，则A (-3，0)、B (3，0)，设P (x ，y )(y ≠0)，则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0)∴P 的轨迹是(B)1AA 3A立体几何中的轨迹问题（教师版）1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（D ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分 简析本题主要考查点到直线距离的概念，线面垂直及抛物线的定义．因为B 1C 1面AB 1，所以⊥PB 1就是P 到直线B 1C 1的距离，故由抛物线的定义知：动点的轨迹为抛物线的一段，从而选D ．2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（B ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（C ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（A ）．A ．圆或圆的一部分B ．抛物线或其一部分C ．双曲线或其一部分D ．椭圆或其一部分 简析由条件易知：AC 是平面BB 1D 1D 的法向量，所以EP 与直线AC 成等角，得到EP 与平面BB 1D 1D 所成的角都相等，故点P 的轨迹有可能是圆或圆的一部分．5．已知正方体的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD A B C D -1111ABCD 内的动点，且点P 到直线的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为A D 11（A ）．A ．抛物线B ．双曲线C ．直线D ．圆简析在正方体中，过P 作PF AD ，过F 作FE A 1D 1，垂足分别为F 、E ，ABCD A B C D -1111⊥⊥连结PE ．则PE 2=a 2+PF 2，又PE 2-PM 2=a 2，所以PM 2=PF 2，从而PM ＝PF ，故点P 到直线AD 与到点M 的距离相等，故点P 的轨迹是以M 为焦点，AD 为准线的抛物线．6．在正方体中，点P 在侧面BCC 1B 1及其边界上运动，总有AP BD 1，则动点P 的轨迹ABCD A B C D -1111⊥为__________． 简析在解题中，我们要找到运动变化中的不变因素，通常将动点聚焦到某一个平面．易证BD 1面ACB 1，所以满足BD 1AP 的所有点P 都在一个平面ACB 1上．而已知条件中的点P 是在侧面BCC 1B 1及⊥⊥其边界上运动，因此，符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上，故所求的轨迹为线段B 1C ．本题的解题基本思路是：利用升维，化“动”为“静”，即先找出所有点的轨迹，然后缩小到符合条件的点的轨迹．7．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面SCD 内及其边界上运动，总有PE AC ，则动点∆⊥P 的轨迹为_______________． 答案线段MN （M 、N 分别为SC 、CD 的中点）8．若A 、B 为平面的两个定点，点P 在外，PB ，动点C （不同于A 、B ）在内，且PC AC ，则αα⊥αα⊥动点C 在平面内的轨迹是________．（除去两点的圆）9．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成的图形可能是：（D ）∆A A A AB C B C B C B C A B C D简析动点P 在侧面ABC 内，若点P 到AB 的距离等于到棱BC 的距离，则点P 在的内角∠ABC 平分线上．现在P 到平面BCD 的距离等于到棱AB 的距离，而P 到棱BC 的距离大于P 到底面BCD 的距离，于是，P 到棱AB 的距离小于P 到棱BC 的距离，故动点P 只能在的内角平分线与AB 之间的区域∠ABC 内．只能选D ．10．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（B ）． A ．圆B ．椭圆 C ．双曲线D ．抛物线解题的要领就是化空间问题为平面问题，把一些重要元素集中在某一个平面内，利用相关的知识去解答，象平面几何知识、解析几何知识等．11．已知正方体的棱长为1，在正方体的侧面上到点A 距离为的点的轨迹形ABCD A B C D -1111BCC B 11233成一条曲线，那么这条曲线的形状是_________，它的长度为__________．12．已知长方体中，，在线段BD 、上各有一点P 、Q ，PQ 上有一点ABCD A B C D -1111AB BC ==63,A C 11M ，且，则M 点轨迹图形的面积是 ．PM MQ =2提示轨迹的图形是一个平行四边形．13．已知棱长为3的正方体中，长为2的线段MN 的一个端点在上运动，另一个端点ABCD A B C D -1111DD 1N 在底面ABCD 上运动，求MN 中点P 的轨迹与正方体的面所围成的几何体的体积．14．已知平面平面，直线，点，平面、间的距离为4，则在内到点P 的距离为5且到直//αβl α⊂l P ∈αββ线的距离为的点的轨迹是（ ）l 29A ．一个圆B ．两条平行直线C ．四个点D ．两个点简析：如图，设点P 在平面内的射影是O ，则OP 是、的公垂线，OP=4．在βαβ点的轨迹是四个点，故选C ．16．在四棱锥中，面PAB ，面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，ABCD P -⊥AD ⊥BC ，满足上述条件的四棱锥的顶点P 的轨迹是（ ）CPB APD ∠=∠A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分简析：因为面PAB ，面PAB ，所以AD//BC ，且．⊥AD ⊥BC ︒=∠=∠90CBP DAP 又，8BC ,4AD ,CPB APD ==∠=∠由于点P 不在直线AB 上，故此轨迹为一个不完整的圆，选B ．17．如图，定点A 和B 都在平面内，定点P C 是内异于A 和B α,PB ,α⊥α∉α的动点．且，那么动点C 在平面内的轨迹是（ ）AC PC ⊥αA ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点简析：因为，且PC 在内的射影为BC ，所以，即．所以点C 的轨迹是PC AC ⊥αBC AC ⊥︒=∠90ACB 以AB 为直径的圆且去掉A 、B 两点，故选B ．18．如图，在正方体中，P 是侧面内一动点，若P 到直线1111D C B A ABCD -1BC BC 与直线的距离相等，则动点P 的轨迹所在的曲线是（ ）11D C A ．直线B ．圆C ．双曲线D ．抛物线简析：因为P 到的距离即为P 到的距离，所以在面内，P 到定点11D C 1C 1BC 的距离与P 到定直线BC 的距离相等．由圆锥曲线的定义知动点P 的轨迹为抛物线，故选D ．1C 19．已知正方体的棱长为1，点P 是平面AC 内的动点，若点P 到直线的距离等于点1111D C B A ABCD -11D A P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（ ）A ．抛物线B ．双曲线C ．椭圆D ．直线简析：如图4，以A 为原点，AB 为x 轴、AD 为y 轴，建立平面直角坐标系．设P （x ，y ），作于E 、于F ，连结EF ，易知AD PE ⊥11D A PF ⊥建议收藏下载本文，以便随时学习！1x |EF ||PE ||PF |2222+=+=又作于N ，则．依题意，CD PN ⊥|1y ||PN |-=|PN ||PF |=故动点P 的轨迹为双曲线，选B ．20．如图，AB 是平面的斜线段，A 为斜足，若点P 在平面内运动，使得△ABP a a 的面积为定值，则动点P 的轨迹是（ ）（A ）圆 （B ）椭圆 （C ）一条直线 （D ）两条平行直线分析：由于线段AB 是定长线段，而△ABP 的面积为定值，所以动点P 到线段AB 的距离也是定值．由此可知空间点P 在以AB 为轴的圆柱侧面上．又P 在平面内运动，所以这个问题相当于一个平面去斜切一个圆柱(AB 是平面的斜线段)，得到的切痕是椭圆．P 的轨迹就是圆柱侧面与平面的交线 ．a 21．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正P 1111ABCD A B C D -1BD P 11BB D D 方体表面相交于．设，，则函数的图象大致是（ ）M N ，BP x =MN y =()y f x=ABCD MN P A 1B 1C 1D 1分析：将线段MN 投影到平面ABCD 内，易得y 为x 一次函数．22．已知异面直线a ，b 成角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且︒60线段AB 长等于4，求线段AB 中点的轨迹方程．图5简析：如图5，易知线段AB 的中点P 在公垂线段MN 的中垂面上，直线、为平面内过MN 的中α'a 'b α点O 分别平行于a 、b 的直线，于，于，则，且P 也为的中点．'a 'AA ⊥'A 'b 'BB ⊥'B P 'B 'A AB =⋂'B 'A 由已知MN=2，AB=4，易知得．,2AP ,1'AA ==32'B 'A =则问题转化为求长等于的线段的两个端点、分别在、上移动时其中点P 的轨迹．现以32'B 'A 'A 'B 'a 'b 的角平分线为x 轴，O 为原点建立如图6所示的平面直角坐标系．'OB 'A ∠图6设，，)y ,x (P n |'OB |,m |'OA |==则)n 21,n 23('B ),m 21,m 23('A -)n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++-消去m 、n ，得线段AB 的中点P 的轨迹为椭圆，其方程为．1y 9x 22=+点评：例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起，相互交汇和渗透，有利于培养运用多学科知识解决问题的能力．立体几何中的轨迹问题1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为 （ ）A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（ ） A ．圆或圆的一部分 B ．抛物线或其一部分 C ．双曲线或其一部分 D ．椭圆或其一部分5．已知正方体的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD A B C D -1111ABCD 内的动点，且点P 到直线的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（ A D 11）A ．抛物线B ．双曲线C ．直线D ．圆6．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与ABC 组成的图形可能是（ ∆）A A AB C B C B C B CA B C D7．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（ ） A ．圆B ．椭圆 C ．双曲线D ．抛物线8．已知平面平面，直线，点，平面、间的距离为4，则在内到点P 的距离为5且到直//αβl α⊂l P ∈αββ线的距离为的点的轨迹是（l 29）A ．一个圆B ．两条平行直线C ．四个点D ．两个点9．在四棱锥中，面PAB ，面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，ABCD P -⊥AD ⊥BC ，满足上述条件的四棱锥的顶点P 的轨迹是（ ）CPB APD ∠=∠A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分10．如图，定点A 和B 都在平面内，定点P C 是内异于A 和B α,PB ,α⊥α∉α的动点．且，那么动点C 在平面内的轨迹是（ ）AC PC ⊥αA ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点11．已知正方体的棱长为1，点P 是平面AC 内的动点，若点P 到直线的距离等于点1111D C B A ABCD -11D A P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（）A ．抛物线B ．双曲线C ．椭圆D ．直线12．如图，AB 是平面的斜线段，A 为斜足，若点P 在平面内运动，使得△ABP a a 的面积为定值，则动点P 的轨迹是（ ）A ．圆B ．椭圆C ．一条直线D ．两条平行直线13．如图，动点在正方体的对角线上．过点作垂直于平面的直线，与正P 1111ABCD A B C D -1BD P 11BB D D 方体表面相交于．设，，则函数的图象大致是（ ）M N ，BP x =MN y =()y f x =ABCD MN P A 1B 1C 1D 114．在正方体中，点P 在侧面BCC 1B 1及其边界上运动，总有AP BD 1，则动点P 的轨迹ABCD A B C D -1111⊥为________．15．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面SCD 内及其边界上运动，总有PE AC ，则动点∆⊥P 的轨迹为_______________．16．若A 、B 为平面的两个定点，点P 在外，PB ，动点C （不同于A 、B ）在内，且PC AC ，则αα⊥αα⊥动点C 在平面内的轨迹是________．17．已知正方体的棱长为1，在正方体的侧面上到点A 距离为的点的轨迹形ABCD AB C D -1111BCC B 11233成一条曲线，那么这条曲线的形状是_________，它的长度为__________．18．已知长方体中，，在线段BD 、上各有一点P 、Q ，PQ 上有一点ABCD A B C D -1111AB BC ==63,A C 11M ，且，则M 点轨迹图形的面积是．PM MQ =219．已知棱长为3的正方体中，长为2的线段MN 的一个端点在上运动，另一个端点ABCD A B C D -1111DD 1N 在底面ABCD 上运动，则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是．20．已知异面直线a ，b 成角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且︒60线段AB 长等于4，求线段AB 中点的轨迹方程．。

第12课时 平面与平面位置关系学习要求1.理解并掌握两平面平行, 两平面相交的定义.2.会画平行或相交平面的空间图形, 并会用符号表示.3.掌握两个平面平行的判定定理和性质定理,并能运用其解决一些具体问题.【课堂互动】自学评价１. 两个平面的位置关系位置关系 两平面平行 两平面相交公共点符号表示图形表示２．两个平面平行的判定定理：符号表示：３．两个平面平行的性质定理：已知：求证：证明：４．思考： (1)一个平面内的直线是否平行于另一个平面 (2)分别在两个平行平面内的两条直线是否平行？ ５．两个平行平面间的距离 ６．直线和平面的距离： 【精典范例】 例1：如图, 在长方体ABCD-A 1B 1C 1D 1中, 求证: 平面C 1DB//平面AB 1D 1. 证明：见书40例1听课随笔 C A例2.求证: 如果一条直线垂直于两个平行平面中的一个平面, 那么它也垂直于另一个平面.证明：见书40例2例 3.求证: 如果一条直线垂直于两个平面, 那么这两个平面平行．.已知求证：证明：仿例2证思维点拨：两个平面平行的判定定理和性质定理体现了在一定条件下，线线平行，线面平行，面面平行之间可以互相转化．追踪训练1.判断下列命题是否正确，并说明理由：(1).若平面α内的两条直线分别与平面β平行，则α与β平行；(2) 若平面α内的有无数条直线与平面β平行，则α与β平行；(3)平行于同一条直线的两个平面平行；(4)过已知平面外一点，有且仅有一个平面与已知平面平行；(5) 过已知平面外一条直线，必能作出与已知平面平行的平面。

2.六棱柱的表面中，互相平行的面最多有多少对？3.如图，设E,F,E1,F1分别是长方体ABCD-A1B1C1D1的棱AB,CD,A1B1,C1D1的中点，求证：平面ED1//平面BF1证明：略4.求证：夹在两个平行平面间的平行线段相等。

证明：略A听课随笔。

必修二立体几何复习讲义一、基础知识梳理：1、柱、锥、台、球的结构特征￥2、空间几何体的三视图 ^定义三视图：正视图（光线从几何体的前面向后面正投影）；侧视图（从左向右）、俯视图（从上向下） 注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度； 俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度；侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。

3、空间几何体的直观图——斜二测画法斜二测画法特点：①原来与x 轴平行的线段仍然与x 平行且长度不变；②原来与y 轴平行的线段仍然与y 平行，长度为原来的一半。

】4、柱体、锥体、台体的表面积与体积（1）几何体的表面积为几何体各个面的面积的和。

（2）特殊几何体表面积公式（c 为底面周长，h 为高，'h 为斜高，l 为母线）ch S =直棱柱侧面积 rh S π2=圆柱侧 '21ch S =正棱锥侧面积 rlS π=圆锥侧面积')(2121h c c S +=正棱台侧面积 l R r S π)(+=圆台侧面积 ()l r r S +=π2圆柱表()l r r S +=π圆锥表 ()22R Rl rl r S +++=π圆台表（3）柱体、锥体、台体的体积公式V Sh =柱 2V Sh r h π==圆柱 13V Sh =锥 h r V 231π=圆锥 ''1()3V S S S S h =台"[（4）球体的表面积和体积公式：V 球=343R π ； S 球面=24R π5、空间点、直线、平面的位置关系 （1）平面① 平面的概念： A.描述性说明； B.平面是无限伸展的；② 平面的表示：通常用希腊字母α、β、γ表示，如平面α（通常写在一个锐角内）；也可以用两个相对顶点的字母来表示，如平面BC 。

】③ 点与平面的关系：点A 在平面α内，记作A α∈；点A 不在平面α内，记作A α∉点与直线的关系：点A 的直线l 上，记作：A ∈l ； 点A 在直线l 外，记作A ∉l ； 直线与平面的关系：直线l 在平面α内，记作l ⊂α；直线l 不在平面α内，记作l ⊄α。

必修二立体几何复习讲义一、基础知识梳理：1、柱、锥、台、球的结构特征2、空间几何体的三视图定义三视图：正视图（光线从几何体的前面向后面正投影）；侧视图（从左向右）、俯视图（从上向下）注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度；俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度；侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。

3、空间几何体的直观图——斜二测画法斜二测画法特点：①原来与x轴平行的线段仍然与x平行且长度不变；②原来与y轴平行的线段仍然与y平行，长度为原来的一半。

4、柱体、锥体、台体的表面积与体积（1）几何体的表面积为几何体各个面的面积的和。

（2）特殊几何体表面积公式（c为底面周长，h为高，'h为斜高，l为母线）chS=直棱柱侧面积rhSπ2=圆柱侧'21chS=正棱锥侧面积rlSπ=圆锥侧面积')(2121hccS+=正棱台侧面积lRrSπ)(+=圆台侧面积()lrrS+=π2圆柱表()lrrS+=π圆锥表()22RRlrlrS+++=π圆台表（3）柱体、锥体、台体的体积公式V Sh=柱2V S h r hπ==圆柱13V S h=锥hrV231π=圆锥''1()3V S S S S h=++台（4）球体的表面积和体积公式：V球=343Rπ；S球面=24Rπ5、空间点、直线、平面的位置关系（1）平面①平面的概念： A.描述性说明； B.平面是无限伸展的；②平面的表示：通常用希腊字母α、β、γ表示，如平面α（通常写在一个锐角内）；也可以用两个相对顶点的字母来表示，如平面BC。

③ 点与平面的关系：点A 在平面α内，记作A α∈；点A 不在平面α内，记作A α∉点与直线的关系：点A 的直线l 上，记作：A ∈l ； 点A 在直线l 外，记作A ∉l ；直线与平面的关系：直线l 在平面α内，记作l ⊂α；直线l 不在平面α内，记作l ⊄α。