2011年高考数学真题分类汇编3

四川省各地市2011年高考数学最新联考试题分类大汇编第3部分:函数与导数 一、选择题：5．(四川省成都市外国语学校2011年3月高三考试理科)若函数()y f x =存在反函数1()y f x -=，且函数2()y x f x =-的图像过点(2,1)，则函数1()2y f x x -=-的图象一定过点（ D ）A ．(3,2)B ．(2,3)-C ．(4,3)-D ．(3,4)-2. (四川省成都石室中学2011届髙三二诊模拟考试理科)当a 、b R 时，下列总能成立的是（ B )(A) (B)(C) (D)5.(四川省成都石室中学2011届髙三二诊模拟考试理科)已知函数的反函数的图象的对称中心为(-1，5),则实数a 的是（ D ）(A) —3 (B) 1 (C) 5 (D) 710. (四川省成都石室中学2011届髙三二诊模拟考试理科)下图是的图象，则的值是（ D ）（A ） (B) (C) (D)[来源:学科网ZXXK]11. (四川省成都石室中学2011届髙三二诊模拟考试理科)一给定函数的图象在下列图中，并且对任意，由关系式得到的数列满足，则该函数的图象是（ A ）2．(四川省成都市外国语学校2011年3月高三考试理科)命题p ：若0a b ⋅< ，则a 与b的夹角为钝角。

命题q ：定义域为R 的函数()f x 在(,0)-∞及(0,)+∞上都是增函数，则()f x 在(,)-∞+∞上是增函数。

下列说法正确的是（ B ）A ．“p 或q ”是真命题B ．“p 且q ”是假命题C ．“p ⌝”为假命题D ．“q ⌝”为假命题12．(四川省成都市外国语学校2011年3月高三考试理科)下列命题中：①函数()2()sin (0,)sin f x x x xπ=+∈的最小值是22②在ABC ∆中，若sin 2sin 2A B =，则ABC ∆是等腰或直角三角形；③如果正实数,,a b c 满足a b c +>，则111a b ca b c +>+++；④如果()y f x =是可导函数，则0()0f x '=是函数()y f x =在0x x =处取到极值的必要不充分条件。

2011年全国各地高考数学试题及解答分类汇编大全（14统计、统计案例、算法初步、框图、推理与证明）一、选择题：1. (2011北京文)执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为( )(A)2 (B)3 (C)4 (D)51.【答案】C【解析】执行三次循环，12S A =≤=成立，112p =+=，1131122S P =+=+=，322S A =≤=成立，213p =+=，3131112236S P =+=+=，1126S A =≤=成立，314p =+=1111112566412S p =+=+=，25212S A =≤=不成立，输出4p =，故选C2.(2011北京理)执行如图所示的程序框图，输出的s 值为（ ）（A ）-3 （B ）-12（C ）13 （D ）22.【答案】D【解析】：循环操作4次时S 的值分别为11,,3,232--，选D 。

3. (2011福建文)某校选修乒乓球课程的学生中，高一年级有30名， 高二年级有40名。

现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为（ ）A. 6B. 8C. 10D.12解析：由30:406:,n =可得8n =，答案应选B 。

4. (2011福建文)阅读右图所示的程序框图，运行相应的程序，输出的结果是（ ）A.3B.11C.38D.1234.解析：110,12310,a a =<=+=<2321110,11a a =+=>=,答案应选B 。

5. (2011广东理) 设S 是整数集Z 的非空子集，如果S b a ∈∀,,有S ab ∈,则称S 关于数的乘法是封闭的，若T,V 是Z 的两个不相交的非空子集，T ∪V=Z, 且T c b a ∈∀,,,有T c ab ∈,;V z y x ∈∀,,,有V xyz ∈,则下列结论恒成立的是（ ）A. T,V 中至少有一个关于乘法是封闭的B. T,V 中至多有一个关于乘法是封闭的C. T,V 中有且只有一个关于乘法是封闭的D. T,V 中每一个关于乘法是封闭的5. 解析：（A ）．若T 为奇数集，V 为偶数集，满足题意，此时T 与V 关于乘法都是封闭的，排除B 、C ，若T 为负整数集，V 为非负整数集，也满足题意，此时只有V 关于乘法是封闭的，排除D 。

导数2.（2012·某某高考卷·T9·5分）函数的图像大致为【答案】D【解析】函数x x x x f --=226cos )(，)(226cos )(x f xx f xx -=-=--为奇函数， 当0→x ，且0>x 时+∞→)(x f ；当0→x ，且0<x 时-∞→)(x f ； 当+∞→x ，+∞→--xx 22，0)(→x f ；当-∞→x ，-∞→--x x 22，0)(→x f .答案应选D 。

【点评】本题考查了函数的奇偶性的性质特点，结合图象语言，考查了数形结合法的思想，函数图象是考点中重要内容，估计明年还会继续考察。

5.( 2011年某某) 函数()()m nf x ax x =1-在区间〔0,1〕上的图像如图所示，则m ，n 的值 可能是（A ）1,1m n == (B) 1,2m n == (C) 2,1m n == (D) 3,1m n ==【答案】B 【命题意图】本题考查导数在研究y0.51xO0.5函数单调性中的应用，考查函数图像，考查思维的综合能力.难度大.【解析】代入验证，当1,2m n ==，()()()f x ax x n x x x 232=1-=-2+，则 ()()f x a x x 2'=3-4+1，由()()f x a x x 2'=3-4+1=0可知，121,13x x ==，结合图像可知函数应在10,3⎛⎫ ⎪⎝⎭递增，在1,13⎛⎫ ⎪⎝⎭递减，即在13x =取得最大值，由 ()()f a 21111=⨯1-=3332，知a 存在.故选B.7.（2011年某某）1(2)0xe x dx+⎰等于A ．1B ．1e -C ．eD ．1e +【答案】C8.（2011年某某）对于函数()sin f x a x bx c =++ (其中，,,a b R c Z ∈∈)，选取,,a b c 的一组值计算(1)f 和(1)f -，所得出的正确结果一定不可能是A ．4和6B ．3和1C ．2和4D ．1和2【答案】D9.（2011年某某）已知函数()xf x e x =+，对于曲线()y f x =上横坐标成等差数列的三个点A ，B ，C ，给出以下判断： ①△ABC 一定是钝角三角形 ②△ABC 可能是直角三角形 ③△ABC 可能是等腰三角形 ④△ABC 不可能是等腰三角形 其中，正确的判断是A ．①③B ．①④C ．②③D ．②④【答案】B10.（2011年某某）若关于x 的方程x2＋mx ＋1＝0有两个不相等的实数根，则实数m 的取值X 围是A ．（－1，1）B ．（－2，2）C ．（－∞，－2）∪（2，＋∞）D ．（－∞，－1）∪（1，＋∞） 【答案】C13.（2011年某某）函数1()lg(1)1f x x x =++-的定义域是 （ ）A ．(,1)-∞-B ．(1,)+∞C ．(1,1)(1,)-+∞D ．(,)-∞+∞【答案】C14.（2011年某某）已知定义在R 上的奇函数()x f 和偶函数()x g 满足()()2+-=+-x x a a x g x f()1,0≠>a a 且，若()a g =2，则()=2fA. 2B. 415C. 417D. 2a【答案】B【解析】由条件()()22222+-=+-a a g f ，()()22222+-=-+--a a g f ，即 ()()22222+-=+--a a g f ，由此解得()22=g ，()222--=a a f ，所以2=a ，()41522222=-=-f ，所以选B.15.（2011年某某）放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象成为衰变，假设在放射性同位素铯137的衰变过程中，其含量M （单位：太贝克）与时间t （单位：年）满足函数关系：()3002t M t M -=，其中M 为0=t 时铯137的含量，已知30=t 时，铯137的含量的变化率是2ln 10-（太贝克/年），则()=60MA. 5太贝克B. 2ln 75太贝克C. 2ln 150太贝克D. 150太贝克 【答案】D【解析】因为()300/22ln 301tM t M -⨯-=，则()2ln 1022ln 3013030300/-=⨯-=-M M ，解得6000=M ，所以()302600t t M -⨯=，那么()150416002600603060=⨯=⨯=-M （太贝克），所以选D.16.（2011年某某）曲线sin 1sin cos 2x y x x =-+在点(,0)4M π处的切线的斜率为（ ）A ．12-B ．12 C． D．【答案】B【解析】22cos (sin cos )sin (cos sin )1'(sin cos )(sin cos )x x x x x x y x x x x +--==++，所以2411'|2(sincos )44x y πππ===+。

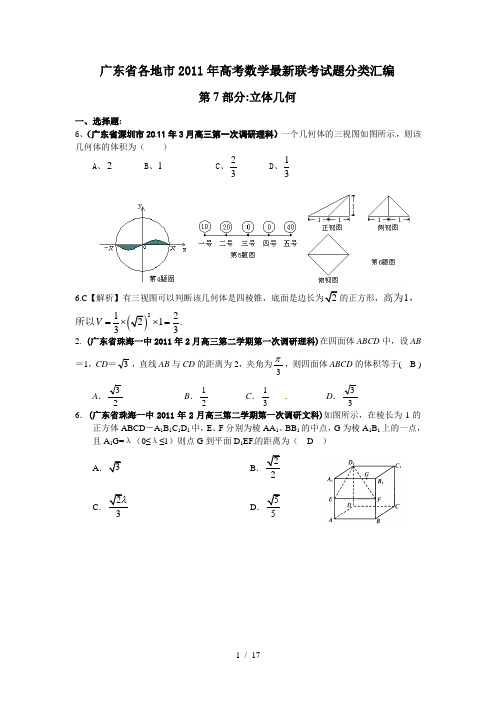
广东省各地市2011年高考数学最新联考试题分类汇编第7部分:立体几何一、选择题: 6、（广东省深圳市2011年3月高三第一次调研理科）一个几何体的三视图如图所示，则该几何体的体积为（ ）A 、2B 、1C 、23D 、136.C 【解析】有三视图可以判断该几何体是四棱锥，底面是边长为2的正方形，高为1，所以()21221.33V =⨯⨯=2. (广东省珠海一中2011年2月高三第二学期第一次调研理科)在四面体ABCD 中，设AB ＝1，CD ＝3，直线AB 与CD 的距离为2，夹角为3π，则四面体ABCD 的体积等于( B ) A ．23 B ．21 C ．31 D ．33 6．(广东省珠海一中2011年2月高三第二学期第一次调研文科)如图所示，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别为棱AA 1、BB 1的中点，G 为棱A 1B 1上的一点，且A 1G=λ（0≤λ≤1）则点G 到平面D 1EF 的距离为（ D ）A ．3B ．22 C ．23λD ．53. (广东省珠海一中2011年2月高三第二学期第一次调研文科)一个几何体的三视图如下图所示，其中正视图是一个边长为2的正三角形，俯视图是一正方形，那么该几何体的侧．视图．．的面积为( C )A．1 B．2C．D．4⒌(广东省江门市2011年高考一模文科)某型号儿童蛋糕上半部分是半球，下半部分是圆锥，三视图如图1，则该型号蛋糕的表面积=S( A )A．π115B．π110C．π105D．π100⒌(广东省江门市2011年高考一模理科)一个底部水平放置的几何体，下半部分是圆柱，上半部分是正四棱锥，其三视图如图1所示，则这个几何体的体积=V( D )A．3054+πB．π69C．π66D．2454+π7.(广东省广雅金山佛一中2011年2月高三联考理科)已知某一几何体的正视图与侧视图如图，则下列图形中，可以是该几何体的俯视图的图形有（ D ）正视图侧视图图2侧视图俯视图正视图4x33x 4A ．①②③⑤B ．②③④⑤C ．①②④⑤D ． ①②③④6. (广东省东莞市2011年高三一模理科)一空间几何体的三视图如图2所示, 该几何体的体积为85123π+，则正视图中x 的值为( C ) A. 5 B. 4 C. 3 D. 28．(广东省东莞市2011年高三一模文科)一个几何体的三视图及部分数据如图所示，侧视图为等腰三角形，俯视图为正方形，则这个几何体的体积等于( A ) A ．13B ．23C ．156D ．62243．(广东执信中学2011年2月高三考试文科)已知,αβ为不重合的两个平面，直线,m α⊂那么“m β⊥”是“αβ⊥”的（ A ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．(广东执信中学2011年2月高三考试文科)已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是 （ B ）A ．383cm B ．343cm C ．323cm D ．313cm二、填空题:2312．（广东省深圳市2011年3月高三第一次调研文科）已知正三棱柱（侧棱与底面垂直，底面是正三角形）的高与底面边长均为2，其直观图和正(主)视图如下，则 它的左(侧)视图的面积是 ．12. 2 3.【解析】画出左(侧)视图如图,其面积为2 3.14. (广东省珠海一中2011年2月高三第二学期第一次调研理科)在0120的二面角内，放一个半径为10cm 的球切两半平面于A,B 两点，那么这两切点在球面上的最短距离是___________310π11．(广东省广雅金山佛一中2011年2月高三联考文科)已知空间四边形ABCD 中，AB ⊥BC ，BC ⊥CD ， CD ⊥AB ，且AB ＝2，BC ＝5，CD ＝7，则AD ＝ 4 。

2011年—2019年全国卷（Ⅰ、Ⅱ、Ⅲ卷）理科数学试题分类汇编8．函数与导数一、填空题(2019·全国卷Ⅰ，理3)已知0.20.32log 0.220.2a b c ===，，，则（ ） A ．a b c <<B ．a c b <<C ．c a b <<D ．b c a <<(2019·全国卷Ⅰ，理5)函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为（ ） A ．B ．C ．D ．(2019·全国卷Ⅱ，理6)若a b >，则（ ）A ．ln()0a b ->B ．33a b <C ．330a b ->D ．a b >(2019·全国卷Ⅱ，理12)设函数()f x 的定义域为R ，满足(1) 2 ()f x f x +=，且当(0,1]x ∈时，()(1)f x x x =-．若对任意(,]x m ∈-∞，都有8()9f x ≥-，则m 的取值范围是（ ）A ．9,4⎛⎤-∞ ⎥⎝⎦ B ．7,3⎛⎤-∞ ⎥⎝⎦ C ．5,2⎛⎤-∞ ⎥⎝⎦ D ．8,3⎛⎤-∞ ⎥⎝⎦(2019·全国卷Ⅲ，理6)已知曲线ln xy ae x x =+在(1,)ae 处的切线方程为y =2x +b ，则（ ）A ．,1a e b ==-B ．,1a e b ==C ．1,1a e b -==D ．1,1a e b -==-2019·全国卷Ⅲ，理7) 函数3222x xx y -=+在[6,6]-的图像大致为（ ）A ．B ．C ．D ． (2019·全国卷Ⅲ，理11)设f (x )是定义域为R 的偶函数，且在(0,+∞)单调递减，则（ ）A ．233231(log )(2)(2)4f f f -->> B ．233231(log )(2)(2)4f f f -->>C ．233231(2)(2)(log )4f f f -->>D ．233231(2)(2)(log )4f f f -->>(2018·新课标Ⅰ，理5)设函数()32(1)f x x a x ax =+-+，若()x f 为奇函数，则曲线()x f y =在点()0,0处的切线方程为（ ）A ．x y 2-= B. x y -= C. x y 2= D.x y =(2018·新课标Ⅰ，理9)已知函数()0ln 0x e x f x x x ⎧=⎨>⎩，≤，，()()g x f x x a =++，若()g x 存在2个零点，则a 的取值范围是（ ） A ．[)10-，B ．[)0+∞，C ．[)1-+∞，D ．[)1+∞，（2018·新课标Ⅱ，3）函数()2x xe ef x x --=的图象大致是（ ）（2018·新课标Ⅱ，10）若()cos sin f x x x =-在[]a a -，是减函数，则a 的最大值是（ ）A ．2πB ．2π C ．34π D ．π（2018·新课标Ⅱ，11）已知()f x 是定义域为()-∞+∞，的奇函数，满足()()11f x f x -=+．若()12f =，则()()()()12350f f f f +++⋅⋅⋅+=（ ） A ．50-B ．0C ．2D ．50（2018·新课标Ⅲ，理7）函数422y x x =-++的图像大致为（ ）（2018·新课标Ⅲ，理12）设0.2log 0.3a =，2log 0.3b =，则（ ）A ．0a b ab +<<B ．0ab a b <+<C ．0a b ab +<<D ．0ab a b <<+（2017·新课标Ⅰ，5）函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是（ ） A ．[2,2]- B ． [1,1]-C ． [0,4]D ． [1,3]（2017·新课标Ⅰ，11）设,,x y z 为正数，且235x y z ==，则（ ）A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z （2017·新课标Ⅱ，11）若2x =-是函数21`()(1)x f x x ax e-=+-的极值点，则()f x 的极小值为（ ）A.1-B.32e --C.35e -D.1 （2017·新课标Ⅲ，11）已知函数()()2112ee x xf x x x a --+=-++有唯一零点，则a =（ ）A ．12-B ．13C ．12D ．1（2016·新课标Ⅰ，7）函数xe x y -=22在]2,2[-的图像大致为（ ）C ．D ． （2016·新课标Ⅰ，8）若1>>b a ，10<<c ，则（ ）A ．c c b a <B ．c c ba ab <C ．c b c a a b log log <D ．c c b a log log <（2016·新课标Ⅱ，12）已知函数()()f x x ∈R 满足()2()f x f x -=-，若函数1x y x+=与()y f x =图像的交点为11(,)x y ，22(,)x y ，…，(,)m m x y ，则1()mi i i x y =+=∑ （ ）A ．0B ．mC ．2mD ．4m（2016·新课标Ⅲ，6）已知4213332,3,25a b c ===，则（ ）A. b a c <<B. a b c <<C. b c a <<D. c a b <<（2015·新课标Ⅰ，12）设函数()f x =(21)xe x ax a --+,其中1a <，若存在唯一的整数0x ，使得0()0f x <，则a 的取值范围是（ ）A ．3,12e ⎡⎫-⎪⎢⎣⎭ B ．33,2e 4⎡⎫-⎪⎢⎣⎭ C ．33,2e 4⎡⎫⎪⎢⎣⎭ D ．3,12e ⎡⎫⎪⎢⎣⎭（2015·新课标Ⅱ，5）设函数211log (2)(1)()2(1)x x x f x x -+-<⎧=⎨≥⎩，则2(2)(l og 12)f f -+=（ ）A．3 B．6 C．9 D．12（2015·新课标Ⅱ，10）如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP=x. 将动点P到A，B两点距离之和表示为x的函数f（x），则f（x）的图像大致为（）A．B．C．D．（2015·新课标Ⅱ，12）设函数()f x'是奇函数()()f x x R∈的导函数，(1)0f-=，当x>0时，()()0xf x f x'-<，则使得f (x) >0成立的x的取值范围是（）A．(,1)(0,1)-∞-B．(1,0)(1,)-+∞C．(,1)(1,0)-∞--D．(0,1)(1,)+∞（2014·新课标Ⅰ，3）设函数()f x，()g x的定义域都为R，且()f x是奇函数，()g x是偶函数，则下列结论正确的是（）A.()f x()g x是偶函数B.|()f x|()g x是奇函数C.()f x|()g x|是奇函数D.|()f x()g x|是奇函数（2014·新课标Ⅰ，11）已知函数()f x=3231ax x-+，若()f x存在唯一的零点x，且x＞0，则a的取值范围为（）A.（2，+∞）B.（-∞，-2）C.（1，+∞）D.（-∞，-1）（2014·新课标Ⅱ，8）设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x，则a=（）A．0 B．1 C．2 D．3（2014·新课标Ⅱ，12）设函数()3xf xmπ=，若存在()f x的极值点x满足22200[()]x f x m+<，则m 的取值范围是（）A．(,6)(6,+)-∞-∞B．(,4)(4,+)-∞-∞C．(,2)(2,+)-∞-∞D．(,1)(4,+)-∞-∞（2013·新课标Ⅰ，11）已知函数f(x)＝220ln(1)0.x x xx x⎧-+≤⎨+>⎩，，，若|f(x)|≥ax，则a的取值范围是()．A．(－∞，0] B．(－∞，1] C．[－2,1] D．[－2,0]（2013·新课标Ⅱ，8）设3log6a=，5log10b=，7log14c=，则（）A.c b a>> B.b c a>> C.a c b>> D.a b c>>（2013·新课标Ⅱ，10）已知函数32()f x x ax bx c=+++，下列结论中错误的是（）A.00,()0x f x∃∈=RB.函数()y f x =的图像是中心对称图形C.若0x 是()f x 的极小值点，则()f x 在区间0(,)x -∞单调递减D.若0x 是()f x 的极值点，则0()0f x '= （2012·新课标Ⅰ，10）已知函数1()ln(1)f x x=+，则()y f x =的图像大致为（ ）（2012·新课标Ⅰ、Ⅱ，12）设点P 在曲线12xy e =上，点Q 在曲线ln(2)y x =上，则||PQ 的最小值为（ ） A ．1ln2-B ln 2)-C ．1ln2+D ln 2)+（2011·新课标Ⅰ、Ⅱ，2）下列函数中，既是偶函数又在+∞（0，）单调递增的函数是（ ） A ．3y x = (B) 1y x =+ C ．21y x =-+ (D) 2xy -=（2011·新课标Ⅰ、Ⅱ，9）由曲线y =2y x =-及y 轴所围成的图形的面积为（ ）A ．103 B ．4 C ．163D ．6 （2011·新课标Ⅰ、Ⅱ，12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于（ ）A ．2B ．4C ．6D ．8 二、填空题(2019·全国卷Ⅰ，理13)曲线23()e xy x x =+在点(0)0，处的切线方程为____________．(2019·全国卷Ⅱ，理14)已知()f x 是奇函数，且当0x <时，()e a x f x =-．若(ln 2)8f =，则a =__________．（2018·新课标Ⅱ，理13）曲线()2ln 1y x =+在点()00，处的切线方程为__________．（2018·新课标Ⅲ，理14）曲线()1x y ax e =+在点()01，处的切线的斜率为2-，则a =________． （2017·新课标Ⅲ，15）设函数()1020x x x f x x +⎧=⎨>⎩，，，，则满足()112f x f x ⎛⎫+-> ⎪⎝⎭的x 的取值范围是________.（2016·新课标Ⅱ，16）若直线y = kx +b 是曲线y = ln x +2的切线，也是曲线y = ln(x +1)的切线，则b = . （2016·新课标Ⅲ，15）已知f (x )为偶函数，当0x <时，()()ln 3f x x x =-+，则曲线()y f x =在点()1,3-处A ．B ．D ．的切线方程是______（2015·新课标Ⅰ，13）若函数f (x )=x ln （x a =（2014·新课标Ⅱ，15）已知偶函数f (x )在[0, +∞)单调递减，f (2)=0. 若f (x -1)>0，则x 的取值范围是_________. （2013·新课标Ⅰ，16）若函数f (x )＝(1－x 2)(x 2＋ax ＋b )的图像关于直线x ＝－2对称，则f (x )的最大值为_____． 三、解答题(2019·全国卷Ⅰ，理20)已知函数()sin ln(1)f x x x =-+，()f x '为()f x 的导数．证明：（1）()f x '在区间(1,)2π-存在唯一极大值点； （2）()f x 有且仅有2个零点．(2019·全国卷Ⅱ，理20)已知函数()11ln x f x x x -=-+．（1）讨论()f x 的单调性，并证明()f x 有且仅有两个零点；（2）设0x 是()f x 的一个零点，证明曲线ln y x =在点00(,ln )A x x 处的切线也是曲线e xy =的切线．(2019·全国卷Ⅲ，理20)已知函数32()2f x x ax b =-+．（1）讨论f (x )的单调性；（2）是否存在a ，b ，使得f (x )在区间[0,1]的最小值为-1且最大值为1？若存在，求出a ，b 的所有值；若不存在，说明理由．（2018·新课标I ，理21）已知函数()1ln f x x a x x=-+. （1）讨论()f x 的单调性；（2）若()f x 存在两个极值点1x ，2x ，证明：()()12122f x f x a x x -<--.（2018·新课标Ⅱ，理21）已知函数()2x f x e ax =-．（1）若1a =，证明：当0x ≥时，()1f x ≥； （2）若()f x 在()0+∞，只有一个零点，求a ．（2018·新课标Ⅲ，理21）已知函数()()()22ln 12f x x ax x x =+++-．（1）0a =，证明：当10x -<<时，()0f x <；当0x >时，()0f x >； （2）若0x =是()f x 的极大值点，求a ．（2017·新课标Ⅰ，21）已知函数()()22xx f x aea e x =+--．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．（2017·新课标Ⅱ，21）已知函数2()ln ,f x ax ax x x =--且()0f x ≥.（1）求a ；（2）证明：()f x 存在唯一的极大值点0x ，且220()2e f x --<<.（2017·新课标Ⅲ，）21.已知函数()1ln f x x a x =--. （1）若()0f x ，求a 的值；（2）设m 为整数，且对于任意正整数n ，21111+1++222n m ⎛⎫⎛⎫⎛⎫< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭1，求m 最小值.（2016·新课标Ⅰ，12）已知函数2)1()2()(-+-=x a e x x f x 有两个零点．（Ⅰ）求a 的取值范围；（Ⅱ）设21,x x 是)(x f 的两个零点，证明：221<+x x ．（2016·新课标Ⅱ，21）（Ⅰ）讨论函数2()2x x f x e x -=+ 的单调性，并证明当x >0时，(2)20xx e x -++>；（Ⅱ）证明：当[0,1)a ∈时，函数2()=(0)x e ax ag x x x -->有最小值.设g (x )的最小值为()h a ，求函数()h a 的值域.（2015·新课标Ⅰ，12）已知函数31()4f x x ax =++，()ln g x x =-. （Ⅰ）当a 为何值时，x 轴为曲线()y f x =的切线；（Ⅱ）用min{,}m n 表示,m n 中的最小值，设函数min{),()(}()h x f x g x =（0x >），讨论()h x 零点的个数.（2016·新课标Ⅲ，21）设函数()()()cos 21cos 1f x a x a x =+-+，其中0a >，记()f x 的最大值为A .(1)求()'f x ；(2)求A ；(3)证明：()'2f x A ≤.（Ⅰ）证明：f (x)在（-∞，0）单调递减，在（0，+∞）单调递增；（Ⅱ）若对于任意x1,，x2∈[-1，1]，都有｜f (x1)- f (x2)｜≤ e-1，求m的取值范围．（2014·新课标Ⅰ，21）设函数1(0lnxxbef x ae xx-=+，曲线()y f x=在点（1，(1)f处的切线为(1)2y e x=-+.(Ⅰ)求,a b；（Ⅱ）证明：()1f x>.（Ⅰ）讨论()f x 的单调性；（Ⅱ）设()(2)4()g x f x bf x =-，当0x >时，()0g x >，求b 的最大值；（Ⅲ）已知1.4142 1.4143<，估计ln2的近似值（精确到0.001）.（2013·新课标Ⅰ，理21）设函数f (x )＝x 2＋ax ＋b ，g (x )＝e x (cx ＋d )．若曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)，且在点P 处有相同的切线y ＝4x ＋2.(1)求a ，b ，c ，d 的值；(2)若x ≥－2时，f (x )≤kg (x )，求k 的取值范围．（Ⅰ）设0x =是()f x 的极值点，求m ，并讨论()f x 的单调性； （Ⅱ）当2m ≤时，证明()0f x >.（2012·新课标Ⅰ、Ⅱ，21）已知函数)(x f 满足2121)0()1(')(x x f e f x f x +-=-． （1）求)(x f 的解析式及单调区间；（2）若b ax x x f ++≥221)(，求b a )1(+的最大值．（2011·新课标Ⅰ、Ⅱ，21）已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=．（Ⅰ）求a 、b 的值；（Ⅱ）如果当0x >，且1x ≠时，ln ()1x kf x x x>+-，求k 的取值范围．2011年—2018年新课标全国卷理科数学试题分类汇编8．函数与导数（解析版）一、填空题(2019·全国卷Ⅰ，理3)已知0.20.32log 0.220.2a b c ===，，，则（ ） A ．a b c <<B ．a c b <<C ．c a b <<D ．b c a <<【答案】B 解析：2log 0.20a =<；0.221b =>，0.300.21c <=<，得a c b <<. (2019·全国卷Ⅰ，理5)函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为（ ） A ．B ．C ．D ．【答案】D 解析：因为()2(sin )()cos x x f x f x x x -+-==-+故函数为奇函数，排除A ；又2()01f πππ=>-，排除B ，C 。

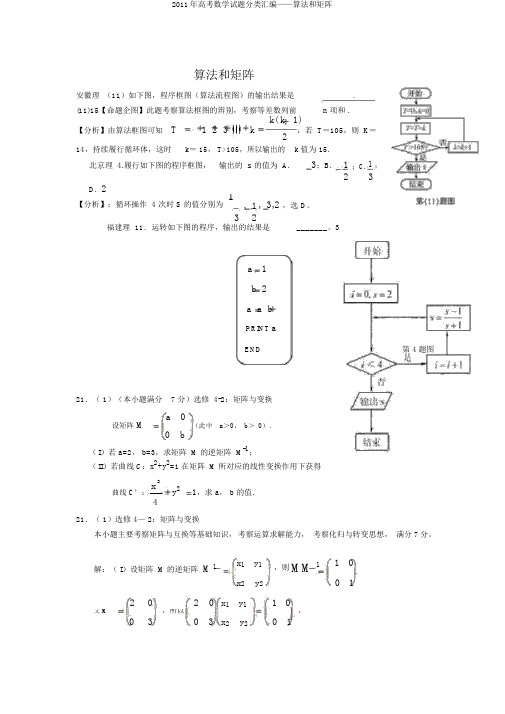
算法和矩阵安徽理 （11）如下图，程序框图（算法流程图）的输出结果是.(11)15【命题企图】此题考察算法框图的辨别，考察等差数列前n 项和 .【分析】由算法框图可知 T1 2 3kk( k 1)2，若 T ＝105，则 K ＝14，持续履行循环体，这时 k ＝ 15， T>105，所以输出的 k 值为 15.北京理 4.履行如下图的程序框图， 输出的 s 的值为 A.3；B.1 ；C. 1 ；2 3D. 2【分析】：循环操作 4 次时 S 的值分别为1, 1 , 3,2 ，选 D 。

3 2福建理 11．运转如下图的程序，输出的结果是 _______。

3a 1b 2a a bPRINT aEND第 4题图21．（ 1）（本小题满分 7 分）选修 4-2：矩阵与变换a 0设矩阵 M（此中 a ＞0， b ＞ 0）．0 b（ I ）若 a=2， b=3，求矩阵 M 的逆矩阵 M -1；（ II ）若曲线 C ：x 2+y 2=1 在矩阵 M 所对应的线性变换作用下获得2曲线 C ’：xy 21，求 a ， b 的值．421．（ 1）选修 4— 2：矩阵与变换本小题主要考察矩阵与互换等基础知识， 考察运算求解能力， 考察化归与转变思想， 满分7分。

解：（ I ）设矩阵 M 的逆矩阵 M1x 1 y 1 ，则MM 11 0x 2 y 2 0 .12 0 2 0 x 1 y 1 1 0又 M3，所以3 x 2 y 20 ，1所以 2x 1 1,2 y 10,3x 20,3 y 2 1,即 x 11 1 , y 1 0, x2 0, y 2,231 012故所求的逆矩阵 M.13（ II ）设曲线 C 上随意一点 P(x, y) ，它在矩阵 M 所对应的线性变换作用下获得点P '( x ', y') ，则a0 x x ' ,即 axx '，又点 P '( x', y ') 在曲线 C '上，0 byy ' by y '所以x '2y '21 ,,则 a2 x 2b 2 y 2 1为曲线 C 的方程，44又已知曲线 C 的方程为 x 2y 2 1,故a 24,b 21.又 a0,b 0,所以a2,b 1.福建文 5．阅读右图所示的程序框图，运转相应的程序，输出的结果是A ． 3B ．11C ． 38D ． 123B开始湖南理 13 、若履行如图 3 所示的框图，输入x1, x2, x3,x2 ，则输出的数等于。

专题35不等式选讲年份题号考点考查内容2011文理24不等式选讲绝对值不等式的解法2012文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法2013卷1文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲多元不等式的证明2014卷1文理24不等式选讲基本不等式的应用卷2文理24不等式选讲绝对值不等式的解法2015卷1文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理24不等式选讲不等式的证明2016卷1文理24不等式选讲分段函数的图像，绝对值不等式的解法卷2文理24不等式选讲绝对值不等式的解法，绝对值不等式的证明卷3文理24不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法2017卷1文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷2文理23不等式选讲不等式的证明卷3文理23不等式选讲绝对值不等式的解法，绝对值不等式解集非空的参数取值范围问题2018卷1文理23不等式选绝对值不等式的解法，不等式恒成立参数取值范围问题的解法讲卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲绝对值函数的图象，不等式恒成立参数最值问题的解法2019卷1文理23不等式选讲三元条件不等式的证明卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件最值问题的解法，三元条件不等式的证明2020卷1文理23不等式选讲绝对值函数的图像，绝对值不等式的解法卷2文理23不等式选讲绝对值不等式的解法，不等式恒成立参数取值范围问题的解法卷3文理23不等式选讲三元条件不等式的证明考点出现频率2021年预测考点120绝对值不等式的求解23次考4次2021年主要考查绝对值不等式的解法、绝对值不等式的证明，不等式恒成立参数取值范围问题的解法等．考点121含绝对值不等式的恒成立问题23次考12次考点122不等式的证明23次考7次考点120绝对值不等式的求解1．(2020全国Ⅰ文理22)已知函数 3121f x x x ．(1)画出 y f x 的图像；(2)求不等式 1f x f x 的解集．2．(2020江苏23)设x R ，解不等式2|1|||4x x ．3．(2016全国I 文理)已知函数()|1||23|f x x x ．(I)在图中画出()y f x 的图像；(II)求不等式|()|1f x 的解集．4．(2014全国II 文理)设函数 f x =1(0)x x a a a(Ⅰ)证明： f x ≥2；(Ⅱ)若 35f ，求a 的取值范围．5．(2011新课标文理)设函数()3f x x a x ，其中0a ．(Ⅰ)当1a 时，求不等式()32f x x 的解集；(Ⅱ)若不等式()0f x 的解集为 |1x x ，求a 的值．考点121含绝对值不等式的恒成立问题6．(2020全国Ⅱ文理22)已知函数 221f x x a x a ．(1)当2a 时，求不等式 4f x 的解集；(2)若 4f x ，求a 的取值范围．7．(2019全国II 文理23)[选修4-5：不等式选讲](10分)已知()|||2|().f x x a x x x a (1)当1a 时，求不等式()0f x 的解集；(2)若(,1)x 时，()0f x ，求a 的取值范围．8．(2018全国Ⅰ文理)已知()|1||1|f x x ax ．(1)当1a 时，求不等式()1f x 的解集；(2)若(0,1)x 时不等式()f x x 成立，求a 的取值范围．9．(2018全国Ⅱ文理)设函数()5|||2| f x x a x ．(1)当1a 时，求不等式()0≥f x 的解集；(2)若()1≤f x ，求a 的取值范围．10．(2018全国Ⅲ文理)设函数()|21||1|f x x x ．(1)画出()y f x 的图像；(2)当[0,)x 时，()f x ax b ≤，求a b 的最小值．11．(2018江苏)若x ，y ，z 为实数，且226x y z ，求222x y z 的最小值．12．(2017全国Ⅰ文理)已知函数2()4f x x ax ，()|1||1|g x x x ．(1)当1a 时，求不等式()()f x g x ≥的解集；(2)若不等式()()f x g x ≥的解集包含[1,1] ，求a 的取值范围．13．(2017全国Ⅲ文理)已知函数()|1||2|f x x x ．(1)求不等式()1f x ≥的解集；(2)若不等式2()f x x x m ≥的解集非空，求m 的取值范围．14．(2016全国III 文理)已知函数()|2|f x x a a(Ⅰ)当a=2时，求不等式()6f x ≤的解集；(Ⅱ)设函数()|21|g x x ，当x R 时，()()3f x g x ≥，求a 的取值范围．15．(2015全国I 文理)已知函数()|1|2||f x x x a ，0a ．(Ⅰ)当1a 时，求不等式()1f x 的解集；(Ⅱ)若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围．16．(2014全国I 文理)若0,0a b ，且11a b．(Ⅰ)求33a b 的最小值；(Ⅱ)是否存在,a b ，使得236a b ？并说明理由．16．(2013全国I 文理)已知函数()f x =|21||2|x x a ，()g x =3x ．(Ⅰ)当a =-2时，求不等式()f x ＜()g x 的解集；(Ⅱ)设a ＞-1，且当x ∈[2a ，12)时，()f x ≤()g x ，求a 的取值范围．17．(2012新课标文理)已知函数|2|||)( x a x x f ．(Ⅰ)当|3 a 时，求不等式()3f x 的解集；(Ⅱ)若()|4|f x x 的解集包含]2,1[，求a 的取值范围．考点122不等式的证明18．(2020全国Ⅲ文理23)设,,,0,1a b c a b c abc R ．(1)证明：0ab bc ca ；(2)用 max ,,a b c 表示,,a b c 的最大值，证明： max ,,a b c 19．(2019全国I 文理23)已知a ，b ，c 为正数，且满足abc=1．证明：(1)222111a b c a b c；(2)333()()()24a b b c c a ．20．(2019全国III 文理23)设,,x y z R ，且1x y z ．(1)求222(1)(1)(1)x y z 的最小值；(2)若2221(2)(1)()3x y z a 成立，证明：3a 或1a ．21．(2017全国Ⅱ文理)已知0a ，0b ，332a b ，证明：(1)554a b a b ；(2)2a b ．23．(2016全国II 文理)已知函数 1122f x x x，M 为不等式 2f x 的解集．(I)求M ；(II)证明：当a ，b M 时，1a b ab ．24．(2015全国II 文理)设,,,a b c d 均为正数，且a b c d ，证明：(Ⅰ)若ab >cd(Ⅱ ||||a b c d 的充要条件．25．(2013全国II 文理)设,,a b c 均为正数，且1a b c ，证明：(Ⅰ)13ab bc ca ；(Ⅱ)2221a b c b c a ．。

五、解析几何
一、选择题
22x?y?2x?6y?0内，过点E（0，1）的最长弦和最短弦分别是AC1.（重庆理8）在圆
和BD，则四边形ABCD的面积为
A．52 B．2 C
．D．2
【答案】B
x2y2y2
2C1:2?2?1(a＞b＞0)C1:x??1ab42.（浙江理8）已知椭圆与双曲线有公共的焦点，
C1的一条渐近线与以C1的长轴为直径的圆相交于A,B两点，C若1恰好将线段AB三等分，则
a2?
A．
【答案】C 1312b?2 B．a2?13 C．2 2D．b?2
2x2?2x??4y?x?ax?5(a≠0)13.（四川理10）在抛物线上取横坐标为，的两点，过
225x?5y?36相切，则这两点引一条割线，有平行于该割线的一条直线同时与抛物线和圆
抛物线顶点的坐标为
A．(?2,?9) B．(0,?5) C．(2,?9) D．(1,?6)
【答案】C
【解析】由已知的割线的坐标(?4,11?4a),(2,2a?1),K?2?a,设直线方程为
36b2
?2y?(a?2)x?b51?(2?a)，则
?y?x2?ax?5?b??6?a?4?(?2,?9)?y?(a?2)x?b又?
4.（陕西理2）设抛物线的顶点在原点，准线方程为x??2，则抛物线的方程是222y??8xy?8xy??4x A． B． C．2y?4x D．
【答案】B
x2y2
?2?1(a＞0，b＞0)2b5.（山东理8）已知双曲线a的两条渐近线均和圆
22x?y?6x?5?0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为 C:
第1页考名牌大学，上高考试题库。

（安徽）双曲线x y 222-=8的实轴长是（A ）2 (B)（福建）设圆锥曲线r 的两个焦点分别为F 1，F 2，若曲线r 上存在点P 满足1122::PF F F PF =4:3:2，则曲线r 的离心率等于 A.1322或 B.23或 2C.12或2 D.2332或（湖北）将两个顶点在抛物线22(0)y px p =>上，另一个顶点是此抛物线焦点的正三角形个数记为n ，则A. n=0 B. n=1 C. n=2 D. n ≥3（湖南）设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=，则a 的值为（ ）A ．4 B ．3 C ．2 D ．1答案：C 解析：由双曲线方程可知渐近线方程为3y x a=±，故可知2a =。

（江西）若曲线02221=-+x y x C ：与曲线0)(2=--m mx y y C ：有四个不同的交点,则实数m 的取值范围是 ( ) A. )33,33(-B. )33,0()0,33(⋃-C. ]33,33[-D. ),33()33,(+∞⋃--∞ 答案：B 曲线0222=-+x y x 表示以()0,1为圆心，以1为半径的圆，曲线()0=--m mx y y 表示0,0=--=m mx y y 或过定点()0,1-，0=y 与圆有两个交点，故0=--m mx y 也应该与圆有两个交点，由图可以知道，临界情况即是与圆相切的时候，经计算可得，两种相切分别对应3333=-=m m 和，由图可知，m 的取值范围应是⎪⎪⎭⎫⎝⎛⋃⎪⎪⎭⎫ ⎝⎛-33,00,3310.（江西）如右图，一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方 向滚动，M 和N 是小圆的一条固定直径的两个端点.那么，当小圆这 样滚过大圆内壁的一周，点M ，N 在大圆内所绘出的图形大致是( )答案：A解析：根据小圆 与大圆半径1：2的关系，找上下左右四个点，根据这四个点的位置，小圆转半圈，刚好是大圆的四分之一，因此M 点的轨迹是个大圆，而N 点的轨迹是四条线，刚好是M 产生的大圆的半径。

2011年高考数学试题分类汇编——函数1．(2011安徽理)设()f x 是定义在R 上的奇函数，当x ≤0时，()f x x x 2=2-，则()f 1=（ ） （A ）-3 (B) -1 （Ｃ）１ （Ｄ）３2．（2011安徽文）若点(a,b)在lg y x = 图像上，a ≠1,则下列点也在此图像上的是（ ）（A ）（a1，b ） (B ) (10a,1-b) (C) (a10,b+1) (D)(a 2,2b)3．（2011北京理）根据统计，一名工人组装第x件某产品所用的时间（单位：分钟）为()x A f x c x A <=≥（A ，c 为常数）。

已知工人组装第4件产品用时30分钟，组装第A 件产品时用时15分钟，那么c 和A 的 值分别是（ ） A. 75，25B. 75，16C. 60，25D. 60，164．（2011福建文）已知函数f (x )＝⎩⎨⎧2x ， x ＞0x ＋1，x ≤0，若f (a )＋f (1)＝0，则实数a 的值等于（ ）A ．－3B ．－1C ．1D ．35．（2011广东理）设函数()f x 和g(x )分别是R 上的偶函数和奇函数，则下列结论恒成立的是 （ ） A ．()f x +|g(x)|是偶函数 B ．()f x -|g(x)|是奇函数 C ．|()f x | +g(x)是偶函数 D ．|()f x |- g(x)是奇函数6．（2011广东文）设)(),(),(x h x g x f 是R 上的任意实值函数．如下定义两个函数()()x g f 和()()x g f ∙；对任意R x ∈,()()())(x g f x g f = ；()()())(x g x f x g f =∙．则下列等式恒成立的是（ ） A ．()()()()()())(x h g h f x h g f ∙∙=∙ B ．()()()()()())(x h g h f x h g f ∙=∙ C ．()()()()()())(x h g h fx h g f =D ．()()()()()())(x h g h fx h g f ∙∙∙=∙∙7．（2011湖北理）已知定义在R 上的奇函数()x f 和偶函数()x g 满足()()2+-=+-x x a a x g x f ()1,0≠>a a 且，若()a g =2，则()=2f （ ） A. 2 B .415 C.417 D. 2a8．（2011江苏）已知实数0≠a ，函数⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ，若)1()1(a f a f +=-，则a 的值为________9．（2011辽宁理）设函数⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x ，则满足2)(≤x f 的x 的取值范围是（ ）A ．1[-，2]B ．[0，2]C ．[1，+∞]D ．[0，+∞]10．（2011全国Ⅰ理）函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于（ ）（A ）2 (B) 4 (C) 6 (D)811．（2011全国Ⅱ理）设()f x 是周期为2的奇函数，当01x ≤≤时，()2(1)f x x x =-，则5()2f -=（ ）(A)12-(B)14-(C)14(D)1212．（2011山东理文）函数2sin 2x y x =-的图象大致是（ ）13．（2011山东理）已知()f x 是R 上最小正周期为2的周期函数，且当02x ≤<时,3()f x x x =-,则函数()y f x =的图象在区间[0,6]上与x 轴的交点的个数为（ ）（A ）6 （B ）7 （C ）8 （D ）914．（2011山东理）已知函数f x （）=log (0a 1).a x x b a +-≠＞，且当2＜a ＜3＜b ＜4时，函数f x （）的零点*0(,1),,n=x n n n N ∈+∈则 .15．（2011陕西理）设函数()f x （x ∈R ）满足()()f x f x -=，(2)()f x f x +=，则函数()y f x =的图像是16．（2011陕西文）函数13y x =的图像是 （ ）17．（2011陕西文）设lg ,0()10,0x x x f x x >⎧=⎨⎩…，则((2))f f -=______.18．（2011上海理）设()g x 是定义在R 上，以1为周期的函数，若函数()()f x x g x =+在区间[3,4]上的值域为[2,5]-，则()f x 在区间[10,10]-上的值域为 .19．（2011上海理）下列函数中，既是偶函数，又是在区间(0,)+∞上单调递减的函数是（ ）（A ）1ln||y x =. （B ）3y x =. （C ）||2x y =. （D ）cos y x =.20．（2011四川理）若()f x 是R 上的奇函数，且当0x >时，1()()12x f x =+，则()f x 的反函数的图象大致是（ ）21.(2011年天津理)对实数a 与b ，定义新运算“⊗”：,1,,1.aa b a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =--∈若函数()y f x c =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是（ ）A ．(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭ B ．(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭C ．11,,44⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭ D ．311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭22．（2011天津理）已知324log 0.3log 3.4log 3.615,5,,5a b c ⎛⎫=== ⎪⎝⎭则A ．a b c >>B ．b a c >>C ．a c b >>D ．c a b >> 23．（2011浙江理）若函数2()f x x x a =-+为偶函数，则实数a =24．（2011重庆文）设,,,则,,的大小关系是(A) (B) (C) (D)25．（2011重庆文）若函数在处取最小值,则 （ ）(A) (B) (C)3 (D)4。