数制与码制M优秀课件

位权 2i
bn1 2n1 bn2 2n2 L L b1 21 b0 20 b1 21 b2 22 L L bm 2m
n1
bi 2i im
bi 0, 1
（公式1.1.2）
三、八进制（Octal）
1. 数码
n1
ci 8i im
ci 0, 1,L L ,7
（公式1.1.3）
四、十六进制(Hexadecimal)
1. 数码
0、1、2、3、4、5、6、7、8、9、 A、B、C、D、E、F（10、11、12、13、14、15）
2. 基数
16
3. 计数规则
逢十六进一
即
F 1 10H
第一章 数制和代码
•概
述
•数
制
•数 制 间 的 转 换
• 二进制正负数表示法
•二 进 制 代 码
返回
概
述
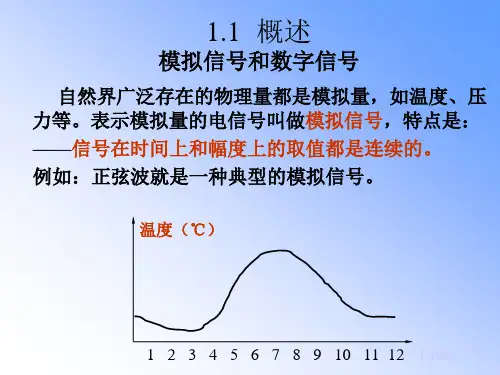
一个数通常可以用两种不同的方法来表示。
一、按“值”表示
所谓按“值”表示，即选择某种进位制来确定某个数的值或大小，这就是所谓的数制。
按“值”表示时需要注意三个问题 1. 恰当地选择数字符号（数码）及其组合规律； 2. 确定小数点的位置； 3. 正确地表示出数的正、负符号。
10 逢十进一
即
9 1 10D
4. 位权展开式
一个有n位整数和m位小数的任意十进制数的位权展开式为：
ND an1an2 L L a1a0.a1a2 L L am
位权10i
an1 10n1 an2 10n2 L L a1 101 a0 100 a1 101 a2 102 L L am 10m
例 1.1.3

③ 十六进制
十六进制数的每一位有十六个不同的数码，分别用
0—9、(10)A、(11)B、(12)C、(13)D、(14)E、(15)F
表示。
n1
D
ki (16)i
im
十六进制用H(Hexadecimal) 下标。由于目前在微型
计算机中普遍采用8位、16位和32位二进制并行运算，
而8位、16位和32位的二进制数可以用2位、4位和8位
2. 数制之间的转换
①二—十转换：把二进制数转换为等值的十进 制数称为二—十转换。 方法：按权展开。
②十—二转：分为整数部分和小数部分两种情 况处理。
⑴ 整数部分的转换:“除2取余倒排列” 假定十进制整数为(S)10 ,等值的二进制数则为：
( k n 1 k n 2 k 2 k 1 k 0 ) 2
模拟量信号
热电偶在工作时输出的电压信号就属于模拟信号 RC电路中电容两端电压随时间的变化在时间上还
是在数量上也都是连续的。
RC充电回路
S
R
Va
图1-1-3 RC电路
Vc
Vc
Va
C
t
图1-1-4 电容两端电压Vc 随时间t的变化
离散量信号
表示时间上离散的量的信号是离散信号。将 离散量进行量化和编码叫做数字量
⑵ 小数部分的转换：“乘2取整依次排列”
若(S)10是一个十进制的小数则对应的二进制小数为：
( 0 . k 1 k 2 k 3 • • • • • • k i• • • • • k m ) 2
( S ) 1 0 0 . k 1 2 1 k 2 2 2 k n 3 2 3 k m 2 m
将上式两边同乘以2得到: 2 ( S ) 1 k 0 1 ( k 2 2 1 k 3 2 2 k m 2 m 1 ) 将小数(S)10乘以2得到的整数部分即k-1同理， 将乘积的小数部分两边再同乘以2又可得到：

▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
数字电子技术课件 数制和码制
21、没有人陪你走一辈子，所以你要 适应孤 独，没 有人会 帮你一 辈子， 所以你 要奋斗 一生。 22、当眼泪流尽的时候，留下的应该 是坚强 。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之 首，因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿． 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ，它只 是让人 们的脚 放上一 段时间 ，以便 让别一 只脚能 够再往 上登。

▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
35

＝(135.0625)10
十六进制数的权展开式： 如：(D8.A)2＝ 13×161 ＋8×160＋10 ×16－1
＝(216.625)10
４、十进制数转换为二进制数
采用的方法 — 基数连除、连乘法 原理：将整数部分和小数部分分别进行转换。
整数部分采用基数连除法，小数部分 采用基数连乘法。转换后再合并。
＝(135.0625)10
各数位的权是8的幂
4、十六进制
数码为：0～9、A～F；基数是16。 运算规律：逢十六进一，即：F＋1＝10。 十六进制数的权展开式： 如：(D8.A)16＝ 13×161 ＋8×160＋10 ×16－1
＝(216.625)10
各数位的权是16的幂
结论
①一般地，N进制需要用到N个数码，基数是N；运算规 律为逢N进一。
典型的模拟电子系统
DAC
典型的模拟和数字混合系统
对模拟信号进行传输、处理的电子线路 称为模拟电路。
对数字信号进行传输、处理的电子线路 称为数字电路。
每个数字信号只有0、1两种取值，如何表 示模拟信号各种不同的幅度呢？
——用组合数字信号来描述这个幅度。
模拟量和数字量的相互转换
数字电路、逻辑电路
②从低位向高位的进位规则
一般地，N进制需要用到N个数码，基数 是N；运算规律为逢N进一。
十进制，二进制，八进制，十六
进制
逢二进一
逢八进一
逢十进一
逢十六进一
十进制数
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
几种进制数之间的对应关系
二进制数
八进制数 十六进制数
0000
运算 加法规则：0+0=0， 0+1=1， 1+0=1， 1+1=10 规则 乘法规则：0 × 0=0， 0 × 1=0 ，1 × 0=0，1 × 1=1

1.1.3 计算机中带符号数的表示
一、机器数及其真值
•带符号的正数 +100 0101B（+45H），可以表示成 0100 0101B；（45H） •带符号的负数 - 101 0101B（- 55H），可以表示成 1101 0101B。（D5H）
数在计算机内的表示形式称为机器数。而这 个数本身称为该机器数的真值。
ASCII码
41H 42H 43H ∶ 5AH
字符
a b c ∶ z
ASCII码
61H 62H 63H ∶ 7AH
字符
SP(空格) CR(回车) LF(换行) BEL(响铃) BS(退格)
ASCII码
20H 0DH 0AH 07H 08H
二、二进制编码的十进制数----BCD码
用二进制码表示十进制数的代码称为BCD码 。
1 0000B 10H
1 0001B 11H
1.1.2 编码
计算机中数以及数以外的其它信息（如字符或字符串） 要用二进制代码来表示。这些二进制代码称为二进制编码。
一、字符的二进制编码----ASCII码
常用字符的ASCII码
字符
0 1 2 ∶ 9
ASCII码
30H 31H 32H ∶ 39H
字符
A B C ∶ Z
补码 0111 1111B（7FH） 0000 0001B（01H） 0000 0000B（00H） 0000 0000B（00H） 1111 1111B（FFH） 1000 0001B（81H） 1000 0000B（80H）
采用补码时，“0”只有一种表示方式，单字节 表示的范围是：+127 ~ -128。
已知一个负数的补码求其真值的方法是：对该补码求补 （符号位不变，数值位取反加1）即得到该负数的原码（符号 位+数值位），依该原码可知其真值。

数字量：其变化在时间上和数量上都是不连续的。 电子电路中的电信号可分为: 模拟信号： 连续变化的电压和电流 数字信号： 离散的电压值（高、低电平）
数字电路的特点

以逻辑代数为数学基础，适合工作在存储、控制、 决策等系统中
系统可靠性高、精度高 集成度高、体积小、功耗低

数字电路的应用

计算机系统：主板、内存、硬盘、显卡…… 消费类电子产品：手机、电子表、MP3\4……
方法：将二进制数按权展开后相加，即得到 等值的十进制数。 例：
(1011.01)
3
2
2 1 0 －1
1 2 ＋ 0 2 ＋1 2 ＋ 1 2 ＋ 0 2
＋1 2
－2
＝（ 11 . 25 ) 10
简便算法：将为1的那些位的位权直接相加即可。
二、十－二转换
整数部分: 除二取余法
如：十进制基数是10，二进制基数是2

位权：数制中每位数字所对应的权重；
位权的大小=基数i，i是数字的位序，
数字的大小=数码乘上该位的权重 例如：十进制数243.15： 3的位权是100 4的位权是101 1的权重为10-1……

按权展开式：将数码写成加权和的形式
例如：243.15= 2×102+4×101+3×100 +1×10-1+5×10-2 十进制数的通用形式：
二进制补码运算原理
引例：将表从10点调到5点
法一：往回拨5格，10-5=5 法二：往前拨7格，超过12以 后产生进位，舍弃进位， 则10+7-12=5 可见： 1、10-5可以在舍弃进位的 条件下，用10+7代替。 2、而7是-5对12的补码

十六进制先转成二进制，再从二进制转成八进制
(6EA)16=(110 1110 1010)2 (11 011 101 010)2 =(3352)8
十六进制先转成十进制，再从十进制转成八进制
(6EA)16=(1770)10 (1770)10=(3352)8
目录
2.1 2.2 2.3 2.4 2.5
2.3 计算机中数据的表示
2.3.1 数值型数据
（4）原码、补码和反码 例如，［X］补 =（11100001）２，但
X ≠（-1100001）２， 而是 X =（-00111111）２＝（-31）10。 采用补码可以把减法转换为加法，且可证明两数和的补码等 于两数补码的和，即：［X＋Y］补 ＝［X］补 ＋［Y］补
例：在字长为８位的二进制数字系统中，当 X=(64)10， Y=(10)10，求 X-Y=？
2.3 计算机中数据的表示
2.3.2 字符型数据
字符编码实际上就是为每个字符确定一个对应的整型二进制 数值编码。
由于字符与整型数值之间没有必然的联系，某个字符究竟对 应哪个整数完全可以人为规定，一旦规定好，就固定下来， 以便应用。
任一数制的数都由一串数码表示，其中每一位数码所 表示的实际值大小，除与数码本身的数值有关外，还 与它所处的位置有关，由位置决定的值就叫位权。
2.1 数制
2.1.1 常用数制 （1）十进制
十进制数制系统有十个计数符号：0，1，2，3，4，5 ，6，7，8，9。
十进制数具有以下特点：
① 基数为10； ② 位权值为10i； ③ 逢十进一，借一当十。
2.1 数制
2.1.3 计算机中的二进制运算 （2）逻辑运算
逻辑非运算
2.1 数制