SPSS多元方差分析
- 格式:pdf
- 大小:176.77 KB
- 文档页数:15

方差分析是用于两个及两个以上样本均数差别的显著性检验。
由于各种因素的影响,研究所得的数据呈现波动状,造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
方差分析的基本思想是:通过分析研究不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
方差分析主要用途:①均数差别的显著性检验,②分离各有关因素并估计其对总变异的作用,③分析因素间的交互作用,④方差齐性检验。
在科学实验中常常要探讨不同实验条件或处理方法对实验结果的影响。
通常是比较不同实验条件下样本均值间的差异。
例如医学界研究几种药物对某种疾病的疗效;农业研究土壤、肥料、日照时间等因素对某种农作物产量的影响;不同化学药剂对作物害虫的杀虫效果等,都可以使用方差分析方法去解决。
方差分析原理方差分析的基本原理是认为不同处理组的均数间的差别基本来源有两个:(1) 随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示,记作SS w,组内自由度df w。
(2) 实验条件,实验条件,即不同的处理造成的差异,称为组间差异。
用变量在各组的均值与总均值之偏差平方和表示,记作SS b,组间自由度df b。
总偏差平方和 SS t = SS b + SS w。
组内SS t、组间SS w除以各自的自由度(组内dfw =n-m,组间dfb=m-1,其中n为样本总数,m为组数),得到其均方MS w和MS b,一种情况是处理没有作用,即各组样本均来自同一总体,MS b/MS w≈1。
另一种情况是处理确实有作用,组间均方是由于误差与不同处理共同导致的结果,即各样本来自不同总体。
那么,MS b>>MS w(远远大于)。
MS b/MS w比值构成F分布。
用F值与其临界值比较,推断各样本是否来自相同的总体。
方差分析的假设检验假设有m个样本,如果原假设H0:样本均数都相同即μ1=μ2=μ3=…=μm=μ,m个样本有共同的方差。

使用SPSS软件进行多因素方差分析使用SPSS软件进行多因素方差分析一、引言多因素方差分析是一种重要的统计方法,用于分析多个自变量对因变量的影响。
它可以帮助研究人员确定不同因素对研究对象的差异产生的影响,以及这些因素之间是否存在交互作用。
SPSS软件是一款功能强大且易于使用的统计分析工具,可以帮助用户在进行多因素方差分析时快速、准确地得出结果。
本文将介绍使用SPSS软件进行多因素方差分析的步骤,并通过一个案例来具体说明。
二、SPSS软件介绍SPSS(Statistical Package for the Social Sciences)是一款专业的统计分析软件,被广泛应用于社会科学、医学、商业等领域。
它提供了丰富的统计方法和分析工具,并具备数据清洗、可视化、报告生成等功能。
在多因素方差分析中,SPSS 可以帮助用户进行方差分析表的生成、方差分析的可视化、方差齐性检验和事后比较等操作,大大简化了分析过程。
三、多因素方差分析的步骤1. 数据准备:将需要分析的数据录入SPSS软件,并确定自变量和因变量的测量水平。
一般自变量为定类变量,而因变量可以是定量或定类变量。
2. 方差分析表的生成:选择“分析”菜单中的“一元方差分析”选项,然后将因变量添加到依赖变量框中,将自变量添加到因子框中。
接下来,点击“选项”按钮设置参数,如设定显著性水平和置信区间。
点击“确定”后,SPSS会生成方差分析表。
3. 方差分析的可视化:在方差分析表中,用户可以查看各个因素的主效应和交互作用,以及统计指标如F值、p值等。
此外,SPSS还提供了绘制效应图、交互作用图等功能,帮助用户更直观地理解分析结果。
4. 方差齐性检验:方差齐性检验用于验证因变量的变异是否在各组间具有相同的方差。
SPSS软件可以通过选择“分析”菜单中的“Compare Means”选项,进而进行多个组间方差齐性检验。
5. 事后比较:当发现方差分析存在显著差异时,需要进一步进行事后比较以确定差异所在。
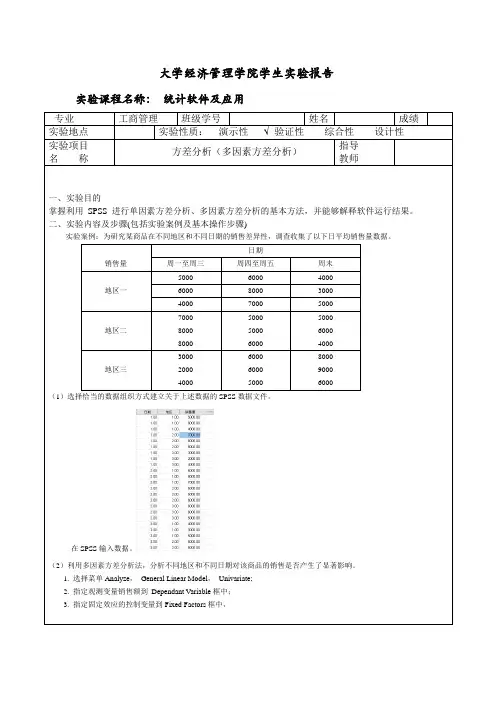
大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 4000 6000 8000 3000 4000 7000 5000地区二700080008000500050006000500060004000地区三300020004000600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)SPSS输出的多因素方差分析的饱和模型分析:表的第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是方差;第五列是F检验统计量的观测值;第六列是检验统计量的概率P-值。
F日期,,F地区,F日期*地区概率P-值分别为0.254,0.313,0.000。
如果显著性水平α为0.05,由于F日期、,F地区大于显著性水平α,所以不应拒绝原假设,不同地区和不同日期对该商品没有显著性影响。

22. 方差分析一、方差分析原理1. 方差分析概述方差分析可用来研究多个分组的均值有无差异,其中分组是按影响因素的不同水平值组合进行划分的。
方差分析是对总变异进行分析。
看总变异是由哪些部分组成的,这些部分间的关系如何。
方差分析,是用来检验两个或两个以上均值间差别显著性(影响观察结果的因素:原因变量(列变量)的个数大于2,或分组变量(行变量)的个数大于1)。
一元时常用F检验(也称一元方差分析),多元时用多元方差分析(最常用Wilks’∧检验)。
方差分析可用于:(1)完全随机设计(单因素)、随机区组设计(双因素)、析因设计、拉丁方设计和正交设计等资料;(2)可对两因素间交互作用差异进行显著性检验;(3)进行方差齐性检验。
要比较几组均值时,理论上抽得的几个样本,都假定来自正态总体,且有一个相同的方差,仅仅均值可以不相同。
还需假定每一个观察值都由若干部分累加而成,也即总的效果可分成若干部分,而每一部分都有一个特定的含义,称之谓效应的可加性。
所谓的方差是离均差平方和除以自由度,在方差分析中常简称为均方(Mean Square)。
2. 基本思想基本思想是,将所有测量值上的总变异按照其变异的来源分解为多个部份,然后进行比较,评价由某种因素所引起的变异是否具有统计学意义。
根据效应的可加性,将总的离均差平方和分解成若干部分,每一部分都与某一种效应相对应,总自由度也被分成相应的各个部分,各部分的离均差平方除以各自的自由度得出各部分的均方,然后列出方差分析表算出F检验值,作出统计推断。
方差分析的关键是总离均差平方和的分解,分解越细致,各部分的含义就越明确,对各种效应的作用就越了解,统计推断就越准确。
效应项与试验设计或统计分析的目的有关,一般有:主效应(包括各种因素),交互影响项(因素间的多级交互影响),协变量(来自回归的变异项),等等。
当分析和确定了各个效应项S后,根据原始观察资料可计算出各个离均差平方和SS,再根据相应的自由度df,由公式MS=SS/df,求出均方MS,最后由相应的均方,求出各个变异项的F值,F值实际上是两个均方之比值,通常情况下,分母的均方是误差项的均方。



体育统计与SPSS读书笔记(八)—多因素方差分析(1)具有两个或两个以上因素的方差分析称为多因素方差分析。
多因素是我们在试验中会经常遇到的,比如我们前面说的单因素方差分析的时候,如果做试验的不是一个年级,而是多个年纪,那就成了双因素了:不同教学方法的班级,不同年级。
如果再加上性别上的因素,那就成了三因素了。
如果我们把实验前和试验后的数据用一个时间的变量来表示,那又多了一个时间的因素。
如果每个年级都是不同的老师来上,那又多了一个老师的因素,等等等等,所以我们在设计试验的时候都要进行充分考虑,并确定自己只研究哪些因素。
下面用例子的形式来说说多因素方差分析的运用。
还是用前面说单因素的例子,前面的例子说了只在五年级抽三个班进行不同教学方法的试验,现在我们还要在初二和高二各抽三个班进行不同教学方法的试验。
形成年级和不同教学法班级双因素。
分析:1.根据实验方案我们划出双因素分析的表格,可以看出每个单元格都是有重复数据(也就是不只一个数据),年级不同教学方法的班级定性班定量班定性定量班五年级(班级每个人)(班级每个人)(班级每个人)初中二年级(班级每个人)(班级每个人)(班级每个人)高中二年级(班级每个人)(班级每个人)(班级每个人)2.因为有重复数据,所以存在在数据交互效应的可能。
我们来看看交效应的含义:如果在A因素的不同水平上,B因素对因变量的影响不同,则说明A、B两因素间存在交互作用。
交互作用是多因素实验分析的一个非常重要的内容。
如因素间存在交互作用而又被忽视,则常会掩盖因素的主效应的显著性,另一方面,如果对因变量Y,因素A与B之间存在交互作用,则已说明这两个因素都Y对有影响,而不管其主效应是否具有显著性。
在统计模型中考虑交互作用,是系统论思想在统计方法中的反映。
在大多数场合,交互作用的信息比主效应的信息更为有用。
根据上面的判断。
根据上面的说法,我也无法判断是否有交互作用,不像身高和体重那么直接。
这里假设他们之间有交互作用。

第八讲多因素方差分析第一部分前一讲复习与回顾第二部分多因素方差分析的概念第三部分多因素方差分析的SPSS过程第四部分协方差分析的过程SPSS的方差分析SPSS方差分析主要用到以下两个模块One-Way ANOVA 单因素方差分析模型GLM general linear model一般线性模型可进行多因素方差分析协方差分析重复测量的方差分析等方差分析表变差来源自由度df平方和均方差FFα组间组内dfBdfWLBLWLB/dfBMSBLW/dfWMSWFMSB/MSW 查表总和dfTLTSPSS调用分析过程输出结果SPSS操作演示定义yield为指标变量定义factor为因素变量单击选择对比方法单击定义多重比较的检验方法单击设置其他选项最后单击输出分析结果用于选择进行趋势检验的曲线类型。
有5个选项Linear线性、Quadratic 二次、Cubic三次、4th四次、5th五次选择是否对方差分析的组间平方和进行分解并进行趋势检验精确定义均值比较的多项式系数因素A有3个水平想要比较A1和A3水平下的样本均值就在该框输入“1”单击Add 再按相同方法分别添加“0”、“-1”。
需要注意的是所有添加的系数加盐业必须0。
同时可通过Next定义多组多项式系数。
最后单击返回主对话框该对话框主要用于定义多重比较的检验方法。
比如方差分析的结果认为因素A各水平之间的差异会对指标X造成显著影响。
但并不意味差任意两个水平之间的差异都会给指标X造成显著影响。
这解决这个问题就有必要将各个水平的均值进行两两比较。
这种两两比较的方法就称为多重比较。
之对话框主要包括如下几项定义样本方差齐次情况下多重比较的检验方法。
SPSS共提供了14种检验方法。
其中最常用的是LSD法雪费最小显著差异法。
定义样本方差不齐情况下多重比较的检验方法。
定义两两比较的显著性水平最后单击返回主对话框其他选项设置最后单击返回主对话框是否绘制图形直观比较各组间均值统计指标复选框□输出各组的描述性统计量□输出不变效应和随机效应模型的标准差、标准误以及95的置信区间□计算Levene统计量检验各组方差齐性□计算Brown-Rorsythe统计量检验各组的均值是否相等。

SPSS统计分析教程-多因素方差分析多因素方差分析是对一个变量是否受一个或多个因素或变量影响而进行的方差分析oSPSS调用“Univariate ”过程,检验不同水平组合之间因变量均数,由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用,也可以分析因素之间的交互作用,以及分析协方差,以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来,且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量,协变量与因变量不彼此。
因素变量是分类变量,可以是数值型也可以是长度不超过8 的字符型变量。
固定因素变量(Fixed Factor) 是反应处理的因素; 随机因素是随机地从总体中抽取的因素。
[ 例子] 研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表相对湿度( %)温度C 重复1 2 3 4 100 25 91.2 95.0 93.8 93.0 27 87.6 84.7 81.2 82.429 79.2 67.0 75.7 70.6 31 65.2 63.3 63.6 63.3 80 25 93.2 89.3 95.1 95.527 85.8 81.6 81.0 84.4 29 79.0 70.8 67.7 78.8 31 70.7 86.5 66.9 64.9 4025 100.2 103.3 98.3 103.8 27 90.6 91.7 94.5 92.2 29 77.2 85.8 81.7 79.731 73.6 73.2 76.4 72.5 数据保存在“ DATA5 2.SAV'文件中,变量格式如图5-1。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量,因素变量温度“ A”,湿度为“B'变量,重复变量“重复”。

SPSS学习笔记之重复测量的多因素方差分析报告学习笔记之重复测量的多因素方差分析报告SPSS(Statistical Package for the Social Sciences,社会科学统计软件包)是一款功能强大的数据分析工具,广泛应用于各个领域的研究。
在SPSS中,重复测量的多因素方差分析被视为一项重要的统计方法,用于研究相同参与者在不同条件下的测试结果。
本篇学习笔记以重复测量的多因素方差分析为主题,将介绍如何使用SPSS进行该项分析,并给出详细的分析报告。
1. 研究目的和问题描述2. 数据采集和处理3. 研究设计和假设4. 数据分析5. 结果解释与讨论1. 研究目的和问题描述本次研究的目的是考察不同刺激条件对参与者注意力的影响。
具体而言,我们想了解参与者在三种刺激条件下的注意力水平是否存在显著差异。
2. 数据采集和处理我们招募了40位参与者,并随机将其分为三组。
每组参与者分别接受三次测试,每次测试采用不同的刺激条件。
我们记录了每位参与者的测试结果,并进行数据整理和清洗。
3. 研究设计和假设本研究采用的是重复测量的多因素方差分析设计。
考察因素为刺激条件,对应的水平为A、B和C。
我们的研究假设如下:- H0(零假设):不同刺激条件下的注意力水平无显著差异。
- H1(备择假设):不同刺激条件下的注意力水平存在显著差异。
4. 数据分析为了进行重复测量的多因素方差分析,我们打开SPSS软件,并导入数据集。
接下来,我们按照以下步骤进行分析:步骤一:打开SPSS软件,点击“打开”按钮,导入数据集。
步骤二:选择“分析”菜单,然后选择“一般线性模型”和“重复测量”。
步骤三:将待分析的因子变量(刺激条件)拖动到“因子”框中,并设置不同刺激条件的水平。
步骤四:选择适当的因变量(注意力水平),并将其拖动到“依赖变量”框中。
步骤五:点击“选项”按钮,可以对分析进行更多设置,比如是否计算偏斜度和峰度等。
步骤六:点击“确定”按钮,SPSS将自动进行重复测量的多因素方差分析,并生成分析结果。
《SPSS数据分析教程》——方差分析方差分析(Analysis of Variance,缩写为ANOVA)是统计学中用来测量和分析两个或多个样本之间变量差异的统计方法。
方差分析检验的是不同实验条件下样品的均值是否存在显著性差异,以此来判断实验条件对样品响应是否有影响。
简而言之,方差分析能够判断不同处理条件下样本变量的总体均值是否有显著差异,以便检验实验条件是否有效。
方差分析实际上是将实验条件分成实验组和非实验组,然后对试验组与非实验组的结果进行比较,看看实验处理是否有显著的结果。
另一种情况是将不同的实验条件分成若干组,然后将不同组之间的结果进行比较,看看不同的实验条件是否有显著的差别。
SPSS采取一步法方差分析,在用户指定自变量和因变量后,可以自动给出方差分析的结果,包括方差分析表,均值表,均方差表,以及F检验的统计量和显著性水平等。
另外,它还可以提供多元变量分析(MVA)结果,包括每个变量的贡献率,方差膨胀因子,皮尔逊相关系数,单变量分析等。
为了使用SPSS进行方差分析,首先要指定变量和实验条件。
然后,点击菜单栏“分析”,选择“双因素方差分析”。
SPSS如何实现多个条件的多重比较在使用SPSS进行数据分析时,我们常常需要进行多个条件下的多重比较。
SPSS提供了一些简单的策略来实现这一目标。
下面将介绍一些常见的方法。
1. 单因素方差分析(One-way ANOVA)如果我们有一个自变量(组别)和一个因变量(数值型),并且希望比较多个组之间的均值差异,我们可以使用单因素方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
然后将因变量移至“因变量”框中,将自变量移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
2. 重复测量方差分析(Repeated Measures ANOVA)在某些情况下,我们可能有多个因变量,并且希望比较这些因变量在多个时间点或条件下的均值差异。
这时可以使用重复测量方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
在“因变量”框中选择所有的因变量,将自变量(时间点或条件)移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
3. 多元方差分析(Multivariate ANOVA)在某些情况下,我们可能有多个自变量,并且想要比较这些自变量在多个因变量上的均值差异。
这时可以使用多元方差分析。
在SPSS中,选择“分析”菜单下的“一元方差分析”选项。
在“因变量”框中选择所有的因变量,将自变量移至“因子”框中。
点击“选项”,勾选“描述性统计”和“多重比较”。
4. 进一步的多重比较分析除了上述方法,SPSS还提供了更多的多重比较分析方法,如LSD(最小显著差异法)、Bonferroni法、Tukey法等。
这些方法可在上述分析的结果中找到。
需要注意的是,在进行多重比较时,我们应该根据实际情况选择最适合的方法。
在选择方法时,应综合考虑样本大小、数据分布和研究假设等因素。
以上就是在SPSS中实现多个条件的多重比较的一些基本方法。
希望对您有帮助!。
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze—〉General Linear Model —>Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM e rror,即无法分开MM intercept和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze—〉General Linear Model-〉Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21。
SPSS重复测量地多因素方差分析报告
一、实验结果的总体分析
1、总体数据及描述性统计
首先我们来分析实验的总体数据,主要包括对被试者的一般信息及参
与实验的各个变量的描述统计及分布情况。
基本信息:本次实验共有30名参与者,其平均年龄为31岁。
其中男
性占比为53.3,女性占比为46.7%。
变量的描述性统计:检测变量的标准差为0.614,最小值为1.4,最
大值为3.0,平均值为2.2,中位数为2.2,偏度为0.00,峰度为0.61变量的分布情况:根据变量分布图可以看出,变量的分布情况接近正
态分布。
2、数据检验
完成数据收集后需要对数据进行检验,以确保数据的准确性和可靠性。
检验的方法包括残差检验、异方差分析以及 Shapiro-Wilk 检验等。
经过
检验后,发现所有数据满足检验条件,可以用于进一步的分析。
二、多因素重复测量方差分析
本次实验使用多因素重复测量方差分析,用来检验被试者对不同环境
条件下的反应差异。
由于本次实验中因素为环境条件A、B、C,为三因素
实验,所以本次实验的实验设计为3X3实验设计。
1、方差分析表
计算完毕后,计算结果如下所示:。
SPSS多因素方差分析一、问题对小白鼠喂以三种不同的营养素,目的是了解不同营养素增重的效果。
采用随机区组设计方法,以窝别作为划分区组的特征,以消除遗传因素对体重增长的影响。
现将同品系同体重的24只小白鼠分为8个区组,每个区组3只小白鼠。
三周后体重增量结果(克)列于下表,问小白鼠经三种不同营养素喂养后所增体重有无差别?SPSS软件版本:18.0中文版。
二、统计操作:1、建立数据文件变量视图:建立3个变量,如下图数据视图:如下图:区组号用1-8表示,营养素号用1-3表示。
数据文件见“小白鼠喂3种不同的营养素增重数量.sav”,可以直接使用。
2、统计分析菜单选择:分析-> 一般线性模型-> 单变量点击进入“单变量”对话框将“体重”选入“因变量”框,“区组”、“营养素”选入固定因子框点击右边“模型”按钮,进入“单变量:模型对话框”点击“设定”单选按钮,在“构建项”下拉菜单中选择“主效应”把左边的因子与协变量框中区组和营养素均选入右边的模型框中其余选项取默认值就行,点击“继续”按钮,回到“单变量”界面点击“两两比较”按钮,进入下面对话框将左边框中“区组”、“营养素”均选入右边框中再选择两两比较的方法,LSD、S-N-K,Duncan为常用的三种方法,点击“继续”按钮回到“单变量”主界面。
点击“选项”按钮勾选“统计描述”及“方差齐性检验”,设置显著性水平,点击“继续”按钮,回到“单变量”主界面点击下方“确定”按钮,开始分析。
3、结果解读这是一个所分析因素的取值情况列表。
变量的描述性分析这是一个典型的方差分析表,有2个因素“营养素”和“区组”,首先是所用方差分析模型的检验,F值为11.517,P小于0.05,因此所用的模型有统计学意义,即认为至少有一个因素对体重增长有显著影响,可以用它来判断模型中系数有无统计学意义;第二行是截距,它在我们的分析中没有实际意义,忽略即可;第三行是变量是区组,P<0.001,可见有统计学意义(即认为区组对体重增长有显著影响),不过通常我们关心的也不是他;第四行是我们真正要分析的营养素,非常遗憾,它的P值为0.084,没有统计学意义(即认为营养素对体重增长没有显著影响)。