当前位置：文档之家 › 高中数学人教版双曲线上课课件PPT1

高中数学人教版双曲线上课课件PPT1

  • 格式：ppt
  • 大小：2.51 MB
  • 文档页数：65

下载文档原格式

  / 65

合集下载

3.2.1双曲线及其标准方程课件(人教版)(1)

3.2.1双曲线及其标准方程课件(人教版)(1)


方法归纳
(1)求双曲线标准方程的步骤：
①定位:确定与坐标系的相对位置，在标准方程的前提下,确定焦点位
于哪条坐标轴上，以确定方程的情势.
②定量:确定a2、b2的值，常由条件列方程组求解.
(2)双曲线标准方程的两种求法：
①定义法:根据双曲线的定义得到相应的a、b、c,再写出双曲线的标准
方程.
②待定系数法:先设出双曲线的标准方程，然后根据条件求出待定的
的点的轨迹叫做双曲线.
M
| |MF1| - |MF2| |= 2a (0<2a<|F1F2|)
这两个定点叫做双曲线的焦点，
两焦点间的距离叫做双曲线的焦距=2c，
焦距的一半称为半焦距.
F1
F2
概念辨析
思考：
（1）如果定义中去掉“绝对值”三个字会有什么影响？
如果不加绝对值，那得到的轨迹只是双曲线的一支.
使得|OB|=b吗?
新知探究
3.双曲线的标准方程
y
y
M
F1
O
•
F2 x
x2 y2
焦点在x轴上： 2 2 1(a 0, b 0)
a
b
焦点坐标：
F1(-c,0)、F2(c,0)
a,b,c关系： c2=a2+b2
M
F2
O
x
F1
y2 x2
焦点在y轴上： 2 2 1(a 0, b 0)
段PB为半径作圆.
（1）当点P在线段AB上运动时，如果|F1F2|>|AB|，两圆不相交，不存在
交点轨迹;
（2）如果|F1F2|<|AB|，那么两圆相交，其交点M的轨迹是 椭圆 .
l
A
双曲线的简单几何性质 第1课时(上课课件)

双曲线的简单几何性质 第1课时(上课课件)

4
人A数学选择性必修第一册
返回导航 上页 下页
(3)设与双曲线x22－y2＝1 有公共渐近线的双曲线方程为x22－y2＝k(k≠0)， 将点 M(2，－2)的坐标代入得 k＝222－(－2)2＝－2，∴双曲线的标准方 程为y22－x42＝1.
人A数学选择性必修第一册
返回导航 上页 下页
2.求满足下列条件的双曲线的标准方程：
人A数学选择性必修第一册
返回导航 上页 下页
3．2.2 双曲线的简单几何性质 第一课时 双曲线的简单几何性质(1)
人A数学选择性必修第一册
返回导航 上页 下页
根据双曲线的方程研究其几何性质
标准方程
ax22－by22＝1(a>0，b>0)
ay22－bx22＝1(a>0，b>0)
性 图形
质
人A数学选择性必修第一册
人A数学选择性必修第一册
返回导航 上页 下页
3.若双曲线的渐近线方程为 y＝±34x，则双曲线的离心率 为__54_或__53___．
―→
依题意列 出不等式
―→
求出e的 取值范围
人A数学选择性必修第一册
返回导航 上页 下页
[解析] 由题意可知直线 l 的方程为ax＋by＝1，即 bx＋ay－ab＝0.点(1,0)
到直线 l 的距离 d1＝ baa2－＋1b2，点(－1,0)到直线 l 的距离 d2＝ baa2＋＋1b2，
s＝d1＋d2＝ a22a＋b b2＝2acb，由 s≥45c，得2acb≥45c，
返回导航 上页 下页
标准方程
ax22－by22＝1(a>0，b>0)
ay22－bx22＝1(a>0，b>0)
3.2.1双曲线及其标准方程课件(人教版)(1)

3.2.1双曲线及其标准方程课件(人教版)(1)

2 =5
2

则有 25 4
,解得 2
,双曲线的标准方程为 5 －y2＝1.
− 2 = 1
=1
2
法二∵焦点在x轴上，c＝
25
2
y2
6，∴设所求双曲线方程为 λ －6−λ＝1(其中0<λ<6)．
4
∴ λ －6−λ＝1，∴λ＝5或λ＝30(舍去)．
2
∴所求双曲线的标准方程是 5 －y2＝1.
P到焦点F2的距离．
【错解一】
a=4，由|PF1|－|PF2|＝8，即9－|PF2|＝8，得|PF2|＝1.
【错解二】
a=4，由双曲线的定义得||PF1|－|PF2||＝8，所以|9－|PF2||＝8，
所以|PF2|＝1或17.
【错因】 错解一是对双曲线的定义中的差的绝对值掌握不够，是概念性的错误．错解二没有验证两解
将P、Q两点坐标代入可得
y2
225
9
−
=1
162
2
25
256
−
=1
2
92
2
2 =9

,解得 2
,
= 16
y2
2
（三）典型例题
1.求双曲线的标准方程
例1.根据下列条件，求双曲线的标准方程．
15
16
(1)经过点P(3， 4 )，Q(－ 3 ，5)．
2 y2
法二：设双曲线方程为 ＋ ＝1(mn<0)．
焦点
两个定点叫做双曲线的焦点
焦距
两焦点间的距离叫做双曲线的焦距
集合
语言
P＝{M|||MF1|－|MF2||＝2a,0<2a<|F1F2|}
3.2.2双曲线的简单几何性质(第1课时)课件-高二上学期数学人教A版(2019)选择性必修第一册

3.2.2双曲线的简单几何性质(第1课时)课件-高二上学期数学人教A版(2019)选择性必修第一册

双曲线的渐近线方程？

=−


2 2
对于双曲线 2 − 2 = 1和它的渐近线 = ± ，




=

y
(, )
将方程中的与互换，就得到双曲线


即 = ± ．
− 2 = 1 的渐近线方程 = ± ，
2



2
2
(−, )
规律方法：由双曲线方程求渐近线方程，只需把1变成0,

∴当 ∈
2
+
2


2
> 1.
=

(1, +∞)时，

∈

1+

2

(0, +∞),且增大, 也增大

b
离心率越大, 渐近线y x的斜率越大 双曲线的“张口”越大
a
新知探究
方程
2 2
− 2=1
2


2 2
− 2=1
2


图像
范围
对称性
≤ −，或 ≥
≤ −，或 ≥
≤ −，或 ≥
关于轴、轴、原点对称
（ − ，），（，） （， − ），（，）
a
b
y x
y x
渐近线
b
a

= >
离心率

顶点
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线方程.
2
2
x
y
2
2
2
2
2
2
(1) x 8 y 32; (2) 9 x y 81; (3) x y 4; (4)
人教高中数学必修《双曲线》精品PPT1

人教高中数学必修《双曲线》精品PPT1


双曲线定义
平面内与两个定点F1，F2的距离的差 的绝对值等于常数(小于|F1F2|)的点的轨迹 叫做双曲线. ||MF1|－|MF2||=2a ① 两个定点F1、F2 ——双曲线的焦点; ② |F1F2|=2c——焦距. 说明：(1) 2a<2c；(2) 2a>0；
① |MF1|－|MF2|=|F2F|=2a ② |MF2|-|MF1|=|F1F|=2a 由①②可得：
2.3.1双曲线及其标准方程
1. 椭圆平: 面内与两定点F1、F2的距离的和 等于常数2a(2a>|F1F2|>0)的点的轨迹.
|MF1|+|MF2|=2a( 2a>2c>0) 点M的轨迹是椭圆
若2a=2c,
点M的轨迹是线段F1F2；
若2a＜2c，
点M的轨迹不存在。
3.引入问题： 若把椭圆中的距离“和”改为距离”差”
[例2] 如果方程
x2
y2
1
2m m1
表示双曲线，求m的取值范围.
思考：
方程 x2 y2 1表示焦点在y轴
2m m1
双曲线时，则m的取值范围__________.
[例2] 如果方程
x2
y2
1
2m m1
表示双曲线，求m的取值范围.
思考：
方程 x2 y2 1表示焦点在y轴
2m m1
双曲线时，则m的取值范围___m_<_－__2___.
[例3] 已知A,B两地相距800m,在A地 听到炮弹爆炸声比在B地晚2s,且声速为 340m/s,求炮弹爆炸点的轨迹方程.
yP
x
A
B
[例3] 已知A,B两地相距800m,在A地 听到炮弹爆炸声比在B地晚2s,且声速为 340m/s,求炮弹爆炸点的轨迹方程.
人教A版高中数学《双曲线》PPT完美课件1

人教A版高中数学《双曲线》PPT完美课件1


O
X
问题三: 人教A版高中数学《双曲线》PPT完美课件1
若直线y=kx-1与双曲线4x2-y2=1无公共点，实数k的取值 范围是什么？说明位置关系。
人教A版高中数学《双曲线》PPT完美 课件1
问题三: 人教A版高中数学《双曲线》PPT完美课件1
若直线y=kx-1与双曲线4x2-y2=1无公共点，实数k的取值 范围是什么？说明位置关系。
问题一:
直线y=kx-1与双曲线4x2-y2=1有且只有一个公共点，求直 线方程，说明位置关系。
解 ： 联 立 4 y x 2 k y x 2 1 1 得 (4 - k 2 )x 2 + 2 k x - Y2 = 0
O
X
问题二
若直线y=kx-1与双曲线4x2-y2=1有两个不同公共点，实数 k的取值范围是什么？说明位置关系。
得到一元二次方程
计算判别式
>0
=0
<0
相交 相切 相离
人教A版高中数学《双曲线》PPT完美 课件1
练习:
1、已知直线y=kx-1与双曲线x2-y2=4,试讨论实数k的取值范围,使直 线与双曲线
(1)交于异支两点；
-1＜k＜1 ；
(2)与左支交于两点.
- 5 k 1 2
解 ： x y 2 = -k y 2 由 - = x 1 4 得 x （ 2 ， 1 -k 2 ） 2 k x 5 0
问题二: 人教A版高中数学《双曲线》PPT完美课件1
若直线y=kx-1与双曲线4x2-y2=1有两个不同公共点，实数 k的取值范围是什么？说明位置关系。
解 ： 联 立 4 y x 2 k y x 2 1 1 得 (4 - k 2 )x 2 + 2 k x Y- 2 = 0
《双曲线》_PPT完整版人教版1

《双曲线》_PPT完整版人教版1

94
1.
a 3 ，b 2， c 9 4 5 . 4
2
4
2
∴ 离心率 e 5 . 3
《双曲线》教学分析人教版1-精品课 件ppt( 实用版)
《双曲线》教学分析人教版1-精品课 件ppt( 实用版)
变式1
求以椭圆
x2 13
y2 3
1的焦点为焦点，以直线
y
1 2
x为
渐近线的双曲线方程。
所求双曲线的渐近线为 x y 0 21
4 （2）焦点在 y 轴，焦距是 16， e 4 ;
3 （3）以椭圆 x2 y2 1 的焦点为顶点，以椭圆的顶点为焦点；
85
（4）一个焦点是 F1（-6，0）的等轴双曲线.
解：(1) 2a 8, c 5 , a4
a 4, c 5, b2 c2 a2 9. 故所求标准方程为：x2 y2 1.
例3 求与双曲线
x2 y2 1 共渐近线且过点 (2
16 9
3， 3)
的双曲线方程及离心率．
解：设与已知双曲线共渐近线的双曲线方程为 x2 y2 0
16 9
∵ 点 (2 3， 3)在双曲线上，
12 9 1
16 9 4 故所求双曲线方程为：x2 y2
16 9
1 4
即
y2 x2
2.3.2 双曲线的简单几何性质（1）
思考回顾 椭圆的简单几何性质 ？
①范围; ②对称性; ③顶点; ④离心率等
双曲线是否具有类似的性质呢?
图象
方程 性质
A1 F1
y B1
O
B2
M
A2
F2 x
范围
| x | a，| y | b
B1 A1 A2
B2
双曲线及其标准方程ppt课件

双曲线及其标准方程ppt课件

所以 2 mm 1 0 ，解得 m 2 或 m 1， 即实数 m 的取值范围是,2 1, .
总结一下
1.双曲线的定义 2.双曲线的标准方程
Fresh and simple general ppt template
谢谢观看
2.焦点在y轴上的双曲线的标准方程
如图，双曲线的焦距为 2c，焦点分别是
F1(0, c) ， F2 (0,c) ，a，b 的意义同上，这时
双曲线的方程是
y2 a2
x2 b2
1(a
0, b
0)
，这个
方程也是双曲线的标准方程.
y
M
F2
x O
F1
双曲线标准方程
图形
y M x
F1 O F2
y M F2
3.2.1 双曲线及其标准方程
人教A版（2019）选择性必修一
学习目标
01 经历从具体情境中抽象出双曲线模型的过程 02 了解双曲线的定义、几何图形和标准方程
03 通过双曲线标准方程的推导过程理解数形结合思想
学习重点
双曲线的定义、标准方程
学习难点
双曲线标准方程的推导
新课导入
我们知道，平面内与两个定点F1，F2的距离的和等于常数的点的轨
由双曲线的定义，双曲线就是下列点的集合：
P {M || MF1 | | MF2 || 2a ， 0 2a | F1F2 |} .
因为 | MF1 | (x c)2 y2 ，| MF2 | (x c)2 y2 ， 所以 (x c)2 y2 (x c)2 y2 2a .①
类比椭圆标准方程的化简过程，化简①，得 (c2 a2 )x2 a2 y2 a2 (c2 a2 ) ，
x2 b2
1a
第三章3.2.2第1课时双曲线的简单几何性质PPT课件(人教版)

第三章3.2.2第1课时双曲线的简单几何性质PPT课件(人教版)


4.双曲线x2－y2＝1的顶点到其渐近线的距离等于
A.12
√B.
2 2
C.1
D. 2
解析 双曲线x2－y2＝1的渐近线方程为x±y＝0，顶点坐标为(1,0) 2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
5.已知双曲线 C：ax22－by22＝1(a>0，b>0)的离心率为 25，则双曲线 C 的渐近线方
∴b＝2，∴－m1 ＝b2＝4， ∴m＝－41，故选 C.
12345
3.中心在原点，焦点在x轴上，且一个焦点在直线3x－4y＋12＝0上的等轴双曲
线的方程是
√A.x2－y2＝8
B.x2－y2＝4
C.y2－x2＝8
D.y2－x2＝4
解析 令y＝0，得x＝－4， ∴等轴双曲线的一个焦点为(－4,0)， ∴c＝4，a2＝b2＝21c2＝21×16＝8，故选 A.
实轴长2a＝6，虚轴长2b＝4，
离心率 e＝ac＝ 313， 渐近线方程为 y＝±bax＝±23x.
延伸探究 求双曲线nx2－my2＝mn(m>0，n>0)的实半轴长、虚半轴长、焦点坐标、离心 率、顶点坐标和渐近线方程.
解 把方程 nx2－my2＝mn(m>0，n>0)化为标准方程为xm2－yn2＝1(m>0，n>0)， 由此可知，实半轴长 a＝ m，
所以双曲线的离心率为 1＋ 2.
3 随堂演练
PART THREE
1.(多选)已知双曲线方程为x2－8y2＝32，则
√A.实轴长为 8 2
√B.虚轴长为 4
C.焦距为 6
√D.离心率为3 4 2
解析 双曲线方程 x2－8y2＝32 化为标准方程为3x22 －y42＝1， 可得 a＝4 2，b＝2，c＝6，
双曲线及其标准方程 课件(人教版)

双曲线及其标准方程 课件(人教版)


()D.45
解析：(1)因为由双曲线的定义有|PF1|－|PF2|＝|PF2| ＝2a＝2 2，
所以|PF1|＝2|PF2|＝4 2， |PF1|2＋|PF2|2－|F1F2|2
则 cos ∠F1PF2＝ 2|PF1|·|PF2| ＝
（4 22）×24＋（2×2 22）2 2－42＝34. 答案：C
解：(1)法一：由题意知双曲线的两焦点为 F1(0，－
3)，F2(0，3)． 设双曲线方程为ay22－xb22＝1(a＞0，b＞0)， 将点 A(4，－5)代入双曲线方程得2a52－1b62＝1. 又 a2＋b2＝9，解得 a2＝5，b2＝4. 所以双曲线的标准方程为y52－x42＝1.
法二：||AF1|－|AF2||＝| 20－ 80|＝2 5＝2a，
[迁移探究 2] (变换条件)上例中将条件“|PF1|＝ 2|PF2|”改为“P→F1·P→F2＝0”，则△F1PF2 的面积是 ________．
解：不妨设点 P 在双曲线的右支上，则|PF1|－|PF2|
＝2a＝2 2， 由于P→F1·P→F2＝0，所以P→F1⊥P→F2.
所以在△F1PF2 中，有|PF1|2＋|PF2|2＝|F1F2|2， 即|PF1|2＋|PF2|2＝16，所以|PF1|·|PF2|＝4， 所以 S△F1PF2＝12|PF1|·|PF2|＝2. 答案：2
双曲线及其标准方程
1．双曲线的定义 把平面内与两个定点 F1、F2 的距离的差的绝对值等 于常数(小于|F1F2|)的点的轨迹叫做双曲线，这两个定点 叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．
温馨提示 把定常数记为 2a，当 2a＜|F1F2|时，其轨迹是双曲线； 当 2a＝|F1F2|时，其轨迹是以 F1、F2 为端点的两条射线(包 括端点)；当 2a＞|F1F2|时，其轨迹不存在．
高二数学人教A版选修一《3.2双曲线》完整课件(85页)

高二数学人教A版选修一《3.2双曲线》完整课件(85页)


)
A．[－4,1)
B．(－∞，－4)∪(1，＋∞)
C．(－4,1)
D．(－∞，－4]∪[1，＋∞)
解析：根据题意，若曲线k＋x24＋k－y2 1＝1 表示双曲线，则有 (k＋4)(k－1)<0，解得－4<k<1.
答案：C
题型三 双曲线标 (1)只有当双曲线的两焦点 F1，F2 在坐标轴上，并且线段 F1F2 的垂直平分线也是坐标轴时得到的方程才是双曲线的标准 方程． (2)标准方程中的两个参数 a 和 b，确定了双曲线的形状和大 小，是双曲线的定形条件，这里的 b2＝c2－a2 与椭圆中的 b2＝a2 －c2 相区别，且椭圆中 a>b>0，而双曲线中 a，b 大小不确定．
()
(3)方程 mx2＋ny2＝1(mn<0)表示双曲线．
()
答案：(1)× (2)× (3)√
2．双曲线1x02－y22＝1 的焦距为
A．2 2
B．4 2
C．2 3
D．4 3
()
解析：因为 c2＝10＋2＝12，所以 c＝2 3，从而焦距为 4 3. 答案：D
3．已知双曲线的 a＝5，c＝7，则该双曲线的标准方程为( ) A．2x52－2y42 ＝1 B．2y52 －2x42＝1 C．2x52－2y42 ＝1 或2y52 －2x42＝1 D．2x52－2y42 ＝0 或2y52 －2x42＝0
数 m 的取值范围是
()
A．m>2
B．m<1 或 m>2
C．－1<m<2
D．－1<m<1 或 m>2
(2)“3<m<5”是“方程mx－2 5＋m2－ym2 －6＝1 表示的图形为双曲

《双曲线》课件人教版1


《双曲线》课件人教版1
如何求双曲线的标准方程？
1. 建系. 以F1,F2所在的直线为X轴，线
段F1F2的垂直平分线为y轴，建立直 角坐标系Oxy
y
M
2.设点 设M（x , y）,双曲线的焦
距为2c（c>0）,F1(-c,0),F2(c,0) F1
o F2 x
常数=2a
3.列式．||MF1 |- |MF2||= 2a
y2 b2
1
y2 a2
x2 b2
1
(a0， b0)
c2 a2 b2
《双曲线》课件人教版1
《双曲线》课件人教版1
思考：如何判断双曲线的焦点在哪个轴上？
看 x 2 , y 2 前的系数，哪一个为正，
则在哪一个轴上
练习：写出以下双曲线的焦点坐标.
(1) x 2 - y 2 =1; 16 9
(5,0)，（-5,0）
(2)常数要小于|F1F2|大于0
F1 o F2
0<2a<2c
①如图(A)，
|PF1|-|PF2|=2a ②如图(B)，
|PF2|-|PF1|=2a 由①②可得： | |PF1|-|PF2| | = 2a
（差的绝对值）
上面 两条合起来叫做双曲线
拉链画双曲线
双曲线定义
| |MF1| - |MF2| | = 2a 0<2a<2c
时，则m的取值范围___m_______2___.
P121 T4
《双曲线》课件人教版1
《双曲线》课件人教版1
小结
定义 | |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
图象
y
M
F1 o F2 x

选择性必修第一册3.2.1双曲线及其标准方程课件(人教版)

a>b>0, a2=b2+c2 a, b, c中a最大
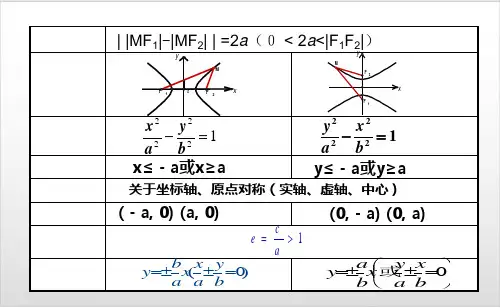
双曲线
||MF1|－|MF2||=2a (a<c)
x2 a2
y2 b2
1(a
0, b
0)
y2 x2 a2 b2 1(a 0, b 0)
F1(－c, 0), F2(c, 0) F1(0, －c), F2(0, c)
a>0, b>0, c2=a2+b2 a, b, c中c最大
练习 已知1－x2k －|k|y－2 3 ＝－1，当 k 为何值时： (1)方程表示双曲线；(2)方程表示焦点在 x 轴上的双曲线．
解：(1)原方程可变形为|k|y－2 3 －1－x2k ＝1. 要使方程表示双曲线，必须满足(|k|－3)(1－k)>0， 即|1k－|－k3>>00， 或|1k－|－k3<<00，， 解得 k<－3 或 1<k<3.
们的斜率之积是 4 ,求点M的轨迹方程. 9
解：设M( x,
y ), 则k AM
kBM
4 ,
9
即
x
y 5
x
y 5
4(x 9
5).
A
y
M •
O
Bx
化简得 4x2 9 y2 100,即 x2 y2 1( x 5). 25 100
9
∴点M的轨迹方程为 x2 y2 1( x 5). 25 100
o A•
B• x
利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点
所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲
线的一个重要应用 .

双曲线及其标准方程ppt课件


课后提升
1.必做题：P127页课本习题3.2第1，2，5题
2. 思考题（选做）:定位问题
某中心接到其正东、正西、正北方向三个观测点的报告，正西、
正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其
它两个观测点晚4秒。已知各观测点到该中心的距离都是1020m，试
确定该巨响发生的位置。
（假定声音传播的速度为340m/s,相关各点均在同一平面内。）


−
= 令 = −



−
你能在y轴上找一点B，使得|OB|=b吗？
1
验证
设点
2
坐标法
4
化简
列式
3
绝对值
教学过程分析
3
通过图象，生成定义
绘制图象，合作探究
2
1
类比启发，方程推导
重
点
4
5
类比推理，举一反三
列表对比，加深理解
教学过程分析
方程推导
在学生脑海里留下更加深刻的印象。
通过学生的自主学习、小组合作、师生互
动，让学生学会交流、表达、质疑、反思。
04
01
02
03
谢
大
谢
家
5.及时练习，巩固所学
6.回顾小结，思维提升
7.课后延伸，探究发现
教学过程分析
复习回顾，课题导入
复习回顾：
椭圆及其标准方程
创设情境
导入课题：双曲线及其标准方程
教学过程分析
3
通过图象，生成定义
绘制图象，合作探究
2
1
类比启发，方程推导
4
类比推理，举一反三
5

《双曲线》ppt高中人教版1


Δ>0
直线与双曲线相交（两个交点）
Δ=0
直线与双曲线相切
Δ<0
直线与双曲线相离
人教A版数学选修2—1ቤተ መጻሕፍቲ ባይዱ2.3 直线与双曲线的位置关系
代数法判断直线与双曲线的位置关系: 人教A版数学选修2—1 2.3 直线与双曲线的位置关系
把直线方程代入双曲线方程
得到一元一次方程
直线与双曲线的 渐进线平行或重合
相交（一个交点）或相离
•
2.许地山这样说，也是这样做的，他 长大后 埋头苦 干，默 默奉献 ，成为 著名的 教授和 作家， 他也因 此取了 个笔名 叫落花 生，这 就是他 笔名的 由来。
•
3.在伟大庄严的教堂里，从彩色玻璃 窗透进 一股不 很明亮 的光线 ，沉重 的琴声 好像是 把人的 心都洗 淘了一 番似的 ，我感 到了我 自己的 渺小。
人教A版数学选修2—1 2.3 直线与双曲线的位置关系
问题二: 人教A版数学选修2—1 2.3直线与双曲线的位置关系
若直线y=kx-1与双曲线4x2-y2=1有两个不同公共点，实数 k的取值范围是什么？说明位置关系。
解 ： 联 立 4 y x 2 k y x 2 1 1 得 (4 - k 2 )x 2 + 2 k x Y- 2 = 0
人教A版数学选修2—1 2.3 直线与双曲线的位置关系
yax或yx0 b a b
教学目标:
1.知识与能力: （1）理解并熟练掌握直线与双曲线的各种位置关系，
能类比直线与椭圆的位置关系进行判断求解， 培养分析、归纳、推理、类比的能力。 （2）掌握判断位置关系的两种思路：几何法、代数 法。 （3）加强运算能力的训练，培养良好的思维习惯。
2.过程与方法： 强化数形结合、函数方程、转化化归、分类讨论等数学思想方法在直线与双曲
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【解析】 双曲线C1的一条渐近线方程为bx－ay＝0， 圆心(2，0)到渐近线的距离为1，
即 a|22＋b| b2＝1，得a2＝3b2，
Hale Waihona Puke 即ba＝3 3.所以双曲线C1的渐近线方程为y＝± 33x.故选D.
(2)(2020·唐山市第一次模拟)已知F是双曲线C：
x2 a2
－
y2 b2
＝
1(a>0，b>0)的右焦点，M是C的渐近线上一点，且MF⊥x轴，过
第二课时 双曲线与抛物线小题
热点调研
一、基础知识 双曲线的方程与性质
标准方程
xa22－yb22＝1(a>0，b>0) ya22－xb22＝1(a>0，b>0)
图形
范围 x≥a或x≤－a，y∈R
x∈R，y≥a或y≤－a
对称轴：坐标轴 对称 对称性
中心：原点
顶点坐标：
顶点坐标：
顶点
A1(－a，0)，A2(a，0)
押题一 双曲线
(1)(2020·百校联考)双曲线C1：xa22－yb22＝1(a>0，b>0)的
渐近线与圆C2：(x－2)2＋y2＝1相切，则双曲线C1的渐近线方程 为( D )
A．y＝±12x
B．y＝±13x
C．y＝±
2 2x
D．y＝±
3 3x
【分析】 双曲线C1的一条渐近线方程为bx－ay＝0，根据 渐近线与圆C2：(x－2)2＋y2＝1相切，则有 a|22＋b| b2＝1求解．
A1(0，－a)，A2(0，a)
性 轴
实轴：线段A1A2，虚轴：B1B2
质 焦距
|F1F2|＝2c
离心率
e＝ca，e∈(1，＋∞)，e越大，开口越大
a，b，c 的关系
c2＝a2＋b2
渐近线
y＝±bax
y＝±bax
等轴双曲线 (1)定义：中心在原点，以坐标轴为对称轴，实半轴长与虚 半轴长相等的双曲线叫做等轴双曲线． (2)性质：①a＝b；②e＝ 2；③渐近线互相垂直；④等轴双 曲线上任意一点到中心的距离是它到两焦点距离的等比中项．
共轭双曲线 (1)定义：如果一条双曲线的实轴和虚轴分别是另一条双曲 线的虚轴和实轴，那么这两条双曲线互为共轭双曲线． (2)性质：①它们有共同的渐近线；②它们的四个焦点共 圆；③它们的离心率的倒数的平方和等于1.
抛物线的标准方程和几何性质
标准 方程
y2＝2px (p>0)
y2＝－2px (p>0)
x2＝2py (p>0)
x2＝－2py (p>0)
图形
顶点 对称轴
焦点
准线
(0，0)
x轴
y轴
Fp2，0
F－p2，0
F0，p2
F0，－p2
x＝－p2
x＝p2
y＝－p2
y＝p2
二、常见方法结论
双曲线 (1)双曲线的焦点到其渐近线的距离为b. (2)若P是双曲线右支上一点，F1，F2分别为双曲线的左、右 焦点，则|PF1|min＝a＋c，|PF2|min＝c－a. (3)同支的焦点弦中最短的为通径(过焦点且垂直于实轴的 弦)，其长为2ab2；异支的弦中最短的为实轴，其长为2a. (4)若P是双曲线上不同于实轴两端点的任意一点，F1，F2分 别为双曲线的左、右焦点，则S△PF1F2＝ b2θ，其中θ为∠F1PF2.
关于抛物线的切线 (1)以焦点弦为直径的圆与准线相切；以焦半径为直径的圆 与y轴相切(开口向右)． (2)过抛物线焦点弦的两个端点作抛物线的两条切线，则切 线互相垂直，且交点在抛物线准线上． (3)过抛物线的准线上任意一点作抛物线的两条切线，则切 线互相垂直，两切点与抛物线焦点共线．
如果OA，OB是抛物线y2＝2px上的两条弦(O是原点)，则
，
|AF| |BF|
＝
1－cosθ 1＋cosθ
，
1 |AF|
＋
1 |BF|
＝
2 p
，
|AB|＝sin22pθ.
(2)过抛物线x2＝2py(p>0)的焦点F作倾斜角为θ的直线交抛物 线于点A(x1，y1)，B(x2，y2)，其中x1<0<x2，则有|AF|＝ 1＋spinθ，|BF|＝1－spinθ，||ABFF||＝11＋－ssiinnθθ，|A1F|＋|B1F|＝2p，|AB| ＝co2sp2θ.
∵MN⊥ON，且kMN＝
bac＋b2ca c－2c
＝
3b a
，kON＝－
b a
，∴kMN·kON＝－
3b2 a2
＝－1，∴
b2 a2
＝
1 3
，因此，双曲线C的离心率为e＝
c a
＝
a2＋b2 a2
＝
1＋ba2＝2 33.故选A.
(3)(2020·河南省鹤壁第二次模拟)已知双曲线C：
x2 a2
－
y2 b2
tan 2
(5)若P是双曲线
x2 a2
－
y2 b2
＝1(a>0，b>0)右支上不同于实轴端点
的任意一点，F1，F2分别为双曲线的左、右焦点，I为△PF1F2内 切圆的圆心，则圆心I的横坐标为定值a.
(6)设F1，F2是双曲线
x2 a2
－
y2 b2
＝1(a>0，b>0)的左、右焦点，
AB是过F1的弦，则|AF2|＋|BF2|－|AB|＝4a.
F作直线OM的平行线交C的渐近线于点N(O为坐标原点)，若
MN⊥ON，则双曲线C的离心率是( A )
A.2 3 3
B. 3
6 C. 2
D．2
【解析】
设点M为双曲线C的渐近线y＝
b a
x上的一点，易知点
F(c，0)，所以点M
c，bac
，直线FN的方程为y＝
b a
(x－c)，联立
yy＝＝－ba（baxx－，c），解得xy＝＝－2c，b2ca，则点N2c，－2bac，
(1)若OA，OB互相垂直，则直线AB过定点(2p，0)；
(2)若直线AB过定点(2p，0)，则OA，OB互相垂直．
(1)过抛物线y2＝2px(p>0)的焦点F作倾斜角为θ的直线交
抛物线于点A(x1，y1)，B(x2，y2)，其中y1<0<y2，则有|AF|＝
p 1＋cosθ
，|BF|＝
p 1－cosθ
(7)AB为双曲线
x2 a2
－
y2 b2
＝1(a>0，b>0)的弦，A(x1，y1)，
B(x2，y2)，弦中点M(x0，y0)．则
①弦长l＝ 1＋k2|x1－x2|＝ ②直线AB的斜率kAB＝ba22yx00.
1＋k12|y1－y2|；
关于抛物线的焦点弦 线段AB为抛物线y2＝2px(p>0)的焦点弦，A(x1，y1)，B(x2， y2)，则 (1)x1x2＝p42； (2)y1y2＝－p2； (3)焦半径|AF|＝x1＋p2； (4)弦长l＝x1＋x2＋p.当弦AB⊥x轴时，弦长最短为2p，此时 的弦又叫通径．
＝