人教版高中数学双曲线
- 格式:pptx
- 大小:562.60 KB
- 文档页数:10

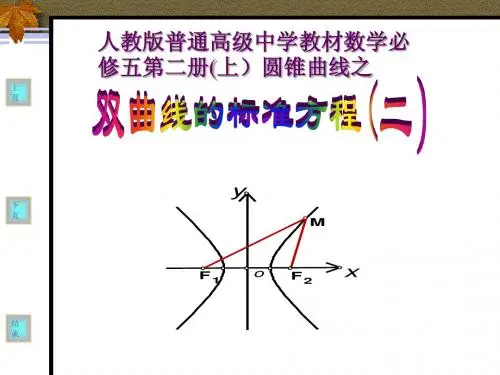



双曲线及标准方程、几何性质一、双曲线的定义及标准方程【知识要点】1. 双曲线的定义第一定义:平面内与两定点21,F F 的距离之差的绝对值为常数(小于21F F )的点的轨迹叫双曲线.第二定义:平面内与一个定点F 和一条定直线)(l F l ∉的距离之比是常数)),1((+∞∈e e 的点的轨迹叫做双曲线。
2. 双曲线的方程(1)标准方程:12222=-b y a x 或12222=-b x a y ,其中222,0,0b a c b a +=>>。
(2)一般方程:122=+By Ax ,其中0<AB【基础训练】1.已知点)0,5(1-F ,)0,5(2-F ,动点P 满足821=-PF PF ,则动点P 的轨迹是( ) A.椭圆 B.双曲线 C.两条射线 D.线段 2.已知双曲线19422=-y x 上一点P 到一个焦点的距离为5,则P 到另一个焦点的距离为( )A.1B.9C.1或9D.4或93.到两定点)5,0(),5,0(B A -的距离之差的绝对值为6的动点的轨迹方程为 。
4.两个焦点的坐标分别为)0,2(),0,2(-,并且经过)2,3(的双曲线的标准方程是 。
5.已知平面内有一长度为4的定线段AB ,动点P 满足3=-PB PA ,O 为AB 的中点,则OP 的最小值为 。
【典例精析】例1.方程13122=-+-my m x 表示焦点在y 轴上的双曲线,则m 的范围是( ) A. 3<m 且1≠m B.1>m 且3≠m C.31<<mD.3>m 或1-<m例2.已知双曲线的中心在原点,焦点在坐标轴上,分别求满足下列条件的双曲线的方程.(1)一个焦点为)0,4(-,且一条渐近线的方程是023=-y x ;(2)离心率为2,且过点)10,4(-P .例3.求与圆4)2(22=++y x 外切,并过定点)0,2(B 的动圆圆心M 的轨迹方程。


人教版高中数学双曲线教案
教学目标:
1. 了解双曲线的定义和性质。
2. 掌握双曲线的标准方程和图像。
3. 能够利用双曲线方程解决实际问题。
教学重点:
1. 双曲线的定义。
2. 双曲线的标准方程和图像。
3. 利用双曲线求解实际问题。
教学难点:
1. 确定双曲线的焦点和渐近线。
2. 利用双曲线方程解决实际问题。
教学准备:
1. 教师准备双曲线的相关知识讲解。
2. 准备多媒体教学资料,用于展示双曲线的图像。
3. 准备练习题,用于学生巩固练习。
教学过程:
一、引入:
教师通过举例引入双曲线的概念,并讲解双曲线的定义和性质。
二、概念讲解:
1. 讲解双曲线的标准方程和图像。
2. 解释双曲线的焦点和渐近线的概念。
三、例题演练:
1. 讲解双曲线的方程与图像的对应关系。
2. 解答一些实际问题,让学生应用双曲线方程进行求解。
四、课堂练习:
教师出示多个双曲线练习题,让学生在课堂上进行解答。
五、总结:
教师总结本节课的重点内容,强调学生需要重点掌握的知识点。
六、作业布置:
布置相关的练习题作业,要求学生在家中完成,并在下节课上进行讲解和批改。
教学反思:
通过本节课的教学,发现学生在理解双曲线的概念和性质上存在一定的困难,需要进一步加强讲解和练习。
在下节课上会结合学生的实际情况进行有针对性的教学。

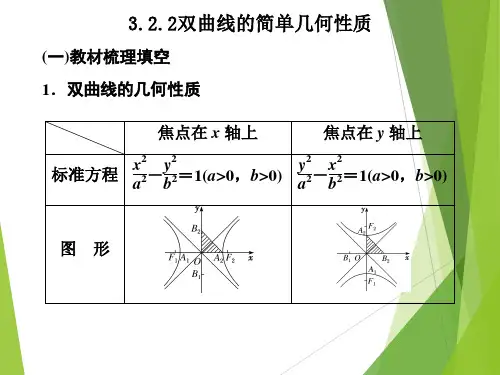


3.2.1双曲线及其标准方程
一、学习目标:1.了解双曲线的定义、几何图形和标准方程的推导过程;
2.掌握双曲线的标准方程;
3.会利用双曲线的定义和标准方程解决简单的应用问题.
学习重点:双曲线的定义、标准方程及几何图形.
学习难点:双曲线标准方程的推导与化简过程.
二、导学指导与检测
三、巩固诊断
【A 层】
1.双曲线064422=+-y x 上一点P 到它的一个焦点的距离等于1,求P 另一个焦点的距离.
【B 层】
2.求适合下列条件的双曲线的标准方程
(1)焦点在x 轴上,a =4,b =3;
(2)焦点为(0,-6),(0,6),且经过点(2,-5).
【C 层】
3.已知定点A 的坐标为(1,4),点F 是双曲线112
42
2=-y x 的左焦点,点P 是双曲线右支上的动点,求|PF |+|PA |的最小值.
【闯关题】:方程),求该双曲线的标准,(共焦点的双曲线过点已知与双曲线62
5191622--=-P y x .。
3.2.1双曲线及其标准方程本节课选自《2019人教A 版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习双曲线及其标准方程学生初步认识圆锥曲线是从椭圆开始的,双曲线的学习是对其研究内容的进一步深化和提高。
如果双曲线研究的透彻、清楚,那么抛物线的学习就会顺理成章。
所以说本节课的作用就是纵向承接椭圆定义和标准方程的研究,横向加深对双曲线的标准方程及简单几何性质的理解与应用。
从高考大纲要求和课程标准角度来讲,双曲线的定义、标准方程作为了解内容,在高考的考查当中以选择、填空为主。
正因如此,学生在学习过程当中对双曲线缺少应有的重视,成为了学生的一个失分点。
而且由于学生对椭圆与双曲线的区别与联系认识不够,无法做到知识与方法的迁移,在学习双曲线时极易与椭圆混淆。
在教学中要时刻注意运用类比的方法,让学生充分的类比体会椭圆与双曲线的异同点,使得椭圆与双曲线的学习能相互促进。
重点:用双曲线的定义和标准方程解决简单实际问题. 难点:双曲线的标准方程及其求法.多媒体双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定定位等都要用到双曲线的性质。
本节我们将类比椭圆的研究方法研究双曲线的有关问题。
我们知道,平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹是椭圆,一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?l A B P l如图,在直线上取两个定点,,是直线上的动点。
12如图,在>的条件下,让两圆的交点的轨迹是什么形状?F F AB M从椭圆的情形一样,下面我们用坐标法来探讨尝试与发现中的问题,并求出双曲线的标准方程。
解:建立平面直角坐标系,使并且原点与线段的中点重合。
设炮弹爆炸点的坐标为(3402AB P PA PB -=⨯=2 4−所以双曲线方程为x轴负半轴上的一段,又因为|PF1|-|PF2|=2a,说明|PF1|>|PF2|,所以应该是起点为(5,0),与x轴重合向x轴正方向延伸的射线.答案:D2.已知双曲线x2a2−y2b2=1(a>0,b>0),F1,F2为其两个焦点,若过焦点F1的直线与双曲线的同一支相交,且所得弦长|AB|=m,则△ABF2的周长为()A.4aB.4a-mC.4a+2mD.4a-2m解析:不妨设|AF2|>|AF1|,由双曲线的定义,知|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,所以|AF2|+|BF2|=(|AF1|+|BF1|)+4a=m+4a,于是△ABF2的周长l=|AF2|+|BF2|+|AB|=4a+2m.故选C.答案:C3.已知方程x21+m +y2m-2=1表示双曲线,则m的取值范围是()A.(-1,+∞)B.(2,+∞)C.(-∞,-1)∪(2,+∞)D.(-1,2)解析:∵方程x 21+m +y2m-2=1,∴(m-2)(m+1)<0,解得-1<m<2,∴m的取值范围是(-1,2).答案:D4. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知tan∠PEF=12,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦点且过点P的双曲线方程.解:以E,F所在直线为x轴,EF的垂直平分线为y轴建立直角坐标系,如图.设以E,F为焦点且过点P的双曲线方程为x 2a2−y2b2=1,∵在△EFP中,|EF|=2c,EF4五、课时练学生已经系统的学习了直线的方程,双曲线的方程以及简单几何性质,会根据题目条件求简单的双曲线的标准方程。
人教版高中数学双曲线的标准方程与性质1. 了解双曲线的定义、几何图形和标准方程及简单性质.2. 了解双曲线的实际背景及双曲线的简单应用.3. 理解数形结合的思想.1.双曲线的定义平面内动点与两个定点F1,F2(|F1F2|=2c>0)的距离差的绝对值等于常数(小于|F1F2|大于零),则点的轨迹叫双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0:(1)若a<c时,则集合P为双曲线;(2)若a=c时,则集合P为两条射线;(3)若a>c时,则集合P为空集.2.双曲线的标准方程和几何性质标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)图形性质范围x ≥a 或x ≤-a ,y ∈Rx ∈R ,y ≤-a 或y ≥a对称性对称轴:坐标轴;对称中心:原点顶点A1(-a ,0),A2(a ,0) A1(0,-a),A2(0,a)渐近线y =±b axy =±abx离心率e =ca,e ∈(1,+∞)实虚轴线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a叫做双曲线的半实轴长,b叫做双曲线的半虚轴长a,b,c的关系c2=a2+b2(c>a>0,c>b>0)类型一双曲线的定义及应用例1:(1)已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程为________.【解析】利用动圆M同时与圆及圆外切,可得的轨迹为到定点,距离差为常数2的点的集合,即双曲线的左支,从而可得方程.【答案】动圆的圆心为,动圆的圆心为动圆M同时与圆及圆外切,动圆M的半径,即的轨迹为到定点,距离差为常数2的点的集合,即双曲线的左支的轨迹方程为因此,本题正确答案是:练习1:已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若PF1⊥PF2,则|PF1|+|PF2|的值为________.【答案】23练习2:设P是双曲线x216-y220=1上一点,F1,F2分别是双曲线左、右焦点,若|PF1|=9,则|PF2|=( )A.1 B.17 C.1或17 D.以上答案均不对【答案】B练习3:已知F是双曲线x24-y212=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为( )A.5 B.5+4 3 C.7 D.9【答案】D类型二双曲线的标准方程例2:已知双曲线中心在原点且一个焦点为F1(-5,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程是( )A.2214xyB.2214yxC.22123x yD.22132x y【解析】∵F1(-5,0),PF1的中点坐标为(0,2),∴P的坐标为(5,4).又∵双曲线的一个焦点为F1(-5,0),∴另一个焦点为F2(5,0).∴2a=||PF1|-|PF2||=2.∴a=1.又∵c=5,∴b2=c2-a2=4.∴双曲线方程为x2-y24=1.【答案】B练习1:设双曲线与椭圆x227+y236=1有共同的焦点,且与椭圆相交,一个交点的坐标为(15,4),则此双曲线的标准方程是________.【答案】根据题意可以知道椭圆的焦点在y 轴上,且,故焦点坐标为由双曲线的定义可得,故,,故所求双曲线的标准方程为因此,本题正确答案是:规律方法待定系数法求双曲线方程具体过程是先定形,再定量,即先确定双曲线标准方程的形式,然后再根据a,b,c,e及渐近线之间的关系,求出a,b的值.如果已知双曲线的渐近线方程,求双曲线的标准方程,可设有公共渐近线的双曲线方程为x2a2-y2b2=λ(λ≠0),再由条件求出λ的值即可.练习2:根据下列条件,求双曲线的标准方程:(1)虚轴长为12,离心率为54;(2)焦距为26,且经过点M(0,12);(3)经过两点P(-3,27)和Q(-62,-7).【答案】(1)设双曲线的标准方程为-=1或-=1(a>0,b>0).由题意知,2b=12,e==.∴b=6,c=10,a=8.∴双曲线的标准方程为-=1或-=1. (2)∵双曲线经过点M(0,12),∴M(0,12)为双曲线的一个顶点,故焦点在y轴上,且a=12.又2c=26,∴c=13.∴b2=c2-a2=25.∴双曲线的标准方程为-=1.(3)设双曲线方程为mx2-ny2=1(mn>0).∴∴双曲线的标准方程为-=1.类型三双曲线的几何性质例3:(1)设F1,F2分别为双曲线的左、右焦点.若在双曲线右支上存在点P,满足|PF2|=|F1F2|,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )A.3x±4y=0 B.3x±5y=0 C.4x±3y =0 D.5x+4y=0【解析】等腰三角形中,到的距离为2a化简得所以渐近线方程【答案】C练习1:(2014·浙江卷)设直线x-3y+m=0(m≠0)与双曲线x2a2-y2b2=1(a>0,b>0)的两条渐近线分别交于点A,B.若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是________.【答案】:5 2练习2:设a>1,则双曲线22221(1)x ya a的离心率e的取值范围是( )A.(2,2) B.(2,5) C.(2,5) D.(2,5)【解析】e=ca=1+a+1a2=1+1+1a2.∵a>1,∴0<1a<1,∴1<1+1a<2,∴2<e<5,故选 B.【答案】B类型四直线与双曲线的位置关系例4:已知中心在原点的双曲线C的右焦点为(2,0),实轴长为2 3.(1)求双曲线C的方程;(2)若直线l:y=kx+2与双曲线C左支交于A,B两点,求k的取值范围.【解析】(1),,,C的方程为由与消去y,得,方程有解,判别式大于0,两根之和小于0,解得,【答案】(1),,,C的方程为(2)由与消去y,得,方程有解,判别式大于0,两根之和小于0,解得,研究直线与双曲线位置关系的通法:将直线代入双曲线的方程,消元,得到关于x或y的一元二次方程.当二次项系数等于0时,直线与双曲线相交于某支上一点,这时直线平行于一条渐近线;当二次项系数不等于0时,用判别式Δ来判定.(2)近几年高考对直线与双曲线的考查降低了要求,一般与双曲线的几何性质结合考查.练习1:(2014·湖北卷)设a,b是关于t的方程t2cosθ+tsinθ=0的两个不等实根,则过A(a,a2),B(b,b2)两点的直线与双曲线x2cos2 θ-y2sin2 θ=1的公共点的个数为( )A .0B .1C .2D .3 【答案】A练习2:【2015江苏高考,12】在平面直角坐标系中,为双曲线右支上的一个动点。