准滑动模态控制matlab仿真实例.
- 格式:doc
- 大小:182.00 KB
- 文档页数:12


自动控制原理MATLAB仿真实验(于海春)实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入imulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个imulink仿真环境常规模板。
图1-1SIMULINK仿真界面图1-2系统方框图3.在imulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击imulink下的“Continuou”,再将右边窗口中“TranferFen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在imulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的imulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击imulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。



matlab的simulink仿真建模举例Matlab的Simulink仿真建模举例Simulink是Matlab的一个工具包,用于建模、仿真和分析动态系统。
它提供了一个可视化的环境,允许用户通过拖放模块来构建系统模型,并通过连接和配置这些模块来定义模型的行为。
Simulink是一种功能强大的仿真平台,可以用于解决各种不同类型的问题,从控制系统设计到数字信号处理,甚至是嵌入式系统开发。
在本文中,我们将通过一个简单的例子来介绍Simulink的基本概念和工作流程。
我们将使用Simulink来建立一个简单的电机速度控制系统,并进行仿真和分析。
第一步:打开Simulink首先,我们需要打开Matlab并进入Simulink工作环境。
在Matlab命令窗口中输入"simulink",将会打开Simulink的拓扑编辑器界面。
第二步:创建模型在拓扑编辑器界面的左侧,你可以看到各种不同类型的模块。
我们将使用这些模块来构建我们的电机速度控制系统。
首先,我们添加一个连续模块,代表电机本身。
在模块库中选择Continuous中的Transfer Fcn,拖动到编辑器界面中。
接下来,我们添加一个用于控制电机速度的控制器模块。
在模块库中选择Discrete中的Transfer Fcn,拖动到编辑器界面中。
然后,我们需要添加一个用于输入参考速度的信号源模块。
在模块库中选择Sources中的Step,拖动到编辑器界面中。
最后,我们添加一个用于显示模拟结果的作用模块。
在模块库中选择Sinks 中的To Workspace,拖动到编辑器界面中。
第三步:连接模块现在,我们需要将这些模块连接起来以定义模型的行为。
首先,将Step模块的输出端口与Transfer Fcn模块的输入端口相连。
然后,将Transfer Fcn模块的输出端口与Transfer Fcn模块的输入端口相连。
接下来,将Transfer Fcn模块的输出端口与To Workspace模块的输入端口相连。

实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB 中SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK 功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB 软件,在命令窗口栏“>>”提示符下键入simulink 命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK 仿真环境下。
2.选择File 菜单下New 下的Model 命令,新建一个simulink 仿真环境常规模板。
3.在simulink 仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:图1-1 SIMULINK 仿真界面 图1-2 系统方框图1)进入线性系统模块库,构建传递函数。
点击simulink 下的“Continuous ”,再将右边窗口中“Transfer Fen ”的图标用左键拖至新建的“untitled ”窗口。
2)改变模块参数。
在simulink 仿真环境“untitled ”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK ,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math ”右边窗口“Gain ”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink 下的“Source ”,将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口,形成一个阶跃函数输入模块。
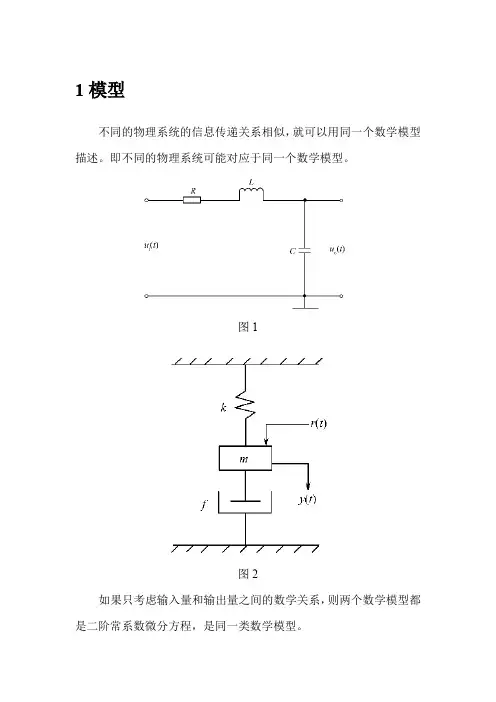

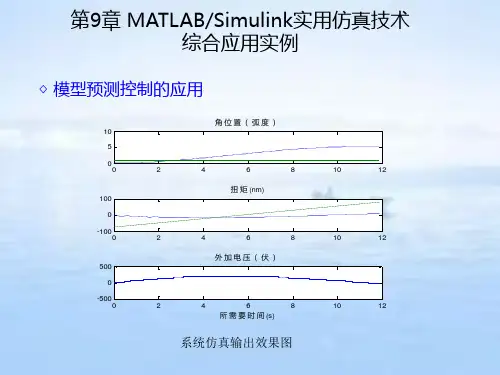


基于MATLABSimulink的控制系统建模与仿真实践控制系统是现代工程领域中一个至关重要的研究方向,它涉及到对系统的建模、分析和设计,以实现对系统行为的控制和调节。
MATLAB Simulink作为一款强大的工程仿真软件,在控制系统领域有着广泛的应用。
本文将介绍基于MATLAB Simulink的控制系统建模与仿真实践,包括建立系统模型、进行仿真分析以及设计控制算法等内容。
1. 控制系统建模在进行控制系统设计之前,首先需要建立系统的数学模型。
MATLAB Simulink提供了丰富的建模工具,可以方便快捷地搭建系统模型。
在建模过程中,可以利用各种传感器、执行器、控制器等组件来描述系统的结构和功能。
通过连接这些组件,并设置其参数和初始条件,可以构建出一个完整的系统模型。
2. 系统仿真分析建立好系统模型后,接下来就是进行仿真分析。
MATLABSimulink提供了强大的仿真功能,可以对系统进行各种不同条件下的仿真实验。
通过改变输入信号、调节参数值等操作,可以观察系统在不同工况下的响应情况,从而深入理解系统的动态特性和性能指标。
3. 控制算法设计在对系统进行仿真分析的基础上,可以针对系统的性能要求设计相应的控制算法。
MATLAB Simulink支持各种常见的控制算法设计方法,如PID控制、状态空间法、频域设计等。
通过在Simulink中搭建控制算法,并与系统模型进行联合仿真,可以验证算法的有效性和稳定性。
4. 系统优化与调试除了基本的控制算法设计外,MATLAB Simulink还提供了优化工具和调试功能,帮助工程师进一步改进系统性能。
通过优化算法对系统参数进行调整,可以使系统响应更加迅速、稳定;而通过调试功能可以检测和排除系统中可能存在的问题,确保系统正常运行。
5. 实例演示为了更好地说明基于MATLAB Simulink的控制系统建模与仿真实践,接下来将通过一个简单的倒立摆控制系统实例进行演示。
准滑动模态控制 2.8.1准滑动模态控制 在滑动模态控制系统中,如果控制结构的切换具有理想的开关特性,则能在切换面上形成理想的滑动模态,这是一种光滑的运动,渐进趋近于原点。但在实际工程中,由于存在时间上的延迟和空间上的滞后等原因,使得滑动模态呈抖振形式,在光滑的滑动上叠加了抖振。理想的滑动模态是不存在的,现实中的滑动模态控制均伴随有抖振,抖振问题是影响滑动模态看控制广泛应用的主要障碍。 所谓准滑动模态,是指系统的运动轨迹被限制在理想滑动模态的某一领域内的模态。从相轨迹方面来说,具有理想滑动模态的控制是使一定范围内的状态点均被吸引至切换面。而准滑动模态控制则是使一定范围内的状态点均被吸引至切换面的某一领域内,通常称此领域为滑动模态切换面的边界层。 在边界层内,准滑动模态不要求满足滑动模态的存在条件,因此准滑动模态不要求在切换面上进行控制结构的切换。它可以在边界层上进行结构变换的控制系统,也可以根本不进行结构变换的连续状态反馈控制系统。准滑动模态控制在实现上的这种差别,使它从根本上避免或削弱了抖振,从而在实际中得到了广泛的应用。 在连续系统中,常用的准滑动模态控制有以下两种方法: (1) 用饱和函数()sats代替理想滑动模态中的符号函数sgn()s。 1()1ssatsksss
1k
(2.46)
其中称为“边界层”。饱和函数()sats如图2-26所示,饱和函数的本质为:在边界层外,采用切换控制;在边界之内,采用线性化反馈控制。 (2) 将继电特性连续化,用连续函数()s取代sgn()s。
()sss (2.47)
式中是很小的正常数。 2.8.2 仿真实例 对象为二阶传递函数: 2()pbGssas
其中25,133ab。 将传递函数描述为位置状态方程的形式: .xxu
其中010a, 0b。 设位置指令信号为r,则 ......[(1)](2)[(1)](2)scrxdrxscrxrxslaw
采用指数趋近律: sgn()slawsks
将(2)(2)xaxbu代入上式,得控制律为 ...1
[((2))(2)]ucrxrslawaxb
系统的初始状态为0.50。在仿真程序中,指令为正弦信号。1M
为指数趋近律,2M为采用饱和函数的指数趋近律,3M为采用继电特性的指数趋近律。取51C,15,30k,进行如下几种仿真: (1)采用指数趋近律。取1M,正弦跟踪结果如图所示。 00.511.522.533.544.55-0.8-0.6-0.4-0.200.20.40.6time(s)r,yout
正弦跟踪(M=1)
00.511.522.533.544.55-0.100.10.20.30.40.50.6
time(s)error
误差曲线(M=1) -0.100.10.20.30.40.50.6-3-2-101234ede
相轨迹(M=1)
00.511.522.533.544.55-10123456
time(s)s
切换函数s(M=1) 00.511.522.533.544.55-0.4-0.200.20.40.60.811.21.41.6time(s)u
控制器输出(M=1) (2)验证准滑动模态控制。2M为采用饱和函数的方法,取5.0,仿真结果如图所示。
00.511.522.533.544.55-0.8-0.6-0.4-0.200.20.40.6
time(s)r,yout
正弦信号跟踪(M=2) 00.511.522.533.544.55-0.100.10.20.30.40.50.6time(s)error
误差曲线(M=2)
-0.100.10.20.30.40.50.6-3-2-101234
ede
相轨迹(M=2) 00.511.522.533.544.55-10123456time(s)s
切换函数s(M=2)
00.511.522.533.544.55-1-0.500.511.52
time(s)u
控制器输出(M=2) (3)3M为采用继电特性的方法,取0.05,仿真结果如图所示 00.511.522.533.544.55-0.8-0.6-0.4-0.200.20.40.6time(s)r,yout
正弦信号跟踪(M=3)
00.511.522.533.544.55-0.100.10.20.30.40.50.6
time(s)error
误差曲线(M=3) -0.100.10.20.30.40.50.6-3-2-101234ede
相轨迹(M=3)
00.511.522.533.544.55-10123456
time(s)s
切换函数s(M=3) 00.511.522.533.544.55-1-0.500.511.52time(s)u
控制器输出(M=3) 仿真程序如下:
(1) 主程序:figure2_8.m clear all; close all; global a b c A F M ep k delta ts=0.001; T=5; TimeSet=[0:ts:T]; c=5.0; para=[]; [t,x]=ode45('figure2_8eq',TimeSet,[-0.5 0],[],para); x1=x(:,1); x2=x(:,2); r=A*sin(2*pi*F*t); dr=A*2*pi*F*cos(2*pi*F*t); ddr=-A*(2*pi*F)^2*sin(2*pi*F*t); s=c*(r-x(:,1))+dr-x(:,2); if M==1 slaw=-ep*sign(s)-k*s; %Exponential velocity trending law u=1/b*(c*(dr-x(2))+ddr-slaw+a*x(2)); elseif M==2 kk=1/delta; for i=1:1:T/ts+1; if s(i)>delta sats(i)=1; elseif abs(s(i))<=delta sats(i)=kk*s(i); elseif s(i)<-delta sats(i)=-1; end slaw(i)=-ep*sats(i)-k*s(i); u(i)=1/b*(c*(dr(i)-x2(i))+ddr(i)-slaw(i)+a*x2(i)); end elseif M==3 for i=1:1:T/ts+1; ths(i)=s(i)/(abs(s(i))+delta); slaw(i)=-ep*ths(i)-k*s(i); u(i)=1/b*(c*(dr(i)-x2(i))+ddr(i)-slaw(i)+a*x2(i)); end end
figure(1); plot(t,r,'r',t,x(:,1),'b'); xlabel('time(s)'); ylabel('r,yout'); figure(2); plot(t,r-x(:,1),'r'); xlabel('time(s)'); ylabel('error'); figure(3); plot(r-x(:,1),dr-x(:,2),'r',r-x(:,1),-c*(r-x(:,1)),'b'); %draw line (s=0) xlabel('e'); ylabel('de'); figure(4); plot(t,s,'r'); xlabel('time(s)'); ylabel('s'); figure(5); plot(t,u,'r'); xlabel('time(s)'); ylabel('u'); (2)控制子程序:figure2_8eq.m
function dx=DynamicModel(t,x,flag,para) global a b c A F M ep k delta
a=25;b=133; A=0.50;F=1.0;