arcgis半变异函数

半变异函数(第一部分)
半变异函数是概率论中一种重要的概率分布。

它属于正态分布的一种变形，属于一类非对称性的分布。

半变异函数的形式是：y = (2/σ√2π) (1+x2/σ2) -1/2 α，其中σ代表标准差，α 代表偏度参数。

4个参数的半变异函数关系性更加紧密，根据参数的不同，它的几何形状形可能会发生改变，这也是其它变异函数的不同之处。

半变异函数有若干重要的特点。

其中，分布的峰值与基线均出现在分布的中心位置，与正态分布在两端出现最大值不同。

并且，它还具有较宽的左右两侧分布，使得半变异性分布在极端情况下也更具有延展性。

此外，半变异函数可用来选择特定的观测值，可应用于差异分析，还能够表征观测值的非线性特征，从而能够更准确地反映数据中存在的模式。

半变异函数经过长期发展，已经成为统计分析中重要的工具，它不仅可以应用于波动分析、风险分析，同时还可以作为进行统计计算和模型构建的重要基础。

通过灵活运用半变异函数，研究人员以及经济相关的决策者可以从不同的层面深入研究问题的解决方案，为社会发展注入新的动力，推动社会经济的发展。

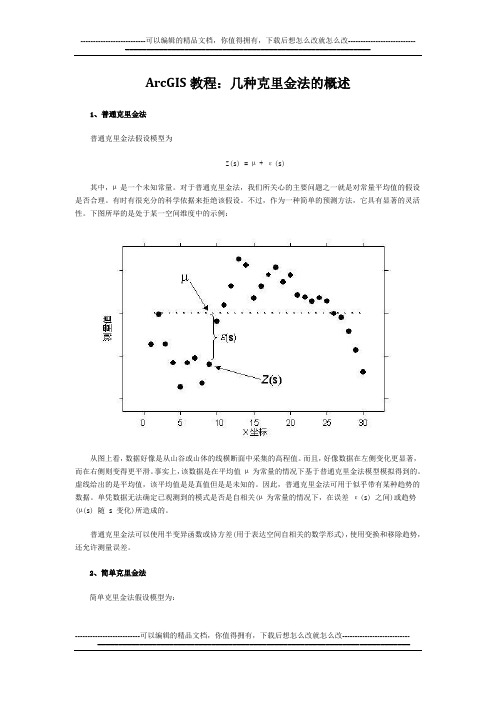
ArcGIS教程：几种克里金法的概述1、普通克里金法普通克里金法假设模型为Z(s) = µ + ε(s)其中，µ 是一个未知常量。

对于普通克里金法，我们所关心的主要问题之一就是对常量平均值的假设是否合理。

有时有很充分的科学依据来拒绝该假设。

不过，作为一种简单的预测方法，它具有显著的灵活性。

下图所举的是处于某一空间维度中的示例：从图上看，数据好像是从山谷或山体的线横断面中采集的高程值。

而且，好像数据在左侧变化更显著，而在右侧则变得更平滑。

事实上，该数据是在平均值µ 为常量的情况下基于普通克里金法模型模拟得到的。

虚线给出的是平均值，该平均值是是真值但是是未知的。

因此，普通克里金法可用于似乎带有某种趋势的数据。

单凭数据无法确定已观测到的模式是否是自相关(µ 为常量的情况下，在误差ε(s) 之间)或趋势(µ(s) 随 s 变化)所造成的。

普通克里金法可以使用半变异函数或协方差(用于表达空间自相关的数学形式)，使用变换和移除趋势，还允许测量误差。

2、简单克里金法简单克里金法假设模型为：Z(s) = µ + ε(s)其中，µ 是已知常量例如，下图中使用的数据与普通克里金法和泛克里金法概念介绍中所使用的数据相同，观测数据以实心圆的形式给出：虚线表示的已知常量为µ。

这点可以与普通克里金法进行比较。

对于简单克里金法，因为假设确切已知µ，那么也确切已知数据位置上的ε(s)。

对于普通克里金法，如果估算了µ，那么也会估算ε(s)。

如果已知ε(s)，可以比估算ε(s)时更好地估算自相关。

通常，已知确切平均值µ 的假设是不现实的。

但是，有时候，假定一个基于物理的模型能够给出已知趋势却是有意义的。

由此可以使用模型和观测值的差值(称为残差)，并且假设残差中的趋势已知为零，可以在残差上使用简单克里金法。

简单克里金法可以使用半变异函数或协方差(用于表达自相关的数学形式)和变换，并且允许测量误差。

ArcGIS地统计分析模块提供三个功能模块，探索性数据分析、地统计分析向导、以及生成数据子集。

利用这些基本功能模块，可以方便的完成多种地统计分析，创建完善的专题地图，其中探索性数据分析模块能帮助我们确定统计数据属性，探测数据分布、全局和局部异常值(过大值或过小值)、寻求全局的变化趋势。

1、首先了解一下直方图，直方图指对采样数据按一定的分级方案(等间隔分级、标准差分，等等)进行分级，统计采样点落入各个级别中的个数或占总采样数的百分比，并通过条带图或柱状图表现出来。

直方图可以直观的反映采样数据分布特征、总体规律，可以用来检验数据分布和寻找数据离群值。

该地区GDP数据分布具有明显的对数分布，符合正态分布的特征。

但在最右侧有一个明显的值段内没有数据。

2、普通QQPlot(General QQPlot)分布图用来评估两个数据集的分布的相似性。

普通QQPlot图揭示了两个物体(变量)之间的相关关系，如果在QQPlot图中曲线呈直线，说明两物体呈一种线性关系，可以用一个一元一次方程式来拟合。

如果QQPlot图中曲线呈抛物线，说明两物体的关系可以用一个二元多项式来拟合。

3、半变异函数云表示的是数据集中所有样点对的理论半变异值和协方差，并把它们用两点间距离的函数来表示，用此函数作图来表示。

半变异函数是事物空间相关系数的表现，当两事物彼此距离较小时，它们是相似的，半变异值较小;反之，半变异值较大。

图中横坐标为样点对之间的距离，纵坐标表示半变异的函数值，图中所示的曲线为理想状态下半变异函数曲线图，而往往数据的函数图不能呈现如此状态，通过图中异常样对点，我们可以对数据的异常点进行判断在地统计分析中，生成数据曲面的插值方法是建立在平稳假设的基础上，这种假设在一定程度上要求所有数据值具有相同的变异性。

另外，一些插值法(比如说：克里格插值)都假设数据服从正态分布。

如果数据不服从正态分布，需要进行一定的数据变换，从而使其服从正态分布。

arcgis克里金插值无法估算半变异函数以arcgis克里金插值无法估算半变异函数为标题克里金插值是一种常用的地理信息系统（GIS）插值方法，可用于估算未知位置的数值。

然而，克里金插值在一些情况下可能无法有效估算半变异函数，这是因为半变异函数的特性与克里金插值的假设之间存在不匹配。

半变异函数是地统计学中常用的工具，用于描述变量值在空间上的变化程度。

它可以通过计算不同距离下的半方差来确定。

半方差表示两个位置之间的变量值差异程度，距离越大，半方差值越大，说明变量值的差异越大。

半变异函数的形状和参数可以提供有关空间变量结构的重要信息，从而可以用于空间数据的插值和预测。

然而，克里金插值方法在估算半变异函数时存在一些限制。

首先，克里金插值假设数据是平稳的，即在空间上具有相似的统计特性。

然而，实际数据往往呈现出空间非平稳性，即在不同位置上具有不同的统计特性。

这导致克里金插值无法准确地估算半变异函数的形状和参数。

克里金插值假设数据的半变异函数是稳定的，即在不同距离下具有相似的半方差值。

然而，实际数据往往呈现出非稳定性，即半方差值在不同距离下发生明显变化。

这使得克里金插值无法准确地估算半变异函数的参数，从而影响插值结果的可靠性。

克里金插值还假设数据的半变异函数是光滑的，即在不同距离下具有连续的半方差值。

然而，实际数据往往呈现出非光滑性，即半方差值在不同距离下出现跳跃或断裂。

这使得克里金插值无法准确地估算半变异函数的形状，从而导致插值结果的不准确性。

为了解决克里金插值无法估算半变异函数的问题，可以尝试使用其他插值方法或改进的克里金插值方法。

例如，可以尝试使用反距离加权插值（IDW）方法，该方法在估算插值值时不需要假设数据的平稳性、稳定性和光滑性。

另外，也可以尝试使用基于样条函数的插值方法，该方法可以更好地拟合非光滑的半变异函数。

克里金插值在估算半变异函数时存在一些限制，特别是在数据呈现空间非平稳性、非稳定性和非光滑性的情况下。

arcgis半变异函数ArcGIS半变异函数在地理信息系统（GIS）中，半变异函数是一种用于描述地理现象空间变异性的统计方法。

ArcGIS作为一款常用的GIS软件，提供了多种半变异函数的计算方法和工具，帮助用户分析地理数据的空间变异性，进而支持决策和规划过程。

本文将介绍ArcGIS中的半变异函数的基本概念、计算方法以及应用案例。

一、半变异函数的基本概念半变异函数是描述地理现象空间变异性的数学函数，用于研究地理现象在空间上的相似性和差异性。

半变异函数包括两个主要参数：距离和方向。

距离参数表示观测点之间的空间间隔，方向参数表示观测点之间的方向关系。

通过计算不同距离和方向下的变异性，可以得到半变异函数的数学模型。

二、ArcGIS中的半变异函数计算方法ArcGIS提供了多种半变异函数的计算方法，包括简单半变异函数、指数半变异函数、高斯半变异函数等。

用户可以根据具体需求选择适合的计算方法。

1. 简单半变异函数简单半变异函数是最基本的半变异函数模型，它假设地理现象的空间变异性在不同距离上呈现简单的线性关系。

ArcGIS中提供了简单半变异函数的计算工具，用户可以根据实际数据进行参数设置和计算。

2. 指数半变异函数指数半变异函数假设地理现象的空间变异性在不同距离上呈现指数关系。

在ArcGIS中，用户可以使用指数半变异函数工具进行计算，通过调整参数来拟合实际数据。

3. 高斯半变异函数高斯半变异函数假设地理现象的空间变异性在不同距离上呈现高斯分布。

ArcGIS中的高斯半变异函数工具可以帮助用户计算高斯半变异函数，并根据实际数据进行参数调整。

三、半变异函数的应用案例半变异函数在GIS中有广泛的应用，具体包括以下几个方面：1. 空间插值半变异函数可以用于空间插值，通过已知观测点的数值和位置信息，推断未知位置上的数值。

通过计算半变异函数，可以确定最佳插值方法和参数，提高插值结果的准确性。

2. 空间分析半变异函数可以用于空间分析，通过计算不同距离和方向下的变异性，揭示地理现象的空间分布规律。

半变异函数的求解克里金差值首先需要求取半变异函数，它是矢量距离h的函数，但这个问题似乎一直是大家纠结的问题，我也很纠结。

实际工作中，采样点位并未位于正规网格节点上，甚至较为离散，所以在计算半变异函数值时，要考虑角度容差和距离容差；也就是说，在理论上，x+h数据是足够的，但实际上，x+h 数据极少，因此必须考虑容差。

在矢量h的角度容差和距离容差范围内，都可以看做是x+h，这样才能计算半变异函数值。

在半变异函数的求解中，最方便又常用的软件就是GS+和Surfer（不要提ArgGIS），两者区别在哪？个人认为主要在以下三个方面：（1）容差。

我们知道，在看各向异性时，一般都是以0度（即x轴正向）为始，45度为间隔，看8个方向上的各向异性。

在GS+中，默认角度容差为22.5度，这个数字化刚刚好（这个容易理解），而Surfer中默认为90度，那也就是说surfer中考虑各向异性仅仅考虑x轴正向和x轴负向两个方向，当然这个似乎可以改变。

（2）距离选择。

GS+中有两个距离，一个是最大滞后距离，一个是计算间隔，其中计算间隔才是决定半变异函数模型的主要参数；surfer中只有一个，是最大滞后距离。

最大滞后距离（是否也就是搜索半径呢？我个人认为是），GS+选择的是x、y轴两者最大距离的1/2，surfer选择的是对角线距离最大值的1/3。

但这个数值我个人认为影响不大（只要不是太离谱），它影响的仅仅是点对数的多少（因为在实际工作中，各自距离的1/2和1/3都应该超出了样品的相关性范围）。

不过对于搜索半径，我也看到一些资料说选择采样间隔的2.5倍到3倍。

（3）各向异性的整体考虑。

GS+中，在半变异函数计算中并未整体考虑各向异性（我个人认为，不知道是否对），而surfer考虑了，但是surfer中的自动拟合参数似乎有些问题；而且，模型得自己选择并进行比较得出最优结果，而GS+默认选择的已经是最优的。

不知道上述观点大家是否同意？大家一起讨论讨论。

ArcGIS 中几种空间插值方法1. 反距离加权法(IDW)ArcGIS 中最常用的空间内插方法之一，反距离加权法是以插值点与样本点之间的距离为权重的插值方法，插值点越近的样本点赋予的权重越大，其权重贡献与距离成反比。

可表示为：1111()()n nip p i i i i Z Z D D ===∑∑其中Z 是插值点估计值，Z i (i=1Λn)是实测样本值，n 为参与计算的实测样本数，D i 为插值点与第i 个站点间的距离，p 是距离的幂，它显著影响内插的结果，它的选择标准是最小平均绝对误差。

2.多项式法多项式内插法(Polynomial Interpolation)是根据全部或局部已知值，按研究区域预测数据的某种特定趋势来进行内插的方法,属统计方法的范畴。

在GA 模块中，有二种类型的多项式内插方法，即全局多项式内插和局部多项式内插。

前者多用于分析数据的全局趋势；后者则是使用多个平面来拟合整个研究区域，能表现出区域内局部变异的情况。

3.样条函数内插法样条函数是一个分段函数，进行一次拟合只有少数点拟合，同时保证曲线段连接处连续，这就意味着样条函数可以修改少数数据点配准而不必重新计算整条曲线。

样条函数的一些缺点是：样条内插的误差不能直接估算，同时在实践中要解决的问题是样条块的定义以及如何在三维空间中将这些“块”拼成复杂曲面,又不引入原始曲面中所没有的异常现象等问题。

4.克里格插值法克里格法是GIS 软件地理统计插值的重要组成部分。

这种方法充分吸收了地理统计的思想，认为任何在空间连续性变化的属性是非常不规则的，不能用简单的平滑数学函数进行模拟，可以用随机表面给予较恰当的描述。

这种连续性变化的空间属性称为“区域性变量”，可以描述象气压、高程及其它连续性变化的描述指标变量。

地理统计方法为空间插值提供了一种优化策略，即在插值过程中根据某种优化准则函数动态的决定变量的数值。

Kriging 插值方法着重于权重系数的确定，从而使内插函数处于最佳状态，即对给定点上的变量值提供最好的线性无偏估计。

ArcGIS教程：几种克里金法的概述1、普通克里金法普通克里金法假设模型为Z(s) = µ + ε(s)其中，µ 是一个未知常量。

对于普通克里金法，我们所关心的主要问题之一就是对常量平均值的假设是否合理。

有时有很充分的科学依据来拒绝该假设。

不过，作为一种简单的预测方法，它具有显著的灵活性。

下图所举的是处于某一空间维度中的示例：从图上看，数据好像是从山谷或山体的线横断面中采集的高程值。

而且，好像数据在左侧变化更显著，而在右侧则变得更平滑。

事实上，该数据是在平均值µ 为常量的情况下基于普通克里金法模型模拟得到的。

虚线给出的是平均值，该平均值是是真值但是是未知的。

因此，普通克里金法可用于似乎带有某种趋势的数据。

单凭数据无法确定已观测到的模式是否是自相关(µ 为常量的情况下，在误差ε(s) 之间)或趋势(µ(s) 随 s 变化)所造成的。

普通克里金法可以使用半变异函数或协方差(用于表达空间自相关的数学形式)，使用变换和移除趋势，还允许测量误差。

2、简单克里金法简单克里金法假设模型为：Z(s) = µ + ε(s)其中，µ 是已知常量例如，下图中使用的数据与普通克里金法和泛克里金法概念介绍中所使用的数据相同，观测数据以实心圆的形式给出：虚线表示的已知常量为µ。

这点可以与普通克里金法进行比较。

对于简单克里金法，因为假设确切已知µ，那么也确切已知数据位置上的ε(s)。

对于普通克里金法，如果估算了µ，那么也会估算ε(s)。

如果已知ε(s)，可以比估算ε(s)时更好地估算自相关。

通常，已知确切平均值µ 的假设是不现实的。

但是，有时候，假定一个基于物理的模型能够给出已知趋势却是有意义的。

由此可以使用模型和观测值的差值(称为残差)，并且假设残差中的趋势已知为零，可以在残差上使用简单克里金法。

简单克里金法可以使用半变异函数或协方差(用于表达自相关的数学形式)和变换，并且允许测量误差。

克里格方法的半变异函数The semivariogram in the Kriging method is a fundamental tool for spatial interpolation and analysis. It quantifies the spatial variability of a variable by measuring the degree of similarity or dissimilarity between values at different locations. The semivariogram represents the variance of the differences between values at various distances, providing insights into the spatial structure and autocorrelation of the data.克里格方法中的半变异函数是空间插值和分析的基本工具。

它通过测量不同位置之间值的相似性或差异性来量化变量的空间变异性。

半变异函数表示在不同距离上值之间差异的方差，为数据的空间结构和自相关性提供了深刻见解。

The semivariogram is typically plotted as a function of distance, with the x-axis representing the separation distance between data points and the y-axis representing the semivariance. This plot helps identify the range, sill, and nugget effect, which are key parameters in Kriging interpolation. The range indicates the distance at which values become spatially independent, the sill represents the maximum semivariance or total spatial variability, and the nugget effect accounts for the variability that cannot be explained by spatial autocorrelation.半变异函数通常作为距离的函数进行绘制，其中x轴表示数据点之间的分离距离，y轴表示半变异值。