2009年兰州大学数学分析考研试题

2009考研数学一真题及答案一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则（ ）()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=. 【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小，则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。

另外201cos lim3x a axbx →--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除D 。

所以本题选A 。

（2）如图，正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14max k k I ≤≤=（ ）()A 1I .()B 2I . ()C 3I .(D 【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰； x{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为A.（3）设函数()y f x =在区间[]1,3-上的图形为：则函数(F()A .()B .()C .()D .【答案】D【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：①[]0,1x ∈时，()0F x ≤，且单调递减。

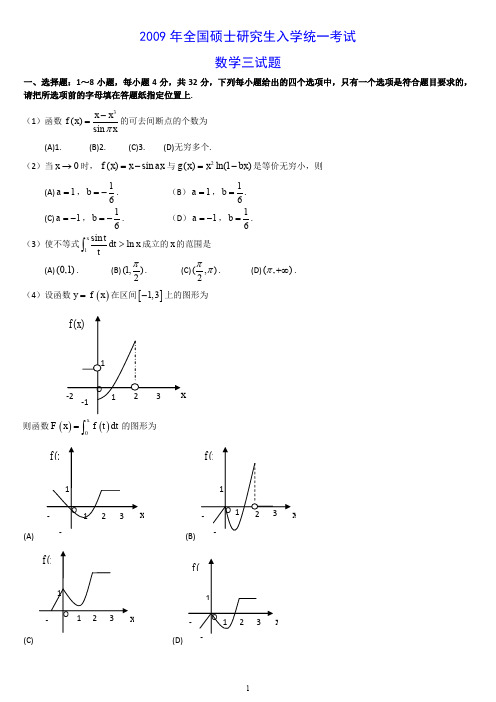
2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为(A)1.(B)2. (C)3.(D)无穷多个.（2）当时，与是等价无穷小，则(A)，. （B ），. (C)，. （D ），.（3）使不等式成立的的范围是(A).(B). (C).(D).（4）设函数在区间上的图形为则函数的图形为(A)(B)(C)(D)3()sin x x f x xπ-=0x →()sin f x x ax =-2()ln(1)g x x bx =-1a =16b =-1a =16b =1a =-16b =-1a =-16b =1sin ln x tdt x t>⎰x(0,1)(1,)2π(,)2ππ(,)π+∞()y f x =[]1,3-()()0xF x f t dt =⎰xxxx（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩阵的伴随矩阵为 (A). (B). (C).(D). （6）设均为3阶矩阵，为的转置矩阵，且，若，则为(A).(B).(C).(D).（7）设事件与事件B 互不相容，则(A).(B).(C).(D).（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为，记为随机变量的分布函数，则函数的间断点个数为 (A) 0.(B)1.(C)2 .(D)3.二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9） .（10）设，则. （11）幂级数的收敛半径为 . （12）设某产品的需求函数为,其对应价格的弹性，则当需求量为10000件时，价格增加1元会使产品收益增加 元.（13）设,，若矩阵相似于，则 .(14)设，,…,为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，则 .三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分）,A B *,A B *,A B ||2,||3A B ==O A B O ⎛⎫⎪⎝⎭**32OB A O ⎛⎫⎪⎝⎭**23O B A O ⎛⎫⎪⎝⎭**32O A B O ⎛⎫⎪⎝⎭**23O A B O ⎛⎫⎪⎝⎭,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭1231223(,,),(,,)P Q ααααααα==+T Q AQ 210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪⎪ ⎪⎝⎭200010002⎛⎫⎪ ⎪ ⎪⎝⎭100020002⎛⎫⎪ ⎪ ⎪⎝⎭A ()0P AB =()()()P AB P A P B =()1()P A P B =-()1P A B ⋃=X Y X (0,1)N Y 1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z cos 0x x →=()y x z x e =+(1,0)zx ∂=∂21(1)n n nn e x n ∞=--∑()Q Q P =P 0.2p ξ=(1,1,1)T α=(1,0,)T k β=T αβ300000000⎛⎫⎪⎪ ⎪⎝⎭k =1X 2X n X (,)B n p X 2S 2T X S =-ET =求二元函数的极值.（16）（本题满分10 分） 计算不定积分 . （17）（本题满分10 分） 计算二重积分，其中. （18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则，得证.（Ⅱ）证明：若函数在处连续，在内可导，且，则存在，且. （19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯形面积值的倍，求该曲线的方程. （20）（本题满分11 分）设,. （Ⅰ）求满足，的所有向量，. （Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关. （21）（本题满分11 分）设二次型. （Ⅰ）求二次型的矩阵的所有特征值.（Ⅱ）若二次型的规范形为，求的值. （22）（本题满分11 分）设二维随机变量的概率密度为（Ⅰ）求条件概率密度； （Ⅱ）求条件概率.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、、分别表示两次取球所取得的红、黑与白球的个数. （Ⅰ）求；（Ⅱ）求二维随机变量的概率分布.()22(,)2ln f x y xy y y =++ln(1dx +⎰(0)x >()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥()f x [],a b (),a b (),a b ξ∈()'()()()f b f a f b a ξ-=-()f x 0x =()0,,(0)σσ>'lim ()x f x A +→='(0)f +'(0)f A +=()y f x =()f x ()0f x >()y f x =0,1y x ==(1)x t t =>x t π111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭21A ξξ=231A ξξ=2ξ3ξ2ξ3ξ1ξ2ξ3ξ2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-f f 2211y y +a (,)X Y 0(,)0xe y xf x y -⎧<<=⎨⎩其他()Y X f y x 11P X Y =⎡≤≤⎤⎣⎦X Y Z 10P X Z ⎡==⎤⎣⎦(,)X Y2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为(A)1. (B)2. (C)3. (D)无穷多个.【答案】C. 【解析】则当取任何整数时，均无意义故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解故可去间断点为3个，即（2）当时，与是等价无穷小，则(A)，. （B ），. (C)，. （D ），.【答案】A.【解析】为等价无穷小，则故排除(B)、(C).另外存在，蕴含了故排除(D).所以本题选(A). （3）使不等式成立的的范围是 (A).(B). (C).(D).3()sin x x f x xπ-=()3sin x x f x xπ-=x ()f x ()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==0,1±0x →()sin f x x ax =-2()ln(1)g x x bx =-1a =16b =-1a =16b =1a =-16b =-1a =-16b =2()sin ,()(1)f x x ax g x x ln bx =-=-222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-201cos lim 3x a axbx →--1cos 0a ax -→()0x → 1.a =1sin ln xtdt x t>⎰x (0,1)(1,)2π(,)2ππ(,)π+∞【答案】A.【解析】原问题可转化为求成立时的取值范围，由，时，知当时，.故应选(A).（4）设函数在区间上的图形为则函数的图形为(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由的图形可见，其图像与轴及轴、所围的图形的代数面积为所求函数，从而可得出几个方面的特征： ①时，，且单调递减. ②时，单调递增. ③时，为常函数.111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 1sin 0t t ->()0,1t ∈()0,1x ∈()0f x >()y f x =[]1,3-()()0xF x f t dt =⎰()y f x =xy 0x x =()F x []0,1x ∈()0F x ≤[]1,2x∈()F x []2,3x ∈()F x④时，为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩阵的伴随矩阵为 (A). (B).(C).(D). 【答案】B.【解析】根据，若 分块矩阵的行列式，即分块矩阵可逆 故答案为(B).（6）设均为3阶矩阵，为的转置矩阵，且，若，则为(A).(B).(C).(D).【答案】A.[]1,0x ∈-()0F x ≤,A B *,A B *,A B ||2,||3A B ==O A B O ⎛⎫⎪⎝⎭**32OB A O ⎛⎫⎪⎝⎭**23O B AO ⎛⎫⎪⎝⎭**32O A BO ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭CC C E *=111,C C C C C C*--*==O A B O ⎛⎫⎪⎝⎭221236O A A B B O ⨯=-=⨯=（）1111661O B BO A O A O A O B B O B O B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O B O B A O A O ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭1231223(,,),(,,)P Q ααααααα==+T Q AQ 210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪⎪ ⎪⎝⎭200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【解析】，即：（7）设事件与事件B 互不相容，则(A).(B).(C).(D).【答案】D.【解析】因为互不相容，所以 (A)，因为不一定等于1，所以(A)不正确.(B)当不为0时，(B)不成立，故排除. (C)只有当互为对立事件的时候才成立，故排除. (D)，故(D)正确.（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为，记为随机变量的分布函数，则函数的间断点个数为（ ） (A) 0. (B)1.(C)2 .(D)3.【答案】 B.【解析】独立（1）若，则（2）当，则为间断点，故选(B).二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦A ()0P AB =()()()P AB P A P B =()1()P A P B =-()1P A B ⋃=,A B ()0P AB =()()1()P AB P AB P AB ==-()P AB (),()P A P B ,A B ()()1()1P AB P AB P AB ==-=X Y X (0,1)N Y 1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z ()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤0z <1()()2Z F z z =Φ0z ≥1()(1())2Z F z z =+Φ0z ∴=（9） .【答案】.【解析】. （10）设，则 . 【答案】.【解析】由，故代入得，.（11）幂级数的收敛半径为 . 【答案】. 【解析】由题意知，所以，该幂级数的收敛半径为（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为10000件时，价格增加1元会使产品收益增加 元. 【答案】8000.【解析】所求即为 因为，所以 所以cos 0x x →=32e cos cos 10xx x x -→→=02(1cos )lim 13x e x x→-=20212lim 13x e x x →⋅=32e =()y x z x e =+(1,0)zx ∂=∂2ln 21+()xyz x e =+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦1x =()ln 21,01ln 22ln 212ze x∂⎛⎫=+=+ ⎪∂⎝⎭21(1)n n nn e x n ∞=--∑1e()210nn n e a n --=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦1e()Q Q P =P 0.2p ξ=()QP Q P Q ''=+0.2p Q PQξ'==-0.2Q P Q '=-()0.20.8QP Q Q Q '=-+=将代入有.（13）设,，若矩阵相似于，则 .【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为 3，0，0.而为矩阵的对角元素之和，，.(14)设，,…,为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，则 .【答案】【解析】由.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.（15）（本题满分9分） 求二元函数的极值.【解析】，，故. . 则，，.而 二元函数存在极小值.（16）（本题满分10 分） 计算不定积分 .得 10000Q =()8000QP '=(1,1,1)T α=(1,0,)T k β=T αβ300000000⎛⎫ ⎪⎪ ⎪⎝⎭k =T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦T αβT αβT αβ1300k ∴+=++2k ∴=1X 2X n X (,)B n p X 2S 2T X S =-ET =2np 222()(1)ET E X S EX ES np np p np =-=-=--=()22(,)2ln f x y xy y y =++2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =12(0,)12(2)xx ef e ''=+1(0,)0xyef ''=1(0,)yyef e ''=0xxf ''>2()0xy xx yy f f f ''''''-<∴11(0,)f e e=-ln(1dx +⎰(0)x >t =22212,1(1)tdtx dx t t -= =--而所以（17）（本题满分10 分） 计算二重积分，其中. 【解析】由得，.（18）（本题满分11 分）2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t =+-+=---+⎰⎰⎰22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C +++=+-+--+=++⎰()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则，得证.（Ⅱ）证明：若函数在处连续，在内可导，且，则存在，且. 【解析】（Ⅰ）作辅助函数，易验证满足：；在闭区间上连续，在开区间内可导，且. 根据罗尔定理，可得在内至少有一点，使，即（Ⅱ）任取，则函数满足：在闭区间上连续，开区间内可导，从而有拉格朗日中值定理可得：存在，使得……又由于，对上式（*式）两边取时的极限可得： 故存在，且.（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯形面积值的倍，求该曲线的方程. 【解析】旋转体的体积为曲边梯形的面积为：，则由题可知两边对t 求导可得继续求导可得，化简可得，解之得()f x [],a b (),a b (),a b ξ∈()'()()()f b f a f b a ξ-=-()f x 0x =()0,,(0)σσ>'0lim ()x f x A +→='(0)f +'(0)f A +=()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ()()a b ϕϕ=()x ϕ[],a b (),a b ''()()()()f b f a x f x b aϕ-=--(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--0(0,)x δ∈()f x []00,x ()00,x ()()000,0,x x ξδ∈⊂()0'00()(0)x f x f f x ξ-=-()*()'0lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-'(0)f +'(0)f A +=()y f x =()f x ()0f x >()y f x =0,1y x ==(1)x t t =>x t π22()()11x x t tV f dx f dx ππ==⎰⎰()1x t s f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dx πππ=⇒=⇒=⎰⎰⎰⎰22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰''2()()()()()f t f t f t tf t f t --='1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y -=⋅+在式中令，则，代入得. 所以该曲线方程为：.（20）（本题满分11 分）设,. （Ⅰ）求满足，的所有向量，. （Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关. 【解析】（Ⅰ）解方程故有一个自由变量，令，由解得， 求特解，令，得故 ，其中为任意常数解方程故有两个自由变量，令，由得 令，由得1t =2(1)(1)0,()0,(1)1f f f t f -=>∴=1223t cyy -=+11,2)33c t y =∴=+230y x -=111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭21A ξξ=231A ξξ=2ξ3ξ2ξ3ξ1ξ2ξ3ξ21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =32x =0Ax =211,1x x =-=120x x ==31x =21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k 231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭231,0x x =-=20A x =11x =230,1x x ==-20A x =10x =求得特解故 ，其中为任意常数（Ⅱ）证明：由于故 线性无关.（21）（本题满分11 分）设二次型. （Ⅰ）求二次型的矩阵的所有特征值.（Ⅱ）若二次型的规范形为，求的值.【解析】（Ⅰ）.（Ⅱ） 若规范形为，说明有两个特征值为正，一个为0.则1) 若，则 ， ，不符题意21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k 12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠123,,ξξξ2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-f f 2211y y +a 0101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+2212y y +10a λ==220λ=-<31λ=2) 若 ，即，则，，符合3) 若 ，即，则 ，，不符题意 综上所述，故（22）（本题满分11 分）设二维随机变量的概率密度为（Ⅰ）求条件概率密度 （Ⅱ）求条件概率 【解析】（Ⅰ）由得其边缘密度函数故 即 （Ⅱ）而.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、、分别表示两次取球所取得的红、黑与白球的个数. ①求.②求二维随机变量的概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，20λ=2a =120λ=>330λ=>30λ=1a =-110λ=-<230λ=-<2a =(,)X Y 0(,)0x e y x f x y -⎧<<=⎨⎩其他()Y X f y x 11P X Y =⎡≤≤⎤⎣⎦0(,)0x y x e f x y -<<⎧= ⎨⎩其它0()0xx x x f x e dy xe x --== >⎰|(,)1(|)0()y x x f x y f y x y x f x x== <<|1(|)0y x y xf y x x⎧ 0<<⎪=⎨⎪ ⎩其它[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤111011[1,1](,)12xx x x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x y Y yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110yyP Y e dy e e e ----∴ ≤==-=-+=-⎰11122[1|1]11e e P X Y e e ----∴ ≤≤==--X Y Z 10P X Z ⎡==⎤⎣⎦(,)X Y其中摸了一个红球.（Ⅱ）X ，Y 取值范围为0，1，2，故12113324(10)9C P X Z C C ⨯∴====⋅()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======。

兰州大学《电子线路》考研真题2009年(总分：74.99，做题时间：90分钟)一、{{B}}填空题{{/B}}(总题数：8，分数：20.00)1.理想二极管组成的电路如下图所示，输出电压U o=______。

（分数：2.00）填空项1:__________________ （正确答案：-6V）解析：2.已知某晶体管电流放大系数β的频率特性如下图所示，由图可判断该管的ωβ=______，ωT=______。

（分数：4.00）填空项1:__________________ （正确答案：4Mrad/s 400Mrad/s）解析：3.某放大电路在负载开路时的输出电压为6V，当接入2kΩ负载电阻后，输出电压降为4V，这表明该放大电路的输出电阻R o= 1。

（分数：2.00）填空项1:__________________ （正确答案：1kΩ）解析：4.某理想乙类OCL功放电路在输出功率最大时，每管的管耗等于1W，则可知该电路所能输出的最大功率P om≈ 1。

（分数：2.00）填空项1:__________________ （正确答案：5W）解析：5.当集成运算放大器的输入偏置电流I IB=0.6μA，输入失调电流I IO=0.2μA时，则两个差分输入管的基极偏流分别为 1。

（分数：2.00）填空项1:__________________ （正确答案：I B1=0.7μA，I B2=0.5μA）解析：6.电流源电路在集成电路中的主要作用是 1。

（分数：2.00）填空项1:__________________ （正确答案：为集成电路中各级电路提供稳定的偏置电流或作为有源负载）解析：7.某MOS场效应管的I DSS为6mA，而I DQ自漏极流出，大小为8mA，由此可判断该管的类型为 1。

（分数：2.00）填空项1:__________________ （正确答案：P沟道耗尽型MOS场效应管）解析：8.用示波器观察由NPN管组成的单管共射电路的输出波形时，发现波形顶部被削平，这说明电路出现了______失真，若要消除此类失真，应将Q点调______。

2009年全国硕士研究生入学统一考试数学二试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）函数()3sin x x f x nx-=的可去间断点的个数，则（ ）()A 1.()B 2. ()C 3.()D 无穷多个.（2）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小，则（ ）()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=. （3）设函数(),z f x y =的全微分为dz xdx ydy =+，则点()0,0（ ）()A 不是(),f x y 的连续点. ()B 不是(),f x y 的极值点. ()C 是(),f x y 的极大值点. ()D 是(),f x y 的极小值点.（4）设函数(),f x y 连续，则()()222411,,yxydx f x y dy dy f x y dx -+=⎰⎰⎰⎰（ ）()A ()2411,xdx f x y dy -⎰⎰. ()B ()241,xxdx f x y dy -⎰⎰.()C ()2411,ydy f x y dx -⎰⎰.()D .()221,y dy f x y dx ⎰⎰（5）若()f x ''不变号，且曲线()y f x =在点()1,1上的曲率圆为222x y +=，则()f x 在区间()1,2内（ ）()A 有极值点，无零点. ()B 无极值点，有零点.()C 有极值点，有零点. ()D 无极值点，无零点.（6）设函数()y f x =在区间[]1,3-上的图形为：则函数()()0xF x f t dt =⎰的图形为（ ）()A .()B .()C .()D .（7）设A 、B 均为2阶矩阵，**A B ，分别为A 、B的伴随矩阵。

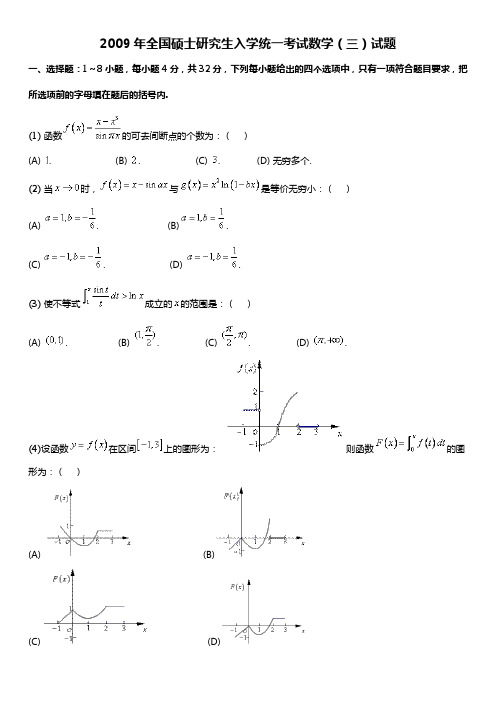
2009年全国硕士研究生入学统一考试数学（三）试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.(1)函数的可去间断点的个数为：（）(A) . (B) . (C) . (D) 无穷多个.(2)当时，与是等价无穷小：（）(A) . (B).(C) . (D) .(3)使不等式成立的的范围是：（）(A) . (B) . (C) . (D) .(4)设函数在区间上的图形为：则函数的图形为：（）(A)(B)(C)(D)(5)设均为阶矩阵，分别为的伴随矩阵，若，则分块矩阵的伴随矩阵为：（）(A) . (B) .(C) . (D).(6)设均为阶矩阵，为的转置矩阵，且.若，则为：（）(A) . (B) . (C). (D) .(7)设事件与事件互不相容，则：（）(A) . (B) .(C) . (D) .(8)设随机变量与相互独立，且服从标准正态分布，的概率分布为.记为随机变量的分布函数，则函数的间断点个数为：（）(A). (B) . (C) . (D) .二、填空题：9~14小题，每小题4分，共24分.请将答案写在答题纸指定位置上.(9)_________.(10)设，则_________.(11)幂级数的收敛半径为_________.(12)设某产品的需求函数为，其对价格的弹性，则当需求量为件时，价格增加元会使产品收益增加_________元.(13)设，.若矩阵相似于，则_________.(14)设为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，则_________.三、解答题：15~23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数的极值.(16) (本题满分10分)计算不定积分.(17) (本题满分10分)计算二重积分，其中.(18)(本题满分11分)(I) 证明拉格朗日中值定理：若函数在上连续，在可导，则存在，使得.(II) 证明：若函数在处连续，在内可导，且，则存在，且.(19)(本题满分10分)设曲线，其中是可导函数，且.已知曲线与直线及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯形面积值的倍，求该曲线方程.(20)(本题满分11分)设，(I) 求满足的所有向量；(II) 对(I)中的任意向量，证明：线性无关.(21)(本题满分11分)设二次型.(I) 求二次型的矩阵的所有特征值；(II) 若二次型的规范形为，求的值.(22)(本题满分11分)设二维随机变量的概率密度为(I) 求条件概率密度；(II) 求条件概率.(23)(本题满分11分)袋中有个红球，个黑球与个白球.现有放回地从袋中取两次，每次取一个球，以分别表示两次取球所取得的红球、黑球与白球的个数.(I) 求；(II) 求二维随机变量的概率分布.。

一、选择题：（1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则()A 11,6a b ==-.()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则2222()sin sin 1cos sin limlimlimlimlim()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bxbx→→→→→---==-⋅---洛洛23sin lim166x a ax ab baxa →==-=-⋅ 36a b ∴=- 故排除,B C 。

另外21cos lim3x a ax bx→--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排D 。

所以本题选A 。

（2）如图，正方形(){},1,1x y x y ≤≤被其对角线划分为 四个区域()1,2,3,4k D k =，cos kk D I y xdxdy =⎰⎰，则{}14m ax kk I ≤≤=()A 1I .()B 2I .()C 3I .()D 4I .【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==;13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是关于x 的偶函数，所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰；{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为A.（3）设函数()y f x =在区间[]1,3-上的图形为： 则函数()()0xF x f t dt =⎰的图形为x()A ()B()C ()D【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征： ①[]0,1x ∈时，()0F x ≤，且单调递减。

2009年1月真题解析一、问题求解：第1～15小题，每小题3分，共45分.下列每题给出的A 、B 、C 、D 、E 五个选项中,有一项是符合试题要求的.请在答题卡上将所选项的字母涂黑.1.一家商店为回收资金，把甲、乙两件商品均以480元一件卖出，已知甲商品赚了20%，乙商品亏了20%，则商店盈亏结果为（）.（A ）不亏不赚（B ）亏了50元（C ）赚了50元（D ）赚了40元（E ）亏了40元【答案】E【考点】盈亏问题【解析】设甲、乙两件商品的成本价分别为,x y 元，则(120%)480,(120%)480,x y +=⎧⎨-=⎩解得400,600,x y =⎧⎨=⎩所以甲、乙两件商品的成本之和为1000x y +=元，而实际卖得的价格为480+480=960元，商店亏了1000-960=40元.2.某国参加北京奥运会的男女运动员比例原为19:12，由于先增加若干名女运动员，使男女运动员比例变为20:13.后又增加了若干名男运动员，于是男女运动员比例最终变为30:19.如果后增加的男运动员比先增加的女运动员多3人，则最后运动员的总人数为（）.（A ）686（B ）637（C ）700（D ）661（E ）600【答案】B【考点】比例问题【解析】方法1：设先增加了x 名女运动员，后增加了3x +名男运动员，最初男女运动员分别有19k 和12k 人则有1920121319(3)301219kk x k x k x⎧=⎪⎪+⎨++⎪=⎪+⎩，解得7,20x k ==所以总人数为1920(73)12207637⨯+++⨯+=（人）.方法2：原来男:女19:12=;增加女运动员后，男:女20:13=,在该过程中男运动员数量没变,故男运动员数能被20和19整除,增加女运动员后，男:女20:13=,再增加男运动员后，男:女30:19=;在该过程中女运动员数量没变,故女运动员数能被13和19整除,.最小就1319247⨯=;又男:女30:19=⇒男1330390=⨯=，390247637+=.3.某工厂定期购买一种原料，已知该厂每天需用该原料6吨，每吨价格1800元.原料的保管费用平均每吨3元，每次购买原料支付运费900元.若该厂要使平均每天支付的总费用最省，则应该每（）天购买一次原料.（A ）11（B ）10（C ）9（D ）8（E ）7【答案】B【考点】均值不等式【解析】设应该每隔n 天购买一次原料则总费用1800663(12)900108009(1)900S n n n n n =⨯+⨯⨯++++=+++ ，所以平均每天的费用900108099S n n =++，根据平均值不等式可知当且仅当9009n n=即10n =时。

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1) 函数()3sin x x f x xπ-=的可去间断点的个数为 ( )(A) 1.(B) 2. (C) 3.(D) 无穷多个.(2) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(3) 使不等式1sin ln x tdt x t>⎰成立的x 的范围是 ( ) (A) (0,1).(B) (1,)2π. (C) (,)2ππ. (D) (,)π+∞.(4) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)(C) (D)(5) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B AO ⎛⎫⎪⎝⎭. (C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭. (6) 设,A P 均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭.若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为 ( )(A) 210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B) 110120002⎛⎫⎪⎪ ⎪⎝⎭.(C) 200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D) 100020002⎛⎫ ⎪⎪ ⎪⎝⎭.(7) 设事件A 与事件B 互不相容,则 ( )(A) ()0P AB =.(B) ()()()P AB P A P B =. (C) ()1()P A P B =-.(D) ()1P A B = .(8) 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 ( )(A) 0. (B) 1. (C) 2. (D) 3.二、填空题：9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.(9) cos 0x x →= .(10) 设()y x z x e =+,则(1,0)zx ∂=∂ _______ .(11) 幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 ______. (12) 设某产品的需求函数为()Q Q p =,其对价格p 的弹性0.2p ε=,则当需求量为10000件时,价格增加1元会使产品收益增加 _______ 元.(13) 设(1,1,1)T α=,(1,0,)T k β=.若矩阵T αβ相似于300000000⎛⎫⎪⎪ ⎪⎝⎭,则k = ____ .(14) 设12,,,m X X X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = _____.三、解答题：15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分10 分)计算不定积分ln 1dx ⎛+ ⎝⎰ (0)x >. (17)(本题满分10 分)计算二重积分()Dx y dxdy -⎰⎰,其中()()(){}22,112,D x y x y y x =-+-≤≥.(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理：若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明：若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线方程. (20)(本题满分11 分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ； (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明：123,,ξξξ线性无关. (21)(本题满分11 分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值；(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为,0,(,)0,x e y x f x y -⎧<<=⎨⎩其他. (I) 求条件概率密度()Y X f y x ； (II) 求条件概率{}11P X Y ≤≤.(23)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==；(Ⅱ)求二维随机变量(),X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)【答案】(C)【解析】由于()3sin x x f x xπ-=,则当x 取任何整数时,()f x 均无意义,故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±.320032113211131lim lim ,sin cos 132lim lim ,sin cos 132lim lim .sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即1,2,30,1x =±. (2) 【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bxa ax ab axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛 即36a b =-,故排除B,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选A.(3) 【答案】(A)【解析】原问题可转化为求1sin ()ln 0xtf x dt x t=->⎰成立时x 的取值范围. 11111sin sin 1()ln sin 11sin 0.xx x x x tt f x dt x dt dt t tt t t dt dt t t =-=---==>⎰⎰⎰⎰⎰由()0,1t ∈时,1sin 0tt->,知当()0,1x ∈时,()0f x >.故应选(A). (4) 【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征：① []1,0x ∈-时,()0F x ≤为线性函数,单调递增； ② []0,1x ∈时,()0F x ≤,且单调递减； ③ []1,2x ∈时,()F x 单调递增； ④ []2,3x ∈时,()F x 为常函数； ⑤ ()F x 为连续函数. 结合这些特点,可见正确选项为(D). (5) 【答案】(B) 【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O⨯=-=⨯=（）,即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B).(6)【答案】(A)【解析】1223123100100(,,)(,,)110110001001Q P ααααααα⎛⎫⎛⎫ ⎪ ⎪=+== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,100100110110001001110100100210010010110110.001002001002TT Q AQ P A P ⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥⎢⎥⎪ ⎪=⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪ ⎪== ⎪⎪⎪ ⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(7) 【答案】(D)【解析】因为,A B 互不相容,所以()0P AB =.(A)()()1()P AB P A B P A B ==- ,因为()P A B 不一定等于1,所以(A)不正确； (B)当(),()P A P B 不为0时,()B 不成立,故排除； (C)只有当,A B 互为对立事件的时候才成立,故排除； (D)()()1()1P A B P AB P AB ==-= ,故()D 正确. (8) 【答案】(B) 【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤. (1) 当0z <时,1()()2Z F z z =Φ；(2) 当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题：9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上. (9) 【答案】32e 【解析】cos cos 10x x x x -→→= 200221(1cos )32lim lim 233x x e x e x e x x→→⋅-===.(10) 【答案】12ln 2+【解析】解法1：由于()xy z x e=+,故()(),01xz x x =+,()ln(1)ln(1)01ln(1)1x x x x x y z x x e e x xx ++=∂'⎡⎤'⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦∂+⎣⎦,代入1x =,得ln 2(1,0)1ln 22ln 212z e x ∂⎛⎫=+=+ ⎪∂⎝⎭.解法2：由于ln()()()ln()yx x e y xy x y y e x e z x x e x e x x x x e +⎡⎤∂⎡⎤∂+∂⎡⎤⎣⎦⎣⎦===+⋅++⎢⎥∂∂∂+⎣⎦, 故000(1,0)1(1)ln(1)2ln 211z e e x e ∂⎡⎤=+⋅++=+⎢⎥∂+⎣⎦. (11) 【答案】1e -【解析】由题意知,()210nn n e a n --=>,()()()()1121211221lim lim 1111lim ,111n n n nn n n nn n n n n e a n a n e e e n e n e e +++→∞→∞++→∞--=⋅+--⎡⎤⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦=⋅=⎡⎤+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以,该幂级数的收敛半径为1e -. (12) 【答案】8000【解析】所求即为()Qp Q p Q ''=+. 因为0.2p Q pQε'=-=,所以0.2Q p Q '=-,所以()0.20.8Qp Q Q Q '=-+=. 将10000Q =代入有()8000Qp '=. (13) 【答案】2【解析】T αβ相似于300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭,根据相似矩阵有相同的特征值,得到Tαβ的特征值为3,0,0.而Tαβ为矩阵T αβ的对角元素之和,1300k ∴+=++,2k ∴=.(14) 【答案】2np【解析】222()(1)ET E X S EX ES np np p np =-=-=--=.三、解答题：15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)【解析】 2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,)21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+= 所以 2212(2)0,B AC e e-=-+<且0A >. 从而1(0,)f e 是(,)f x y 的极小值,极小值为11(0,)f e e=-.(16)(本题满分10 分) 【解析】解法1t =,则21,1x t =-()()2221ln 1ln 11ln 111111dx t d t t dt t t t ⎛⎛⎫+=+ ⎪ -⎝⎭⎝+=-⋅--+⎰⎰⎰而()()()()()()2211112411111111ln 1ln 1,4421dt dt t t t t t t t C t ⎡⎤=--⎢⎥-+-++⎢⎥⎣⎦=--++++⎰⎰所以()()2ln1111ln1ln141211ln1ln41ln1ln211ln1ln.22t tdx Ct t tx Cx Cx x C ⎛+++=+-+--+⎝⎛=++⎝⎛=++⎝⎛=+++-⎝⎰解法21ln1ln11dx x x dx-'⎛⎛⎛=-⎝⎝⎝⎰⎰1ln112x dx⎛⎛⎫=+--⎪⎪⎝⎭⎰11ln122x x⎛=++-⎝⎰(2ln lnuduu C C=++=+分部即)11ln1ln1ln22dx x x C ⎛⎛+=++-+⎝⎝⎰1ln1ln211ln1ln.22x Cx x C⎛=++⎝⎛=++⎝(17)(本题满分10 分)【解析】解法1如右图所示,区域D的极坐标表示为302(sin cos),44rππθθθ≤≤+≤≤.132(sin cos )442(sin cos )33404334433443444()(cos sin )1(cos sin )38(cos sin )(sin cos )38(sin cos )(sin cos )3818(sin cos ).343Dr r x y dxdy d r r rdrr d d d θθππθθππππππππθθθθθθθθθθθθθθθθθ+=+=-=-⎡⎤=-⋅⎢⎥⎢⎥⎣⎦=-+=++=⨯+=-⎰⎰⎰⎰⎰⎰⎰解法2 将区域D 分成12,D D两部分(如右图),其中(){}(){}12,110,,12.D x y y x D x y x y x =-≤≤+-≤=≤≤+≤≤由二重积分的性质知()()()12DD D x y dxdy xy dxdy x y dxdy-=-+-⎰⎰⎰⎰⎰⎰,而()1111)D x y dxdyx y dy-=-⎰⎰⎰⎰103122,33x=-=-=-⎰()221020230)122(21242,23xD x y dxdy dx x y dyx dx -=-⎡=---⎣⎡⎤=-+=-⎢⎥⎢⎥⎣⎦⎰⎰⎰⎰⎰ 所以()()()1228233DD D x y dxdy x y dxdy x y dxdy -=-+-=--=-⎰⎰⎰⎰⎰⎰. (18)(本题满分11 分) 【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且()()()()()(),()()()()()().f b f a F a f a a a f a b af b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()000()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈. 由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10 分) 【解析】解法1 由题意知211()()t tf x dx t f x dx ππ=⎰⎰,两边对t 求导得21()()()tf t f x dx tf t =+⎰,代入1t =得 (1)1f =或(1)0f = (舍去). 再求导得 2()()2()()f t f t f t tf t ''=+,记()f t y =,则112dt t dy y+=, 因此, 111222()()dydyy y t eedy C y C --⎰⎰=+=+⎰132222()33y y C y -=+=+.代入1,1t y ==得13C =,从而23t y =+故所求曲线方程为23x y =+解法2 同解法1,得2()()2()(),(1)1f t f t f t tf t f ''=+=.整理得22dy ydt y t=-. 令y u t =,则 dy du u t dt dt=+, 原方程变成 23221du u u t dt u -=-, 分离变量得211(32)u du dt u u t-=-,即 114332dtdu u u t -⎛⎫+=⎪-⎝⎭, 积分得 21ln (32)ln 3u u Ct --=, 即 1233(32)u u Ct ---=.代入1,1t u ==,得1C =,所以231(32)u u t -=. 代入y u t =化简得2(32)1y t y -=,即23t y =.故所求曲线方程为23x y =(20)(本题满分11 分)【解析】(Ⅰ)对矩阵1()A ξ 施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ⎪---⎛⎫ ⎪⎪⎪=-→ ⎪ ⎪ ⎪--- ⎪⎝⎭ ⎪ ⎪⎝⎭可求得 2122122k kk ξ⎛⎫-+ ⎪ ⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ 施以初等行变换()211110220122201000044020000A ξ⎛⎫-⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭,可求得 312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1 由(Ⅰ)知12311122211,,102222ka ka kbξξξ--+--=-=-≠-, 所以123,,ξξξ线性无关.解法2 由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=, ①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=, ②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠，于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11 分) 【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111aE A aa a a a λλλλλλλ---=-=--+----+, 所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1 由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫ ⎪ ⎪ ⎪⎝⎭,其秩为2,故 1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意. 当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意. 当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +. 综上可知,2a =.解法2 由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零. 又21a a a -<<+,所以2a =.(22)(本题满分11 分)【解析】(I)X 的概率密度0,0,,0,()(,)0,0.0,0xx x X e dy x xe x f x f x y dy x x --+∞-∞⎧⎧>>⎪===⎨⎨≤⎩⎪≤⎩⎰⎰当0x >时,Y 的条件概率密度|1,0,(,)(|)()0,Y X X y x f x y f y x x f x ⎧<<⎪== ⎨⎪⎩其他.(II)Y 的概率密度,0,()(,)0,0.y Y e y f y f x y dx y -+∞-∞⎧>==⎨≤⎩⎰{}{}{}111111,11|11(,)2.11xx y P X Y P X Y P Y dx e dyf x y dxdye e e e dy--∞-∞--≤≤≤≤=≤-===--⎰⎰⎰⎰⎰(23)(本题满分11分)【解析】(Ⅰ) 12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========. (Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,0,0,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为。

2009年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上.（1）函数的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.【答案】C. 【解析】则当取任何整数时，均无意义故的间断点有无穷多个，但可去间断点为极限存在的点，故应是的解故可去间断点为3个，即（2）当时，与是等价无穷小，则(A)，. （B ），. (C)，.（D ），. 【答案】A.【解析】为等价无穷小，则3()sin x x f x xπ-=()3sin x x f x xπ-=x ()f x ()f x 30x x -=1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--==0,1±0x →()sin f x x ax =-2()ln(1)g x x bx =-1a =16b =-1a =16b =1a =-16b =-1a =-16b =2()sin ,()(1)f x x ax g x x ln bx =-=-故排除(B)、(C). 另外存在，蕴含了故排除(D).所以本题选(A).（3）使不等式成立的的范围是 (A). (B). (C).(D).【答案】A.【解析】原问题可转化为求成立时的取值范围，由，时，知当时，.故应选(A).（4）设函数在区间上的图形为则函数的图形为222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅36a b ∴=-201cos lim3x a axbx →--1cos 0a ax -→()0x → 1.a =1sin ln xtdt x t>⎰x (0,1)(1,)2π(,)2ππ(,)π+∞111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t--==>⎰⎰x 1sin 0tt ->()0,1t ∈()0,1x ∈()0f x >()y f x =[]1,3-()()0xF x f t dt =⎰(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核，由的图形可见，其图像与轴及轴、所围的图形的代数面积为所求函数，从而可得出几个方面的特征：①时，，且单调递减. ②时，单调递增. ③时，为常函数.④时，为线性函数，单调递增. ⑤由于F(x)为连续函数结合这些特点，可见正确选项为(D).（5）设均为2阶矩阵，分别为的伴随矩阵，若，则分块矩阵的伴随矩阵为 ()y f x =x y0x x =()F x []0,1x ∈()0F x ≤[]1,2x ∈()F x []2,3x ∈()F x []1,0x ∈-()0F x ≤,A B *,A B *,A B ||2,||3A B ==O A B O ⎛⎫⎪⎝⎭(A). (B). (C).(D). 【答案】B.【解析】根据，若 分块矩阵的行列式，即分块矩阵可逆 故答案为(B).（6）设均为3阶矩阵，为的转置矩阵，且，若，则为(A).(B).(C).(D).【答案】A.**32O B A O ⎛⎫⎪⎝⎭**23O B AO ⎛⎫⎪⎝⎭**32O A BO ⎛⎫⎪⎝⎭**23O A BO ⎛⎫⎪⎝⎭CC C E *=111,C C C C C C*--*==OA BO ⎛⎫⎪⎝⎭221236O A A B B O⨯=-=⨯=（）1111661O B BO A O A O A O B B O B O B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O BOB AO A O ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭,A P T P P 100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭1231223(,,),(,,)P Q ααααααα==+T Q AQ 210110002⎛⎫⎪ ⎪ ⎪⎝⎭110120002⎛⎫⎪⎪ ⎪⎝⎭200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭【解析】，即：（7）设事件与事件B 互不相容，则(A). (B).(C).(D).【答案】D.【解析】因为互不相容，所以 (A)，因为不一定等于1，所以(A)不正确.(B)当不为0时，(B)不成立，故排除. (C)只有当互为对立事件的时候才成立，故排除. (D)，故(D)正确.（8）设随机变量与相互独立，且服从标准正态分布，的概率分布为，记为随机变量的分布函数，则函数的间断点个数为（ ） (A) 0.(B)1. (C)2.(D)3.【答案】 B.【解析】122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦A ()0P AB =()()()P AB P A P B =()1()P A P B =-()1P A B ⋃=,A B ()0P AB =()()1()P AB P AB P AB ==-()P AB (),()P A P B ,A B ()()1()1P AB P AB P AB ==-=X Y X (0,1)N Y 1{0}{1}2P Y P Y ====()z F Z Z XY =()z F Z ()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==独立（1）若，则 （2）当，则 为间断点，故选(B).二、填空题：9~14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9） .【答案】.【解析】. （10）设，则 . 【答案】. 【解析】由，故代入得，.（11）幂级数的收敛半径为 . 1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=,X Y 1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤0z <1()()2Z F z z =Φ0z ≥1()(1())2Z F z z =+Φ0z ∴=cos 0x x →=32e cos cos 10xx x x -→→=02(1cos )lim13x e x x→-=20212lim 13x e x x →⋅=32e =()y x z x e =+(1,0)zx ∂=∂2ln 21+()xy z x e=+()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦1x =()ln 21,01ln 22ln 212ze x∂⎛⎫=+=+ ⎪∂⎝⎭21(1)n n nn e x n ∞=--∑【答案】. 【解析】由题意知，所以，该幂级数的收敛半径为（12）设某产品的需求函数为,其对应价格的弹性，则当需求量为10000件时，价格增加1元会使产品收益增加 元. 【答案】8000.【解析】所求即为 因为，所以 所以 将代入有.（13）设,，若矩阵相似于，则 .【答案】2.【解析】相似于，根据相似矩阵有相同的特征值，得到的特征值为3，0，0.而为矩阵的对角元素之和，，.1e()210nn n e a n --=>()()()()111122122111()11111n n n n n nnn nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦1e()Q Q P =P 0.2p ξ=()QP Q P Q ''=+0.2p Q PQξ'==-0.2Q P Q '=-()0.20.8QP Q Q Q '=-+=10000Q =()8000QP '=(1,1,1)T α=(1,0,)T k β=T αβ300000000⎛⎫ ⎪⎪ ⎪⎝⎭k =T αβ300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦T αβT αβT αβ1300k ∴+=++2k ∴=(14)设，,…,为来自二项分布总体的简单随机样本，和分别为样本均值和样本方差，记统计量，则 .【答案】【解析】由.三、解答题：15～23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. （15）（本题满分9分）求二元函数的极值.【解析】，，故. . 则，，.而 二元函数存在极小值.（16）（本题满分10 分） 计算不定积分 .得而1X 2X n X (,)B n p X 2S 2T X S =-ET =2np 222()(1)ET E X S EX ES np np p np =-=-=--=()22(,)2ln f x y x y y y =++2(,)2(2)0x f x y x y '=+=2(,)2ln 10y f x y x y y '=++=10,x y e= =2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =12(0,)12(2)xx ef e''=+1(0,)0xyef ''=1(0,)yyef e ''=0xxf ''>2()0xy xx yy f f f ''''''-<∴11(0,)f e e=-ln(1dx +⎰(0)x >t =22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t =+-+=---+⎰⎰⎰所以（17）（本题满分10 分）计算二重积分，其中.【解析】由得，.22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C ++=+-+--+=++⎰()Dx y dxdy -⎰⎰22{(,)(1)(1)2,}D x y x y y x =-+-≤≥22(1)(1)2x y -+-≤2(sin cos )r θθ≤+32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-（18）（本题满分11 分）（Ⅰ）证明拉格朗日中值定理，若函数在上连续，在上可导，则，得证.（Ⅱ）证明：若函数在处连续，在内可导，且，则存在，且. 【解析】（Ⅰ）作辅助函数，易验证满足：；在闭区间上连续，在开区间内可导，且. 根据罗尔定理，可得在内至少有一点，使，即（Ⅱ）任取，则函数满足：在闭区间上连续，开区间内可导，从而有拉格朗日中值定理可得：存在，使得……又由于，对上式（*式）两边取时的极限可得： 故存在，且.（19）（本题满分10 分）设曲线，其中是可导函数，且.已知曲线与直线及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯形面积值的倍，求该曲线的方程.【解析】旋转体的体积为()f x [],a b (),a b (),a b ξ∈()'()()()f b f a f b a ξ-=-()f x 0x =()0,,(0)σσ>'0lim ()x f x A +→='(0)f +'(0)f A +=()()()()()()f b f a x f x f a x a b aϕ-=----()x ϕ()()a b ϕϕ=()x ϕ[],a b (),a b ''()()()()f b f a x f x b aϕ-=--(),a b ξ'()0ϕξ='()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--0(0,)x δ∈()f x []00,x ()00,x ()()000,0,x x ξδ∈⊂()0'00()(0)x f x f f x ξ-=-()*()'0lim x f x A +→=00x +→()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-'(0)f +'(0)f A +=()y f x =()f x ()0f x >()y f x =0,1y x ==(1)x t t =>x t π22()()11x x t tV f dx f dx ππ==⎰⎰曲边梯形的面积为：，则由题可知两边对t 求导可得继续求导可得，化简可得，解之得在式中令，则，代入得.所以该曲线方程为：.（20）（本题满分11 分）设,. （Ⅰ）求满足，的所有向量，. （Ⅱ）对（Ⅰ）中的任意向量,，证明,,线性无关. 【解析】（Ⅰ）解方程故有一个自由变量，令，由解得， 求特解，令，得()1x ts f dx =⎰22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dx πππ=⇒=⇒=⎰⎰⎰⎰22()()()()()()11t x t t t x t tf f dx tf f tf f dx =+⇒-=⎰⎰''2()()()()()f t f t f t tf t f t --='1(2())()2()12dt f t t f t f t t dy y-=⇒+=1223t c y y -=⋅+1t =2(1)(1)0,()0,(1)1f f f t f -=>∴=1223t cyy -=+11,2)33c t y =∴=230y x =111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭21A ξξ=231A ξξ=2ξ3ξ2ξ3ξ1ξ2ξ3ξ21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =32x =0Ax =211,1x x =-=120x x ==31x =故 ，其中为任意常数解方程故有两个自由变量，令，由得 令，由得求得特解故 ，其中为任意常数（Ⅱ）证明：由于故 线性无关.（21）（本题满分11 分）21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1k 231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭231,0x x =-=20A x =11x =230,1x x ==-20A x =10x =21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫ ⎪⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭23,k k 12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠123,,ξξξ设二次型. （Ⅰ）求二次型的矩阵的所有特征值.（Ⅱ）若二次型的规范形为，求的值.【解析】（Ⅰ）.（Ⅱ） 若规范形为，说明有两个特征值为正，一个为0.则1) 若，则 ， ，不符题意 2) 若 ，即，则，，符合3) 若 ，即，则 ，，不符题意 综上所述，故（22）（本题满分11 分）设二维随机变量的概率密度为（Ⅰ）求条件概率密度 （Ⅱ）求条件概率 【解析】2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-f f 2211y y +a 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭110||01()1111111aa aE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+2212y y +10a λ==220λ=-<31λ=20λ=2a =120λ=>330λ=>30λ=1a =-110λ=-<230λ=-<2a =(,)X Y 0(,)0x e y x f x y -⎧<<=⎨⎩其他()Y X f y x 11P X Y =⎡≤≤⎤⎣⎦（Ⅰ）由得其边缘密度函数故 即（Ⅱ）而.（23）（本题满分11分）袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以、、分别表示两次取球所取得的红、黑与白球的个数. ①求.②求二维随机变量的概率分布.【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球.（Ⅱ）X ，Y 取值范围为0，1，2，故0(,)0x y xe f x y -<<⎧= ⎨⎩其它0()0xx xx f x e dy xe x --== >⎰|(,)1(|)0()y x x f x y f y x y x f x x== <<|1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪ ⎩其它[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤111011[1,1](,)12xx x x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0x x y Y yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰11122[1|1]11e e P X Y e e ----∴ ≤≤==--X Y Z 10P X Z ⎡==⎤⎣⎦(,)X Y 12113324(10)9C P X Z C C ⨯∴====⋅()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======。