新北师大版七年级数学下册全册教案
- 格式:doc
- 大小:10.06 MB
- 文档页数:136


教案数学北师大版七年级下册教学目标:1. 知识与技能:掌握七年级下册数学的基本概念和运算方法。
2. 过程与方法:通过小组讨论和实际操作,提高解决问题的能力。
3. 情感态度价值观:培养学生对数学的兴趣和合作精神。
教学内容:第一章:整式的乘除乘法公式整式的乘除运算第二章:二元一次方程组方程组的解法实际应用问题第三章:不等式与不等式组不等式的解法不等式组的解法第四章:数据的初步认识数据的收集与表示平均数、中位数、众数的计算教学方法:启发式教学:鼓励学生主动思考和提问。
小组合作:通过小组活动,培养学生的合作能力。
实际操作:通过实际操作,加深对数学概念的理解。
教学步骤:第一节课:整式的乘除1. 导入:通过日常生活中的实例引入整式乘除的概念。
2. 新授:讲解乘法公式和整式乘除的运算方法。
3. 练习:布置练习题,让学生独立完成。
4. 小组讨论:学生分组讨论解题过程中的疑问。
第二节课:二元一次方程组1. 复习:回顾上节课的内容。
2. 新授:讲解二元一次方程组的解法。
3. 实际应用:解决实际问题,如“鸡兔同笼”问题。
4. 小组活动:分组解决实际问题,分享解题过程。
第三节课:不等式与不等式组1. 复习:回顾上节课的内容。
2. 新授:讲解不等式与不等式组的解法。
3. 练习:布置练习题,让学生独立完成。
4. 小组讨论:学生分组讨论解题过程中的疑问。
第四节课:数据的初步认识1. 导入:通过日常生活中的实例引入数据的概念。
2. 新授:讲解数据的收集与表示方法。
3. 实际操作:学生分组进行数据收集和计算。
4. 小组分享:分享数据收集和计算的过程和结果。
教学评价:课堂表现:观察学生在课堂上的参与度和积极性。
作业完成情况:检查学生的作业完成情况和质量。
测试:定期进行测试,评估学生的学习效果。
学生反馈:收集学生的反馈意见,了解学生的学习需求。
教案探索自然界的节奏生物课教学目标:1. 知识与技能:了解自然界中生物的生活节奏和适应性。
2015—2016学年度第二学期教学进度任课教师:学科:数学年(班)级:本学期总目标:培养学生良好的学习习惯,提高他们学习数学的热情,力争取得一个比较优异的学习成绩教研组长签字:说明:此表一式两份,一份作为教案附件之一粘贴在教案本上,一份上交教务处。
1.1 同底数幂的乘法教学目标:知识与技能:使学生在了解同底数幂乘法意义的基础上,掌握幂的运算性质(或称法则),进行基本运算。
过程与方法:在推导“性质”的过程中,培养学生观察、概括与抽象的能力。
情感、态度、价值观:提高学生学习数学的兴趣。
教学重点和难点:幂的运算性质.教学过程:一、实例导入:二、温故:2.,指出下列各式的底数与指数:(1)34;(2)a3;(3)(a+b)2;(4)(-2)3;(5)-23.其中,(-2)3与-23的含义是否相同?结果是否相等?(-2)4与-24呢?三、知新:1.利用乘方的意义,提问学生,引出法则计算103×102.解:103×102=(10×10×10)×(10×10)(幂的意义)=10×10×10×10×10 (乘法的结合律)=105.2.引导学生建立幂的运算法则将上题中的底数改为a,则有a3·a2=(aaa)·(aa)=aaaaa=a5,即a3·a2=a5=a3+2.用字母m,n表示正整数,则有即a m·a n=a m+n.3.引导学生剖析法则(1)等号左边是什么运算?(2)等号两边的底数有什么关系?(3)等号两边的指数有什么关系?(4)公式中的底数a可以表示什么(5)当三个以上同底数幂相乘时,上述法则是否成立?要求学生叙述这个法则:同底数幂相乘,底数不变,指数相加。
注意:强调幂的底数必须相同,相乘时指数才能相加.四、巩固:例1计算:(1) (-3)7×(-3)6;(2)(1/111)3×(1/111).(3) -x3·x5 (4) b2m·b2m+1..例2、光在真空中的速度约为3×108米/秒,泰照射到地球上大约需要5×102秒,地球距离太阳大约有多远?五、拓展:1、计算:(1)105·106;(2)a7·a3;(3)y3·y2;(4)b5·b;(5)a6·a6;(6)x5·x5.2、计算:(1)y12·y6;(2)x10·x;(3)x3·x9;(4)10·102·104;(5)y4·y3·y2·y;(6)x5·x6·x3.六、课堂小结:1.同底数幂相乘,底数不变,指数相加,对这个法则要注重理解“同底、相乘、不变、相加”这八个字.2.解题时要注意a的指数是1.3.解题时,是什么运算就应用什么法则.同底数幂相乘,就应用同底数幂的乘法法则;整式加减就要合并同类项,不能混淆.4.-a2的底数a,不是-a.计算-a2·a2的结果是-(a2·a2)=-a4,而不是(-a)2+2=a4.5.若底数是多项式时,要把底数看成一个整体进行计算。


北师大版七年级数学下册教案一、教学目标1.了解一次函数的定义和性质;2.掌握一次函数图像的绘制和判断;3.学会利用计算器求解一次函数的解;4.掌握一次函数在实际问题中的应用。
二、教学重点难点1.掌握一次函数的图像和性质;2.学会利用计算器求解一次函数的解;3.学会将一次函数应用于实际问题中。
三、教学内容1. 一次函数概念一次函数是指形如y=kx+b的函数,其中k和b都是常数。
其中,k被称为斜率,表示直线的斜率;b被称为截距,表示直线与y轴的交点。
如果k>0,则函数是增函数,图像向右上方延伸;如果k<0,则函数是减函数,图像向右下方延伸。
2. 一次函数图像绘制绘制一次函数图像的步骤如下:1.确定k的正负,以及b的值;2.找到y轴截距点(0,b);3.找到x轴截距点 $(-\\frac{b}{k},0)$;4.将两个点用直线连接,得到函数图像。
3. 一次函数解的求解利用计算器可以求解一次函数的解,其中求解步骤如下:1.打开计算器,进入计算器界面;2.输入一次函数,例如y=2x+1;3.选择求解模式,选择方程求解;4.输入待求解的值,例如y=7;5.计算器即可求出对应的x值。
4. 一次函数应用一次函数在实际问题中有广泛应用,例如以下问题:例1甲、乙两人跑步比赛,已知甲的速度是4千米每小时,乙的速度是6千米每小时,乙比甲先2小时到达终点。
求比赛路程长度。
解:设比赛路程长度为x千米,则甲的运动方程为y1=4t,乙的运动方程为y2=6(t−2),其中t表示时间。
由题意可得:y1=y24t=6(t−2)t=4将t=4代入y1=4t得到甲跑了16千米,故比赛路程长度为$16\\times2=32$ 千米。
例2一张纸片长30厘米,高20厘米,现用它折成一个正方形,求正方形的边长及面积。
解:设正方形的边长为x厘米,则可以列出下列方程:2x+30=20解得x=−5,因此不能构造正方形。
此时回顾问题,发现纸张已给定,且不能裁剪,因此不能折成正方形。

北师大七年级数学下册教案8篇作为一名优秀的教育工作者,可能需要进行教案编写工作,教案是实施教学的主要依据,有着至关重要的作用。
来参考自己需要的教案吧!下面是辛苦为朋友们带来的8篇《北师大七年级数学下册教案》,在大家参考的同时,也可以分享一下给您的好友哦。
北师大七年级数学下册教案篇一教学目标:1.知识与技能结合具体实例,进一步认识三角形的概念,掌握三角形三条边的关系。
2.过程与方法通过观察、操作、想象、推理、交流等活动,发展空间观念,推理能力和有条理地表达能力。
3.情感、态度与价值观联系学生的生活环境、创设情景,帮助学生树立几何知识源于实际、用于实际的观念,激发学生的学习兴趣。
教学重点难点:1.重点让学生掌握三角形的概念及三角形的三边关系,并能运用三边关系解决生活中的实际问题。
2.难点探究三角形的三边关系应用三边关系解决生活中的实际问题。
教学设计:本节课件设计了以下几个环节:回顾与思考、情境引入、三角形的`概念、探索三角形三边关系、练习应用、课堂小结、探究拓展思考、布置作业。
第一环节回顾与思考1、如何表示线段、射线和直线?2、如何表示一个角?第二环节情境引入活动内容:让学生收集生活中有关三角形的图片,课上让学生举例,并观察图片。
活动目的:让学生能从生活中抽象出几何图形,感受到我们生活在几何图形的世界之中。
培养学生善于观察生活、乐于探索研究的学习品质,从而更大地激发学生学习数学的兴趣第三环节三角形概念的讲解(1)你能从中找出四个不同的三角形吗?(2)与你的同伴交流各自找到的三角形。
(3)这些三角形有什么共同的特点?通过上题的分析引出三角形的概念、三角形的表示方法及三角形的边角的表示方法。
并出两道习题加以练习,从练习中归纳出三角形的三要素和注意事项。
北师大七年级数学下册教案篇二一、教学目标1、知识目标:掌握数轴三要素,会画数轴。
2、能力目标:能将已知数在数轴上表示,能说出数轴上的点表示的数,知道有理数都可以用数轴上的点表示;3、情感目标:向学生渗透数形结合的思想。
2015—2016学年度第二学期教学进度任课教师:学科:数学年(班)级:本学期总目标:培养学生良好的学习习惯,提高他们学习数学的热情,力争取得一个比较优异的学习成绩教研组长签字:说明:此表一式两份,一份作为教案附件之一粘贴在教案本上,一份上交教务处。
1.1 同底数幂的乘法教学目标:知识与技能:使学生在了解同底数幂乘法意义的基础上,掌握幂的运算性质(或称法则),进行基本运算。
过程与方法:在推导“性质”的过程中,培养学生观察、概括与抽象的能力。
情感、态度、价值观:提高学生学习数学的兴趣。
教学重点和难点:幂的运算性质.教学过程:一、实例导入:二、温故:2.,指出下列各式的底数与指数:(1)34;(2)a3;(3)(a+b)2;(4)(-2)3;(5)-23.其中,(-2)3与-23的含义是否相同?结果是否相等?(-2)4与-24呢?三、知新:1.利用乘方的意义,提问学生,引出法则计算103×102.解:103×102=(10×10×10)×(10×10)(幂的意义)=10×10×10×10×10(乘法的结合律)=105.2.引导学生建立幂的运算法则将上题中的底数改为a,则有a3·a2=(aaa)·(aa)=aaaaa=a5,即a3·a2=a5=a3+2.用字母m,n表示正整数,则有即a m·a n=a m+n.3.引导学生剖析法则(1)等号左边是什么运算?(2)等号两边的底数有什么关系?(3)等号两边的指数有什么关系?(4)公式中的底数a可以表示什么(5)当三个以上同底数幂相乘时,上述法则是否成立?要求学生叙述这个法则:同底数幂相乘,底数不变,指数相加。
注意:强调幂的底数必须相同,相乘时指数才能相加.四、巩固:例1计算:(1) (-3)7×(-3)6;(2)(1/111)3×(1/111).(3)-x3·x5 (4) b2m·b2m+1..例2、光在真空中的速度约为3×108米/秒,泰阳光照射到地球上大约需要5×102秒,地球距离太阳大约有多远?五、拓展:1、计算:(1)105·106;(2)a7·a3;(3)y3·y2;(4)b5·b;(5)a6·a6;(6)x5·x5.2、计算:(1)y12·y6;(2)x10·x;(3)x3·x9;(4)10·102·104;(5)y4·y3·y2·y;(6)x5·x6·x3.六、课堂小结:1.同底数幂相乘,底数不变,指数相加,对这个法则要注重理解“同底、相乘、不变、相加”这八个字.2.解题时要注意a的指数是1.3.解题时,是什么运算就应用什么法则.同底数幂相乘,就应用同底数幂的乘法法则;整式加减就要合并同类项,不能混淆.4.-a2的底数a,不是-a.计算-a2·a2的结果是-(a2·a2)=-a4,而不是(-a)2+2=a4.5.若底数是多项式时,要把底数看成一个整体进行计算。
北师大七年级数学下册教案北师大七年级数学下册教案教学目标:1.让学生理解和掌握本节课的基本概念和方法;2.培养学生的逻辑思维能力和问题解决能力;3.通过实际应用,让学生了解数学在现实生活中的应用价值。
教学内容:本节课我们将学习“XXXX”章节,包括以下几个部分:1.XXXX的基本概念;2.XXXX的运算规则;3.XXXX在实际生活中的应用。
教学重点与难点:重点:理解和掌握XXXX的基本概念及运算规则;难点:如何运用XXXX解决实际问题。
教具和多媒体资源:1.黑板;2.投影仪(用于展示例题、图片等);3.教学软件(可用于互动环节,增强学生的参与感)。
教学方法:1.激活学生的前知:通过提问,回顾与本节课相关的已学知识;2.教学策略:采用讲解、示范、小组讨论和实例分析的方式进行教学;3.学生活动:让学生参与讨论,动手操作,加深对知识的理解。
教学过程:1.导入:通过问题导入或情境导入,引发学生的思考;2.讲授新课:详细讲解XXXX的基本概念、运算规则,通过例题进行示范;3.巩固练习:让学生动手计算,完成一定数量的练习题,教师进行巡回指导;4.归纳小结:总结本节课的主要内容,回顾学生的学习成果;5.作业布置:布置与本节课内容相关的作业,要求学生按时完成。
评价与反馈:1.设计评价策略:通过课堂练习、小组讨论、教师观察等方式评价学生的学习效果;2.为学生提供反馈:针对学生在课堂上的表现,给予及时的反馈和指导,帮助他们改进。
教师自我反思:通过本节课的教学,我认为自己在以下几个方面表现较好:首先,教学思路清晰,能够有条理地展开教学内容;其次,注重与学生的互动,及时回答学生的问题,引导他们深入思考。
但是,我也发现自己在某些方面仍有提高的空间,如部分例题的选择不够典型,未能很好地体现知识的应用价值。
在今后的教学中,我将更加注重例题的选取,让学生更多地接触到实际问题的应用。
同时,我也会更加关注学生的学习状态,及时调整教学策略,确保学生能够更好地掌握知识。
第1页共137页1.1同底数幂的乘法教学目标:知识与技能:使学生在了解同底数幂乘法意义的基础上,掌握幂的运算性质(或称法则),进行基本运算。过程与方法:在推导“性质”的过程中,培养学生观察、概括与抽象的能力。情感、态度、价值观:提高学生学习数学的兴趣。教学重点和难点:幂的运算性质.教学过程:一、实例导入:二、温故:
2.,指出下列各式的底数与指数:(1)34;(2)a3;(3)(a+b)2;(4)(-2)3;(5)-23.其中,(-2)3与-23的含义是否相同?结果是否相等?(-2)4与-24
呢?三、知新:1.利用乘方的意义,提问学生,引出法则计算103×102.解:103×102=(10×10×10)×(10×10)(幂的意义)
=10×10×10×10×10(乘法的结合律)第2页共137页
=105.
2.引导学生建立幂的运算法则将上题中的底数改为a,则有a3·a2=(aaa)·(aa)
=aaaaa=a5,
即a3·a2=a5=a3+2.用字母m,n表示正整数,则有
即am·an=am+n.3.引导学生剖析法则(1)等号左边是什么运算?(2)等号两边的底数有什么关系?(3)等号两边的指数有什么关系?(4)公式中的底数a可以表示什么(5)当三个以上同底数幂相乘时,上述法则是否成立?
要求学生叙述这个法则:同底数幂相乘,底数不变,指数相加。注意:强调幂的底数必须相同,相乘时指数才能相加.四、巩固:例1计算:第3页共137页
(1)(-3)
7×(-3)6;(2)(1/111)3×(1/111).
(3)-x3·x5(4)b2m·b2m+1..例2、光在真空中的速度约为3×108米/秒,泰阳光照射到地球上大约需要5×102秒,地球距离太阳大约有多远?五、拓展:1、计算:(1)105·106;(2)a7·a3;(3)y3·y2;(4)b5·b;(5)a6·a6;(6)x5·x5.
2、计算:(1)y12·y6;(2)x10·x;(3)x3·x9;(4)10·102·104;(5)y4·y3·y2·y;(6)x5·x6·x3.
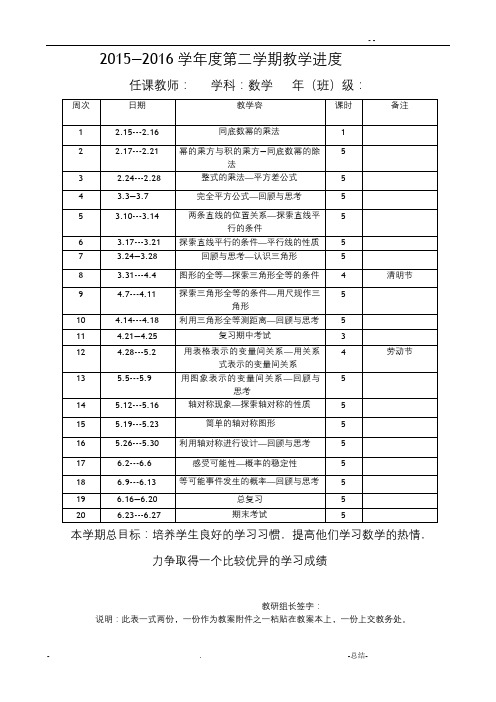
2015—2016学年度第二学期教学进度 任课教师: 学科:数学 年(班)级: 周次 日期 教学内容 课时 备注 1 2.15---2.16 同底数幂的乘法 1 2 2.17---2.21 幂的乘方与积的乘方—同底数幂的除法 5
3 2.24---2.28 整式的乘法—平方差公式 5 4 3.3—3.7 完全平方公式—回顾与思考 5 5 3.10---3.14 两条直线的位置关系—探索直线平行的条件 5
6 3.17---3.21 探索直线平行的条件—平行线的性质 5 7 3.24—3.28 回顾与思考—认识三角形 5
8 3.31---4.4 图形的全等—探索三角形全等的条件 4 清明节 9 4.7---4.11 探索三角形全等的条件—用尺规作三角形 5
10 4.14---4.18 利用三角形全等测距离—回顾与思考 5 11 4.21—4.25 复习期中考试 3 12 4.28---5.2 用表格表示的变量间关系—用关系式表示的变量间关系 4 劳动节
13 5.5---5.9 用图象表示的变量间关系—回顾与思考 5 14 5.12---5.16 轴对称现象—探索轴对称的性质 5 15 5.19---5.23 简单的轴对称图形 5 16 5.26---5.30 利用轴对称进行设计—回顾与思考 5 17 6.2---6.6 感受可能性—概率的稳定性 5 18 6.9---6.13 等可能事件发生的概率—回顾与思考 5 19 6.16—6.20 总复习 5 20 6.23---6.27 期末考试 5 本学期总目标:培养学生良好的学习习惯,提高他们学习数学的热情,
力争取得一个比较优异的学习成绩
教研组长签字: 说明:此表一式两份,一份作为教案附件之一粘贴在教案本上,一份上交教务处。 1.1 同底数幂的乘法 教学目标: 知识与技能:使学生在了解同底数幂乘法意义的基础上,掌握幂的运算性质(或称法则),进行基本运算。 过程与方法:在推导“性质”的过程中,培养学生观察、概括与抽象的能力。 情感、态度、价值观:提高学生学习数学的兴趣。 教学重点和难点: 幂的运算性质. 教学过程: 一、实例导入: 二、温故:
2.,指出下列各式的底数与指数: (1)34;(2)a3;(3)(a+b)2;(4)(-2)3;(5)-23. 其中,(-2)3与-23的含义是否相同?结果是否相等?(-2)4与-24
呢? 三、知新: 1.利用乘方的意义,提问学生,引出法则 计算103×102. 解:103×102=(10×10×10)×(10×10)(幂的意义) =10×10×10×10×10 (乘法的结合律) =105. 2.引导学生建立幂的运算法则 将上题中的底数改为a,则有 a3·a2=(aaa)·(aa) =aaaaa =a5, 即a3·a2=a5=a3+2. 用字母m,n表示正整数,则有
即am·an=am+n. 3.引导学生剖析法则 (1)等号左边是什么运算? (2)等号两边的底数有什么关系? (3)等号两边的指数有什么关系? (4)公式中的底数a可以表示什么 (5)当三个以上同底数幂相乘时,上述法则是否成立?
要求学生叙述这个法则:同底数幂相乘,底数不变,指数相加。 注意:强调幂的底数必须相同,相乘时指数才能相加. 四、巩固: 例1 计算: (1) (-3)7×(-3)6; (2)(1/111)3×(1/111). (3) -x3·x5 (4) b2m·b2m+1. .例2、光在真空中的速度约为3×108米/秒,泰阳光照射到地球上大约需要5×102秒,地球距离太阳大约有多远? 五、拓展: 1、计算:(1)105·106;(2)a7·a3;(3)y3·y2; (4)b5·b; (5)a6·a6;(6)x5·x5. 2、计算:(1)y12·y6;(2)x10·x;(3)x3·x9; (4)10·102·104;(5)y4·y3·y2·y;(6)x5·x6·x3. 六、课堂小结: 1.同底数幂相乘,底数不变,指数相加,对这个法则要注重理解“同底、相乘、不变、相加”这八个字. 2.解题时要注意a的指数是1. 3.解题时,是什么运算就应用什么法则.同底数幂相乘,就应用同底数幂的乘法法则;整式加减就要合并同类项,不能混淆. 4.-a2的底数a,不是-a.计算-a2·a2的结果是-(a2·a2)=-a4,而不是(-a)2+2=a4. 5.若底数是多项式时,要把底数看成一个整体进行计算。 七、板书设计:
八、教学后记: 1.2幂的乘方与积的乘方(1) 教学目标: 知识与技能:了解幂的乘方与积的乘方的运算性质,并能解决一些实际问题。 过程与方法:经历探索幂的乘方与积的乘方的运算性质的过程,进一步体会幂的意义,发展推理能力和有条理的表达能力。 情感、态度、价值观:提高学生学习数学的兴趣。
教学重点:会进行幂的乘方的运算。 教学难点:幂的乘方法则的总结及运用。 教学方法:尝试练习法,讨论法,归纳法。 活动准备:课件 教学过程: 一、温故: 计算(1)(x+y)2·(x+y)3(2)x2·x2·x+x4·x (3)(0.75a)3·(41a)4(4)x3·xn-1-xn-2·x4 通过练习的方式,先让学生复习乘方的知识,并紧接着利用乘方的知识探索新课的内容。 二、知新: 1、64表示_________个___________相乘. (62)4表示_________个___________相乘. a3表示_________个___________相乘. (a2)3表示_________个___________相乘. 在这个练习中,要引导学生观察,推测(62)4与(a2)3的底数、指数。并用乘方的概念解答问题。 2、(62)4=________×_________×_______×________=__________ (33)5=_____×_______×_______×________×_______=__________ (a2)3=_______×_________×_______=__________ (am)2=________×_________=__________ (am)n=________×________×…×_______×__________=__________ 即 (am)n= ______________(其中m、n都是正整数) 通过上面的探索活动,发现了什么? 幂的乘方,底数__________,指数__________. 学生在探索练习的指引下,自主的完成有关的练习,并在练习中发现幂的乘方的法则,从猜测到探索到理解法则的实际意义从而从本质上认识、学习幂的乘方的来历。教师应当鼓励学生自己发现幂的乘方的性质特点(如底数、指数发生了怎样的变化)并运用自己的语言进行描述。然后再让学生回顾这一性质的得来过程,进一步体会幂的意义。 三、巩固: 1、计算下列各题: (1)(102)3 (2)(b5)5 (3)(an)3 (4)-(x2)m (5)(y2)3·y (6)2(a2)6-(a3)4 学生在做练习时,不要鼓励他们直接套用公式,而应让学生说明每一步的运算理由,进一步体会乘方的意义与幂的意义。 2、 判断题,错误的予以改正。 (1)a5+a5=2a10 ( ) (2)(s3)3=x6 ( ) (3)(-3)2·(-3)4=(-3)6=-36 ( ) (4)x3+y3=(x+y)3 ( ) (5)[(m-n)3]4-[(m-n)2]6=0 ( ) 学生通过练习巩固刚刚学习的新知识。在此基础上加深知识的应用. 四、拓展: 1、 1、计算 5(P3)4·(-P2)3+2[(-P)2]4·(-P5)2 [(-1)m]2n+1m-1+02002―(―1)1990 2、 若(x2)n=x8,则m=_____________. 3、 、若[(x3)m]2=x12,则m=_____________。 4、 若xm·x2m=2,求x9m的值。 5、 若a2n=3,求(a3n)4的值。 6、已知am=2,an=3,求a2m+3n的值.
五、课堂小结:会进行幂的乘方的运算。 六、作业设计:课本P6习题1.2:1、2 七、板书设计:
八、教学后记:
1.2幂的乘方与积的乘方(2) 教学目标: 知识与技能:了解积的乘方的运算性质,并能解决一些实际问题。 过程与方法:经历探索积的乘方的运算的性质的过程,进一步体会幂的意义,发展推理能力和有条理的表达能力。 情感、态度、价值观:提高学生学习数学的兴趣。 教学重点:积的乘方的运算 教学难点:正确区别幂的乘方与积的乘方的异同。 教学方法:探索、猜想、实践法 教学用具:课件 教学过程: 一、温故: 1、计算下列各式: (1)_______25xx (2)_______66xx (3)_______66xx (4)_______53xxx(5)_______)()(3xx(6)_______3423xxxx 2、下列各式正确的是( ) (A)835)(aa (B)632aaa (C)532xxx(D)422xxx 二、知新: 1、 计算:333___)(____________________________52 2、 计算:888___)(____________________________52 3、 计算:121212___)(____________________________52 从上面的计算中,你发现了什么规律?_________________________ 4、猜一猜填空:(1)(___)(__)453)53( (2)(___)(__)53)53(m (3)(___)(__))(baabn 你能推出它的结果吗? 结论:积的乘方等于把各个因式分别乘方,再把所得的幂相乘。 三、巩固: 1、 计算下列各题:(1)666(__)(__))(ab