立交匝道计算案例——又一个高速公路立交匝道的计算

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

广州市轨道交通八号线北延段工程（文化公园～白云湖)白云湖车辆段桥梁计算书中铁上海设计院集团有限公司2015年2月计算书工程(项目)编号勘察设计阶段施工图设计工程名称单体名称桥梁工程计算内容结构计算（共页）38计算日期校核日期审核日期1.工程概况1.1 桥型布置本工程中匝道1孔跨布置为（16+10.5+16）+（4×16）m，共两联；匝道2孔跨布置为（3×16）+（（2×13.85+8.3）m，共两联；匝道4孔跨布置为4x16m，该桥为双幅桥，共一联，所有箱梁结构均为等截面钢筋混凝土单箱单室连续箱梁。

1.2 桥面布置桥梁全宽8m，具体布置为0.5m（栏杆）+7m（车行道）+0.5m（栏杆）。

桥梁横断面如下图所示：2.设计技术标准（1）设计荷载：城—B级；（2）桥梁净宽：所有匝道净宽7m；（3）桥下通行净高：跨越城市主干道、快速路和高速公路的净空高≥5.5m；（4）设计洪水频率：1/100；（5）抗震设防烈度： 6度，地震动峰值加速度为0.05g；（6）坐标系：（7）高程系：（8）环境类别：I类；（9）结构设计基准期：100年；（10）结构安全等级：一级。

（11）钢筋混凝土构件的裂缝宽度容许值根据规范要求，Ⅰ、Ⅱ类环境中钢筋混凝土构件限值：0.2mm，本次工程所处环境为沿海潮湿环境，故结构计算时钢筋混凝土构件限值按0.15mm控制。

（12）主要材料a 混凝土：主梁采用C50砼；b 普通钢筋：HPB400、HPB300钢筋；3.设计依据及规范3.1 设计依据3.2 设计规范1.《公路工程技术标准》(JTG B01—2003)2.《公路工程基本建设项目设计文件编制办法》(2007年)3.《公路工程地质勘察规范》(JTJ 064—98)4.《公路勘测规范》(JTG C10—2007)5.《公路工程水文勘测设计规范》(JTG C30-2002)6.《公路桥涵设计通用规范》(JTG D60—2004)7.《城市桥梁设计规范》（CJJ 11-2011）8.《城市桥梁抗震设计规范》（CJJ 166-2011）9.《公路圬工桥涵设计规范》(JTG D61—2005)10.《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)11.《公路涵洞设计细则》(JTG/T D65—04—2007)12.《公路桥涵地基与基础设计规范》(JTG D63—2007)13.《公路桥梁抗震设计细则》(JTG/T B02-01—2008)14.《公路桥涵施工技术规范》（JTG/T F50-2011）15.《公路交通安全设施设计规范》(JTG D81—2006)16.《公路交通安全设施设计细则》(JTG/T D81-2006)17.《混凝土结构耐久性设计规范》（GB/T 50476-2008）18.《城市桥梁桥面防水工程技术规程》CJJ 139-201019.《城市桥梁工程施工与质量验收规范》CJJ2-20083.3 地质情况1、<1>素填土：灰黄色、灰褐色、深灰色，由耕植土，粉质粘土、中粗砂等组成，局部含少量建筑垃圾，欠压实。

匝 道 设 计 数 据 录 入 表
一匝道 起点 ZH HY1 YH1 HY2 YH2 HZ 终点 二匝道 起点 ZH HY1 YH1 HY2 YH2 HZ 终点 K000+090.000 K000+160.000 K000+223.715 K000+271.881 K000+384.032 K000+444.032 K000+544.032 9987.403 9968.981 9910.603 9880.438 9922.316 9981.363 10081.363 10059.378 10125.341 10136.791 10100.904 10007.909 10000.000 10000.000 1.000 50.000 50.000 75.000 75.000 1.000 0.000 桩 号 坐 X(M) 标 Y(M) 半径R（M)
请输入中桩到 左 边桩垂距（M)= 3.50 请输入中桩到 右 边桩垂距（M)= 3.50
请输入自定义逐桩距
ห้องสมุดไป่ตู้ 切线方位角
备 注
输
入
说
明
匝道的组成：起点直线-缓和曲线（ZH)-圆 曲线（HY1)-卵形曲线（YH1)-圆曲线(HY2)缓和曲线(YH2)-直线（HZ)-终点。 1、切线方位角: 136°08′20.6″ 按 136.08206 格式输入。 2、半径输入：缓和曲线接直线端输入“1”， 其余按设计参数输入，直线不作规定。 3、起点或终点无直线段可不作输入，但ZH-HZ 间各行必须输入。如：接直线端无缓和曲线 92.17262 132.23516 205.24336 251.24185 337.04542 0.00000 0.00000 ，HY1、YH1输入同一点参数过度。 4、自定义逐桩距的取值：请按以下线性设计 逐桩点个数及线段长度选择 2、 2.5、5、 10、 20、25、50米7个级数。 直线、圆曲线50个逐桩点，如果自定义 逐桩距为5米，可计算250米长的直线和圆 曲线； 完整缓和曲线50个逐桩点； 不完整缓和曲线40个逐桩点，如果自定义 逐桩距为5米 ，可计算200米长的不完整 缓和曲线。 如果要同时计算两条匝道，请根据长匝道中 的最长线段自定义逐桩距，使其完整显示。

某公路互通立交匝道桥现浇箱梁跨既有高速公路施工方案及安全专项方案**互通 D 匝道第五联跨**施工方案一、工程概述**互通 D 匝道桥全长 1057.595m，共分 12 联。

第五联跨越**高速公路，其中 D 匝道 19#墩（桩基桩径 1.3m，桩长 20m；立柱直径1.2m，柱长 14m。

）位于**高速中央分隔带内。

第五联采用 20m+20+17.03m 预应力混凝土现浇连续箱梁，桥面宽 10.5m，采用单箱双室。

为了不影响**高速公路的通车，在**高速南行和北行线搭设门洞，门洞净高9.9m，净宽8.5m，并且在门洞两端加设警示标牌及限速标志，摆放防撞沙桶，做好安全防护工作。

二、施工工艺（一）、门洞设计D匝道第 18#、19#、20#两跨梁体跨越**高速，其下搭设门洞。

门洞由混凝土基础、钢管柱、工字钢、贝雷梁组成。

门洞搭设步骤：混凝土基础 14 .5*0. 5*1.0m 钢管柱υ46.2cm*900cm*0.8cm I40a 贝雷梁 5mm 钢板（见附图 1）。

1、门洞验算1．1、门洞纵梁验算支架纵梁采用 19 片贝雷梁拼装，每片贝雷梁长 12 米。

①、每孔梁重:131.51m3×26KN/m3=3419KN每米梁体荷载：3419/20=171KN/m②、模板重量:200kg/m2=2KN/m2（含贝雷梁之上的钢管及顶托、底托）（1.3×2+2×2+8）×2=29.2KN/m ③、施工人员及机具200kg/m2 2×12×1=24KN/md、振捣时产生的荷载：2.0KPa2×12×1=24KN/m④、贝雷梁：[M]=788.2KN?m[Q]=245.2KN则贝雷梁荷载集度为：275×19×10/(3×1000)+24+24+29.2+171=265.6KN/m ⑤、弯矩验算梁体底模12*12cm方木碗扣支架10*10cm方木5mm防坠物钢板贝雷梁I40工字钢图 1支架纵梁受力图q9.78mM=1/8×265.6×9.782×1/19=167.1KN?m＜[M]=788.2 KN?m⑥、剪力：Q=1/2×265.6×9.78/19=68.36KN＜[Q]=245.2KN⑦、挠度：fmax=5ql4/384EI=[5×（1.3×1×26+5.3+2+2+2.4）×124]/（2 ×384×1.95×105×250500×10-8）=3.5㎜1.2、横梁验算（1）、荷载集度支架横梁采用双 I40a 型工字钢，自重 135.2kg/mq=275×10/(3×1000)+24+24+29.2+171+1.352=250.5KN/m （2）、横梁受弯应力、剪力计算按 2.5 米跨度简支梁计算，计算简图见下图 2qR R R R R R1 2.5 2.5 2.5 2.5 2.5 1q2.5m图 2支架横梁受力图M =1/8ql2=1/8×250.5×2.52=195.7KN/m σ=M = 195.7 ?10 3 =90Mpa<【σ】=150Mpa W1090 ? 2Q=2.5×250.5/2=313.13KNτmax=QS = 313.13? 86.1 = 44MPa<1.3*85Mpa 2 ?1.42 ? 21720bI（3）、挠度验算f =45ql=5 ? 250.5 ? 25004l384EIx384 ?1.95 ?105 ? 2.17 ?108=3.01mm<400= 6.25mm1.3、钢管柱验算每排横梁处设 6 根Φ42.6㎝×8㎜的钢管柱（计算长度 9m ）R=(12×265.6+1.352×29)×1/2×1/6=268.9KN钢管容许轴应力【σ】=140 Mpa钢管截面特性：截面积：Am=3.14×426×8=105.055㎝2截面最小回转半径：r= Im/ Am = 22952.91/105.055 =14.78㎝长细比：λ=L/r=900/14.78=60.893查稳定系数表得稳定系数：Φ=0.896强度验算：σ= R = 268.9 ?10 3= 26MPa < 【σ】=140MpaA 10506稳定性验算：σ= 268.9 ?103= 29MPa < 【σ】=140MPa0.896 ?105061.4、基底承载力验算每根钢管重：10506×10-6×9×7850=494.83kg=7.27KN混凝土基础自重：1.25×1.0×0.5×26=16.25KN（混凝土基础尺寸：长×宽×高=1.25×1×0.5m）P=268.9+7.27+16.25=292.4KNσ=2.5292.41= 117KPa<【σ】=200MPa既有公路路面承载力大于 200KPa ,可满足要求。

高速公路线路（缓和曲线、竖曲线、圆曲线、匝道）坐标计算公式未知2009-12-27 21:40:34 本站高速公路的一些线路坐标、高程计算公式（缓和曲线、竖曲线、圆曲线、匝道）一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：I②圆曲线的半径：R③缓和曲线的长度：I o④转向角系数：K（1或一1）⑤过ZH点的切线方位角：a⑥点ZH的坐标：x z, y z计算过程：SJ Q , = — + n 180I4)S= j£*y ：⑸ q 二 4+4-90(6)K J = ScosC^⑺比=SsinOjI0]x F + XZl9]y = y L + y E公式中n 的取值如下:当计算第二缓和曲线上的点坐标时，则:I 为到点HZ 的长度 a 为过点HZ 的切线方位角再加上180 °K 值与计算第一缓和曲线时相反x z , y z 为点HZ 的坐标切线角计算公式：二、圆曲线上的点坐标计算6R1,说明：当曲线为左转向时， K=1，为右转向时,K=-1,此文档收集于网络，如有侵权请联系网站删除已知：①圆曲线上任一点离ZH点的长度：I②圆曲线的半径：R③缓和曲线的长度：I o④转向角系数：K（1或一1）⑤过ZH点的切线方位角：a⑥点ZH的坐标：x z, y z计算过程：j I JQ J_ 90 （21■亠h）_ ~~1绯=卫_^—24R 2683R H ⑶珀二丄--+―—} 2240E! 34560R'= [Rd-cos^'）+p]K 旧）叭=Rain0 J+ID（0]q, = arctg —+n- 1E0XoJ盖亠犹侣]4 = 4+』—90[9）Xi= ScosCLj（10]y i = SsinC^II l）X= Ix+Xj11旳二咒+y.说明：当曲线为左转向时，K=1，为右转向时,K=-1 , 公式中n的取值如下：此文档收集于网络，如有侵权请联系网站删除Q > 0<0Zo >0'y t > 0n = 0n = 2n = 1n= 1当只知道HZ点的坐标时，则:I为到点HZ的长度a为过点HZ的切线方位角再加上180 °K值与知道ZH点坐标时相反x z, y z为点HZ的坐标三、曲线要素计算公式⑴緩曲段任意点转角値】6-：2Rlo⑵曲缠段任意虐转角值’ B 二空空I M ZC PCP JI2 ⑶第-缓曲段总转角值吩寻⑷第二缓曲段总转角值鳴.繁⑻第二曲线平移重,Pz =空--亠百2跟 26SSR 3⑸第一切蛙长| T1 -聖二邑十士虫十鹿十2R ） tg-t ril-U 2.2 2tg- 2QD 曲线全扶虧L = R 如乜）2曲圆曲线扶度:L 0 = Ra--(lj + 12)2⑬曲绕段长虧［=丄丄』空邛 ⑭偏窝愛曲D 的边线曲线按度：1=M + D|i公式中各符号说明:I ——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度） I i ――第一缓和曲线长度I 2――第二缓和曲线长度I 0――对应的缓和曲线长度2R1F2⑸第一曲线価移E ）mi -h2 240R Z 34560R'⑹第二曲块顺移藝服=旦2 240^*54 西OR ⑺第一曲統平移董;P1 24R 26881^^2 /%侧第二切线长;廿比晋十;山十现衣叭斤十恥R――圆曲线半径R——曲线起点处的半径F2——曲线终点处的半径P i――曲线起点处的曲率P2――曲线终点处的曲率a――曲线转角值四、竖曲线上高程计算已知：①第一坡度：i i（上坡为“ + ”，下坡为“一”）②第二坡度：i2（上坡为“ + ”，下坡为“―”）③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：sH带有符号）I21R =-------ir _ ii_ 1 ~l f⑶H上也+ ——-_丄--RiA,五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i i第二横坡：i 2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/L23i=(i 2-i 1)(1-3d 2+2d3)+i 1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：a 0⑥曲线起点处曲率：P0( 左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1( 左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：X,y②待求点的切线方位角：a T 计算过程：S=K-K,[H 当 p ( = Pt=0 时 1x=xa+Scos J y^y (j+SsinCU⑵当R = p 冲附Cli = SF'i+OtiX 二比十-sin 4)厲 y=y.-tcos cos CU ) /F\ cir=a[3]当 P^PM=4 SO (P±-P J—Kflt=Nl s R/(P l -R )1=1.+SNC =Ck=S (14-lJ/2/CT-a-NlJ/2Cr —£ i f -ii l 11- ir----- — ---- 十 -------此 S36C 3 42240C 1x=i (>4 NAcosT- BsinTy=y il -F N^sirLT-bBcos注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1 ,当x>0时sgn(x)=1 ,当x=0时sgn(x)=0 。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

立交设计讲座-匝道平面设计方法1、右转匝道曲线布置形式（1）如图1A所示，布置一个半径较大的单圆曲线，其两端应按规定配置缓和曲线（下同）。

（2）如图1b所示，布置不同半径按规定组合的复曲线，以适应地形、地物限制，或减少拆迁、少占良田。

该匝道曲线半径R1<R2，大圆应靠近主线，对于汽车进入主线前可能提前加速行驶有利。

（3）如图1c所示，同样而置了复曲线，但R1>R2，小圆靠近主线，对于车辆进入主线前可能提前加速行驶不利。

如能布置较长的变速车道，或城市道路主线车速不高时方可采用。

（4）如图2所示，把外环匝道布置成连续三个反向曲线，其中中间一个曲线的曲率半径最好与内环曲率半径协调布置为同心圆，使两线在一定范围内互相平行，便于设置桥梁或路基，该类型匝道布置非常紧湊，占地较少，对于城市立交来说，以最大限度节约用地，减少拆迁工程量。

由于三个曲线的半径一般较小，当匝道车速较高时不适用。

当不受条件限制，曲线半径相当大时可以采用，如济青高速公路某处，即采用了不连续三个反向曲线的匝道。

（5）如图3所示，由于某种需要，可以把匝道布置成两个曲线夹一段直线。

这种布置较图2显然会增大占地和拆迁范围，在用地紧张或拆迁过多时不宜采用。

2、左转小环道曲线布置形式（1）图4a所示为单圆曲线两端配置较长的缓和曲线作为内环匝道，是城市道路立交中常采用的一种线形。

此种形式曲率变化单一，行车适顺，线形对称优美，设计施工都较简便，一般情况下常被采用。

（2）如图4b所示，用双心怎复曲线两端配置较长的缓和曲线作为内环匝道，能更好地适应地形、地物变化，减少拆迁，节约工程投资。

但是，为适应汽车进出主线前可能得前加速或未能及时减速行驶，大圆半径曲线以紧靠主线设置这宜。

（3）图4c、d所示的三心复曲线，两端配置必须的缓和曲线作为内环匝道是比较理想的线形。

前者多用于喇叭型立交，后者多用于苜蓿叶型立交。

汽车驶离主线或交叉线进入内环时，经过变速车道变速，车速应该达到内环曲线要求，但往往因为某种原因或驾驶员稍有不慎，车速仍然较高。

辅助车道

设计原则：出入顺畅、安全、线形与正线协调,出入口
应易于辨认，正线与匝道间相互通视。
五 端部设计
一、出口与入口设计
【主线出、入口】：一般情况下主线出、入口应设在主线行 车道的右侧，出口位置应易于识别。
出口：上坡路段－便于减速，一般在构造物前，若在后，
距离>150m 入口：下坡路段－便于加速
一级公路 二（一）
二级公路 三（二）
三级公路 三
四级公路 三
一级公路
二级公路 三级公路 四级公路
二（一）
三（二） 三 三
三（二）
（三） （三） （三）
（三）
/ / /
（三）
/ / /
（三）
/ / /
三、匝道的设计依据
（二）匝道的设计速度 根据立交的类型、转弯交通量的大小以及用地和建

设费用等条件选定。
3 匝道设计
一、匝道的基本形式
按匝道的功能及其与 相交道路的关系划分 右转匝道 左转匝道
1．右转匝道
特点：右出右进， 不设跨线构造物； 方向明确， 车速高。
2．左转匝道
车辆须转约90～270°越过对向车道，除环圈匝道外，至 少需要一座跨线构造物。 1）直接式：又称定向式或左出左进式。 左转车辆直接从左侧驶出，左转弯，到相交道路的左侧驶入。

平行式变速车道端部应设渐变段与正线连接。
五 端部设计
（2）直接式：不设平行路段，由正线斜向渐变加宽，形成一条 与匝道连接的附加车道。 特点：线形平顺与行车轨迹吻合，对行车有利。但起点不易识 别

五 端部设计

采用原则： 减速车道采用直接式
加速车道采用平行式 变速车道为双车道时，加减速车道均采用直接式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式_★★高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

( 7)
d l = r・ dβ=
A
2
l1 + l
dβ
上式积分即得到弧长 l 所对应的非完整缓和曲 线角 : β= l + l 2 R1 2 A 若 R1 < R2 ,则有 : β= 1 - l 2 R1 2 A 再由 :
d l = r・ dβ d x = d l・ cosβ d y = d l・ sinβ
第 28 卷 , 第3 期 2003年9月
中 南 公 路 工 程 Central South Highway Engineering
Vol . 28 ,No . 3 Sep . , 2 0 0 3
高速公路互通立交匝道非完整缓和曲线计算
隋永芹 , 张雪华 , 王家红
江苏 苏州 215001)
[摘 要 ] 在高速公路互通立交匝道线形设计中 ,非完整缓和曲线上任意一点坐标计算较为困难 ,通过公式推
DX < 0 , DY > 0 时 , A O1 = 180 - θ; DX < 0 , DY < 0 时 , A O1 = 180 + θ; DX > 0 , DY < 0 时 , A O1 = 360 - θ。
以 O1 点为局部坐标原点时 , 非完整缓和曲线 任意一点的大地坐标可由式 ( 6) 计算 : X = XO1 + x cos A O1 - ξ y sin A O1
A dl = ・ dβ l
2 2
图2 缓和曲线中桩坐标示意图 Figure 2 Illustration of central stake coordinates of transition curve
式中 :ξ= SG N ( R ) , 右转角为正 , 左转角为负 ; A ZH 为 完整缓和曲线起点的切线坐标方位角 。( x , y ) 为完 整缓和曲线在直角坐标系中的坐标 。

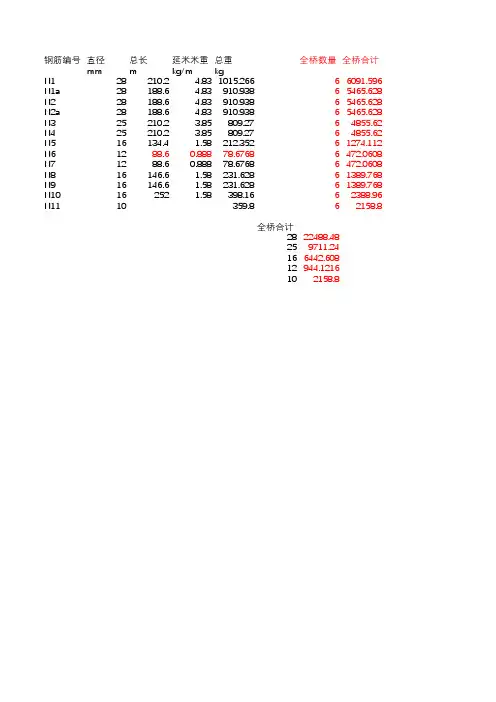
钢筋编号直径总长延米米重总重全桥数量全桥合计
mmmkg/mkg
N128210.24.831015.26666091.596
N1a28188.64.83910.93865465.628
N228188.64.83910.93865465.628
N2a28188.64.83910.93865465.628
N325210.23.85809.2764855.62
N425210.23.85809.2764855.62
N516134.41.58212.35261274.112
N61288.60.88878.67686472.0608
N71288.60.88878.67686472.0608
N816146.61.58231.62861389.768
N916146.61.58231.62861389.768
N10162521.58398.1662388.96
N1110359.862158.8

全桥合计
2822488.48
259711.24
166442.608
12944.1216
102158.8

立交匝道坐标放样正反算CASIO_fx-5800P程序(带数据库功能)
立交匝道坐标放样正反算CASIO fx-5800P程序（带数据库功能）
程序代码（王中伟）qq595077
.
.
.
.
.
.
.
.
d匝道和MR匝道数据库子程序略。

.
.
五、程序变量清单
.
.
.
六、计算流程示例
1．坐标正算示例
计算任务：计算MN互通式立交c匝道K0+315.3中桩坐标及切线方位角，以及该桩左侧4.5米、右侧6米的边桩坐标，假设在导线点（2807544.340，475613.014）上架设全站仪，计算这三个点位的极坐标放样数据。

使用立交匝道坐标放样计算程序RAMP－4的操作流程见下表。

.
.
.
2．坐标反算示例
计算任务：根据上面计算的c匝道K0+315.3中桩坐标，以及该桩左侧4.5米、右侧6米的边桩坐标计算结果，反算对应的c匝道桩号及距中距离，并进行结果的验证。

使用立交匝道坐标放样计算程序RAMP－4的操作流程见下表。

.。

互通式⽴交匝道设计分析总之，平⾯线形要做到“宽松⼀指标上要尽量采⽤规范规定的较⾼要求”，“紧凑⼀在满⾜规范的前提下尽量减少占地”，“流畅⼀平纵横指标协调，保证车辆⾏驶流畅”，“合理⼀总体布局合理，各项指标均衡”。

3．1．2 平曲线半径匝道圆曲线半径的⼤⼩，在考虑⽴交形式、⽤地规模、拆迁数量和⼯程造价等条件下，应与设计速度、超⾼横坡度以及⾏车安全和舒适性相适应。

通常情况下，应采⽤较⼤的圆曲线半径和较⼩的超⾼横坡度，只有当受地形条件或其他特殊情况限制时，才可采⽤极限最⼩⽜径值。

如果采⽤较⼩半径的单曲线或环圈式匝道，除了圆曲线半径满⾜最⼩⽜径规定以外，还应有⾜够的匝道长度，以保证曲率的缓和过渡和上下主线的展线长度要求。

可近似按(2)式计算：Rmin≥57．3H／(a·i) (2)式中，H：上下线要求的最⼩⾼差(m)；a：匝道的转向⾓(°);i:匝道的设计纵坡(％)。

3．1．3 缓和曲线为满⾜汽车⾏驶⼒学及线形顺畅的要求，在匝道及其端部，凡曲率变化较⼤处均应设置缓和曲线。

缓和曲线⼀般采⽤回旋线，回旋线的参数和长度，以及相邻回旋线参数的⽐值应满⾜规范要求。

在⼀般情况下，应尽量采⽤较⼤的回旋线参数或较长的回旋线长度，只有在条件受限时⽅可采⽤最⼩值。

反向曲线间的两个回旋线，其参数宜相等，不相等时，其⽐值应⼩于2．0，有条件时以⼩于1．5为宜，两圆曲线半径之⽐不宜过⼤，以R2／R1=1～1／3为宜(R1为⼤圆曲线半径，R2为⼩圆曲线半径)；卵形曲线回旋线参数宜符合R2／2≤A≤R2的规定，两圆曲线半径之⽐以R2／R1=0．2～0．8为宜；回旋线的长度同时应满⾜超⾼过渡及加宽过渡的长度要求。

3．1．4平曲线加宽匝道平曲线的加宽过渡⽅式与主线相同。

⽴体交叉单向单车道匝道圆曲线半径72m，单向双车道或双向双车道圆曲线半径47m 应设置加宽。

(1)加宽缓和段设置缓和曲线或超⾼缓和段时，加宽缓和段应在缓和曲线或超⾼缓和段内进⾏；不设缓和曲线或超⾼缓和段时，加宽缓和段应按渐变率1：15且长度L0≦10m的要求设置。

<<桥梁工程>>结构计算课程设计任务书题目: （分离式）立交桥结构设计计算1 桥梁概况K45+024.627 县道011分离式立交桥上跨011县道，与被交路成28°38′55″夹角。

全桥由双向六车道分离的两座桥构成，全长86.12m，左幅桥中心桩号为K45+039.627，右幅桥中心桩号为K45+015.373。

2 设计标准及桥型结构设计荷载:公路I级。

地震作用：按8度设防。

桥面布置：双幅26m=0.5m墙式护栏+11.5m行车道+2m中央分隔带+11.5m行车道+0.5m 墙式护栏；桥孔布置：（1）预应力钢筋混凝土连续箱梁建议桥孔布置20+24+20m三孔一联预应力钢筋混凝土连续箱梁。

桥平面位于直线内，桥面横坡为双向1.50％，由墩台身高度不同来调整。

箱梁为等截面，高度为1.60m。

（2）拱桥或其它桥型自定3预应力钢筋混凝土连续箱梁上构预应力体系箱梁采用纵向预应力体系。

预应力钢束采用平弯、竖弯相结合的方式布置，两端张拉， R b y =1860MPa；预应力钢绞线用OVM型锚具，张拉控制应力为1395 MPa。

预应力体系的建立应严格按《公路桥涵施工技术规范》的要求，同时应严格执行张拉过程。

4预应力钢筋混凝土连续箱梁下部构造本桥采用独柱墩，桥台采用肋板式桥台，基础均采用钻孔灌注桩。

独柱墩基础为2根∅150cm 钻孔灌注桩，桩长为34～35.5米，承台边长750 280cm，厚200cm。

桥台基础为4根∅120cm钻孔灌注桩，桩长为32.5～33米。

独柱墩墩身采用φ180cm 的圆截面墩柱，墩身高为6m ～6.8m ，1号墩支座采用GPZ15000GD 盆式支座，2号墩支座采用GPZ15000GX 盆式支座。

5 设计计算基本资料 5.1 主要技术标准（1）桥面净宽：行车道净宽 11.5m ×2；（2）荷载标准：公路I 级； （3）温度：年平均气温6.2℃，一月平均气温-13.1℃，七月平均气温22℃，冬季最低气温-32.8℃，夏季最高气温38.4℃。

浅谈高速公路立交匝道施工坐标的计算作者：马驰来源：《科技视界》 2014年第2期马驰（辽宁省交通高等专科学校，辽宁沈阳 110122）【摘要】高速公路的立交匝道由于设计特殊、线形连接复杂，给施工测量数据的计算带来一定难度。

本文以立交匝道中回旋线计算为例，介绍立交匝道施工测量数据的计算方法与过程。

【关键词】立交匝道；缓和曲线；坐标计算在高速公路设计、施工的过程中，经常遇到高速公路主线与另一条高速公路的主线相互连接以及高速公路主线与普通公路连接的问题。

为了较好地解决上述问题，设计中除了考虑运动学，还应满足视觉、生态、环保等诸多因素，在进行路线连接时，主要采用回旋线。

立交匝道的平面线型以直线、圆曲线、回旋线相互结合，改变了普通公路中回旋线（缓和曲线）的对称形式，以更加灵活的线型组合模式构建了立交匝道的平面线型[1]。

常见的线型包括基本型、S 型、卵型、凸型和复合型五种[2]。

立交匝道的坐标计算与高速公路主线的坐标计算类似，包括直线段、圆曲线段和缓和曲线段的计算。

本文以回旋线为例，介绍立交匝道施工坐标计算的方法。

1 回旋线假定坐标值计算在进行立交匝道的坐标计算，将一条回旋线作为研究对象，并且仅考虑回旋线曲率半径从大到小的方向进行计算，即正向回旋线的计算方法。

而对于反向的回旋线，只需按照正向的计算方法，同理可以计算得到。

图1为一段回旋线，回旋线两端的曲率半径分别为R1、R2，其中R1＞R2。

因为R1＜∞，显然相当于在完整的回旋线TS(ST)至SC段舍去一段长度为1h1=A2/R1，在图中为TS至CS段虚线部分。

那对于回旋线的全部长度为1h2=A2/R2,其中1h2与1h1即为立交匝道中回旋线的长度，在进行计算时，可通过此项计算进项检核图纸数据。

在进行回旋线假定坐标计算时，是以过TS点的切线方向为x轴，与切线相互垂直的曲率半径方向为y轴，建立假定坐标系。

如此建立的坐标系，就是一个完整的回旋线计算，在计算时，充分考虑立交匝道计算时曲率半径较小的因素，因而采用如下的公式，公式中高次项主要为弥补曲率半径小前提下的计算。