C匝道坐标计算
- 格式:xls
- 大小:124.50 KB
- 文档页数:2

免责申明:免费提供;仅供参考。
卡西欧(上海)贸易有限公司不对用户使用本程序发生的任何问题负责。
读者对本程序的问题请发电子邮件到775403338@ 邮箱咨询。
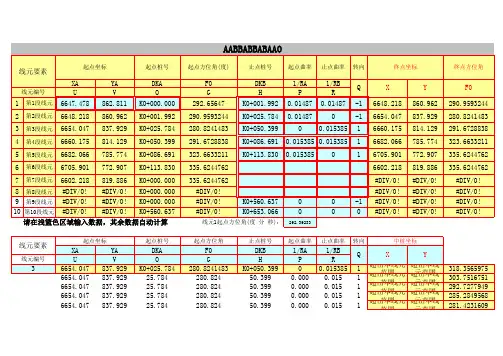
fx-9750GⅡ公路测量程序使用说明一、程序使用流程本程序数据和主程序是分开的,编程时将不同的工程数据存放到不同的数据文件里,如A匝道,文件名为A,将匝道A所有的曲线线元参数输入A文件里。
运行时只要运行文件名A的程序就可以了,具体运行流程见下图:二、数据文件的编写(一)交点法数据文件编辑交点法编写数据文件必须是对称型的,即直线段→缓和曲线段→圆曲线段→缓和曲线段→直线段,(如果任意一端没有直线段,则把直线段长度看做是0),另外圆曲线两侧缓和曲线的旋转常数必须相等,并且和直线段连接处的半径必须是无穷大。
交点法数据文件编写一般是根据设计图纸提供的平面曲线参数一览表提供的参数来编写,每个弯道包括:弯道起点方位角(C),交点X坐标(D),交点Y坐标(E),缓和曲线长度(F,当没有设缓和曲线时,F=0),交点转交(G,向左转弯,G为负值,向右转弯,G取正值),交点桩号(H),弯道圆曲线半径(R)。
下图是一段市政道路设计参数数据。
根据上图提供的数据,可以编辑成如下的数据文件:文件名:CHLNR在上图中,有两个条件转移语句即If L>0:Then 98°39°35.12°→C:4774.384→D: 2415.861→E:140→F:31°17°23°→G:410.007→H:600→R:IfEndIf L>1060:Then 129°56°58.19°→C:4206.421→D: 3093.946→E:70→F:-33°50°48°→G:1285.437→H:600→R:IfEnd……如果还有其他弯道,可以继续完后加。
在这些存放设计参数的语句前后的程序表达式是固定的。

高速公路坐标高程计算程序本软件简要说明:一、平曲线计算(主程序)1、J为起算点里程,C、D为起算点的X、Y坐标,F为起算点的切线方位角,R为圆曲线半径(左偏取负,右偏取正),A、B为第一、第二缓和曲线回旋参数,O为圆曲线长度,Ki为该分段的终点里程;2、对于直线段或圆曲线段,起算点可取直线或圆曲线上的任意一点;3、对于带第一、第二缓和曲线的平曲线段,起算点应取HY点;4、K为所求点的里程,T、P为第一偏距、偏角,S、Z为第二偏距、偏角,偏角取从该点的切线顺时针旋转的夹角;5、分段法则:直线单独分段;单一的圆曲线单独分段;缓和曲线1+圆曲线+缓和曲线2为一个整体单独分段,若不存在第一或第二缓和曲线(即不完全缓和曲线)仍然可以计算,A或B可取任意不为零的值;若不存在圆曲线,则O取零;6、无论任何时候A、B不能取零,否则可能导致被零除的错误;7、F、Q切线方位角输入输出均为度.分秒的格式,例如153°24′05.24″=153.240524。
Q改变时,可按照新方位角为基准,结合第一第二偏距、偏角重新计算所求点;8、输入平曲线参数后,默认为计算全线坐标,可修改来计算某段曲线,默认间距也可修改;9、可参考CAD图《平曲线计算图例》;10、生成的中桩CAD脚本设置成在世界坐标系下生成,注意的是世界坐标系与大地测量坐标系的区别是XY坐标是互换的,否则画出的图形与实际相反。
先打开CAD,设置好图层名称、颜色,并设置为当前层,然后单击CAD的工具==>运行脚本==>选中生成的脚本文件即可。
11、输出的坐标结果可以导入到EXCEL中,操作办法为:打开EXCEL,然后把坐标数据复制到单元格里,然后单击数据==>分列==>选中分隔符号==>下一步==>选中TAB键和逗号==>下一步==>完成即可。
下一次可直接在此表中粘贴,数据自动分列。
二、缓和曲线计算(辅助程序)1、本程序为辅助程序,用来从ZH点或HZ点计算整条完全的缓和曲线,若不知道HY点X、Y、Q参数,可用此程序计算出来,然后输入平曲线参数;2、参数设置参考平曲线计算;3、导出到EXCEL的办法同平曲线计算;三、直线计算(辅助程序)1、本程序为辅助程序,若已知P1(X1,Y1),P1-->P2的距离I及方位角J(度.分秒格式),可计算坐标P2(X2,Y2)。

公路通用复化辛普森公式匝道点位坐标计算4800源程序------------------杭浦高速临平互通---------------------本文利用的是计算公路匝道点位坐标的复化辛普森通用公式数学模型,集直线、圆曲线、回旋线通用,占字符内存较小,计算精度不限的程序一、运行变量名称说明:V=1、2分别进入坐标计算、桩号反算K1、K2-------曲线起点、终点里程F0-----------曲线起点方位角R1、R2------曲线起点、终点半径(ρ左-右+,0为直线)X0、Y0-------曲线起点、终点坐标M------------求和累积次数n的2倍(偶数),精度迭代次数K------------曲线待求点里程BP-----------求点左右偏距(左-右+)ANG-------- -求点的右斜交角X、Y---------曲线求得坐标FW-----------待求点的即时切线方位角XF、YF-------为需求桩号的点坐标DL、K+O、LP分别为桩号误差、求得桩号、左右偏距(左-右+)当曲线的设计半径较小时,为保证点位计算精度,M(即程序中n的2倍)的取值可适当的大些。
M为偶数,直线时M=2即可,经计算M=16即可满足半径为60的小半径曲线精度。
二、曲线计算程序名: Prog "CURVE"Defm 4V"V=1 2"Lbl 0:{KLW}Lbl 4Q"OPT:M0AB1C2D3E4FH5G6I7J8CR9"=0=>Prog "M"△Q=1=>Prog "AB"△Q=2=>Prog "C"△Q=3=>Prog "D"△Q=4=>Prog "E"△Q=5=>Prog "FH"△Q=6=>Prog "G"△Q=7=>Prog "I"△Q=8=>Prog "J"△Q=9=>Prog "CR"△A"K1"B"K2"C"F0"D"R1"E"R2"F"X0"G"Y0"D≠0=>I=1/D:≠=>I=D△E≠0=>J=1/E:≠=>J=E△AbsD+AbsE=0=>M=2:≠=>M=16△V=2=>L=0:W=90△KL"BP"W"ANG"N=0:Z[1]=0:Z[2]=0:Z[3]=0:Z[4]=0 进入坐标迭代计算Lbl2N=N+1:H=2(K-A)/M:R=NH/2+A:R=C+180/π*(I+(J-I)/2(B-A)*(R-A))*(R-A)Int(N/2)=N/2=>Z[1]=Z[1]+cosR:Z[2]=Z[2]+sinR:≠=>Z[3]=Z[3]+cosR:Z[4]=Z[4]+ sinR△N=M=>Goto3:≠=>Goto 2Lbl3X=F+H/6*(cosC+4Z[3]+2Z[1]-cosR)+Lcos(R+W)Y=G+H/6*(sinC+4Z[4]+2Z[2]-sinR)+Lsin(R+W)V=2=>Goto 6△X"X="◢Y"Y="◢R"FW"=R-360Intg(R/360◢Goto 0Lbl 6 进入桩号求算Pol(T"XF"-X,U"YF"-YO=Icos(J-RAbsO≤1e-4=>O"DL"◢K=K+O◢O"LP"=Isin(J-R◢{TU}Goto 6:≠=>K=K+O:L=0:Goto 4三、数据文件:线元要素数据文件每行为一个线元段,逐句执行赋值,直至不满足、运行完成。


立交匝道中边桩坐标放样正反算程序主程序:(RAMP)Deg : Fix 3 : 10→Dim Z↙0.1739274226→Z[1] : 0.0694318442→Z[2] : 0.3260725774→Z[3] : 0.3300094782→Z[4] ↙Z[3]→Z[5] : 1- Z[4]→Z[6] : Z[1]→Z[7] : 1-Z[2]→Z[8]↙“RAMP?[1-N]”?→Z[9]↙(输入匝道代码,比如数字1,2,3...代表a,b,c匝道,并存储在变量Z[9]中)If Z[9]=0 : then“XA”?W :“YA”?Y :“FWJ”?Q:“RS”?A :“RE”?B :“KS”?S : “KE”?E : IfEnd ↙(若Z[9]=0 时,则手工输入原始数据:线元起点X﹑Y坐标,方位角,线元起﹑终点曲率,起﹑终点桩号)Cls :“ZS[1],FS[2]”?→Z[10]:Z[10]=2 =>Goto 2↙“XS”?U :“YS”?V↙(输入测站点坐标)Lbl 0:“KP”?P↙(输入待计算的中桩桩号)Z[9]>0=>Prog“RAMP-DATA”↙(调用匝道数据库子程序)Prog“RAMP-ZBJS”↙(调用子程序计算中桩坐标)Lbl 1:90→H:“YJ”?H : H=0 =>Goto 0 :?D↙(输入右角及距离,若右角为0则返回桩号输入)F+Dcos(Z+H)→R : G+Dsin(Z+H)→T↙(坐标计算)Pol(R-U,T-V) : J<0=>J+360→J↙1→O :Prog“RAMP-XS”: Goto 1↙(调用计算结果显示子程序)Lbl 2:“XB”?U :“YB”?V :“KP”?P↙(坐标反算,输入X,Y,估算的桩号)Lbl 3:Z[9]>0=>Prog“RAMP-DATA”↙Prog“RAMP-ZBJS”↙(调用子程序计算中桩坐标)(V-G)cos(Z-90)-(U-F)sin(Z-90)→H↙If Abs(H)>0.001 : Then P+H→P : Goto 3: IfEnd↙(G-V)÷sin(Z-90)→D↙2→O : Prog“RAMP-XS”: Goto 2↙(调用计算结果显示子程序)子程序1:(RAMP-ZBJS)坐标计算E-S →C : P-S →L : 180÷π→M : (B-A)÷2÷C →N ↙0→F : 0→G : 0→Z:For 0→K To 3:(计算X,Y 坐标值)F+LZ[2K+1]cos(Q+MALZ[2K+2]+MN(LZ[2K+2])2)→F:(计算X,Y 坐标值)G+LZ[2K+1]sin(Q+MALZ[2K+2]+MN(LZ[2K+2])2)→G:(计算X,Y 坐标值)Next :W+F →F : Y+G →G:(计算X,Y 坐标值)Q+MAL+MNL 2→Z:(计算切线方位角)Z<0=>Z+360→Z : Z>360=>Z-360→Z ↙子程序2(RAMP-XS)显示 Cls :If O =1 :Then ↙“X=” :Locate4,1,R: “Y=”: Locate4,2,T : Fix4 : “A=” : Locate4,3,J 。
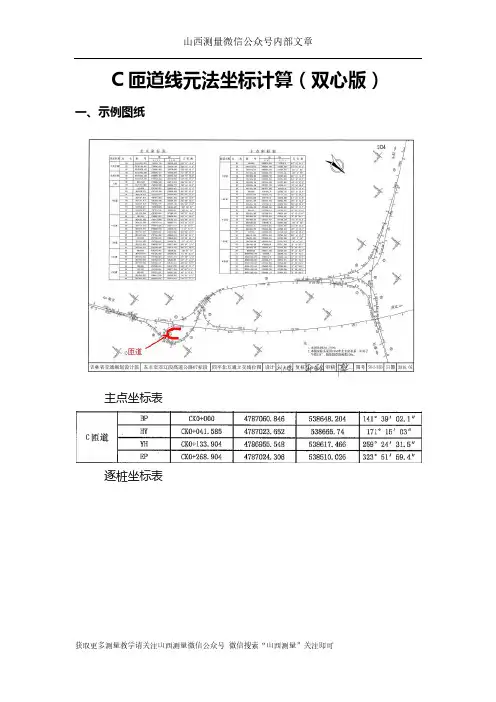
C匝道线元法坐标计算(双心版)一、示例图纸
主点坐标表
逐桩坐标表
线位数据图
二、图纸分析
根据主点坐标表和线位数据图分析出下图:
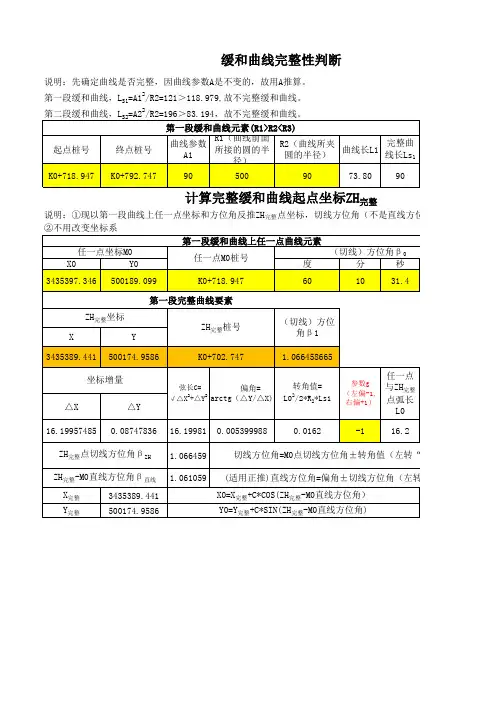
BP—HY为一段缓和曲线,A=70,LS=41.585,由于A²≠LS*R,70²≠41.585*60,所以该段缓和曲线为非完整缓和曲线,起点半径为:
有两个数据值,在用“测量员”或者“轻松测量”时输入哪一个都可以。
此处是双心软件计算不需要考虑。
HY—YH为一段圆曲线,R=60;YH—EP为一段缓和曲线,由于A²=LS*R,90²=135*60,所以该段缓和曲线为完整的,终点半径为无穷大。
三、双心软件输入参数
四、坐标计算结果
五、生成CAD脚本图。

高速公路曲线、匝道的坐标、高程计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
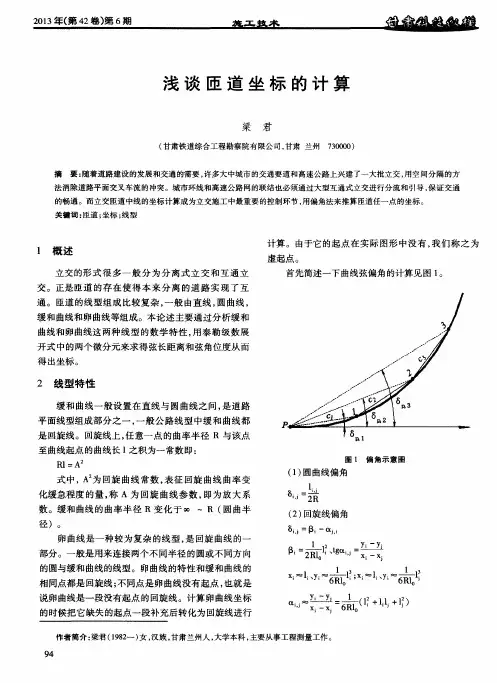
匝道施工中中线和边桩放样坐标的计算方法文艺屏(南宁市政工程XXX 广西南宁530011)【摘要】推导匝道中线和边桩在城市坐标系中的坐标计算公式,介绍实现整条线路连续统一计算的程序设计思路。
【关键词】匝道中线边桩放样坐标计算方法1 引言随着我国城市交通事业的飞速发展,各种立交桥如雨后春笋般拔地而起,线形越来越优美也越来越复杂,多是由圆曲线和缓和曲线组成的全曲线交通线路。
匝道的施工放样是道路施工放样中最复杂、精度要求最高的部分,放样点的密度直接影响到竣工产品的外形美观度甚至使用功能。
一般地,设计文件仅提供线路曲线段主要控制点的当地城市坐标和该工程相对桩号,远远不能满足施工放样的需要,在施工中必须要大量地加密控制点。
同时由于施工现场条件非常复杂,我们不可能也没有必要在室内无限计算曲线上任意一点的坐标备用,只能临时在现场根据需要确定加密点并计算其坐标,这就要求我们能有一种相对简单又能满足精度要求的计算方法。
本文针对构成匝道要素的圆曲线和缓和曲线推导其坐标计算公式,简单介绍实现整条线路连续统一计算的程序设计思路。
在施工放样中仅以线路上任意点桩号作为参数代入就可以计算出自己想要得到的该点任何放样数据,利用全站仪高效、准确地进行匝道施工放样。
2 匝道中线坐标及法线方位角计算公式推导为了方便推导和简化公式的表述,我们约定1)约定中线的法线方位角前进方向的顺时针方向为其正方向;2)线路偏转方向函数LR(A i,A i+1)并在后面的计算中用λ替代,A i为线路转角前方位角,A i+1为线路转角后方位角,约定线路偏转方向函数为3)左手坐标系为计算中默认坐标系,即x为纵坐标,y为横坐标。
1、直线中线坐标、法线方位角计算设直线的起点P(x0,y0)和直线前进方位角A i,计算直线上与起点距离为S的点P0(x1,y1)的坐标、法线方位角N,根据一般测量原理有:(1)2、圆曲线中线及圆心坐标、曲线法线方位角计算设圆曲线的起点为P0(x0,y0),相应点前进方向的切线方位角A i,圆半径r,圆曲线终点切线方位角A i+1,起点法线方位角为α。
浅谈高速公路立交匝道施工坐标的计算作者:马驰来源:《科技视界》 2014年第2期马驰(辽宁省交通高等专科学校,辽宁沈阳 110122)【摘要】高速公路的立交匝道由于设计特殊、线形连接复杂,给施工测量数据的计算带来一定难度。
本文以立交匝道中回旋线计算为例,介绍立交匝道施工测量数据的计算方法与过程。
【关键词】立交匝道;缓和曲线;坐标计算在高速公路设计、施工的过程中,经常遇到高速公路主线与另一条高速公路的主线相互连接以及高速公路主线与普通公路连接的问题。
为了较好地解决上述问题,设计中除了考虑运动学,还应满足视觉、生态、环保等诸多因素,在进行路线连接时,主要采用回旋线。
立交匝道的平面线型以直线、圆曲线、回旋线相互结合,改变了普通公路中回旋线(缓和曲线)的对称形式,以更加灵活的线型组合模式构建了立交匝道的平面线型[1]。
常见的线型包括基本型、S 型、卵型、凸型和复合型五种[2]。
立交匝道的坐标计算与高速公路主线的坐标计算类似,包括直线段、圆曲线段和缓和曲线段的计算。
本文以回旋线为例,介绍立交匝道施工坐标计算的方法。
1 回旋线假定坐标值计算在进行立交匝道的坐标计算,将一条回旋线作为研究对象,并且仅考虑回旋线曲率半径从大到小的方向进行计算,即正向回旋线的计算方法。
而对于反向的回旋线,只需按照正向的计算方法,同理可以计算得到。
图1为一段回旋线,回旋线两端的曲率半径分别为R1、R2,其中R1>R2。
因为R1<∞,显然相当于在完整的回旋线TS(ST)至SC段舍去一段长度为1h1=A2/R1,在图中为TS至CS段虚线部分。
那对于回旋线的全部长度为1h2=A2/R2,其中1h2与1h1即为立交匝道中回旋线的长度,在进行计算时,可通过此项计算进项检核图纸数据。
在进行回旋线假定坐标计算时,是以过TS点的切线方向为x轴,与切线相互垂直的曲率半径方向为y轴,建立假定坐标系。
如此建立的坐标系,就是一个完整的回旋线计算,在计算时,充分考虑立交匝道计算时曲率半径较小的因素,因而采用如下的公式,公式中高次项主要为弥补曲率半径小前提下的计算。
匝道是组成高等及公路立交的基本单元,其形式千变万化,就线形而言,也是由直线段、回旋曲线段、圆曲线段组成。
但是,组成立交的匝道涉及线形的曲率变化特点,利用复化辛普森公式导证了计算公路匝道点位坐标的通用公式。
并利用卡西欧FX-4500P计算器编程计算公路匝道点位坐标。
二、公路匝道点位坐标计算1. 公路匝道中线形式公路匝道中线是由直线—回旋曲线—圆曲线(R1)—回旋曲线—圆曲线(R2)—回旋曲线—直线的顺序组成的,其中R1¹R2。
2. 回旋曲线上点位坐标方位角的计算如图1,设回旋曲线起点A的曲率为r A,其里程为DK A;回旋曲线终点B的曲率为,其里程为DK B,Ax¢y¢为以A为坐标原点,以A点切线为x¢轴的局部坐标系;AXY为线路坐标系。
由此回旋曲线上各点曲率半径为R i和该点离曲线起点的距离ﺎi成反比,故此任意点的曲率为(=R0为常数)(1)由式(1)可知,回旋曲线任意点的曲率按线性变化,由此回旋曲线上里程为DK i点的曲率为(2)当曲线右偏时,取正;当曲线左偏时取负。
在图1中有(3)将式(2)代入式(3)得(4)若已知回旋曲线起点A在线路坐标系下切线坐标方位角αA,则里程为Dk i点切线坐标方位角为(5)将式(4)代入式(5)得(6)对于式(6),当,时,,则a i=a A,式(6)变成计算直线段上任意点切线坐标方位角计算公式;当,时,,,则式(6)代表圆曲线上任意点切线坐标方位角计算公式。
可见,若已知曲线段起点和终点的曲率及起点的切线坐标方位角,式(6)便能计算任意线型点位切线坐标方位角。
3、回旋曲线点位坐标计算由图1可得回旋曲线上点位在坐标系下坐标计算公式:(7)(8)设回旋曲线起点A在线路坐标系下的坐标为将式(6)替代式(8)中的,便得回旋曲线上任意点在线路坐标系下的坐标:(9)对于式(9)的解算,由于后半部分是定积分,我们引入复化辛普森公式对其进行解算。