高速公路互通立交匝道坐标计算 (2)

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z，y Z为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：x Z，y Z计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z，y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：S Z④变坡点高程：H Z⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

互通匝道超高计算方法摘要：一、互通匝道超高计算方法简介二、互通匝道超高计算公式及参数解释三、实例分析四、注意事项正文：互通匝道超高计算方法是高速公路设计中的一项重要内容。

互通匝道超高是指在互通立交中，由于道路线形的变化，使某一部位的纵断面具有较大的高差。

合理的互通匝道超高计算方法能够保证道路线形流畅，提高行驶安全性。

本文将详细介绍互通匝道超高计算方法、公式及实例分析，以期为设计师提供参考。

一、互通匝道超高计算方法简介互通匝道超高计算方法主要包括以下几个步骤：1.根据互通立交的类型，确定匝道的线形组合。

2.分析互通匝道的交通量、车速、路幅宽度等设计参数。

3.依据设计规范，确定互通匝道的最小半径、最大坡度等技术指标。

4.计算互通匝道的超高值，并进行相应的调整。

二、互通匝道超高计算公式及参数解释1.超高计算公式：h = (v^2)/127R其中，h为超高值（m），v为设计速度（km/h），R为曲线半径（m）。

2.参数解释：（1）设计速度：根据互通立交的交通量、车速等因素综合确定。

（2）曲线半径：根据互通立交的类型、地形地貌等因素综合确定。

（3）超高调整系数：根据道路等级、设计年限等因素确定。

三、实例分析以某一等级为高速公路的互通立交为例，已知设计速度为100km/h，曲线半径为150m。

根据公式计算，得到超高值为0.12m。

考虑到道路等级较高，超高调整系数取1.1，最终确定超高值为0.132m。

四、注意事项1.在计算互通匝道超高时，应充分考虑地形地貌、交通量、设计年限等因素，确保计算结果的合理性。

2.超高值不应过大，以免影响道路线形美观和行驶安全性。

3.超高调整系数应根据实际情况确定，以满足不同道路等级的设计要求。

4.在实际设计过程中，应充分了解设计规范，确保互通匝道超高的计算符合相关规定。

通过以上分析，我们可以了解到互通匝道超高计算方法的重要性。

YA V 837.929 837.929 837.929 837.929 837.929
DKA O K0+025.784 25.784 25.784 25.784 25.784
F0 G 280.8241483 280.824 280.824 280.824 280.824
DKB H K0+050.399 50.399 50.399 50.399 50.399
0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
线元编号 起点坐标 起点桩号
K0+560.637 K0+653.066
0 0
292.39233
0 0
292.65647
-1 0
线元1起点方位角(度 分 秒)： 起点方位角 止点桩号
起点曲率
止点曲率
转向
中桩坐标
3
XA U 6654.047 6654.047 6654.047 6654.047 6654.047
6654.047 6654.047 6654.047 6654.047 6654.047 6654.047 6654.047 6654.047 6654.047 6654.047
837.929 837.929 837.929 837.929 837.929 837.929 837.929 837.929 837.929 837.929
50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399 50.399

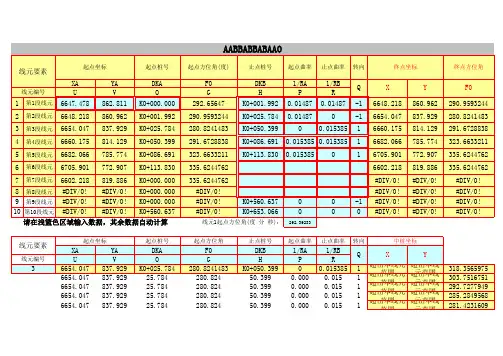
使 用 说 明1、本工作簿共含四张工作表，第一张表为使用说明；第二张表为数据录入（曲线数据库）；第三张表为曲线段张表为曲线任意点坐标正反算.使用前请认真阅读使用说明。

　２、数据录入表的使用：你可将全线路或标段的各线段设计参数依序录入表中。

序号列不需输入，表格根据录入本表设计有供输入310行的线段点参数的单元区间,完全满足全线或标段全程计算需要。

　①、桩号输入：按普通数值输入，表格自动显示为代公里标示的格式。

（全程可逆向输入）　②、切线方位角输入：如：１8２°25′36.2″按 182.25362 输入。

（曲线转向自动判断、曲线属性自动判断③、半径输入：直线段不作规定；圆曲线输入设计半径值；缓和曲线接直线端输入“1”，接圆曲线端输入圆半曲线相接于公切点时，应在第二半径列输入作为下一曲线段起点计算的半径值。

（此类情况可发生在复曲线或反曲④、断链：断链值按长正短负输入；处理在直线末端。

程序自动计算断链桩号。

直线段大于1.2公里时，应分多⑤、曲线段中边桩坐标计算的选择：你可在录入表右上方的黄色单元格中输入需要计算的线段序号，程序自动在中进行计算。

如：输入“5”，程序自动选择5-6序号段进行计算。

3、线段中边桩坐标计算表的使用：打开此表，在逐桩栏输入任意数值或字符，在左边垂距和右边垂距中输入数中边桩坐标，不输入边桩垂距，不计算边桩点坐标；整桩取值：直线段按25或50米；曲线段按5、10、20、25、504、任意点坐标正反算表的使用：①、正算：可直接计算全线范围内的有效桩号值中边桩坐标。

（有桩号范围提示）一次只能进行一个桩号的计②、反算：只能进行一个曲线段中的桩号反算。

方法：在正算栏输入需要反算的曲线段区间的任意桩号值，程作为反算依据，在反算栏输入曲线点的坐标值，该点的桩号自动计算并显示，误差小于3毫米。

一次计算一个点。

③、放样计算：可对正算的桩号点（包括中边桩）自动进行放样计算，得到的放样参数为：以曲线起点为置镜零方向的偏距和偏角。

18.有时设计院没有给出匝道最后一段缓和曲线的结束半径，那么在积木法计算前就需要计算最后一段缓和曲线的结束半径。

公式如下：其中 A 是缓和曲线参数、R 是半径ls 是缓和曲线长度。

回旋线是公路路线设计中最常见的一种缓和曲线。

我国的标准规定缓和曲线采用回旋线。

它的基本公式为：A*A=r*l其中：A是回旋线参数。

r是回旋线上某点的曲率半径(m)l是回旋线上某点到原点的曲线长在回旋线上的任意点上，r是随着l 的变化而变化的。

但是在缓和曲线的终点处，l=Ls,r=R,则上式可写为A*A=R*Ls则 -------A=√R*Ls在设计上可以由已知R和Ls计算A，也可以按各种条件选择R和A，再计算Ls.至于用于计算坐标，你可以综合所有的已知条件进行计算，它只是提供一个计算和你进行复核的条件。

对互通立交端部的一点认识随着经济和交通运输事业的飞速发展，高等级公路的普遍修建，作为高等级公路车辆出入门户的互通式立交也开始大量修建。

立体交叉中主线与交叉线处于不同高程上，需用道路将其互相联系，便于各方向车流四通八达，这些起联系作用的道路通常称为匝道。

匝道两端与主线、交叉线连接区域称之为匝道端部。

匝道端部范围，包括匝道出入口，三角区，变速车道等部分。

匝道的端部形式，就其出入口位置不同，有左出入口和右出入口；就其主线或交叉线几何形状不同，有直线和曲线等。

匝道端部形式多样，几何关系以及设计都较繁琐，而且都应满足各自不同的技术要求，如设计不当，将造成对车辆行驶不利，容易引发事故阻碍交通。

本文就结合自己的设计经验，针对匝道端部设计做一些探讨。

一、匝道端部路线平、纵面要求1、路线平面要求从主线流出的车辆，在进入匝道的短暂运行过程中，其驾驶过程较为复杂，分流、转向、减速对司机都有一定的操作要求，同时司机产生心理压力也有影响。

因此，出口处应为车辆行驶创造良好条件，对路线平面应有较高要求，入口处一般也应如此。

我国公路《规范》规定，驶入匝道的分流点应具有较大的曲率半径，并使曲率变化适应行驶速度的变化。

高速公路的一些线路坐标、高程计算公式缓和曲线、竖曲线、圆曲线、匝道))(缓和曲线、竖曲线、圆曲线、匝道一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

道路曲线高程计算公式 Final revision by standardization team on December 10, 2020.高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

路桥坐标计算圆曲线中边桩坐标计算公式： L=F-H；注：L---所求点曲线长；F---所求点里程；H---圆曲线起点（ZY点桩号里程）X=XZY+2×R×SIN（L÷2R）×COS｛α±(L÷2R)｝+S×COS｛α±(L÷R)+M｝; Y =YZY+2×R×SIN（L÷2R）×SIN｛α±(L÷2R)｝+S×SIN｛α±(L÷R)+M｝. 注：α---线路方位角；M---所求边桩与路线的夹角；S---所求边桩至中桩的距离；"±"---曲线左偏取“-”右偏取“+”；当S=0时为中桩坐标。

经高速公路施工一线使用效果很好。

记住在公式中加入Excel的Radians（）函数将度转为弧度即可轻松方便地使用，从ZY点坐标准确快速推算地计算出整条圆曲线。

注意要分清左偏右偏两种情况。

高速公路线路坐标计算公式:高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K③曲线终点桩号：K1④曲线起点坐标：x0，y⑤曲线起点切线方位角：α⑥曲线起点处曲率：P(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

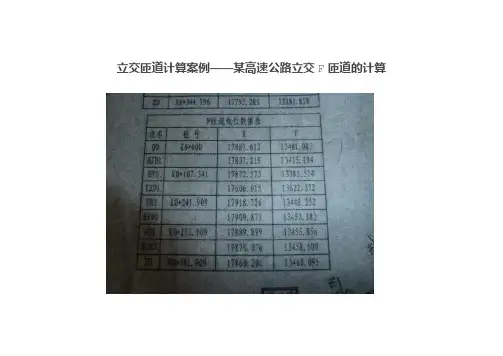
立交匝道计算案例——某高速公路立交F匝道的计算————————————————————————————————————————————————————————————分析F匝道，该匝道设计文件的特殊之处在于，没有标注缓和曲线参数A，同时匝道的起、终点的半径有待确定。

设计单位“偷懒”，但同时也为锻炼一线测量员的计算能力提供了又一个很好的实例。

F匝道共四个线元，为表达方便，分别用1~4来指代。

线元1、3、4为缓和曲线，线元2为圆曲线，其中线元1明显为不完整缓和曲线，线元3、4为完整缓和曲线，要顺利进行F匝道的逐桩坐标计算，需要确定的参数是：1．匝道起点的切线方位角；2．匝道起点的半径；3．匝道终点的半径。

幸运的是，这里，设计单位给出了各曲线的交点坐标，因此，很容易地根据线元1的交点（HJD1）坐标与线元1起点坐标，求得线元1起点切线方位角（也是匝道起点切线方位角）为：236°01′46.95″。

类似地，根据线元1的终点坐标与线元1的交点(HJD)坐标，求得线元1的终点切线方位角为：318°08′13.66″。

这样，线元1的起点、终点切线方位角之差即为线元1的转角：82°06′26.71″。

这里设线元1的起点半径为R1，终点半径为R2，线元1的长度为L，这里已知R2=40m，L=107.341m，根据缓和曲线的相关几何特性，可列方程组如下：根据以上方程组，可求解得：A=67.875m，R1=587.962m。

现在只剩下最后一个问题，就是计算线元4终点半径，即匝道终点半径。

终点半径的计算思路，完全可以参照线元1的起点半径的计算方法，而且由于线元4是完整缓和曲线，方程组更加简单，这里就不再赘述了。

我这里采用的是另一个计算方法，就是试算法，通过不断改变线元1的终点半径值，直到终点坐标与设计文件一致（或差值小于限差）。

这种方法的使用前提是：1．只有一个不确定的变量；2．必须有相关的计算软件或程序；3．必须知道变量的大致范围，并合理地确定一个初值；4．试算法的优点在于不必列出和求解繁杂的数学公式。

高等级公路中桩边桩坐标计算方法一．平面坐标系间的坐标转换公式如图，设有平面坐标系xoy 和x’o’y’（左手系——x 、x’轴正向顺时针旋转90º为y 、y’轴正向）；x 轴与x’轴间的夹角为θ（x 轴正向顺时针旋转至x’轴正向，θ范围：00—3600）。

设o’点在xoy 坐标系中的坐标为（xo’,yo’），则任一点P 在xoy 坐标系中的坐标（x,y ）与其在x’o’y’坐标系中的坐标（x’,y’）的关系式为：⎥⎦⎤⎢⎣⎡''⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎭⎬⎫'+'+='+'-=''''y x y x y x x y y y x y x x o o o o θθθθθθθθcos sin sin cos :sin cos cos sin 即二．公路中桩边桩统一坐标的计算高等级公路中桩边桩统一坐标的计算王 劲 松（广东交通职业技术学院土木系，广东 广州 510650）摘要：对位于直线、缓和曲线、圆曲线几个公路基本平面线形上的点，进行了中桩、边桩统一坐标的计算；并对一些复杂线形中要用到的非完整非对称缓和曲线上点的坐标计算进行了分析。

通过编程计算出各中桩边桩坐标后，能便于全站仪、GPS RTK 的坐标放样。

关键词：中桩；边桩；坐标转换；统一坐标系；缓和曲线The calculation for unified coordinates of center-stake& side-stake in advanced highwayWANG Jin-song（一）引言传统的公路中桩测设，常以设计的交点（JD ）为线路控制，用转点延长法放样直线段，用切线支距法或偏角法放样曲线段；边桩测设则是根据横断面图上左、右边桩距中桩的距离（L d 、R d ），在实地沿横断面方向进行丈量。

随着高等级公路特别是高速公路建设的兴起，公路施工精度要求的提高以及全站仪、GPS 等先进仪器的出现，这种传统方法由于存在放样精度低、自动化程度低、现场测设不灵活（出现虚交，处理麻烦）等缺点，已越来越不能满足现代公路建设的需要，遵照《测绘法》的有关规定，大中型建设工程项目的坐标系统应与国家坐标系统一致或与国家坐标系统相联系，故公路工程一般用光电导线或GPS 测量方法建立线路统一坐标系，根据控制点坐标和中边桩坐标，用“极坐标法”测设出各中边桩。

高速公路坐标高程计算程序本软件简要说明：一、平曲线计算（主程序）1、J为起算点里程，C、D为起算点的X、Y坐标，F为起算点的切线方位角，R为圆曲线半径（左偏取负，右偏取正），A、B为第一、第二缓和曲线回旋参数，O为圆曲线长度，Ki为该分段的终点里程；2、对于直线段或圆曲线段，起算点可取直线或圆曲线上的任意一点；3、对于带第一、第二缓和曲线的平曲线段，起算点应取HY点；4、K为所求点的里程，T、P为第一偏距、偏角，S、Z为第二偏距、偏角，偏角取从该点的切线顺时针旋转的夹角；5、分段法则：直线单独分段；单一的圆曲线单独分段；缓和曲线1+圆曲线+缓和曲线2为一个整体单独分段，若不存在第一或第二缓和曲线（即不完全缓和曲线）仍然可以计算，A或B可取任意不为零的值；若不存在圆曲线，则O取零；6、无论任何时候A、B不能取零，否则可能导致被零除的错误；7、F、Q切线方位角输入输出均为度.分秒的格式，例如153°24′05.24″=153.240524。

Q改变时，可按照新方位角为基准，结合第一第二偏距、偏角重新计算所求点；8、输入平曲线参数后，默认为计算全线坐标，可修改来计算某段曲线，默认间距也可修改；9、可参考CAD图《平曲线计算图例》；10、生成的中桩CAD脚本设置成在世界坐标系下生成，注意的是世界坐标系与大地测量坐标系的区别是XY坐标是互换的，否则画出的图形与实际相反。

先打开CAD，设置好图层名称、颜色，并设置为当前层，然后单击CAD的工具==>运行脚本==>选中生成的脚本文件即可。

11、输出的坐标结果可以导入到EXCEL中，操作办法为：打开EXCEL，然后把坐标数据复制到单元格里，然后单击数据==>分列==>选中分隔符号==>下一步==>选中TAB键和逗号==>下一步==>完成即可。

下一次可直接在此表中粘贴，数据自动分列。

二、缓和曲线计算（辅助程序）1、本程序为辅助程序，用来从ZH点或HZ点计算整条完全的缓和曲线，若不知道HY点X、Y、Q参数，可用此程序计算出来，然后输入平曲线参数；2、参数设置参考平曲线计算；3、导出到EXCEL的办法同平曲线计算；三、直线计算（辅助程序）1、本程序为辅助程序，若已知P1（X1，Y1），P1-->P2的距离I及方位角J（度.分秒格式），可计算坐标P2（X2，Y2）。

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式发布时间:2009-06-06 16:58:25高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

高速公路立交匝道卵形曲线的坐标计算瑞国二航局分公司测试中心摘 要：高速公路立交匝道平曲线普遍采用卵形曲线形式，关于其坐标的计算的原理与方法在众多书籍中介绍的较繁琐或不甚全面，笔者结合施工经历，利用工程实例对卵形曲线的坐标计算进展推导及验证。

关键词：高速公路 立交匝道 卵形曲线 坐标计算1 引言近年来，随着城市的开展需要，我国也逐渐加大对各城市的高速公路建立的资金投入，高速公路已占据我国公路网中的主要地位，设计单位为了使高速公路中立交匝道的线型美观和流畅，不可防止的需要插入卵形曲线，所以对于测量人员而言，掌握卵形曲线的坐标计算原理与方法显得尤为重要，本文通过对卵形曲线原理的分析以及公式推导，并结合工程实例进展计算验证，以此运用于高速公路的施工测量工程实践。

2 卵形曲线的概念卵形曲线是指在两个半径不等的同向圆曲线间插入一段非完整的缓和曲线而构成的复曲线。

即卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

在计算包含卵形曲线的立交匝道时，将卵形曲线转化成完整的缓和曲线后按照缓和曲线公式计算，问题与难点便迎刃而解。

3 卵形曲线坐标计算原理对于初学者，判定某段缓和曲线是否为卵形曲线的技巧为：将该段的缓和曲线参数平方除以该段缓和曲线的长度，计算出数值是否等于与其相连接的圆曲线半径，用公式表达为R LA 2,假设该公式结果成立，那么为正常缓和曲线，假设结果不成立，那么为卵形曲线。

如图1所示，在半径为1R 与2R 的两圆曲线间插入长度为F L 的非完整缓和曲线，此段缓和曲线的端点分别为YH 和HY 点，首先计算出整条完整缓和曲线的起点桩号'ZH 或终点桩号'HZ 〔该图1中计算出点桩号'HZ 〕、'HZ 的坐标)Y ,(X C C 、'HZ 的切线方位角C W 〔即图1中CD 的方位角〕，最后根据以上条件求得卵形曲线上任意一点桩号的坐标和切线方位角。

0
备注 弧度制 1.050259
R2*Ls1 =A12 8100
备注
值（左转“+”，右转“-”）
位角（左转“-”，右转“+”） 利用公式反算
坐标增量 △X 16.19957485 △Y 0.08747836
ZH
任一点 与ZH完整 点弧长 L0 16.2
16.19981 1.066459 1.061059
0.005399988
0.0162
-1
ZH完整点切线方位角β ZH完整-M0直线方位角β X完整 Y完整
切线方位角=M0点切线方位角±转角值（左转“+”，右转“-”）
第一段完整曲线要素 ZH完整坐标 X 3435389.441 Y 500174.9586 ZH完整桩号 K0+702.747
弦长C= 偏角= √△X2+△Y2 arctg（△Y/△X)
（切线）方位 角β 1 1.066458665
转角值= 2 L0 /2*R2*Ls1
参数g （左偏-1, 右偏+1）
直线
(适用正推)直线方位角=偏角±切线方位角（左转“-”，右转“+”） X0=X完整+C*COS(ZH完整-M0直线方位角） Y0=Y完整+C*SIN(ZH完整-M0直线方位角)
3435389.441 500174.9586
缓和曲线 完整性 不完整
备注 A12=Ls1*R2
整
不是直线方位角）

说明：①现以第一段曲线上任一点坐标和方位角反推ZH完整点坐标，切线方位角（不是直线方位角） ②不用改变坐标系 第一段缓和曲线上任一点曲线元素 任一点坐标M0 X0 Y0 3435397.346 500189.099 任一点M0桩号 K0+718.947 度 60 （切线）方位角β 0 分 秒 10 31.4

C匝道线元法坐标计算（双心版）一、示例图纸
主点坐标表
逐桩坐标表
线位数据图
二、图纸分析
根据主点坐标表和线位数据图分析出下图：
BP—HY为一段缓和曲线，A=70,LS=41.585，由于A²≠LS*R，70²≠41.585*60，所以该段缓和曲线为非完整缓和曲线，起点半径为：
有两个数据值，在用“测量员”或者“轻松测量”时输入哪一个都可以。

此处是双心软件计算不需要考虑。

HY—YH为一段圆曲线，R=60；YH—EP为一段缓和曲线，由于A²=LS*R，90²=135*60，所以该段缓和曲线为完整的，终点半径为无穷大。

三、双心软件输入参数
四、坐标计算结果
五、生成CAD脚本图。

在 图 １中有 ：
Ｊ
Ｉ一 ｄ பைடு நூலகம்ｌ
将式 （ ） 入式 （ ） 得 ： ２代 ３，
一
（ ３ ）
（ ） ４
“ 直线 曲线及 转角 一 览 表 ” 其 中线 坐 标 的计 算 不 宜 ，
使用 基本型 曲线 的计算 公式 ， 是使用 线 元法 。 而
ｌ 线元 法 中线 坐 标 的计 算 公 式
ｆ— Ｐ Ｄ ＾＋ （） ２
｛ 一ｆｉ ｄ＝ｌ ｘ ｄ Ｓ ＇ ｉ ，ｃ ｏ ｓ ｌ ｆ
ｆ一 ｏ， ｚ ｊ ｓ１ ｃｄ ｌ ｆ
（ ７）
式 中： Ｌ—ＤＫＢ —ＤＫＡ 为 回旋 曲线长 度 ； —ＤＫ ， ｚ —
（ ８）
Ｄ Ｋ ， 为任 意点距 回旋 曲线 起 点的长 度 。
曲线右 偏 时 ，Ａ 为正 ； 偏 时 ，Ａ Ｐ ｐ、 左 ｐ 、Ｂ为负 。
１一 ｄ ｚ
设 回旋 曲线 起 点 在 路 线 坐标 系 下 的 坐 标 为 Ａ
维普资讯
１ ４ ７
ｖ 运 ｔｏ ｓ Ｈ ｉ ｈ ｙ 路 ｔｍｏ ｉ ｅ ｇ 公 ｗａ ｓ＆ Ａｕ与 ｔ汽 ｐ ｉａ ｉｎ ｏ Ａｐ ｌｃ
广． ￡
．— ＡＩ Ｓｚ ： Ｘ＋‘ａ ｆ Ｘ Ｃ＇ Ｏｄ
ｌ Ｙ— ＋ Ｉｓ ａｄ ‘ｉ ｚ ｎ
Ｌ Ｊ０
㈤
Ｒ” ” Ｒ１ ：Ｒ— Ｏ ＞ 一 ０： ＝Ａ ≠ Ａ一 １ Ｒ ÷
Ｔ” ” Ｒ２ ：Ｔ— Ｏ ＞ ＝ Ｂ一 ０ ≠ Ｂ一 １ Ｔ ： ÷
｛ ：Ｌ—Ｐ— Ｓ Ｐ｝
总 第 １ ６期 ２
Ｈｉｈ ｙ ｇ ｗａ ｓ＆ Ａｕ ｏ ｔｖ ｐｌｃ ｔｏ ｓ ｔｍｏ ｉ ｅＡｐ ｉａ ｉ ｎ