22.1.2-二次函数y=ax2的图象和性质同步练习(含答案)
- 格式:doc
- 大小:333.98 KB
- 文档页数:3

《二次函数的图象和性质》同步测试2讲堂学习检测一、填空题1.已知 a≠0,(1)抛物线 y= ax2的极点坐标为 ______,对称轴为 ______.(2)抛物线 y= ax2+ c 的极点坐标为 ______,对称轴为 ______ .(3)抛物线 y= a(x- m)2的极点坐标为 ______,对称轴为 ______.2.若函数y (m 1) x2 m2m 1是二次函数,则m=______ .23.抛物线 y= 2x2的极点,坐标为______,对称轴是 ______.当 x______时, y 随 x 增大而减小;当 x______时, y 随 x 增大而增大;当x= ______时, y 有最 ______值是 ______.4.抛物线 y=- 2x2的张口方向是 ______,它的形状与y= 2x2的形状 ______,它的极点坐标是 ______ ,对称轴是 ______.5.抛物线y= 2x2+ 3 的极点坐标为______,对称轴为 ______.当 x______ 时, y 随 x 的增大而减小;当x= ______时, y 有最 ______值是 ______,它能够由抛物线y= 2x2向 ______平移______ 个单位获得.6.抛物线 y= 3(x-2)2的张口方向是______,极点坐标为 ______,对称轴是 ______.当 x______时, y 随 x 的增大而增大;当x=______时, y 有最 ______值是 ______,它能够由抛物线y=3x2向 ______平移 ______个单位获得.二、选择题7.要获得抛物线y 1( x4) 2,可将抛物线 y1x2()33A .向上平移 4 个单位B .向下平移 4 个单位C.向右平移 4 个单位D .向左平移 4 个单位8.以下各组抛物线中能够相互平移而相互获得对方的是()A . y=2x2与 y= 3x21x2 2 与 y 2 x21 B . y22C. y=2x2与 y= x2+ 2D. y= x2与 y= x2- 29.极点为 (- 5, 0),且张口方向、形状与函数y1x2的图象同样的抛物线是()3A . y 1( x 5)2 B . y 1 x25 33C. y 1( x 5) 2D. y1( x 5)2 33三、解答题10.在同一坐标系中画出函数y1121x23和 y312的图象,并说明y1, y2 x3, y22x22的图象与函数y1x2的图象的关系.211.在同一坐标系中,画出函数y1= 2x2, y2= 2(x-2) 2与 y3= 2(x+2) 2的图象,并说明y2,y3的图象与y1= 2x2的图象的关系.综合、运用、诊疗一、填空题12.二次函数 y= a(x- h)2+ k( a≠0)的极点坐标是,对称轴是,当 x=时, y 有最值;当 a> 0 时,若 x时, y 随 x 增大而减小.13.填表.分析式张口方向极点坐标对称轴y= (x- 2)2- 3y=- (x+3) 2+ 2y1(x5)252y1( x 5 )2132y=3(x-2)2y=- 3x2+ 214.抛物线 y1( x3)2 1 有最 ______点,其坐标是 ______.当 x= ______时,y 的最 ______ 2值是 ______;当 x______时, y 随 x 增大而增大.15.将抛物线 y1x2向右平移 3 个单位,再向上平移 2 个单位,所得的抛物线的分析式为3______ .二、选择题16.一抛物线和抛物线y=- 2x2的形状、张口方向完整同样,极点坐标是(- 1, 3),则该抛物线的分析式为()A . y=- 2(x- 1)2+ 3B .y=- 2(x+ 1)2+ 3C. y=- (2x+ 1)2+3D. y=- (2x- 1)2+ 317.要获得 y=- 2(x+ 2)2- 3 的图象,需将抛物线y=- 2x2作以下平移()A .向右平移 2 个单位,再向上平移 3 个单位B .向右平移 2 个单位,再向下平移 3 个单位C.向左平移 2 个单位,再向上平移 3 个单位D .向左平移 2 个单位,再向下平移 3 个单位三、解答题18.将以下函数配成y= a(x- h)2+ k 的形式,并求极点坐标、对称轴及最值.(1) y= x2+ 6x+ 10(2) y=- 2x2- 5x+ 7(3) y= 3x2+2x(4) y=- 3x2+ 6x- 2(5) y= 100- 5x2(6) y= (x- 2)(2x+ 1)拓展、研究、思虑19.把二次函数 y= a(x- h)2+ k 的图象先向左平移 2 个单位,再向上平移 4 个单位,获得二次函数y 1(x 1) 2 1 的图象.2(1)试确立 a, h,k 的值;(2)指出二次函数 y= a(x- h)2+ k 的张口方向、对称轴和极点坐标.参照答案1. (1)(0 ,0), y 轴;(2)(0 , c) ,y 轴; (3)( m ,0),直线 x =m .2. m =- 13. (0, 0), y 轴, x ≤0, x > 0, 0,小, 0.4.向下,同样, (0,0) ,y 轴.5. (0, 3), y 轴, x ≤0, 0,小, 3,上, 3.6.向上, (2, 0),直线 x = 2, x ≥2, 2,小, 0,右, 2.7. C . 8. D . 9. C .10.图略, y 1, y 2 的图象是 y1 x 2的图象分别向上和向下平移 3 个单位.211.图略, y 2, y 3 的图象是把 y 1 的图象分别向右和向左平移2 个单位.12. (h , k),直线 x = h ; h , k , x ≤h .13.张口方向极点坐标对称轴y = (x - 2)2-3 向上 (2 ,- 3) 直线 x = 2 y =- (x + 3)2+ 2向下 (-3,2)直线 x =- 3y1( x5) 2 5向下(- 5,- 5) 直线 x =- 52(5,1)直线 x =5y1( x 5 )21向上3222y = 3(x - 2)2 向上 (2,0) 直线 x = 2 y =- 3x 2+ 2向下(0,2)直线 x = 014.高. (-3,- 1),- 3,大,- 1, ≤-3. 15. y1 (x 3) 22 1 x 2 2x 5.3316. B . 17. D .18. (1)y = (x + 3) 2+ 1,极点 ( -3, 1),直线 x =- 3,最小值为 1.(2) y2(x5 )281, 极点 ( 5 , 81), 直线 x 5 , 最大值为 814 84 84 8 (3) y3( x 1 )21 ,极点( 1,1), 直线 x1 , 最小值为1333333(4)y =- 3(x - 1)2+ 1,极点 (1, 1),直线 x = 1,最大值为 1.(5)y=- 5x2+ 100,极点 (0, 100),直线 x=0,最大值为100.(6) y2( x 3 )225,极点 (3,25), 直线x3, 最小值为251 , h 48484819. (1) a1, k5;2(2)张口向上,直线x=1,极点坐标 (1,- 5).。


22.1.2二次函数()2h x a y -=的图象和性质同步练习 一、选择题1.抛物线12-=x y 的顶点坐标为( )A .(1,0)B .(−1,0)C .(0,−1)D .(2,3)2.抛物线()4232+--=x y 的开口方向、对称轴、顶点坐标分别为( ) A .开口向下,对称轴2-=x ,顶点坐标(−2,4) B .开口向上,对称轴2=x ,顶点坐标(2,4)C .开口向上,对称轴2=x ,顶点坐标(2,−4)D .开口向下,对称轴2=x ,顶点坐标(2,4)3.抛物线()52342-+=--m x y m m 的顶点在x 轴下方,则( )A .5=mB .1-=mC .15-==m m 或D .15=-=m m 或4.把抛物线221x y =向左平移1个单位长度,再向下平移1个单位,得抛物线为( ) A .()22212++=x x y B .()12212-+=x x y C .()12212--=x x y D .()12212+-=x x y 5.二次函数()2122+-=x y 的图象可由22x y =的图象( )得到. A .向左平移1个单位长度,再向下平移2个单位长度B .向左平移1个单位长度,再向上平移2个单位长度C .向右平移1个单位长度,再向下平移2个单位长度D .向右平移1个单位长度,再向上平移2个单位长度6.将抛物线12--=x y 向上平移2个单位得到抛物线的表达式( )A .2x y -=B .22--=x yC .12+-=x yD .12+=x y 7.抛物线b x y +=2与抛物线22-=ax y 的形状相同,只是位置不同,则b a 、值分别是( ) A .2,1-≠=b a B .2,1≠=b a C .2,1-≠±=b a D .2,1≠±=b a 8. 二次函数2ax y =与一次函数a ax y +=在同一坐标系中的图象大致是( ) A.B. C. D. 9. 函数b ax y +=2与b ax y +=在同一坐标系里的图象大致是( )A .B .C .D . 10. 已知二次函数()k x y +-=213的图象上有三点A(2,y 1),B(2,y 2),C(−5,y 3),则321y y y 、、的大小关系为( )A .321y y y >>B .312y y y >>C .213y y y >>D .123y y y >>二、填空题1、抛物线()232+=x y 的开口 ;顶点坐标为 ;对称轴是_________;当3->x 时,y 随x 的增大而 ;当3-=x 时,y 有最 值是_________.2、函数2)1(3+-=x y ,当x 时,函数值y 随x 的增大而减小;当x 时,函数取得最 值,最 值y = .3、若抛物线()21+=x m y 过点(1,-4),则m =__________.4、抛物线()224-=x y 与y 轴的交点坐标是 ,与x 轴的交点坐标为 . 5、把抛物线23x y =向右平移4个单位后,得到的抛物线的表达式为 ,再向上平移4个单位得到的抛物线的表达式为 .6、将抛物线()2131--=x y 向左平移2个单位后得到的抛物线解析式为 . 7、二次函数12+-=mx x y 的图象的顶点在x 轴上,则m 的值是 .8、抛物线()2n x m y +=向左平移2个单位后,得到的函数关系式是()244--=x y ,则m = ,n = .9、二次函数2)2(31+=x y ,若y 恒大于0,则自变量x 的取值范围是 . 10、把抛物线22y x =向左平移使顶点坐标是(-1,0),则所得抛物线的表达式为 .11、写出一个顶点是(5,0),形状、开口方向与抛物线22x y -=都相同的二次函数解析式_________________.12、一条抛物线的对称轴是1x =,且与x 轴有唯一的公共点,并且开口方向向下,则这条抛物线的解析式是 .(任写一个)三、解答题1、已知二次函数7)1(82-+--=k x k x y ,当k 为何值时,此二次函数以y 轴为对称轴?写出其函数关系式.2、二次函数()2h x a y -=的图象如图:已知21=a ,OA OC =,试求该抛物线的解析式.3、将抛物线2ax y =向左平移后所得新抛物线的顶点横坐标为2-,且新抛物线经过点()1,3,求a 的值.4、如图所示,抛物线2()y x m =--的顶点为A ,直线L :y x m =-与y 轴的交点为B ,其中0>m .(1)写出抛物线的对称轴和顶点坐标;(用含m 的式子表示);(2)若点A 在直线L 上,求∠ABO 的大小.5、如图,河上有一座抛物线桥洞,已知桥下的水面离桥拱顶部3m 时,水面宽AB 为6m ,当水位上升0.5m 时:(1)求抛物线的解析式。

2的图象和性质教学目标:1、使学生会用描点法画出y=ax2的图象,理解抛物线的有关概念。
2、使学生经历、探索二次函数y=ax2图象性质的过程,培养学生观察、思考、归纳的良好思维习惯重点难点:重点:使学生理解抛物线的有关概念,会用描点法画出二次函数y=ax2的图象是教学的重点。
难点:用描点法画出二次函数y=ax2的图象以及探索二次函数性质是教学的难点。
教学过程:一、提出问题1,同学们可以回想一下,一次函数的性质是如何研究的?(先画出一次函数的图象,然后观察、分析、归纳得到一次函数的性质)2.我们能否类比研究一次函数性质方法来研究二次函数的性质呢?如果可以,应先研究什么?(可以用研究一次函数性质的方法来研究二次函数的性质,应先研究二次函数的图象) 3.一次函数的图象是什么?二次函数的图象是什么?二、范例例1、画二次函数y=ax2的图象。
解:(1)列表:在x的取值范围内列出函数对应值表:x …-3 -2 -1 0 1 2 3 …y …9 4 1 0 1 4 9 …(2)在直角坐标系中描点:用表里各组对应值作为点的坐标,在平面直角坐标系中描点(3)连线:用光滑的曲线顺次连结各点,得到函数y=x2的图象,如图所示。
提问:观察这个函数的图象,它有什么特点?让学生观察,思考、讨论、交流,归结为:它有一条对称轴,且对称轴和图象有一点交点。
抛物线概念:像这样的曲线通常叫做抛物线。
顶点概念:抛物线与它的对称轴的交点叫做抛物线的顶点.三、做一做1.在同一直角坐标系中,画出函数y=x2与y=-x2的图象,观察并比较两个图象,你发现有什么共同点?又有什么区别?2.在同一直角坐标系中,画出函数y=2x2与y=-2x2的图象,观察并比较这两个函数的图象,你能发现什么?3.将所画的四个函数的图象作比较,你又能发现什么?对于1,在学生画函数图象的同时,教师要指导中下水平的学生,讲评时,要引导学生讨论选几个点比较合适以及如何选点。

人教版九年级数学上册22.1 二次函数的图象和性质同步训练一、选择题1. 二次函数y=2x2,y=-2x2,y=12x2的共同性质是()A.其图象开口都向上B.其图象的对称轴都是y轴C.其图象都有最高点D.y随x的增大而增大2. 若y=ax2+bx+c,则由表格中的信息可知y与x之间的函数解析式是()A.y=x2-4x+3 B.y=x2-3x+4C.y=x2-3x+3 D.y=x2-4x+83. 若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为()A. x1=0,x2=6B. x1=1,x2=7C. x1=1,x2=-7D. x1=-1,x2=74. 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是()A.b≥-1 B.b≤-1C.b≥1 D.b≤15. 二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是()A. 抛物线开口向下B. 抛物线经过点(2,3)C. 抛物线的对称轴是直线x=1D. 抛物线与x轴有两个交点6. 将函数y=x2的图象用下列方法平移后,所得的图象不经过点A(1,4)的是() A.向左平移1个单位长度B.向右平移3个单位长度C.向上平移3个单位长度D.向下平移1个单位长度7. 已知抛物线y=2x2+bx+c的顶点坐标是(-1,-2),则b与c的值分别为() A.-1,-2 B.4,-2C.-4,0 D.4,08. 已知二次函数y=x2+bx+c与x轴只有一个交点,且图象过A(x1,m)、B(x1+n,m)两点,则m、n的关系为()A. m=12n B. m=14n C. m=12n2 D. m=14n2二、填空题9. 某抛物线的形状、开口方向与抛物线y=12x2-4x+3相同,顶点坐标为(-2,1),则该抛物线的函数解析式为________________.10. 已知抛物线y=2(x-1)2上有两点(x1,y1),(x2,y2),且1<x1<x2,则y1与y2的大小关系是________.11. 抛物线y=-8x2的开口向________,对称轴是________,顶点坐标是________;当x>0时,y随x的增大而________,当x<0时,y随x的增大而________.12. 已知二次函数的图象经过原点及点(-12,-14),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析式为________________.13. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值为________.14. 顶点坐标是(2,0),且与抛物线y=-3x2的形状、开口方向都相同的抛物线的解析式为________.15. 如图,抛物线y=ax2+bx+c与x轴相交于点A,B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是________.16. 如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是________.三、解答题17. 已知抛物线y=ax2经过点A(-2,-8).(1)求此抛物线的解析式;(2)判断点B(-1,-4)是否在此抛物线上;(3)求出抛物线上纵坐标为-6的点的坐标.18. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=-12x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.19. 如图,等腰直角三角形ABC的直角边与正方形MNPQ的边长均为10 cm,边CA与边MN在同一直线上,开始时点A与点M重合,△ABC沿MN方向以1 cm/s 的速度匀速运动,当点A与点N重合时,停止运动.设运动的时间为t s,运动过程中△ABC与正方形MNPQ重叠部分的面积为S cm2.(1)试写出S关于t的函数关系式,并指出自变量t的取值范围;(2)当MA=2 cm时,重叠部分的面积是多少?20. 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;(2)根据图象,写出你发现的一条结论;(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.人教版九年级数学上册22.1 二次函数的图象和性质同步训练-答案一、选择题1. 【答案】B2. 【答案】A[解析] ∵x =1时,ax 2=1,∴a =1.将(-1,8),(0,3)分别代入y =x 2+bx +c ,得⎩⎨⎧1-b +c =8,c =3,解得⎩⎨⎧b =-4,c =3.∴y 与x 之间的函数解析式是y =x 2-4x +3.故选A.3. 【答案】D【解析】∵二次函数y =x 2+mx 的对称轴为x =-m2=3,解得m =-6,则关于x 的方程为x 2-6x =7,解得,x 1=-1,x 2=7.4. 【答案】D [解析] 先根据抛物线的性质得到其对称轴为直线x =b ,且当x >b 时,y 的值随x 值的增大而减小.因为当x >1时,y 的值随x 值的增大而减小,所以b≤1.5. 【答案】D【解析】本题考查了二次函数的性质,由于2>0,所以抛物线的开口向上,所以A 选项错误;由于当x =2时,y =8-3=5,所以B 选项错误;由于y =2x 2-3的对称轴是y 轴,所以C 选项错误;由2x 2-3=0得b 2-4ac =24>0,则该抛物线与x 轴有两个交点,所以D 选项正确.6. 【答案】D [解析] A .将函数y =x 2的图象向左平移1个单位长度得到函数y =(x +1)2的图象,它经过点(1,4);B.将函数y =x 2的图象向右平移3个单位长度得到函数y =(x -3)2的图象,它经过点(1,4);C.将函数y =x 2的图象向上平移3个单位长度得到函数y =x 2+3的图象,它经过点(1,4);D.将函数y =x 2的图象向下平移1个单位长度得到函数y =x 2-1的图象,它不经过点(1,4).故选D.7. 【答案】D8. 【答案】D【解析】因为二次函数y =x 2+bx +c 的图象与x 轴只有一个交点,∴b 2-4c =0,即c =b 24,由题意知,点A ,B 关于抛物线的对称轴对称,∴12AB=|n|2=-b 2-x 1,b =-|n|-2x 1, ∴c =(-|n|-2x 1)24=|n|2+4|n|x 1+4x 214,∵A(x 1,m)在y =x 2+bx +c 上,∴m =x 21+bx 1+c ,∴ m =x 21+(-|n|-2x 1)· x 1+|n|2+4|n|x 1+4x 214,化简整理得m =14n 2,故选D .二、填空题9. 【答案】y =12(x +2)2+1 [解析] 已知抛物线的顶点坐标,可以设顶点式y =a(x -h)2+k.又因为该抛物线的形状、开口方向与抛物线y =12x 2-4x +3相同,所以a =12,所以该抛物线的函数解析式是y =12(x +2)2+1.10. 【答案】y 1<y 2[解析] ∵抛物线的解析式是y =2(x -1)2,∴其对称轴是直线x =1,抛物线的开口向上, ∴在对称轴右侧,y 随x 的增大而增大.又∵抛物线y =2(x -1)2上有两点(x 1,y 1),(x 2,y 2),且1<x 1<x 2,∴y 1<y 2.11. 【答案】下y 轴 (0,0) 减小 增大12. 【答案】y =x 2+x 或y =-13x 2+13x 【解析】依题意,所求函数有可能经过(-1,0),(-12,-14) 或(1,0),(-12,-14) .设所求函数解析式为y =ax 2+bx +c ,图象经过原点,则c =0,当图象经过(-1,0),(-12,-14)时,代入可求得a =b =1,即所求解析式为y =x 2+x ; 当图象经过(1,0),(-12,-14)时,代入可求得a =-13,b =13,即所求解析式为y =-13x 2+13x .综上所述,所求函数的解析式为y=x 2+x 或y =-13x 2+13x .13. 【答案】0 【解析】设抛物线与x 轴的另一个交点是Q ,∵抛物线的对称轴是过点(1,0)的直线,与x 轴的一个交点是P(4,0),∴与x 轴的另一个交点Q(-2,0),把(-2,0)代入解析式得:0=4a -2b +c ,∴4a -2b +c =0.14. 【答案】y =-3(x -2)215. 【答案】(-2,0)【解析】如解图,过D 作DM ⊥x 轴于点M ,∴M(m ,0),又B(m +2,0),∴MB =2,由C(0,c),D(m ,c)知:OC =DM ,即点C 、D 关于对称轴对称,故点O 、M 也关于对称轴对称,∴OA =MB =2,∴A(-2,0).16. 【答案】-2 [解析] 抛物线y =ax 2+bx 的顶点C 的坐标为(-b 2a ,-b 24a).把x =-b 2a 代入y =ax 2,得点B 的坐标为(-b 2a ,b 24a ).在y =ax 2+bx 中,令y =0,则ax 2+bx =0,解得x 1=0,x 2=-b a ,∴A(-ba ,0).∵四边形ABOC 为正方形,∴BC =OA ,∴2·b 24a =-b a ,即b 2+2b =0.解得b =-2或b =0(不符合题意,舍去).三、解答题17. 【答案】解:(1)∵抛物线y =ax 2经过点A(-2,-8),∴4a =-8,解得a =-2,∴此抛物线的解析式为y =-2x 2.(2)当x =-1时,y =-2,∴点B(-1,-4)不在此抛物线上.(3)把y =-6代入y =-2x 2,得-2x 2=-6,解得x =±3,∴抛物线上纵坐标为-6的点的坐标为(3,-6),(-3,-6).18. 【答案】解:(1)把B(-2,6),C(2,2)代入抛物线的解析式得: ⎩⎨⎧6=a·(-2)2+b·(-2)+22=a·22+b·2+2,(1分)解得⎩⎪⎨⎪⎧a =12b =-1,(2分)∴抛物线的解析式为y =12x 2-x +2.(3分)(2)抛物线解析式化为顶点式:y =12(x -1)2+32,则抛物线顶点D(1,32),(4分) 如解图①所示,过点B 、D 、C 分别向x 轴作垂线,垂足分别为点M 、N 、H ,则有:S △BCD =S 梯形BMHC -S 梯形BMND -S 梯形DNHC =12(6+2) ×4-12(6+32)×3-12(32+2) ×1 =3.(6分)解图①解图② (3)如解图②所示,连接BC ,∵直线BC 斜率k BC =2-62-(-2)=-1<-12,∴过点C 作直线MN 与直线y =-12x 平行,设直线MN 的解析式为y =-12x +b 1,代入C(2,2), ∴b 1=3.(7分)作直线EF 与抛物线相切,且与直线y =-12x 平行, 设直线EF 的解析式为y =-12x +b 2,联立抛物线解析式得, ⎩⎪⎨⎪⎧y =12x 2-x +2y =-12x +b 2, ∴x 2-x +4-2b 2= 0, ∵直线EF 与抛物线相切,∴b 2-4ac =0,即(-1)2-4(4-2b 2)=0,(9分)∴b 2=158,(11分) ∴158<b ≤3.(12分)注:斜率知识为高中知识,但常渗透于中考压轴题,与二次函数相结合考查,做题时注意其性质的应用.19. 【答案】解:(1)设AB 与MQ 交于点R.∵△ABC 是等腰直角三角形,四边形MNPQ 是正方形, ∴△AMR 是等腰直角三角形. 由题意知,AM =MR =t ,∴S =S △AMR =12t·t =12t 2(0≤t≤10).(2)当MA =2 cm ,即t =2时,重叠部分的面积是12×2×2=2(cm 2).20. 【答案】解:(1)当k =0时,y =-(x -1)(x +3),所画图象如解图所示.(2分)(2)①k 取0和2时的函数图象关于点(0,2)中心对称,②函数y =(x -1)[(k -1)x +(k -3)](k 是常数)的图象都经过(1,0)和(-1,4).(5分)(3)由题意可得y 2=(x -1)[(2-1)x +(2-3)]=(x -1)2,平移后的函数y 3的表达式为y 3=(x -1+4)2-2=(x +3)2-2, 所以当x =-3时,函数y 3的最小值是-2.(8分)。
人教版数学九年级上册《22.1.2二次函数y=ax2 的图象和性质》说课稿1一. 教材分析人教版数学九年级上册《22.1.2二次函数y=ax^2 的图象和性质》这一节,是在学生已经掌握了函数的概念、一次函数的图象和性质的基础上,进一步引导学生学习二次函数的图象和性质。
通过这一节的学习,使学生能够掌握二次函数的一般形式,了解二次函数的图象特征,以及掌握二次函数的性质。
教材通过丰富的例题和练习题,帮助学生巩固所学知识,提高解决问题的能力。
二. 学情分析九年级的学生已经具备了一定的函数知识,对一次函数的图象和性质有了初步的了解。
但是,二次函数相对于一次函数来说,图象和性质更加复杂,需要学生有一定的抽象思维能力。
此外,学生可能对二次函数的图象和性质在实际问题中的应用还不够清晰,需要教师在教学中进行引导和启发。
三. 说教学目标1.知识与技能目标:让学生掌握二次函数的一般形式,了解二次函数的图象特征,掌握二次函数的性质。
2.过程与方法目标:通过观察、分析、归纳等方法,引导学生自主探究二次函数的图象和性质。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的探究精神和合作意识。
四. 说教学重难点1.教学重点:二次函数的一般形式,二次函数的图象特征,二次函数的性质。
2.教学难点:二次函数的图象和性质在实际问题中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组讨论法等,引导学生主动探究,提高学生的参与度和积极性。
2.教学手段:利用多媒体课件,展示二次函数的图象和性质,使抽象的知识更加直观形象。
同时,利用练习题和案例,帮助学生巩固所学知识。
六. 说教学过程1.导入:通过复习一次函数的图象和性质,引出二次函数的一般形式,激发学生的学习兴趣。
2.探究二次函数的图象特征:让学生观察二次函数的图象,引导学生发现二次函数的顶点、开口方向等特征。
3.探究二次函数的性质:通过小组讨论,让学生归纳出二次函数的增减性、对称性等性质。
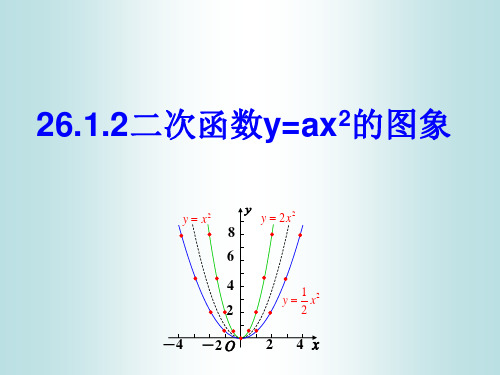
- 1 -
二次函数2axy的图象和性质
知识点:
1.用描点发画函数图象的步骤是 , , 。
2.二次函数图象是 ,开口方向由 决定,开口大小的程度又是由谁决定的?
3.一般地,抛物线2axy的对称轴是 ,顶点坐标是 .当0a时,抛物线开口向 ,
顶点是抛物线的 ,a 越大,抛物线的开口越 ;当0a时,抛物线开口向 ,顶点是
抛物线的 ,a 越大,抛物线的开口越 。
一.选择题
1.关于函数23xy 的性质的叙述,错误的是( ).
A.对称轴是y 轴 B.顶点是原点 C.当0x时,y随x 的增大而增大 D.y有最大值
2.在同一坐标系中,抛物线22221,,xyxyxy的共同点是( ).
A.开口向上,对称轴是y轴,顶点是原点 B.对称轴是y轴,顶点是原点
C.开口向下,对称轴是y 轴,顶点是原点 D.有最小值为0
3.函数2axy与baxy的图象可能是( )
A B C D
4.在同一平面直角坐标系中,同一水平线上开口最大的抛物线是( )
A. 2xy B. 231xy C. 233xy D. 22xy
5.下列函数中,具有过原点,且当0x时,y 随x增大而减小,这两个特征的有( ).
①)0(2aaxy;②)1()1(2axay;③)0(22aaxy;④)0(23aaxy
A.1个 B.2个 C.3个 D.4个
6.若对任意实数x,二次函数2)1(xay的值总是非负数,则a 的取值范围是( ).
A.1a B.1a C.1a D.1a
7.下列说法错误的是( ).
- 2 -
x
y
o
A.在二次函数23xy 中,当0x时,y随x的增大而增大
B.在二次函数26xy 中,当0x时,y 有最大值0
C.a越大图象开口越小,a 越小图象开口越大
D.不论a是正数还是负数,抛物线)0(2aaxy的顶点一定是坐标原点
8.已知点),2(),,1(),,3(321yCyByA在抛物线232xy 上,则321,,yyy 的大小关系是( ).
A.321yyy B.321yyy C.231yyy D.132yyy
二.填空题
1.抛物线221xy的对称轴是 (或 ),顶点坐标是 ,抛物线上 的点都在x轴的
方,当x 时,y随x的增大而增大,当x 时,y随x的增大而减小,当x= 时,该函
数有最 值是 。
2..抛物线26xy的对称轴是 (或 ),顶点坐标是 ,抛物线上 的点都在x轴的
方,当x 时,y随x的增大而增大,当x 时,y随x的增大而减小,当x 时,该函
数有最 值是 。
3.二次函数223xy,当x1>x2>0时,试比较1y和2y的大小:1y _2y(填“>”,“<”或“=”)
4.二次函数12mmxy在其图象对称轴的左则,y随x的增大而增大,m 。
5.对于函数22xy下列说法:①当x取任何实数时,y的值总是正的;②x的值增大,y的值也增大;③y随x
的增大而减小;④图象关于y轴对称。其中正确的是 。
6.抛物线12xy的最小值是 。
7.如图所示,在同一坐标系中,作出①23xy②221xy③2xy的图
象,则图象从里到外的三条抛物线对应的函数依次是 (填序号)
8.直线2xy与抛物线2xy 的交点坐标是 。
9.已知点)7,(1x和点))(7,(212xxx均在抛物线2axy上,则当21xxx时,y的值 是 。
10.抛物线 22xy与直线bxy3的一个交点坐标是),3(m,则另一个交点坐标是 。
11.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛
物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是 _________ .
- 3 -
12.如图,⊙O的半径为2.C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是 _________ .
三.解答题
1. 已知函数422mmxmy是关于x的二次函数,求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最底点?求出这个最底点,当x为何值时,y随x的增大而增大;
(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?
3.已知二次函数2axy的图象与直线12xy交于点),1(mP.
(1)求ma,的值;
(2)写出二次函数的解析式,并指出x在和范围内时,y随x的增大而增大.
4.如图,某涵洞的截面是抛物线的一部分,现水面宽mAB6.1,涵洞顶点O到水面的距离为m4.2,求涵洞所
在抛物线的解析式。