全等三角形证明与直角三角形经典88题
- 格式:doc
- 大小:296.00 KB
- 文档页数:17
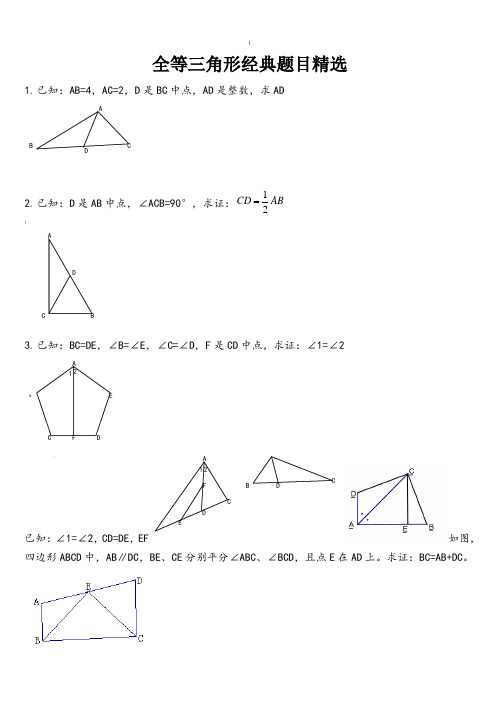
[全等三角形经典题目精选1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB!3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2已知:∠1=∠2,CD=DE ,EF 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
A& CD EF 21 AD B CDA BC ACDF21 E CD B `8.已知:AB 知:AB=CD ,∠A=∠D ,求证:∠B=∠C是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB> 11.已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC13.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .14.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA>DC】 A F E A B CP DA CBF A E D}B15.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PEDCBA16.如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD,求证:∠C=2∠BDCBA《17.如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立若成立请给予证明;若不成立请说明理由.18.已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):O E DC B A19.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .|FEDCB A20、如图:DF=CE ,AD=BC ,∠D=∠C 。

全等三角形的证明基础题定A 篇(一)三角形全等的识别方法1、如图:△ABC 与△DEF 中2、如图:△ABC 与△DEF 中∴△ABC ≌△DEF(SSS) ∴△ABC ≌△DEF(SAS)3、如图:△ABC 与△DEF 中4、如图:△ABC 与△DEF 中∵{ ∵{∴△ABC ≌△DEF(ASA) ∴△ABC ≌△DEF(AAS)(全等三角形的对应边 )∠A= ,∠B= ,∠C= .B :运用篇 1.如图(1)求证△ABC ≌△ADC. 如图(2). AE=BC.∠A.∠B 是直角.求证△ABC ≌△BCD.〔 = ∵=∵{ =-5、如图: Rt△ABC与Rt△DEF中, ∠ =∠ =90°::{∴Rt△ABC≌Rt△DEF( )(二)全等三角形的特征 ∵△ABC≌△DEF∴AB= . AC= BC= .2、已知: 如图: BE=CF, AB=DE, AC=DF,求证: AB∥DE 4. 已知:AB=AC、AD=AE、∠1=∠2. 求证: △ABD≌△ACE.B .F3.如图,点E,F在 BC上,BE=CF,AB=DC, ∠B=∠C,求证:∠A=∠B。
5、如图, AB=CD, AE⊥BC, DF⊥BC,CE=BF。
求证: AE=DF。
7.已知:如图,CF ⊥AB 于E, 且AE-EB,已知∠B-40°,求∠ACD,∠DCF 的度数.8.如图,已知AB=AC,∠A=40°,AB 的垂直平分线MN 交AC 于点D,求∠DBC 的度数.6.如图:在△ABC中,∠C -90°,AD是∠BAC的平分线,DE⊥AB于E, F 在AC 上,BD=DF;求证:CF=EB9. 如右图所示,△ABC 为等边三角形,AD ∥BC,CD ⊥AD,若△ABC 的周长为36cm,求AD 的长.10.如图,在等边△ABC中,D 是AC 的中点,E 是BC 延长线上一点,且CE=CD.求证: BD=DE.。

三角形全等的判定专题训练题(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--- 2 -三角形全等的判定专题训练题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE 。
求证:AC ⊥CE 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF=EG ,(2)BF ∥DG 。
7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。
求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM 。
(图1)D CB A F E (图2)DC B A FE (图3)DC B A E(图4)D CBA E (图5)DB AG FE(图6)D C B AN M(图7)CBA- 3 -8、如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
12、如图(12)AB ∥CD ,OA=OD ,点F 、D 、O 、A 、E AE=DF 。

三角形全等20个经典试题(图形变换).1.四边形ABC配正方形(提示:正方形四边相等,四个角都是90 )(1)如图1,点G是BC边上任意一点(不与点B、C重合),连接AG作BFLAG于点F, D」AG于点E.求证:△ ABF^A DAE(2)直接写出(1)中,线段EF与AF、BF的等量关系(3)①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG 作BJAG丁点F, DNAG丁点E,则图中全等三角形是 ,线段EF与AF、BF的等量关系是②如图3,若点G是CD延长线上任意一点,连接AG作BFLAG于点F, DE ± AG丁点E,线段EF与AF、BF的等量关系是(4)若点G是BC延长线上任意一点,连接AG作BFLAG丁点F, DNAG 丁点E,请画图、探究线段EF与AF、BF的等量关系.2小明、小敏两人一起做数学作业,小敏把题读到如图(1)所示,CdA己BE ± AC时,还没把题读完,就说:这题一定是求证Z B=Z C,也太容易了. ”她的证法是:由Cd AB, B」AC,得Z ADC=AEB=90,公共角Z DAC= BAE所以△ DA(^A EAB由全等三角形的对应角相等得Z B=ZC.小明说:小敏你错了,你未弄活本题的条件和结论,即使有CEUA己B」AG 公共角Z DAC=BAE你的推理也是错误的.看我画的图(2),显然△DAC^A EAB是不全等的.再说本题不是要证明Z B=ZC,而是要证明BE=CD ”(1) 根据小敏所读的题,判断2 B=Z C”对吗?她的推理对吗?若不对,请做出正确的推理.(2) 根据小明说的,要证明BE=CD必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD勺正确推理.(3 )要判断三角形全等,从这个问题中你得到了什么启发?3请阅读下列材料:问题:如图1,在正方形ABC的正方形CEFG^,点巳C E在同一条直线上,M是线段AF 的中点,连接DM MG探究线段DM巨MGR量与位置有何关系. 小聪同学的思路是:延长DM咬GF丁H,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题:(1) 直接写出上面问题中线段DM巨MGfc!与位置有何关系(2) 将图1中的正方形CEF敬点C顺时针旋转,使正方形CEFG亏角线CF恰好与正方形ABCD勺边BC在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3) 如图3,将正方形CEF硫点C顺时针旋转任意角度,原问题中的其他条件不变,写出你的猜想.4在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知^ABC ZACB=90, ZABC=45,分别以AB BC为边向外ABE^A BCE 且DA=DB EB=EC Z ADB£ BEC=90,连接DE交AB于点 F.探究线段DF与EF的数量关系.小慧同学的思路是:过点D作D& AB丁G,构造全等三角形,通过推理使问题得解.小东同学说:我做过一道类似的题目,不同的是Z ABC=30, ZADB^ BEC=60小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:(1) 写出原问题中DF与EF的数量关系;(2) 如图2,若ZABC=30, ZADB^ BEC=60,原问题中的其他条件不变,你在(1) 中得到的结论是否发生变化?请写出你的猜想并加以证明;(3) 如图3,若ZADB^ BEC=Z ABC原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明。
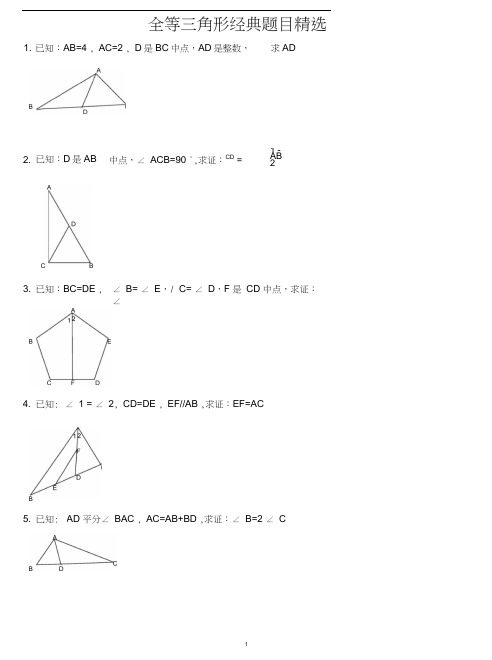
1.全等三角形经典题目精选已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD2. 中点,∠ ACB=90 °,求证:CD =1 -AB23.已知:D是AB∠ B= ∠ E,/ C= ∠ D,F 是CD 中点,求证:∠已知:BC=DE ,4. ∠ 1 = ∠ 2, CD=DE , EF//AB ,求证:EF=AC已知:5. AD 平分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ C已知:6.已知:AC 平分∠ BAD , CE ⊥ AB , ∠ B+ ∠ D=180 °,求证:AE=AD+BE 7. 如图,四边形 ABCD 中,AB Il DC , BE 、CE 分别平分∠ ABC 、/ BCD ,且点E 在AD 上 求证:BC=AB+DC 。
8. 已知:AB//ED ,∠ EAB= ∠ BDE ,AF=CD ,EF=BC ,求证:∠ F= ∠ C9. 已知:AB=CD ,∠ A= ∠ D ,求证:∠ B= ∠ C12. 已知,E 是 AB 中点,AF=BD ,BD=5,AC=7,求 DC10. P 是∠ BAC 平分线 AD 上一点,AC>AB ,求证: PC-PB<AC-ABAC-AB=2BECDBE 丄AE ,求证:D13. 如图,在△ ABC 中,BD=DC , ∠ 1 = ∠ 2,求证:AD 丄BC .14. 如图,OM 平分∠ POQ , MA 丄OP,MB 丄OQ , A 、B 为垂足,AB 交OM 于点N .求证:∠OAB= ∠ OBA15. 如图,已知AD Il BC , ∠ PAB 的平分线与∠ CBA 的平分线相交于 E , CE 的连线交 AP 于D .求 证:AD+BC=AB .16. 如图,△ ABC 中,AD 是∠ CAB 的平分线,且 AB=AC+CD ,求证:∠ C=2∠ B17 .如图①,E 、F 分别为线段 AC 上的两个动点,且 DE 丄AC 于E , BF 丄AC 于F ,若AB=CD,F CAAF=CE , BD 交AC 于点M . (1)求证:MB = MD , ME=MF (2)当E 、F 两点移动到如图②的位18. 已知:如图, DC Il AB ,且 DC=AE , E 为 AB 的中点,(1)求证:△ AEDEBC . (2)观 看图前,在不添辅助线的情况下,除厶EBC 夕卜,请再写出两个与△ AED 的面积相等的三角形.(直 接写出结果,不要求证明):19. 如图,△ ABC 中,∠ BAC=90度,AB=AC , BD 是∠ ABC 的平分线,BD 的延长线垂直于过C 点的直线于 E ,直线CE 交BA 的延长线于 F .求证:BD=2CE .20、如图:DF=CE AD=BC ∠ D=∠ C 。
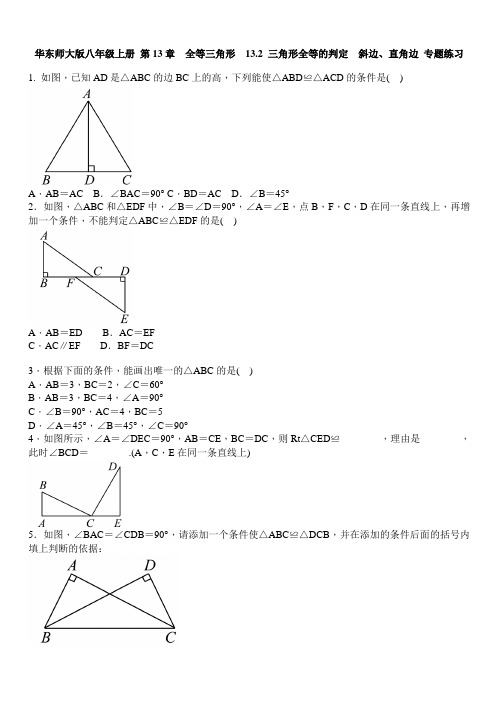
华东师大版八年级上册第13章全等三角形13.2 三角形全等的判定斜边、直角边专题练习1. 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )A.AB=AC B.∠BAC=90° C.BD=AC D.∠B=45°2.如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是( )A.AB=ED B.AC=EFC.AC∥EF D.BF=DC3.根据下面的条件,能画出唯一的△ABC的是( )A.AB=3,BC=2,∠C=60°B.AB=3,BC=4,∠A=90°C.∠B=90°,AC=4,BC=5D.∠A=45°,∠B=45°,∠C=90°4.如图所示,∠A=∠DEC=90°,AB=CE,BC=DC,则Rt△CED≌________,理由是________,此时∠BCD=________.(A,C,E在同一条直线上)5.如图,∠BAC=∠CDB=90°,请添加一个条件使△ABC≌△DCB,并在添加的条件后面的括号内填上判断的依据:(1)________________( );(2)________________( );(3)_________________________( );(4)_________________________( ).6.在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.7.已知AC=BD,AF=BE,CE⊥AB,FD⊥AB.求证:CE=DF.8.已知点B,E,C在一条直线上,AB⊥BC,DC⊥BC,AB=EC,且AE=DE.求证:AB+DC=BC.9.下列说法中正确的有( )①两直角边分别相等的两直角三角形全等;②两锐角分别相等的两直角三角形全等;③斜边和一条直角边分别相等的两直角三角形全等;④一锐角和斜边分别相等的两直角三角形全等.A.4个B.3个C.2个D.1个10.如图,矩形ABCD中,E为CD的中点,连结AE并延长交BC的延长线于点F,连结BD,DF,则图中全等的直角三角形共有( )A.3对B.4对C.5对D.6对11.如图AD,A′D′分别是锐角△ABC和△A′B′C′中BC,B′C′边上的高且AB=A′B′,AD=A′D′,若使△ABC≌△A′B′C′.请你补充条件(只填写一个你认为适当的条件)12.已知:如图AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.求证:BE⊥AC.13.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图①,若点O在BC上,求证:∠B=∠C;(2)如图②,若点O在△ABC的内部,求证:∠ABO=∠ACO.14.如图,AB 与CD 相交于点O ,∠ACF =∠BDE =90°,F 在AB 上,且AC =BD ,AE =BF ,求证:CO =DO.15.如图,在△ABC 中,AB =AC ,∠A =90°,D 是AC 上的一点,CE ⊥BD 于点E ,且CE =12BD ,求证:BD 平分∠ABC.答案:1. A2. C3. B4. Rt △BAC H.L. 90°5. (1) AC =DB(H .L .)(2) AB =DC(H.L.)(3) ∠ABC =∠DCB(A.A.S.)(4) ∠ACB =∠DBC(A.A.S.)依据:略6. ∵∠ABC =90°,∴∠CBF =∠ABE =90°,在Rt △ABE 和Rt △CBF 中,AE =CF ,AB =CB ,∴Rt △ABE ≌△Rt △CBF(H .L .)7. ∵AF =BE ,∴AF -EF =BE -EF ,即AE =BF ,∵EC ⊥AB ,FD ⊥AB ,∴∠AEC =∠BFD =90°,在Rt △ACE 和Rt △BDF 中,⎩⎨⎧AC =BD AE =BF,∴Rt △ACE ≌Rt △BDF(H .L .),∴CE =DF 8. ∵AB ⊥BC ,DC ⊥BC ,∴∠B =∠C =90°,在Rt △AEB 和Rt △EDC 中,⎩⎨⎧AE =DE AB =EC, ∴Rt △AEB ≌Rt △EDC(H .L .),∴DC =BE ,∵BC =BE +CE ,∴AB +DC =BC9. B10. B11. BC =B ′C ′或∠C =∠C ′或∠BAC =∠B ′A ′C ′12. ∵AD ⊥BC ,∴∠BDA =∠ADC =90°,又∵BF =AC ,FD =CD ,∴Rt △BDF ≌Rt △ADC(H .L .),∴∠C =∠BFD ,∵∠DBF +∠BFD =90°,∴∠C +∠DBF =90°,∵∠C +∠DBF +∠BEC =180°,∴∠BEC =90°,即BE ⊥AC13. (1)在Rt △OEC 和Rt △OFB 中,∵⎩⎨⎧OE =OF OB =OC ,∴Rt △OEC ≌Rt △OFB(H .L .),∴∠B =∠C(全等三角形的对应角相等)(2)在Rt △OEC 和Rt △OFB 中,∵⎩⎨⎧OE =OF OB =OC ,∴Rt △OEC ≌Rt △OFB(H .L .),∴∠ABO =∠ACO 14. 利用H .L .证Rt △ACF ≌Rt △BDE ,∴∠AFC =∠BED ,CF =DE ,再利用A .A .S .,证△COF ≌△DOE ,∴OC =OD15. 延长CE 与BA 的延长线相交于F ,证△ABD ≌△ACF ,∴BD =CF ,∵CE =12BD ,∴CE =12CF ,再证:△FBE ≌△CBE.∴BD 平分∠ABC。
. Word 资料 第一讲全等三角形的性质及判定 【例1】 如图,ACDE∥,BCEF∥,ACDE.求证:AFBD.
【补充】如图所示:ABCD∥,ABCD.求证:ADBC∥. 【例2】 已知:如图,B、E、F、C四点在同一条直线上,ABDC,BECF,BC.求证:OAOD.
【补充】已知:如图,ADBC,ACBD,求证:CD.
【补充】如图,在梯形ABCD中,ADBC∥,E为CD中点,连结AE并延长AE交BC的延长线于点F.求证:FCAD.
FED
CBA
【例3】 如图,ABCD,相交于点O,OAOB,E、F为CD上两点,AEBF∥,CEDF.求证:ACBD∥.
FEDCBA
DCBA
FEODCBA
ODCBA .
Word 资料 OF
E
DCB
A
【补充】已知,如图,ABAC,CEAB,BFAC,求证:BFCE. FE
CB
A
【例4】 如图,90DCECDCEADACBEAC,,,,垂足分别为AB,,试说明ADABBE E
DC
B
A
【例10】 如图所示, 已知ABDC,AEDF,CEBF,证明:AFDE.
【例11】 E、F分别是形ABCD的BC、CD边上的点,且BECF.求证:AEBF. PFE
DCBA
【补充】E、F、G分别是形ABCD的BC、CD、AB边上的点,GEEF,GEEF.求证:BGCFBC.
FEDCBA .
Word 资料 GA
BCD
EF 【例12】 在凸五边形中,BE,CD,BCDE,M为CD中点.求证:AMCD.
【补充】如图所示:AFCD,BCEF,ABDE,AD.求证:BCEF∥. A
BCDE
F
【例13】 (1)如图,△ABC的边AB、AC为边分别向外作形ABDE和形ACFG,连结EG,试判 断△ABC与△AEG面积之间的关系,并说明理由. (2)园林小路,曲径通幽,如图所示,小路由白色的形理石和黑色的三角形理石铺成.已知中间的所有形的面积之和是a平方米,圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?