高二数学(选修1-2)检测题

2010级高二数学（文科）选修1-2单元测试题（六）班级______________姓名______________一、选择题（42080''⨯=）1．[ ]已知命题P ：“2,230x R x x ∀∈++≥”，则命题P 的否定为 A ．2,230x R x x ∀∈++< B ．2,230x R x x ∃∈++≥ C ．2,230x R x x ∃∈++< D ．2,230x R x x ∃∈++≤ 2．[ ]对任意实数c b a ,,,下列命题中,真命题是A ．“bc ac >”是“b a >”的必要条件B ．“bc ac =”是“b a =”的必要条件C ．“bc ac >”是“b a >”的充分条件D ．“bc ac =”是“b a =”的充分条件 3．[ ] “2a =-”是“直线02=+y ax 垂直于直线1=+y x ”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件4．[ ]椭圆14922=+y x 的焦点坐标是A ．)5,0(±B ．)0,5(±C ．)13,0(±D ．)0,13(±5．[ ] “α为锐角”是“sin 0α＞”的A ．充分非必要条件B ．必要非充分条件C ．非充分非必要条件D ．充要条件6．[ ]命题“所有能被2整除的数都是偶数”的否定．．是 A ．所有不能被2整除的数都是偶数 B ．所有能被2整除的数都不是偶数 C ．存在一个不能被2整除的数是偶数 D ．存在一个能被2整除的数不是偶数 7．[ ]曲线()ln f x x x x =+在点1x =处的切线方程为A ．1y x =-B ．1y x =+C ．21y x =-D ．21y x =+8．[ ]已知函数),2[,32)(2+∞-∈+-=x mx x x f 当时是增函数，则m 的取值范围是 A ．[－8，+∞） B ．[8，+∞） C ．（－∞，－ 8] D ．（－∞，8]9．[ ]下列四种说法中，错误．．的个数是 ①命题“2,320x R x x ∀∈--≥均有”的否定是：“2,320x R x x ∃∈--≤使得”； ②“命题q p ∨为真”是“命题q p ∧为真”的必要不充分条件； ③“若b a bm am <<则,22”的逆命题为真； ④{}0,1A =的子集有3个． A ．0个 B ．1个 C ．2 个D ．3个10．[ ]已知椭圆2215x y m +=的离心率e =，则m 的值为A ．3BCD ．253或311．[ ] “关于x 的不等式220x ax a -+>的解集为R ”是“01a ≤≤”的 A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 12．[ ]椭圆123222=+y x 的半焦距等于A ．10B ．102C ．22D ．2 13．[ ]设双曲线的焦点在x 轴上，两条渐近线为x y 21±=，则该双曲线的离心率为 A ．5 B ．5 C ．45 D ．2514．[ ]焦点为()6,0，且与双曲线1222=-y x 有相同的渐近线的双曲线方程是 A ．1241222=-y xB ．1241222=-x yC ．1122422=-x y D ．1122422=-y x 15．[ ]抛物线2ax y =的准线方程是2y =，则a 的值为 A ．81 B ．－81 C ．8 D ．－816．[ ]已知双曲线2221x y a-=的一个焦点为(2,0)，则它的离心率为A B C ．32 D ．217．[ ]规定记号“⊗”表示一种运算，即2a b ab a b ⊗=++ （,a b 为正实数）， 若31=⊗k ，则k =A ．1B ．2-C ．2- 或1D ．218．[ ]若椭圆12222=+by a x （0>>b a ）的离心率21=e ，右焦点为()0,c F ，方程022=++c bx ax 的两个实数根分别是1x 和2x ，则点),(2,1x x P 到原点的距离为A ．2B ．27C ．2D ．4719．[ ]观察图形规律，在其右下角的空格内画上合适的图形为A ．■B ．▢C ．□D ．○20．[ ]在右表格中,每格填上一个数字后,使每一 行成等差数列,每一列成等比数列,则a b c ++的值是 A ．1 B ．2 C ．3 D ．4二、填空题（4520''⨯=）21．抛物线x y =2的准线方程是 ． 22．已知复数z 满足(34)5i z i -=，则||z = ．23．已知整数对的序列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4）， ，则第80个数对是 ．24．双曲线221916x y -=的焦点到渐近线的距离为 ． 25．观察下列式子：474131211,3531211,23211222222<+++<++<+,… …,根据以上式子可以猜想：<++++22220111...31211____ _____．三、解答题（10550''⨯=）26．已知正数a ，b 满足a b s +=，且1s a x =+，1sb y =+．证明：1xy =．27．观察等式：sin 220°＋sin 240°＋sin 20°·sin 40°＝34；sin 210°＋sin 250°＋sin 10°·sin 50°＝34；sin 228°＋sin 232°＋sin 28°·sin 32°＝34．请写出一个与以上三个等式规律相同的一般性等式．（不必证明）28．已知离心率为53的双曲线与椭圆2214015x y +=有公共焦点，求双曲线的方程．29．已知椭圆中心在原点，以坐标轴为对称轴且经过两点()()2,3,1,621--P P ， 求椭圆的方程．30．若a 、b 、c 均为实数，且a ＝x 2－2y ＋π2，b ＝y 2－2z ＋π3，c ＝z 2－2x ＋π6．请用反证法证明：a ，b ，c 中至少有一个大于0．2010级高二数学（文科）选修1-2单元测试题（六）参考答案一、选择题（42080''⨯=）1-----------5 CBCBA 6----------10 DCCDD 11--------15 ADDBB 16--------20 AAAAA二、填空题（4520''⨯=）21．14x =- 22．１ 23．(2,12) 24．4 25．40212011三、解答题（10550''⨯=） 26．证明：∵1s a x =+ ∴s a x a -=------------------------------------------------2分 ∵1sb y =+ ∴s b y b -=--------------------------------4分∴xy =s a s b a b --⨯＝a b a a b b a b +-+-⨯＝1b aa b⨯=------10分 另证：∵a b s +=，且1s a x =+，1sb y =+ ∴11s s s x y +=++，又0s >∴11111x y +=++ 去分母得：11(1)(1)y x x y +++=++ ∴1xy =27．解：若060αβ+=，则223sin sin sin sin 4αβαβ++=----------10分28．解： 在椭圆2214015x y +=中，240a =，215b =-----------------2分 ∴2401525c =-=，焦点为12(5,0),(5,0)F F ------------------------4分 ∴设双曲线的方程为22221(0,0)x y a b a b-=>>------------------------5分又∵35==a c e ，且5c =------------------------------------------7分3,4a b ∴== ------------------------------------------------9分故双曲线的方程为221916x y -=--------------------------------------10分29．解：（1）若椭圆焦点在x 轴上，设椭圆方程为12222=+by a x (0)a b >>---1分椭圆过点()()2,3,1,621--P P ，∴⎪⎩⎪⎨⎧=+=+1231162222b ab a ------------------------------3分 解得：⎩⎨⎧==3922b a ---------------------------------------------------------------------------------5分∴椭圆方程为13922=+y x -----------------------------------------------------------------6分 （2）若椭圆焦点在y 轴上，设椭圆方程为22221(0)x y a b b a+=>>----------7分椭圆过点()()2,3,1,621--P P ，2222611321b a ba ⎧+=⎪⎪⎨⎪+=⎪⎩--------------------8分 解得： 2239a b ⎧=⎪⎨=⎪⎩ 这与0a b >>矛盾，故无解----------------------------9分综上所述：椭圆方程为13922=+y x -------------------------------------------10分30．证明： 假设a 、b 、c 都不大于0----------------------------------------------1分即a ≤0，b ≤0，c ≤0---------------------------------------------------------------2分 所以a ＋b ＋c ≤0---------------------------------------------------------------------3分 而a ＋b ＋c＝⎝⎛⎭⎫x 2－2y ＋π2＋⎝⎛⎭⎫y 2－2z ＋π3＋⎝⎛⎭⎫z 2－2x ＋π6-----------------------------------4分 ＝(x 2－2x )＋(y 2－2y )＋(z 2－2z )＋π＝(x －1)2＋(y －1)2＋(z －1)2＋π－3----------------------------------------------7分 所以a ＋b ＋c >0----------------------------------------------------------------------8分 这与a ＋b ＋c ≤0矛盾--------------------------------------------------------------9分 故a 、b 、c 中至少有一个大于0-------------------------------------------------10分。

普通高中课程标准实验教科书——数学选修2—1（文科）[人教版]高中学生学科素质训练新课标高二数学同步测试（9）（1-2第四章）说明：本试卷分第一卷和第二卷两部分，第一卷74分，第二卷76分，共150分；答题时间120分钟。

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）。

1．如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为（）A．26 B．24 C．20 D．192．有一堆形状、大小相同的珠子,其中只有一粒重量比其它的轻,某同学经过思考,他说根据科学的算法,利用天平,三次肯定能找到这粒最轻的珠子,则这堆珠子最多有几粒（）A．21 B．24 C．27 D．303．“对于大于2的整数，依次从2～n 检验是不是n的因数，即整除n的数。

若有这样的数，则n不是质数；若没有这样的数，则n是质数”，对上面流程说法正确的是（）A．能验证B．不能验证C．有的数可以验证，有的不行D．必须依次从2～n－1检验4．“韩信点兵”问题：韩信是汉高祖手下大将，他英勇善战，谋略超群，为建立汉朝立下不朽功勋。

据说他在一次点兵的时候，为保住事秘密，不让敌人知道自己里的事实力，采用下述点兵方法：先令士兵1~3报数，结果最后一个士兵报2；又令士兵1~5报数，结果最后一个士兵报3；又令士兵1~7报数，结果最后一个士兵报4；这样韩信很快算出自己士兵的总数。

士兵至少有多少人（）A．20 B．46 C．53 D．395．注的数字表示该段网线单位时间内可以通过的最大信息量，现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递，则单如图，小圆圈表示网络的结点，结点之间的连线表示他们有网线相连，连线标位时间内传递的最大信息量为（）A．26 B．24 C．20 D．196．“烧开水泡壶茶喝”是我国著名数学家华罗庚教授作为“统筹法”的引子，虽然是生活中的小事，但其中有不少的道理。

综合检测卷一、选择题(本大题共10小题，每小题5分，共50分) 1．i 是虚数单位，复数1－3i1－i 的共轭复数是( )A ．2＋iB ．2－iC ．－1＋2iD ．－1－2i答案 A解析 ∵1－3i 1－i ＝(1－3i)(1＋i)(1－i)(1＋i)＝4－2i 2＝2－i ，∴1－3i 1－i的共轭复数是2＋i. 2．数列2,5,11,20，x,47，…中的x 等于( ) A ．28 B ．32 C ．33 D ．27 答案 B解析 5－2＝3,11－5＝6,20－11＝9， 推出x －20＝12，x ＝32.3．演绎推理“因为对数函数y ＝log a x(a>0且a ≠1)是增函数，而函数y ＝log 12x 是对数函数，所以y ＝log 12x 是增函数”所得结论错误的原因是( )A ．大前提错误B ．小前提错误C ．推理形式错误D ．大前提和小前提都错误 答案 A解析 对数函数y ＝log a x(a>0，且a ≠1)，当a>1时是增函数，当0<a<1时是减函数，故大前提错误．4．已知变量x 与y 正相关，且由观测数据算得样本平均数x ＝3，y ＝3.5，则由该观测数据算得的线性回归方程可能是( ) A ．y ＝0.4x ＋2.3 B ．y ＝2x －2.4 C ．y ＝－2x ＋9.5D ．y ＝－0.3x ＋4.4答案 A解析 因为变量x 和y 正相关，则回归直线的斜率为正，故可以排除选项C 和D. 因为样本点的中心在回归直线上，把点(3,3.5)的坐标分别代入选项A 和B 中的直线方程进行检验，可以排除B ，故选A.5．观察下列各式：a ＋b ＝1，a 2＋b 2＝3，a 3＋b 3＝4，a 4＋b 4＝7，a 5＋b 5＝11，…，则a 10＋b 10等于( ) A ．28 B ．76C ．123D ．199答案 C解析 观察规律，归纳推理．从给出的式子特点观察可推知，等式右端的值，从第三项开始，后一个式子的右端值等于它前面两个式子右端值的和，照此规律，则a 10＋b 10＝123.6．用反证法证明命题：“若a ，b ∈N ，ab 能被3整除，那么a ，b 中至少有一个能被3整除”时，假设应为( ) A ．a ，b 都能被3整除 B ．a ，b 都不能被3整除 C ．a ，b 不都能被3整除 D ．a 不能被3整除 答案 B解析 “至少有一个”的否定为“一个也没有”．7．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：由χ2＝n(ad －bc)2(a ＋b)(c ＋d)(a ＋c)(b ＋d)算得，χ2＝110×(40×30－20×20)260×50×60×50≈7.8.附表：A ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”B ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”C ．有99%以上的把握认为“爱好该项运动与性别有关”D ．有99%以上的把握认为“爱好该项运动与性别无关” 答案 C解析 根据独立性检验的定义，由χ2≈7.8>6.635可知我们有99%以上的把握认为“爱好该项运动与性别有关”．8．下面给出了关于复数的四种类比推理：①复数的加减法运算可以类比多项式的加减法运算法则；②由向量a 的性质|a|2＝a 2类比得到复数z 的性质|z|2＝z 2；③方程ax 2＋bx ＋c ＝0(a ，b ，c ∈R)有两个不同实数根的条件是b 2－4ac>0可以类比得到：方程az 2＋bz ＋c ＝0(a ，b ，c ∈C)有两个不同复数根的条件是b 2－4ac>0；④由向量加法的几何意义可以类比得到复数加法的几何意义． 其中类比得到的结论错误的是( ) A ．①③ B ．②④ C ．②③ D ．①④ 答案 C9．执行如图所示的算法框图，若输入n ＝10，则输出S 等于( )A.511B.1011C.3655D.7255 答案 A解析 执行第一次循环后，S ＝13，i ＝4；执行第二次循环后，S ＝25，i ＝6；执行第三次循环后，S ＝37，i ＝8；执行第四次循环后，S ＝49，i ＝10；执行第五次循环后，S ＝511，i ＝12，此时i ≤n 不成立，退出循环，输出S ＝511.10.已知x>0，由不等式x ＋1x≥2x·1x ＝2，x ＋4x 2＝x 2＋x 2＋4x 2≥33x 2·x 2·4x 2＝3，…，可以推出结论：x ＋ax n ≥n ＋1(n ∈N ＋)，则a 等于( )A ．2nB ．3nC ．n 2D ．n n 答案 D解析 由两个不等的结构特点知， x ＋a x n ＝x n ＋x n ＋…＋x n ＋a xn ≥ (n ＋1)n ＋1x n ·x n ·…·x n ·a x n ＝(n ＋1)n ＋1a n n ＝n ＋1.所以a ＝n n .二、填空题(本大题共5小题，每小题5分，共25分)11．若P ＝a ＋a ＋7，Q ＝a ＋3＋a ＋4(a ≥0)，则P ，Q 的大小关系为________． 答案 P<Q解析 要比较P 与Q 的大小，只需比较P 2与Q 2的大小，只需比较2a ＋7＋2a(a ＋7)与2a ＋7＋2(a ＋3)(a ＋4)的大小，只需比较a 2＋7a 与a 2＋7a ＋12的大小，即比较0与12的大小，而0<12，故P<Q.12．若复数z ＝cos θ－sin θi 所对应的点在第四象限，则θ为第________象限角． 答案 一解析 由已知得⎩⎪⎨⎪⎧cos θ>0－sin θ<0，所以θ为第一象限角．13．如图所示，A ，B ，C 表示3种开关，若在某段时间内它们正常工作的概率分别为0.9，0.8，0.7，那么此系统的可靠性为______． ①0.504；②0.994；③0.496；④0.06. 答案 ②解析 A 、B 、C 三个开关相互独立，三个中只要至少有一个正常工作即可，由间接法知 P ＝1－(1－0.9)×(1－0.8)×(1－0.7) ＝1－0.1×0.2×0.3＝0.994. 14．复数11－x2＋(2－2x)i(x ∈R)在复平面内的对应点位于第________象限．答案 一 解析 由题意可得11－x 2>0，解得－1<x<1，故2－2x >0，所以复数11－x2＋(2－2x)i(x ∈R)在复平面内对应点位于第一象限．15．已知下列框图，若a ＝5，则输出b ＝________.答案 26解析 因a ＝5，所以5>5不成立， 判断框执行“否”，即b ＝52＋1＝26. 三、解答题(本大题共6小题，共75分)16．已知复数z ＝a 2－7a ＋6a 2－1＋(a 2－5a －6)i(a ∈R)，试求实数a 取什么值时，z 分别为(1)实数；(2)虚数；(3)纯虚数．解 (1)当z 为实数时，则a 2－5a －6＝0，且a 2－7a ＋6a 2－1有意义，∴a ＝－1，或a ＝6，且a ≠±1， ∴当a ＝6时，z 为实数．(2)当z 为虚数时，则a 2－5a －6≠0，且a 2－7a ＋6a 2－1有意义，∴a ≠－1，且a ≠6，且a ≠±1.∴当a ≠±1，且a ≠6时，z 为虚数，即当a ∈(－∞，－1)∪(－1,1)∪(1,6)∪(6，＋∞)时，z 为虚数． (3)当z 为纯虚数时，则有a 2－5a －6≠0， 且a 2－7a ＋6a 2－1＝0.∴⎩⎪⎨⎪⎧a ≠－1，且a ≠6，a ＝6. ∴不存在实数a 使z 为纯虚数．17．数列{a n }的前n 项和记为S n ，已知a 1＝1，a n ＋1＝n ＋2n S n(n ∈N ＋)，证明：(1)数列⎩⎨⎧⎭⎬⎫S n n 是等比数列；(2)S n ＋1＝4a n .证明 (1)∵a n ＋1＝S n ＋1－S n ，a n ＋1＝n ＋2n S n ，∴(n ＋2)S n ＝n(S n ＋1－S n )，即nS n ＋1＝2(n ＋1)S n . ∴S n ＋1n ＋1＝2·S n n ，又S 11＝1≠0，(小前提)故⎩⎨⎧⎭⎬⎫S n n 是以1为首项，2为公比的等比数列．(结论) (大前提是等比数列的定义，这里省略了) (2)由(1)可知S n ＋1n ＋1＝4·S n －1n －1(n ≥2)， ∴S n ＋1＝4(n ＋1)·S n －1n －1＝4·n －1＋2n －1·S n －1＝4a n (n ≥2)(小前提)又a 2＝3S 1＝3，S 2＝a 1＋a 2＝1＋3＝4＝4a 1，(小前提) ∴对于任意的正整数n ，都有S n ＋1＝4a n .(结论)(第(2)问的大前提是第(1)问的结论以及题中的已知条件)18．为了研究教师工作积极性和对待教育改革态度的关系，随机抽取了278名教师进行问卷调查，所得数据如下表：0.01的前提下认为态度与工作积极性有关？ 解 利用公式得χ2＝278×(55×52－73×98)2153×125×128×150≈13.959>6.635，故在犯错误的概率不超过0.01的前提下认为该单位教师对待教育改革的态度与其工作积极性是有关的．19．某种产品的广告费支出x 与销售额y(单位：百万元)之间有如下对应数据：(1)画出散点图；(2)求线性回归方程；(3)试预测广告费支出为10百万元时，销售额多大？ 解 (1)根据表中所列数据可得散点图如下：(2)列出下表，并用科学计算器进行有关计算：因此，x ＝255＝5，y ＝2505＝50，∑5i ＝1x 2i ＝145，∑5i ＝1y 2i ＝13 500，∑5i ＝1x i y i ＝1 380. 于是可得：b ＝∑5i ＝1x i y i －5x ·y∑5i ＝1x 2i －5x 2＝1 380－5×5×50145－5×5×5＝6.5；a ＝y －b x ＝50－6.5×5＝17.5.因此，所求线性回归方程为：y ＝6.5x ＋17.5.(3)根据上面求得的线性回归方程，当广告费支出为10百万元时，y ＝6.5×10＋17.5＝82.5(百万元)，即这种产品的销售收入大约为82.5百万元．20．画出计算函数y ＝|2x －3|的函数值的框图．(x 由键盘输入) 解21．f(x)＝13x＋3，先分别求f(0)＋f(1)，f(－1)＋f(2)，f(－2)＋f(3)，然后归纳猜想一般性结论，并给出证明．解 f(0)＋f(1)＝130＋3＋131＋3＝11＋3＋13(1＋3)＝33(1＋3)＋13(1＋3)＝33，同理可得：f(－1)＋f(2)＝33， f(－2)＋f(3)＝33. 由此猜想f(x)＋f(1－x)＝33. 证明：f(x)＋f(1－x)＝13x ＋3＋131－x ＋3＝13x ＋3＋3x 3＋3·3x ＝13x ＋3＋3x3(3＋3x ) ＝3＋3x 3(3＋3x )＝33.。

流程图（简答题：一般）1、执行如图所示的程序框图．（1）若输入的，，求输出的的值；（2）若输入的，输出的，求输入的（）的值．2、已知函数，对每输入的一个值，都得到相应的函数值，画出程序框图并写出程序.3、已知数列的递推公式，且，请画出求其前5项的流程图.4、已知某算法的算法框图如图所示.(1)求函数的解析式；(2)求的值.5、的取值范围为[0,10]，给出如图所示的程序框图，输入一个数．（1）请写出程序框图所表示的函数表达式；（2）求输出的（）的概率；（3）求输出的的概率．6、已知数列的各项均为正数，观察程序框图，当，时，.（1）求数列的通项；（2）令，求的值．7、某药厂生产某种产品的过程如下：(1)备料、前处理、提取、制粒、压片、包衣、颗粒分装包装；(2)提取环节经检验，合格，进入下一工序，否则返回前处理；(3)包衣、颗粒分装两环节分别检验合格进入下一工序，否则为废品，画出生产该产品的工序流程图．8、根据下面的要求，求┅值.（Ⅰ）请将程序框图补充完整；（Ⅱ）求出（I）中输出S的值.9、求满足的最小正整数，写出算法的程序并画出程序框图．10、执行如下程序框图：（1）如果在判断框内填入“”，请写出输出的所有数值；（2）如果在判断框内填入“”，试求出所有输出数字的和。

11、根据下面的程序，画出其对应的程序框图．12、读下列程序，写出此程序表示的函数，并求当输出的时，输入的的值.13、执行如图所示的程序框图．（1）若输入的，，求输出的的值；（2）若输入的，输出的，求输入的（）的值．14、某算法的程序框图如图所示，其中输入的变量在1，2，3，…30这30个整数中等可能随机产生. （1）分别求出（按程序框图正确编程运行时）输出的值为的概率；（2）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行次后，统计记录了输出的值为的频数，下面是甲、乙所作频数统计表的部分数据：甲的频数统计表（部分）乙的频数统计表（部分）当时，根据表中的数据，分别写出甲、乙所编程序各自输出的值为的频率（用分数表示），并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.15、（2015秋•宁德期末）阅读如图所示程序框图，根据框图的算法功能回答下列问题：（Ⅰ）当输入的x∈[﹣1，3]时，求输出y的值组成的集合；（Ⅱ）已知输入的x∈[a，b]时，输出y的最大值为8，最小值为3，求实数a，b的值．16、的取值范围为[0,10]，给出如图所示程序框图，输入一个数．（1）请写出程序框图所表示的函数表达式；（2）求输出的（）的概率；（3）求输出的的概率．17、（本题满分16分）对任意函数f（x），x∈D，可按如图构造一个数列发生器，记由数列发生器产生数列{x n}．（1）若定义函数，且输入，请写出数列{x n}的所有项；（2）若定义函数f（x）=xsinx（0≤x≤2π），且要产生一个无穷的常数列{x n}，试求输入的初始数据x0的值及相应数列{x n}的通项公式x n；（3）若定义函数f（x）=2x+3，且输入x0=﹣1，求数列{x n}的通项公式x n．18、在某校趣味运动会的颁奖仪式上，为了活跃气氛，大会组委会决定在颁奖过程中进行抽奖活动，用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座，其中高二代表队有6人．（1）把在前排就座的高二代表队6人分别记为a，b，c，d，e，f，现从中随机抽取2人上台抽奖，求a和b至少有一人上台抽奖的概率；（2）抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖"，则该代表中奖；若电脑显示“谢谢”，则不中奖．求该代表中奖的概率．19、（本小题满分12分）如图所示程序框图中,有这样一个执行框=f（）其中的函数关系式为，程序框图中的D为函数f（x）的定义域.，（1）若输入，请写出输出的所有；（2）若输出的所有xi都相等,试求输入的初始值.20、（本小题满分12分）已知数列的各项均为正数，观察流程图，当时，；当时，，（1）写出时，的表达式（用等来表示）；（2）求的通项公式；（3）令，求．21、（本小题满分12分）如下图，给出了一个程序框图,其作用是输入的值,输出相应的的值，（I）请指出该程序框图所使用的逻辑结构；（Ⅱ）若视为自变量，为函数值，试写出函数的解析式；（Ⅲ）若要使输入的的值与输出的的值相等,则输入的值的集合为多少？22、（本小题满分13分）从某企业生产的某种产品中抽取20件，测量这些产品的一项质量指标值，由测量得到如图的频率分布直方图，从左到右各组的频数依次记为，，，，．（1）求图中的值；（2）下图是统计图中各组频数的一个算法流程图，求输出的结果；（3）从质量指标值分布在、的产品中随机抽取2件产品，求所抽取两件产品的质量指标值之差大于10的概率．23、对任意函数，，可按如图构造一个数列发生器，记由数列发生器产生数列{}．（1）若定义函数，且输入，请写出数列{}的所有项；（2）若定义函数（0≤x≤2π），且要产生一个无穷的常数列{}，试求输入的初始数据的值及相应数列{}的通项公式；（3）若定义函数，且输入，求数列{}的通项公式．参考答案1、（1）；（2）．2、见解析3、见解析4、(1)；(2)5、（1）（2）（3）6、（1）（2）7、见解析8、（I）；（II）.9、程序见解析，程序框图见解析．10、（1）（2）11、程序框图见解析．12、，.13、（1）；（2）．14、（1），，；（2）乙.15、（Ⅰ）输入x∈[﹣1，3]，输出y的值组成的集合为[0，8]；（Ⅱ）所求实数a，b的值为或16、（1）；（2）；（3）．17、（1）；（2）故当，；当；（3）18、（1）；（2）19、（1）（2）或20、（1）；（2）；（3）．21、（I）条件结构和顺序结构（Ⅱ）（Ⅲ）22、（1）0.005；（2）18；（3）23、（1），，；（2）当时，；当时，；（3）.【解析】1、试题分析：（1）根据程序框图的循环结构，根据判断框的条件，即可求解；（2）根据第一次运算，第二次运算，即可得出，即可求解的值．试题解析：（1）第一次运算：，，；第二次运算：，，；第三次运算：，，；第四次运算：，，；第五次运算：，，，输出．（2）第一次运算：，，，此时不成立，则．第二次运算：，，，此时成立，则，∴，又，∴．考点：程序框图的运算．2、试题分析：利用条件结构和条件语句可实现分段函数求值的算法，进而可得程序框图并编写相应的程序。

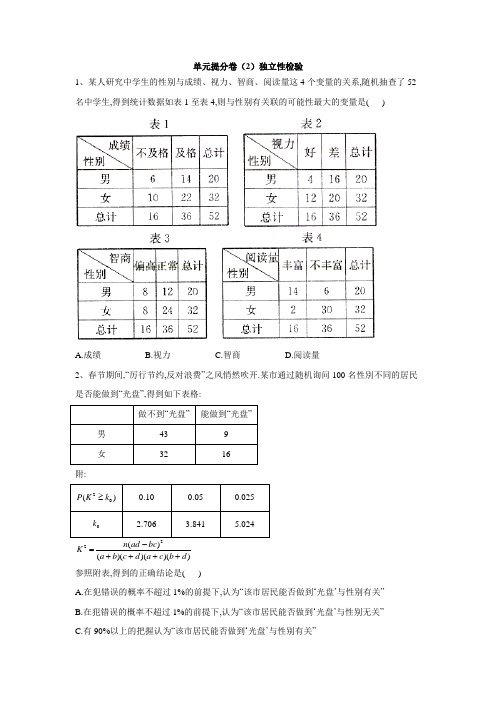
单元提分卷（2）独立性检验1、某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )A.成绩B.视力C.智商D.阅读量2、春节期间,“厉行节约,反对浪费”之风悄然吹开.某市通过随机询问100名性別不同的居民是否能做到“光盘”,得到如下表格:做不到“光盘” 能做到“光盘”男 43 9 女 3216附:20()P K k ≥0.10 0.05 0.025 0k2.7063.8415.0242()()()()()n ad bc K a b c d a c b d -=++++ 参照附表,得到的正确结论是( )A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别有关”B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到‘光盘’与性别无关”C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关” 3、分类变量X 和Y 的列联表如下,则( )A.ad bc -越小,说明X 与Y 的关系越弱B.ad bc -越大,说明X 与Y 的关系越强C.2()ad bc -越大,说明X 与Y 的关系越强D.2()ad bc -越接近于0,说明X 与Y 的关系越强4、某班主任对全班50名学生进行了作业量的调查,数据如下表:则学生的性别与认为作业量的大小有关系的把握大约为( ) A.99%B.95%C.90%D.无充分根据5、高二第二学期期中考试,按照甲、乙两个班级学生数学考试成绩优秀和及格统计人数后,得到如下列联表:则随机变量2K 的观测值约为( ) A.0.600B.0.828C.2.712D.6.0046、假设两个分类变量X 与Y ,它们的可能取值分别为{}12,x x 和{}12,y y ,其列联表为对于同一样本的以下各组数据,能说明X 与Y 有关的可能性最大的一组为( ) A.5,4,3,2a b c d ==== B.5,3,4,2a b c d ==== C.2,3,4,5a b c d ====D.2,3,5,4a b c d ====7、有两个分类变量X 与Y 的一组数据,由其列联表计算得2 4.523K ≈,则认为X 与Y 有关系是错误的可信度为( ) A.95%B.90%C.5%D.10%8、为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:经计算,统计量2K 的观测值 4.762k ≈.已知独立性检验中统计量2K 的临界值参考表为:则认为药物有效,犯错误的概率不超过( ) A.0.005B.0.05C.0.010D.0.0259、下列关于2K 的说法中正确的是( ) A.2K 越大,“变量,A B 有关联”的可信度越小 B.2K 越大,“变量,A B 无关”的可信度越大 C.2K 越小,“变量,A B 有关联”的可信度越小 D.2K 越小,“变量,A B 无关”的可信度越小10、为了调查中学生假期里玩手机的情况，某校200名男生中有120名假期里玩过手机，150名女生中有70名假期里玩过手机，在检验这些中学生玩手机是否与性别有关时最有说服力的方法是( )A.平均数B.方差C.回归分析D.独立性检验11、下表是关于喜欢抢红包与性别是否有关的列联表,依据表中的数据,得到2K的观测值k 为_____________(结果保留到小数点后三位).12、统计推断,当___________时,有95%的把握说事件A与B有关;当___________时,认为没有充分的证据显示事件A与B是有关的.13、若由一个22⨯列联表中的数据计算得 4.013k=,则有__________的把握认为两个变量有关系.14、为了调查患慢性支气管炎是否与吸烟有关，调查了339名50岁以下的人，调查结果如下表：K的观测值k≈__________.根据列联表数据，求得215、某校为了研究学生的性别与对待某一活动的态度(支持和不支持两种态度)的关系,运用K=,则所得到的统计学结论是:有22⨯列联表进行独立性检验,经计算26.669__________%的把握认为“学生性别与支持活动有关系”.附:16、以下结论正确的序号有__________.①根据22⨯列联表中的数据计算得出2 6.635K ≥，而2( 6.635)0.01P K ≥≈，则有99%的把握认为两个分类变量有关系；②独立性检验是判断两个分类变量是否有关系的唯一方法；③事件,X Y 关系越密切，则由观测数据计算得到的2K 的观测值越大；④由独立性检验可知，有99%的把握认为物理成绩优秀与数学成绩有关，某人数学成绩优秀，则他有99%的可能物理也优秀. 参考数据：,具体数据如下:根据上述数据,如果判断“科类与数学是否优秀有关系”,那么这种判断出错的概率为__________18、为了判断高中二年级学生是否喜欢足球运动与性别的关系,现随机抽取50名学生,得到的前提下认为“喜欢足球与性别有关”.答案以及解析1答案及解析： 答案：D解析：因为222152(6221410)5281636322016363220K ⨯⨯-⨯⨯==⨯⨯⨯⨯⨯⨯, 222252(4201612)521121636322016363220K ⨯⨯-⨯⨯==⨯⨯⨯⨯⨯⨯, 222352(824128)52961636322016363220K ⨯⨯-⨯⨯==⨯⨯⨯⨯⨯⨯, 222452(143062)524081636322016363220K ⨯⨯-⨯⨯==⨯⨯⨯⨯⨯⨯, 则22224231K K K K >>>, 所以阅读量与性别有关联的可能性最大.2答案及解析： 答案：C解析：由22⨯列联表得到43,9,32,16a b c d ====,则52a b +=,48c d +=,75a c +=,25b d +=,688ad =,288bc =,100n =. 代入22()()()()()n ad bc K a b c d a c b d -=++++,得2K 的观测值2100(688288) 3.41954487525k ⨯-=≈⨯⨯⨯.因为2.706 3.419 3.841<<,所以有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”.3答案及解析： 答案：C解析：2()()()()()n ad bc k a b c d a c b d -=++++(其中n a b c d =+++),若2()bd bc -越大,则k 越大,说明X 与Y 的关系越强.4答案及解析： 答案：B解析：250(181598) 5.059 3.84127232624k ⨯⨯-⨯=≈>⨯⨯⨯,所以有关系的把握大约为95%.5答案及解析：答案：A解析：2K 的观测值290(1137348)0.60045451971k ⨯⨯-⨯=≈⨯⨯⨯.6答案及解析：答案：D解析：利用||ad bc -越大越有关进行判断; 对于A,|||1012|2ad bc -=-=; 对于B,|||1012|2ad bc -=-=; 对于C,|||1012|2ad bc -=-=; 对于D,|||815|7ad bc -=-=. 故选D.7答案及解析： 答案：C解析：2( 3.841)0.05P K ≥=.故选C.8答案及解析： 答案：B解析：由题意算得, 4.762 3.841k =>,参照附表,可得在犯错误的概率不超过0.05的前提下,认为药物有效.9答案及解析： 答案：C解析：2K 越大,“变量,A B 有关联”的可信度越大,“变量,A B 无关”的可信度越小;相反,2K 越小,“变量,A B 有关联”的可信度越小,“变量,A B 无关”的可信度越大.10答案及解析： 答案：D解析：分析已知条件，易得如下22⨯列联表.根据列联表可得2K 的观测值，再与临界值比较，检验这些中学生玩手机是否与性别有关，故利用独立性检验的方法最有说服力.故选D.11答案及解析： 答案：4.772解析：2K 的观测值285(4012285) 4.77268174540k ⨯⨯-⨯=≈⨯⨯⨯.12答案及解析：答案：2 3.841K ≥;2 2.706K < 解析：结合2K 的临界值表可知,当2 3.841K ≥时有95%的把握说事件A 与B 有关;当2 2.706K <时认为没有充分的证明显示事件A 与B 是有关的.13答案及解析： 答案：95%解析：因为 4.013 3.841k =>,所以有95%的把握认为两个变量有关系.14答案及解析： 答案：7.469解析：22339(4312116213)7.46920513456283K ⨯⨯-⨯=≈⨯⨯⨯.15答案及解析：答案：99解析：因为6.669与附表中的6.635最接近,所以得到的统计学结论是:有10.0100.9999%-==的把握认为“学生性别与支持该活动有关系”.16答案及解析： 答案：①③解析：对于①，根据22⨯列联表中的数据计算得出2 6.635K ≥，而2( 6.635)0.01P K ≥≈，则有99%的把握认为两个分类变量有关系，故①正确；②独立性检验不是判断两个分类变量是否相关的唯一方法，频率等高条形图等也能用来作初步判断，故②不正确；③由临界值表K的观测值k越大，事情发生的概率就越小——即作出有关系判断犯错的概率可以看出，2就越小，故③正确；④有99%的把握认为物理成绩优秀与数学成绩有关，和如果数学优秀那么有99%可能物理也优秀是两回事，④错误.故填①③.17答案及解析：答案：0.05解析：18答案及解析：答案：0.005解析：由Ruize收集整理。

最新人教A版高二数学选修1-2综合测试题带答案解析2套模块综合测评（一）（时间120分钟,满分150分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给岀的四个选项中，只冇一项是符合题目要求的・）1.设i为虚数单位,则复数（1+址=（）A.0 B・ 2C. 2iD. 2 + 2i【解析】（1 + i）2 = 1 + 2i + i2 = 2i.【答案】C2•根据二分法求方程?-2=0的根得到的程序框图町称为（）A.工序流程图B.程序流程图C.知识结构图D.组织结构图【解析】由于该框图是动态的且可以通过计算机来完成，故该程序框图称为程序流程图・【答案】B3.利用独立性检测来考查两个分类变量X, 丫是否冇关系，当随机变量K?的值（）A.越大，“X与丫有关系”成立的可能性越大B.越大，“X与丫有关系”成立的可能性越小C.越小，“X与丫有关系”成立的可能性越大D.与“X与Y有关系”成立的可能性无关【解析】由K?的意义可知，K?越大，说明X与y有关系的可能性越大.【答案】A4.用反证法证明命题“a, bGN,如果必可被5整除”,那么d, b至少冇一个能被5 整除.则假设的内容是（）A.a, b都能被5整除B.ci, b都不能被5整除C・a不能被5整除D. a, b右一个不能被5整除【解析】“至少有一个”的否定为“一个也没有”石攵应假设“Q力都不能被5整除”.【答案】B5.有一段演绎推理是这样的“有些右理数是真分数，整数是有理数，则整数是真分数” 结论显然是错误的，是因为()A.大前提错误B.小前提错误C.推理形式错误D.非以上错误【解析】一般的演绎推理是三段论推理：大前提——已知的一般原理；小前提——所研究的特殊情况；结论——根据一般原理对特殊情况作出的判断・此题的推理不符合上述特征，故选C.【答案】C6.设i是虚数单位，如果复数尖的实部与虚部相等，那么实数Q的值为()1 1A3 B・一亍C・3 D・—3【解析】貯二2— 1 ；(° + 2)1,由题意知2— 1二Q +2 ,解得Q =3.【答案】C7.在两个变量的回归分析中，作散点图是为了()A.直接求出回归直线方程B.直接求出回归方程C.根据经验选定回归方程的类型D.估计回归方程的参数【解析】散点图的作用在于判断两个变量更近似于什么样的函数关系，便于选择合适的函数模型•【答案】C8.给出下而类比推理：①“若2a<2b9贝lj a<b v类比推出“若a2<b29贝lj a<b"；②“(a + b)c=Qc+bc(cHO)” 类比推出“厲也=E+°(cHO)” ；C C C③“a, bWR,若a—b = O,则a=b”类比推出“a, b^C,若a~b=O f贝a=b v；④“°, /)GR,若Q —b>0,贝类比推岀"ci, bWC,若a~b>O f则a>b(C为复数其中结论正确的个数为（）【解析】 第一次循环S=2 , /; = 2 ,第二次循环S=6Z H = 3 ,第三次循环S = 2 ,n = 4f 弟四次循环S - 18 , n = 5 ,弟五次循环5 = 14 , A ? = 6 ,弟7X 次循环S 二78 , /? = 7 ,需满足S2K , 此时输出//= 7 ,所以18VKW78 ,所以整数K 的最大值为7&【答案】C10. 已知 Q1=3, Q2 = 6, A a n+2=a n+\—a n ,则的3 为（ ） B. —3C- 6［角军析］ Q1 = 3 , Q2 = 6 ,幺3 = Q2 ・ Q ］ = 3 ,幺4 = 03 ・ ^2 二・ 3 , ^5 = ^4 ・ ^3 = ~ 6 , <26 = ^5■ 04 = ■ 3 ,= 3 卩= 07 ■= 6观察可知仏｝是周期为6的周期数列,故的3 = 03 = 3.A. 1B. 2C. 3D. 4【解析】 ①显然是错误的；因为复数不能比较大小，所以④错误，②③正确，故选B. 【答案】B9. 执行如图1所示的程序框图，若输出的〃 =7,则输入的整数K 的最大值是（）A. 18B. 50 C- 78D. 306A. 311.下列推理合理的是（）A.fix)是增函数，则f (x)>0B・因为ci>b(a, bWR),贝U+2i>6+2i(i是虚数单位)C.g ”是锐角AMC的两个内角，贝ijsiz>cos"D.%是三角形/EC的内角，若cos/f>0,则此三角形为锐角三角形【解析】A不正确，若/(工)是增函数，则f (x)^0 ；B不正确・复数不能比较大小；C7C正确，•/«+/?> 2 ,兀、a > 2 - sin a > cos “ ； D 不正确,只有cos A> 0 , cos B> 0 , cos C> 0 ,才能说明此三角形为锐角三角形・【答案】C12.有人收集了春节期间平均气温X与某取暖商品销售额尹的有关数据如下表：A A根据以上数据，用线性冋归的方法，求得销售额y与平均气温X之间线性冋归方^.y=bxA A+a的系数-2.4,则预测平均气温为一8°C时该商品销售额为()A. 34.6万元B. 35.6万元C. 36.6万元D. 37.6万元-.,- —_2-3-5_6【角牛析】x = 彳=■ 4 ,—20 + 23 + 27 + 30y = 4 =25”所以这组数据的样本中心点是(・4,25)・A因为b 二-2.4 ,把样本中心点代入线性回归方程得>15.4 ,所以线性回归方程为彳二-2.4X+15.4.当x =・8时,y = 346故选A.二、填空题(本大题共4小题，每小题5分，共20分.将答案填在题中的横线上・)13. ___________________________________________________________ 已知复数z=m2( 1 + i)—m(m + i)(mR),若z是实数，则加的值为_____________________________ ・【解析1 z二〃，+加2).加2 . 〃打二(加2 . m y x ,m - m = 0 ,・•・加=0或1.【答案】0或114.心理学家分析发现视觉和空间想彖能力与性别有关，某数学兴趣小组为了验证这个结论，从所在学校屮按分层抽样的方法抽取50名同学（男30女20）,给所有同学儿何题和代数题各一题，让各位同学自由选择一道题进行解答.选题情况如下表：（单位：人）几何题代数题总计男同学22830女同学81220总计302050根拯上述数据，推断视觉和空间想象能力与性别有关系，则这种推断犯错误的概率不超过 .附表：P 艮2k)0.150.100.050.0250.0100.0050.001k 2.072 2.706 3.841 5.024 6.6357.87910.828【解析】由列联表计算疋的观测值50X(22X 12 - 8X8)2〜5.556 >5.02430X20X20X30・•・推断犯错误的概率不超过0.025.【答案】0.02515.二维空间屮圆的一维测度（周长）/=2血，二维测度（面积）S=十，观察发现s，=1；三维空间小球的二维测度（表面积）S=4兀三维测度（体积）7=兑/,观察发现厂=S.则四维空间屮“超球”的四维测度W=2nr\猜想其三维测度V= _______________ .【解析】由已知,可得圆的一维测度为二维测度的导函数；球的二维测度是三维测度的导函数.类比上述结论•“超球”的三维测度是四维测度的导函数,即V=旷二（2兀/）' =8兀尸3.【答案】如彳16.已知等差数列｛如中，右5十常•+20/十2事•+30,贝恠等比数列©｝中, 会有类似的结论【解析】 由寺比数列的性质可知/ b\hyo - /?2^29 =…=伤］/?20 /"Q®ibi2・・・b20 =先如仇…加).【答案】 1守如1伤2・・・仇0 =彳躺血…加）三、解答题（木大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤•）l+i ・ 4i + 4 + 2 + 4i 7 + i z=3+4i =3+4i z・・・|z| =18.（木小题满分12分）我校学生会有如下部门：文娱部、体育部、宣传部、生活部、学 习部•请画出学生会的组织结构图.【解】 学生会的组织结构图如图.19・（本小题满分12分）给岀如下列联表:由以上数拯判断高血压与患心肌病之间在多大程度上有关系?（参考数据：卩（疋26.635） = 0.010, P （^2>7.879） = 0.005） 【解】 由列联表中数据可得110X （20X50 ・ 10X30）2k = ------- ------------------- —^7 48630X80X50X60又卩（疋26.635）二 0.010 ,17. （本小题满分 10分）设(l —4i)(l+i) + 2+4i3+4i,求|z|.【解】所以在犯错误的概率不超过0.010的前提下,认为高血压与患心脏病有关系・20.（本小题满分12分）已知非零实数a, b, c构成公差不为0的等差数列，求证：十，丄不能构成等差数列.【证明】假设+ /1, +能构成等差数列,则| = ~ + |,因此b(a + c) = lac.而由于a , h , c构成等差数列，且公差,可得2b = a^c f:.(a + c)2 = 4ac ,即(a - c)1 2 3 = 0 ,于是得a-b-c ,这与a ,h ,c构成公差不为0的等差数列矛盾・故假设不成立，即+不能构成等差数列・21.(本小题满分12分)已知a2 + b2=i f x2+y2=i f求证：分别用综合法、分析法证明).【证明】综合法：•・・2axW/+x2,2/?yW Z)2+b ,・・・ 2(ax + + b2) + (x2 +/)・又•.•/ + 护=1 , x2 = 1 ,/. 2(ax + by)W2 , ax + byW 1.分析法：要证ax + byW 1成立，只要证1・(ax +切20 ,只要证2 - 2ax - 2by$0 ,又•・• / + 护二1 t x1 +y2= I ,・°・只要证cr + A2 + x2 +y2 ・2ax - 2byM0 ,即证(a - x)2 + (b - y)2^0 ,显然成立・22.(木小题满分12分)某班5名学生的数学和物理成绩如下表：1 画出散点图；2 求物理成绩y对数学成绩x的冋归直线方程；3 —名学生的数学成绩是96,试预测他的物理成绩.附：回归直线的斜率和截距的最小二乘法估计公式分别为:n ____»少厂〃兀yf=lAA ------------ A ______h=, a= y ~b x .■7x 2/=1【解】（1）散点图如图,~0.625・A —— A .a= y ・ bx ^67.8 ・ 0.625X73.2 = 22.05.所以y 对x 的回归直线方程是Aj^ = 0.625x +22.05.⑶当x = 96 ,贝I© = 0.625X96+ 22.05 = 82 r 即可以预测他的物理成绩是82分・模块综合测评（二）（时间120分钟，满分150分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只 有9080 • 70 • 60 ■ • •50l.~~-_-_-_«__一55 60 65 70 75 80 85 90 x(2)7 二*X(88 + 76 + 73 + 66 + 63) = 73.2 , 7 =|x (78 + 65 + 71 + 64 + 61) = 67.8.5为効= 88X78+ 76X65 + 73X71 +66X64 + 63X61 =25 054. /=!= 882 + 762 + 732 + 662 + 632 = 27 174.z=l5》＞閃・5x y A /=!所以b 二一; ------- fx?-5x 2 /=125 054 ・ 5X73.2X67.8=~27 174 - 5X73.22一项是符合题目要求的.）1.冇下列关系：①人的年龄与他（她）拥冇的财富之间的关系；②曲线上的点与该点的坐 标之间的关系；③苹果的产量与气候之间的关系；④森林中的同一种树木，其横断面宜径与 高度Z 间的关系.其中有和关关系的是（）A.①②③C.②③B.①② D.①③④【解析】 曲线上的点与该点的坐标之间是确定关系——函数关系,故②不正确・其余 均为相关关系・【答案】DZ2・若z —4 + 3i,则恻—( )A. 1B ・一1cMi r 十5】D Mu5 51【解析】・.・z = 4 + 3i ,・•・ z =4 ・ 3i , |z| = ^/42 + 32 = 5 , z4・ 3i 4 3. •・|z| 5 5 51-【答案】D3. 有一段演绎推理：直线平行于平面，则平行于平面内所有直线；已知直线庆平面°, 直线QU 平而直线b 〃平而6（,则直线b 〃直线Q.这个结论显然是错误的，这是因为（ ）A.大前提错误C.推理形式错误B.小前提错误 D.非以上错误【解析】 大前提错误,直线平行于平面,未必平行于平面内的所有直线・ 【答案】A4. 如图1所示的知识结构图为什么结构（）A.树形 C.对称性【解析】 由题图可知结构图为树形结构・ 【答案】A5. 执行如图2所示的程序框图，若输入的〃的值为8,则输出的s 的值为（） （开始）/綸人聽/*图2 A. 4 B ・ 8 C- 10【解析】 初始值 \ n = S f i = 2 , k = \ , s = \ } z<A7 /5=1X(1X2) = 2 9 z = 2 + 2 = 4 , k=1 + 1=2 ； i < n , 5 = ^X(2X4) = 4 r 24 + 2 = 6 , Z: = 2 + 1 = 3 ； i < n , 5 = |x (4X6) = 8 r i 6 + 2 = 8 ,^=3+1=4；/ = /?,退出循环・故输出的s 的值为&【答案】B6. 已知回归直线的斜率的估计值是1.23,样本点的中心为（4,5）,则回归直线的方程是B.环形 D.左右形D. 12图1k=k+]1=2,5=i=i+2AAAy = 1.23x+4 By = 1.23x+5 C.J=1.23x+0.08D.J=0.08x+1.23【解析】 由题意可设回归直线方程为;=1.23x + d ，又样本点的中心(4,5)在回归直线上, 故 5 二 1.23X4 + ^ ,即 ° 二 0.08 , 故回归直线的方程为尹=1.23% + 0.08. 【答案】C7. 设的三边长分别为a, b, g N4BC 的面积为S,内切圆半径为r,则r=类比这个结论可知：四而体S-ABC 的四个而的而积分别为Si ，S2, S3, S4,内切球半径为7?, 四面体S-ABC 的体积为兀则/?=(V A ---SI+S2+S3+S4【解析】 四面体中以内切球的球心为顶点,四面体的各个面为底面,可把四面体分割37• R = ------------------S1+S2+S3 + S,【答案】c8. 已知数列仇｝的前n 项和S”=/・d 〃(Q2),而°] = 1,通过计算。

课时跟踪检测（十二）结构图层级一学业水平达标1．在结构图中，常在表示逻辑先后关系时出现的结构是()A．“树”形结构B．“环”形结构C．知识结构图D．组织结构图答案：B2．如图所示的框图中“幂函数的定义”“幂函数的图象与性质”与“幂函数”的关系是()A．并列关系B．从属关系C．包含关系D．交叉关系答案：B3．如图是一商场制订销售计划时的局部结构图，则“计划”受影响的主要要素有()A．经理B．政府行为C．政府行为、策划部、社会需求D．社会需求解析：选C影响“计划”的主要要素应是三个“上位”要素，即“政府行为”“策划部”“社会需求”，故选C.4．下列结构图中，各要素之间表示从属关系的是()解析：选D A，B，C中的结构图表示的是逻辑关系，只有D中结构图表示的是从属关系．5．在如图所示的知识结构图中，“求简单函数的导数”的“上位”要素有________个．解析：基本导数公式、导数的运算法则、复合函数求导法则都是其“上位”要素． 答案：36．如图所示为《数学5》第三章“不等式”的知识结构图，填空：①________________________________________________________________________；②________________________________________________________________________.答案：二元一次不等式(组)与简单的线性规划问题 基本不等式：ab ≤a ＋b27．在工商管理学中，MRP(Material Requirement Planning)指的是物资需求计划，基本MRP 的体系结构如图所示．从图中可以看出，基本MRP 直接受________、________和________的影响．解析：从结构图中可以看出，影响“基本MRP ”的主要要素应是其3个“上位”要素：主生产计划、产品结构、库存状态．答案：主生产计划 产品结构 库存状态8．我们学过圆的有关知识及应用，试画出有关圆的知识结构图． 解：知识结构图如图所示．9．某公司局域网设置如下：由服务器联结经理室、市场部、销售部、客户服务部、系统管理员，与外部联结是通过服务器，试画出该公司局域网设置结构图．解：结构图如下：层级二应试能力达标1．下图所示的是“概率”知识的()A．流程图B．结构图C．程序框图D．直方图解析：选B这是关于“概率”知识的结构图．2．下图是“集合”的知识结构图，如果要加入“子集”，则应该放在()A．“集合的概念”的下位B．“集合的表示”的下位C．“基本关系”的下位D．“基本运算”的下位解析：选C子集是集合与集合之间的基本关系，故应为“基本关系”的下位．3．如图是人教A版教材选修1－2第二章“推理与证明”的知识结构图(部分)，如果要加入知识点“三段论”，那么应该放在图中()A．“①”处B．“②”处C．“③”处D．“④”处解析：选B三段论是演绎推理的内容，因此应放在“②”处．4．某自动化仪表公司组织结构图如图，其中采购部的直接领导是()A．副总经理(甲) B．副总经理(乙)C．总经理D．董事会解析：选B由组织结构图可知：采购部由副总经理(乙)直接领导．5．下图是一种信息管理系统的结构图，则其构成有________部分．解析：由框图的结构知共4个部分．答案：46．某市质量技术监督局质量认证审查流程图如图所示，从图中可得在审查过程中可能不被审查通过的环节有________处．解析：这是一个实际问题，观察流程图可知有3处判断框，即3处环节可能不被审查通过．答案：37．试画出我们认识的“数”的知识结构图．解：从大范围到小范围，逐步细化．知识结构图如图所示．8．下面是中国移动关于发票的表述：我们在充分考虑您的个性化需求的基础上提供了以下几种话费发票方式：后付费话费发票、预付费话费发票、充值发票、全球通发票，其中全球通简单发票和单一发票是为满足全球通客户的个性化需要而制定的．您可以根据您的实际情况选择其中的话费发票方式．试写出关于发票的结构图．解：。

1．下列变量之间是线性相关关系的是________． ①人的身高与视力；②角的大小与所对的圆弧长； ③收入水平与纳税水平；④某地人的出生率与树林覆盖率．解析：②为确定性关系，①④不具有线性相关关系． 答案：③2．散点图在回归分析过程中的作用是________． ①查找个体个数；②比较个体数据大小关系； ③探究个体分类；④粗略判断变量是否线性相关．解析：散点图在回归分析中，能粗略判断变量间的相关关系． 答案：④3．已知x ，y 之间的一组数据：x 1.081.121.191.28y2.25 2.37 2.40 2.55 y 与x 之间的线性回归方程y ＝a ＋b x 必过定点________．解析：由已知可知线性回归方程一定过定点(x ，y )，因此求出x ＝1.1675，y ＝2.3925，故填(1.1675,2.3925)．答案：(1.1675,2.3925)4．设有一个回归方程为y ^＝2－2.5x ，则变量x 增加一个单位时，y 平均________个单位．解析：线性回归方程y ^＝a ^＋b ^x 中a ^，b ^的意义是：以a ^为基数，x 每增加1个单位，y 相应地平均增加b ^个单位．答案：减少2.5一、填空题1．下列说法：①回归方程适用于一切样本和总体；②样本取值的范围会影响回归方程的适用范围；③回归方程得到的预报值，是预报变量的精确值．其中正确的是________．解析：回归方程反映的是两个线性相关变量间的相关关系，它能预测变量的值，但不是精确值．答案：②2．关于相关系数r 的临界值r 0.05的说法：①临界值r 0.05是一个定值；②若|r |≤r 0.05，则否定假设H 0，表明有95%的把握认为x ，y 具有较强的线性相关关系；③若|r |＞r 0.05，则没有理由拒绝假设H 0，即没有充分的理由认为y 与x 之间有线性相关关系；④临界值r 0.05不是一个定值，它的值可由检验水平0.05及n －2在附表中查到．其中正确的序号为________．解析：②中应改为“|r |＞r 0.05”；③中应改为“|r |≤r 0.05”才正确；①、④矛盾，其中④中的表述正确．答案：④3．如图所示，有5组(x ，y )数据，去掉一组数据后，要使剩下的4组数据的相关系数最大，应去掉________点．解析：由散点图可知，D 点偏离最远，所以去掉D 点后，剩下4组数据的相关系数最大．答案：D4．若某地财政收入x 与支出y 满足线性回归方程y ＝bx ＋a ＋e (单位：亿元)，其中b ＝0.8，a ＝2，|e |≤0.5，如果今年该地区财政收入10亿元，年支出预计不会超过________亿．解析：代入数据得y ＝10＋e ，因为|e |≤0.5，所以|y |≤10.5，故不会超过10.5亿． 答案：10.55．(2011年高考广东卷)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x (单位：小时)与当天投篮命中率y 之间的关系：时间x 12345命中率0.4 0.5 0.6 0.6 0.4小李这5天的平均投篮命中率为________；用线性回归分析的方法，预测小李每月6号打篮球6小时的投篮命中率为________．解析：小李这5天的平均投篮命中率 y ＝0.4＋0.5＋0.6＋0.6＋0.45＝0.5.可求得小李这5天的平均打篮球时间x ＝3.根据表中数据可求得b ^＝0.01，a ^＝0.47，故回归直线方程为y ^＝0.47＋0.01x ，将x ＝6代入得6号打6小时篮球的命中率约为0.53. 答案：0.5 0.536．已知回归直线的斜率的估计值为 1.23.样本点的中心为(4,5)，则回归直线方程是________．解析：由斜率的估计值为 1.23，且回归直线一定经过样本点的中心(4,5)，可得y ^－5＝1.23(x －4)，即y ^＝1.23x ＋0.08.答案：y ^＝1.23x ＋0.087．(2011年高考山东卷改编)某产品的广告费用x 与销售额y 的统计数据如下表广告费用x (万元)4235销售额y (万元) 49 26 39 54 根据上表可得回归方程y ＝b x ＋a 中的b 为9.4，据此模型预报广告费用为6万元时销售额为________．解析：∵x ＝4＋2＋3＋44＝72，y ＝49＋26＋39＋544＝42，又y ^＝b ^x ＋a ^必过(x ，y )，∴42＝72×9.4＋a ^，∴a ^＝9.1.∴线性回归方程为y ^＝9.4x ＋9.1.∴当x ＝6时，y ^＝9.4×6＋9.1＝65.5(万元)． 答案：65.5万元8．观测两相关变量得如下数据：x－1－2－3－4－553421 y －9 －7 －5 －3 －1 1 5 3 79根据表中数据可得y 与x 之间的线性回归方程是________．(填序号)①y ^＝12x －1；②y ^＝x ；③y ^＝2x ＋13；④y ^＝x ＋1.解析：由表中数据可求得x ＝0，y ＝0，所以填②. 答案：②9．(2011年高考陕西卷改编)设(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线(如图)，以下结论中正确的是________．①x 和y 的相关系数为直线l 的斜率； ②x 和y 的相关系数在0到1之间；③当n 为偶数时，分布在l 两侧的样本点的个数一定相同；④直线l 过点(x ，y )．解析：因为相关系数是表示两个变量是否具有线性相关关系的一个值，它的绝对值越接近于1，两个变量的线性相关程度越强，所以①②错误．当n 为偶数时，分布在l 两侧的样本点的个数不一定相同，所以③错误．因为回归直线一定过样本点的中心，所以④正确．答案：④ 二、解答题10．某矿山采煤的单位成本y 与采煤量x 有关，其数据如下： 采煤量/千克 289298316322327329 329 331 350 单位成本/元43.5 42.9 42.1 39.6 39.138.5383837(1)作出散点图；(2)求出y 对x 的回归直线方程(结果保留3位小数)． 解：(1)作出散点图，如图所示．(2)由图表可得x ≈321.222，y ≈39.856，∑i ＝19x 2i ＝931337，∑i ＝19x i y i ＝114892.7.所以b ^＝∑i ＝19x i y i －9x y∑i ＝19x 2i －9(x )2≈－0.123，a ^＝y －b ^x ≈79.366.故y 对x 的回归直线方程为y ^＝－0.123x ＋79.366.11．一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器运转速度的变化而变化，下表为抽转速x (转/秒)1614128每小时生产有缺点的零件数y (件)11 9 8 5(1)利用散点图或相关系数r 的大小判断变量y 对x 是否线性相关？为什么？ (2)如果y 对x 有线性相关关系，求线性回归方程；(3)若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？(最后结果精确到0.001，参考数据：656.25≈25.617,16×11＋14×9＋12×8＋8×5＝438,162＋142＋122＋82＝660,112＋92＋82＋52＝291)解：(1)x ＝12.5，y ＝8.25，∑4i ＝1(x i －x )(y i －y )＝25.5， ∑4i ＝1(x i －x)2∑4i ＝1(y i －y )2＝656.25≈25.617，∴r 0.05≈0.995，由检验水平0.05及n －2＝2，在附录1中查得r 0.05＝0.950， 因为0.995>0.950，∴y 与x 具有线性相关关系．(2)∑4i ＝1(x i －x )2＝35， ∴b ^≈0.729，a ^＝y －b ^x ≈－0.863. ∴线性回归方程为y ^＝0.729x －0.863. (3)0.729x －0.863≤10，解得x ≤14.901， 故机器运转速度应在每秒14转之内．12．下表为某百货公司1～6月份销售量与利润之间的数量关系：月份1月2月3月4月5月6月现从具有线性相关关系这六组数据中选取4组数据求线性回归方程，再用剩下的2组数据进行检验．(1)根据2至5月份的数据，求出y 关于x 的线性回归方程y ^＝b ^x ＋a ^；(2)若由线性回归方程得到的估计数据与剩下的检验数据的误差均不超过2万元，则认为得到的线性回归方程是理想的，试问所得线性回归方程是否理想？解：(1)由表中数据求得x ＝11，y ＝24，∑5i ＝2x i y i ＝11×25＋13×29＋12×26＋8×16＝1092，∑5i ＝2x 2i ＝112＋132＋122＋82＝498，∴b ^＝∑5i ＝2x i y i －4x －y －∑5i ＝2x 2i －4x 2＝1092－4×11×24498－4×112＝3614＝187， a ^＝y －b ^x ＝24－187×11＝－307.所以y 关于x 的线性回归方程为y ^＝187x －307.(2)当x ＝10时，y ＝187×10－307＝1507，此时|1507－22|<2；当x ＝6时，y ＝187×6－307＝787，此时|787－12|<2.所以所得的线性回归方程是理想的．。

阶段质量检测（一）(时间120分钟，满分150分)一、选择题(本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．根据如下样本数据x 345678y 4.0 2.5－0.50.5－2.0－3.0得到的回归方程为y＝bx＋a，则( )A．a>0，b>0 B．a>0，b<0C．a<0，b>0 D．a<0，b<0解析：由表中数据画出散点图，如图，由散点图可知b<0，a>0.答案：B2．在某段时间内，甲地下雨的概率为0.3，乙地下雨的概率为0.4，假设在这段时间内两地是否下雨之间没有影响，则这段时间内，甲、乙两地都不下雨的概率为( ) A．0.12 B．0.88C．0.28 D．0.42解析：P＝(1－0.3)(1－0.4)＝0.42.答案：D3．某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )A．y＝－10x＋200 B．y＝10x＋200C．y＝－10x－200 D．y＝10x－200解析：由题意知选项B、D为正相关，选项C不符合实际意义．答案：A4．坛子中放有3个白球和2个黑球，从中进行不放回地摸球，用A1表示第一次摸得白球，A2表示第二次摸得白球，则A1和A2是( )A．互斥的事件B．相互独立的事件C．对立的事件 D．不相互独立的事件解析：由互斥事件、对立事件、相互独立事件的定义可知，A1与A2不互斥也不对立，同时A1与A2也不相互独立．答案：D5．如图，用K，A1，A2三类不同的元件连接成一个系统．当K正常工作且A1，A2至少有一个正常工作时，系统正常工作．已知K，A1，A2正常工作的概率依次为0.9,0.8,0.8，则系统正常工作的概率为( )A．0.960 B．0.864C．0.720 D．0.576解析：可知K，A1，A2三类元件正常工作相互独立．所以当A1，A2至少有一个能正常工作的概率为P＝1－(1－0.8)2＝0.96，所以系统能正常工作的概率为P K·P＝0.9×0.96＝0.864.答案：B6．对有线性相关关系的两个因素建立的回归直线方程y＝bx＋a中，回归系数b( ) A．可以小于0 B．大于0C．能等于0 D．只能小于0解析：∵b＝0时，则r＝0，这时不具有线性相关关系，但b可以大于0也可以小于0.答案：A7．某班主任对全班50名学生进行了作业量多少的调查，数据如下表：认为作业多认为作业不多总数喜欢玩电脑游戏18927不喜欢玩电脑游戏81523总数262450已知P(χ2≥3.841)≈0.05，则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )A．99% B．95%C．90% D．无充分依据解析：由题表中数据得χ2＝50×18×15－8×9226×24×27×23≈5.060>3.841.所以有95%的把握认为两变量之间有关系．答案：B8．2017年7月持续高温，下表是某同学记录的7月11日至7月22日每天因中暑去某医院的人数，及根据这些数据绘制出的散点图如下：日期7.117.127.137.147.157.16人数100109115118121134日期7.177.187.197.207.217.22人数141152168175186203下列说法：①根据此散点图，可以判断日期与人数具有线性相关关系；②根据此散点图，可以判断日期与人数具有正相关关系；③根据此散点图，可以判断日期与人数具有一次函数关系．其中正确的个数为( )A．0 B．1C．2 D．3解析：由散点图可知日期与人数具有线性相关关系而不是一次函数关系，故①正确，③错误．由散点图可知，人数随日期的增加而增多，故②正确．答案：C9．下表是x与y之间的一组数据，则y关于x的线性回归方程必过( )x 123 4y 57910A．点(2,8) B．点(2.5,8)C．点(10,31) D．点(2.5,7.75)解析：线性回归方程必过样本点的中心(x，y)，即(2.5,7.75)．答案：D10．硕士学位与博士学位的一个随机样本给出了关于所获取学位类别与学生性别的分类数据如表所示：根据以上数据，则( ) A ．性别与获取学位类别有关 B ．性别与获取学位类别无关 C ．性别决定获取学位的类别 D ．以上都是错误的解析：由列联表可得：博士：男性占2735≈77%，女性占835≈23%，相差很大，所以性别与获取学位的类别有关． 答案：A11．已知x ，y 的取值如表所示：如果y 与x 线性相关，且线性回归方程为y ＝bx ＋2，则b 的值为( )A ．－12B.12C ．－110D.110解析：计算得x ＝3，y ＝5，代入到y ＝bx ＋132中，得b ＝－12.答案：A12．为了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机抽取了60名高中生，通过问卷调查，得到以下数据：由以上数据，计算得到χ2≈9.643，根据临界值表，以下说法正确的是( ) A ．没有充足的理由认为课外阅读量大与作文成绩优秀有关 B ．有1%的把握认为课外阅读量大与作文成绩优秀有关 C ．有99.9%的把握认为课外阅读量大与作文成绩优秀有关 D ．有99%的把握认为课外阅读量大与作文成绩优秀有关解析：根据临界值表，9.643＞6.635，在犯错误的概率不超过0.01的前提下，认为课外阅读量大与作文成绩优秀有关，即有99%的把握认为课外阅读量大与作文成绩优秀有关．答案：D二、填空题(本大题共4小题，每小题5分，满分20分．把答案填写在题中的横线上) 13．有两组问题，其中第一组中有数学题6个，物理题4个；第二组中有数学题4个，物理题6个．甲从第一组中抽取1题，乙从第二组中抽取1题．甲、乙都抽到物理题的概率是________，甲和乙至少有一人抽到数学题的概率是________．解析：设A ＝{甲抽到物理题}，B ＝{乙抽到物理题}． 则P (A )＝410＝25，P (B )＝610＝35，P (AB )＝P (A )P (B )＝625，∴甲、乙至少有一人抽到数学题的概率为P ＝1－P (AB )＝1925.答案：625192514．已知某车间加工零件的个数x 与所花费时间y (h)之间的线性回归方程为y ＝0.01x ＋0.5，则加工600个零件大约需要________h.解析：当x ＝600时，y ＝0.01×600＋0.5＝6.5. 答案：6.515．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据(如下表)，由最小二乘法求得回归方程y ^＝0.67x ＋54.9.零件数x (个) 10 203040 50 加工时间y (min) 62758189现发现表中有一个数据模糊看不清，请你推断出该数据的值为________． 解析：由表知x ＝30，设模糊不清的数据为m ， 则y ＝15(62＋m ＋75＋81＋89)＝307＋m5，因为y ＝0.67x ＋54.9， 即307＋m5＝0.67×30＋54.9，解得m ＝68. 答案：6816．为了判断高中一年级学生选修文科与选修理科是否与性别有关，现随机抽取50名学生，得到2×2列联表如下：理科 文科 总计 男 13 10 23 女 7 20 27 总计203050已知P (χ2≥3.841)≈0.05，P (χ2≥5.024)≈0.025. 根据表中数据，得到χ2＝50×13×20－10×7223×27×30×20≈4.844.则认为选修文科与性别有关出错的可能性是________．解析：由χ2≈4.844>3.841，得选修文科与性别无关是不成立的，即有关的概率是95%，出错的可能性是1－95%＝5%.答案：5%三、解答题(本大题共6小题，满分70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)甲、乙、丙3位大学生同时应聘某个用人单位的职位，3人能被选中的概率分别为25，34，13，且各自能否被选中互不影响．(1)求3人同时被选中的概率； (2)求3人中至少有1人被选中的概率．解：记甲、乙、丙能被选中的事件分别为A ，B ，C ， 则P (A )＝25，P (B )＝34，P (C )＝13.(1)3人同时被选中的概率P 1＝P (ABC )＝P (A )P (B )P (C )＝25×34×13＝110.(2)3人中有2人被选中的概率P 2＝P (AB C ∪A B C ∪A BC )＝25×34×⎝ ⎛⎭⎪⎫1－13＋25×⎝ ⎛⎭⎪⎫1－34×13＋⎝ ⎛⎭⎪⎫1－25×34×13＝2360.3人中只有1人被选中的概率P 3＝P (A B C ∪A B C ∪A B C )＝25×⎝ ⎛⎭⎪⎫1－34×⎝ ⎛⎭⎪⎫1－13＋⎝⎛⎭⎪⎫1－25×34×⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫1－25×⎝ ⎛⎭⎪⎫1－34×13＝512.故3人中至少有1人被选中的概率为110＋2360＋512＝910.18．(本小题满分12分)某企业的某种产品产量与单位成本数据如下：月份 1 2 3 4 5 6 产量(千件) 2 3 4 3 4 5 单位成本(元)737271736968(1)试确定回归直线；(2)指出产量每增加1 000件时，单位成本下降多少？(3)假定产量为6 000件时，单位成本是多少？单位成本为70元时，产量应为多少件？ 解：(1)设x 表示每月产量(单位：千件)，y 表示单位成本(单位：元)作散点图．由图知y 与x 间呈线性相关关系， 设线性回归方程为y ＝bx ＋a ，x ＝3.5，y ＝71，S xy ＝－53，S 2x ＝1112， 故由公式可求得b ＝S xyS 2x＝－1.818，a ＝77.363， ∴线性回归方程为y ＝－1.818x ＋77.363.(2)由线性回归方程知，每增加1 000件产量，单位成本下降1.818元． (3)当x ＝6 000时，y ＝－1.818×6＋77.363＝66.455(元)， 当y ＝70时，70＝－1.818x ＋77.363，得x ＝4.05(千件)．19．(本小题满分12分)为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：性别是否需要志愿者男 女 需要4030不需要160 270(1)估计该地区老年人中，需要志愿者提供帮助的老年人的比例；(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关？解：(1)调查的500位老年人中有70位需要志愿者提供帮助，因此该地区老年人中，需要帮助的老年人的比例的估计值为70500＝14%.(2)χ2＝500×40×270－30×1602200×300×70×430≈9.967.由于9.967>6.635，所以能在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要帮助与性别有关．20．(本小题满分12分)(全国卷Ⅱ)某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：A 地区：62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89B 地区：73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79(1)根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值，给出结论即可)；(2)根据用户满意度评分，将用户的满意度从低到高分为三个等级：满意度评分 低于70分 70分到89分不低于90分 满意度等级不满意满意非常满意记事件C ：“A 地区用户的满意度等级高于B 地区用户的满意度等级”．假设两地区用户的评价结果相互独立．根据所给数据，以事件发生的频率作为相应事件发生的概率，求C 的概率．解：(1)两地区用户满意度评分的茎叶图如下：通过茎叶图可以看出，A 地区用户满意度评分的平均值高于B 地区用户满意度评分的平均值；A 地区用户满意度评分比较集中，B 地区用户满意度评分比较分散．(2)记C A1表示事件：“A 地区用户的满意度等级为满意或非常满意”；C A2表示事件：“A 地区用户的满意度等级为非常满意”； C B1表示事件：“B 地区用户的满意度等级为不满意”； C B2表示事件：“B 地区用户的满意度等级为满意”，则C A1与C B1独立，C A2与C B2独立，C B1与C B2互斥，C ＝C B1C A1∪C B2C A2.P (C )＝P (C B1C A1∪C B2C A2)＝P (C B1C A1)＋P (C B2C A2) ＝P (C B1)P (C A1)＋P (C B2)P (C A2)．由所给数据得C A1，C A2，C B1，C B2发生的频率分别为1620，420，1020，820，即P (C A1)＝1620，P (C A2)＝420，P (C B1)＝1020，P (C B2)＝820，P (C )＝1020×1620＋820×420＝0.48.21．(本小题满分12分)如图是我国2012年到2018年生活垃圾无害化处理量(单位：亿吨)的折线图．(1)由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； (2)建立y 关于t 的回归方程(系数精确到0.01)，预测2020年我国生活垃圾无害化处理量．附注：参考数据：∑i ＝17y i ＝9.32，∑i ＝17t i y i ＝40.17,∑i ＝17y i －y2＝0.55，7≈2.646.参考公式：相关系数r ＝∑i ＝1nt i －ty i －y∑i ＝1nt i －t2∑i ＝1n y i －y2，回归方程y ^＝a ^＋b ^t 中斜率和截距的最小二乘估计公式分别为：b ^＝∑i ＝1nt i －ty i －y∑i ＝1nt i －t2，a ^＝y －b ^t .解：(1)由折线图中数据和附注中参考数据得t ＝4，∑i ＝17(t i －t )2＝28,∑i ＝17y i －y2＝0.55，∑i ＝17 (t i －t )(y i －y )＝∑i ＝17t i y i －t ∑i ＝17y i＝40.17－4×9.32＝2.89，r ≈2.892×2.646×0.55≈0.99.因为y 与t 的相关系数近似为0.99，说明y 与t 的线性相关程度相当高，从而可以用线性回归模型拟合y 与t 的关系．(2)由y ＝9.327≈1.331及(1)得b ^＝∑i ＝17t i －ty i －y∑i ＝17t i －t2＝2.8928≈0.103， a ^＝y －b ^t ≈1.331－0.103×4≈0.92.所以y 关于t 的回归方程为y ^＝0.92＋0.10t . 将2020年对应的t ＝9代入回归方程得y^＝0.92＋0.10×9＝1.82.所以预测2020年我国生活垃圾无害化处理量将约为1.82亿吨．22．(本小题满分12分)(全国卷Ⅱ)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量(单位：kg)，其频率分布直方图如下：(1)记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；(2)填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：箱产量＜50 kg箱产量≥50 kg旧养殖法新养殖法(3)根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较．附：P(K2≥k0)0.0500.0100.001k0 3.841 6.63510.828K2＝n ad－bc2a＋b c＋d a＋c b＋d.解：(1)旧养殖法的箱产量低于50 kg的频率为(0.012＋0.014＋0.024＋0.034＋0.040)×5＝0.62. 因此，事件A的概率估计值为0.62.(2)根据箱产量的频率分布直方图得列联表箱产量＜50 kg箱产量≥50 kg旧养殖法 62 38 新养殖法3466根据表中数据及χ2的计算公式得， χ2＝200×62×66－34×382100×100×96×104≈15.705.由于15.705＞6.635，故有99%的把握认为箱产量与养殖方法有关．(3)箱产量的频率分布直方图表明：新养殖法的箱产量平均值(或中位数)在50 kg 到55 kg 之间，旧养殖法的箱产量平均值(或中位数)在45 kg 到50 kg 之间，且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高，因此，可以认为新养殖法的箱产量较高且稳定，从而新养殖法优于旧养殖法．。