2012届高考数学知识点复习测试题

2012届高考数学第一轮复习精品试题：集合§1.1 集合的含义及其表示经典例题：若x ∈R ，则｛3，x ，x2－2x ｝中的元素x 应满足什么条件? 当堂练习1．下面给出的四类对象中，构成集合的是（ ）A ．某班个子较高的同学B ．长寿的人CD ．倒数等于它本身的数2下面四个命题正确的是（ ）A ．10以内的质数集合是{0，3，5，7}B ．由1，2，3组成的集合可表示为{1，2，3}或{3，2，1}C ．方程2210x x -+=的解集是{1，1} D ．0与{0}表示同一个集合3． 下面四个命题： （1）集合N 中最小的数是1； （2）若 -a ∉Z ，则a ∈Z ； （3）所有的正实数组成集合R+；（4）由很小的数可组成集合A ； 其中正确的命题有（ ）个A ．1B ．2C ．3D ．44．下面四个命题： （1）零属于空集； （2）方程x2-3x+5=0的解集是空集； （3）方程x2-6x+9=0的解集是单元集； （4）不等式 2 x-6>0的解集是无限集； 其中正确的命题有（ ）个A ．1B ．2C ．3D ．4 5． 平面直角坐标系内所有第二象限的点组成的集合是( ) A ． {x,y 且0,0x y <>} B ． {(x,y)0,0x y <>}C. {(x,y)0,0x y <>} D. {x,y 且0,0x y <>}6．用符号∈或∉填空：0__________{0}， a__________{a}， π__________Q ， 21__________Z ，－1__________R ，0__________N ， 0 Φ． 7．由所有偶数组成的集合可表示为{x x =}．8．用列举法表示集合D={2(,)8,,x y y x x N y N=-+∈∈}为 ．9．当a 满足 时, 集合A ＝{30,x x a x N +-<∈}表示单元集．10．对于集合A ＝{2，4，6}， 若a ∈A ，则6－a ∈A ，那么a 的值是__________． 11．数集{0，1，x2－x}中的x 不能取哪些数值？12．已知集合A ＝{x ∈N|126x －∈N }，试用列举法表示集合A ．13.已知集合A={2210,,x ax x a R x R++=∈∈}.(1)若A 中只有一个元素,求a 的值; (2)若A 中至多有一个元素,求a 的取值范围.14.由实数构成的集合A 满足条件:若a ∈A, a ≠1,则11Aa∈-,证明：（1）若2∈A ，则集合A 必还有另外两个元素，并求出这两个元素； （2）非空集合A 中至少有三个不同的元素。

指数与指数函数一、选择题：(本大题共6小题，每小题6分，共36分，将正确答案的代号填在题后的括号内．)1．下列结论中正确的个数是( )①当a <0时，(a 2)32＝a 3；②n a n ＝|a |；③函数y ＝(x －2)12－(3x －7)0的定义域是(2，＋∞)；④若100a ＝5,10b ＝2，则2a ＋b ＝1.A ．0B ．1C ．2D ．3 2．(36a 9)4·(63a 9)4(a ≥0)的化简结果是( ) A ．a 16 B ．a 8C ．a 4D ．a 23．若函数y ＝(a 2－5a ＋5)·a x 是指数函数，则有( )A ．a ＝1或a ＝4B ．a ＝1C ．a ＝4D ．a >0，且a ≠14．在平面直角坐标系中，函数f (x )＝2x ＋1与g (x )＝21－x 图象关于( )A ．原点对称B ．x 轴对称C ．y 轴对称D ．直线y ＝x 对称5．若函数f (x )＝a |2x －4|(a >0，a ≠1)，满足f (1)＝19，则f (x )的单调递减区间是( ) A ．(－∞，2] B ．[2，＋∞)C ．[－2，＋∞)D ．(－∞，－2]6．已知函数f (x )＝⎝⎛⎭⎫13x －log 2x ，实数a 、b 、c 满足f (a )f (b )f (c )<0(0<a <b <c )，若实数x 0是方程f (x )＝0的一个解，那么下列不等式中，不可能成立的是( )A ．x 0<aB ．x 0>bC ．x 0<cD ．x 0>c二、填空题：(本大题共4小题，每小题6分，共24分，把正确答案填在题后的横线上．)7．已知不论a 为何正实数，y ＝a x ＋1－2的图象恒过定点，则这个定点的坐标是________．8．函数y ＝(13)x －3x 在区间[－1,1]上的最大值为________． 9．定义：区间[x 1，x 2](x 1<x 2)的长度为x 2－x 1.已知函数y ＝2|x |的定义域为[a ，b ]，值域为[1,2]，则区间[a ，b ]的长度的最大值与最小值的差为________．10．设f (x )＝e x ＋e －x 2，g (x )＝e x －e －x2，计算f (1)g (3)＋g (1)f (3)－g (4)＝________，f (3)g (2)＋g (3)f (2)－g (5)＝________，并由此概括出关于函数f (x )和g (x )的一个等式，使上面的两个等式是你写出的等式的特例，这个等式是________．三、解答题：(本大题共3小题，11、12题13分，13题14分，写出证明过程或推演步骤．)11．已知函数f (x )＝b ·a x(其中a ，b 为常量且a >0，a ≠1)的图象经过点A (1,6)，B (3,24)．(1)试确定f (x )；(2)若不等式⎝⎛⎭⎫1a x ＋⎝⎛⎭⎫1b x －m ≥0在x ∈(－∞，1]时恒成立，求实数m 的取值范围．12．已知函数f (x )＝⎝⎛⎭⎫13ax 2－4x ＋3.(1)若a ＝－1，求f (x )的单调区间；(2)若f (x )有最大值3，求a 的值．(3)若f (x )的值域是(0，＋∞)，求a 的取值范围．13．已知函数f (x )＝2x －12|x |(1)若f (x )＝2，求x 的值；(2)若2t f (2t )＋mf (t )≥0对于t ∈[1,2]恒成立，求实数m 的取值范围．。

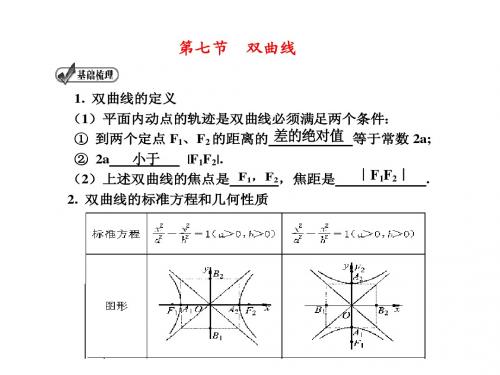
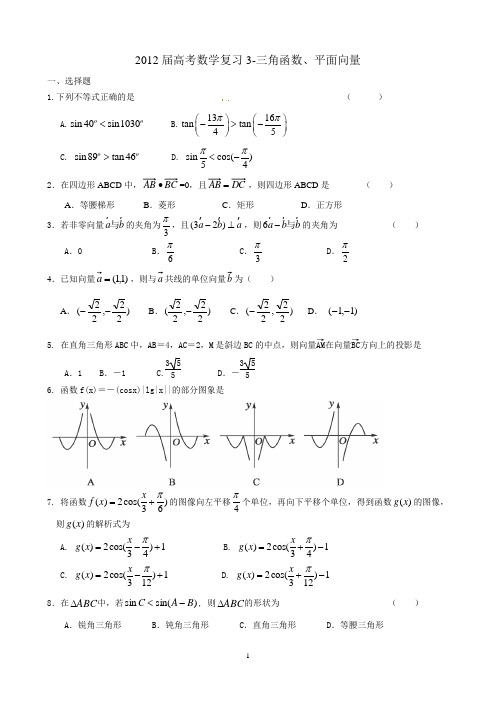
2012届高考数学复习3-三角函数、平面向量一、选择题1.下列不等式正确的是 （ ） A.sin 40sin 1030oo< B.1316tan tan 45ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭ C. sin 89tan 46o o> D. sinco s()54ππ<-2．在四边形ABCD 中，BC AB ∙=0，且DC AB =，则四边形ABCD 是 （ ）A ．等腰梯形B ．菱形C ．矩形D ．正方形3．若非零向量a b 与的夹角为3π，且(32)a b a -⊥ ，则6a b b - 与的夹角为（ ）A ．0B ．6π C ．3π D ．2π4．已知向量)1,1(=a ，则与a 共线的单位向量b 为（ ）A ．)22,22(-- B ．)22,22(- C ．)22,22(- D ． )1,1(--5. 在直角三角形ABC 中，AB ＝4，AC ＝2，M 是斜边BC 的中点，则向量AM →在向量BC →方向上的投影是A ．1B ．－1 C.355D ．－3556. 函数f(x)＝－(cosx)|lg|x||的部分图象是7. 将函数()2co s()36x f x π=+的图像向左平移4π个单位，再向下平移个单位，得到函数()g x 的图像，则()g x 的解析式为 A. ()2co s()134x g x π=-+ B. ()2co s()134x g x π=+- C. ()2co s()1312x g x π=-+ D. ()2co s()1312xg x π=+-8．在ABC ∆中，若)sin(sin B A C -<, 则ABC ∆的形状为 （ ）A ．锐角三角形B ．钝角三角形C ．直角三角形D ．等腰三角形9. 已知ABC∆，D 是BC 边上的一点，4||,2||,==⎭⎫ ⎝⎛+=AC AB AD λ，若记,A B a A C b == ，则用b a,表示B D 所得的结果为 （ ）A ．b a 2121-B ．b a 3131-C ．b a 3131+- D ．b a 3121+二、填空题 10．函数2()sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是 。

2012届高考数学第一轮复习精品试题：函数§2.1.1 函数的概念和图象经典例题：设函数f （x ）的定义域为［0，1］，求下列函数的定义域： （1）H （x ）=f （x2+1）；（2）G （x ）=f （x+m ）+f （x －m ）（m ＞0）.当堂练习：1． 下列四组函数中,表示同一函数的是（ ） A．(),()f x x g x ==B．2(),()f x x g x ==C ．21(),()11x f x g x x x -==+- D．()()f x g x ==2函数()y f x =的图象与直线x a =交点的个数为（ ）A ．必有一个B ．1个或2个C ．至多一个D ．可能2个以上3．已知函数1()1f x x =+，则函数[()]f f x 的定义域是（ ）A ．{}1x x ≠ B ．{}2x x ≠- C ．{}1,2xx ≠-- D ．{}1,2x x ≠-4．函数1()1(1)f x x x =--的值域是（ ）A ．5[,)4+∞B ．5(,]4-∞C ． 4[,)3+∞D ．4(,3-∞ 5．对某种产品市场产销量情况如图所示，其中：1l 表示产品各年年产量的变化规律；2l 表示产品各年的销售情况．下列叙述： （ ）（1）产品产量、销售量均以直线上升，仍可按原生产计划进行下去；（2）产品已经出现了供大于求的情况，价格将趋跌；（3）产品的库存积压将越来越严重，应压缩产量或扩大销售量；（4）产品的产、销情况均以一定的年增长率递增．你认为较合理的是( ) A ．（1），（2），（3） B ．（1），（3），（4） C ．（2），（4） D ．（2），（3）6．在对应法则,,,x y y x b x R y R→=+∈∈中,若25→,则2-→ ， →6．7．函数()f x 对任何x R +∈恒有1212()()()f x x f x f x ⋅=+，已知(8)3f =，则f = ．8．规定记号“∆”表示一种运算，即a b a b a b R+∆++∈，、. 若13k ∆=，则函数()fx k x=∆的值域是___________．9．已知二次函数f(x)同时满足条件： (1) 对称轴是x=1； (2) f(x)的最大值为15；(3) f(x)的两根立方和等于17．则f(x)的解析式是 ．10．函数2522y x x =-+的值域是 ．11． 求下列函数的定义域 ： (1)()121x f x x =-- (2)(1)()x f x x x+=-12．求函数y x =13．已知f(x)=x2+4x+3，求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t)．14．在边长为2的正方形ABCD 的边上有动点M ，从点B 开始，沿折线BCDA 向A 点运动，设M 点运动的距离为x ，△ABM 的面积为S ． （1）求函数S=的解析式、定义域和值域； （2）求f[f(3)]的值．§2.1.2 函数的简单性质经典例题：定义在区间（－∞，＋∞）上的奇函数f （x ）为增函数，偶函数g （x ）在［0，＋∞ )上图象与f （x ）的图象重合.设a ＞b ＞0，给出下列不等式，其中成立的是 f （b ）－f （－a ）＞g （a ）－g （－b ） ②f （b ）－f （－a ）＜g （a ）－g （－b ）③f （a ）－f （－b ）＞g （b ）－g （－a ） ④f （a ）－f （－b ）＜g （b ）－g （－a ） A ．①④ B ．②③ C ．①③ D ．②④ 当堂练习：1．已知函数f(x)=2x2-mx+3，当()2,x ∈-+∞时是增函数，当(),2x ∈-∞-时是减函数，则f(1)等于 （ ）A ．-3B ．13C ．7D ．含有m 的变量2．函数1()x f x -=是（ ）A ． 非奇非偶函数B ．既不是奇函数,又不是偶函数奇函数C ． 偶函数D ． 奇函数3．已知函数(1)()11f x x x =++-,(2)()f x =2()33f x x x =+(4)0()()1()R x Q f x x C Q ∈=∈⎧⎨⎩,其中是偶函数的有（ ）个 A ．1 B ．2 C ．3 D ．44．奇函数y=f （x ）（x ≠0），当x ∈（0，+∞）时，f （x ）=x －1，则函数f （x －1）的图象为（ ）5．已知映射f:A →B,其中集合A={-3,-2,-1,1,2,3,4},集合B 中的元素都是A 中元素在映射f 下的象,且对任意的A a ∈,在B 中和它对应的元素是a,则集合B 中元素的个数是（ ）A ．4B ．5C ．6D ．76．函数2()24f x x tx t =-++在区间[0, 1]上的最大值g(t)是 ．7． 已知函数f(x)在区间(0,)+∞上是减函数,则2(1)f x x ++与()34f 的大小关系是 ．8．已知f(x)是定义域为R 的偶函数,当x<0时, f(x)是增函数,若x1<0,x2>0,且12x x <,则1()f x 和2()f x 的大小关系是 ．9．如果函数y=f(x+1)是偶函数，那么函数y=f(x)的图象关于_________对称．10．点(x,y)在映射f作用下的对应点是(,)22y x +-,若点A 在f 作用下的对应点是B(2,0),则点A 坐标是 ．13. 已知函数2122()x x f x x++=,其中[1,)x ∈+∞，(1)试判断它的单调性；(2)试求它的最小值．14．已知函数2211()a f x aa x+=-，常数0>a 。

2012年全国各地高考数学试题及解答分类汇编大全（06数列）一、选择题：1. (2012安徽文)公比为2的等比数列{n a } 的各项都是正数，且 3a 11a =16，则5a =（ ） （A ）1 ()B 2 ()C 4 ()D 8 【解析】选A2231177551616421a a a a a a =⇔=⇔==⨯⇔=2. (2012安徽理){}n a 的各项都是正数，且31116a a =，则162log a =（ ） ()A 4 (B ) 5 ()C 6 ()D 7 【解析】选B29311771672161616432log 5a a a a a a q a =⇔=⇔=⇒=⨯=⇔=3．(2012北京文)已知为等比数列，下面结论种正确的是（ ）（A ）a 1+a 3≥2a 2 （B ）2223212a a a ≥+ （C ）若a 1=a 3，则a 1=a 2（D ）若a 3＞a 1，则a 4＞a 2 【解析】当01<a ，0<q ，时，可知01<a ，03<a ，02>a ，所以A 选项错误；当1-=q 时，C 选项错误：当0<q 时，241313a a q a q a a a <⇒<⇒>，与D 选项矛盾，因此描述均值定理的B 选项为正确答案，故选B 。

【答案】B4. (2012福建理) 等差数列{a n }中，a 1+a 5=10,a 4=7,则数列{a n }的公差为（ ）A.1B.2C.3D.4 【答案】B【解析】153210a a a +==，35a =，所以432d a a =-= 【点评】本题考查等差数列的中项公式，定义．5. (2012福建文)数列{a n }的通项公式2cosπn n a n =，其前n 项和为S n ，则S 2012等于（ ） A.1006 B.2012 C.503 D.06．(2012湖北文、理)定义在(,0)(0,)-∞+∞上的函数()f x ，如果对于任意给定的等比数列{}n a ，{()}n f a 仍是等比数列，则称()f x 为“保等比数列函数”. 现有定义在(,0)(0,)-∞+∞上的如下函数：①2()f x x =； ②()2x f x =； ③()f x =④()ln ||f x x =.则其中是“保等比数列函数”的()f x 的序号为 （ ）A ．① ②B ．③ ④C ．① ③D ．② ④ 考点分析：本题考察等比数列性质及函数计算. 难易度：★【解析1】设数列{}n a 的公比为q .对于①，22112()()n n n nf a a q f a a ++==,是常数，故①符合条件;对于②，111()22()2n n n n a a a n a n f a f a ++-+==，不是常数，故②不符合条件;对于③，1()()n nf a f a +===;对于④,11()ln ||()ln ||n n n n f a a f a a ++=，不是常数，故④不符合条件.由“保等比数列函数”的定义知应选C.解析2：等比数列性质，212++=n n n a a a ，①()()()()122212222++++===n n n n n n a f a a a a f a f ；②()()()12221222222+++=≠==+++n a a a a an n a f a f a f n n n n n ；③()()()122122++++===n n n n n n a f a a a a f a f ；④()()()()122122ln ln ln ++++=≠=n n n n n n a f a a a a f a f .选C【点评】本题考查等比数列的新应用，函数的概念.对于创新性问题，首先要读懂题意，然后再去利用定义求解，抓住实质是关键.来年需要注意数列的通项，等比中项的性质等. 7. (2012江西文) 观察下列事实|x|+|y|=1的不同整数解（x,y ）的个数为4 ， |x|+|y|=2的不同整数解（x,y ）的个数为8， |x|+|y|=3的不同整数解（x,y ）的个数为12 ….则|x|+|y|=20的不同整数解（x ，y ）的个数为（ ）A.76B.80C.86D.92 【答案】B【解析】本题主要为数列的应用题，观察可得不同整数解的个数可以构成一个首先为4，公差为4的等差数列，则所求为第20项，可计算得结果.8. (2012辽宁文)在等差数列{a n }中，已知a 4+a 8=16，则a 2+a 10=（ ）(A) 12 (B) 16 (C) 20 (D)24 【答案】B【解析】48111(3)(7)210,a a a d a d a d +=+++=+21011121048()(9)210,16a a a d a d a d a a a a +=+++=+∴+=+=，故选B【点评】本题主要考查等差数列的通项公式、同时考查运算求解能力，属于容易题。

第十四讲 导数的概念及其运算一、选择题：(本大题共6小题，每小题6分，共36分，将正确答案的代号填在题后的括号内．)1．下列结论不正确的是( )A ．若y ＝3，则y ′＝0B ．若y ＝1x ，则y ′＝－12xC ．若y ＝－x ，则y ′＝－12x D ．若y ＝3x ，则y ′＝32．已知奇函数y ＝f (x )在区间(－∞，0]上的解析式为f (x )＝x 2＋x ，则切点横坐标为1的切线方程是( )A ．x ＋y ＋1＝0B ．x ＋y －1＝0C ．3x －y －1＝0D ．3x －y ＋1＝0 3．已知直线y ＝kx ＋1与曲线y ＝x 3＋ax ＋b 切于点(1,3)，则b 的值为( )A ．3B ．－34．(2010·江西)若函数f (x )＝ax 4＋bx 2＋c 满足f ′(1)＝2，则f ′(－1)＝( )A ．－1B ．－2C ．2D ．05．(2010·全国Ⅱ)若曲线y ＝x 2＋ax ＋b 在点(0，b )处的切线方程是x －y ＋1＝0，则( )A ．a ＝1，b ＝1B ．a ＝－1，b ＝1C ．a ＝1，b ＝－1D ．a ＝－1，b ＝－16．(2010·辽宁)已知点P 在曲线y ＝4e x ＋1上，α为曲线在点P 处的切线的倾斜角，则α的取值范围是( ) A.⎝⎛⎭⎫0，π4 B.⎝⎛⎭⎫π4，π2 C.⎝⎛π2，3π4 D.⎣⎡⎭⎫3π4，π 二、填空题：(本大题共4小题，每小题6分，共24分，把正确答案填在题后的横线上．)7．曲线y ＝x 2－2x ＋a 与直线y ＝3x ＋1相切时，常数a 的值是________．8．已知函数f (x )的导函数为f ′(x )，且满足f (x )＝3x 2＋2xf ′(2)，则f ′(5)＝________.9．若曲线f (x )＝ax 3＋ln x 存在垂直于y 轴的切线，则实数a 的取值范围是________．10．(2010·江苏)函数y ＝x 2(x >0)的图象在点(a k ，a 2k )处的切线与x 轴的交点的横坐标为a k ＋1，其中k ∈N *.若a 1＝16，则a 1＋a 3＋a 5的值是________．三、解答题：(本大题共3小题，11、12题13分，13题14分，写出证明过程或推演步骤．)11．已知曲线y ＝x 3＋x －2在点P 0处的切线l 1平行于直线4x －y －1＝0，且点P 0在第三象限．(1)求P 0的坐标；(2)若直线l ⊥l 1，且l 也过切点P 0，求直线l 的方程．12．已知函数f (x )＝x 3＋x －16，(1)求曲线y ＝f (x )在点(2，－6)处的切线的方程；(2)直线l 为曲线y ＝f (x )的切线，且经过原点，求直线l 的方程及切点坐标；(3)如果曲线y ＝f (x )的某一切线与直线y ＝－14x ＋3垂直，求切点坐标与切线的方程．13．设函数f (x )＝ax ＋1x ＋b(a ，b ∈Z )，曲线y ＝f (x )在点(2，f (2))处的切线方程为y ＝3. (1)求f (x )的解析式；(2)证明：函数y ＝f (x )的图象是一个中心对称图形，并求其对称中心；(3)证明：曲线y ＝f (x )上任一点的切线与直线x ＝1和直线y ＝x 所围的三角形的面积为定值，并求出此定值．。

2012年普通高等学校招生全国统一考试理科数学（必修+选修II ）一、 选择题（1）、复数131i i-++= A. 2 B. 2 C. 12 D. 12i i i i +-+- 【考点】复数的计算【难度】容易【答案】C 【解析】13(13)(1)24121(1)(1)2i i i i i i i i -+-+-+===+++-. 【点评】本题考查复数的计算。

在高二数学（理）强化提高班下学期，第四章《复数》中有详细讲解，其中第02节中有完全相同类型题目的计算。

在高考精品班数学（理）强化提高班中有对复数相关知识的总结讲解。

（2）、已知集合A ＝{1.3. m }，B ＝{1，m } ,A B ＝A , 则m =A. 0或3B. 0或3C. 1或3D. 1或3【考点】集合【难度】容易【答案】B【解析】(1,3,),(1,)30,1()3A B A B A A m B m m A m m m m m m ⋃=∴⊆==∴∈∴==∴===或舍去.【点评】本题考查集合之间的运算关系，及集合元素的性质。

在高一数学强化提高班下学期课程讲座1，第一章《集合》中有详细讲解，其中第02讲中有完全相同类型题目的计算。

在高考精品班数学（理）强化提高班中有对集合相关知识及综合题目的总结讲解。

（3） 椭圆的中心在原点，焦距为4， 一条准线为x =﹣4 ，则该椭圆的方程为 A. 216x +212y =1 B. 212x +28y =1 C. 28x +24y =1 D. 212x +24y =1 【考点】椭圆的基本方程【难度】容易【答案】C【解析】椭圆的一条准线为x =﹣4,∴2a =4c 且焦点在x 轴上，∵2c =4∴c =2，a =22∴椭圆的方程为22=184x y + 【点评】本题考查椭圆的基本方程，根据准线方程及焦距推出椭圆的方程。

在高二数学（理）强化提高班，第六章《圆锥曲线与方程》中有详细讲解，其中在第02讲有相似题目的详细讲解。

第十七讲 同角三角函数的基本关系式及诱导公式一、选择题：(本大题共6小题，每小题6分，共36分，将正确答案的代号填在题后的括号内．)1．(2010·全国Ⅰ)记cos(－80°)＝k ，那么tan100°＝( ) A.1－k 2k B ．－1－k 2kC.k 1－k 2 D ．－k 1－k 2解析：cos(－80°)＝cos80°＝k ，sin80°＝1－k 2，tan80°＝1－k 2k ，tan100°＝－tan80°＝－1－k 2k，故选B.答案：B 2．已知1＋sin x cos x ＝－12，那么cos x sin x －1的值是( ) A.12 B ．－12C ．2D ．－2 解析：因为1＋sin x cos x ·sin x －1cos x ＝sin 2x －1cos 2x ＝－1，从而由已知1＋sin x cos x ＝－12得cos x sin x －1＝12. 答案：A3．若cos α＋2sin α＝－5，则tan α＝( )A.12 B ．2 C ．－12D ．－2 解析：由cos α＋2sin α＝－5,①,sin 2α＋cos 2α＝1,②)将①代入②得(5sin α＋2)2＝0，∴sin α＝－255，cos α＝－55.故选B. 答案：B4．若tan α＝2，则sin α－3cos αsin α＋cos α的值是( ) A ．－13 B ．－53 C.13 D.53解析：由tan α＝2，则sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－13，选A. 答案：A5．设f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)，其中a 、b 、α、β都是非零实数，若f (2008)＝－1，那么f (2009)等于( )A ．－1B ．0C ．1D ．2解析：∵f (2008)＝a sin(2008π＋α)＋b cos(2008π＋β)＝a sin α＋b cos β＝－1，∴f (2009)＝a sin(2009π＋α)＋b cos(2009π＋β)＝－(a sin α＋b cos β)＝1.答案：C6．已知sin α＋cos α＝1，则sin n α＋cos n α等于( )A ．1B ．0C.12n －1 D ．不能确定 解析：由⎩⎪⎨⎪⎧ sin α＋cos α＝1，sin 2α＋cos 2α＝1，解得⎩⎪⎨⎪⎧ sin α＝1，cos α＝0，或⎩⎪⎨⎪⎧sin α＝0，cos α＝1. ∴sin n α＋cos n α＝1.答案：A二、填空题：(本大题共4小题，每小题6分，共24分，把正确答案填在题后的横线上．)7．已知tan α＝2，则(1)2sin α－3cos α4sin α－9cos α＝________； (2)2sin 2α－3cos 2α4sin 2α－9cos 2α＝________； (3)4sin 2α－3sin αcos α－5cos 2α＝________.解析：(1)注意到分式的分子与分母均是关于sin α、cos α的一次齐次式，将分子、分母同除以cos α(∵cos α≠0)，然后整体代入tan α＝2的值．2sin α－3cos α4sin α－9cos α＝2tan α－34tan α－9＝2×2－34×2－9＝－1. (2)注意到分子、分母都是关于sin α、cos α的二次齐次式，∵cos 2α≠0，分子、分母同除以cos 2α，有2sin 2α－3cos 2α4sin 2α－9cos 2α＝2tan 2α－34tan 2α－9＝2×4－34×4－9＝57.∴应填57. (3)要注意到sin 2α＋cos 2α＝1，4sin 2α－3sin αcos α－5cos 2α＝4sin 2α－3sin αcos α－5cos 2αsin 2α＋cos 2α＝4tan 2α－3tan α－5tan 2α＋1＝4×4－3×2－54＋1＝55＝1.应填1. 答案：(1)－1 (2)57(3)1 评析：这是一组在已知tan α＝m 的条件下，求关于sin α、cos α的齐次式(即次数相同)的问题，解答这类“已知某个三角函数，求其余三角函数值”的问题的常规思路是：利用同角间的三角函数关系，求出其余三角函数值，这就需要根据m 的取值符号，确定α角所在的象限，再对它进行讨论．这样计算相当繁琐，而在这里灵活地运用“1”的代换，将所求值的式子的分子、分母同除以cos n α，用tan n α表示出来，从而简化了解题过程，我们应熟练掌握这种解法．更主要的是由此进一步领悟“具体问题、具体分析”的辩证思想方法．8．化简cos(－θ)cos(360°－θ)·tan 2(180°－θ)－cos(90°＋θ)cos 2(270°＋θ)·sin(－θ)＝________.解析：直接利用三角函数的诱导公式进行化简可得原式＝－1.答案：－19．(2010·广州模拟)已知sin ⎝⎛⎭⎫α－π4＝13，则 cos ⎝⎛⎭⎫π4＋α＝________.解析：cos ⎝⎛⎭⎫π4＋α＝cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4－α ＝sin ⎝⎛⎭⎫π4－α＝－sin ⎝⎛⎭⎫α－π4＝－13. 答案：－1310．设α＝sin(sin2008°)，b ＝sin(cos2008°)，c ＝cos(sin2008°)，d ＝cos(cos2008°)，则a ，b ，c ，d 从小到大的顺序是________．解析：∵2008°＝5×360°＋180°＋28°，∴a ＝sin(－sin28°)＝－sin(sin28°)<0，b ＝sin(－cos28°)＝－sin(cos28°)<0，c ＝cos(－sin28°)＝cos(sin28°)>0，d ＝cos(－cos28°)＝cos(cos28°)>0，又sin28°<cos28°，∴b <a <d <c .答案：b <a <d <c三、解答题：(本大题共3小题，11、12题13分，13题14分，写出证明过程或推演步骤．)11．(2011·兰州模拟题)已知3cos 2(π＋x )＋5cos ⎝⎛⎭⎫π2－x ＝1，求6sin x ＋4tan 2x －3cos 2(π－x )的值． 解：由已知得3cos 2x ＋5sin x ＝1，即3sin 2x －5sin x －2＝0，解得sin x ＝－13(sin x ＝2舍去)．这时cos 2x ＝1－⎝⎛⎭⎫－132＝89，tan 2x ＝sin 2x cos 2x ＝18， 故6sin x ＋4tan 2x －3cos 2(π－x )＝6×⎝⎛⎭⎫－13＋4×18－3×89＝－256. 12．(1)已知tan α＝3，求23sin 2α＋14cos 2α的值． (2)已知1tan α－1＝1，求11＋sin αcos α的值． 解：(1)23sin 2α＋14cos 2α＝23sin 2α＋14cos 2αsin 2α＋cos 2α＝23tan 2α＋14tan 2α＋1＝23×32＋1432＋1＝58. (2)由1tan α－1＝1得tan α＝2， 11＋sin αcos α＝sin 2α＋cos 2αsin 2α＋cos 2α＋sin αcos α＝tan 2α＋1tan 2α＋tan α＋1＝22＋122＋2＋1＝57. 13．已知在△ABC 中，sin A ＋cos A ＝15， (1)求sin A ·cos A ；(2)判断△ABC 是锐角三角形还是钝角三角形；(3)求tan A 的值．分析：可先把sin A ＋cos A ＝15两边平方得出sin A ·cos A ，然后借助于A ∈(0，π)及三角函数符号法则可得sin A 与cos A 的符号，从而进一步构造sin A －cos A 的方程，最后联立求解．解：(1)∵sin A ＋cos A ＝15① ∴两边平方得1＋2sin A cos A ＝125， ∴sin A ·cos A ＝－1225. (2)由(1)sin A cos A ＝－1225<0，且0<A <π， 可知cos A <0，∴A 为钝角，∴△ABC 是钝角三角形．(3)∵(sin A －cos A )2＝1－2sin A cos A＝1＋2425＝4925， 又sin A >0，cos A <0，∴sin A －cos A >0，∴sin A －cos A ＝75② ∴由①，②可得sin A ＝45，cos A ＝－35， ∴tan A ＝sin A cos A ＝45－35＝－43. 评析：sin α·cos α与sin α－cos α，sin α＋cos α存在内在联系，即：sin α·cos α＝12[(sin α＋cos α)2－1]，sin α·cos α＝12[1－(sin α－cosα)2]．可“知一求二”．。