高中数学必修2立体几何专题-线面垂直方法总结
- 格式:ppt
- 大小:723.50 KB
- 文档页数:36
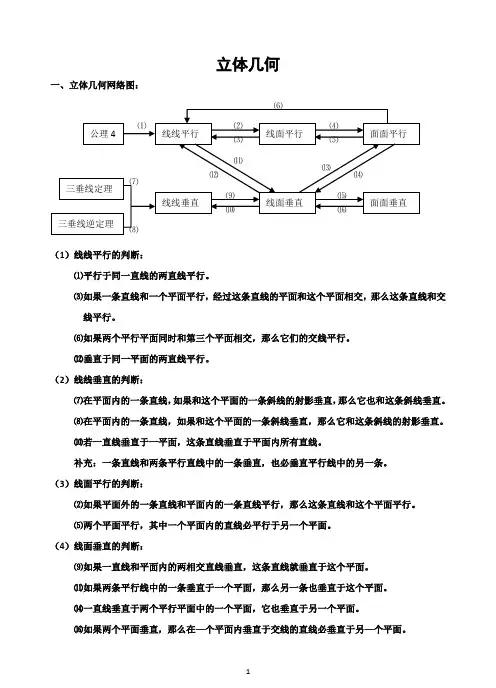
立体几何一、立体几何网络图:(1)线线平行的判断:⑴平行于同一直线的两直线平行。
⑶如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
⑹如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
⑿垂直于同一平面的两直线平行。
(2)线线垂直的判断:⑺在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
⑻在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直。
⑽若一直线垂直于一平面,这条直线垂直于平面内所有直线。
补充:一条直线和两条平行直线中的一条垂直,也必垂直平行线中的另一条。
(3)线面平行的判断:⑵如果平面外的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
⑸两个平面平行,其中一个平面内的直线必平行于另一个平面。
(4)线面垂直的判断:⑼如果一直线和平面内的两相交直线垂直,这条直线就垂直于这个平面。
⑾如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
⒁一直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⒃如果两个平面垂直,那么在—个平面内垂直于交线的直线必垂直于另—个平面。
(5)面面平行的判断:⑷一个平面内的两条相交直线分别平行于另一个平面,这两个平面平行。
⒀垂直于同一条直线的两个平面平行。
(6)面面垂直的判断:⒂一个平面经过另一个平面的垂线,这两个平面互相垂直。
二、其他定理:(1)确定平面的条件:①不公线的三点;②直线和直线外一点;③相交直线;(2)直线与直线的位置关系:相交;平行;异面;直线与平面的位置关系:在平面内;平行;相交(垂直是它的特殊情况);平面与平面的位置关系:相交;;平行;(3)等角定理:如果两个角的两边分别平行且方向相同,那么这两个角相等;如果两条相交直线和另外两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等;(4)射影定理(斜线长、射影长定理):从平面外一点向这个平面所引的垂线段和斜线段中,射影相等的两条斜线段相等;射影较长的斜线段也较长;反之,斜线段相等的射影相等;斜线段较长的射影也较长;垂线段比任何一条斜线段都短。


那么另一条也垂直于这个平 a 的无数条直线”是“ I 丄a B.必要不充分条件线面垂直与面面垂直专题复习【知识点】一.线面垂直(1) 直线与平面垂直的定义:如果直线l 和平面a 的 __________________ 一条直线都垂直,我们就说直线 I 与平面a 垂直,记作 _____________ .重要性质: ____________________________________________________________________________(2) 直线与平面垂直的判定方法:①判定定理:一条直线与一个平面的两条 ___________________ 都垂直,那么这条直线就垂直于这 个平面.用符号表示为:②常用结论:如果两条平行直线中的一条垂直于一个平面, 面.用符号可表示为:(3)直线与平面垂直的性质:① 由直线和平面垂直的定义知:直线与平面垂直,则直线垂直于平面的 ________ 直线.② 性质定理:垂直于同一平面的两条直线平行.用符号可表示为: 二、面面垂直(1) 平面与平面垂直的定义:两平面相交,如果它们所成的二面角是 _____________________ ,就说这两个平面互相垂直.(2) 平面与平面垂直的判定定理:如果一个平面经过另一个平面的一条 _____________________ ,那么这两个平面互相垂直.简述为 "线面垂直,则面面垂直”,用符号可表示为:(3)平面与平面垂直的性质:如果两个平面互相垂直,那么在一个平面垂直于它们交线的直线垂直于另一个平面. 用符号可表示为:【题型总结】 题型一小题:判断正误1. “直线I 垂直于平面 A.充分不必要条件C.充要条件D.既不充分又不必要条件2. 已知如图,六棱锥 P — ABCDE 的底面是正六边形, 下列结论不正确的是( ).A.CD// 平面 PAFB. DF 丄平面 PAFC. CF//平面 PAB 2.设m n, I 是三条不同的直线,,,是三个不同的平面,判断命题正误:理科数学复习专题立体几何①m,m ,则//⑥m n, m// ,则n②m,// ,则m⑦m n,n 1,则m//l③m,m//n,则n⑧, ,则〃④m,n ,则m//n⑨m n,n//I,则m 1⑤m,m n,则n//⑩,//,则题型「二证明线面垂直P归纳:①证明异面直线垂直的常用方法:_________________________________________②找垂线(线线垂直)的方法一:______________________________________________ 2.四棱锥P ABCD中,底面ABCD的边长PD PB 4, BAD 600, E 为PA 中点•1如图,四棱锥P-ABCD中,底面ABCD为平行四边形,/ DAB = 60° AB= 2AD, PD 丄底面ABCD .(1)证明:BD丄面PAD (2)证明:PA丄BD;求证:BD 平面PAC ;4的菱形,归纳:找垂线(线线垂直)的方法找垂线(线线垂直)的方法三:3、如图,AB是圆0的直径,C是圆0上不同于A, B的一点,PA 平面ABC , E是PC 的中点,AB 3 , PA AC 1.求证:AE PB•Z归纳:找垂线(线线垂直)的方法四:____________________________________4.如图,在三棱锥P ABC中,PA 底面ABC, BCA 900,AP=AC,点D , E分别为棱PB、PC的中点,且BC〃平面ADE求证:DE丄平面PAC ;归纳:_____________________________________________________________________________________ 题型三面面垂直的证明(关键:找线面垂直)1、如图所示,四边形ABCD是菱形,O是AC与BD 的交点,SA 平面ABCD.求证:平面SAC 平面SBD ;2. (2016理数)如图,在以A,B,C,D,E,F为顶点的五面体中面ABEF 为正方形,AF=2FD, AFD 90:,证明:平面ABEF 平面EFDC ;题型四面面垂直的性质(注意:交线)1、如图所示,平面EAD 平面ABCD , ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点, 求证:EG 平面ABCD ;2、如图,平行四边形ABCD中,CD 1, BCD 600, BD CD,正方形ADEF,且面ADEF 面ABCD •求证:BD 平面ECD ;综合运用如图所示,PA丄矩形ABCD所在平面,M、N分别是AB、PC的中点.(1) 求证:MN //平面PAD.(2) 求证:MN丄CD.⑶若/ PDA = 45 °求证:面BMN丄平面PCD.【练习】1.设M表示平面,a、b表示直线,给出下列四个命题:金a〃b a M a M a//M① b M ②a//b ③b/ M ④b± Ma Mb M a b a b其中正确的命题是( )A.①②B.①②③C.②③④D.①②④2.给出以下四个命题:CD如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。

立体几何知识点总结一、平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:a)A∈l—点A在直线l上;A∉α—点A不在平面α内;b)l⊂α—直线l在平面α内;c)a⊄α—直线a不在平面α内;d)l∩m=A—直线l与直线m相交于A点;e)α∩l=A—平面α与直线l交于A点;f)α∩β=l—平面α与平面β相交于直线l.二、平面的基本性质公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.公理3 经过不在同一直线上的三个点,有且只有一个平面.根据上面的公理,可得以下推论.推论1 经过一条直线和这条直线外一点,有且只有一个平面.推论2 经过两条相交直线,有且只有一个平面.推论3 经过两条平行直线,有且只有一个平面.公理4 平行于同一条直线的两条直线互相平行三、证题方法四、空间线面的位置关系共面平行—没有公共点(1)直线与直线相交—有且只有一个公共点异面(既不平行,又不相交)直线在平面内—有无数个公共点(2)直线和平面直线不在平面内平行—没有公共点(直线在平面外) 相交—有且只有一公共点(3)平面与平面相交—有一条公共直线(无数个公共点)平行—没有公共点五、异面直线的判定证明两条直线是异面直线通常采用反证法.有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.六、线面平行与垂直的判定(1)两直线平行的判定①定义:在同一个平面内,且没有公共点的两条直线平行.②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,a ∥β④垂直于同一平面的两直线平行,即若a⊥α,b⊥α,则a∥b(线面垂直的性质定理)⑤两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b(面面平行的性质公理)⑥中位线定理、平行四边形、比例线段……,α∩β=b,则a∥b.(线面平行的判定定理)③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.(公理4)(2)两直线垂直的判定①定义:若两直线成90°角,则这两直线互相垂直.②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c③一条直线垂直于一个平面,则垂直于这个平面内的任意一条直线.即若a⊥α,b⊂α,a⊥b.④三垂线定理和逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.⑤如果一条直线与一个平面平行,那么这条直线与这个平面的垂线垂直.即若a∥α,b⊥α,则a⊥b.(3)直线与平面平行的判定①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.即若a⊄α,b⊂α,a∥b,则a∥α.(线面平行的判定定理)③两个平面平行,其中一个平面内的直线平行于另一个平面,即若α∥β,l⊂α,则l∥β.(4)直线与平面垂直的判定①定义:若一条直线和一个平面内的任何一条直线垂直,则这条直线和这个平面垂直.②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.即若m⊂α,n⊂α,m∩n=B,l⊥m,l⊥n,则l⊥α.(线面垂直判定定理)③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.④一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面,即若α∥β,l⊥β,则l⊥α.⑤如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即若α⊥β,a∩β=α,l⊂β,l⊥a,则l⊥α.(面面垂直的性质定理)(5)两平面平行的判定①定义:如果两个平面没有公共点,那么这两个平面平行,即无公共点⇔α∥β.②如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,即若a,b⊂α,a∩b=P,a∥β,b ∥β,则α∥β.(面面平行判定定理)推论:一个平面内的两条直线分别平行于另一平面内的两条相交直线,则这两个平面平行,即若a,b⊂α,c,d⊂β,a∩b=P,a∥c,b∥d,则α∥β.(6)两平面垂直的判定①定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直,即二面角α-a-β=90°⇔α⊥β.②如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直,即若l⊥β,l⊂α,则α⊥β.(面面垂直判定定理)七、空间中的各种角等角定理及其推论定理若一个角的两边和另一个角的两边分别平行,并且方向相同,则这两个角相等.推论若两条相交直线和另两条相交直线分别平行,则这两组直线所成的锐角(或直角)相等.1、异面直线所成的角(1)定义:a 、b 是两条异面直线,经过空间任意一点O ,分别引直线a ′∥a,b ′∥b,则a ′和b ′所成的锐角(或直角)叫做异面直线a 和b 所成的角.(2)取值范围:0°<θ≤90°. (3)求解方法①根据定义,通过平移,找到异面直线所成的角θ; ②解含有θ的三角形,求出角θ的大小. 2、直线和平面所成的角——斜线和射影所成的锐角 (1)取值范围0°≤θ≤90° (2)求解方法①作出斜线在平面上的射影,找到斜线与平面所成的角θ. ②解含θ的三角形,求出其大小. 3、二面角及二面角的平面角(1)半平面 直线把平面分成两个部分,每一部分都叫做半平面.(2)二面角 条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个平面叫做二面角的面,即二面角由半平面一棱一半平面组成.若两个平面相交,则以两个平面的交线为棱形成四个二面角.二面角的大小用它的平面角来度量,通常认为二面角的平面角θ的取值范围是0°<θ≤180° (3)二面角的平面角①以二面角棱上任意一点为端点,分别在两个面内作垂直于棱的射线,这两条射线所组成的角叫做二面角的平面角.如图,∠PCD 是二面角α-AB-β的平面角.平面角∠PCD 的大小与顶点C 在棱AB 上的位置无关. ②二面角的平面角具有下列性质:(i)二面角的棱垂直于它的平面角所在的平面,即AB ⊥平面PCD.(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.(iii)二面角的平面角所在的平面与二面角的两个面都垂直,即平面PCD ⊥α,平面PCD ⊥β. ③找(或作)二面角的平面角的主要方法.(i)定义法 (ii)垂面法 (iii)三垂线法 (Ⅳ)根据特殊图形的性质 (4)求二面角大小的常见方法先找(或作)出二面角的平面角θ,再通过解三角形求得θ的值. 八.空间的各种距离 点到平面的距离(1)定义 面外一点引一个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离. (2)求点面距离常用的方法: 1)直接利用定义求①找到(或作出)表示距离的线段;②抓住线段(所求距离)所在三角形解之.2)体积法其步骤是:①在平面内选取适当三点,和已知点构成三棱锥;②求出此三棱锥的体积V 和所取三点构成三角形的面积S ;③由V=31S ·h ,求出h 即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.直线和平面的距离、平行平面的距离将线面、面面距离转化为点面距离,然后运用解三角形或体积法求解之.空间直线和平面(一)知识结构(二)平行与垂直关系的论证1、线线、线面、面面平行关系的转化:线线∥线面∥面面∥公理4 (a//b,b//ca//c)线面平行判定αβαγβγ//,//==⇒⎫⎬⎭a ba b面面平行判定1a ba ba//,//⊄⊂⇒⎫⎬⎭ααα面面平行性质a ba b Aa b⊂⊂=⇒⎫⎬⎪⎭⎪ααββαβ,//,////线面平行性质aaba b////αβαβ⊂=⇒⎫⎬⎪⎭⎪面面平行性质1αβαβ////aa⊂⇒⎫⎬⎭面面平行性质αγβγαβ//////⎫⎬⎭⇒A bα aβabα2. 线线、线面、面面垂直关系的转化:a a OA a PO a PO a AO⊂⊥⇒⊥⊥⇒⊥αα在内射影则面面垂直判定线面垂直定义l a l a⊥⊂⇒⊥⎫⎬⎭αα面面垂直性质,推论2αβαββα⊥=⊂⊥⇒⊥⎫⎬⎪⎭⎪ b a a b a , αγβγαβγ⊥⊥=⇒⊥⎫⎬⎪⎭⎪ a a面面垂直定义αβαβαβ =--⇒⊥⎫⎬⎭l l ,且二面角成直二面角3. 平行与垂直关系的转化:面面∥面面平行判定2 线面垂直性质2面面平行性质3a b a b //⊥⇒⊥⎫⎬⎭ααa b a b ⊥⊥⇒⎫⎬⎭αα//a a ⊥⊥⇒⎫⎬⎭αβαβ//αβαβ//a a ⊥⊥⎫⎬⎭a4. 应用以上“转化”的基本思路——“由求证想判定,由已知想性质。

垂直的证明【方法总结】1、证明线面垂直的方法:①利用线面垂直定义:如果一条直线垂直于平面内任一条直线,则这条直线垂直于该平面;②用线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,则这条直线与平面垂直;③用线面垂直性质:两条平行线中的一条垂直于一个平面,则另一条也必垂直于这个平面.2、证明线线(或线面)垂直有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.3、证明面面垂直一般要先找到两个面的交线,然后再在两个面内找能与交线垂直的直线,最后通过证明线面垂直证明面面垂直。
【分类练习】考向一线面垂直例1、在四棱锥P ABCD -中,PA ⊥底面ABCD ,//AB CD ,AB BC ⊥,1AB BC ==,2DC =,点E 在PB 上求证:CA ⊥平面PAD ;【答案】(1)证明见解析;(2)2.【解析】(1)过A 作AF ⊥DC 于F ,则CF =DF =AF ,所以∠DAC =90°,即AC ⊥DA ,又PA ⊥底面ABCD ,AC ⊂面ABCD ,所以AC ⊥PA ,因为PA 、AD ⊂面PAD ,且PA ∩AD =A ,所以AC ⊥平面PAD .例2、如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;解析:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .例3、如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点求证:AC ⊥平面BEF ;【解析】(1)在三棱柱111ABC A B C -中,∵1CC ⊥平面ABC ,∴四边形11A ACC 为矩形.又E ,F 分别为AC ,11A C 的中点,∴AC ⊥EF .∵AB BC =.∴AC ⊥BE ,∴AC ⊥平面BEF .例4、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,CD ⊥AD ,BC ∥AD ,12BC CD AD ==.(Ⅰ)求证:BD ⊥平面PAB ;【解析】因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以BD ⊥PA .所以222AD AB BD =+,所以BD AB ⊥.因为PA AB A = ,所以BD ⊥平面PAB .【巩固练习】1、如图,在三棱柱ABC-A 1B 1C 1中,AB=AC,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.证明:A 1D⊥平面A 1BC;【答案】见解析【解析】证明:设E 为BC 的中点,连接A 1E,AE.由题意得A 1E⊥平面ABC,所以A 1E⊥AE.因为AB=AC,所以AE⊥BC.故AE⊥平面A 1BC.连接DE,由D,E 分别为B 1C 1,BC 的中点,得DE∥B 1B 且DE=B 1B,从而DE∥A 1A 且DE =A 1A,所以AA 1DE 为平行四边形.于是A 1D∥AE.因为AE⊥平面A 1BC,所以A 1D⊥平面A 1BC.2.(2019·上海格致中学高三月考)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,作EF PB ⊥交PB 于点F .(1)证明:PA ∥平面EDB ;(2)证明:PB ⊥平面EFD .【答案】(1)详见解析;(2)详见解析.【解析】(1)设AC 与BD 相交于O ,连接OE ,由于O 是AC 中点,E 是PC 中点,所所以PA ∥平面EDB .(2)由于PD ⊥底面ABCD ,所以PD BC ⊥,由于,BC CD PD CD D ⊥⋂=,所以BC ⊥平面PCD ,所以BC DE ⊥.由于DP DC =且E 是PC 中点,所以DE PC ⊥,而PC BC C ⋂=,所以DE ⊥平面PBC ,所以DE PB ⊥.依题意EF PB ⊥,DE EF E = ,所以PB ⊥平面EFD .3.(2019·江苏高三月考)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AC ,BD 相交于点O ,OP OC =,E 为PC 的中点,PA PD ⊥.(1)求证://PA 平面BDE ;(2)求证:PA ⊥平面PCD【答案】(1)详见解析(2)详见解析【解析】(1)连结OE .因为四边形ABCD 是平行四边形,AC ,BD 相交于点O ,所以O 为AC 的中点.因为E 为PC 的中点,所以//OE PA .因为OE ⊂平面BDE ,PA ⊄平面BDE ,所以//PA 平面BDE .(2)因为OP OC =,E 为PC 的中点,所以OE PC ⊥.由(1)知,//OE PA ,所以PA PC ⊥.因为PA PD ⊥,PC ,PD ⊂平面PCD ,PC PD P ⋂=,所以PA ⊥平面PCD .考向二面面垂直例1、如图,在四棱锥P ABCD -中,已知底面ABCD 为矩形,且AB =,1BC =,E ,F 分别是AB ,PC 的中点,PA DE ⊥.(1)求证://EF 平面PAD ;(2)求证:平面PAC ⊥平面PDE .【答案】(1)详见解析(2)详见解析【解析】证明:(1)取PD 中点G ,连AG ,FG ,F ,G 分别是PC ,PD 的中点又E 为AB 中点//AE FG ∴,AE FG=四边形AEFG 为平行四边形//EF AG ∴,又EF ⊄平面PAD ,AG ⊂平面PAD//EF ∴平面PAD(2)设AC DE H= 由AEH CDH ∆∆ 及E 为AB 中点又BAD ∠为公共角GAE BAC∴∆∆ 90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥,PA AC A= DE ⊥平面PAC ,又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图,边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直,M 是 CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为 CD上异于C ,D 的点,且DC 为直径,所以DM ⊥CM .又BC CM =C ,所以DM ⊥平面BMC .而DM ⊂平面AMD ,故平面AMD ⊥平面BMC .例3、如图,在梯形ABCD 中,AB ∥CD ,AD=DC=CB=a ,∠ABC=3π,平面ACFE ⊥平面ABCD ,四边形ACFE 是矩形,AE=AD ,点M 在线段EF 上。

高中数学知识点:证明线面垂直的方法
直线与平面垂直定义:如果一条直线与平面内任意一条直线都垂直,那么这条直线与这个平面垂直。
是将“三维”问题转化为“二维”解决是一种重要的立体几何数学思想方法。
一、证明线面垂直的方法
1、线面垂直的判定定理
直线与平面内的两相交直线垂直
2、面面垂直的性质
若两平面垂直则在一面内垂直于交线的直线必垂直于另一平面
3、线面垂直的性质
两平行线中有一条与平面垂直,则另一条也与平面垂直
4、面面平行的性质
一线垂直于二平行平面之一,则必垂直于另一平面
5、定义法
直线与平面内任一直线垂直
二、线面垂直证法
由性质定理2可知,过空间内一点(无论是否在已知平面上),有且只有一条直线与平面垂直。
下面就讨论如何作出这条唯一的直线。
点在平面外
设点P是平面α外的任意一点,求作一条直线PQ使PQ⊥α。
作法:
①在α内任意作一条直线l,并过P作PA⊥l,垂足为A。
此时,若PA⊥α,则所需PQ已作出;若不是这样,
②在α内过A作m⊥l。
③过P作PQ⊥m,垂足为Q,则PQ是所求直线。
证明:
由作法可知,l⊥PA,l⊥QA
∵PA∩QA=A
∴l⊥平面PQA
∴PQ⊥l
又∵PQ⊥m,且m∩l=A,m?α,l?α
∴PQ⊥α
点在平面内
设点P是平面α内的任意一点,求作一条直线PQ使PQ⊥α。
作法:
①过平面外一点A作AB⊥α,作法见上。
②过P作PQ∥AB,PQ是所求直线。
证明:
由性质定理3可知,若作出了AB⊥α,PQ∥AB,那么PQ⊥α。


专题二:立体几何—--线面垂直、面面垂直一、知识点(1)线面垂直性质定理(2)线面垂直判定定理(3)面面垂直性质定理(2)面面垂直判定定理线面垂直的证明中的找线技巧通过计算,运用勾股定理寻求线线垂直1.如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1A O ⊥平面MBD .证明:连结MO ,1A M ,∵DB ⊥1A A ,DB ⊥AC ,1A AAC A =,∴DB ⊥平面11A ACC ,而1AO ⊂平面11A ACC ∴DB ⊥1A O . 设正方体棱长为a ,则22132A O a =,2234MO a =. 在Rt △11A C M 中,22194A M a =.∵22211A O MO A M +=,∴1AO OM ⊥. ∵OM ∩DB =O ,∴ 1A O ⊥平面MBD . 评注:在证明垂直关系时,有时可以利用棱长、角度大小等数据,通过计算来证明.利用面面垂直寻求线面垂直2.如图2,P 是△ABC 所在平面外的一点,且P A ⊥平面ABC ,平面P AC ⊥平面PBC .求证:BC ⊥平面P AC .证明:在平面P AC 内作AD ⊥PC 交PC 于D .因为平面P AC ⊥平面PBC ,且两平面交于PC ,AD ⊂平面P AC ,且AD ⊥PC , 由面面垂直的性质,得AD ⊥平面PBC . 又∵BC ⊂平面PBC ,∴AD ⊥BC .∵P A ⊥平面ABC ,BC ⊂平面ABC ,∴P A ⊥BC . ∵AD ∩P A =A ,∴BC ⊥平面P AC .评注:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直⇒线面垂直⇒线线垂直.一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面是判定定理,而从后面推出前面是性质定理.同学们应当学会灵活应用这些定理证明问题.下面举例说明.3.如图1所示,ABCD 为正方形,SA ⊥平面ABCD ,过A 且垂直于SC 的平面分别交SB SC SD ,,于E F G ,,.求证:AE SB ⊥,AG SD ⊥.证明:∵SA ⊥平面ABCD , ∴SA BC ⊥.∵AB BC ⊥,∴BC ⊥平面SAB .又∵AE ⊂平面SAB ,∴BC AE ⊥.∵SC ⊥平面AEFG ,∴SC AE ⊥.∴AE ⊥平面SBC .∴AE SB ⊥.同理可证AG SD ⊥. 评注:本题欲证线线垂直,可转化为证线面垂直,在线线垂直与线面垂直的转化中,平面起到了关键作用,同学们应多注意考虑线和线所在平面的特征,从而顺利实现证明所需要的转化.4.如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD . 证明:取AB 的中点F,连结CF ,DF . ∵AC BC =,∴CF AB ⊥.∵AD BD =,∴DF AB ⊥.又CF DF F =,∴AB ⊥平面CDF . ∵CD ⊂平面CDF ,∴CD AB ⊥. 又CD BE ⊥,BE AB B =,∴CD ⊥平面ABE ,CD AH ⊥.∵AH CD ⊥,AH BE ⊥,CD BE E =,∴ AH ⊥平面BCD .评注:本题在运用判定定理证明线面垂直时,将问题转化为证明线线垂直;而证明线线垂直时,又转化为证明线面垂直.如此反复,直到证得结论.5.如图3,AB是圆O的直径,C是圆周上一点,PA⊥平面ABC.若AE⊥PC,E为垂足,F是PB上任意一点,求证:平面AEF⊥平面PBC.⊥.证明:∵AB是圆O的直径,∴AC BC∵PA⊥平面ABC,BC⊂平面ABC,⊥.∴BC⊥平面APC.∴PA BC∵BC⊂平面PBC,∴平面APC⊥平面PBC.∵AE⊥PC,平面APC∩平面PBC=PC,∴AE⊥平面PBC.∵AE⊂平面AEF,∴平面AEF⊥平面PBC.评注:证明两个平面垂直时,一般可先从现有的直线中寻找平面的垂线,即证线面垂直,而证线面垂直则需从已知条件出发寻找线线垂直的关系.10.如图, 在空间四边形SABC中, SA⊥平面ABC,∠ABC = 90︒,AN⊥SB于N, AM⊥SC于M.求证:①AN⊥BC;②SC⊥平面ANM分析:①要证AN⊥BC,转证,BC⊥平面SAB。

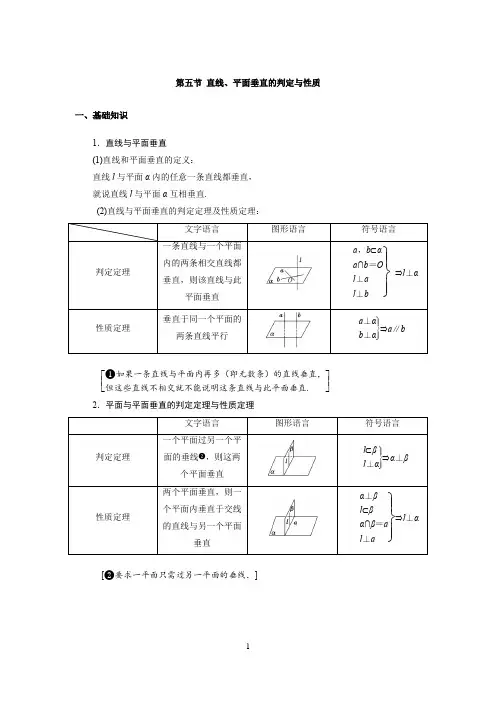
第五节 直线、平面垂直的判定与性质一、基础知识1.直线与平面垂直 (1)直线和平面垂直的定义:直线l 与平面α内的任意一条直线都垂直, 就说直线l 与平面α互相垂直.(2)直线与平面垂直的判定定理及性质定理:文字语言 图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a ,b ⊂αa ∩b =Ol ⊥a l ⊥b⇒l ⊥α 性质定理 垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b⎣⎢⎡⎦⎥⎤❶如果一条直线与平面内再多(即无数条)的直线垂直,但这些直线不相交就不能说明这条直线与此平面垂直. 2.平面与平面垂直的判定定理与性质定理文字语言 图形语言符号语言判定定理一个平面过另一个平面的垂线❷,则这两个平面垂直⎭⎪⎬⎪⎫l ⊂βl ⊥α⇒α⊥β 性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直⎭⎪⎬⎪⎫α⊥βl ⊂βα∩β=a l ⊥a ⇒l ⊥α[❷要求一平面只需过另一平面的垂线.]二、常用结论直线与平面垂直的五个结论(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线.(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直.(5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.考点一直线与平面垂直的判定与性质[典例]如图,在四棱锥PABCD中,P A⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC的中点.求证:(1)CD⊥AE;(2)PD⊥平面ABE.[证明](1)在四棱锥PABCD中,∵P A⊥底面ABCD,CD⊂底面ABCD,∴P A⊥CD,又∵AC⊥CD,且P A∩AC=A,∴CD⊥平面P AC.∵AE⊂平面P AC,∴CD⊥AE.(2)由P A=AB=BC,∠ABC=60°,可得AC=P A.∵E是PC的中点,∴AE⊥PC.由(1)知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.∵PD⊂平面PCD,∴AE⊥PD.∵P A⊥底面ABCD,AB⊂底面ABCD,∴P A⊥AB.又∵AB⊥AD,且P A∩AD=A,∴AB⊥平面P AD,∵PD⊂平面P AD,∴AB⊥PD.又∵AB∩AE=A,∴PD⊥平面ABE.[解题技法]证明线面垂直的4种方法(1)线面垂直的判定定理:l ⊥a ,l ⊥b ,a ⊂α,b ⊂α,a ∩b =P ⇒l ⊥α. (2)面面垂直的性质定理:α⊥β,α∩β=l ,a ⊂α,a ⊥l ⇒a ⊥β. (3)性质:①a ∥b ,b ⊥α⇒a ⊥α,②α∥β,a ⊥β⇒a ⊥α. (4)α⊥γ,β⊥γ,α∩β=l ⇒l ⊥γ.(客观题可用) [口诀归纳]线面垂直的关键,定义来证最常见, 判定定理也常用,它的意义要记清. 平面之内两直线,两线相交于一点, 面外还有一直线,垂直两线是条件. [题组训练]1.(2019·安徽知名示范高中联考)如图,在直三棱柱ABC A 1B 1C 1中,AB =BC =BB 1,AB 1∩A 1B =E ,D 为AC 上的点,B 1C ∥平面A 1BD .(1)求证:BD ⊥平面A 1ACC 1;(2)若AB =1,且AC ·AD =1,求三棱锥A BCB 1的体积. 解: (1)证明:如图,连接ED ,∵平面AB 1C ∩平面A 1BD =ED ,B 1C ∥平面A 1BD , ∴B 1C ∥ED , ∵E 为AB 1的中点, ∴D 为AC 的中点, ∵AB =BC ,∴BD ⊥AC .∵A 1A ⊥平面ABC ,BD ⊂平面ABC ,∴A 1A ⊥BD . 又∵A 1A ,AC 是平面A 1ACC 1内的两条相交直线, ∴BD ⊥平面A 1ACC 1.(2)由AB =1,得BC =BB 1=1,由(1)知AD =12AC ,又AC ·AD =1,∴AC 2=2,∴AC 2=2=AB 2+BC 2,∴AB ⊥BC , ∴S △ABC =12AB ·BC =12,∴V A BCB 1=V B 1ABC =13S △ABC ·BB 1=13×12×1=16.2.如图,S是Rt△ABC所在平面外一点,且SA=SB=SC,D为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.证明:(1)如图所示,取AB的中点E,连接SE,DE,在Rt△ABC中,D,E分别为AC,AB的中点.∴DE∥BC,∴DE⊥AB,∵SA=SB,∴SE⊥AB.又SE∩DE=E,∴AB⊥平面SDE.又SD⊂平面SDE,∴AB⊥SD.在△SAC中,∵SA=SC,D为AC的中点,∴SD⊥AC.又AC∩AB=A,∴SD⊥平面ABC.(2)∵AB=BC,∴BD⊥AC,由(1)可知,SD⊥平面ABC,又BD⊂平面ABC,∴SD⊥BD,又SD∩AC=D,∴BD⊥平面SAC.考点二面面垂直的判定与性质[典例](2018·江苏高考)在平行六面体ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.[证明](1)在平行六面体ABCDA1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCDA1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.[解题技法] 证明面面垂直的2种方法 定义法利用面面垂直的定义,即判定两平面所成的二面角为直二面角,将证明面面垂直问题转化为证明平面角为直角的问题定理法 利用面面垂直的判定定理,即证明其中一个平面经过另一个平面的一条垂线,把问题转化成证明线线垂直加以解决[题组训练]1.(2019·武汉调研)如图,三棱锥P ABC 中,底面ABC 是边长为2的正三角形,P A ⊥PC ,PB =2.求证:平面P AC ⊥平面ABC .证明:取AC 的中点O ,连接BO ,PO . 因为△ABC 是边长为2的正三角形, 所以BO ⊥AC ,BO = 3.因为P A ⊥PC ,所以PO =12AC =1.因为PB =2,所以OP 2+OB 2=PB 2,所以PO ⊥OB . 因为AC ∩OP =O , 所以BO ⊥平面P AC . 又OB ⊂平面ABC , 所以平面P AC ⊥平面ABC .2.(2018·安徽淮北一中模拟)如图,四棱锥P ABCD 的底面是矩形,P A ⊥平面ABCD ,E ,F 分别是AB ,PD 的中点,且P A =AD .求证:(1)AF ∥平面PEC ; (2)平面PEC ⊥平面PCD .证明:(1)取PC 的中点G ,连接FG ,EG , ∵F 为PD 的中点,G 为PC 的中点, ∴FG 为△CDP 的中位线, ∴FG ∥CD ,FG =12CD .∵四边形ABCD 为矩形,E 为AB 的中点, ∴AE ∥CD ,AE =12CD .∴FG =AE ,FG ∥AE , ∴四边形AEGF 是平行四边形,∴AF ∥EG ,又EG ⊂平面PEC ,AF ⊄平面PEC ,∴AF∥平面PEC.(2)∵P A=AD,F为PD中点,∴AF⊥PD,∵P A⊥平面ABCD,CD⊂平面ABCD,∴P A⊥CD,又∵CD⊥AD,AD∩P A=A,∴CD⊥平面P AD,∵AF⊂平面P AD,∴CD⊥AF.又PD∩CD=D,∴AF⊥平面PCD.由(1)知EG∥AF,∴EG⊥平面PCD,又EG⊂平面PEC,∴平面PEC⊥平面PCD.[课时跟踪检测]A级1.设a,b是两条不同的直线,α,β是两个不同的平面,则能得出a⊥b的是() A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β解析:选C对于C项,由α∥β,a⊂α可得a∥β,又b⊥β,得a⊥b,故选C.2.(2019·湘东五校联考)已知直线m,l,平面α,β,且m⊥α,l⊂β,给出下列命题:①若α∥β,则m⊥l;②若α⊥β,则m∥l;③若m⊥l,则α⊥β;④若m∥l,则α⊥β.其中正确的命题是()A.①④B.③④C.①②D.①③解析:选A对于①,若α∥β,m⊥α,l⊂β,则m⊥l,故①正确,排除B.对于④,若m∥l,m⊥α,则l⊥α,又l⊂β,所以α⊥β.故④正确.故选A.3.已知P A垂直于以AB为直径的圆所在的平面,C为圆上异于A,B两点的任一点,则下列关系不正确的是()A.P A⊥BC B.BC⊥平面P ACC.AC⊥PB D.PC⊥BC解析:选C由P A⊥平面ACB⇒P A⊥BC,故A不符合题意;由BC⊥P A,BC⊥AC,P A∩AC=A,可得BC⊥平面P AC,所以BC⊥PC,故B、D不符合题意;AC⊥PB显然不成立,故C符合题意.4.如图,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么点D在平面ABC内的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部解析:选A因为AB⊥AC,BD⊥AC,AB∩BD=B,所以AC⊥平央ABD,又AC⊂平面ABC,所以平面ABC⊥平面ABD,所以点D在平面ABC内的射影H必在直线AB上.5.如图,在正四面体PABC中,D,E,F分别是AB,BC,CA的中点,则下面四个结论不成立的是()A.BC∥平面PDFB.DF⊥平面P AEC.平面PDF⊥平面P AED.平面PDE⊥平面ABC解析:选D因为BC∥DF,DF⊂平面PDF,BC⊄平面PDF,所以BC∥平面PDF,故选项A正确.在正四面体中,AE⊥BC,PE⊥BC,AE∩PE=E,所以BC⊥平面P AE,又DF∥BC,则DF⊥平面P AE,从而平面PDF⊥平面P AE.因此选项B、C均正确.6.如图,已知∠BAC=90°,PC⊥平面ABC,则在△ABC,△P AC的边所在的直线中,与PC垂直的直线有________个;与AP垂直的直线有________个.解析:∵PC⊥平面ABC,∴PC垂直于直线AB,BC,AC.∵AB⊥AC,AB⊥PC,AC∩PC=C,∴AB⊥平面P AC,又∵AP⊂平面P AC,∴AB⊥AP,与AP垂直的直线是AB.答案:317.设α和β为不重合的两个平面,给出下列命题:①若α内的两条相交直线分别平行于β内的两条直线,则α∥β;②若α外的一条直线l与α内的一条直线平行,则l∥α;③设α∩β=l,若α内有一条直线垂直于l,则α⊥β;④直线l⊥α的充要条件是l与α内的两条直线垂直.其中所有的真命题的序号是________.解析:①正确;②正确;满足③的α与β不一定垂直,所以③错误;直线l⊥α的充要条件是l与α内的两条相交直线垂直,所以④错误.故所有的真命题的序号是①②.答案:①②8.在直三棱柱ABCA1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确命题的序号是________.解析:如图所示,因为AA1∥平面α,平面α∩平面AA1B1B=EH,所以AA1∥EH.同理AA1∥GF,所以EH∥GF,又ABCA1B1C1是直三棱柱,易知EH=GF=AA1,所以四边形EFGH是平行四边形,故①正确;若平面α∥平面BB1C1C,由平面α∩平面A1B1C1=GH,平面BCC1B1∩平面A1B1C1=B1C1,知GH∥B1C1,而GH∥B1C1不一定成立,故②错误;由AA1⊥平面BCFE,结合AA1∥EH知EH⊥平面BCFE,又EH⊂平面α,所以平面α⊥平面BCFE,故③正确.答案:①③9.(2019·太原模拟)如图,在四棱锥PABCD中,底面ABCD是菱形,∠BAD=60°,P A=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.(1)求证:AD⊥平面PNB;(2)若平面P AD⊥平面ABCD,求三棱锥PNBM的体积.解:(1)证明:连接BD.∵P A=PD,N为AD的中点,∴PN⊥AD.又底面ABCD是菱形,∠BAD=60°,∴△ABD为等边三角形,∴BN⊥AD,又PN∩BN=N,∴AD⊥平面PNB.(2)∵P A=PD=AD=2,∴PN=NB= 3.又平面P AD⊥平面ABCD,平面P AD∩平面ABCD=AD,PN⊥AD,∴PN⊥平面ABCD,∴PN⊥NB,∴S△PNB=12×3×3=32.∵AD⊥平面PNB,AD∥BC,∴BC ⊥平面PNB .又PM =2MC , ∴V P NBM =V M PNB =23V C PNB =23×13×32×2=23.10.如图,在直三棱柱ABC A 1B 1C 1中,D ,E 分别为AB ,BC 的中点,点F 在侧棱B 1B 上,且B 1D ⊥A 1F ,A 1C 1⊥A 1B 1.求证:(1)直线DE ∥平面A 1C 1F ; (2)平面B 1DE ⊥平面A 1C 1F .证明:(1)在直三棱柱ABC A 1B 1C 1中,AC ∥A 1C 1, 在△ABC 中,因为D ,E 分别为AB ,BC 的中点. 所以DE ∥AC ,于是DE ∥A 1C 1,又因为DE ⊄平面A 1C 1F ,A 1C 1⊂平面A 1C 1F , 所以直线DE ∥平面A 1C 1F .(2)在直三棱柱ABC A 1B 1C 1中,AA 1⊥平面A 1B 1C 1, 因为A 1C 1⊂平面A 1B 1C 1,所以AA 1⊥A 1C 1,又因为A 1C 1⊥A 1B 1,A 1B 1∩AA 1=A 1,AA 1⊂平面ABB 1A 1,A 1B 1⊂平面ABB 1A 1, 所以A 1C 1⊥平面ABB 1A 1, 因为B 1D ⊂平面ABB 1A 1, 所以A 1C 1⊥B 1D ,又因为B 1D ⊥A 1F ,A 1C 1∩A 1F =A 1,A 1C 1⊂平面A 1C 1F ,A 1F ⊂平面A 1C 1F , 所以B 1D ⊥平面A 1C 1F , 因为直线B 1D ⊂平面B 1DE , 所以平面B 1DE ⊥平面A 1C 1F .B 级1.(2018·全国卷Ⅱ)如图,在三棱锥P ABC 中,AB =BC =22,P A =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC =2MB ,求点C 到平面POM 的距离. 解:(1)证明:因为P A =PC =AC =4,O 为AC 的中点, 所以PO ⊥AC ,且PO =2 3. 连接OB , 因为AB =BC =22AC , 所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2.所以PO 2+OB 2=PB 2,所以PO ⊥OB . 又因为AC ∩OB =O ,所以PO ⊥平面ABC . (2)作CH ⊥OM ,垂足为H , 又由(1)可得OP ⊥CH , 所以CH ⊥平面POM .故CH 的长为点C 到平面POM 的距离.由题设可知OC =12AC =2,CM =23BC =423,∠ACB =45°,所以OM =253,CH =OC ·MC ·sin ∠ACB OM =455.所以点C 到平面POM 的距离为455.2.(2019·河南中原名校质量考评)如图,在四棱锥P ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD ,E ,F 分别是CD ,PC 的中点.求证:(1)BE ∥平面P AD ; (2)平面BEF ⊥平面PCD .证明:(1)∵AB ∥CD ,CD =2AB ,E 是CD 的中点, ∴AB ∥DE 且AB =DE , ∴四边形ABED 为平行四边形,∴AD ∥BE ,又BE ⊄平面P AD ,AD ⊂平面P AD , ∴BE ∥平面P AD .(2)∵AB ⊥AD ,∴四边形ABED 为矩形, ∴BE ⊥CD ,AD ⊥CD ,∵平面P AD ⊥底面ABCD ,平面P AD ∩底面ABCD =AD ,P A ⊥AD , ∴P A ⊥底面ABCD , ∴P A ⊥CD ,又P A ∩AD =A , ∴CD ⊥平面P AD ,∴CD ⊥PD , ∵E ,F 分别是CD ,PC 的中点, ∴PD ∥EF ,∴CD ⊥EF ,又EF ∩BE =E , ∴CD ⊥平面BEF ,∵CD ⊂平面PCD ,∴平面BEF ⊥平面PCD .。
立体几何(线面平行、垂直的有关结论)空间中线面平行、垂直关系有关的定理:1、【线面平行的判定】平面外的一条直线和平面内的一条直线平行,则这条直线和这个平面平行。
2、【线面平行的性质】如果一条直线和一个平面平行,经过这条直线的平面和这平面相交,那么这条直线就和两平面的交线平行。
3、如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行。
4、如果两个平面平行,其中一个平面内的任意一条直线平行于另一个平面。
5、如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
6、如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
7、一条直线与两条平行直线中的一条直线相垂直,则这条直线也与另一条直线垂直。
8、与同一条直线都垂直的两条直线相互平行。
()9、与同一个平面都垂直的两条直线相互平行。
10、两条平行直线中的一条直线与一个平面相垂直,则另一条直线也垂直于这个平面。
11、两条相互垂直的直线中的一条平行于一个平面,则另一条直线垂直于这个平面。
()12、两条相互垂直的直线中的一条垂直于以个平面,则另一条直线平行于这个平面。
()13、平面外的两条相互垂直的直线中的一条垂直于一个平面,则另一条直线平行于这个平面。
14、一条直线垂直于两个平行平面中的一个平面,那么该直线也垂直于另一个平面。
15、如果两个平面垂直于同一条直线,那么这两个平面平行。
16、两个平面都与另一个平面相垂直,则这两个平面平行。
()17、一个平面垂直于两平行平面中的一个平面,则此平面也垂直于另一个平面。
18、如果一条直线与平面内的两条相交直线都垂直,则这条直线与这个平面垂直。
19、如果一条直线垂直于一个平面,那么这条直线垂直于该平面内的任意一条直线。
20、如果一个平面过另一个平面的一条垂线,则这两个平面互相垂直。
21、如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
【知识归纳】:【典型例题】:【高考小题】:。
空间点、线、面的位置关系:垂直【背一背基础知识】1.判定两直线垂直,可供选用的定理有:①若a ∥b ,b ⊥c ,则a ⊥c .②若a ⊥α,b ⊂α,则a ⊥b .2.线面垂直的定义:一直线与一平面垂直⇔这条直线与平面内任意直线都垂直;3.线面垂直的判定定理,可选用的定理有:①若a ⊥b ,a ⊥c ,b ,c ⊂α,且b 与c 相交,则a ⊥α.②若a ∥b ,b ⊥α,则a ⊥α.③若α⊥β,α∩β=b ,a ⊂α,a ⊥b ,则a ⊥β.4.判定两平面垂直,可供选用的定理有:若a ⊥α,a ⊂β,则α⊥β.线面垂直1.如图,在三棱台ABC-DEF 中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=F C=1,BC=2,AC=3.(I)求证:BF⊥平面ACFD;2.如图,在四棱锥P ABCD -中,底面ABCD 是︒=∠60DAB 且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD ⊥底面ABCD ,G 为AD 的中点.求证:BG ⊥平面PAD .线线垂直1、如图,在三棱锥P ABC -中,90PAC BAC ∠=∠=︒,PA PB =,点D ,F 分别为BC ,AB 的中点.(1)求证:PF ⊥AD .2、如图,在三棱柱111ABC A B C -中,面11ABB A 为矩形,11,2,AB BC AA D ===为1AA 的中点,BD与1AB 交于点1,O BC AB ⊥.(Ⅰ)证明:1CD AB ⊥3、下图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,//EC PD ,且22PD AD EC ===,N 为线段PB 的中点.(Ⅰ)证明:NE PD ⊥;4、如图所示,在三棱柱111ABC A B C -中,11AA B B 为正方形,11BB C C 为菱形,1160BB C Ð=°,平面11AA B B ^平面11BB C C 。
垂直证明题常见模型及方法证明空间线面垂直需注意以下几点:①由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
②立体几何论证题的解答中,利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
③明确何时应用判定定理,何时应用性质定理,用定理时要先申明条件再由定理得出相应结论。
垂直转化:线线垂直 线面垂直 面面垂直;基础篇类型一:线线垂直证明(共面垂直、异面垂直)(1) 共面垂直:实际上是平面内的两条直线的垂直 (只需要同学们掌握以下几种模型)○1 等腰(等边)三角形中的中线○2 菱形(正方形)的对角线互相垂直 ○3勾股定理中的三角形 ○4 1:1:2 的直角梯形中 ○5 利用相似或全等证明直角。
例:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1A O OE ⊥(2) 异面垂直 (利用线面垂直来证明,高考中的意图) 例1 在正四面体ABCD 中,求证AC BD ⊥变式 1 如图,在四棱锥ABCD P -中,底面A B C D 是矩形,已知60,22,2,2,3=∠====PAB PD PA AD AB .证明:AD PB ⊥;变式2 如图,在边长为2的正方形ABCD 中,点E 是AB 的中点,点F 是BC 的中点,将△AED,△DCF 分别沿,DE DF 折起,使,A C 两点重合于'A . 求证:'A D EF ⊥;BE'ADFG变式3如图,在三棱锥P ABC -中,⊿PAB 是等边三角形,∠P AC =∠PBC =90 º证明:AB ⊥PC类型二:线面垂直证明方法○1 利用线面垂直的判断定理例2:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1A O BDE ⊥平面变式1:在正方体1111ABCD A B C D -中,,求证:11AC BDC ⊥平面 变式2:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90︒.E为BB 1的中点,D 点在AB 上且DE = 3 . 求证:CD ⊥平面A 1ABB 1;变式4 如图,在底面为直角梯形的四棱锥P ABCD -中,AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,AB =6BC =CE变式1, 在四棱锥P ABCD-,底面ABCD是正方形,侧面PAB是等腰三角形,且PAB ABCD⊥面底面,求证:BC PAB⊥面类型3:面面垂直的证明。
立体几何垂直证明题常见模型及方法证明空间线面垂直需注意以下几点:①由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
②立体几何论证题的解答中,利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
③明确何时应用判定定理,何时应用性质定理,用定理时要先申明条件再由定理得出相应结论。
垂直转化:线线垂直 线面垂直 面面垂直;基础篇类型一:线线垂直证明(共面垂直、异面垂直)(1) 共面垂直:实际上是平面内的两条直线的垂直○1 等腰(等边)三角形中的中线 ②菱形(正方形)的对角线互相垂直 ③勾股定理中的三角形 ④1:1:2 的直角梯形中 ⑤ 利用相似或全等证明直角。
例:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1A O OE ⊥(2) 异面垂直 (利用线面垂直来证明,高考中的意图) 例1 在正四面体ABCD 中,求证AC BD ⊥变式 1 如图,在四棱锥ABCD P -中,底面ABCD 是矩形,已知60,22,2,2,3=∠====PAB PD PA AD AB .证明:AD PB ⊥;变式2 如图,在边长为的正方形中,点是的中点,点是的中点,将△AED,△DCF 分别沿折起,使两点重合于.求证:;变式3如图,在三棱锥P ABC -中,⊿PAB 是等边三角形, ∠P AC =∠PBC =90 º证明:AB ⊥PC类型二:线面垂直证明方法○1 利用线面垂直的判断定理例2:在正方体1111ABCD A B C D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1A O BDE ⊥平面变式1:在正方体1111ABCD A B C D -中,,求证:11AC BDC ⊥平面 变式2:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90︒.E 为BB 1的中点,D 点在AB 上且DE = 3 . 求证:CD ⊥平面A 1ABB 1;2ABCD E AB F BC ,DE DF ,A C 'A 'A D EF ⊥变式3:如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2, 2.CA CB CD BD AB AD ======求证:AO ⊥平面BCD ;变式4 如图,在底面为直角梯形的四棱锥P ABCD -中,AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,23AB =,6BC =()1求证:BD ⊥平面PAC○2 利用面面垂直的性质定理 例3:在三棱锥P-ABC 中,PA ABC ⊥底面,PAC PBC ⊥面面,BC PAC ⊥求证:面。