【素材】第一章第五节_证明线面垂直的四种方法

线面垂直判定定理证明几何法线面垂直判定定理是几何学中的重要定理之一。

通过这个定理，我们可以判定一条线段与一个平面是否垂直，从而在解决几何问题时提供了一个有效的方法。

接下来，我将为大家详细介绍线面垂直判定定理的证明过程。

首先，让我们来了解一下线段与平面的垂直关系是什么意思。

当一条线段与一个平面相交，并且线段上的任意一点到平面的距离都垂直于平面时，我们就说这条线段与平面垂直。

这种垂直关系在现实生活中也有很多应用，比如我们常见的直角墙角或者立柱与地面的垂直关系。

现在，让我们开始证明线面垂直判定定理。

假设有一条线段AB与平面P相交，我们需要证明线段AB与平面P垂直。

首先，我们来假设线段AB与平面P不垂直，也即线段AB与平面P 的某一点C处的线段AB与平面P不垂直。

根据平面几何性质，我们可以得知线段AB所在的直线与平面P相交于一点D。

这样，我们就得到了两个不同的直线AB和AD，其中点A是共有的。

接下来，我们利用线面垂直的定义，即线段上的任意一点到平面的距离都垂直于平面。

以线段AB上的另一点E为例，根据垂直关系可知AE与平面P垂直。

那么根据几何性质，直线AE与直线AB在点A处相交，与前面所假设的情况矛盾。

根据这种矛盾，我们可以推知假设的线段AB与平面P的某一点C 处的线段AB与平面P不垂直是错误的。

因此，原假设不成立，即可以得出结论：线段AB与平面P垂直。

根据上述证明过程，我们得到了线面垂直判定定理的证明结果。

这个定理的证明过程简明直观，通过逻辑推理和几何性质的应用，我们可以清晰地理解线段与平面的垂直关系。

线面垂直判定定理在解决几何问题时具有重要的指导意义。

通过这个定理，我们可以根据线段与平面的相交关系，判断它们之间是否垂直。

这为我们解决一些与线段与平面垂直关系相关的问题提供了方向。

总之，线面垂直判定定理的证明过程简单明了，通过逻辑推理和几何性质的应用，我们可以清晰地理解线段与平面的垂直关系。

这个定理具有重要的指导意义，可用于解决与线段与平面垂直关系相关的几何问题。

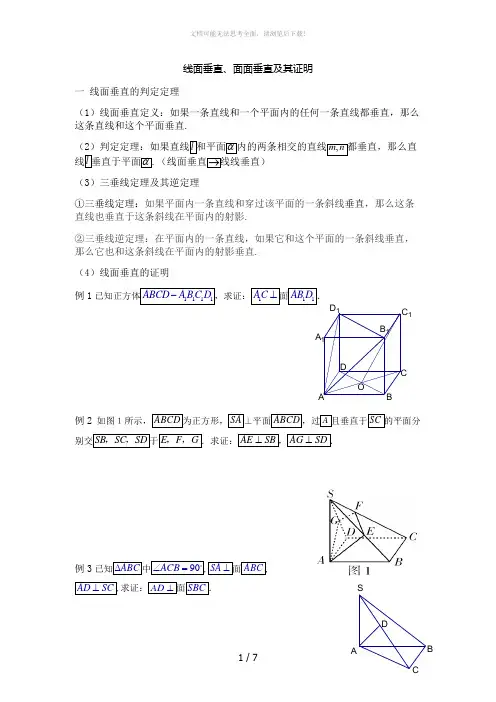
线面垂直、面面垂直及其证明一 线面垂直的判定定理（1）线面垂直定义：如果一条直线和一个平面内的任何一条直线都垂直，那么这条直线和这个平面垂直.（2（3）三垂线定理及其逆定理①三垂线定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影.②三垂线逆定理：在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直. （4）线面垂直的证明例1例2例3SDD 1ODBA C 1B 1A 1C例4在正方体1111ABCD A BC D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD .练习1 在正方体1111ABCD A BC D -中. （1）求证：AC ⊥平面11B D BD .（2）求证：1BD ⊥平面1ACB .练习2在三棱锥A BCD -中，BC AC =，AD BD =，作BE CD ⊥，E 为垂足，作AH BE ⊥于H .求证：AH ⊥平面BCD .在四棱锥P ABCD -中，PA ⊥底面ABCD ，AB AD ⊥，AC CD ⊥，60ABC ︒∠=，PA AB BC ==，E 是PC 的中点.（1）求证：CD AE ⊥. （2）求证：PD ⊥面ABE .二 面面垂直（1条直线叫做二面角的棱，每个半平面叫做二面角的面，若棱为l ，两个面分别为，,αβ二面角记作为l αβ--.（2）二面角的平面角定义：在二面角l αβ--棱l 上取一点O ，在半平面α和β内，从点O 分别作垂直于棱l 的射线,OA OB ，射线组成AOB ∠.则AOB ∠叫做二面角的平面角.二面角的取值范围为[0,180]︒︒.（3）面面垂直定义：若两个平面的二面角为直二面角(平面角是直角的二面角)，则这两个平面互相垂直.（4）面面判定定理：一个平面过另一个平面，则这两个面相互垂直. （5）面面垂直的正面即：面面垂直→线面垂直→线线垂直. 例1如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点.（1）求证：1//AC 平面BDE ； （2）求证：平面1A AC ⊥平面BDE . .例2如图，直三棱柱111C B A ABC -中，侧棱垂直于底面，90ACB ︒∠=121AA BC AC ==，D 是棱1AA 的中点，求证：平面1BDC 平面BDC ．AC B1B 1A D1C练习 如图，过S 引三条长度相等但不共面的线段,,SA SB SC ，且60ASB ASC ︒∠=∠=，90BSC ︒∠=，求证：平面ABC ⊥平面BSC ．三 立体几何高考证明例1（2013江苏）如图，在三棱锥中，平面平面，，，过作，垂足为，点分别是棱的中点．求证：（1）平面平面； （2）．例2（2012江苏）如图，在直三棱柱111ABC A B C -中，1111A B A C =，D E，分别是棱1BC CC ，上的点（点D 不同于点C ），且AD DE F⊥，为11B C 的中点．求证：（1） 平面ADE ⊥平面11BCC B ； （2） 直线1//A F 平面ADE ．ABC S -⊥SAB SBC BC AB ⊥AB AS =A SB AF ⊥F G E ，SC SA ，//EFG ABC SA BC ⊥ABCSGFE例3如图，四棱锥P ABCD -中，底面ABCD 为平行四四边形，60DAB ︒∠=，2AB AD =，PD ⊥底面ABCD .（1）证明：PA BD ⊥（2）设1PD AD ==，求棱锥D PBC -的高.练习1如图，几何体E ABCD -是四棱锥，ABD 为正三角形，,CB CD EC BD =⊥.(Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =︒，M 为线段AE 的中点，求证：DM ∥平面BEC .练习2（2011天津）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，45ADC ∠=︒，1AD AC ==，O 为AC 的中点，PO ABCD ⊥平面，2PO =，M为PD 的中点．(Ⅰ) 证明：//PB ACM 平面；MP(Ⅱ)(Ⅲ)。

线面垂直证线面垂直定理
线面垂直证线面垂直定理是几何学中的一个基本定理，它描述了一条直线和一个平面的垂直关系。

该定理的表述如下：
如果一条直线与一个平面相交，且垂直于该平面上的任意一条直线，则这条直线与该平面垂直。

下面我将对该定理进行详细的解释和证明。

一、定义
在几何学中，我们定义了以下几个基本概念：
1. 直线：在平面上没有宽度的、无限延伸的线段。

2. 平面：在空间中没有厚度的、无限延伸的平面。

3. 垂直：两个物体之间的垂直关系是指它们之间的夹角为90度。

二、证明
我们可以通过以下步骤来证明线面垂直证线面垂直定理：
1. 假设一条直线L与一个平面P相交，且垂直于该平面上的任意一条直线。

2. 在平面P上任取一点A，并以该点为圆心画一个圆。

3. 以直线L为轴，将平面P分为两个部分。

4. 在直线L上任取一点B，并以该点为圆心画一个圆。

5. 由于直线L与平面P垂直，所以点B到平面P的距离等于点A到平面P的距离。

6. 由于点A和点B都在圆上，所以它们到圆心的距离相等。

7. 因此，点A和点B到平面P的距离相等。

8. 由于点A和点B到平面P的距离相等，所以直线AB与平面P垂直。

9. 由于直线AB在平面P上，所以直线AB与直线L重合。

10. 因此，直线L与平面P垂直。

三、总结
线面垂直证线面垂直定理是几何学中的一个基本定理，它描述了一条直线和一个平面的垂直关系。

通过上述证明过程，我们可以看出该定理的正确性。

在实际应用中，该定理可以用于解决许多几何问题，例如求解直线和平面的交点、求解平面的法向量等。

浅谈线面垂直判定定理的证明
答：
1、线面垂直判定定理的证明
线面垂直的判定定理指的是：如果一条直线与某平面都有两个不同的交点，则这条直线与该平面垂直。

因此，线面垂直判定定理的证明实际上就是证明这一定理。

2、证明步骤
(1) 设直线L与平面R有两个不同的交点P、Q，即△PQR为非平行三角形。

1
(2) 设PQ之间的距离为d。

(3) 将点P固定，取任意一点Q′在直线L上，构成△PQ′R′，
若线段PQ′与线段PQ相等，即d，则△PQ′R′也是非平行三角形。

(4) 由等比变换的原理有：等边相等（等偏角的两边也相等）的三角形间必存在等比变换，即它们的相同边之比等于相应的对角线之比。

(5) 由△PQR和△PQ′R′的相同边相等的条件有：
（1）△PQR的相同边PQ=PQ′
（2）△PQ′R′的相同边PQ′=PQ
(6) 将等式（1）和（2）代入等比变换的原理，有：
PR:QR=PR′:QR′
(7) 由三角形PRQ、PR′Q′垂直的条件，有：
PR:QR=QR:QR′
(8) 由（6）和（7），有：
PR=PR′
(9) 由（8）可知，线段PR和PR′的长度相等，即∠PRQ=∠PR′Q′。

(10) 所以，直线L与平面R垂直。

3、证明结论
由上面步骤我们得出了结论：如果一条直线与某平面都有两个不同的交点，则这条直线与该平面垂直。

线面垂直判定定理的证明到此完毕。

P
所在的平面,则PA与BC
的位置关系是_垂__直__.
A
3·如右图，PA平面ABC， p A B C 中 ， B CA B
则图中直角三角形的个
数是（ A ）
A
A4 B3 C2 D 1
2021
B
C B
C
10
例1: 有一根旗杆AB高8 m，它的顶端A 挂 有一条长10 m的绳子，拉紧绳子并把它的 下端放在地面 上的(和旗杆脚不在同一条直线上) C、D。如果这两点都和旗杆脚B 的距离是6 m， 那么旗杆就 和地面垂直，为什么？ A
线面垂直的定义 线面垂直
线面垂直的判定定理
2021
17
小结：
1、入手指南：碰到证明线面垂直的问题，应转 化为证明线线垂直；反之亦然.
2、小心提醒：平面内的这两条直线应该相交；
3、重点总结：证明线线垂直的方法有哪些？
①勾股定理的逆定理（已知长度）
②等腰三角形的三线合一
③利用线面垂直的性质
④利用平行移动不改变夹角大小
⑤正方体（长方体）中的线线垂直、线面垂直
⑥菱形(正方形）的对角线互相垂直
⑦相似
2021
18
作业：1、P66－探究题，请你先写出一个 条件，然后用你的这个条件来证明
A’C⊥B’D’
2、（如图）在正方体AC1中， D1
求证：(1)AC⊥平面D1DB A1
(2)D1B⊥平面ACB1
D
C1 B1
C
A
B
2021
3、如果一条直线垂直于平面内的无数条直线， 能否判断这条直线和这个平面垂直？
Байду номын сангаас
2021
7
线面垂直判定定理：

立体几何证明【知识梳理】1.直线与平面平行判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和这个平面平行.（“线线平行线面平行”）性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行线线平行”）2.．直线与平面垂直判定定理一如果一条直线和一个平面内的两条相交直线都垂直，那么这两条直线垂直于这个平面.（“线线垂直线面垂直”）判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.性质1.如果一条直线垂直于一个平面，那么这条直线垂直于这个平面内的所有直线。

（线面垂直线线垂直）性质2：如果两条直线同垂直于一个平面，那么这两条直线平行.三。

平面与平面空间两个平面的位置关系：相交、平行.1. 平面与平面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行.（“线面平行面面平行”）2. 两个平面垂直判定定理：如果一条直线与一个平面垂直，那么经过这条直线的平面垂直于这个平面.（“线面垂直面面垂直”）性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.（面面垂直线面垂直）知识点一【例题精讲】3.在棱长为2 的正方体A BCD A1B C D 中，E、F 分别为DD1 、DB的中点。

1 1 1（1）求证：EF// 平面ABC1 D1 ；（2）求证：平面B D1C1 B1C EF B1C ；（3）求三棱锥 B EFC1 的体积V.4.如图所示, 四棱锥P ABCD底面是直角梯形,BA AD, CD AD, CD 2AB, PA 底面A B C D, E为PC的中点, PA＝AD＝AB＝1.（1）证明: EB // 平面PAD ;（2）证明: BE 平面PDC ;（3）求三棱锥 B PDC的体积V.3、如图所示，在四棱锥P﹣ABCD 中，PA⊥底面ABCD，AB⊥AD ，AC⊥CD，∠ABC=60°，PA=AB=BC ，E 是PC 的中点，证明：（1）AE⊥CD（2）PD⊥平面ABE．4、.如图，三棱柱ABC ﹣A1B1C1 中，CA=CB ，AB=AA 1，∠BAA 1=60°（Ⅰ）证明：AB ⊥A1C；练习1、如图，菱形ABCD 与等边△PAD 所在的平面相互垂直，AD=2 ，∠DAB=60°．（Ⅰ）证明：AD⊥PB；（Ⅱ）求三棱锥C﹣PAB 的高．5.如图1-4 所示，△ABC 和△BCD 所在平面互相垂直，且AB＝BC＝BD＝2，6.∠ABC＝∠DBC＝120°，E，F，G 分别为AC，DC，AD 的中点．求证：EF⊥平面BCG；7.如图1-1 所示，三棱柱ABC - A1B1C1 中，点A1 在平面ABC 内的射影 D 在AC8.上，∠ACB＝90°，BC＝1，AC＝CC1＝2.(1)证明：AC1⊥A1B；4、如图，在三棱台ABC ﹣DEF 中，平面BCFE ⊥平面ABC ，∠ACB=90°，BE=EF=FC=1 ，BC=2，AC=3 ．（Ⅰ）求证：BF⊥平面ACFD ；（Ⅱ）求直线BD 与平面ACFD 所成角的余弦值．35、三棱锥P﹣ABC 中，∠BAC=90°，PA=PB=PC=BC=2AB=2 ，（1）求证：面PBC⊥面ABC9.已知四棱锥P-ABCD中, 底面四边形为正方形, 侧面PDC为正三角形, 且平面PDC⊥底面ABCD,E为PC的中点.(1) 求证:PA∥平面EDB;(2) 求证: 平面EDB⊥平面PBC;7、如图，在四棱锥P-ABCD 中，底面ABCD 为矩形，平面PAB⊥平面ABCD，PA⊥PB，BP=BC ，E 为PC 的中点．（1）求证：AP∥平面BDE；3.求证BE 垂直平面PAC8、将如图一的矩形ABMD 沿CD 翻折后构成一四棱锥M﹣ABCD（如图二），若在四棱锥M﹣ABCD 中有MA= ．（1）求证：AC⊥MD ；（2）求四棱锥M ﹣ABCD 的体积．作业1、如图1，菱形ABCD 的边长为12，∠BAD=60°，AC 交BD 于点O．将菱形ABCD 沿对角线AC 折起，得到三棱锥B﹣ACD，点M，N 分别是棱BC，AD 的中点，且DM=6 ．（Ⅰ）求证：OD⊥平面ABC；2、如图，在斜三棱柱ABC ﹣A1B1C1 中，O 是AC 的中点，A 1O⊥平面ABC ，∠BCA=90°，AA 1=AC=BC ．（Ⅰ）求证：A1B⊥AC1；3、如图所示，四棱锥P﹣ABCD 的侧面PAD 是边长为2的正三角形，底面ABCD 是∠ABC=6°0的菱形，M 为PC 的中点，PC= ．（Ⅰ）求证：PC⊥AD；4、如图，四棱锥P-ABCD 中，AP⊥平面PCD，AD∥BC，AB=BC=F 分别为线段AD，PC 的中点．12AD，E，（Ⅰ）求证：AP∥平面BEF；（Ⅱ）求证：BE⊥平面PAC．5、如图，四棱锥S﹣ABCD 中，AB ∥CD，BC⊥CD，侧面SAB 为等边三角形．AB=BC=2 ，CD=1，SD= ．（1）证明：CD⊥SD；10.如图，四棱锥S﹣ABCD 中，△ABD 是正三角形，CB=CD ，SC⊥BD ．（Ⅰ）求证：SB=SD；（Ⅱ）若∠BCD=12°0，M 为棱SA 的中点，求证：DM ∥平面SBC．7、如图，在矩形ABCD 中，点E 为边AD 上的点，点 F 为边CD 的中点，2AB AE AD 4,现将ABE 沿BE 边折至PBE 位置，且平面PBE 平面3BCDE .PEADEDFB C B C（1）求证：平面PBE 平面PEF ；8、如图5．在椎体P-ABCD 中，ABCD 是边长为 1 的棱形，且∠DAB=60 ，PA PD 2 ,PB=2,E,F 分别是BC,PC 的中点．（1）证明：AD 平面DEF;9、在如图所示的多面体ABCDEF 中，ABCD 为直角梯形，AB / /CD ，DAB 90 ，四边形ADEF 为等腰梯形，EF / / AD ，已知AE EC ，AB AF EF 2，AD CD 4．（Ⅰ）求证：平面ABCD 平面ADEF11.如图，在底面为平行四边形的四棱锥P ABCD 中，AB AC ，PA 平面12. ABCD ，且PA AB ，点E 是PD 的中点.（Ⅱ）求证：PB // 平面AEC ；。

如何证明线面垂直的判定定理线面垂直的判定定理是几何学中一个重要的定理，它能够帮助我们判断一条直线与一个平面是否垂直。

在本文中，我们将从几何学的角度出发，详细阐述如何证明线面垂直的判定定理。

我们先来明确一下线和面的概念。

在几何学中，线是由一系列无限延伸的点构成的，它没有宽度和厚度；而面是由一系列无限延伸的点构成的，它有宽度和厚度。

在三维空间中，一条直线和一个平面的相交情况有三种可能：相交于一点、相交于一条直线或者不相交。

现在，我们来证明线面垂直的判定定理。

假设有一条直线l和一个平面P，我们要证明l与P垂直。

首先，我们需要找到平面P上的两个不共线的向量a和b，这两个向量既不能平行于线l，也不能共线于线l。

然后，我们需要证明向量a与线l上的任意一个向量的点积为零，同时向量b与线l上的任意一个向量的点积也为零。

只有当这两个条件同时满足时，我们才能够得出结论：线l与平面P 垂直。

为了证明这个定理，我们可以采用反证法。

假设线l与平面P不垂直，即存在线l上的一个向量与向量a的点积不为零，或者存在线l上的一个向量与向量b的点积不为零。

我们将这两种情况分别进行讨论。

假设存在线l上的一个向量与向量a的点积不为零。

我们知道，两个向量的点积等于它们的模长乘积与它们夹角的余弦值。

因此，如果线l上的一个向量与向量a的点积不为零，那么它们的夹角一定不是90度。

根据三角学的知识，我们可以得出结论：线l与平面P 不垂直。

这与我们的假设相矛盾，因此我们可以排除这种情况。

接下来，假设存在线l上的一个向量与向量b的点积不为零。

同样地，我们可以得出结论：线l与平面P不垂直。

这也与我们的假设相矛盾，因此我们可以排除这种情况。

我们可以得出结论：线l与平面P垂直。

根据以上的证明过程，我们可以得出线面垂直的判定定理：如果一条直线上的任意一个向量与平面上的两个不共线的向量的点积都为零，那么这条直线与这个平面垂直。

线面垂直的判定定理在几何学中具有重要的应用价值。

课堂练 习
3.(2018全国Ⅰ,18,12分)如图，在平行四边形 ABCM 中，AB=AC=3 ， ∠ACM=90° ，以AC 为折痕将△ ACM折起，使点M 到达点D 的位置， 且AB⊥DA ． （1）证明：平面ACD⊥平面ABC ；
证明: （1）由已知可得， ∠BAC=90°， BA⊥AC ．又BA⊥AD，所以AB⊥平面ACD． 又AB 平面ABC，所以平面ACD⊥平面ABC．
方法总 结
证明直线与平面垂直的方法
1．判定定理(常用方法)； 2．若两平面垂直，则在一个平面内垂直于交线的直线必垂直于另一
个平面(常用方法); 3．若两条平行直线中的一条垂直于一个平面，则另一条也垂直于这
个平面； 4．若一条直线垂直于两个平行平面中的一个平面，则它必垂直于另
一个平面； 5．若两相交平面同时垂直于第三个平面，则这两个平面的交线垂直
线与此平面垂直
_a_，__b_⊂__α_
_a_∩__b_＝__O_
l_⊥__a_

⇒l⊥α
_l⊥__b_
性质 垂直于同一个平面 定理 的两条直线平__行__
ab__⊥⊥____αα__⇒a∥b
双基落 实
2.平面与平面垂直
（1）、平面与平面垂直的定义 两个平面相交，如果所成的二面角是 __直__二__面__角__,就说这两个平面互相垂直
双基落 实
1．直线与平面垂直 (1)直线和平面垂直的定义：
直线 l 与平面 α 内的任意一条直线都垂直，就说直线 l 与平面 α 互相垂直．
双基落 实
(2)直线与平面垂直的判定定理及性质定理：
文字Байду номын сангаас言
图形语言
符号语言
一条直线与一个平 判定 面内的_两__条__相__交__直_ 定理 线__都垂直，则该直

空间点、线、面的位置关系:垂直【背一背基础知识】1.判定两直线垂直，可供选用的定理有：①若a ∥b ，b ⊥c ，则a ⊥c .②若a ⊥α，b ⊂α，则a ⊥b .2.线面垂直的定义：一直线与一平面垂直⇔这条直线与平面内任意直线都垂直；3.线面垂直的判定定理，可选用的定理有：①若a ⊥b ，a ⊥c ，b ，c ⊂α，且b 与c 相交，则a ⊥α.②若a ∥b ，b ⊥α，则a ⊥α.③若α⊥β，α∩β＝b ，a ⊂α，a ⊥b ，则a ⊥β.4.判定两平面垂直，可供选用的定理有：若a ⊥α，a ⊂β，则α⊥β.线面垂直1.如图，在三棱台ABC-DEF 中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=F C=1，BC=2，AC=3.（I）求证：BF⊥平面ACFD；2.如图，在四棱锥P ABCD -中，底面ABCD 是︒=∠60DAB 且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD ⊥底面ABCD ,G 为AD 的中点.求证：BG ⊥平面PAD .线线垂直1、如图，在三棱锥P ABC -中，90PAC BAC ∠=∠=︒，PA PB =，点D ，F 分别为BC ，AB 的中点．（1）求证：PF ⊥AD ．2、如图，在三棱柱111ABC A B C -中，面11ABB A 为矩形，11,2,AB BC AA D ===为1AA 的中点，BD与1AB 交于点1,O BC AB ⊥.（Ⅰ）证明：1CD AB ⊥3、下图为一简单组合体，其底面ABCD 为正方形，PD ⊥平面ABCD ，//EC PD ，且22PD AD EC ===，N 为线段PB 的中点．（Ⅰ）证明：NE PD ⊥；4、如图所示，在三棱柱111ABC A B C -中，11AA B B 为正方形，11BB C C 为菱形，1160BB C Ð=°,平面11AA B B ^平面11BB C C 。

空间向量证明线面垂直
空间向量是描述空间中的位置和方向的工具。

线面垂直是指一
条直线与一个平面垂直相交。

现在我们来利用空间向量来证明线面
垂直的性质。

假设有一条直线上的两个点A和B，以及一个平面上的一个点C。

我们可以用空间向量来表示这三个点的位置。

假设向量OA表示点A
的位置，向量OB表示点B的位置，向量OC表示点C的位置。

那么
向量AB可以表示直线AB的方向，而向量AC和向量BC可以表示平
面ABC的法向量。

现在我们来证明线AB与平面ABC垂直。

根据向量的性质，如果
两个向量的点积为0，则它们垂直。

所以我们可以计算向量AB与向
量AC的点积，以及向量AB与向量BC的点积。

如果它们都等于0，
那么我们就证明了线AB与平面ABC垂直。

点积的计算公式为，向量a·向量b = |a||b|cos(θ)，其中
|a|和|b|分别表示向量a和向量b的模长，θ表示向量a和向量b
之间的夹角。

假设向量AB为a，向量AC为b，向量BC为c。

那么我们可以计算点积：
a·b = |a||b|cos(θ1)。

a·c = |a||c|cos(θ2)。

如果θ1和θ2都是90度（即cos(θ1)和cos(θ2)都等于0），那么a·b和a·c都等于0，根据点积的性质，我们就可以得出结论，线AB与平面ABC垂直。

通过空间向量的方法，我们成功地证明了线面垂直的性质。

这种方法可以很好地应用于空间几何中的各种问题，为我们理解空间中的几何关系提供了一种有效的工具。

线面垂直判定定理的证明方法标题：线面垂直判定定理的证明方法导言：线面垂直判定定理（Perpendicularity Criterion）是几何学中一个非常重要的定理，用来判定两个几何对象（线与面）是否垂直。

本文将深入探讨线面垂直判定定理的证明方法，并分享我对该定理的观点和理解。

第一节：线面垂直判定定理的声明在本节中，我们将详细说明线面垂直判定定理的声明，并给出几个实际应用的例子。

通过这些例子，读者将对这个定理有一个直观的认识，并能理解为什么证明这个定理的方法非常重要。

第二节：利用向量和法向量证明线面垂直判定定理在本节中，我们将介绍一种基于向量和法向量的证明方法来证明线面垂直判定定理。

首先，我们将简要回顾向量和法向量的基本概念，然后引入线面垂直的定义，并在此基础上给出证明的步骤和逻辑。

通过这个证明方法，读者将能够深入理解线面垂直的本质，并能够在实际问题中应用该定理。

第三节：利用直角三角形证明线面垂直判定定理在本节中，我们将介绍一种基于直角三角形的证明方法来证明线面垂直判定定理。

首先，我们将回顾直角三角形的基本性质和定理，然后介绍线面垂直判定定理和直角三角形之间的关系。

通过这个证明方法，读者将能够进一步加深对线面垂直的理解，并能够在不同几何对象之间建立直观的联系。

第四节：总结与回顾在本节中，我们将对线面垂直判定定理的证明方法进行总结和回顾。

我们将强调证明过程中的关键步骤和技巧，并提供一些实例说明如何应用这些技巧。

此外，我们将讨论该定理的一些拓展和相关的研究方向，以便读者能够进一步深入研究和应用线面垂直的相关问题。

观点和理解：线面垂直判定定理是几何学中非常重要的定理之一，它在实际问题中有着广泛的应用。

通过学习和理解线面垂直判定定理的证明方法，我们能够增强我们在几何学方面的思考能力和问题解决能力。

此外，线面垂直判定定理也为我们提供了一种切入点，来深入研究更复杂的几何问题，例如平面垂直和曲线面垂直的相关定理。

线面垂直的判定定理证明今天我们要聊聊“线面垂直的判定定理”，这可真是一个有趣的话题！什么是线面垂直呢？其实简单来说，就是线和面之间的关系。

我们会把一个线段垂直于一个平面，意思就是这条线与平面上的任何一条直线都没有交角，全都是“90度”的关系。

这个看起来好像挺抽象的，但是如果用身边的东西做个比喻就更容易理解了。

你可以想象一下，当你把一根铅笔直立插进一本打开的书里，那根铅笔就和书页的平面垂直，完全没有任何倾斜，完全正着插进去。

好啦，接下来我们就来深入讲讲，怎么判断一条直线是不是和一个平面垂直。

这个方法也没啥难度，给你们一个小小的秘诀，那就是：只要线和面上任意一条直线的夹角是90度，就能证明线垂直于面！是不是听起来很简单呢？对，就是这么轻松。

想象一下，假设你站在一个平面上，假如这条线跟你脚下的地面垂直，你的身体就完全没有倾斜，站得稳稳当当，完全是90度嘛。

这个就是它的意思。

我们来讲讲具体怎么做。

判定这条线与平面垂直的方法也不复杂，我们可以通过向量的方式来推导一下。

想象一下你有一个平面，上面有两条向量，分别是平面内的两条直线。

然后，如果有一条线和这两个向量分别形成了90度角，那么这条线一定是垂直于这个平面的。

是不是很直观呢？就像你站直了，眼睛不斜不歪地看着前方，保持正直的姿态，这样你肯定就不会和旁边的物体形成倾斜的角度，对吧？说到这里，很多小伙伴可能就会想：“呃，这些都是公式和向量之类的东西啊，能不能给个实际点的例子？”哈哈，别急，咱们继续。

假如你家里有个立式风扇，那个扇子头垂直于风扇的支架，你能想象到那根支架和扇叶之间，完全是个直角吗？你站在旁边瞧一眼，完全不会觉得它有任何歪斜的地方。

只要风扇支架跟地面没有倾斜，那支架就与地面垂直。

再拿这个例子举例，想象一下风扇的支架是一条直线，地面是一片平面。

如果你能证明这条支架和地面上的任意一条直线都呈90度角，那就能证明风扇支架是垂直于地面的。

这时候是不是觉得这道题还挺有意思的呢？如果换个角度理解，这个“线面垂直的判定定理”其实就在告诉我们一个道理：只有当某些条件满足，才能得出一个结论。

线面垂直、面面垂直及其证明一线面垂直的判定定理1）线面垂直定义：如果一条直线和一个平面内的任何一条直线都垂直，那么这条直线和这个平面垂直•（2）判定定理：如果直线I和平面内的两条相交的直线m,n都垂直，那么直线I垂直于平面.（线面垂直线线垂直）（3）三垂线定理及其逆定理①三垂线定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影.②三垂线逆定理：在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直.（4）线面垂直的证明例1已知正方体ABCD A1B1C1D1，求证：AC 面AB1D1.例2如图1所示，ABCD为正方形，SA丄平面ABCD，过A且垂直于SC的平面分别交SB SC, SD于E，F，G .求证：AE SB，AG SD .例3 已知ABC 中ACB 90°, SA 面ABC,AD SC,求证：AD 面SBC.D例4在正方体ABCD A i B1C1D1中，M为CG的中点，AC交BD于点0 ,求证:A0 平面MBD .练习1在正方体ABCD ABGD I中.(1)求证：AC 平面BD i BD.(2)求证：BD1平面ACB1.练习2在三棱锥A BCD中，BC AC , AD BD，作BE CD , E为垂足，作AH BE于H.求证：AH 平面BCD.练习3在四棱锥P ABCD中，PA 底面ABCD，AB AD，AC CD，ABC 60，PA AB BC，E 是PC 的中点•(1)求证：CD AE .(2)求证：PD 面ABE.面面垂直(1) 二面角定义：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面，若棱为 I ，两个面分别为， ,二面角记作为 I . (2)二面角的平面角定义：在二面角 I 棱I 上取一点0,在半平面 和 内， 从点0分别作垂直于棱I 的射线0A,0B ，射线组成 A0B .则 A0B 叫做二面角的平 面角•二面角的取值范围为[0 ,180].(3) 面面垂直定义： 若两个平面的二面角为直二面角 (平面角是直角的二面角)， 则这两个平面互相垂直.(4)面面判定定理：一个平面过另一个平面，则这两个面相互垂直 .(5) 面面垂直的正面即：面面垂直 线面垂直 线线垂直.例1如图，在正方体ABCD A 1B 1C 1D 1中，E 是AA 的中点.(1)求证： AC//平面 BDE ;例2如图，直三棱柱 ABC AB 1C 1中，侧棱垂直于底面, 1 ____________________________________AC BC 一 AA ，D 是棱AA 1的中点，求证：平面 BDG 平面BDC • 2(2)求证：平面 AAC 平面BDE .ACB 90(1) 平面EFG//平面ABC ; (2) BC SA •例2 （2012江苏）如图，在直三棱柱ABC ABG 中，AQ , D ,E 分别是棱BC，CCl上的点（点D 不同于点C ），且A D D E ，F 为BlCl的中点.求证： (1) 平面 ADE 平面 BCC 1B 1 ; (2)直线A.F //平面ADE .练习如图，过S 引三条长度相等但不共面的线段 SASB,SC ，且 ASB ASC 60 , BSC 90，求证：平面 ABC 丄平面 BSC .三立体几何高考证明例1 （2013江苏）如图，在三棱锥SAB BC , AS AB ，过 A 作 AF SA, SC 的中点•求证：ABC 中，平面 SAB 平面SBC ,SB ，垂足为F ，点E , G 分别是棱BBCi£C例3如图，四棱锥P ABCD 中，底面ABCD 为平行四四边形，DAB 60 ,(I )求证：BE DE ;(II)若/ BCD 120 ，M 为线段AE 的中点，求证：DM //平面BEC .练习2 (2011天津)如图，在四棱锥 P ABCD 中，底面ABCD 是平行四边形,AB 2AD ， PD 底面ABCD . (1) 证明： PA BD (2) 设PD AD1，求棱锥D PBC 的高练习1如图，几何体E ABCD 是四棱锥V ABD 为正三角形CB CD,EC BD.ADC 45，AD AC 1，O 为 AC 的中点，PO 为PD 的中点. 平面 ABCD ，PO 2，M(I )证明：PB//平面ACM ； (I)证明：AD 平面PAC ；(m)求直线AM与平面ABCD所成角的正切值.。

如何证明线线垂直问题一：空间几何中如何证明线线垂直线l和线m相互垂直的证明方法：1、l⊥ m所在平面2、l⊥ m的平行线3、l m在第三个平面上的投影线相互垂直问题二：如何证明面面垂直？证明面面垂直的基本方法有：（1）利用定义证明，即利用两平面相交成直二面角来证明；（2）利用面面垂直的判定定理证明，即若a⊥ ，a ，则⊥在证明两平面垂直时，一般方法是先从现有的直线中寻找平面的垂线，若没有这样的直线，则可通过作辅助线来解决，而作辅助线则应有理论根据并且要有利于证明，不能随意添加.在有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直.解决这类问题的关键是熟练掌握“线线垂直”“线面垂直”“面面垂直”间的转化条件和转化应用.问题三：怎么证明线线垂直从给的图看，题中的数据有误，应该是：AB=BC=4，AD=2设，EG∩BF=M，AG∩BD=N则四边形BGFE是正方形，所以，DF⊥EG且，M是EG的中点，翻折后的四边形ABGD是矩形，所以，点N是AG的中点，所以，MN∥AE易证，AE⊥平面BCFE，所以，MN⊥平面BCFE所以，MN⊥EG所以，EG⊥平面BDF，所以，EG⊥BD问题四：线面垂直可以证明线线垂直吗？可以证明。

具体解答如下：不妨先设有两条直线为m,n.有平面A。

直线m与平面A垂直，直线n属于平面A。

若可以证明直线m与直线n垂直，则即线面垂直而可以证线线垂直。

线面垂直（即直线m与平面A垂直），那么这条线与这个面上的所有直线垂直（即m与平面A上所有直线垂直)；另一条直线属于这个面上（即直线n属于平面A）；那么这两条直线两两垂直（即直线m垂直于直线n）。

问题五：线线垂直如何证明定义法：两直线夹角90度三垂线定理：在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直直线与平面的定义：若1条直线垂直于一个平面,则它垂直于这个平面的所有直线法向量：在空间直角坐标系中,三点两向量确定一个平面,分别于这两个向量垂直的向量也就是分别与这两个向量乘积为0的向量垂直于这个平面,也就叫这个平面的法向量.问题六：如何证明两条线垂直？ 185分假如不平行,就会有一个焦点,那么这个焦点和两个垂足会构成一个三角形,这个三角形的内角有2个90度,那么内角和就比180度大了,所以是错的,所以……分页：123。

线面垂直、线面夹角1.线面垂直：如果一条直线和一个平面内的任何一条直线都垂直，就说这条直线和这个平面垂直.2.线面垂直判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面. 推论：如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于同一平面. 推论：一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面. 性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行.3.三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它和这条斜线垂直.逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线在该平面上的射影垂直.4.线面角：平面的一条斜线和它在平面内的射影所成的锐角，叫做这条直线和这个平面所成的角；求线面角：“一作，二证，三计算”。

①平面的平行线与平面所成的角：规定为0。

②平面的垂线与平面所成的角：规定为90。

线线垂直⇒线面垂直 （线面垂直⇒线线垂直） 例1.如图：AB 是⊙O 的直径，PA 垂直于⊙O 所在的平面，C 是圆周上不同于B A ,的任意一点，求证： PAC BC 平面⊥例 2. 三棱柱111ABC A B C -的侧棱1A A 垂直于底面ABC ，12A A =，1AC CB ==，90BCA ︒∠=，M 、N 分别是AB 、1A A 的中点．（1）求BN 的长；（2）求证：1A B CM ⊥．例3. 如图，在四棱锥P －ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，AC ⊥CD ，∠ABC ＝60°，PA ＝AB ＝BC ，E 是PC 的中点(1)求证：CD ⊥AE ；(2)求证：PD ⊥面ABE. 线面角例4. 在长方体ABCD ﹣A 1B 1C 1D 1中，AB=BC=2，AA 1=1，则AC 1与平面A 1B 1C 1D 1所成角的正弦值为 ．例5. 如图，在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中，E 是BC 1的中点，则直线DE 与平面ABCD 所成角的正切值为 _________ ．例6. 在正三棱柱ABC ﹣A 1B 1C 1中，侧棱长为，底面三角形的边长为1，则BC 1与侧面ACC 1A 1所成的角是 ________例7.a 是平面α的斜线，b α⊂，a 与b 成3π角，b 与a 在α内的射影成4π角，则a 与α所成角的大小为 。