第18讲 系统的频率特性总结
- 格式:pdf
- 大小:1.26 MB
- 文档页数:28



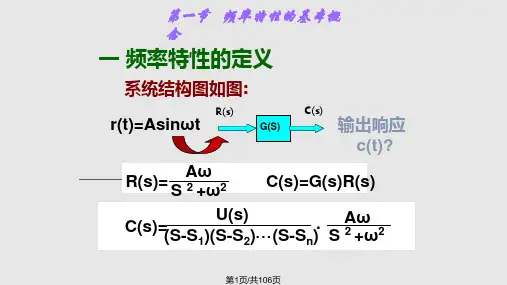




频率特性(frequencycharacteristic)百科物理大全
频率特性(frequencycharacteristic)百科物
理大全
广泛的阅读有助于学生形成良好的道德品质和健全的
人格,向往真、善、美,摈弃假、恶、丑;有助于沟通个人与外部世界的联系,使学生认识丰富多彩的世界,获取信息和知识,拓展视野。
快一起来阅读频率特性(frequencycharacteristic)百科物理大全吧~
频率特性(frequencycharacteristic)
频率特性(frequencycharacteristic)
是表征系统动态功能特性的频域物理模型。
系统的频率特性是传递函数,在电路系统控制中亦称网络函数。
只要知道了系统的传递函数,对于任何刺激(输入)均可预测系统相应的反应(输出)。
对于单一输入和输出的线性定常系统,其状态方程为常系数线性特征方程。
由状态方程的拉普拉斯(Laplace)变换的常系数特征方程,可求得系统的传递函数。
对系统施以不同的激励信号,由系统响应的频率特性实验曲线也可求得传递函数。
频率特性分析是系统辨识的重要方法,如20世纪50年代以来,对瞳孔系统的物理模型的研究,取得了模型与生物实验结果广泛一致的吻合,阐明了生理学难以解释的虹膜震颤、瞳孔收缩的大小效应等,成为生物控制论定量研究的成功典范。
由查字典物理网独家提供频率特性。
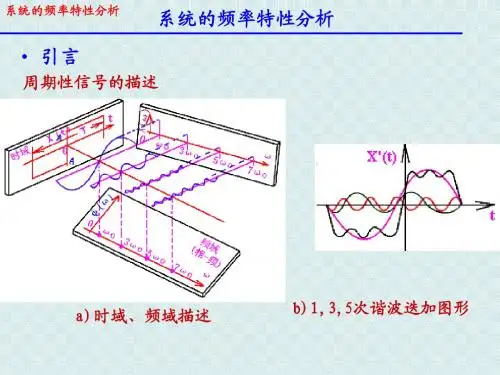


第三章 系统频率特性系统的时域分析是分析系统的直接方法,比较直观,但离开计算机仿真,分析高阶系统是困难的。
系统频域分析是工程广为应用的系统分析和综合的间接方法。
频率分析不仅可以了解系统频率特性,如截止频率、谐振频率等,而且可以间接了解系统时域特性,如快速性,稳定性等,为分析和设计系统提供更简便更可靠的方法。
本章首先阐明频率响应的特点,给出计算频率响应的方法,接着介绍Nyquist 图和Bode 图的绘制方法、系统的稳定裕度及系统时域性能指标计算。
3.1 频率响应和频率特性3.1.1 一般概念频率响应是指系统对正弦输入的稳态响应。
考虑传递函数为G(s)的线性系统,若输入正弦信号t X t x i i ωsin )(= (3.1-1)根据微分方程解的理论,系统的稳态输出仍然为与输入信号同频率的正弦信号,只是其幅值和相位发生了变化。
输出幅值正比于输入的幅值i X ,而且是输入正弦频率ω的函数。
输出的相位与i X 无关,只与输入信号产生一个相位差ϕ,且也是输入信号频率ω的函数。
即线性系统的稳态输出为)](sin[)()(00ωϕωω+=t X t x (3.1-2)由此可知,输出信号与输入信号的幅值比是ω的函数,称为系统的幅频特性,记为)(ωA 。
输出信号与输入信号相位差也是ω的函数,称为系统的相频特性,记为)(ωϕ。
幅频特性:)()()(0ωωωi X X A = (3.1-3)相频特性:)()()(0ωϕωϕωϕi -= (3.1-4)频率特性是指系统在正弦信号作用下,稳态输出与输入之比对频率的关系特性,可表示为:)()()(0ωωωj X j X j G i = (3.1-5)频率特性)(ωj G 是传递函数)(s G 的一种特殊形式。
任何线性连续时间系统的频率特性都可由系统传递函数中的s 以ωj 代替而求得。
)(ωj G 有三种表示方法:)()()(ωϕωωj e A j G = (3.1-6))()()(ωωωjV U j G += (3.1-7))(sin )()cos()()(ωϕωωωωjA A j G +=(3.1-8) 式中,实频特性:)(cos )()(ωϕωωA U =虚频特性:)()(arctan )()()()()(sin )()(22ωωωϕωωωωϕωωU V V U A A V =+==一般在分析系统的结构及参数变化对系统性能的影响时,频域分析比时域分析要容易些。
频率特性的基本概念大中小在稳定的线性系统(或线性环节)的输入端作用一个正弦信号,当系统相对稳定后,系统的稳态输出也必定是一个同频率的正弦信号。
稳态输出与输入的振幅比值以及它们之间的相位差取决于系统本身的结构和输入信号的频率。
这种现象在如图5-1所示的强迫振动实验中可以观察得到。
(图5-1)图中的系统为稳定的线性定常系统。
当输入信号R为时,输出C在稳态时也为正弦信号两者的频率相同,但振幅和相位角不同。
当输入信号的频率改变时,输出信号的振幅和相位角会发生变化。
一、频率特性的数学本质以上介绍的是频率响应特性(简称频率特性)的实验现象,下面我们将证明频率特性和传递函数之间的数学关系,以便可以很方便地由系统传递函数得到频率特性,反之也能够由频率特性得到传递函数。
输出的拉普拉斯变换式为设输入R(t)为正弦函数,表示为由拉普拉斯变换表查得故部分分式中及B、D均为待定系数。
对于一个稳定的系统,由于特征方程的所有特征根均具有负实数部分,的第一个分量总是随着t的增长逐渐消失,系统最终将以作稳态运动。
上式恰恰是我们需要求解的,其中系数由上式得到同理将系数B、D代入,则式中Im为G(jω)的虚部,Re为G(jω)的实部。
而输出端响应的振幅和输入端的振荡之比为输出端响应和输入端的相位差为由此可见,作用有正弦输入时的稳定线性定常系统,输出响应具有与输入同一频率的正弦稳定信号。
但是输出的振幅和相位角通常不等于输入量的振幅和相角,输出响应的振幅是输入量的倍,输出响应和输入量相位差为。
因此,系统的频率特性可以直接由G(jω)表示,系统的频率特性为式中是ω的函数,称为幅频特性,也是频率特性的模;是ω的函数,称为相频特性。
在上述数学推导中,我们可以清楚地看到所以,在已知系统或环节的传递函数时,只要令,就可以很方便地得到系统或环节的频率特性。
为了进一步说明频率特性的意义,现以图5-2所示的R-C电路为例。
图5-2频率特性可通过传递函数来求取,当电容两端电压uc为输出量,输入电压ui为输入量时,传递函数可用复阻抗串联的知识求取式中 T=RC频率特性只要将S以jω代替,频率特性为幅频特性(模)为相频特性(幅角)为当ui以低频信号输入时();这表明,当输入正弦电压ui的频率很低,则输出电压uc的振幅与的振幅几乎相等,相位近似同相。
第四章控制系统的频率特性本章要点本章主要介绍自动控制系统频域性能分析方法。
内容包括频率特性的基本概念,典型环节及控制系统Bode图的绘制,用频域法对控制系统性能的分析。
用时域分析法分析系统的性能比较直观,便于人们理解和接受。
但它必须直接或间接地求解控制系统的微分方程,这对高阶系统来说是相当复杂的。
特别是当需要分析某个参数改变对系统性能的影响时,需反复重新计算,而且还无法确切了解参数变化量对系统性能影响的程度。
而频率特性不但可以用图解的方法分析系统的各种性能,而且还能分析有关参数对系统性能的影响,工程上具有很大的实用意义。
第一节频率特性的基本概念一、频率特性的定义频率特性是控制系统的又一种数学模型,它是系统(或元件)对不同频率正弦输入信号的响应特性。
对线性系统,若输入信号为正弦量,则其稳态输出信号也将是同频率的正弦量,但是输出信号的幅值和相位一般不同于输入量,如图4-1。
若设输入量为r(t)=A r sin(ωt+υr)其输出量为c(t)=A c sin(ωt+υc)若保持输入信号的幅值A r不变,改变输入信号的角频率ω,则输出信号的角频率也变化,并且输出信号的幅值和相位也随之变化。
横坐标表示角频率ω,单位为弧度/秒(rad/s),按lgω均匀分度,但对ω而言是不均匀的,纵坐标表示υ(ω),单位为度(o),均匀分度,如图4-4所示。
图4-3 Bode图坐标系2)对数相频特性υ(ω) υ(ω)为一条-90o 的水平直线。
如图4-5所示。
图4-5 积分环节的Bode图2)对数相频特性υ(ω) υ(ω)为一条90o 的水平直线。
图4-6 理想微分环节的Bode图点,然后用一条光滑曲线与渐近线连接起来,就得到精确曲线。
图4-7 惯性环节的Bode图图4-8 比例微分环节的Bo0de图nω图4-9 振荡环节的Bode图计算表明,在ω=ωn处,当0.4<ξ<0.7时,误差小于3dB,可以不对渐近线进行修正;但当ξ<0.4或ξ>0.7时,误差较大,必须对渐近线进行修正。