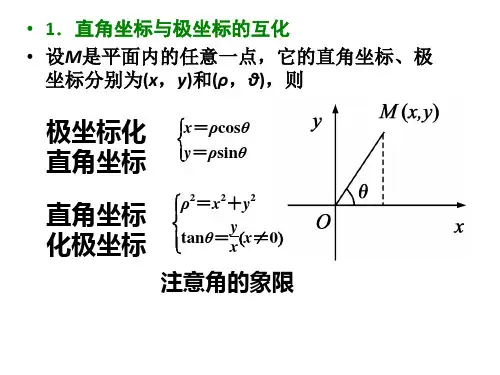
x
x=ρcos , y=ρsin
互化公式的三个前提条件: (限定ρ≥0,0≤θ<2π)
1. 极点与直角坐标系的原点重合; 2. 极轴与直角坐标系的x轴的正半轴重合; 3. 两种坐标系的单位长度相同.
数学运用
例1、把下列点的极坐标化 成直角坐标:
(1)M(8,2 ) (2) (6,7 )
3
4
练习: 已知下列点的极坐标,求它们的直角坐标。
D(0,-2), E(-3,-3) 总结:点的直角坐标化成极坐标的步骤,极角是 如何确定的?
数学运用
例3 已知两点A(2,π/3),B(3,π/2),求AB两
点间的距离.
B
A
o
x
A (3, )
6
B (2, ) 2
C (1, )
2
D ( 3 , ) E (2, 3 )
24
4
数学运用
例2. 把下列点的直角坐标化成极坐标:
(1)P( 6, 2) (2)Q( 6, 2);
(3)R( 2, 2) (限定ρ≥0,0≤θ<2π)
练习2: 已知点的直角坐标, 求它们的极坐标.
A(3,- 3),B(1, 3 ), C(5,0),
极坐标系(2)
问题情境
情境1:若点作平移变动时,则点的位置采用直角坐标 系描述比较方便;
情境2:若点作旋转变动时,则点的位置采用极坐标系 描述比较方便
问题1: 极坐标系是怎样定义的?
问题2: 极坐标系与直角坐标系有何异同?
问题3: 平面内的一个点的直角坐标是(1, 3),
这个点如何用极坐标表示?
在直角坐标系中, 以原点作为极点, x轴的正半轴作为极轴, 并且两种坐 标系中取相同的长度单位。